函数的单调性及奇偶性(含答案)

函数的单调性与最值[A 组 基础保分练]1.下列函数中，在区间（－1，1）上为减函数的是（ ）A.y ＝11－xB.y ＝cos xC.y ＝ln （x ＋1）D.y ＝2－x解析：函数y ＝11－x，y ＝ln （x ＋1）在（－1，1）上都是增函数，函数y ＝cos x 在（－1，0）上是增函数，在（0，1）上是减函数，而函数y ＝2－x ＝⎝⎛⎭⎫12x 在（－1，1）上是减函数. 答案：D2.函数y ＝x 2－2x ＋3有（ ） A.最小值2 B.最小值2 C.最大值2 D.最大值2解析：易知y ＝（x －1）2＋2，因为（x －1）2＋2≥2，所以y ≥ 2. 答案：B3.函数f （x ）＝11－x （1－x ）的最大值是（ ）A.45B.54C.34D.43解析：由f （x ）＝1⎝⎛⎭⎫x －122＋34≤43，则f （x ）max ＝43.答案：D4.设偶函数f （x ）的定义域为R ，当x ∈[0，＋∞）时，f （x ）是增函数，则f （－2），f （π），f （－3）的大小关系是（ ） A.f （π）＞f （－3）＞f （－2） B.f （π）＞f （－2）＞f （－3） C.f （π）＜f （－3）＜f （－2） D.f （π）＜f （－2）＜f （－3）解析：因为f （x ）是偶函数，所以f （－3）＝f （3），f （－2）＝f （2）.又因为函数f （x ）在[0，＋∞）上是增函数，所以f （π）＞f （3）＞f （2），即f （π）＞f （－3）＞f （－2）. 答案：A5.函数f （x ）＝log a （x 2－4x －5）（a ＞1）的单调递增区间是（ ） A.（－∞，－2） B.（－∞，－1） C.（2，＋∞） D.（5，＋∞）解析：根据题意，得x 2－4x －5＞0，解得x ＜－1或x ＞5，设u ＝x 2－4x －5＝（x －2）2－9，易知u ＝x 2－4x －5的单调递增区间为（2，＋∞），所以f （x ）＝log a （x 2－4x －5）的单调递增区间是（5，＋∞）. 答案：D6.已知函数f （x ）＝log 2x ＋11－x，若x 1∈（1，2），x 2∈（2，＋∞），则（ ）A.f （x 1）＜0，f （x 2）＜0B.f （x 1）＜0，f （x 2）＞0C.f （x 1）＞0，f （x 2）＜0D.f （x 1）＞0，f （x 2）＞0解析：因为函数f （x ）＝log 2x ＋11－x在（1，＋∞）上为增函数，且f （2）＝0，所以当x 1∈（1，2）时，f （x 1）＜f （2）＝0；当x 2∈（2，＋∞）时，f （x 2）＞f （2）＝0， 即f （x 1）＜0，f （x 2）＞0. 答案：B7.函数f （x ）＝xx －1（x ≥2）的最大值为__________.解析：易得f （x ）＝x x －1＝1＋1x －1，当x ≥2时，x －1＞0，易知f （x ）在[2，＋∞）上是减函数，∴f （x ）max ＝f （2）＝1＋12－1＝2.答案：28.设函数f （x ）＝⎩⎪⎨⎪⎧－x 2＋4x ，x ≤4，log 2x ，x >4.若函数y ＝f （x ）在区间（a ，a ＋1）上是增加的，则实数a 的取值范围是__________.解析：作出函数f （x ）的图像如图所示，由图像可知f （x ）在（a ，a ＋1）上是增加的，需满足a ≥4或a ＋1≤2，即a ≤1或a ≥4.答案：（－∞，1]∪[4，＋∞）9.已知f （x ）＝xx －a（x ≠a ）.（1）若a ＝－2，试证f （x ）在（－∞，－2）上单调递增；（2）若a ＞0且f （x ）在（1，＋∞）上单调递减，求a 的取值范围. 解析：（1）证明：设x 1＜x 2＜－2，则f （x 1）－f （x 2）＝x 1x 1＋2－x 2x 2＋2＝2（x 1－x 2）（x 1＋2）（x 2＋2）.因为（x 1＋2）（x 2＋2）＞0，x 1－x 2＜0，所以f （x 1）－f （x 2）＜0，即f （x 1）＜f （x 2）， 所以f （x ）在（－∞，－2）上单调递增. （2）设1＜x 1＜x 2，则f （x 1）－f （x 2）＝x 1x 1－a －x 2x 2－a ＝a （x 2－x 1）（x 1－a ）（x 2－a ）.因为a ＞0，x 2－x 1＞0，所以要使f （x 1）－f （x 2）＞0， 只需（x 1－a ）（x 2－a ）＞0恒成立，所以a ≤1.综上所述，a 的取值范围是（0，1].[B 组 能力提升练]1.下列函数f （x ）中，满足“对任意的x 1，x 2∈（0，＋∞）时，均有（x 1－x 2）[f （x 1）－f （x 2）]＞0”的是（ ）A.f （x ）＝12B.f （x ）＝x 2－4x ＋4C.f （x ）＝2xD.f （x ）＝log 12x解析：（x 1－x 2）[f （x 1）－f （x 2）]＞0等价于x 1－x 2与f （x 1）－f （x 2）正负号相同，故函数f（x ）在（0，＋∞）上单调递增.显然只有函数f （x ）＝2x 符合. 答案：C2.已知函数f （x ）满足f （x －1）＝f （5－x ），且对任意的x 1，x 2∈[2，＋∞），x 1≠x 2，都有f （x 1）－f （x 2）x 1－x 2＜0成立，若p ＝f （log 216），q ＝f （log 47），m ＝f ⎝ ⎛⎭⎪⎫⎝⎛⎭⎫1525，则p ，q ，m 的大小关系为（ ） A.q ＜m ＜p B.p ＜m ＜q C.q ＜p ＜m D.p ＜q ＜m 解析：∵f （x －1）＝f （5－x ），∴函数f （x ）的图像关于直线x ＝2对称.又对任意的x 1，x 2∈[2，＋∞），x 1≠x 2，都有f （x 1）－f （x 2）x 1－x 2＜0成立，∴f （x ）在区间[2，＋∞）上单调递减，在（－∞，2）上单调递增.∵log 216＝4，∴f （log 216）＝f （4）＝f （0），又1＜log 47＜log 48＝32，0＜⎝⎛⎭⎫1525＜1，∴0＜⎝⎛⎭⎫1525＜1＜log 47＜2，∴p ＜m ＜q . 答案：B3.定义新运算⊕：当a ≥b 时，a ⊕b ＝a ；当a <b 时，a ⊕b ＝b 2，则函数f （x ）＝（1⊕x ）x －（2⊕x ），x ∈[－2，2]的最大值等于（ ） A.－1 B.1 C.6 D.12解析：由已知得当－2≤x ≤1时，f （x ）＝x －2，当1<x ≤2时，f （x ）＝x 3－2， 因为f （x ）＝x －2在[－2，1]上是增函数， 所以f （x ）≤f （1）＝－1，因为f （x ）＝x 3－2在（1，2]上是增函数，所以f （x ）≤f （2）＝6，所以f （x ）max ＝f （2）＝6. 答案：C4.（2021·西安模拟）已知函数y ＝log 2（ax －1）在（1，2）上单调递增，则实数a 的取值范围是（ ） A.（0，1] B.[1，2] C.[1，＋∞） D.[2，＋∞）解析：要使y ＝log 2（ax －1）在（1，2）上单调递增，则a ＞0且a －1≥0，∴a ≥1. 答案：C5.（2021·衡阳模拟）若函数f （x ）＝2x －a ＋1＋x －a －a 的定义域与值域相同，则a ＝（ ） A.－1 B.1 C.0 D.±1解析：∵函数f （x ）＝2x －a ＋1＋x －a －a ， ∴函数f （x ）的定义域为[a ，＋∞）. ∵函数f （x ）的定义域与值域相同， ∴函数f （x ）的值域为[a ，＋∞）.又∵函数f （x ）在[a ，＋∞）上是单调递增函数，∴当x ＝a 时，f （a ）＝2a －a ＋1－a ＝a ，解得a ＝1. 答案：B6.函数y ＝－x 2＋2|x |＋3的单调递减区间是__________.解析：由题意知，当x ≥0时，y ＝－x 2＋2x ＋3＝－（x －1）2＋4；当x ＜0时，y ＝－x 2－2x ＋3＝－（x ＋1）2＋4，二次函数的图像如图所示，由图像可知，函数y ＝－x 2＋2|x |＋3的单调递减区间为[－1，0]，[1，＋∞）.答案：[－1，0]，[1，＋∞）7.设f （x ）＝⎩⎪⎨⎪⎧（x －a ）2，x ≤0，x ＋1x＋a ，x ＞0.若f （0）是f （x ）的最小值，则a 的取值范围为__________.解析：因为当x ≤0时，f （x ）＝（x －a ）2，f （0）是f （x ）的最小值，所以a ≥0.当x ＞0时，f （x ）＝x ＋1x＋a ≥2＋a ，当且仅当x ＝1时取“＝”.要满足f （0）是f （x ）的最小值，需2＋a ≥f （0）＝a 2，即a 2－a －2≤0，解得－1≤a ≤2， 所以a 的取值范围是[0，2]. 答案：[0，2]8.已知函数f （x ）＝x 2＋a |x －2|－4.（1）当a ＝2时，求f （x ）在[0，3]上的最大值和最小值；（2）若f （x ）在区间[－1，＋∞）上单调递增，求实数a 的取值范围.解析：（1）当a ＝2时，f （x ）＝x 2＋2|x －2|－4＝⎩⎪⎨⎪⎧x 2＋2x －8，x ≥2，x 2－2x ，x ＜2＝⎩⎪⎨⎪⎧（x ＋1）2－9，x ≥2，（x －1）2－1，x ＜2，当x ∈[0，2）时，－1≤f （x ）≤0，当x ∈[2，3]时，0≤f （x ）≤7， 所以f （x ）在[0，3]上的最大值为7，最小值为－1.（2）因为f （x ）＝⎩⎪⎨⎪⎧x 2＋ax －2a －4，x ＞2，x 2－ax ＋2a －4，x ≤2，又f （x ）在区间[－1，＋∞）上单调递增，所以当x ＞2时，f （x ）单调递增，则－a2≤2，即a ≥－4.当－1≤x ≤2时，f （x ）单调递增，则a2≤－1.即a ≤－2，且4＋2a －2a －4≥4－2a ＋2a －4恒成立， 故a 的取值范围为[－4，－2].[C 组 创新应用练]1.定义运算⎪⎪⎪⎪⎪⎪a b c d ＝ad －bc ，若函数f （x ）＝⎪⎪⎪⎪⎪⎪x －1 2－x x ＋3在（－∞，m ）上单调递减，则实数m 的取值范围是（ ） A.（－2，＋∞） B.[－2，＋∞） C.（－∞，－2） D.（－∞，－2]解析：∵⎪⎪⎪⎪⎪⎪a b c d ＝ad －bc ，∴f （x ）＝⎪⎪⎪⎪⎪⎪x －1 2－x x ＋3＝（x －1）（x ＋3）－2×（－x ）＝x 2＋4x －3＝（x ＋2）2－7，∴f （x ）的单调递减区间为（－∞，－2）， ∵函数f （x ）在（－∞，m ）上单调递减， ∴（－∞，m ）⊆（－∞，－2），即m ≤－2. 答案：D2.如果函数y ＝f （x ）在区间I 上是增函数，且函数y ＝f （x ）x在区间I 上是减函数，那么称函数y ＝f （x ）是区间I 上的“缓增函数”，区间I 叫做“缓增区间”.若函数f （x ）＝12x 2－x ＋32是区间I 上的“缓增函数”，则“缓增区间”I 为（ ） A.[1，＋∞） B.[0，3] C.[0，1] D.[1，3]解析：因为函数f （x ）＝12x 2－x ＋32的对称轴为x ＝1，所以函数y ＝f （x ）在区间[1，＋∞）上是增函数，又当x ≥1时，f （x ）x ＝12x －1＋32x .令g （x ）＝12x －1＋32x （x ≥1），则g ′（x ）＝12－32x 2＝x 2－32x2，由g ′（x ）≤0得1≤x ≤3，即函数f （x ）x ＝12x －1＋32x在区间[1，3]上单调递减，故“缓增区间”I 为[1，3].答案：D3.已知定义在区间（0，＋∞）上的函数f （x ）满足f ⎝⎛⎭⎫x 1x 2＝f （x 1）－f （x 2），且当x ＞1时，f （x ）＞0，f （3）＝1.（1）判断f （x ）的单调性；（2）解关于x 的不等式f （3x ＋6）＋f ⎝⎛⎭⎫1x ＞2；（3）若f （x ）≤m 2－2am ＋1对所有x ∈（0，3]，a ∈[－1，1]恒成立，求实数m 的取值范围.解析：（1）设x 1＞x 2＞0，则x 1x 2＞1，因为当x ＞1时，f （x ）＞0，所以f （x 1）－f （x 2）＝f ⎝⎛⎭⎫x 1x 2＞0， 所以f （x 1）＞f （x 2），所以函数f （x ）在区间（0，＋∞）上为增函数.（2）在f （x 1）－f （x 2）＝f ⎝⎛⎭⎫x 1x 2中， 令x 1＝9，x 2＝3，所以f （9）－f （3）＝f （3）. 又f （3）＝1，所以f （9）＝2.所以不等式f （3x ＋6）＋f ⎝⎛⎭⎫1x ＞2，可转化为f （3x ＋6）＋f ⎝⎛⎭⎫1x ＞f （9）， 所以f （3x ＋6）＞f （9）－f ⎝⎛⎭⎫1x ＝f （9x ）， 由函数f （x ）为（0，＋∞）上的增函数，可得3x ＋6＞9x ＞0，所以0＜x ＜1， 所以原不等式的解集为（0，1）.（3）因为函数f （x ）在（0，3]上是增函数， 所以f （x ）在（0，3]上的最大值为f （3）＝1，所以不等式f （x ）≤m 2－2am ＋1对所有x ∈（0，3]，a ∈[－1，1]恒成立转化为1≤m 2－2am ＋1对所有a ∈[－1，1]恒成立，即m 2－2am ≥0对所有a ∈[－1，1]恒成立. 设g （a ）＝－2ma ＋m 2，所以需满足⎩⎪⎨⎪⎧g （－1）≥0，g （1）≥0，即⎩⎪⎨⎪⎧2m ＋m 2≥0，－2m ＋m 2≥0，解该不等式组，得m ≤－2或m ≥2或m ＝0，即实数m 的取值范围为（－∞，－2]∪{0}∪[2，＋∞）.函数的奇偶性与周期性[A 组 基础保分练]1.（2021·石家庄模拟）下列函数中，既是偶函数又在区间（0，＋∞）上单调递增的是（ ）A.y ＝1xB.y ＝|x |－1C.y ＝lg xD.y ＝⎝⎛⎭⎫12|x |解析：∵函数y ＝|x |－1和y ＝⎝⎛⎭⎫12|x |是偶函数，其中y ＝|x |－1在（0，＋∞）上单调递增，y ＝⎝⎛⎭⎫12|x |在（0，＋∞）上单调递减.答案：B2.若函数f （x ）＝（x －a ）（x ＋2）为偶函数，则实数a ＝（ ） A.0 B.1 C.－1 D.2 解析：f （x ）＝（x －a ）（x ＋2）＝x 2＋（2－a ）x －2a 为偶函数，则2－a ＝0，即a ＝2. 答案：D3.已知f （x ）为定义在R 上的奇函数，当x ≥0时，f （x ）＝2x ＋m ，则f （－2）＝（ ）A.－3B.－54C.54D.3 解析：因为f （x ）为R 上的奇函数，所以f （0）＝0，即f （0）＝20＋m ＝0，解得m ＝－1，则f （－2）＝－f （2）＝－（22－1）＝－3. 答案：A4.已知函数f （x ）是奇函数，在（0，＋∞）上是减函数，且在区间[a ，b ]（a ＜b ＜0）上的值域为[－3，4]，则在区间[－b ，－a ]上（ ） A.有最大值4 B.有最小值－4 C.有最大值－3 D.有最小值－3解析：根据题意作出y ＝f （x ）的简图如图所示，由图知，选B.答案：B5.定义在R 上的偶函数f （x ）满足f （x ＋3）＝f （x ）.若f （2）＞1，f （7）＝a ，则实数a 的取值范围为（ ） A.（－∞，－3） B.（3，＋∞） C.（－∞，－1） D.（1，＋∞） 解析：因为f （x ＋3）＝f （x ），所以f （x ）是定义在R 上的以3为周期的周期函数，所以f （7）＝f （7－9）＝f （－2）.又因为函数f （x ）是偶函数， 所以f （－2）＝f （2），所以f （7）＝f （2）＞1， 所以a ＞1，即a ∈（1，＋∞）. 答案：D6.已知函数y ＝f （x ），满足y ＝f （－x ）和y ＝f （x ＋2）是偶函数，且f （1）＝π3，设F （x ）＝f （x ）＋f （－x ），则F （3）＝（ ） A.π3 B.2π3C.πD.4π3解析：由y ＝f （－x ）和y ＝f （x ＋2）是偶函数知，f （－x ）＝f （x ），f （x ＋2）＝f （－x ＋2）＝f （x －2），故f （x ）＝f （x ＋4），则F （3）＝f （3）＋f （－3）＝2f （3）＝2f （－1）＝2f（1）＝2π3.答案：B7.若函数f （x ）＝x ln （x ＋a ＋x 2）为偶函数，则a ＝__________.解析：因为f （x ）为偶函数，所以f （－x ）－f （x ）＝0恒成立，所以－x ln （－x ＋a ＋x 2）－x ln （x ＋a ＋x 2）＝0恒成立，所以x ln a ＝0恒成立，所以ln a ＝0，即a ＝1. 答案：18.（2021·乐山模拟）已知函数f （x ）满足：f （－x ）＋f （x ）＝0，且当x ≥0时，f （x ）＝2＋m2x－1，则f （－1）＝__________. 解析：因为f （－x ）＋f （x ）＝0， 所以f （x ）为奇函数，又当x ≥0时，f （x ）＝2＋m2x －1，则f （0）＝2＋m1－1＝0，所以m ＝－1.所以当x ≥0时，f （x ）＝12x －1，所以f （－1）＝－f （1）＝－⎝⎛⎭⎫12－1＝12.答案：129.已知函数f （x ）＝⎩⎪⎨⎪⎧－x 2＋2x ，x ＞0，0， x ＝0，x 2＋mx ，x ＜0是奇函数.（1）求实数m 的值；（2）若函数f （x ）在区间[－1，a －2]上单调递增，求实数a 的取值范围. 解析：（1）设x ＜0，则－x ＞0，所以f （－x ）＝－（－x ）2＋2（－x ）＝－x 2－2x . 又f （x ）为奇函数，所以f （－x ）＝－f （x ），于是x ＜0时，f （x ）＝x 2＋2x ＝x 2＋mx ，所以m ＝2. （2）要使f （x ）在[－1，a －2]上单调递增，结合f （x ）的图像知⎩⎪⎨⎪⎧a －2＞－1，a －2≤1，所以1＜a ≤3，故实数a 的取值范围是（1，3].[B 组 能力提升练] 1.已知函数f （x ）＝a sin x ＋b 3x ＋4，若f （lg 3）＝3，则f ⎝⎛⎭⎫lg 13＝（ ） A.13 B.－13C.5D.8解析：因为f （x ）＝a sin x ＋b 3x ＋4，则f （－x ）＝－a sin x －b 3x ＋4，所以f （x ）＋f （－x ）＝8，由于f ⎝⎛⎭⎫lg 13＝f （－lg 3），因此f （lg 3）＋f （－lg 3）＝8，即3＋f （－lg 3）＝8，所以f （－lg 3）＝5，即f ⎝⎛⎭⎫lg 13＝f （－lg 3）＝5. 答案：C2.已知定义在R 上的奇函数f （x ）满足当x ≥0时f （x ）＝log 2（x ＋2）＋x ＋b ，则|f （x ）|＞3的解集为（ ）A.（－∞，－2）∪（2，＋∞）B.（－∞，－4）∪（4，＋∞）C.（－2，2）D.（－4，4）解析：由题意知，f （0）＝1＋b ＝0，所以b ＝－1，所以f （x ）＝log 2（x ＋2）＋x －1，所以f （2）＝3，且该函数在R 上单调递增.因为|f （x ）|＞3＝f （2），所以f （x ）＞f （2）或f （x ）＜－f （2）＝f （－2），所以x ＞2或x ＜－2. 答案：A3.设f （x ）是周期为2的奇函数，当0≤x ≤1时，f （x ）＝2x （1－x ），则f ⎝⎛⎭⎫－52等于（ ） A.－12 B.－14C.14D.12解析：f ⎝⎛⎭⎫－52＝f ⎝⎛⎭⎫－52＋2＝f ⎝⎛⎭⎫－12＝－f ⎝⎛⎭⎫12＝－2×12×⎝⎛⎭⎫1－12＝－12. 答案：A4.（2021·郴州模拟）已知f （x ）是定义在[2b ，1－b ]上的偶函数，且在[2b ，0]上为增函数，则f （x －1）≤f （2x ）的解集为（ ）A.⎣⎡⎦⎤－1，23B.⎣⎡⎦⎤－1，13 C.[－1，1] D.⎣⎡⎦⎤13，1解析：因为f （x ）是定义在[2b ，1－b ]上的偶函数，所以2b ＋1－b ＝0，所以b ＝－1，因为f （x ）在[2b ，0]上为增函数，即函数f （x ）在[－2，0]上为增函数，故函数f （x ）在（0，2]上为减函数，则由f （x －1）≤f （2x ），可得|x －1|≥|2x |，即（x －1）2≥4x 2，解得－1≤x ≤13.又因为定义域为[－2，2]，所以⎩⎪⎨⎪⎧－2≤x －1≤2，－2≤2x ≤2，解得⎩⎪⎨⎪⎧－1≤x ≤3，－1≤x ≤1.综上，－1≤x ≤13.答案：B5.已知偶函数f （x ）在[0，＋∞）上单调递增，则对任意实数a ，b ，“a ＞|b |”是“f （a ）＞f （b ）”的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件解析：因为f （x ）为偶函数，所以f （x ）＝f （－x ）＝f （|x |），由于f （x ）在[0，＋∞）上单调递增，因此若a ＞|b |≥0，则f （a ）＞f （|b |），即f （a ）＞f （b ），所以a ＞|b |是f （a ）＞f （b ）的充分条件；若f （a ）＞f （b ），则f （|a |）＞f （|b |），可得|a |＞|b |≥0，由于a ，b 的正负不能判断，因此无法得到a ＞|b |，则a ＞|b |不是f （a ）＞f （b ）的必要条件，所以“a ＞|b |”是“f （a ）＞f （b ）”的充分不必要条件. 答案：A 6.函数y ＝f （x ）在[0，2]上单调递增，且函数f （x ＋2）是偶函数，则下列结论成立的是（ ）A.f （1）＜f ⎝⎛⎭⎫52＜f ⎝⎛⎭⎫72 B.f ⎝⎛⎭⎫72＜f （1）＜f ⎝⎛⎭⎫52 C.f ⎝⎛⎭⎫72＜f ⎝⎛⎭⎫52＜f （1） D.f ⎝⎛⎭⎫52＜f （1）＜f ⎝⎛⎭⎫72 解析：因为函数f （x ＋2）是偶函数，所以f （x ＋2）＝f （－x ＋2）， 所以函数f （x ）的图像关于x ＝2对称，所以f ⎝⎛⎭⎫52＝f ⎝⎛⎭⎫32，f ⎝⎛⎭⎫72＝f ⎝⎛⎭⎫12.因为y ＝f （x ）在[0，2]上单调递增，且12＜1＜32，所以f ⎝⎛⎭⎫12＜f （1）＜f ⎝⎛⎭⎫32，即f ⎝⎛⎭⎫72＜f （1）＜f ⎝⎛⎭⎫52. 答案：B7.定义在R 上的函数f （x ）满足f （x ）＝f （2－x ）及f （x ）＝－f （－x ），且在[0，1]上有f （x ）＝x 2，则f ⎝⎛⎭⎫2 01912＝__________. 解析：函数f （x ）的定义域是R ，f （x ）＝－f （－x ），所以函数f （x ）是奇函数.又f （x ）＝f （2－x ），所以f （－x ）＝f （2＋x ）＝－f （x ），所以f （4＋x ）＝－f （2＋x ）＝f （x ），故函数f （x ）是以4为周期的奇函数，所以f ⎝⎛⎭⎫2 01912＝f ⎝⎛⎭⎫2 020－12＝f ⎝⎛⎭⎫－12＝－f ⎝⎛⎭⎫12.因为在[0，1]上有f （x ）＝x 2，所以f ⎝⎛⎭⎫12＝⎝⎛⎭⎫122＝14，故f ⎝⎛⎭⎫2 01912＝－14. 答案：－148.（2021·柳州模拟）已知函数f （x ）对任意x ∈R 都有f （x ＋6）＋f （x ）＝2f （3），y ＝f （x －1）的图像关于点（1，0）对称且f （2）＝4，则f （22）＝__________.解析：因为y ＝f （x －1）的图像关于点（1，0）对称，所以y ＝f （x ）的图像关于点（0，0）对称，即函数f （x ）为奇函数，由f （x ＋6）＋f （x ）＝2f （3）得，f （x ＋12）＋f （x ＋6）＝2f （3），所以f （x ＋12）＝f （x ），T ＝12，因此f （22）＝f （－2）＝－f （2）＝－4. 答案：－49.已知函数f （x ）对任意x ∈R 满足f （x ）＋f （－x ）＝0，f （x －1）＝f （x ＋1），若当x ∈[0，1）时，f （x ）＝a x ＋b （a ＞0且a ≠1），且f ⎝⎛⎭⎫32＝12. （1）求实数a ，b 的值；（2）求函数g （x ）＝f 2（x ）＋f （x ）的值域. 解析：（1）因为f （x ）＋f （－x ）＝0， 所以f （－x ）＝－f （x ），即f （x ）是奇函数. 因为f （x －1）＝f （x ＋1），所以f （x ＋2）＝f （x ）， 即函数f （x ）是周期为2的周期函数， 所以f （0）＝0，即b ＝－1.又f ⎝⎛⎭⎫32＝f ⎝⎛⎭⎫－12＝－f ⎝⎛⎭⎫12＝1－a ＝12， 解得a ＝14.（2）当x ∈[0，1）时f （x ）＝a x＋b ＝⎝⎛⎭⎫14x －1∈⎝⎛⎦⎤－34，0， 由f （x ）为奇函数知，当x ∈（－1，0）时，f （x ）∈⎝⎛⎭⎫0，34， 又因为f （x ）是周期为2的周期函数，所以当x ∈R 时，f （x ）∈⎝⎛⎭⎫－34，34， 设t ＝f （x ）∈⎝⎛⎭⎫－34，34， 所以g （x ）＝f 2（x ）＋f （x ）＝t 2＋t ＝⎝⎛⎭⎫t ＋122－14， 即g （x ）＝⎝⎛⎭⎫t ＋122－14∈⎣⎡⎭⎫－14，2116.故函数g （x ）＝f 2（x ）＋f （x ）的值域为⎣⎡⎭⎫－14，2116. [C 组 创新应用练]1.（2021·兰州模拟）对任意实数x ，定义[x ]为不大于x 的最大整数（例如[3.4]＝3，[－3.4]＝－4等）.设函数f （x ）＝x －[x ]，给出下列四个结论：①f （x ）≥0；②f （x ）＜1；③f （x ）是周期函数；④f （x ）是偶函数.其中正确结论的个数是（ ） A.1 B.2 C.3 D.4解析：由题意有[x ]≤x ＜[x ]＋1，∴f （x ）＝x －[x ]≥0，且f （x ）＜1，∴①②正确；∵f （x ＋1）＝x ＋1－[x ＋1]＝x ＋1－（[x ]＋1）＝x －[x ]＝f （x ），∴f （x ）为周期函数，③正确；∵f （－0.1）＝－0.1－[－0.1]＝－0.1－（－1）＝0.9，f （0.1）＝0.1－[0.1]＝0.1－0＝0.1≠f （－0.1），∴f （x ）不是偶函数，④错误. 答案：C2.（2019·高考全国卷Ⅱ）设函数f （x ）的定义域为R ，满足f （x ＋1）＝2f （x ），且当x ∈（0，1] 时，f （x ）＝x （x －1）.若对任意x ∈（－∞，m ]，都有f （x ）≥－89，则m 的取值范围是（ ）A.⎝⎛⎦⎤－∞，94B.⎝⎛⎦⎤－∞，73C.⎝⎛⎦⎤－∞，52D.⎝⎛⎦⎤－∞，83 解析：当x ∈（0，1]时，f （x ）＝x （x －1），∴当x ∈（0，1]时，f （x ）∈⎣⎡⎦⎤－14，0. ∵f （x ＋1）＝2f （x ），∴当x ∈（－1，0]时，x ＋1∈（0，1]，f （x ）＝12f （x ＋1）＝12（x ＋1）x ，f （x ）∈⎣⎡⎦⎤－18，0； 当x ∈（－2，－1]时，x ＋1∈（－1，0]，f （x ）＝12f （x ＋1）＝14f （x ＋2）＝14（x ＋2）（x ＋1），f （x ）∈⎣⎡⎦⎤－116，0； …；当x ∈（1，2]时，x －1∈（0，1]，f （x ）＝2f （x －1）＝2（x －1）（x －2），f （x ）∈⎣⎡⎦⎤－12，0； 当x ∈（2，3]时，x －1∈（1，2]，f （x ）＝2f （x －1）＝4f （x －2）＝4（x －2）（x －3），f （x ）∈[－1，0]； ….f （x ）的图像如图所示.11若对任意x ∈（－∞，m ]，都有f （x ）≥－89，则有2＜m ≤3. 设f （m ）＝－89，则4（m －2）（m －3）＝－89， ∴m ＝73或m ＝83.结合图像可知，当m ≤73时，符合题意. 答案：B3.（2021·湘潭模拟）已知定义在R 上的偶函数y ＝f （x ＋2）的图像连续，当x ＞2时，函数y＝f （x ）是单调函数，则满足f （x ）＝f ⎝⎛⎭⎫1－1x ＋4的所有x 之积为__________. 解析：因为函数y ＝f （x ＋2）是连续的偶函数，所以直线x ＝0是它的图像的对称轴，所以直线x ＝2就是函数y ＝f （x ）图像的对称轴.因为f （x ）＝f ⎝⎛⎭⎫1－1x ＋4，所以x ＝1－1x ＋4或x ＋1－1x ＋4＝4.由x ＝1－1x ＋4，得x 2＋3x －3＝0，设方程的两根为x 1，x 2，所以x 1x 2＝－3；由x ＋1－1x ＋4＝4，得x 2＋x －13＝0，设方程的两根为x 3，x 4，所以x 3x 4＝－13.所以x 1x 2x 3x 4＝39. 答案：39。

第三讲 函数的单调性与奇偶性★知识与方法1、奇偶函数的定义、图象特征.2、奇、偶函数的性质：①若奇函数y =f (x )在x =0处有意义，则f (0)=0；偶函数y =f (x )必满足f (x )=f (|x |). ②偶函数（奇函数）在其定义域内关于原点对称的两个区间单调性相反（相同）.③若函数f (x )的定义域关于原点对称，则函数f (x )能表示成一个偶函数与一个奇函数的和的形式. ④复合函数的奇偶性原理：内偶则偶，两奇为奇.⑤两个函数通过四则运算所得的函数的奇偶性可根据定义直接判断. 3、单调函数的定义及等价定义. 4、单调函数的性质：①对于运算函数有如下结论：增+增=增，减+减=减，增－减=增，减－增=减；（特别对于乘除没有必然的结论）②若f (x )为增函数，且f (x )>0（或f (x )<0），则1()f x 为减函数，若f (x )为减函数，且f (x )>0（或f (x )<0），则1()f x 为增函数；③复合函数的单调性：同增异减.5、判断单调性主要的方法：定义法、图象法、复合函数单调性判定法.★典型例题【例1】下列函数中，在区间(],0-∞上为减函数的是（ ）A.11y x=+B.()21y x =-+ C.y = D.2y x = 【答案】D【例2】求下列函数的单调区间：（1）223y x x =-+；（2）223y x x =--；（3）y （4）y .【答案】（1）单调增区间：[][)1,0,1,-+∞，单调减区间：(][],1,0,1-∞-； （2）单调增区间：[][)1,1,3,-+∞，单调减区间：(][],1,1,3-∞-； （3）单调增区间：[)3,+∞，单调减区间：(],3-∞-； （4）单调增区间：[]5,2--，单调减区间：[]2,1-.【例3】讨论函数()()211,01axf x x a x =-<<≠-的单调性。

函数的单调性和奇偶性经典例题透析类型一、函数的单调性的证明1.证明函数上的单调性.证明：在(0，+∞)上任取x1、x2(x1≠x2)，令△x=x2-x1＞0则∵x1＞0，x2＞0，∴∴上式＜0，∴△y=f(x2)-f(x1)＜0∴上递减.总结升华：[1]证明函数单调性要求使用定义；[2]如何比较两个量的大小？(作差)[3]如何判断一个式子的符号？(对差适当变形)举一反三：【变式1】用定义证明函数上是减函数.思路点拨：本题考查对单调性定义的理解，在现阶段，定义是证明单调性的唯一途径.证明：设x1，x2是区间上的任意实数，且x1＜x2，则∵0＜x1＜x2≤1 ∴x1-x2＜0，0＜x1x2＜1∵0＜x1x2＜1故，即f(x1)-f(x2)＞0∴x1＜x2时有f(x1)＞f(x2)上是减函数.总结升华：可以用同样的方法证明此函数在上是增函数；在今后的学习中经常会碰到这个函数，在此可以尝试利用函数的单调性大致给出函数的图象.类型二、求函数的单调区间2. 判断下列函数的单调区间；(1)y=x2-3|x|+2；(2)解：(1)由图象对称性，画出草图∴f(x)在上递减，在上递减，在上递增.(2)∴图象为∴f(x)在上递增.举一反三：【变式1】求下列函数的单调区间：(1)y=|x+1|；(2)(3).解：(1)画出函数图象，∴函数的减区间为，函数的增区间为(-1，+∞)；(2)定义域为，其中u=2x-1为增函数，在(-∞，0)与(0，+∞)为减函数，则上为减函数；(3)定义域为(-∞，0)∪(0，+∞)，单调增区间为：(-∞，0)，单调减区间为(0，+∞).总结升华：[1]数形结合利用图象判断函数单调区间；[2]关于二次函数单调区间问题，单调性变化的点与对称轴相关.[3]复合函数的单调性分析：先求函数的定义域；再将复合函数分解为内、外层函数；利用已知函数的单调性解决.关注：内外层函数同向变化复合函数为增函数；内外层函数反向变化复合函数为减函数.类型三、单调性的应用(比较函数值的大小，求函数值域，求函数的最大值或最小值)3. 已知函数f(x)在(0，+∞)上是减函数，比较f(a2-a+1)与的大小.解：又f(x)在(0，+∞)上是减函数，则.4. 求下列函数值域：(1)；1)x∈[5，10]；2)x∈(-3，-2)∪(-2，1)；(2)y=x2-2x+3；1)x∈[-1，1]；2)x∈[-2，2].思路点拨：(1)可应用函数的单调性；(2)数形结合.解：(1)2个单位，再上移2个单位得到，如图1)f(x)在[5，10]上单增，；2)；(2)画出草图1)y∈[f(1)，f(-1)]即[2，6]；2).举一反三：【变式1】已知函数.(1)判断函数f(x)的单调区间；(2)当x∈[1，3]时，求函数f(x)的值域.思路点拨：这个函数直接观察恐怕不容易看出它的单调区间，但对解析式稍作处理，即可得到我们相对熟悉的形式.，第二问即是利用单调性求函数值域.解：(1)上单调递增，在上单调递增；(2)故函数f(x)在[1，3]上单调递增∴x=1时f(x)有最小值，f(1)=-2x=3时f(x)有最大值∴x∈[1，3]时f(x)的值域为.5. 已知二次函数f(x)=x2-(a-1)x+5在区间上是增函数，求：(1)实数a的取值范围；(2)f(2)的取值范围.解：(1)∵对称轴是决定f(x)单调性的关键，联系图象可知只需；(2)∵f(2)=22-2(a-1)+5=-2a+11又∵a≤2，∴-2a≥-4∴f(2)=-2a+11≥-4+11=7.类型四、判断函数的奇偶性6. 判断下列函数的奇偶性：(1)(2)(3)f(x)=x2-4|x|+3 (4)f(x)=|x+3|-|x-3| (5)(6)(7)思路点拨：根据函数的奇偶性的定义进行判断.解：(1)∵f(x)的定义域为，不关于原点对称，因此f(x)为非奇非偶函数；(2)∵x-1≥0，∴f(x)定义域不关于原点对称，∴f(x)为非奇非偶函数；(3)对任意x∈R，都有-x∈R，且f(-x)=x2-4|x|+3=f(x)，则f(x)=x2-4|x|+3为偶函数；(4)∵x∈R，f(-x)=|-x+3|-|-x-3|=|x-3|-|x+3|=-f(x)，∴f(x)为奇函数；(5)，∴f(x)为奇函数；(6)∵x∈R，f(x)=-x|x|+x ∴f(-x)=-(-x)|-x|+(-x)=x|x|-x=-f(x)，∴f(x)为奇函数；(7)，∴f(x)为奇函数.举一反三：【变式1】判断下列函数的奇偶性：(1)；(2)f(x)=|x+1|-|x-1|；(3)f(x)=x2+x+1；(4).思路点拨：利用函数奇偶性的定义进行判断.解：(1)；(2)f(-x)=|-x+1|-|-x-1|=-(|x+1|-|x-1|)=-f(x) ∴f(x)为奇函数；(3)f(-x)=(-x)2+(-x)+1=x2-x+1∴f(-x)≠-f(x)且f(-x)≠f(x) ∴f(x)为非奇非偶函数；(4)任取x＞0则-x＜0，∴f(-x)=(-x)2+2(-x)-1=x2-2x-1=-(-x2+2x+1)=-f(x)任取x＜0，则-x＞0 f(-x)=-(-x)2+2(-x)+1=-x2-2x+1=-(x2+2x-1)=-f(x)x=0时，f(0)=-f(0) ∴x∈R时，f(-x)=-f(x) ∴f(x)为奇函数.举一反三：【变式2】已知f(x)，g(x)均为奇函数，且定义域相同，求证：f(x)+g(x)为奇函数，f(x)·g(x)为偶函数.证明：设F(x)=f(x)+g(x)，G(x)=f(x)·g(x)则F(-x)=f(-x)+g(-x)=-f(x)-g(x)=-[f(x)+g(x)]=-F(x)G(-x)=f(-x)·g(-x)=-f(x)·[-g(x)]=f(x)·g(x)=G(x)∴f(x)+g(x)为奇函数，f(x)·g(x)为偶函数.类型五、函数奇偶性的应用(求值，求解析式，与单调性结合)7.已知f(x)=x5+ax3-bx-8，且f(-2)=10，求f(2).解：法一：∵f(-2)=(-2)5+(-2)3a-(-2)b-8=-32-8a+2b-8=-40-8a+2b=10∴8a-2b=-50 ∴f(2)=25+23a-2b-8=8a-2b+24=-50+24=-26法二：令g(x)=f(x)+8易证g(x)为奇函数∴g(-2)=-g(2) ∴f(-2)+8=-f(2)-8∴f(2)=-f(-2)-16=-10-16=-26.8. f(x)是定义在R上的奇函数，且当x＜0时，f(x)=x2-x，求当x≥0时，f(x)的解析式，并画出函数图象.解：∵奇函数图象关于原点对称，∴x＞0时，-y=(-x)2-(-x)即y=-x2-x又f(0)=0，，如图9. 设定义在[-3，3]上的偶函数f(x)在[0，3]上是单调递增，当f(a-1)＜f(a)时，求a 的取值范围.解：∵f(a-1)＜f(a) ∴f(|a-1|)＜f(|a|)而|a-1|，|a|∈[0，3].类型六、综合问题10.定义在R上的奇函数f(x)为增函数，偶函数g(x)在区间的图象与f(x)的图象重合，设a＞b＞0，给出下列不等式，其中成立的是_________.①f(b)-f(-a)＞g(a)-g(-b)；②f(b)-f(-a)＜g(a)-g(-b)；③f(a)-f(-b)＞g(b)-g(-a)；④f(a)-f(-b)＜g(b)-g(-a).答案：①③.11. 求下列函数的值域：(1)(2)(3)思路点拨：(1)中函数为二次函数开方，可先求出二次函数值域；(2)由单调性求值域，此题也可换元解决；(3)单调性无法确定，经换元后将之转化为熟悉二次函数情形，问题得到解决，需注意此时t范围.解：(1)；(2)经观察知，，；(3)令.12. 已知函数f(x)=x2-2ax+a2-1.(1)若函数f(x)在区间[0，2]上是单调的，求实数a的取值范围；(2)当x∈[-1，1]时，求函数f(x)的最小值g(a)，并画出最小值函数y=g(a)的图象.解：(1)∵f(x)=(x-a)2-1 ∴a≤0或a≥2(2)1°当a＜-1时，如图1，g(a)=f(-1)=a2+2a2°当-1≤a≤1时，如图2，g(a)=f(a)=-13°当a＞1时，如图3，g(a)=f(1)=a2-2a，如图13. 已知函数f(x)在定义域(0，+∞)上为增函数，f(2)=1，且定义域上任意x、y都满足f(xy)=f(x)+f(y)，解不等式：f(x)+f(x-2)≤3.解：令x=2，y=2，∴f(2×2)=f(2)+f(2)=2 ∴f(4)=2再令x=4，y=2，∴f(4×2)=f(4)+f(2)=2+1=3 ∴f(8)=3∴f(x)+f(x-2)≤3可转化为：f[x(x-2)]≤f(8).14. 判断函数上的单调性，并证明.证明：任取0＜x1＜x2，∵0＜x1＜x2，∴x1-x2＜0，x1·x2＞0(1)当时0＜x1·x2＜1，∴x1·x2-1＜0∴f(x1)-f(x2)＞0即f(x1)＞f(x2)上是减函数.(2)当x1，x2∈(1，+∞)时，上是增函数.难点：x1·x2-1的符号的确定，如何分段.15. 设a为实数，函数f(x)=x2+|x-a|+1，x∈R，试讨论f(x)的奇偶性，并求f(x)的最小值.解：当a=0时，f(x)=x2+|x|+1，此时函数为偶函数；当a≠0时，f(x)=x2+|x-a|+1，为非奇非偶函数.(1)当x≥a时，[1]且[2]上单调递增，上的最小值为f(a)=a2+1.(2)当x＜a时，[1]上单调递减，上的最小值为f(a)=a2+1[2]上的最小值为综上：.学习成果测评基础达标一、选择题1．下面说法正确的选项( )A．函数的单调区间就是函数的定义域B．函数的多个单调增区间的并集也是其单调增区间C．具有奇偶性的函数的定义域定关于原点对称D．关于原点对称的图象一定是奇函数的图象2．在区间上为增函数的是( )A．B．C．D．3．已知函数为偶函数，则的值是( )A. B. C. D.4．若偶函数在上是增函数，则下列关系式中成立的是( )A．B．C．D．5．如果奇函数在区间上是增函数且最大值为，那么在区间上是( )A．增函数且最小值是B．增函数且最大值是C．减函数且最大值是D．减函数且最小值是6．设是定义在上的一个函数，则函数，在上一定是( )A．奇函数B．偶函数C．既是奇函数又是偶函数D．非奇非偶函数.7．下列函数中，在区间上是增函数的是( )A．B．C．D．8．函数f(x)是定义在[-6，6]上的偶函数，且在[-6，0]上是减函数，则( )A. f(3)+f(4)＞0B. f(-3)-f(2)＜0C. f(-2)+f(-5)＜0D. f(4)-f(-1)＞0二、填空题1．设奇函数的定义域为，若当时，的图象如右图，则不等式的解是____________.2．函数的值域是____________.3．已知，则函数的值域是____________.4．若函数是偶函数，则的递减区间是____________.5．函数在R上为奇函数，且，则当，____________.三、解答题1．判断一次函数反比例函数，二次函数的单调性.2．已知函数的定义域为，且同时满足下列条件：(1)是奇函数；(2)在定义域上单调递减；(3)求的取值范围.3．利用函数的单调性求函数的值域；4．已知函数.①当时，求函数的最大值和最小值；②求实数的取值范围，使在区间上是单调函数.能力提升一、选择题1．下列判断正确的是( )A．函数是奇函数B．函数是偶函数C．函数是非奇非偶函数D．函数既是奇函数又是偶函数2．若函数在上是单调函数，则的取值范围是( )A．B．C．D．3．函数的值域为( )A．B．C．D．4．已知函数在区间上是减函数，则实数的取值范围是( )A．B．C．D．5．下列四个命题：(1)函数在时是增函数，也是增函数，所以是增函数；(2)若函数与轴没有交点，则且；(3)的递增区间为；(4) 和表示相等函数.其中正确命题的个数是( )A．B．C．D．6．定义在R上的偶函数，满足，且在区间上为递增，则( )A．B．C．D．二、填空题1．函数的单调递减区间是____________________.2．已知定义在上的奇函数，当时，，那么时，______.3．若函数在上是奇函数，则的解析式为________.4．奇函数在区间上是增函数，在区间上的最大值为8，最小值为-1，则__________.5．若函数在上是减函数，则的取值范围为__________.三、解答题1．判断下列函数的奇偶性(1)(2)2．已知函数的定义域为，且对任意，都有，且当时，恒成立，证明：(1)函数是上的减函数；(2)函数是奇函数.3．设函数与的定义域是且，是偶函数，是奇函数，且，求和的解析式.4．设为实数，函数，.(1)讨论的奇偶性；(2)求的最小值.综合探究1．已知函数，，则的奇偶性依次为( )A．偶函数，奇函数B．奇函数，偶函数C．偶函数，偶函数D．奇函数，奇函数2．若是偶函数，其定义域为，且在上是减函数，则的大小关系是( )A．＞B．＜C．D．3．已知，那么＝_____.4．若在区间上是增函数，则的取值范围是________.5．已知函数的定义域是，且满足，，如果对于，都有，(1)求；(2)解不等式.6．当时，求函数的最小值.7．已知在区间内有一最大值，求的值.8．已知函数的最大值不大于，又当，求的值.答案与解析基础达标一、选择题1.C.2.B.3.B. 奇次项系数为4.D.5.A. 奇函数关于原点对称，左右两边有相同的单调性6.A.7.A. 在上递减，在上递减，在上递减8.D.二、填空题1.. 奇函数关于原点对称，补足左边的图象2.. 是的增函数，当时，3.. 该函数为增函数，自变量最小时，函数值最小；自变量最大时，函数值最大4..5..三、解答题1．解：当，在是增函数，当，在是减函数；当，在是减函数，当，在是增函数；当，在是减函数，在是增函数，当，在是增函数，在是减函数.2．解：，则，3．解：，显然是的增函数，，4．解：对称轴∴(2)对称轴当或时，在上单调∴或.能力提升一、选择题1.C. 选项A中的而有意义，非关于原点对称，选项B中的而有意义，非关于原点对称，选项D中的函数仅为偶函数；2.C. 对称轴，则，或，得，或3.B. ，是的减函数，当4.A. 对称轴5.A. (1)反例；(2)不一定，开口向下也可；(3)画出图象可知，递增区间有和；(4)对应法则不同6.A.二、填空题1．. 画出图象2. . 设，则，，∵∴，3. .∵∴即4. . 在区间上也为递增函数，即5. . .三、解答题1．解：(1)定义域为，则，∵∴为奇函数.(2)∵且∴既是奇函数又是偶函数.2．证明：(1)设，则，而∴∴函数是上的减函数;(2)由得即，而∴，即函数是奇函数.3．解：∵是偶函数，是奇函数，∴，且而，得，即，∴，.4．解：(1)当时，为偶函数，当时，为非奇非偶函数；(2)当时，当时，，当时，不存在；当时，当时，，当时，.综合探究1.D. ，画出的图象可观察到它关于原点对称或当时，，则当时，，则2.C. ，3.. ，4.. 设则，而，则5.解：(1)令，则(2)，则.6.解：对称轴当，即时，是的递增区间，；当，即时，是的递减区间，；当，即时，.7．解：对称轴，当即时，是的递减区间，则，得或，而，即；当即时，是的递增区间，则，得或，而，即不存在；当即时，则，即；∴或. 8．解：，对称轴，当时，是的递减区间，而，即与矛盾，即不存在；当时，对称轴，而，且即，而，即∴.。

高中数学：函数的单调性、奇偶性、最值问题练习及答案1.已知奇函数f（x）的定义域为（－∞，0）∪（0，＋∞），且不等式>0对任意两个不相等的正实数x1，x2都成立，则下列不等式中，正确的是（）A.f（－5）>f（3）B.f（－5）<f（3）C.f（－3）>f（－5）D.f（－3）<f（－5）2.设f（x）是R上的偶函数，且在（0，＋∞）上是减函数，若x1<0且x1＋x2>0，则（）A.f（－x1）>f（－x2）B.f（－x1）＝f（－x2）C.f（－x1）<f（－x2）D.f（－x1）与f（－x2）的大小不确定3.已知函数f（x）是奇函数，且在（－∞，＋∞）上为增函数，若x，y满足等式f（2x2－4x）＋f（y）＝0，则4x＋y的最大值是（）A.10B.－6C.8D.94.已知f（x）＝ax2＋bx＋c（a≠0），且方程f（x）＝x无实根.现有四个说法：①若a>0，则不等式f（f （x））>x对一切x∈R成立；②若a<0，则必存在实数x0使不等式f（f（x0））>x0成立；③方程f（f（x））＝x一定没有实数根；④若a＋b＋c＝0，则不等式f（f（x））<x对一切x∈R成立.其中说法正确的个数是（）A.1B.2C.3D.45.区间[a，b]和[－b，－a]关于原点对称.（1）若f（x）为奇函数，且在[a，b]上有最大值M，则f（x）在[－b，－a]上有最________值________. （2）若f（x）为奇函数，f（x）＋2在[a，b]上有最大值M，则f（x）＋2在[－b，－a]上有最________值________.6.设定义在（－1,1）上的奇函数f（x）在[0,1）上单调递增，且有f（1－m）＋f＜0，求实数m的取值范围.7.已知定义在R上的奇函数f（x），当x>0时，f（x）＝－x2＋2x.（1）求函数f（x）在R上的解析式；（2）若函数f（x）在区间[－1，a－2]上单调递增，求实数a的取值范围.8.定义在R上的函数y＝f（x），f（0）≠0，当x>0时，f（x）>1，且对任意的a，b∈R，有f（a＋b）＝f（a）f（b）.（1）求证：f（0）＝1；（2）求证：对任意的x∈R，恒有f（x）>0；（3）求证：f（x）是R上的增函数.9.若f（x）是定义在（0，＋∞）上的增函数，且对一切x，y>0，满足f（）＝f（x）－f（y）.（1）求f（1）的值；（2）若f（6）＝1，解不等式f（x＋3）－f（）<2.10.定义在（0，＋∞）上的函数f（x）满足f（mn）＝f（m）＋f（n）（m，n>0），且当x>1时，f（x）>0. （1）求f（1）的值；（2）求证f＝f（m）－f（n）；（3）求证f（x）在（0，＋∞）上是增函数；（4）若f（2）＝1，解不等式f（x＋2）－f（2x）>2；（5）比较f的大小.11.若函数f（x）的定义域是R，且对任意x，y∈R，都有f（x＋y）＝f（x）＋f（y）成立.（1）试判断f（x）的奇偶性；（2）若f（8）＝4，求f（－）的值.12.已知f（x）是定义在R上的不恒为0的函数，且对于任意的x，y∈R，有f（x·y）＝xf（y）＋yf（x）. （1）求f（0），f（1）的值；（2）判断函数f（x）的奇偶性，并证明你的结论.13.已知函数f（x）对任意实数x，y恒有f（x＋y）＝f（x）＋f（y），且当x>0时，f（x）<0，又f（1）＝－2.（1）判断f（x）的奇偶性；（2）求证：f（x）是R上的减函数；（3）求f（x）在区间[－3,3]上的值域；（4）若对任意x∈R，不等式f（ax2）－2f（x）<f（x）＋4恒成立，求a的取值范围.14.设f（x）是定义在[－1,1]上的奇函数，且对任意a，b∈[－1,1]，当a＋b≠0时，都有>0.（1）若a>b，试比较f（a）与f（b）的大小；（2）解不等式f（x－）<f（x－）；（3）如果g（x）＝f（x－c）和h（x）＝f（x－c2）这两个函数的定义域的交集是空集，求c的取值范围.15.已知函数f（x）是定义在区间[－1,1]上的奇函数，且f（1）＝1，若对于任意的m，n∈[－1,1]有>0. （1）判断函数的单调性（不要求证明）；（2）解不等式f<f（1－x）；（3）若f（x）≤－2at＋2对于任意的x∈[－1,1]，a∈[－1,1]恒成立，求实数t的取值范围.16.已知函数f（x）＝x－.（1）判断函数f（x）的奇偶性，并加以证明；（2）用定义证明函数f（x）在区间[1，＋∞）上为增函数；（3）若函数f（x）在区间[2，a]上的最大值与最小值之和不小于，求a的取值范围.17.已知函数f（x）＝x2＋2.（1）求函数f（x）的定义域和值域；（2）判断函数f（x）的奇偶性和单调性；（3）求函数f（x）在区间（－1,2]上的最大值和最小值.18.已知函数f（x）＝ax2＋bx＋1（a，b均为实数），x∈R，F（x）＝（1）若f（－1）＝0，且函数f（x）的值域为[0，＋∞），求F（x）的解析式；（2）在（1）的条件下，当x∈[－2,2]时，g（x）＝f（x）－kx是单调函数，求实数k的取值范围；（3）设mn<0，m＋n>0，a>0，且f（x）为偶函数，判断F（m）＋F（n）是否大于零，并说明理由.19.已知函数f（x）＝－（常数a>0）.（1）设m·n>0，证明：函数f（x）在[m，n]上单调递增；（2）设0<m<n，且f（x）的定义域和值域都是[m，n]，求n－m的最大值.20.已知函数y＝f（x）是定义在R上的奇函数，且当x≥0时，f（x）＝－x2＋ax.（1）若a＝－2，求函数f（x）的解析式；（2）若函数f（x）为R上的单调减函数，①求a的取值范围；②若对任意实数m，f（m－1）＋f（m2＋t）<0恒成立，求实数t的取值范围.21.已知二次函数f（x）的最小值为1，且f（0）＝f（2）＝3.（1）求f（x）的解析式；（2）若f（x）在区间[3a，a＋1]上不单调，求实数a的取值范围；（3）在区间[－1,1]上，y＝f（x）的图象恒在y＝2x＋2m＋1的图象上方，试确定实数m的取值范围.22.已知f（x）是定义在[－1,1]上的奇函数，且f（1）＝1，若a，b∈[－1,1]，a＋b≠0时，有>0成立. （1）判断f（x）在[－1,1]上的单调性；（2）解不等式f（x＋）<f（）；（3）若f（x）≤m2－2am＋1对所有的a∈[－1,1]恒成立，求实数m的取值范围.答案1.已知奇函数f（x）的定义域为（－∞，0）∪（0，＋∞），且不等式>0对任意两个不相等的正实数x1，x2都成立，则下列不等式中，正确的是（）A.f（－5）>f（3）B.f（－5）<f（3）C.f（－3）>f（－5）D.f（－3）<f（－5）【答案】C【解析】设0<x1<x2，则x1－x2<0，由>0，得f（x1）－f（x2）<0，即f（x1）<f（x2），∴f（x）在（0，＋∞）上为增函数，∴f（x）在（－∞，0）上也是增函数，∴由－3>－5，可得f（－3）>f（－5）.2.设f（x）是R上的偶函数，且在（0，＋∞）上是减函数，若x1<0且x1＋x2>0，则（）A.f（－x1）>f（－x2）B.f（－x1）＝f（－x2）C.f（－x1）<f（－x2）D.f（－x1）与f（－x2）的大小不确定【答案】A【解析】∵x1<0，x1＋x2>0，∴x2>－x1>0，又f（x）在（0，＋∞）上是减函数，∴f（x2）<f（－x1），∵f（x）是偶函数，∴f（－x2）＝f（x2）<f（－x1）.3.已知函数f（x）是奇函数，且在（－∞，＋∞）上为增函数，若x，y满足等式f（2x2－4x）＋f（y）＝0，则4x＋y的最大值是（）A.10B.－6C.8D.9【答案】C【解析】∵奇函数f（x）在（－∞，＋∞）上是增函数，∴f（2x2－4x）＝－f（y）＝f（－y），∴2x2－4x＝－y，∴4x＋y＝4x－2x2＋4x＝－2（x－2）2＋8≤8，故选C.4.已知f（x）＝ax2＋bx＋c（a≠0），且方程f（x）＝x无实根.现有四个说法：①若a>0，则不等式f（f （x））>x对一切x∈R成立；②若a<0，则必存在实数x0使不等式f（f（x0））>x0成立；③方程f（f（x））＝x一定没有实数根；④若a＋b＋c＝0，则不等式f（f（x））<x对一切x∈R成立.其中说法正确的个数是（）A.1B.2C.3D.4【答案】C【解析】∵方程f（x）＝x无实根，∴f（x）－x>0或f（x）－x<0.∵a>0，∴f（x）－x>0对一切x∈R成立，∴f（x）>x，用f（x）代替x，∴f（f（x））>f（x）>x，∴说法①正确；同理若a<0，则有f（f（x））<x，∴说法②错误；说法③正确；∵a＋b＋c＝0，∴f（1）－1<0，∴必然归为a<0，有f（f（x））<x，∴说法④正确.故选C.填空5.区间[a，b]和[－b，－a]关于原点对称.（1）若f（x）为奇函数，且在[a，b]上有最大值M，则f（x）在[－b，－a]上有最________值________. （2）若f（x）为奇函数，f（x）＋2在[a，b]上有最大值M，则f（x）＋2在[－b，－a]上有最________值________.【答案】（1）小－M（2）小－M＋4【解析】（1）设x∈[－b，－a]，则－x∈[a，b]，∴f（－x）≤M且存在x0∈[a，b]，使f（x0）＝M.∵f（x）为奇函数，∴－f（x）≤M，f（x）≥－M，且存在－x0∈[－b，－a]，使f（－x0）＝－M.∴f（x）在[－b，－a]上有最小值－M.（2）由（1）知，f（x）在[a，b]上有最大值M－2时，f（x）在[－b，－a]上有最小值－M＋2.∴f（x）＋2在[－b，－a]上有最小值－M＋4.解答6.设定义在（－1，1）上的奇函数f（x）在[0，1）上单调递增，且有f（1－m）＋f＜0，求实数m的取值范围.【答案】由于函数f（x）的定义域为（－1，1），则有解得0＜m＜.又f（1－m）＋f＜0，所以f（1－m）＜－f.而函数f（x）为奇函数，则有f（1－m）＜f.因为函数f（x）是奇函数，且在[0，1）上单调递增，所以函数f（x）在定义域（－1，1）上单调递增，则有1－m＜2m－，解得m＞，故实数m的取值范围为.7.已知定义在R上的奇函数f（x），当x>0时，f（x）＝－x2＋2x.（1）求函数f（x）在R上的解析式；（2）若函数f（x）在区间[－1，a－2]上单调递增，求实数a的取值范围.【答案】（1）设x<0，则－x>0，f（－x）＝－（－x）2＋2（－x）＝－x2－2x.又f（x）为奇函数，所以f（－x）＝－f（x）.于是当x<0时f（x）＝x2＋2x，又因为f（x）为奇函数，所以f（0）＝0，所以f（x）＝（2）要使f（x）在[－1，a－2]上单调递增，结合f（x）的图象知所以1<a≤3，故实数a的取值范围是（1，3].8.定义在R上的函数y＝f（x），f（0）≠0，当x>0时，f（x）>1，且对任意的a，b∈R，有f（a＋b）＝f（a）f（b）.（1）求证：f（0）＝1；（2）求证：对任意的x∈R，恒有f（x）>0；（3）求证：f（x）是R上的增函数.【答案】（1）令a＝b＝0，则f（0）＝[f（0）]2，∵f（0）≠0，∴f（0）＝1.（2）令a＝x，b＝－x，则f（0）＝f（x）f（－x），∴f（－x）＝.由已知当x>0时，f（x）>1>0，则当x<0时，－x>0，f（－x）>0，∴f（－x）＝>0，又当x＝0时，f（0）＝1>0，∴对任意x∈R，f（x）>0.（3）任取x2>x1，则f（x2）>0，f（x1）>0，x2－x1>0，∴＝（（x 2）·f（－x1）＝f（x2－x1）>1，∴f（x2）>f（x1），∴f（x）在R上是增函数.9.若f（x）是定义在（0，＋∞）上的增函数，且对一切x，y>0，满足f（）＝f（x）－f（y）.（1）求f（1）的值；（2）若f（6）＝1，解不等式f（x＋3）－f（）<2.【答案】（1）在f（）＝f（x）－f（y）中，令x＝y＝1，则有f（1）＝f（1）－f（1），∴f（1）＝0.（2）∵f（6）＝1，∴f（x＋3）－f（）<2＝f（6）＋f（6），∴f（3x＋9）－f（6）<f（6）.即f（）<f（6）.∵f（x）是定义在（0，＋∞）上的增函数，∴解得－3<x<9，即不等式的解集为（－3，9）.10.定义在（0，＋∞）上的函数f（x）满足f（mn）＝f（m）＋f（n）（m，n>0），且当x>1时，f（x）>0. （1）求f（1）的值；（2）求证f＝f（m）－f（n）；（3）求证f（x）在（0，＋∞）上是增函数；（4）若f（2）＝1，解不等式f（x＋2）－f（2x）>2；（5）比较f与的大小.【答案】（1）令m＝n＝1，由条件得f（1）＝f（1）＋f（1），∴f（1）＝0.（2）f（m）＝f（·n）＝f（）＋f（n），即f（）＝f（m）－f（n）.（3）任取x1，x2∈（0，＋∞），且x1<x2，则>1.由（2）得f（x2）－f（x1）＝f（）>0，即f（x2）>f（x1）.∴f（x）在（0，＋∞）上是增函数.（4）由于f（2）＝1，∴2＝f（2）＋f（2）＝f（4），∴f（x＋2）－f（2x）>2⇒f（x＋2）>f（2x）＋f（4）⇒f（x＋2）>f（8x）.又f（x）在（0，＋∞）上为增函数，∴解得0<x<.故不等式f（x＋2）－f（2x）>2的解集为{x|0<x<}.（5）∵f（mn）＝f（m）＋f（n），∴＝f（mn），f（）＝[f（）＋f（）]＝f[（）2]，∵（）2－mn＝（）2≥0，∴（）2≥mn（当且仅当m＝n时取等号），又f（x）在（0，＋∞）上是增函数，∴f[（）2]≥f（mn）.∴f（）≥11.若函数f（x）的定义域是R，且对任意x，y∈R，都有f（x＋y）＝f（x）＋f（y）成立.（1）试判断f（x）的奇偶性；（2）若f（8）＝4，求f（－）的值.【答案】（1）在f（x＋y）＝f（x）＋f（y）中，令x＝y＝0，得f（0＋0）＝f（0）＋f（0），∴f（0）＝0.再令y＝－x，得f（x－x）＝f（x）＋f（－x），即f（x）＋f（－x）＝0，∴f（－x）＝－f（x），故f （x）为奇函数.（2）令y＝x，由条件f（x＋y）＝f（x）＋f（y），得f（2x）＝2f（x）.由此可得f（8）＝2·f（4）＝2·2f（2）＝2·2·2f（1）＝24·f＝4，∴f＝，∴f＝－f＝－.12.已知f（x）是定义在R上的不恒为0的函数，且对于任意的x，y∈R，有f（x·y）＝xf（y）＋yf（x）. （1）求f（0），f（1）的值；（2）判断函数f（x）的奇偶性，并证明你的结论.【答案】（1）∵f（x·y）＝xf（y）＋yf（x），令x＝y＝0，得f（0）＝0＋0＝0，即f（0）＝0.令x＝y＝1，得f（1）＝1·f（1）＋1·f（1），∴f（1）＝0.（2）∵f（1）＝f[（－1）·（－1）]＝（－1）f（－1）＋（－1）f（－1）＝0，∴f（－1）＝0.对任意的x∈R，f（－x）＝f[（－1）·x]＝（－1）f（x）＋xf（－1）＝－f（x），∴f（x）是奇函数.13.已知函数f（x）对任意实数x，y恒有f（x＋y）＝f（x）＋f（y），且当x>0时，f（x）<0，又f（1）＝－2.（1）判断f（x）的奇偶性；（2）求证：f（x）是R上的减函数；（3）求f（x）在区间[－3，3]上的值域；（4）若对任意x∈R，不等式f（ax2）－2f（x）<f（x）＋4恒成立，求a的取值范围.【答案】（1）取x＝y＝0，则f（0＋0）＝2f（0），∴f（0）＝0.取y＝－x，则f（x－x）＝f（x）＋f（－x），∴f（－x）＝－f（x）对任意x∈R恒成立，∴f（x）为奇函数.（2）任取x1，x2∈（－∞，＋∞），且x1<x2，则x2－x1>0，f（x2）＋f（－x1）＝f（x2－x1）<0，∴f（x2）<－f（－x1）.又f（x）为奇函数，∴f（x1）>f（x2），∴f（x）是R上的减函数.（3）由（2）知f（x）在R上为减函数，∴对任意x∈[－3，3]，恒有f（3）≤f（x）≤f（－3），∵f（3）＝f（2）＋f（1）＝f（1）＋f（1）＋f（1）＝－2×3＝－6，∴f（－3）＝－f（3）＝6，f（x）在[－3，3]上的值域为[－6，6].（4）f（x）为奇函数，整理原式得f（ax2）＋f（－2x）<f（x）＋f（－2），则f（ax2－2x）<f（x－2），∵f（x）在（－∞，＋∞）上是减函数，∴ax2－2x>x－2，当a＝0时，－2x>x－2在R上不是恒成立，与题意矛盾；当a>0时，ax2－2x－x＋2>0，要使不等式恒成立，则Δ＝9－8a<0，即a>；当a<0时，ax2－3x＋2>0在R上不是恒成立，不合题意.综上所述，a的取值范围为（，＋∞）.14.设f（x）是定义在[－1，1]上的奇函数，且对任意a，b∈[－1，1]，当a＋b≠0时，都有>0.（1）若a>b，试比较f（a）与f（b）的大小；（2）解不等式f（x－）<f（x－）；（3）如果g（x）＝f（x－c）和h（x）＝f（x－c2）这两个函数的定义域的交集是空集，求c的取值范围. 【答案】（1）任取－1≤x 1<x2≤1，则f（x2）－f（x1）＝f（x2）＋f（－x1）＝·（x2－x1）>0，∴f（x2）>f（x1），∴f（x）在[－1，1]上是增函数.∵a，b∈[－1，1]，且a>b，∴f（a）>f（b）.（2）∵f（x）是[－1，1]上的增函数，∴由不等式f（x－）<f（x－）得解得∴－≤x≤，∴原不等式的解集是{x|－≤x≤}.（3）设函数g（x），h（x）的定义域分别是P和Q，则P＝{x|－1≤x－c≤1}＝{x|c－1≤x≤c＋1}，Q＝{x|－1≤x－c2≤1}＝{x|c2－1≤x≤c2＋1}于是P∩Q＝∅的条件是c－1＞c2＋1（无解），或c＋1＜c2－1，即c2－c－2＞0，解得c＞2或c＜－1.故c的取值范围是{c|c＞2或c＜－1}.15.已知函数f（x）是定义在区间[－1，1]上的奇函数，且f（1）＝1，若对于任意的m，n∈[－1，1]有>0. （1）判断函数的单调性（不要求证明）；（2）解不等式f<f（1－x）；（3）若f（x）≤－2at＋2对于任意的x∈[－1，1]，a∈[－1，1]恒成立，求实数t的取值范围.【答案】（1）函数f（x）在区间[－1，1]上是增函数.（2）由（1）知函数f（x）在区间[－1，1]上是增函数，由f<f（1－x），得解得0≤x<.所以不等式f<f（1－x）的解集为.（3）因为函数f（x）在区间[－1，1]上是增函数，且f（1）＝1，要使得对于任意的x∈[－1，1]，a∈[－1，1]都有f（x）≤－2at＋2恒成立，只需对任意的a∈[－1，1]，－2at＋2≥1恒成立.令y＝－2at＋1，此时y可以看作a的一次函数，且在a∈[－1，1]时，y≥0恒成立.因此只需解得－≤t≤，所以实数t的取值范围为.16.已知函数f（x）＝x－.（1）判断函数f（x）的奇偶性，并加以证明；（2）用定义证明函数f（x）在区间[1，＋∞）上为增函数；（3）若函数f（x）在区间[2，a]上的最大值与最小值之和不小于，求a的取值范围. 【答案】（1）函数f（x）＝x－是奇函数，∵函数f（x）＝x－的定义域为（－∞，0）∪（0，＋∞），在x轴上关于原点对称，且f（－x）＝－x－＝－（x－）＝－f（x），∴函数f（x）＝x－是奇函数.（2）证明设任意实数x1，x2∈[1，＋∞），且x1<x2，则f（x1）－f（x2）＝（x1－）－（x2－）＝，∵1≤x1<x2，∴x1－x2<0，x1x2>0，x1x2＋1>0，∴<0，∴f（x1）－f（x2）<0，即f（x1）<f（x2），∴函数f（x）在区间[1，＋∞）上为增函数.（3）∵[2，a]⊆[1，＋∞），∴函数f（x）在区间[2，a]上也为增函数.∴f（x）max＝f（a）＝a－，f（x）min＝f（2）＝，若函数f（x）在区间[2，a]上的最大值与最小值之和不小于，则a－＋≥－，∴a≥4，∴a的取值范围是[4，＋∞）.17.已知函数f（x）＝x2＋2.（1）求函数f（x）的定义域和值域；（2）判断函数f（x）的奇偶性和单调性；（3）求函数f（x）在区间（－1，2]上的最大值和最小值.【答案】（1）定义域为R，值域为{y|y≥2}.（2）因为f（x）定义域关于原点对称，且f（－x）＝f（x），所以f（x）为偶函数；在区间（0，＋∞）上单调递增，在区间（－∞，0]上单调递减.（3）f（x）的对称轴为x＝0，f（x）min＝f（0）＝2，f（－1）＝3，f（2）＝6，所以f（x）max＝6.18.已知函数f（x）＝ax2＋bx＋1（a，b均为实数），x∈R，F（x）＝（1）若f（－1）＝0，且函数f（x）的值域为[0，＋∞），求F（x）的解析式；（2）在（1）的条件下，当x∈[－2，2]时，g（x）＝f（x）－kx是单调函数，求实数k的取值范围；（3）设mn<0，m＋n>0，a>0，且f（x）为偶函数，判断F（m）＋F（n）是否大于零，并说明理由. 【答案】（1）∵若f（－1）＝0，∴a－b＋1＝0，①又∵函数f（x）的值域为[0，＋∞），∴a≠0.由y＝a（x＋）2＋，知＝0，即4a－b2＝0.②解①②，得a＝1，b＝2.∴f（x）＝x2＋2x＋1＝（x＋1）2.∴F（x）＝（2）由（1）得g（x）＝f（x）－kx＝x2＋2x＋1－kx＝x2＋（2－k）x＋1＝（x＋）2＋1－. 又∵当x∈[－2，2]时，g（x）＝f（x）－kx是单调函数.∴≤－2或≥2，即k≤－2或k≥6，故实数k的取值范围为（－∞，－2]∪[6，＋∞）.（3）大于零，理由如下：∵f（x）为偶函数，∴f（x）＝ax2＋1，∴F（x）＝不妨设m>n，则n<0.由m＋n>0，得m>－n>0，∴|m|>|－n|，又a>0，∴F（m）＋F（n）＝f（m）－f（n）＝（am2＋1）－（an2＋1）＝a（m2－n2）>0，∴F（m）＋F（n）大于零.19.已知函数f（x）＝－（常数a>0）.（1）设m·n>0，证明：函数f（x）在[m，n]上单调递增；（2）设0<m<n，且f（x）的定义域和值域都是[m，n]，求n－m的最大值.【答案】（1）证略；（2）因为f（x）在[m，n]上单调递增，f（x）的定义域、值域都是[m，n]⇔f（m）＝m，f（n）＝n，即m，n是方程f（x）＝x的两个根，即方程－＝x有两个正根.整理得a2x2－（2a2＋a）x＋1＝0，所以n－m＝＝，令＝t（t>0），n－m＝＝，所以当t＝时，n－m最大值为.20.已知函数y＝f（x）是定义在R上的奇函数，且当x≥0时，f（x）＝－x2＋ax.（1）若a＝－2，求函数f（x）的解析式；（2）若函数f（x）为R上的单调减函数，①求a的取值范围；②若对任意实数m，f（m－1）＋f（m2＋t）<0恒成立，求实数t的取值范围.【答案】（1）当x<0时，－x>0，又∵f（x）为奇函数，且a＝－2，∴当x<0时，f（x）＝－f（－x）＝x2－2x，∴f（x）＝（2）①当a≤0时，对称轴x＝≤0，∴f（x）＝－x2＋ax在[0，＋∞）上单调递减，由于奇函数在关于原点对称的区间上单调性相同，∴f（x）在（－∞，0）上单调递减，又在（－∞，0）上f（x）>0，在（0，＋∞）上f（x）<0，∴当a≤0时，f（x）为R上的单调减函数.当a>0时，f（x）在上单调递增，在上单调递减，不合题意.∴函数f（x）为单调减函数时，a的取值范围为a≤0.②∵f（m－1）＋f（m2＋t）<0，∴f（m－1）<－f（m2＋t），又∵f（x）是奇函数，∴f（m－1）<f（－t－m2），又∵f（x）为R上的单调减函数，∴m－1>－t－m2恒成立，∴t>－m2－m＋1＝－2＋对任意实数m恒成立，∴t>.即t的取值范围是.21.已知二次函数f（x）的最小值为1，且f（0）＝f（2）＝3.（1）求f（x）的解析式；（2）若f（x）在区间[3a，a＋1]上不单调，求实数a的取值范围；（3）在区间[－1，1]上，y＝f（x）的图象恒在y＝2x＋2m＋1的图象上方，试确定实数m的取值范围. 【答案】（1）由已知，得函数f（x）图象的对称轴为直线x＝1，可设f（x）＝a（x－1）2＋1，由f（0）＝3，得a＝2，故f（x）＝2x2－4x＋3.（2）要使函数f（x）在区间[3a，a＋1]上不单调，则3a<1<a＋1，解得0<a<.（3）由已知y＝f（x）的图象恒在y＝2x＋2m＋1的图象上方，得2x2－4x＋3>2x＋2m＋1恒成立，化简得x2－3x＋1－m>0恒成立，其中－1≤x≤1.设g（x）＝x2－3x＋1－m，则只要g（x）min>0即可，而g（x）min ＝g（1）＝－1－m，由－1－m>0，得m<－1.22.已知f（x）是定义在[－1，1]上的奇函数，且f（1）＝1，若a，b∈[－1，1]，a＋b≠0时，有>0成立.（1）判断f（x）在[－1，1]上的单调性；（2）解不等式f（x＋）<f（）；（3）若f（x）≤m2－2am＋1对所有的a∈[－1，1]恒成立，求实数m的取值范围. 【答案】（1）任取x1，x2∈[－1，1]，且x1<x2，则－x2∈[－1，1].∵f（x）为奇函数，∴f（x 1）－f（x2）＝f（x1）＋f（－x2）＝·（x1－x2）.由已知得>0，又x1－x2<0，∴f（x1）－f（x2）<0，即f（x1）<f（x2），∴f（x）在[－1，1]上单调递增.（2）∵f（x）在[－1，1]上单调递增，∴结合不等式的性质及二次函数的图象，得－≤x＜－1.故原不等式的解集为{x|－≤x＜－1}.（3）∵f（1）＝1，且f（x）在[－1，1]上单调递增，∴在[－1，1]上，f（x）≤1.问题转化为m2－2am＋1≥1，即m2－2am≥0，对a∈[－1，1]成立.设g（a）＝－2m·a＋m2，①若m＝0，则g（a）＝0≥0，对a∈[－1，1]恒成立.②若m≠0，则g（a）为关于a的一次函数，若g（a）≥0对a∈[－1，1]恒成立，必须有g（－1）≥0，且g（1）≥0，即结合相应各函数图象，得m≤－2或m≥2.综上所述，实数m的取值范围是（－∞，－2]∪{0}∪[2，＋∞）.。

2004－2005学年度上学期 高一数学同步测试（7）—函数的单调性、奇偶性一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内。

1．设()f x 为定义在R 上的奇函数，满足()()2f x f x +=-，当01x ≤≤时()f x x =，则()7.5f 等于 （ ）A ．0.5B ．0.5-C ．1.5D ． 1.5-2．设()f x 是定义在R 上的偶函数,且在(－∞,0)上是增函数,则()2f -与()223f a a -+（a R ∈）的大小关系是 （ ）A ．()2f -<()223f a a -+B ．()2f -≥()223f a a -+C ．()2f ->()223f aa -+D ．与a 的取值无关3．若函数()f x 为奇函数，且当0x >时，()1f x x =-，则当0x <时，有 （ ）A ．()f x 0>B ．()f x 0<C ．()f x ()f x -≤0D ．()f x －()f x -0> 4．已知函数()()2212f x x a x =+-+在区间(]4,∞-上是减函数，则实数a 的取值范围是（ ）A ．a ≤3B ．a ≥－3C ．a ≤5D ．a ≥35．已知函数()()0f x x a x a a =+--≠，()(1g x x =-()()()2200x x x h x x x x ⎧-+>⎪=⎨+≤⎪⎩，则 ()()(),,f x g x h x 的奇偶性依次为 （ ）A ．奇函数，偶函数，奇函数B ．奇函数，奇函数，偶函数C ．奇函数，奇函数，奇函数D ．奇函数，非奇非偶函数，奇函数6．已知函数()()221,f x x ax b b a b R =-++-+∈对任意实数x 都有()()11f x f x -=+ 成立，若当[]1,1x ∈-时，()0f x >恒成立,则b 的取值范围是 （ ）A ．10b -<<B ．2b >C ．12b b <->或D ．不能确定7．已知函数()()2223f x x x =+-，那么（ ）A ．()y f x =在区间[]1,1-上是增函数B ．()y f x =在区间(],1-∞-上是增函数C ．()y f x =在区间[]1,1-上是减函数D ．()y f x =在区间(],1-∞-上是减函数8．函数()y f x =在()0,2上是增函数，函数()2y f x =+是偶函数，则下列结论中正确的 是（ ）A ．()57122f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭B ．()57122f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭C ．()75122f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭D ．()75122f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭9．设函数()f x 是R 上的奇函数，且当0x >时，()23x f x =-，则()2f -等于（ ）A ．1-B ．114C ．1D ．114-10．函数()y f x =与()y g x =的定义域相同，且对定义域中任何x 有()()0f x f x -+=，()()1g x g x -=，若()1g x =的解集是{}0，则函数()()()()21f x F x f xg x =+-是（ ） A ．奇函数 B ．偶函数C ．既奇又偶函数D ．非奇非偶函数二、填空题：请把答案填在题中横线上。

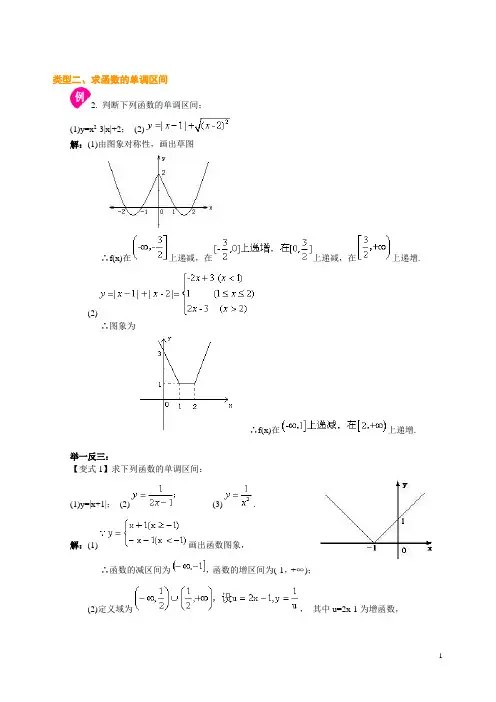
类型二、求函数的单调区间2. 判断下列函数的单调区间；(1)y=x2-3|x|+2；(2)解：(1)由图象对称性，画出草图∴f(x)在上递减，在上递减，在上递增.(2)∴图象为∴f(x)在上递增.举一反三：【变式1】求下列函数的单调区间：(1)y=|x+1|；(2)(3).解：(1)画出函数图象，∴函数的减区间为，函数的增区间为(-1，+∞)；(2)定义域为，其中u=2x-1为增函数，在(-∞，0)与(0，+∞)为减函数，则上为减函数；(3)定义域为(-∞，0)∪(0，+∞)，单调增区间为：(-∞，0)，单调减区间为(0，+∞). 类型三、单调性的应用(比较函数值的大小，求函数值域，求函数的最大值或最小值)3. 已知函数f(x)在(0，+∞)上是减函数，比较f(a2-a+1)与的大小.解：又f(x)在(0，+∞)上是减函数，则.4. 求下列函数值域：(1)；1)x∈[5，10]；2)x∈(-3，-2)∪(-2，1)；(2)y=x2-2x+3；1)x∈[-1，1]；2)x∈[-2，2].1)f(x)在[5，10]上单增，；2)；(2)画出草图1)y∈[f(1)，f(-1)]即[2，6]；2).举一反三：【变式1】已知函数.(1)判断函数f(x)的单调区间；(2)当x∈[1，3]时，求函数f(x)的值域.解：(1)上单调递增，在上单调递增；(2)故函数f(x)在[1，3]上单调递增∴x=1时f(x)有最小值，f(1)=-2 x=3时f(x)有最大值∴x∈[1，3]时f(x)的值域为.5. 已知二次函数f(x)=x2-(a-1)x+5在区间上是增函数，求：(1)实数a的取值范围；(2)f(2)的取值范围.解：(1)∵对称轴是决定f(x)单调性的关键，联系图象可知只需；(2)∵f(2)=22-2(a-1)+5=-2a+11又∵a≤2，∴-2a≥-4∴f(2)=-2a+11≥-4+11=7 .举一反三：【变式1】（2011 北京理13）已知函数，若关于x的方程有两个不同的实根，则实数k的取值范围是________.解：单调递减且值域(0,1]，单调递增且值域为，由图象知，若有两个不同的实根，则实数k的取值范围是（0,1）.类型四、判断函数的奇偶性6. 判断下列函数的奇偶性：(1)(2)(3)f(x)=x2-4|x|+3 (4)f(x)=|x+3|-|x-3| (5)(6(7)解：(1)∵f(x)的定义域为，不关于原点对称，因此f(x)为非奇非偶函数；(2)∵x-1≥0，∴f(x)定义域不关于原点对称，∴f(x)为非奇非偶函数；(3)对任意x∈R，都有-x∈R，且f(-x)=x2-4|x|+3=f(x)，则f(x)=x2-4|x|+3为偶函数；(4)∵x∈R，f(-x)=|-x+3|-|-x-3|=|x-3|-|x+3|=-f(x)，∴f(x)为奇函数；(5)，∴f(x)为奇函数；(6)∵x∈R，f(x)=-x|x|+x ∴f(-x)=-(-x)|-x|+(-x)=x|x|-x=-f(x)，∴f(x)为奇函数；(7)，∴f(x)为奇函数.举一反三：【变式1】判断下列函数的奇偶性：(1)；(2)f(x)=|x+1|-|x-1|；(3)f(x)=x2+x+1；(4).思路点拨：利用函数奇偶性的定义进行判断.解：(1)；(2)f(-x)=|-x+1|-|-x-1|=-(|x+1|-|x-1|)=-f(x) ∴f(x)为奇函数；(3)f(-x)=(-x)2+(-x)+1=x2-x+1∴f(-x)≠-f(x)且f(-x)≠f(x) ∴f(x)为非奇非偶函数；(4)任取x>0则-x<0，∴f(-x)=(-x)2+2(-x)-1=x2-2x-1=-(-x2+2x+1)=-f(x)任取x<0，则-x>0 f(-x)=-(-x)2+2(-x)+1=-x2-2x+1=-(x2+2x-1)=-f(x)x=0时，f(0)=-f(0) ∴x∈R时，f(-x)=-f(x) ∴f(x)为奇函数.类型五、函数奇偶性的应用(求值，求解析式，与单调性结合)7．已知f(x)=x5+ax3-bx-8，且f(-2)=10，求f(2).解：法一：∵f(-2)=(-2)5+(-2)3a-(-2)b-8=-32-8a+2b-8=-40-8a+2b=10∴8a-2b=-50 ∴f(2)=25+23a-2b-8=8a-2b+24=-50+24=-26法二：令g(x)=f(x)+8易证g(x)为奇函数∴g(-2)=-g(2) ∴f(-2)+8=-f(2)-8∴f(2)=-f(-2)-16=-10-16=-26.举一反三：【变式1】（2011 湖南文12）已知为奇函数，，则为：解：，又为奇函数，所以．8. f(x)是定义在R上的奇函数，且当x<0时，f(x)=x2-x，求当x≥0时，f(x)的解析式，并画出函数图象.解：∵奇函数图象关于原点对称，∴x>0时，-y=(-x)2-(-x)即y=-x2-x又f(0)=0，，如图9．设定义在[-3，3]上的偶函数f(x)在[0，3]上是单调递增，当f(a-1)<f(a)时，求a的取值范围.解：∵f(a-1)<f(a) ∴f(|a-1|)<f(|a|)而|a-1|，|a|∈[0，3].类型六、综合问题10．定义在R上的奇函数f(x)为增函数，偶函数g(x)在区间的图象与f(x)的图象重合，设a>b>0，给出下列不等式，其中成立的是_________.①f(b)-f(-a)>g(a)-g(-b)；②f(b)-f(-a)<g(a)-g(-b)；③f(a)-f(-b)>g(b)-g(-a)；④f(a)-f(-b)<g(b)-g(-a).答案：①③.11. 求下列函数的值域：(1)(2)(3)思路点拨：(1)中函数为二次函数开方，可先求出二次函数值域；(2)由单调性求值域，此题也可换元解决；(3)单调性无法确定，经换元后将之转化为熟悉二次函数情形，问题得到解决，需注意此时t 的范围.解：(1)；(2)经观察知，，；(3)令.12. 已知函数f(x)=x2-2ax+a2-1.(1)若函数f(x)在区间[0，2]上是单调的，求实数a的取值范围；(2)当x∈[-1，1]时，求函数f(x)的最小值g(a)，并画出最小值函数y=g(a)的图象.解：(1)∵f(x)=(x-a)2-1 ∴a≤0或a≥2(2)1°当a<-1时，如图1，g(a)=f(-1)=a2+2a2°当-1≤a≤1时，如图2，g(a)=f(a)=-13°当a>1时，如图3，g(a)=f(1)=a2-2a，如图13. 已知函数f(x)在定义域(0，+∞)上为增函数，f(2)=1，且定义域上任意x、y都满足f(xy)=f(x)+f(y)，解不等式：f(x)+f(x-2)≤3.解：令x=2，y=2，∴f(2×2)=f(2)+f(2)=2 ∴f(4)=2再令x=4，y=2，∴f(4×2)=f(4)+f(2)=2+1=3 ∴f(8)=3∴f(x)+f(x-2)≤3可转化为：f[x(x-2)]≤f(8).14. 判断函数上的单调性，并证明.证明：任取0<x1<x2，∵0<x1<x2，∴x1-x2<0，x1·x2>0(1)当时0<x1·x2<1，∴x1·x2-1<0∴f(x1)-f(x2)>0即f(x1)>f(x2)上是减函数.(2)当x1，x2∈(1，+∞)时，上是增函数.15. 设a为实数，函数f(x)=x2+|x-a|+1，x∈R，试讨论f(x)的奇偶性，并求f(x)的最小值. 解：当a=0时，f(x)=x2+|x|+1，此时函数为偶函数；当a≠0时，f(x)=x2+|x-a|+1，为非奇非偶函数.(1)当x≥a时，[1]且[2]上单调递增，上的最小值为f(a)=a2+1.(2)当x<a时，[1]上单调递减，上的最小值为f(a)=a2+1[2]上的最小值为综上：.。

函数的单调性、奇偶性与周期性基础知识一、函数的单调性 1． 单调性概念如果函数y= f (x )对于定义域I 内某个区间上的任意两个自变量的值x 1、、x 2，当x 1、<x 2时， ①都有f (x 1)< f (x 2)，则称f (x )在这个区间上是增函数（或单调递增），而这个区间称函数的一个单调递增区间 ；②都有f (x 1)> f (x 2)，则称f (x )在这个区间上是减函数（或单调递减），而这个区间称函数的一个单调减区间.注意，若函数f (x )在整个定义域I 内只有唯一的一个单调（递增或递减）区间，则f (x )称单调函数.2． 函数的单调性与其导函数的正负有如下关系：在某个区间(,)a b 内，如果/()0f x >，那么函数()y f x =在这个区间内是单调递增； 如果/()0f x <，那么函数()y f x =在这个区间内是单调递减。

二、函数的奇偶性 3．奇偶性概念如果对于函数f (x )定义域内的任意x ，①都有f (－x )=－f (x )，则称f (x )为奇函数；②都有f (－x )= f (x )，则称f (x )为偶函数；③如果函数f (x )不具有上述性质，则f (x )不具有奇偶性.④如果函数同时具有上述两条性质，则f (x )既是奇函数，又是偶函数。

注意：函数f (x )具有奇偶性的必要条件是其定义域关于原点对称。

4．性质：一个函数是奇函数的充要条件是它的图象关于原点对称；一个函数是偶函数的充要条件是它的图象关于y 轴对称。

5．函数f (x )为奇函数，且在0x =处有定义，则(0)0f =三、函数的周期性 6．周期性概念如果存在一个非零常数T ，使得对于函数定义域内的任意x ，都有f (x+T )= f (x )，则称f (x )为周期函数。

T 是f (x )的一个周期。

若f (x )的周期中，存在一个最小的正数，则称它为f (x )的最小正周期。

函数的单调性和奇偶性例1 (1)画出函数y= -X2+2 I x | +3的图像，并指出函数的单调区间.解：函数图像如下图所示，当X>0时，y = -X2+2X+3 = - (X-1 ) 2+4;当X V 0 时，y = -X2-2X+3 = - ( X+1) 2 +4 .在(4, -1 ］和［0, 1 ］上，函数是增函数：在［-1 , 0］和［1 , +〜上，函数是减函数.评析函数单调性是对某个区间而言的，对于单独一个点没有增减变化，所以对于区间端点只要函数有意义，都可以带上.(2)已知函数f ( X)=X2+2 (a-1) X+2在区间(亠,4］上是减函数，求实数a的取值范围.分析要充分运用函数的单调性是以对称轴为界线这一特征.解：f ( X ) = X2+2 (a-1) X+2 =［X+ (a-1)］2- (a-1) 2+2，此二次函数的对称轴是X = 1-a.因为在区间(-a, 1-a］上f (x)是单调递减的，若使f (X)在(4, 4］上单调递减，对称轴X= 1-a必须在X=4的右侧或与其重合，即1-a>4 a<3.评析这是涉及逆向思维的问题，即已知函数的单调性，求字母参数范围，要注意利用数形结合.例2判断下列函数的奇偶性：(1) f ( X)=-2 f ( X)=(X-1 ) •1 .解：(1) f (x)的定义域为R.因为f ( -X )=| -X+1 | - | -X-1 |=| X-1 | - | X+1 | = -f (X).所以f ( X )为奇函数.(2) f ( X)的定义域为｛X | -1WV 1｝，不关于原点对称.所以 f ( X )既不是奇函数，也不是偶函数.评析用定义判断函数的奇偶性的步骤与方法如下：(1 )求函数的定义域，并考查定义域是否关于原点对称.(2)计算f (-x)，并与f ( x)比较，判断f (-x) = f ( x)或f (-x) = -f (x)之一是否成立.f(-x)与-f (x)的关系并不明确时，可考查f (-x) ± (x)= 0是否成立，从而判断函数的奇偶性.例3已知函数f (x)= 1 +「.(1)判断f (x)的奇偶性.(2)确定f (x)在(-a, 0) 上是增函数还是减函数？在区间(0, +8)上呢？证明你的结论. 解：因为f (x)的定义域为R,又] 1f ( -x )= j 亠- J = j ： ... = f (x),所以f (x)为偶函数.(2) f ( 乂)在(-8, 0) 上是增函数，由于f (x)为偶函数，所以f (x)在(0, +8)上为减函数. 其证明：取X i V X2V0,] ] £_彳(心-珂)(乃+可)f (x i) -f (X2)= J「- j = I—「= r — h .因为x1v X2v 0,所以X2-X1> 0, X什X2< 0 ,2 2x 1+1 > 0, x 2+1 > 0,得 f (X1) -f (X2)V 0,即 f (X1)V f (X2).所以f ( X )在(-8, 0) 上为增函数.评析奇函数在(a,b)上的单调性与在(-b,-a)上的单调性相同，偶函数在(a,b)与(-b,-a)的单调性相反.1例4已知y=f (x)是奇函数，它在(0, +8)上是增函数，且 f (x)v 0，试问F (x)= 在(-8, 0)上是增函数还是减函数？证明你的结论.1 ]分析根据函数的增减性的定义，可以任取X1V X2< 0，进而判定F( X1)-F( X2)==「：• ' ■■-的正负•为此，需分别判定 f (X1)、f (X2)与f (X2)的正负，而这可以从已条件中推出.解：任取X1、X2^( -8, 0)且X1< X2，则有-X1 > -X2> 0 .T y = f (x)在(0, +8)上是增函数，且f (X)< 0,二 f (-x2)< f (-x1)< 0. ①又••• f (x)是奇函数，• •• f ( -X2)= -f (X2), f ( -X i)= -f (X i) ②由①、②得 f ( X2)> f (X i)> 0 •于是F (x i) -F (X2)= * '…一 >0，即F (X i)> F (X2),1所以F ( X)=在(-m, 0)上是减函数.评析本题最容易发生的错误，是受已知条件的影响，一开始就在( 0 , +8)内任取X i< X2，展开证明.这样就不能保证-X i , -X2,在(-8, 0)内的任意性而导致错误.避免错误的方法是：要明确证明的目标，有针对性地展开证明活动.ax例5讨论函数f (x)= 1-/ (a^0在区间(-1, 1)内的单调性.分析根据函数的单调性定义求解.解：设-1 < x1< x2< 1,贝Uf (X i) -f (X2)= • 一' 1 - _以帀―X?)(l+可巧)=''-'l'lT x1, x2€( -1, 1),且x1< x2 ,•- X1-X2< 0, 1+X1X2> 0,(1-x21)( 1-X22)> 0于是，当a> 0 时，f (X1)< f (X2);当a< 0 时，f (X1)> f (X2).故当a> 0时，函数在(-1, 1)上是增函数；当a< 0时，函数在(-1, 1) 上为减函数.评析根据定义讨论(或证明)函数的单调性的一般步骤是：(1 )设x1、X2是给定区间内任意两个值，且X1< X2；(2)作差f (X1) -f (X2)，并将此差式变形；(3)判断f (X1) -f (X2)的正负，从而确定函数的单调性.例6求证：f (x) = x+ .■. ( k> 0)在区间(0, k］上单调递减.解：设0 < X1 < X2 < k 贝Uf (X1) -f (X2)= X<|+ -X2---■ 0 V x1< X2w k2二X i-X2< 0, 0< X i X2< k ,••• f ( X1) -f (x2)> 0••• f ( X1)> f ( X2),• f ( X) = X+一中(0, k］上是减函数.评析函数f ( X)在给定区间上的单调性反映了函数 f (X)在区间上函数值的变化趋势，是函数在区间上的整体性质.因此，若要证明 f (X)在］a,b］上是增函数(减函数)，就必须证明对于区间［a,b］上任意两点X1 , X2,当X1< X2 时，都有不等式 f ( X1)< f ( X2)( f(X1)> f ( X2))类似可以证明:函数f (X)= X+ 二(k > 0)在区间［k, +8］上是增函数.例7判断函数f (x)= 工-'二的奇偶性.分析确定函数的定义域后可脱去绝对值符号.)—2 01^ - 2| + x 0解：由II 1得函数的定义域为］-1, 1］.这时，丨X-2 | = 2-X.• f ( X)= - ,• f (-X) = - = - = f (X)是偶函数，不是奇函数.且注意到f ( X)不恒为零，从而可知，f ( X )评析由于函数解析式中的绝对值使得所给函数不像具有奇偶性，若不作深入思考，便会作出其非奇非偶的判断.但隐含条件(定义域)被揭示之后，函数的奇偶性就非常明显了.这样看来，解题中先确定函数的定义域不仅可以避免错误，而且有时还可以避开讨论，简化解题过程.函数奇偶性练习、选择题1 .已知函数f (X) = ax2+ bx+ c (a^ 0)是偶函数，那么g (X) = ax3+ bx2+ ex ( )已知函数f (x ) = ax + bx + 3a + b 是偶函数，且其定义域为］a — 1, 2a ］，则(2义在R 上的奇函数，当x >0时，f (x ) = x — 2x ,则f (x )在R 上的表达式是()二、填空题X —2 —2-「的奇偶性为,1-x 2(填奇函数或偶函数)2若y =( m — 1) x + 2mx+ 3是偶函数，则m =1已知f (x )是偶函数，g (X )是奇函数，若 f(x) ■ g (x):X 一 1 则f (x )的解析式为 10•已知函数f( x )为偶函数，且其图象与x 轴有四个交点，贝y 方程f( x )= 0的所有实根之和为 三、解答题 11.设定义在［—2, 2］上的偶函数 f (x )在区间［0, 2］上单调递减，若f (1 — n ) v f (m ),求实 数m 的取值范围. 12.已知函数f (x )满足f (x + y ) + f (x — y )= 2f (x ) • f (y ) (x R, y R ),且 f (0)工 0, 试证f (x )是偶函数. 13.已知函数f (x )是奇函数，且当x >0时，f (x )= x 3 + 2x 2— 1，求f (x )在R 上的表达式.A .奇函数B .偶函数 C.既奇又偶函数D.非奇非偶函数A . a — — , b = 03B. a =— 1, b = oC. a = 1, b = 0D. a = 3, b = 0已知f (x )是定.A . y = x (x — 2)B . y = x (| x |— 1)C. y =1 x | (x — 2)D. y = x (| x | — 2)已知 f (x )= x 5 + ax 3 + bx — 8,且 f (— 2)= 10, 那么f (2)等于( A . — 26B.— 18C.— 10D. 10函数f (x) a Y —x ：—x 二1 是 (J x 2A .偶函数B.奇函数C.非奇非偶函数D.既是奇函数又是偶函数 若:(x) , g (x )都是奇函数, f (x^ bg (x) 2 在(0,+m )上有最大值 5,则 f (x ) 在(—a,0)上有(A. 最小值—5B .最大值—5 C.最小值—1 D.最大值—3函数f (x)二14. f (x )是定义在(—s,— 5: : 5,+^)上的奇函数，且试判断f (x )在(— s,— 5］上的单调性，并用定义给予证明.15.设函数y =f (x ) (R 且x 丰0)对任意非零实数 求证f (x )是偶函数.函数的奇偶性练习参考答案1. 解析：f (x ) = ax 2 + bx + c 为偶函数，：：(x)二x 为奇函数，••• g (x )= ax 3 + bx 2 + cx = f (x ) • :(x)满足奇函数的条件.答案：A2 .解析：由f (x ) = ax 2 + bx + 3a + b 为偶函数，得b = 0.1 又定乂域为］a — 1, 2a ］, • a — 1 = 2a ,「・ a =—.故选 A .33.解析：由x > 0时，f (x ) = x 2— 2x , f (x )为奇函数，2 2•••当 X V 0 时，f (x )=— f (— x )=—( x + 2x )=— x — 2x = x (— x — 2).f (x )在］5,+s)上单调递减,X i 、X 2 满足 f ( x i • X 2)= f ( x i )+ f ( X 2),(X—O)，即f (x)= x( |x| - 2)(X 0),答案：D4.解析：f (x) + 8=x5+ ax3+ bx 为奇函数，f (- 2)+ 8= 18,「.f (2)+ 8=- 18,「. f (2)=- 26. 答案：A5•解析：此题直接证明较烦，可用等价形式 f ( —x)+ f (x)= 0. 答案：B6. 解析：(x)、g (x)为奇函数，••• f (x) - 2 二a「(x) • bg (x)为奇函数.又f (x)在(0,+s)上有最大值5, • f (x)—2有最大值3.• f (x)—2在(—a, 0) 上有最小值—3, • f (x)在(—a, 0) 上有最小值—1 . 答案:C7. 答案：奇函数8. 答案：0解析：因为函数y =( m—1) x2+ 2mx^ 3为偶函数，2 2••• f ( —x)= f (x),即(m—1) (—x) + 2m(—x)+ 3 =( m-1) x + 2m好3，整理，得m= 0.9. 解析：由f (x)是偶函数，g (x)是奇函数，可得1丄1立f(x) g(x)=X - 1F 八 _ 八—联1 \人)5入丿“，_ x T1111 f (X):(.- )22x -1_ X - 1X -1答案：f (X)二1210.答案：0 11.答案:1m -x -1 212. 证明：令x = y= 0，有f (0)+ f (0)= 2f (0) • f (0),又f (0)工0,二可证f (0)= 1.令x=0,•-f (y) + f ( —y)= 2f (0) • f (y)二f (—y) = f (y),故f (x)为偶函数.13. 解析：本题主要是培养学生理解概念的能力.f (x)= x3+ 2x2—1.因f (x)为奇函数，• f ( 0)= 0.当X V0 时，一x>0, f (—x) = (—x) 3+ 2 (—x) 2— 1 = —x3+ 2x2—1,• f (x)= x3—2x2+ 1.'X3+2X2-1 (x>0),因此，f(x)=20 (x = 0),X3一2x2 1 (x ：： 0).点评：本题主要考查学生对奇函数概念的理解及应用能力.14. 解析：任取X1<X2W —5，则一X1>—X2》一5.因f (X )在［5 ,+a］上单调递减，所以 f (—X1)V f (—X2)= f (X1)V—f (X2)= f ( X1) f(x)”2)> f ( X2),即单调减函数.精品文档点评：此题要注意灵活运用函数奇偶性和单调性，并及时转化.15. 解析：由X1, X2E R且不为0的任意性，令X1 = X2 = 1代入可证，f (1 )= 2f (1), ••• f (1)= 0.又令X1 = X2=—1 ,•f :—1 x(—1) = 2f (1 )= 0,•(—1)= 0.又令X1 = —1, X2= X,•f (—X) = f (—1) + f (X)= 0+ f (X)= f (X),即f (x)为偶函数.点评：抽象函数要注意变量的赋值，特别要注意一些特殊值，如，X1 = X2= 1, X1 X2= 0等，然后再结合具体题目要求构造出适合结论特征的式子即可. X2=—1 或X=。

专题02 函数的奇偶性与单调性【方法点拨】1. 若函数f (x )为偶函数，则f (x )＝f (|x |)，其作用是将“变量化正”，从而避免分类讨论．2. 以具体的函数为依托，而将奇偶性、单调性内隐于函数解析式去求解参数的取值范围，是函数的奇偶性、单调性的综合题的一种重要命题方式，考查学生运用知识解决问题的能力，综合性强，体现能力立意，具有一定难度.【典型题示例】例1 （2022·江苏新高考基地高三第一次联考·19改编）已知函数f (x )＝1－a5x ＋1为奇函数，且存在m ∈[－1，1]，使得不等式f (x 2)＋f (mx －2)≤2－x 2－mx 成立，则x 的取值范围是 ． 【答案】[－2,2]【解析】求得a =2，且f (x )为R 上的增函数，f (x 2)＋f (mx －2)≤2－x 2－mx 可化为f (x 2)＋x 2≤2－mx －f (mx －2) 由f (x )为奇函数，得2－mx －f (mx －2)= 2－mx ＋f (2－mx )令F (x )=f (x )＋x ，则F (x 2)≤F (2－mx )，故有x 2≤2－mx ，即x 2＋mx －2≤0 令G (x )= x 2＋mx －2因为存在m ∈[－1，1]，使G (x )= x 2＋mx －2≤0 故G (－1)= x 2－x －2≤0或G (1)= x 2＋x －2≤0 解之得－2≤x ≤2.例2 已知函数f (x )＝x 3－2x ＋e x －1e x ，其中e 是自然对数的底数，在f (a －1)＋f (2a 2)≤0，则实数a 的取值范围是________. 【答案】1[1,]2-【分析】直接发现函数的单调性、奇偶性，将2(1)(2)0f a f a -+≤移项，运用奇偶性再将负号移入函数内，逆用单调性脱“f ”．【解析】 ∵f (－x )＝(－x )3＋2x ＋e －x －e x ＝－f (x )且x ∈R ， ∴f (x )是奇函数∵函数f (x )＝x 3－2x ＋e x －1ex ，∴f ′(x )＝3x 2－2＋e x ＋1e x ≥3x 2－2＋2e x ·1ex ≥0(当且仅当x ＝0时取等号)，∴f (x )在R 上单调递增.，由f (a －1)＋f (2a 2)≤0，得f (2a 2)≤f (1－a ). 所以2a 2≤1－a ，解之得－1≤a ≤12.所以实数a 的取值范围是⎣⎡⎦⎤－1，12. 例3 已知函数()e +1e x x f x -=-（e 为自然对数的底数），若2(21)42)(f x f x +->-，则实数x 的取值范围为 ． 【答案】()1,3-【分析】本题是例2的进一步的延拓，其要点是需对已知函数适当变形，构造出一个具有奇偶性、单调性的函数,其思维能力要求的更高，难度更大.【解析】令()()1e e x xx F x f -=-=-，易知()F x 是奇函数且在R 上单调递增由2(21)42)(f x f x +->-得[]2(4)11(21)(21)1f x f x f x -->--=--- 即2(4)(21)F x F x ->--由()F x 是奇函数得(21)(12)F x F x ---=，故2(4)(12)F x F x ->-由()F x 在R 上单调递增，得2412x x ->-，即2302x x -<-，解得13x -<<， 故实数x 的取值范围为()1,3-.例4 已知函数()222131x x f x x =-++．若存在()1,4m ∈使得不等式()()2432f ma f m m -++>成立，则实数a 的取值范围是________．【答案】(),8-∞【分析】令()()1F x f x =-，判断函数()F x 的奇偶性与单调性，从而将不等式转化为234m m ma +>-，分离参数可得43a m m<++，令4()3g m m m =++，(1,4)m ∈，利用对勾函数的单调性可得()8g m <，结合题意即可求解a 的取值范围． 【解析】函数222()()131xx f x f x x ==-++，若存在(1,4)m ∈使得不等式2(4)(3)2f ma f m m -++>成立，令2222()()1(31)3131xx x x x F x f x x =-=-=-++，22(31)(13)()()3113x x xxx x F x F x -----===-++， 所以，()F x 为奇函数．不等式2(4)(3)2f ma f m m -++>，即2(4)1(3)10f ma f m m --++->， 即2(4)(3)0F ma F m m -++>，所以2(3)(4)(4)F m m F ma F ma +>--=-， 因为20y x=>在(0,)+∞上为增函数，21031x y =->+在(0,)+∞上为增函数，所以22()(1)31x F x x =-+在(0,)+∞上为增函数， 由奇函数的性质可得()F x 在R 上为增函数，所以不等式等价于234m m ma +>-，分离参数可得43a m m<++， 令4()3g m m m=++，(1,4)m ∈， 由对勾函数的性质可知()g m 在(1,2)上单调递减，在(2,4)上单调递增，g （1）8=，g （4）8=，所以，()8g m <，所以由题意可得8a <， 即实数a 的取值范围是(,8)-∞． 故答案为：(,8)-∞．例5 已知函数112,1()2,1x x x f x x --⎧≥=⎨<⎩，若()2(22)2f x f x x -≥-+，则实数x 的取值范围是（ ） A ．[2,1]-- B ．[1,)+∞C ．RD ．(,2][1,)-∞-+∞【答案】D【解析】函数1112,1()22,1x x x x f x x ----⎧==⎨<⎩，故()f x 关于直线1x =对称，且在[1，)+∞上单减，函数()f x 的图象如下： 2(22)(2)x f x x --+，且f22172()124x x x -+=-+>恒成立，2|221|21x x x ∴---+-，即2|23|1x x x --+，当32x时，不等式化为：2231x x x --+，即2340x x -+，解得x ∈R ，即32x ；当32x <时，不等式化为：2321x x x --+，即220x x +-，解得2x -或1x ，即2x -或312x <；综上，2(22)(2)f x f x x --+时，实数x 的取值范围是(-∞，2][1-，)+∞． 故选：D ．例6 已知函数，，则t 的取值范围是 ． 【答案】[1,)+∞【分析】将已知按照“左右形式相当，一边一个变量”的原则，移项变形为3133(3log 1)log (12log )f t t f t -≥--，易知是奇函数，故进一步变为3333(3log 1)(3log 1)(2log 1)(2log 1)f t t f t t -+-≥-+-（#），故下一步需构造函数()()F x f x x =+，转化为研究()()F x f x x =+的单调性，而()()F x f x x =+单增，故（#）可化为3log 0t ≥，即333log 12log 1t t -≥-，解之得1t ≥.例7 (2022·江苏南通期末·8)已知函数()422xf x x =-+，()3log 2a f =，()4log 3b f =，43c f ⎛⎫= ⎪⎝⎭,则（ ）A. a b c <<B. b c a <<C. c a b <<D.c b a <<【答案】B【分析】分析可知函数()f x 在()1,+∞上为增函数，推导出函数()f x 的图象关于直线1x =对称，则函数()f x 在(),1-∞上为减函数，可得出23c f ⎛⎫= ⎪⎝⎭，利用函数()f x 在(),1-∞上()33x xf x -=-3313(12log )(3log 1)log f t f t t -+-≥3313(12log )(3log 1)log f t f t t -+-≥()33x xf x -=-的单调性可得出a 、b 、c 的大小关系.【解析】令()422xg x x =-+，其中x ∈R ，则()10g =， 因为函数y x =、422x y =-+均为R 上的增函数，故函数()g x 也为R 上的增函数，当1x >时，()()10g x g >=，此时()442222x x f x x x =-=-++，故函数()f x 在()1,+∞上为增函数，因为()()2322222244222222222x xxx x f x x x x -----+--=--=-=-+++ ()()3222442222222xxx x x x x x x f x --⋅=-=-=-=+++故函数()f x 的图象关于直线1x =对称，则函数()f x 在(),1-∞上为减函数， 所以，4233c f f ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭， 3223<，则3lg 22lg3<，即3lg 22log 2lg 33=<， 2343<，则2lg 43lg3<，则4lg 32log 3lg 43=>，即342log 2log 313<<<， 因此，b c a <<. 故选：B.【巩固训练】1．若函数(()=ln f x x x +为偶函数，则实数a = 2.设函数()()21ln 11f x x x=+-+，则使得()()1f x f >成立的x 的取值范围是（ ）． A ．()1,+∞ B ．()(),11,-∞-+∞ C ．()1,1- D ．()()1,00,1-3.已知函数1()22x x f x =-，则满足2(5)(6)0f x x f -+>的实数x 的取值范围是 ．4. 已知函数()||31f x x x x =⋅++，若()2()22f a f a +-<，则实数a 的取值范围__________.5.已知函数222,0()2,0x x x f x x x x ⎧+≥=⎨-<⎩，若()()22f a f a ->，则实数a 的取值范围是__________.6.已知函数()x xg x e e -=-，()()f x xg x =，若1ln 3a f ⎛⎫= ⎪⎝⎭，140.2b f ⎛⎫= ⎪⎝⎭，()1.25c f =，则a 、b 、c 的大小关系为（ ）A ．b a c <<B ．c b a <<C ．b c a <<D ．a b c <<7. （多选题）关于函数12()11xf x x e ⎛⎫=+ ⎪-⎝⎭下列结论正确的是（ ） A ．图像关于y 轴对称 B ．图像关于原点对称 C ．在(),0-∞上单调递增D ．()f x 恒大于08.已知函数())20202020log 20201xx f x x -=+-+，则关于x 的不等式()()21120f x f x +++->的解集为（ ）.A ．1,2020⎛⎫-+∞ ⎪⎝⎭B ．()2020,-+∞C ．2,3⎛⎫-+∞ ⎪⎝⎭D ．2,3⎛⎫-∞-⎪⎝⎭9.已知函数222()131x x f x x =-++.若存在m ∈(1,4)使得不等式(4)f ma -+2(3)2f m m +>成立，则实数a 的取值范围是A . (),7-∞B . (],7-∞C . (),8-∞D . (],8-∞ 10. 已知函数()e e 2sin xxf x x -=--，则关于x不等式()()2320f x f x -+<的解集为（ ） A. ()3,1-B. ()1,3-C. ()(),31,-∞-⋃+∞D. []1,3-11. 已知()sin xxf x e e x x -=-+-，若2(2ln(1))02x f a x f ⎛⎫-++≥ ⎪⎝⎭恒成立，则实数a 的取值范围___．12.已知()sin xxf x e ex x -=-+-，若2(2ln(1))02x f a x f ⎛⎫-++≥ ⎪⎝⎭恒成立，则实数a 的取值范围_ __． 13. 已知函数()1e e 21x x xf x -=+-+，若不等式()()2121f ax f ax +-≥对x ∀∈R 恒成立，则实数a 的取值范围是（ ） A ．(]0,eB ．[]0,eC ．(]0,1D ．[]0,114.已知函数()())2+1sin lnf x x x x =++，若不等式()()39334x x xf f m -+⋅-<对任意x ∈R 均成立，则m 的取值范围为（ ）A ．(),1-∞B ．(),1-∞-C ．()1-D ．()1,-+∞【答案或提示】1．【答案】1【解析】(g()=ln x x +奇函数，g(0)=0=，1a =.2. 【答案】B【解析】()f x 偶函数，且在(0,)+∞单增，()()1f x f >转化为1x >，解得1x >或1x <-. 3.【答案】（2,3）【解析】()f x 奇函数，且单减，2(5)(6)0f x x f -+>转化为2560x x -+<，解得23x <<.4. 【答案】(2,1)-【解析】设()||3g x x x x =⋅+，则()g x 奇函数，且单增，而()()1f x g x =+，由()2()22f a f a +-<得()2211()f a f a --<-即()22()()g a g a g a -<-=-，故22a a -<-，解之得21a -<<.5.【答案】(2,1)-【解析】22y x x =+在[0,)+∞上单调递增，22y x x =-在(,0)-∞上单调递增，且220+20=200⨯⨯-，()f x ∴在R 上单调递增，因此由()()22f a f a ->得2221aa a ->∴-<<，，故答案为：()2,1-6. 【答案】A 【解析】()()()x x f x xg x x e e -==-，该函数的定义域为R ，()()()x x x x f x x e e x e e ---=--=-，所以，函数()y f x =为偶函数，当0x >时，()0xxg x e e-=->，任取120x x >>，12x x -<-，则12x xe e >，12x x e e --<，所以，1122x x x x e e e e --->-，()()120g x g x ∴>>，()()1122x g x x g x ∴>，即()()12f x f x >，所以，函数()y f x =在()0,∞+上单调递增，()11ln lnln333a f f f ⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭， 10 1.2400.20.21ln355<<=<<<，则()()1 1.240.2ln 35f f f ⎛⎫<< ⎪⎝⎭，即b a c <<.故选：A. 7.【答案】ACD 8. 【答案】C【解析】构造函数()())202012020log 2020xx F x fx x -=-=+-，x>=0x>，所以()F x 的定义域为R .())20202020log 2020x xF x x --=+-20202020log 2020x x xx -⎡⎤=+-20202020log 2020x x-⎡⎤=+-)()20202020log 2020x x x F x -=--=-，所以()F x 为奇函数， ()00F =.当0x >时，)20202020,2020,log x xy y y x -==-=都为增函数，所以当0x >时，()F x 递增，所以()F x 在R 上为增函数.由()()21120f x f x +++->，得()()211110f x f x +-++->， 即()()2110F x F x +++>，所以2110x x +++>，解得23x >-. 所以不等式的解集为2,3⎛⎫-+∞ ⎪⎝⎭.故选：C 9. 【答案】C【解析】22222231()1111313131xx x x x f x x x x -⎛⎫=-+=-+=⋅+ ⎪+++⎝⎭设231()()131x x g x f x x -=-=⋅+，则()g x 为定义在R 的奇函数所以()f x 关于点()0,1对称又2223131312ln 33()231313131x x x xx x x x x g x x x x '⎡⎤---⋅⋅''⎡⎤=⋅+⋅=⋅+⎢⎥⎣⎦++++⎣⎦所以当0x >时，()0g x '>，()g x 在()0,+∞上单增 故()g x 在(),-∞+∞上也单增因为2(4)(3)2f ma f m m -++>可化为2(4)1(3)1f ma f m m -->-++所以2(4)(3)g ma g m m ->-+因为()g x 为R 的奇函数，22(4)(3)(3)g ma g m m g m m ->-+=--所以243ma m m ->--又因为存在m ∈(1,4)使得不等式243ma m m ->--成立，分参得43a m m<++ 易得[)437,8m m++∈，所以8a <，故选C . 10.【答案】A【分析】根据题意可判断函数()e e 2sin xxf x x -=--为奇函数且在R 上单调递增，进而根据奇偶性与单调性解不等式即可.【解析】函数()e e 2sin xxf x x -=--的定义域为R ，()()()e e 2sin e e 2sin x x x x f x x x f x ---=---=-+=-，所以函数()e e 2sin xxf x x -=--为奇函数，因为()'e e 2cos 22cos 0xxf x x x -=+-≥-≥，所以函数()e e 2sin xxf x x -=--在R 上单调递增，所以()()()()()22320322f x f x f x f x f x -+<⇔-<-=-，所以232x x -<-，即2230x x +-<，解得31x -<< 所以不等式()()2320f x f x -+<的解集为()3,1-故选：A11.【答案】12ln 2,2⎡⎫-+∞⎪⎢⎣⎭【分析】先分析()f x 的奇偶性和单调性，则2(2ln(1))02x f a x f ⎛⎫-++≥ ⎪⎝⎭等价于2(2ln(1))2x f a x f ⎛⎫-+≥- ⎪⎝⎭，所以22ln(1)2x a x -+≥-，可转化为2()2ln(1)2x a g x x ≥=-++，即max ()a g x ≥，求max ()g x 即得解【解析】因为()()sin xx f x ee x xf x --=--+=-，所以()f x 是R 上的奇函数，()cos 1x xf x e e x -'=++-，()cos 1cos 11cos 0x x f x e e x x x -'=++-≥-=+≥，所以()f x 是R 上的增函数，2(2ln(1))02x f a x f ⎛⎫-++≥ ⎪⎝⎭等价于22(2ln(1))22x x f a x f f ⎛⎫⎛⎫-+≥-=- ⎪ ⎪⎝⎭⎝⎭，所以22ln(1)2x a x -+≥-，所以22ln(1)2x a x ≥-++，令2()2ln(1)2x g x x =-++，则max ()a g x ≥， 因为()()g x g x -=且定义域为R ，所以()g x =22ln(1)2x x -++是R 上的偶函数， 所以只需求()g x 在()0,∞+上的最大值即可.当[)0,x ∈+∞时，2()2ln(1)2x g x x =-++，()()22122()111x x x x g x x x x x +---+'=-+==-+++， 则当[)0,1x ∈时，()0g x '>；当[)1,x ∈+∞时，()0g x '<；所以()g x 在[)0,1上单调递增，在[)1,+∞上单调递减， 可得：max 1()(1)2ln 22g x g ==-，即12ln 22a ≥-. 故答案为：12ln 2,2⎡⎫-+∞⎪⎢⎣⎭. 12.【答案】12ln 2,2⎡⎫-+∞⎪⎢⎣⎭【分析】先分析()f x 的奇偶性和单调性，则2(2ln(1))02x f a x f ⎛⎫-++≥ ⎪⎝⎭等价于2(2ln(1))2x f a x f ⎛⎫-+≥- ⎪⎝⎭，所以22ln(1)2x a x -+≥-，可转化为2()2ln(1)2x a g x x ≥=-++，即max ()a g x ≥，求max ()g x 即得解 【解析】因为()()sin x x f x e e x x f x --=--+=-，所以()f x 是R 上的奇函数，()cos 1x x f x e e x -'=++-，()cos 1cos 11cos 0x x f x e e x x x -'=++-≥-=+≥，所以()f x 是R 上的增函数，2(2ln(1))02x f a x f ⎛⎫-++≥ ⎪⎝⎭等价于22(2ln(1))22x x f a x ff ⎛⎫⎛⎫-+≥-=- ⎪ ⎪⎝⎭⎝⎭， 所以22ln(1)2x a x -+≥-，所以22ln(1)2x a x ≥-++， 令2()2ln(1)2x g x x =-++，则max ()a g x ≥，因为()()g x g x -=且定义域为R ，所以()g x =22ln(1)2x x -++是R 上的偶函数，所以只需求()g x 在()0,∞+上的最大值即可.当[)0,x ∈+∞时，2()2ln(1)2x g x x =-++，()()22122()111x x x x g x x x x x +---+'=-+==-+++，则当[)0,1x ∈时，()0g x '>；当[)1,x ∈+∞时，()0g x '<；所以()g x 在[)0,1上单调递增，在[)1,+∞上单调递减， 可得：max 1()(1)2ln 22g x g ==-，即12ln 22a ≥-. 故答案为：12ln 2,2⎡⎫-+∞⎪⎢⎣⎭. 13.【答案】D【分析】构造函数()()12g x f x =-，判断函数的奇偶性与单调性，将所求不等式转化为()()2111222f ax f ax ⎡⎤-≥---⎢⎥⎣⎦，即()()221g ax g ax ≥-，再利用函数单调性解不等式即可. 【解析】()1e e 21x x x f x -=+-+， ()()1111e e e e 121212121x x x x x x x x f x f x ----∴+-=+-+-+=++=+++令()()12g x f x =-，则()()0g x g x +-=，可得()g x 是奇函数，又()()()2121e e e e e 21e 21ln 2ln 2++2122x x x x x x x x x x x g x --'⎛⎫''=+-== ⎪+⎝++--+⎭， 又利用基本不等式知e 2+1e x x ≥当且仅当1e ex x =，即0x =时等号成立； ln 2ln 214222x x ≤++当且仅当122x x =，即0x =时等号成立； 故()0g x '>，可得()g x 是单调增函数，由()()2121f ax f ax +-≥得()()()21111212222f ax f ax f ax ⎡⎤-≥--+=---⎢⎥⎣⎦， 即()()()21221g ax g ax g ax ≥--=-，即2210ax ax -+≥对x ∀∈R 恒成立. 当0a =时显然成立；当0a ≠时，需20440a a a >⎧⎨∆=-≤⎩，得01a <≤， 综上可得01a ≤≤，故选：D.14.【答案】A【分析】由题设，构造()()2g x f x =-，易证()g x 为奇函数，利用导数可证()g x 为增函数，结合题设不等式可得(39)(33)x x x g g m -<-⋅，即3313x x m <+-对任意x ∈R 均成立，即可求m 的范围.【解析】由题设，令()()22sin )g x f x x x x =-=++，∴()2sin())2sin )()g x x x x x x x g x -=-+-+=---=-，∴()g x 为奇函数，又()2cos 0g x x '=++>，即()g x 为增函数，∴()()39334x x x f f m -+⋅-<，即(39)2[(33)2]x x x f f m --<-⋅--， ∴(39)(33)(33)x x x x g g m g m -<-⋅-=-⋅，则3933x x x m -<-⋅，∴3313x x m <+-对任意x ∈R 均成立，又331113x x +-≥=，当且仅当12x =时等号成立，∴1m <，即m ∈(),1-∞.故选：A。

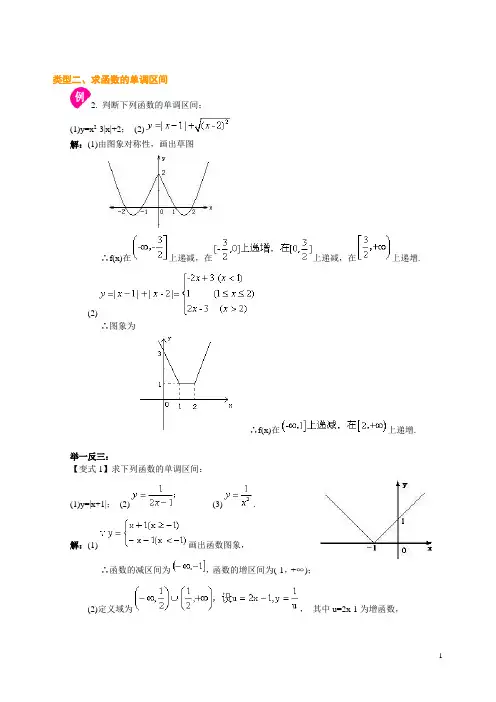
类型二、求函数的单调区间2. 判断下列函数的单调区间；(1)y=x2-3|x|+2；(2)解：(1)由图象对称性，画出草图∴f(x)在上递减，在上递减，在上递增.(2)∴图象为∴f(x)在上递增.举一反三：【变式1】求下列函数的单调区间：(1)y=|x+1|；(2)(3).解：(1)画出函数图象，∴函数的减区间为，函数的增区间为(-1，+∞)；(2)定义域为，其中u=2x-1为增函数，在(-∞，0)与(0，+∞)为减函数，则上为减函数；(3)定义域为(-∞，0)∪(0，+∞)，单调增区间为：(-∞，0)，单调减区间为(0，+∞). 类型三、单调性的应用(比较函数值的大小，求函数值域，求函数的最大值或最小值)3. 已知函数f(x)在(0，+∞)上是减函数，比较f(a2-a+1)与的大小.解：又f(x)在(0，+∞)上是减函数，则.4. 求下列函数值域：(1)；1)x∈[5，10]；2)x∈(-3，-2)∪(-2，1)；(2)y=x2-2x+3；1)x∈[-1，1]；2)x∈[-2，2].1)f(x)在[5，10]上单增，；2)；(2)画出草图1)y∈[f(1)，f(-1)]即[2，6]；2).举一反三：【变式1】已知函数.(1)判断函数f(x)的单调区间；(2)当x∈[1，3]时，求函数f(x)的值域.解：(1)上单调递增，在上单调递增；(2)故函数f(x)在[1，3]上单调递增∴x=1时f(x)有最小值，f(1)=-2 x=3时f(x)有最大值∴x∈[1，3]时f(x)的值域为.5. 已知二次函数f(x)=x2-(a-1)x+5在区间上是增函数，求：(1)实数a的取值范围；(2)f(2)的取值范围.解：(1)∵对称轴是决定f(x)单调性的关键，联系图象可知只需；(2)∵f(2)=22-2(a-1)+5=-2a+11又∵a≤2，∴-2a≥-4∴f(2)=-2a+11≥-4+11=7 .举一反三：【变式1】（2011 北京理13）已知函数，若关于x的方程有两个不同的实根，则实数k的取值范围是________.解：单调递减且值域(0,1]，单调递增且值域为，由图象知，若有两个不同的实根，则实数k的取值范围是（0,1）.类型四、判断函数的奇偶性6. 判断下列函数的奇偶性：(1)(2)(3)f(x)=x2-4|x|+3(4)f(x)=|x+3|-|x-3| (5)(6(7)解：(1)∵f(x)的定义域为，不关于原点对称，因此f(x)为非奇非偶函数；(2)∵x-1≥0，∴f(x)定义域不关于原点对称，∴f(x)为非奇非偶函数；(3)对任意x∈R，都有-x∈R，且f(-x)=x2-4|x|+3=f(x)，则f(x)=x2-4|x|+3为偶函数；(4)∵x∈R，f(-x)=|-x+3|-|-x-3|=|x-3|-|x+3|=-f(x)，∴f(x)为奇函数；(5)，∴f(x)为奇函数；(6)∵x∈R，f(x)=-x|x|+x ∴f(-x)=-(-x)|-x|+(-x)=x|x|-x=-f(x)，∴f(x)为奇函数；(7)，∴f(x)为奇函数.举一反三：【变式1】判断下列函数的奇偶性：(1)；(2)f(x)=|x+1|-|x-1|；(3)f(x)=x2+x+1；(4).思路点拨：利用函数奇偶性的定义进行判断.解：(1)；(2)f(-x)=|-x+1|-|-x-1|=-(|x+1|-|x-1|)=-f(x) ∴f(x)为奇函数；(3)f(-x)=(-x)2+(-x)+1=x2-x+1∴f(-x)≠-f(x)且f(-x)≠f(x) ∴f(x)为非奇非偶函数；(4)任取x>0则-x<0，∴f(-x)=(-x)2+2(-x)-1=x2-2x-1=-(-x2+2x+1)=-f(x)任取x<0，则-x>0 f(-x)=-(-x)2+2(-x)+1=-x2-2x+1=-(x2+2x-1)=-f(x)x=0时，f(0)=-f(0) ∴x∈R时，f(-x)=-f(x) ∴f(x)为奇函数.类型五、函数奇偶性的应用(求值，求解析式，与单调性结合)7．已知f(x)=x5+ax3-bx-8，且f(-2)=10，求f(2).解：法一：∵f(-2)=(-2)5+(-2)3a-(-2)b-8=-32-8a+2b-8=-40-8a+2b=10∴8a-2b=-50 ∴f(2)=25+23a-2b-8=8a-2b+24=-50+24=-26法二：令g(x)=f(x)+8易证g(x)为奇函数∴g(-2)=-g(2) ∴f(-2)+8=-f(2)-8∴f(2)=-f(-2)-16=-10-16=-26.举一反三：【变式1】（2011 湖南文12）已知为奇函数，，则为：解：，又为奇函数，所以．8. f(x)是定义在R上的奇函数，且当x<0时，f(x)=x2-x，求当x≥0时，f(x)的解析式，并画出函数图象.解：∵奇函数图象关于原点对称，∴x>0时，-y=(-x)2-(-x)即y=-x2-x又f(0)=0，，如图9．设定义在[-3，3]上的偶函数f(x)在[0，3]上是单调递增，当f(a-1)<f(a)时，求a的取值范围.解：∵f(a-1)<f(a) ∴f(|a-1|)<f(|a|)而|a-1|，|a|∈[0，3].类型六、综合问题10．定义在R上的奇函数f(x)为增函数，偶函数g(x)在区间的图象与f(x)的图象重合，设a>b>0，给出下列不等式，其中成立的是_________.①f(b)-f(-a)>g(a)-g(-b)；②f(b)-f(-a)<g(a)-g(-b)；③f(a)-f(-b)>g(b)-g(-a)；④f(a)-f(-b)<g(b)-g(-a).答案：①③.11. 求下列函数的值域：(1)(2)(3)思路点拨：(1)中函数为二次函数开方，可先求出二次函数值域；(2)由单调性求值域，此题也可换元解决；(3)单调性无法确定，经换元后将之转化为熟悉二次函数情形，问题得到解决，需注意此时t 的范围.解：(1)；(2)经观察知，，；(3)令.12. 已知函数f(x)=x2-2ax+a2-1.(1)若函数f(x)在区间[0，2]上是单调的，求实数a的取值范围；(2)当x∈[-1，1]时，求函数f(x)的最小值g(a)，并画出最小值函数y=g(a)的图象.解：(1)∵f(x)=(x-a)2-1 ∴a≤0或a≥2(2)1°当a<-1时，如图1，g(a)=f(-1)=a2+2a2°当-1≤a≤1时，如图2，g(a)=f(a)=-13°当a>1时，如图3，g(a)=f(1)=a2-2a，如图13. 已知函数f(x)在定义域(0，+∞)上为增函数，f(2)=1，且定义域上任意x、y都满足f(xy)=f(x)+f(y)，解不等式：f(x)+f(x-2)≤3.解：令x=2，y=2，∴f(2×2)=f(2)+f(2)=2 ∴f(4)=2再令x=4，y=2，∴f(4×2)=f(4)+f(2)=2+1=3 ∴f(8)=3∴f(x)+f(x-2)≤3可转化为：f[x(x-2)]≤f(8).14. 判断函数上的单调性，并证明.证明：任取0<x1<x2，∵0<x1<x2，∴x1-x2<0，x1·x2>0(1)当时0<x1·x2<1，∴x1·x2-1<0∴f(x1)-f(x2)>0即f(x1)>f(x2)上是减函数.(2)当x1，x2∈(1，+∞)时，上是增函数.15. 设a为实数，函数f(x)=x2+|x-a|+1，x∈R，试讨论f(x)的奇偶性，并求f(x)的最小值. 解：当a=0时，f(x)=x2+|x|+1，此时函数为偶函数；当a≠0时，f(x)=x2+|x-a|+1，为非奇非偶函数.(1)当x≥a时，[1]且[2]上单调递增，上的最小值为f(a)=a2+1.(2)当x<a时，[1]上单调递减，上的最小值为f(a)=a2+1[2]上的最小值为综上：.。

一、关于函数的奇偶性的定义：定义说明：对于函数)(x f 的定义域内任意一个x ：（1）)()(x f x f =- ⇔)(x f 是偶函数；（2）)()(x f x f -=-⇔)(x f 奇函数；（3）判断函数的奇偶性有时可以用定义的等价形式： ()()0f x f x ±-=，()1()f x f x =±- 二、函数的奇偶性的几个性质：（1）具有奇偶性的函数，其定义域关于原点对称（2）奇函数的图象关于原点对称，偶函数的图象关于y 轴对称.（3）若奇函数的定义域包含数0，则f （0）=0.（4）奇函数对称区间上的单调性相同，偶函数对称区间上的单调性相反（5）奇函数+奇函数=奇函数 偶函数+偶函数=偶函数奇函数*奇函数=偶函数 偶函数*偶函数=偶函数 奇函数*偶函数=奇函数三、函数的奇偶性的判断利用奇、偶函数的定义，主要考查)(x f 是否与)(x f -、)(x f 相等，步骤如下：（1） 首先确定函数的定义域，并判其定义域是否关于原点对称；（2）确定f(－x)与f(x)的关系；（3）作出相应结论：1、判断下列函数的奇偶性（1）()(f x x =- （2）22(0)()(0)x x x f x x x x ⎧+<⎪=⎨-+>⎪⎩(3)()f x =1122-⋅-x x (4)()f x = (5)f(x)＝2-x +x -2 解：（1）由101x x+≥-，得定义域为[1,1)-，关于原点不对称，∴()f x 为非奇非偶函数 （2）当0x <时，0x ->，则22()()()()f x x x x x f x -=---=-+=-，当0x >时，0x -<，则22()()()()f x x x x x f x -=--=--+=-，综上所述，对任意的(,)x ∈-∞+∞，都有()()f x f x -=-，∴()f x 为奇函数（3）∴f(x)是偶函数.事实上函数的定义域为{-1，1}，将=)(x f 1122-⋅-x x化简得f(x)=0.∴f(x)既是偶函数，又是奇函数.（4）奇函数 （5）此函数定义域为｛2｝，故f(x)是非奇非偶函数。

函数性质—抽象函数奇偶性、单调性综合解答题参考答案与试题解析一．解答题（共 12 小题）1. 函数 f (x ) 对于任意的实数 x ， y 都有 f (x + y ) = f (x ) + f ( y ) 成立，且当 x > 0 时 f (x ) < 0 恒成立． （1） 求 f (0) 的值，并证明函数 f (x ) 为奇函数；（2） 求证 f (x ) 在 R 上为减函数；（3） 若 f （1） = -2 且关于 x 的不等式 f (x 2 - x + k ) < 4 恒成立，求k 的取值范围．【解答】解：（1）令 x = y = 0 得 f (0) = 0 ．令 y = -x 代入原式得 f (x - x ) = f (x ) + f (-x ) = f (0) = 0 ， 所以 f (-x ) = - f (x ) ，故该函数是奇函数． （2）由已知得 f (x + y ) - f (x ) = f ( y ) = f [(x + y ) - x ] ． 所以任取 x 2 > x 1 ，则f (x 2 - x 1 ) = f (x 2 ) + f (-x 1 ) = f (x 2 ) - f (x 1 ) ，因为 x 2 - x 1 > 0 且当 x > 0 时 f (x ) < 0 ，所以 f (x 2 - x 1 ) < 0 ，即 f (x 2 ) - f (x 1 ) < 0 ，所以 f (x 2 ) < f (x 1 ) ，故该函数在 R 上是减函数．（3）因为 f （1） = -2 ，所以 f (-1) = - f （1） = 2 ，所以 f (-2) = 2 f (-1) = 4 ． 所以原不等式可化为： f (x 2 - x + k ) < f (-2) ． 结合（2）知，函数 f (x ) 在 R 上是增函数．所以 x 2 - x + k > -2 恒成立．即 k > -x 2 + x - 2 = -(x - 1)2 + 9恒成立．24 所以只需k > 9即可．42. 已知函数 f (x ) 对一切 x ， y ∈ R ，都有 f (x + y ) = f (x ) + f ( y ) ，当 x > 0 ，有 f (x ) < 0 ．（1）求： f (0) = 0 ；（2）证明：函数 f (x ) 为奇函数；（3）若 f （1） = -2 ，求 f (x ) 在[-3 ， 3] 上的最值；（4） 若对任意t ∈ R ，不等式 f (t 2 - 2t ) + f (2t 2 - k ) < 0 恒成立，求k 的取值范围．【解答】解：（1）令 x = y = 0 ，可得 f (0) = f (0) + f (0) ， ∴ f (0) = 0 ．（2）证明：令 y = -x 可得： f (0) = f (x ) + f (-x ) ，∴ f (-x ) + f (x ) = 0 ， 又 f (x ) 的定义域为 R ， ∴ f (x ) 是奇函数．（3）设 x 1 ， x 2 是 R 上任意两个数，且 x 1 < x 2 ，则 x 2 - x 1 > 0 ，∴ f (x 2 - x 1) < 0 ，∴ f (x 2 ) - f (x 1 ) = f (x 2 ) + f (-x 1 ) = f (x 2 - x 1 ) < 0 ，∴ f (x ) 在 R 上是减函数，（1） = -2 ，∴ f （2） = 2 f （1） = -4 ， ∴ f （3） = f （1） + f （2） = -6 ． ∴ f (-3) = 6 ．∴ f (x ) 在[-3 ， 3] 上的最小值是 f （3） = -6 ，最大值是 f (-3) = 6 ．（4）由 f (t 2 - 2t ) + f (2t 2 - k ) < 0 得： f (t 2 - 2t ) < - f (2t 2 - k ) = f (k - 2t 2 ) ，∴t 2 - 2t > k - 2t 2 ， 即 k < 3t 2 - 2t ．= 3(t - 1)2- 1- 1 ，∴ k < - 1．33 3 3 3．已知 f (x ) 是定义在[-1 ，1] 上的奇函数，且 f （1） = 3 ，若a ， b ∈[-1 ，1] ， a + b ≠ 0 时，有 f (a ) + f (b ) > 0 成a + b立．（1） 判断 f (x ) 在[-1 ，1] 上的单调性，并证明； （2） 解不等式： f (x + 1) < f (21) ；x - 1（3） 若当a ∈[-1 ，1] 时， f (x ) m 2 - 2am + 3 对所有的 x ∈[-1，1] 恒成立，求实数m 的取值范围．【解答】解：（1）任取 x 1 ， x 2 ∈[-1，1] ，且 x 1 < x 2 ，则-x 2 ∈[-1，1] ，f (x ) 为奇函数，∴ f (x ) - f (x ) = f (x ) + f (-x ) = f (x 1 ) + f (-x 2 ) (x- x ) ， 1212x - x 1 2由已知得 f (x 1 ) + f (-x 2 ) > 0 ， x - x 1 2< 0 ，∴ f (x ) - f (x ) < 0 ，即 f (x ) < f (x ) ．x - x1 21 2 1 2 1 2∴ f (x ) 在[-1 ，1] 上单调递增．f 3t 2- 2tf ⎨ 22 ⎪ ⎧x + 1 < 1 ⎪x -1 （2） f (x ) 在[-1 ，1] 上单调递增，∴ ⎪-1 ⎪ ⎪-1 ⎩x + 1 2 1 x - 1 1 ，解得-3 1 x < -1， ∴不等式的解集为{x | - 3 2x < -1} ．（3） （1） = 3 ， f (x ) 在[-1 ，1] 上单调递增，∴在[-1 ，1] 上， f (x ) 3 ，即m 2 - 2am + 3 3 ，∴m 2 - 2am 0 对 a ∈[-1 ，1] 恒成立，求m 的取值范围．设 g （a ） = -2m a + m 2 0 ，①若m = 0 ，则 g （a ） = 0 0 ，自然对a ∈[-1 ，1] 恒成立．②若m ≠ 0 ，则 g （a ）为a 的一次函数，若 g （a ） 0 对 a ∈[-1 ，1] 恒成立， 则必须 g (-1) 0 ，且 g （1） 0 ，∴ m ∴ m 的取值范围是m = 0 或 m - 2 或m - 2 或m 2 ．2 或 m = 0 ． 4. 已知定义在 R 上的函数 f (x ) 对任意 x ， y ∈ R ，总有 f (x ) + f ( y ) = f (x + y ) +1 ，且当 x > 0 时， f (x ) > 1 ．( I ) 若令h (x ) = f (x ) -1 ，证明：函数h (x ) 为奇函数； ( II ) 证明：函数 f (x ) 在 R 上是增函数；( III ) 解关于 x 的不等式 f (x 2 ) - f (3tx ) + f (2t 2 + 2t - x ) < 1 ．其中t ∈ R ．【解答】解： ( I ) 证明：令 x = y = 0 ，则 f (0) = 1 令 y = -x ，即 f (x ) + f (-x ) = f (0) +1 ，即 f (x ) + f (-x ) = 2 所以： f (-x ) -1 = - f (x ) + 1，即h (-x ) = -h (x )故函数h (x ) 为奇函数； （3 分）( II ) 证明：设任意 x 1 ， x 2 ∈ R 且 x 1 > x 2则 f (x 1 ) - f (x 2 ) = f (x 1 ) + f (-x 2 ) - 2 = f (x 1 - x 2 ) +1 - 2 = f (x 1 - x 2 ) -1因为： x 1 > x 2 所以 x 1 - x 2 > 0 ，故 f (x 1 - x 2 ) > 1所以 f (x 1 ) > f (x 2 ) ，故函数 f (x ) 在 R 上是增函数； （7 分）( III ) 因为 f (x 2 ) - f (3tx ) + f (2t 2 + 2t - x ) < 1所以 f (x 2 ) + f (2t 2 + 2t - x ) < f (3tx ) +1即 f (x 2 + 2t 2 + 2t - x ) +1 < f (3tx ) +1即 f (x 2 + 2t 2 + 2t - x ) < f (3tx )又因为函数 f (x ) 在 R上是增函数所以 x 2 + 2t 2 + 2t - x < 3tx即： x 2 - (3t + 1)t + 2t 2 + 2t < 0即： (x - 2t )(x - t -1) < 0 ⅰ ) 当t = 1 时，原不等式无解；ⅱ ) 当t > 1 时，原不等式的解集{x | t + 1 < x < 2t }ⅲ ) 当t < 1 时，原不等式的解集{x | 2t < x < t + 1}⋯ （12 分）5. 已知函数 f (x ) 为奇函数，且当 x 0 时， f (x ) = (x -1)2 - 3x + a ．（1） 求a 的值，并求 f (x ) 在(-∞, 0) 上的解析式；（2） 若函数 g (x ) = f (x ) + kx 在[-3 ， -1] 上单调递减，求k 的取值范围．【解答】解：（1） f (x ) 为奇函数，∴ f (0) = 0 ，即1 + a = 0 ，∴ a = -1 ，令 x < 0 ，则-x > 0 ，∴ f (-x ) = (-x -1)2 + 3x -1 = (x + 1)2 + 3x -1 = - f (x ) ，∴ f (x ) = -(x + 1)2 - 3x + 1 ，故 f (x ) 在(-∞, 0) 上的解析式为 f (x ) = -(x + 1)2 - 3x + 1．（2） g (x ) = f (x ) + kx = -(x +1)2 - 3x +1 + kx = -x 2 + (k - 5)x ，开口向下，对称轴为 x = k - 5 ，2g (x ) 在[-3 ， -1] 上单调递减，∴ k - 52- 3 ，解得k -1． 故 k 的取值范围为(-∞ ， -1] ．6. 设函数 f (x ) 是实数集 R 上的单调增函数，令 F (x ) = f (x ) - f (2 - x ) ． （1） 求证： F (x ) 在 R 上是单调增函数；（2）若 F (x 1 ) + F (x 2 ) > 0 ，求证： x 1 + x 2 > 2 ．【解答】解：（1）任取 x 1 ， x 2 ∈ R ，且 x 1 < x 2 ，则 F (x 1 ) - F (x 2 ) = [ f (x 1 ) - f (2 - x 1 )] -[ f (x 2 ) - f (2 - x 2 )] = [ f (x 1 ) - f (x 2 )] +[ f (2 - x 2 ) - f (2 - x 1 )] ；f (x ) 是实数集 R 上的增函数，且 x 1 < x 2 ，则 f (x 1 ) - f (x 2 ) < 0 ， 由 x 1 < x 2 ，得-x 1 > -x 2 ，∴2 - x 1 > 2 - x 2 ，∴f (2 -x1) >f (2 -x2 ) ，5f ∴ f (2 - x 2 ) - f (2 - x 1) < 0 ，∴[ f (x 1 ) - f (x 2 )] +[ f (2 - x 2 ) - f (2 - x 1 )] < 0 ；即 F (x 1) < F (x 2 ) ；∴ F (x ) 是 R 上的增函数．（2） 证明： F (x 1 ) + F (x 2 ) > 0 ，∴ F (x 1) > -F (x 2 ) > 0 ；由 F (x ) = f (x ) - f (2 - x ) 知，-F (x 2 ) = -[ f (x 2 ) - f (2 - x 2 )] = f (2 - x 2 ) - f (x 2 ) = f (2 - x 2 ) - f [2 - (2 - x 2 )] = F (2 - x 2 ) ，∴ F (x 1) > F (2 - x 2 ) ；又 F (x ) 是实数集 R 上的增函数， 所以 x 1 + > 2 - x 2 ．， 即 x 1 + x 2 > 2 ．7. 已知函数 y = f (x ) 对任意的实数ab 都有： f (a + b ) = f （a ） + f （b ） -1 ，且 x > 0 时， f (x ) > 1 ，（1）求证： f (x ) 是 R 上的增函数；（2）若 f （4） = 5 ，求 f （2）的值，并解不等式 f (3m 2 - m - 2) < 3 ．【解答】解：（1）证明： f (a + b ) = f （a ） + f （b ） -1 ，且 x > 0 时， f (x ) > 1 ，设 x 1 < x 2 ，则 x 2 - x 1 > 0 ， f (x 2 - x 1 ) > 1 ，∴ f (x 2 ) - f (x 1 ) = f [(x 2 - x 1 ) + x 1 ] - f (x 1 ) = f (x 2 - x 1 ) + f (x 1 ) -1 - f (x 1 ) = f (x 2 - x 1 ) -1 > 1 -1 = 0 ，∴ f (x ) 是 R 上的增函数；（2） （4） = f (2 + 2) = f （2） + f （2） -1 = 5 ， ∴ f （2） = 3 ．∴ f (3m 2 - m - 2) < 3 = f （2），又 f (x ) 是 R 上的增函数；∴3m 2 - m - 2 < 2 ，∴-1 < m < 43∴不等式 f (3m 2 - m - 2) < 3 的解集为：{m | -1 < m < 4} ．38. 已知定义域为 R 的函数 f (x ) 对任意的实数a ， b 均有 f (a + b ) = f （a ）（b ），且当 x < 0 时， f (x ) > 1 ．（1） 求 f (0) 的值；（2） 求证：对任意的 x ∈ R 都有 f (x ) > 0 ；ff f （3） 求证： f (x ) 在 R 上为减函数；（4）当 f （4） = 1 16 时，解不等式 f (x - 3) < 1．4【解答】（1）解：由于 f (a + b ) = f （a ） （b ），则 f (0) = f 2 (0) ，即有 f (0) = 0 或 1．若 f (0) = 0 ，则令a = x ， b = 0 ，有 f (x ) = 0 不成立， 故 f (0) = 1．（2）证明：由于 f (a + b ) = f （a ） （b ），可令a = b = x，则 f (x ) = f 2 ( x) 0 ，由当 x < 0 时， f (x ) > 1 ，22则 f (x ) ≠ 0 ，故有对任意的 x ∈ R 都有 f (x ) > 0 ；（3）证明：设 x 1 > x 2 ，则 x 2 - x 1 < 0 ，当 x < 0 时， f (x ) > 1 恒成立，则 f (x 2 - x 1 ) > 1 ，∴ f (x 1 ) + f (x 2 - x 1 ) = f (x 2 ) > f (x 1 ) ，∴函数 y = f (x ) 是 R 上的减函数；（4）解：当 f （4） = 1 16即有 f （2） = 1，4时，则有 f （4） = f 2 （2），不等式 f (x - 3) < 1，即为 f (2 + x - x 2 ) < f （2）， 4由于函数 y = f (x ) 是 R 上的减函数， 则 2 + x - x 2 > 2 ，解得0 < x < 1． 即有解集为(0,1) ．9. 已知 f (x ) 对任意实数a ， b 都有 f (a + b ) = f （a ） + f （b ） -2 且当 x > 2 时，有 f (x ) > 2 ． （1） 求证： f (x ) 在 R 上为增函数；（2） 若 f （1） = 2 ，求满足不等式 f (3t - 2) + f (t - t 2 ) < 4 的实数t 的取值范围．【解答】（1）证明：任取 x 1 ， x 2 ∈ R 且 x 1 < x 2 ， 则 x 2 - x 1 > 0 ， f (x 2 - x 1 ) > 2 ．f (a + b ) = f （a ） + f （b ） -2 ，∴ f (x 2 ) = f [(x 2 - x 1 ) + x 1 ] = f (x 2 - x 1 ) + f (x 1 ) - 2 > 2 + f (x 1 ) - 2 = f (x 1 ) ，∴ f (x 2 ) > f (x 1) ，∴ f (x ) 在 R 上为增函数．f (5 - x 2 ) f (5 - x 2 )1 x （2）解： f (3 - 2) + f (t - t2 ) < 4 ，即 f (3t - 2) + f (t - t 2 ) - 2 < 2 ，∴ f (3t - 2 + t - t 2 ) < 2 ．（1） = 2 ，∴ f (4t - 2 - t 2 ) < f （1），又 f (x ) 在 R 上为增函数， ∴4t - 2 - t 2 < 1， 即t 2 - 4t + 3 > 0 解得t > 3 或t < 1故实数t 的取值范围为(-∞ ，1) ⋃(3 ， +∞) ．10. 已知函数 f (x ) 的定义域为(0, +∞) ，当 x > 1 时， f (x ) > 0 且 f (xy ) = f (x ) + f ( y )（1）求 f （1），并求证： f ( 1) =- f (x )x（2） 证明 f (x ) 在定义域上是增函数．（3） 如果 f (1) = -1求满足不等式 f ( 31 x - 2) 2 的 x 的取值范围．【解答】解：（1） f (xy ) = f (x ) + f ( y ) 令 x = y = 1 ，则 f （1） = f （1） + f （1） 解得 f （1） = 0令 y = 1 ，则 f (x 1) = f (x ) + f ( ) = f （1） = 0xx x故 1f ( ) =- f (x )x（2）设0 < x < x ，则 x 2 > 1 ，则 f ( x2 ) > 0 ，1 211 则令 x = x ， y = x2 ，1则 f (x ) = f (x x 1 x 2 ) = f (x ) + x 2> f (x )2 1 x f ( ) 1 x11 1故 f (x ) 在定义域上是增函数 1f ( ) 3 = -1 ，∴ f （3） = 1， f （9） = f （3） + f （3） = 2 又 f (x ) 在定义域上是增函数， 故不等式 f (即1x - 21x - 2 ) 2 可化为 f ( （9） f 1 ) f x - 29 （3） xf (x + y ) = f (x ) f ( y ) ，解得2 < x即满足条件的 x 的取值范围为(2 ， 19]911. 已知函数 y = f (x ) 满足对任意实数 x ， y 有 f (x + y ) = f (x ) （1）求 f (0) 的值；（2）求证： x < 0 ， f (x ) > 1 ； （3）讨论函数 y = f (x ) 的单调性；（4）解不等式 f (x 2 + x ) < f (3 - x ) ．f ( y ) ，且当 x > 0 ， 0 < f (x ) < 1 ．【解答】解：（1）令 y = 0 ，可得 f (x + 0) = f (x ) （2）设 x < 0 ，则-x > 0 ， 当 x > 0 ， 0 < f (x ) < 1， ∴0 < f (-x ) < 1 ，f (x - x ) = f (x ) f (-x ) = 1，f (0) ，∴ f (0) = 1 ；∴ f (-x ) = 1 ，f (x )∴0 <1f (x )< 1 ， ∴ f (x ) > 1 ；（3）在函数 f (x ) 定义域 R 上任取自变量 x 1 ， x 2 且 x 1 < x 2 ，∴ x 2 - x 1 > 0 ．∴ f (x 2 ) - f (x 1 ) = f [x 1 + (x 2 - x 1 )] - f (x 1 ) = f (x 1 ) f (x 2 - x 1 )] - f (x 1 ) = f (x 1 )[ f (x 2 - x 1 ) -1] ． 当 x > 0 时，有0 < f (x ) < 1， ∴ f (x 2 - x 1) < 1．∴函数 f (x ) 定义域 R 上单调递减．（4） f (x 2 + x ) < f (3 - x ) ，∴ x 2 + x > 3 - x ． ∴ x 2 + 2x - 3 > 0 ，∴ x < -3 或 x > 1 ，∴不等式的解集为： (-∞ ， -3) ⋃(1， +∞) ．12. 已知函数 f (x ) 定义域为[-1 ，1] ，若对于任意的 x ，y ∈[-1 ，1] ，都有 f (x + y ) = f (x ) + f ( y ) ，且x > 0 时，有 f (x ) > 0 ．（Ⅰ）证明函数 f (x ) 是奇函数；19 9⎩ ⎩ （Ⅱ）讨论函数 f (x ) 在区间[-1 ，1] 上的单调性；（Ⅲ）设 f （1） = 1，若 f (x ) < m 2 - 2am + 1，对所有 x ∈[-1，1] ， a ∈[-1 ，1] 恒成立，求实数m 的取值范围．【解答】证明：（Ⅰ）因为有 f (x + y ) = f (x ) + f ( y ) ，令 x = y = 0 ，得 f (0) = f (0) + f (0) ，所以 f (0) = 0 ， 令 y = -x 可得： f (0) = f (x ) + f (-x ) = 0 ， 所以 f (-x ) = - f (x ) ， 所以 f (x ) 为奇函数．（Ⅱ）由（Ⅰ）可知 f (x ) 是定义在[-1 ，1] 上的奇函数，由题意设-1 x 1 < x 2 1 ，则 f (x 2 ) - f (x 1 ) = f (x 2 ) + f (-x 1 ) = f (x 2 - x 1 )由题意 x > 0 时，有 f (x ) > 0 ，∴ f (x 2 ) > f (x 1 )∴ f (x ) 是在[-1 ，1] 上为单调递增函数；（Ⅲ）根据（Ⅰ）（Ⅱ）结论可得 f (x ) 在[-1 ，1] 上为单调递增函数，所以 f (x ) 在[-1 ，1] 上的最大值为 f （1） = 1，所以要使 f (x ) < m 2 - 2am + 1，对所有 x ∈[-1，1] ， a ∈[-1 ，1] 恒成立， 只要m 2 - 2am + 1 > 1，即m 2 - 2am > 0 ， 令 g （a ） = m 2 - 2am = -2am + m 2⎧g (-1) > 0由⎨g (1) > 0 ⎧2m + m 2 > 0 ，可得⎨-2m + m 2 > 0解得： m > 2 或m < -2故实数m 的取值范围是(-∞ ， -2) ⋃(2 ， +∞)。

函数的性质练习(奇偶性，单调性，周期性，对称性)1、定义在R 上的奇函数)(x f ，周期为6，那么方程0)(=x f 在区间[6,6-]上的根的个数可能是A.0B.1C.3D.52、f (x )是定义在R 上的以3为周期的偶函数，且f (2)＝0，则方程f (x )＝0在区间(0,6)内解的个数至少是( )A ．1B ．4C ．3D ．23、已知)(x f 是R 上的偶函数,)(x g 是R 上的奇函数,且)(x g =)1(-x f ,那么=)3120(fA.0B.2C. 2-D.2± 4、已知112)(-+=x x x f ，那么=+++++-+-+-)8()6()4()2()0()2()4()6(f f f f f f f f A.14 B.15 C. 16- D.165、已知)(x f 的定义域为R ，若)1()1(+-x f x f 、都为奇函数，则A.)(x f 为偶函数B.)(x f 为奇函数C.)(x f =)2(+x fD.)3(+x f 为奇函数6、定义在R 上的函数)(x f 对任意的实数x 都有)1()1(--=+x f x f ，则下列结论一定成立的是A.)(x f 的周期为4B. )(x f 的周期为6C. )(x f 的图像关于直线1=x 对称D. )(x f 的图像关于点(1 , 0) 对称 7、定义在R 上的函数)(x f 满足:)()(x f x f -=-,)1()1(x f x f -=+，当∈x [1-, 1] 时，3)(x x f =，则=)2013(fA.1-B.0C.1D.28、定义在R 上的函数)(x f 对任意的实数x 都有)2()2(x f x f -=+，并且)1(+x f 为 偶函数. 若3)1(=f ，那么=)101(fA.1B.2C.3D.49、已知f (x )(x ∈R)为奇函数，f (2)＝1，f (x ＋2)＝f (x )＋f (2)，则f (3)等于( )A.12 B ．1 C.32 D ．2 10、若奇函数f (x )(x ∈R)满足f (3)＝1，f (x ＋3)＝f (x )＋f (3)，则f ⎝⎛⎭⎫32 等于( )A ．0B ．1 C.12 D ．－1211、已知定义在R 上的奇函数f (x )满足f (x －4)＝－f (x )，且在区间[0,2]上是增函数，则( )A ．f (－25)<f (11)<f (80)B ．f (80)<f (11)<f (－25)C ．f (11)<f (80)<f (－25)D ．f (－25)<f (80)<f (11)12、设()f x 为定义在R 上的奇函数，满足()()2f x f x +=-，当01x ≤≤时()f x x =，则 ()7.5f 等于 （ ）A ．0.5B ．0.5-C ．1.5D ． 1.5-13、设()f x 是定义在R 上的偶函数,且在(－∞,0)上是增函数,则()2f -与()223f a a -+ （a R ∈）的大小关系是 （ ）A ．()2f -<()223f a a -+B ．()2f -≥()223f a a -+C ．()2f ->()223f aa -+D ．与a 的取值无关14、若函数()f x 为奇函数，且当0x >时，()1f x x =-，则当0x <时，有 （ ）A ．()f x 0>B ．()f x 0<C ．()f x ()f x -≤0D ．()f x －()f x -0> 15、已知函数()()2212f x x a x =+-+在区间(]4,∞-上是减函数，则实数a 的取值范围是（ ）A ．a ≤－3B ．a ≥－3C ．a ≤5D ．a ≥317、已知函数()()221,f x x ax b b a b R =-++-+∈对任意实数x 都有()()11f x f x -=+ 成立，若当[]1,1x ∈-时，()0f x >恒成立,则b 的取值范围是 （ ） A ．10b -<< B ．2b >C ．12b b <->或 D ．不能确定 18、已知函数()()2223f x x x =+-，那么（ ）A ．()y f x =在区间[]1,1-上是增函数B ．()y f x =在区间(],1-∞-上是增函数C ．()y f x =在区间[]1,1-上是减函数D ．()y f x =在区间(],1-∞-上是减函数19、函数()y f x =在()0,2上是增函数，函数()2y f x =+是偶函数，则下列结论中正确的 是 （ ） A ．()57122f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭B ．()57122f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭ C ．()75122f f f ⎛⎫⎛⎫<<⎪ ⎪⎝⎭⎝⎭D ．()75122f f f ⎛⎫⎛⎫<< ⎪ ⎪⎝⎭⎝⎭20、设函数()f x 是R 上的奇函数，且当0x >时，()23xf x =-，则()2f -等于（ ）A ．1-B ．114C ．1D ．114-21、设函数)(x f 是R 上的偶函数,且在()+∞,0上是减函数,且12210x x x x >>+，,则 A.)()(21x f x f > B.)()(21x f x f = C.)()(21x f x f < D.不能确定23、已知函数=)(x f ⎩⎨⎧<-≥-0,10,sin x e x x x x ，若)()2(2a f a f >-，则实数a 取值范围是A. (1,-∞-)),2(+∞YB. (1,2-)C. (2,1-)D. (2,-∞-)+∞,1(Y )A ．0B ．1C ．2D ．3二、填空题：24、设()y f x =是R 上的减函数，则()3y fx =-的单调递减区间为25、已知()f x 为偶函数，()g x 是奇函数，且()f x ()22g x x x -=+-，则()f x 、()g x 分别为 ; 26、定义在()1,1-上的奇函数()21x mf x x nx +=++，则常数m = ，n = ；28、．已知函数(),f x 当,x y R ∈时，恒有()()()f x y f x f y +=+.(1)求证: ()f x 是奇函数;(2)若(3),(24)f a a f -=试用表示.29、若()f x 是定义在()0,+∞上的增函数，且()()x f f x f y y ⎛⎫=- ⎪⎝⎭⑴求()1f 的值；⑵若()61f =，解不等式()132f x f x ⎛⎫+-< ⎪⎝⎭．30．函数()f x 对于x>0有意义，且满足条件(2)1,()()(),()f f xy f x f y f x ==+是减函数。

专题07 函数的单调性、奇偶性、周期性与对称性（知识梳理）一、函数的单调性(一)函数的单调性和单调区间定义：1、增函数与减函数的定义：设函数)(x f y =的定义域为A ，区间A M ⊆，如果取区间M 中的任意两个值1x 、2x ，改变量012>-=∆x x x ，则当0)()(12>-=∆x f x f y 时，就称函数)(x f y =在区间M 上是增函数；当0)()(12<-=∆x f x f y 时，就称函数)(x f y =在区间M 上是减函数。

2、函数的单调性与单调区间：如果一个函数在某个区间M 上是增函数或是减函数，就说这个函数在这个区间M 上具有单调性(区间M 称为单调区间)。

此时也说函数是这一区间上的单调函数。

在单调区间上，增函数的图像是上升的，减函数的图像是下降的。

例1-1．下列给定函数中，在区间)10(，上单调递减的函数是( )。

A 、x x f =)(B 、)1(log )(21+=x x g C 、|1|)(+=x x h D 、12)(+=x x w【答案】B【解析】x x f =)(在)0[∞+，上是增函数，)1(log )(21+=x x g 在)1(∞+-，上是减函数，|1|)(+=x x h 在]1(--∞，上是减函数，在)1[∞+-，上是增函数，12)(+=x x w 在R 上是增函数，则)(x g 在区间)10(，上单调递减的函数，选B 。

(二)对函数单调性定义的理解1、函数的单调性是局部性质：从定义上看，函数的单调性是指函数在定义域的某个子区间上的性质，即单调区间是定义域的子集，是函数的局部特征。

函数的单调性只在定义域内讨论，可以是整个定义域，也可以是定义域的某个子区间；如果一个函数在某个区间上是单调的，那么在这个区间的子区间上也是单调的。

但在某个区间上单调，在整个定义域上不一定单调。

如函数2x y =的定义域为R ，当)0[∞+∈，x 时是增函数，当]0(，-∞∈x 时是减函数。

专题八 函数奇偶性与单调性的综合问题奇偶性与单调性的综合问题主要包括：奇偶性与单调性的判断，利用函数的奇偶性与单调性比较函数值的大小以及解不等式等．考点一 奇偶性与单调性的判断【方法总结】对于函数奇偶性与单调性的判断问题主要是应用奇偶性与单调性的定义及相关结论解决．当然对于选填题也可用特值法秒杀．【例题选讲】[例1](1)下列函数中，既是偶函数，又在(0，1)上单调递增的函数是( )A ．y ＝|log 3x |B ．y ＝x 3C ．y ＝e |x |D ．y ＝cos |x |答案 C 解析 对于A 选项，函数定义域是(0，＋∞)，故是非奇非偶函数，显然B 项中，y ＝x 3是奇函数．对于C 选项，函数的定义域是R ，是偶函数，且当x ∈(0，＋∞)时，函数是增函数，故在(0，1)上单调递增，正确．对于D 选项，y ＝cos |x |在(0，1)上单调递减．(2)已知函数f (x )＝x e|x |，则下列说法正确的是( ) A ．函数f (x )是奇函数，且在(－∞，－1)上是减函数B ．函数f (x )是奇函数，且在(－∞，－1)上是增函数C ．函数f (x )是偶函数，且在(－∞，－1)上是减函数D ．函数f (x )是偶函数，且在(－∞，－1)上是增函数答案 A 解析 由题意，函数f (x )＝x e |x |，可得其定义域为R ，又由f (－x )＝－x e|－x |＝－x e |x |＝－f (x )，即f (－x )＝－f (x )，所以函数f (x )是奇函数，当x ∈(－∞，－1)时，f (x )＝x e－x ＝x ·e x ，则f ′(x )＝e x ＋x e x ＝(1＋x )e x ，则f ′(x )<0，函数f (x )在(－∞，－1)上单调递减，故选A.(3) (2017·全国Ⅰ)已知函数f (x )＝ln x ＋ln(2－x )，则( )A ．f (x )在(0，2)上单调递增B ．f (x )在(0，2)上单调递减C ．y ＝f (x )的图象关于直线x ＝1对称D ．y ＝f (x )的图象关于点(1，0)对称答案 C 解析 f (x )的定义域为(0，2)．f (x )＝ln x ＋ln(2－x )＝ln[x (2－x )]＝ln(－x 2＋2x )．设u ＝－x 2＋2x ，x ∈(0，2)，则u ＝－x 2＋2x 在(0，1)上单调递增，在(1，2)上单调递减．又y ＝ln u 在其定义域上单调递增，∴f (x )＝ln(－x 2＋2x )在(0，1)上单调递增，在(1，2)上单调递减．∴选项A ，B 错误；∵f (x )＝ln x ＋ln(2－x )＝f (2－x )，∴f (x )的图象关于直线x ＝1对称，∴选项C 正确；∵f (2－x )＋f (x )＝[ln(2－x )＋ln x ]＋[ln x ＋ln(2－x )]＝2[ln x ＋ln(2－x )]，不恒为0，∴f (x )的图象不关于点(1，0)对称，∴选项D 错误．故选C ．(4)设函数f (x )＝ln(1＋x )＋m ln(1－x )是偶函数，则( )A ．m ＝1，且f (x )在(0，1)上是增函数B ．m ＝1，且f (x )在(0，1)上是减函数C ．m ＝－1，且f (x )在(0，1)上是增函数D ．m ＝－1，且f (x )在(0，1)上是减函数答案 B 解析 因为函数f (x )＝ln(1＋x )＋m ln(1－x )是偶函数，所以f ⎝⎛⎭⎫12＝f ⎝⎛⎭⎫－12，则(m －1)ln 3＝0，即m ＝1，则f (x )＝ln(1＋x )＋ln(1－x )＝ln(1－x 2)，因为当x ∈(0，1)时，y ＝1－x 2是减函数，故f (x )在(0，1)上是减函数．故选B ．(5)(2019·北京)设函数f (x )＝e x ＋a e －x (a 为常数)．若f (x )为奇函数，则a ＝________；若f (x )是R 上的增函数，则a 的取值范围是________．答案 －1 (－∞，0] 解析 因为f (x )＝e x ＋a e －x (a 为常数)的定义域为R ，所以f (0)＝e 0＋a e －0＝1＋a＝0，所以a ＝－1．因为f (x )＝e x ＋a e －x ，所以f ′(x )＝e x －a e －x ＝e x －a e x ．因为f (x )是R 上的增函数，所以f ′(x )≥0在R 上恒成立，即e x ≥a e x 在R 上恒成立，所以a ≤e 2x 在R 上恒成立．又e 2x ＞0，所以a ≤0，即a 的取值范围是(－∞，0]．【对点训练】1．下列函数中，既是偶函数又在区间(0，＋∞)上单调递增的是( )A ．y ＝1xB ．y ＝|x |－1C ．y ＝lg xD ．y ＝⎝⎛⎭⎫12|x | 1．答案 B 解析 y ＝1x为奇函数；y ＝lg x 的定义域为(0，＋∞)，不具备奇偶性；y ＝⎝⎛⎭⎫12|x |在(0，＋∞)上 为减函数；y ＝|x |－1在(0，＋∞)上为增函数，且在定义域上为偶函数．2．下列函数中，既是奇函数又在(0，＋∞)上单调递增的是( )A ．y ＝e x ＋e －xB ．y ＝ln(|x |＋1)C ．y ＝sin x |x |D ．y ＝x －1x2．答案 D 解析：选项A ，B 是偶函数，排除；选项C 是奇函数，但在(0，＋∞)上不是单调函数，不符合题意；选项D 中，y ＝x －1x 是奇函数，且y ＝x 和y ＝－1x 在(0，＋∞)上均为增函数，故y ＝x －1x在(0，＋∞)上为增函数，所以选项D 正确．故选D.3．已知函数f (x －1)是定义在R 上的奇函数，且在[0，＋∞)上是增函数，则函数f (x )的图象可能是( )3．答案 B 解析：选函数f (x －1)的图象向左平移1个单位，即可得到函数f (x )的图象．因为函数f (x －1)是定义在R 上的奇函数，所以函数f (x －1)的图象关于原点对称，所以函数f (x )的图象关于点(－1，0)对称，排除A ，C ，D ，故选B.4．已知f (x )＝e x －e －x 2，则下列正确的是( ) A ．奇函数，在R 上为增函数 B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数4．答案 A 解析 定义域为R ，∵f (－x )＝e －x －e x 2＝－f (x )，∴f (x )是奇函数，∵e x 是R 上的增函数，－ e －x 也是R 上的增函数，∴e x －e －x 2是R 上的增函数，故选A ． 5．已知函数f (x )满足以下两个条件：①任意x 1，x 2∈(0，＋∞)且x 1≠x 2，(x 1－x 2)·[f (x 1)－f (x 2)]<0；②对定义域内任意x 有f (x )＋f (－x )＝0，则符合条件的函数是( )A ．f (x )＝2xB ．f (x )＝1－|x |C ．f (x )＝－x 3D ．f (x )＝ln(x 2＋3)5．答案 C 解析 由条件①可知，f (x )在(0，＋∞)上单调递减，则可排除A 、D 选项，由条件②可知，f (x )为奇函数，则可排除B 选项，故选C ．考点二 比较函数值的大小【方法总结】比较函数值大小的思路：比较函数值的大小时，若自变量的值不在同一个单调区间内，要利用其函数性质，转化到同一个单调区间上进行比较，对于选择题、填空题能数形结合的尽量用图象法求解．同时要充分利用奇函数在关于原点对称的两个区间上具有相同的单调性，偶函数在关于原点对称的两个区间上具有相反的单调性．【例题选讲】[例2](1) (2019·全国Ⅰ)设f (x )是定义域为R 的偶函数，且在(0，＋∞)单调递减，则( )A ．233231(log )(2)(2)4f f f -->>B ．233231(log )(2)(2)4f f f -->> C ．233231(2)(2)(log )4f f f -->> D ．233231(2)(2)(log )4f f f -->> 答案 C 解析 根据函数f (x )为偶函数可知，f (log 314)＝f (－log 34)＝f (log 34)，因为0<322-<232-<20<log 34，且函数f (x )在(0，＋∞)单调递减，所以f (322-)>f (232-)>f (log 314)．故选C ． (2)已知函数y ＝f (x )是R 上的偶函数，当x 1，x 2∈(0，＋∞)时，都有(x 1－x 2)·[f (x 1)－f (x 2)]＜0．设a ＝ln 1m，b ＝(ln m )2，c ＝ln m ，其中m ＞e ，则( )A ．f (a )＞f (b )＞f (c )B ．f (b )＞f (a )＞f (c )C ．f (c )＞f (a )＞f (b )D ．f (c )＞f (b )＞f (a )答案 C 解析 根据已知条件知f (x )在(0，＋∞)上是减函数，且f (a )＝f (|a |)，f (b )＝f (|b |)，f (c )＝f (|c |)，|a |＝ln m ＞1，b ＝(ln m )2＞|a |，0＜c ＝12ln m ＜|a |，∴f (c )＞f (a )＞f (b )． (3)函数f (x )是定义在R 上的奇函数，对任意两个正数x 1，x 2(x 1<x 2)，都有x 2f (x 1)>x 1f (x 2)，记a ＝12f (2)，b ＝f (1)，c ＝－13f (－3)，则a ，b ，c 之间的大小关系为( ) A ．a >b >c B ．b >a >c C ．c >b >a D ．a >c >b答案 B 解析 因为对任意两个正数x 1，x 2(x 1<x 2)，都有x 2f (x 1)>x 1f (x 2)，所以f (x 1)x 1>f (x 2)x 2，得函数g (x )＝f (x )x 在(0，＋∞)上是减函数，又c ＝－13f (－3)＝13f (3)，所以g (1)>g (2)>g (3)，即b >a >c ，故选B ． 【对点训练】6．已知f (x )是定义在R 上的偶函数，且f (x )在(0，＋∞)上单调递增，则( )A ．f (0)>f (log 32)>f (－log 23)B ．f (log 32)>f (0)>f (－log 23)C ．f (－log 23)>f (log 32)>f (0)D ．f (－log 23)>f (0)>f (log 32)6．答案 C 解析 ∵log 23>log 22＝1＝log 33>log 32>0，且函数f (x )在(0，＋∞)上单调递增，∴f (log 23)>f (log 32)>f (0)，又函数f (x )为偶函数，∴f (log 23)＝f (－log 23)，∴f (－log 23)>f (log 32)>f (0)．7．函数y ＝f (x )在[0，2]上单调递增，且函数f (x ＋2)是偶函数，则下列结论成立的是( )A ．f (1)<5()2f <7()2fB ．7()2f <f (1)<5()2fC ．7()2f <5()2f <f (1)D ．5()2f <f (1)<7()2f7．答案 B 解析 ∵函数y ＝f (x )在[0，2]上单调递增，且函数f (x ＋2)是偶函数，∴函数y ＝f (x )在[2，4]上单调递减，且在[0，4]上函数y ＝f (x )满足f (2－x )＝f (2＋x )，∴f (1)＝f (3)，7()2f <f (3)<5()2f ，即7()2f <f (1)<5()2f ．8．定义在R 上的偶函数f (x )满足：对任意的x 1，x 2∈[0，＋∞)(x 1≠x 2)，有f (x 2)－f (x 1)x 2－x 1<0，则( ) A ．f (3)＜f (－2)＜f (1) B ．f (1)＜f (－2)＜f (3)C ．f (－2)＜f (1)＜f (3)D ．f (3)＜f (1)＜f (－2)8．答案 A 解析 ∵f (x )是偶函数∴f (－2)＝ f (2)，又∵任意的x 1，x 2∈[0，＋∞)(x 1≠x 2)，有f (x 2)－f (x 1)x 2－x 1<0， ∴f (x )在[0，＋∞)上是减函数，又∵1＜2＜3∴f (1)＞f (2)＝f (－2)＞f (3)，故选A ．9．(2017·全国Ⅰ)已知奇函数f (x )在R 上是增函数，g (x )＝xf (x )．若a ＝g (－log 25.1)，b ＝g (20.8)，c ＝g (3)，则a ，b ，c 的大小关系为( )A ．a <b <cB ．c <b <aC ．b <a <cD ．b <c <a9．答案 C 解析 法一 易知g (x )＝xf (x )在R 上为偶函数，∵奇函数f (x )在R 上是增函数，且f (0)＝0．∴g (x )在(0，＋∞)上是增函数．又3>log 25.1>2>20.8，且a ＝g (－log 25.1)＝g (log 25.1)，∴g (3)>g (log 25.1) >g (20.8)，则c >a >b ．法二 (特殊化)取f (x )＝x ，则g (x )＝x 2为偶函数且在(0，＋∞)上单调递增，又3>log 25.1>20.8，从而可得c >a >b ．10．已知函数y ＝f (x )是R 上的偶函数，对任意x 1，x 2∈(0，＋∞)，都有(x 1－x 2)·[f (x 1)－f (x 2)]＜0．设a ＝ln1π，b ＝(lnπ)2，c ＝ln π，则( ) A ．f (a )＞f (b )＞f (c ) B ．f (b )＞f (a )＞f (c ) C ．f (c )＞f (a )＞f (b ) D ．f (c )＞f (b )＞f (a )10．答案 C 解析 由题意易知f (x )在(0，＋∞)上是减函数，因为f (x )是R 上的偶函数，所以f (－x )＝f (x )＝f (|x |)．又因为|a |＝ln π＞1，b ＝(ln π)2＞|a |，0＜c ＝ln π2＜|a |，所以f (c )＞f (|a |)＞f (b )．又由题意知，f (a )＝f (|a |)．所以f (c )＞f (a )＞f (b )．11．已知函数f (x )＝a x (a >0，a ≠1)的反函数的图象经过点⎝⎛⎭⎫22，12．若函数g (x )的定义域为R ，当x ∈[－2， 2]时，有g (x )＝f (x )，且函数g (x ＋2)为偶函数，则下列结论正确的是( )A ．g (π)<g (3)<g (2)B ．g (π)<g (2)<g (3)C ．g (2)<g (3)<g (π)D ．g (2)<g (π)<g (3)11．答案 C 解析：因为函数f (x )的反函数的图象经过点⎝⎛⎭⎫22，12，所以函数f (x )的图象经过点⎝⎛⎭⎫12，22， 所以a 12＝22，即a ＝12，函数f (x )在R 上单调递减．函数g (x ＋2)为偶函数，所以函数g (x )的图象关于直线x ＝2对称，又x ∈[－2，2]时，g (x )＝f (x )且g (x )单调递减，所以x ∈[2，6]时，g (x )单调递增，根据对称性，可知在[－2，6]上距离对称轴x ＝2越远的自变量，对应的函数值越大，所以g (2)<g (3)<g (π)．故选C.12．已知定义在R 上的函数f (x )满足下列三个条件：①对任意的x ∈R 都有f (x ＋2)＝－f (x )；②对任意的0≤x 1<x 2≤2，都有f (x 1)<f (x 2)；③f (x ＋2)的图象关于y 轴对称．则f (4.5)，f (6.5)，f (7)的大小关系是________．(用“<”连接)12．答案 f (4.5)<f (7)<f (6.5) 解析：由①可知，f (x )是一个周期为4的函数；由②可知，f (x )在[0，2]上是增函数；由③可知，f (x )的图象关于直线x ＝2对称．故f (4.5)＝f (0.5)，f (6.5)＝f (2.5)＝f (1.5)，f (7)＝f (3)＝f (1)，f (0.5)<f (1)<f (1.5)，即，f (4.5)<f (7)<f (6.5)．考点三 解不等式(抽象函数)【方法总结】含“f ”不等式的解法：首先根据函数的性质把不等式转化为f (g (x ))>f (h (x ))的形式，然后根据函数的单调性去掉“f ”，转化为具体的不等式(组)，此时要注意g (x )与h (x )的取值应在外层函数的定义域内．要注意奇偶性中结论8：奇函数在两个对称的区间上具有相同的单调性；偶函数在两个对称的区间上具有相反的单调性的应用．特别应用奇偶性中结论2：如果函数f (x )是偶函数，那么f (x )＝f (|x |)，可避免分类讨论．【例题选讲】[例3](1)(2017·全国Ⅰ)函数f (x )在(－∞，＋∞)上单调递减，且为奇函数．若f (1)＝－1，则满足－1≤f (x －2)≤1的x 的取值范围是( )A ．[－2，2]B ．[－1，1]C ．[0，4]D ．[1，3]答案 D 解析 ∵f (x )为奇函数，∴f (－x )＝－f (x )．∵f (1)＝－1，∴f (－1)＝－f (1)＝1．故由－1≤f (x －2)≤1，得f (1)≤f (x －2)≤f (－1)．又f (x )在(－∞，＋∞)上单调递减，∴－1≤x －2≤1，∴1≤x ≤3．(2)已知定义域为(－1，1)的奇函数f (x )是减函数，且f (a －3)＋f (9－a 2)<0，则实数a 的取值范围是( )A ．(22，3)B ．(3，10)C ．(22，4)D ．(－2，3)答案 A 解析 由f (a －3)＋f (9－a 2)<0得f (a －3)<－f (9－a 2)．又由奇函数性质，得f (a －3)<f (a 2－9)．因为f (x )是定义域为(－1，1)的减函数，所以⎩⎪⎨⎪⎧ －1<a －3<1，－1<a 2－9<1，a －3>a 2－9，解得22<a <3．(3)设f (x )为奇函数，且在(－∞，0)内是减函数，f (－2)＝0，则xf (x )<0的解集为( )A ．(－1，0)∪(2，＋∞)B ．(－∞，－2)∪(0，2)C ．(－∞，－2)∪(2，＋∞)D ．(－2，0)∪(0，2)答案 C 解析 ∵f (x )为奇函数，且在(－∞，0)内是减函数，f (－2)＝0，∴f (－2)＝－f (2)＝0，在(0，＋∞)内是减函数．若xf (x )<0，则⎩⎪⎨⎪⎧ x >0，f (x )<0＝f (2)或⎩⎪⎨⎪⎧x <0，f (x )>0＝f (－2).根据f (x )在(－∞，0)内是减函数，在(0，＋∞)内是减函数，解得：x ∈(－∞，－2)∪(2，＋∞)．故选．(4)已知函数y ＝f (x )是定义域为R 的偶函数，且f (x )在[0，＋∞)上单调递增，则不等式f (2x －1)>f (x －2)的解集为________．答案 (－∞，－1)∪(1，＋∞) 解析 ∵函数y ＝f (x )是定义域为R 的偶函数，∴f (2x －1)>f (x －2)可转化为f (|2x －1|)>f (|x －2|)，又∵f (x )在[0，＋∞)上单调递增，∴f (2x －1)>f (x －2)⇔|2x －1|>|x －2|，两边平方解得：x ∈(－∞，－1)∪(1，＋∞) ，故f (2x －1)>f (x －2)的解集为x ∈(－∞，－1)∪(1，＋∞)．(5)已知f (x )是定义在R 上的偶函数，且在区间(－∞，0)上单调递增．若实数a 满足f (2|a －1|)>f (－2)，则a 的取值范围是________．答案 ⎝⎛⎭⎫12，32 解析 ∵f (2|a －1|)>f (－2)＝f (2)，又由已知可得f (x )在(0，＋∞)上单调递减，∴2|a －1|<2＝122，∴|a －1|<12，∴12<a <32． (6)若函数f (x )是定义在R 上的偶函数，且在区间[0，＋∞)上是单调递增的．如果实数t 满足f (ln t )＋f ⎝⎛⎭⎫ln 1t ≤2f (1)，那么t 的取值范围是________．答案 ⎣⎡⎦⎤1e ，e 解析 由于函数f (x )是定义在R 上的偶函数，所以f (ln t )＝f ⎝⎛⎭⎫ln 1t ，由f (ln t )＋f ⎝⎛⎭⎫ln 1t ≤2f (1)，得f (ln t )≤f (1)．又函数f (x )在区间[0，＋∞)上是单调递增的，所以|ln t |≤1，即－1≤ln t ≤1，故1e≤t ≤e ． (7)已知定义在R 上的函数f (x )在[1，＋∞)上单调递减，且f (x ＋1)是偶函数，不等式f (m ＋2)≥f (x －1)对任意的x ∈[－1，0]恒成立，则实数m 的取值范围是( )A ．[－3，1]B ．[－4，2]C ．(－∞，－3]∪[1，＋∞)D ．(－∞，－4]∪[2，＋∞) 答案 A 解析 因为f (x ＋1)是偶函数，所以f (－x ＋1)＝f (x ＋1)，所以f (x )的图象关于x ＝1对称，由f (m ＋2)≥f (x －1)得|(m ＋2)－1|≤|(x －1)－1|，即|m ＋1|≤|x －2|在x ∈[－1，0]恒成立，所以|m ＋1|≤|x －2|min ，所以|m ＋1|≤2，解得－3≤m ≤1．(8)已知函数y ＝f (x )的定义域为R ，f (x ＋1)为偶函数，且对∀x 1<x 2≤1，满足f (x 2)－f (x 1)x 2－x 1<0．若f (3)＝1，则不等式f (log 2x )<1的解集为( )A ．⎝⎛⎭⎫12，8B ．(1，8)C ．⎝⎛⎭⎫0，12∪(8，＋∞) D ．(－∞，1)∪(8，＋∞) 答案 A 解析 因为对∀x 1<x 2≤1，满足f (x 2)－f (x 1)x 2－x 1<0，所以y ＝f (x )当x ∈(－∞，1]时，是单调递减函数，又因为f (x ＋1)为偶函数，所以函数y ＝f (x )的图象关于x ＝1对称，所以函数y ＝f (x )当x >1时，是增函数，又因为f (3)＝1，所以有f (－1)＝1，当log 2x ≤1时，即当0<x ≤2时，f (log 2x )<1⇒f (log 2x )<f (－1)⇒log 2x >－1⇒x >12，∴12<x ≤2，当log 2x >1时，即当x >2时，f (log 2x )<1⇒f (log 2x )<f (3)⇒log 2x <3⇒x <8，∴2<x <8，综上所述：不等式f (log 2x )<1的解集为⎝⎛⎭⎫12，8，故选A ．(9)已知函数f (x )是定义在R 上的奇函数，若对于任意给定的不等实数x 1、x 2，不等式x 1f (x 1)＋x 2f (x 2)<x 1f (x 2)＋x 2f (x 1)恒成立，则不等式f (1－x )<0的解集为( )A ．(－∞，0)B ．(0，＋∞)C ．(－∞，1)D ．(1，＋∞)答案 C 解析 由条件式得(x 1－x 2)[f (x 1)－f (x 2)]<0，∴x 1<x 2时，f (x 1)>f (x 2)，x 1>x 2时，f (x 1)<f (x 2)，∴f (x )为减函数，又f (x )为R 上的奇函数，∴f (0)＝0，∴不等式f (1－x )<0化为f (1－x )<f (0)，∴1－x >0，∴x <1，故选C ．(10)定义在R 上的函数f (x )对任意0<x 2<x 1都有f (x 1)－f (x 2)x 1－x 2<1，且函数y ＝f (x )的图象关于原点对称，若f (2)＝2，则不等式f (x )－x >0的解集是( )A ．(－2，0)∪(0，2)B ．(－∞，－2)∪(2，＋∞)C ．(－∞，－2)∪(0，2)D ．(－2，0)∪(2，＋∞)答案 C 解析 由f (x 1)－f (x 2)x 1－x 2<1，可得[f (x 1)－x 1]－[f (x 2)－x 2]x 1－x 2<0．令F (x )＝f (x )－x ，由题意知F (x )在(－∞，0)，(0，＋∞)上是减函数，且是奇函数，F (2)＝0，F (－2)＝0，所以结合图象，令F (x )>0，得x <－2或0<x <2．故选C ．【对点训练】13．已知定义在R 上的奇函数y ＝f (x )在(0，＋∞)内单调递增，且f ⎝⎛⎭⎫12＝0，则f (x )>0的解集为_______________． 13．答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪－12<x <0或x >12 解析 由奇函数y ＝f (x )在(0，＋∞)内单调递增，且f ⎝⎛⎭⎫12＝0，可知函数y＝f (x )在(－∞，0)内单调递增，且f ⎝⎛⎭⎫－12＝0．由f (x )>0，可得x >12或－12<x <0． 14．已知f (x )是定义在R 上的奇函数，且在[0，＋∞)上单调递增．若实数m 满足f (log 3|m －1|)＋f (－1)<0，则m 的取值范围是( )A ．(－2，1)∪(1，4)B ．(－2，1)C ．(－2，4)D ．(1，4)14．答案 A 解析 因为f (x )是定义在R 上的奇函数，且在[0，＋∞)上单调递增，所以函数f (x )是R 上的增函数，由题得f (log 3|m －1|)＋f (－1)<0，所以f (log 3|m －1|)<－f (－1)＝f (1)，所以log 3|m －1|<1＝log 33，所以|m －1|＜3，所以－3＜m －1＜3，所以－2＜m ＜4，因为|m －1|>0，所以m ≠1，故m ∈(－2，1)∪(1，4)．故选A ．15．设奇函数f (x )在(0，＋∞)上为增函数，且f (1)＝0，则不等式f (x )－f (－x )x＜0的解集为________． 15．答案 (－1，0)∪(0，1) 解析 ∵f (x )为奇函数，且在(0，＋∞)上是增函数，f (1)＝0，∴f (－1)＝－f (1)＝0，f (x )在(－∞，0)上也是增函数，f (x )－f (－x )x ＝2f (x )x ＜0，即⎩⎪⎨⎪⎧x ＞0，f (x )＜0或⎩⎪⎨⎪⎧x ＜0，f (x )＞0，根据f (x )在(－∞，0)和(0，＋∞)上都是增函数，且f (－1)＝f (1)＝0，解得x ∈(－1，0)∪(0，1)．16．已知函数f (x )是定义在R 上的奇函数，且在区间[0，＋∞)上单调递增，若|f (ln x )－f (ln 1x )|2<f (1)，则x 的 取值范围是( )A ．(0，1e )B ．(0，e)C ．(1e，e) D ．(e ，＋∞) 16．答案 C 解析 因为函数f (x )是定义在R 上的奇函数，所以f (ln x )－f (ln 1x)＝f (ln x )－f (－ln x )＝f (ln x )＋ f (ln x )＝2f (ln x )，所以|f (ln x )－f (ln 1x )|2<f (1)等价于|f (ln x )|<f (1)，又f (x )在区间[0，＋∞)上单调递增，所以－1<ln x <1，解得1e<x <e ． 17．已知偶函数f (x )在区间[0，＋∞)上单调递增，则满足f (2x －1)＜f ⎝⎛⎭⎫13的x 的取值范围是( )A ．⎝⎛⎭⎫13，23B ．⎣⎡⎭⎫13，23C ．⎝⎛⎭⎫12，23D ．⎣⎡⎭⎫12，23 17．答案 A 解析 因为f (x )是偶函数，所以其图象关于y 轴对称，又f (x )在[0，＋∞)上单调递增，f (2x－1)＜f ⎝⎛⎭⎫13，所以|2x －1|＜13，所以13＜x ＜23． 18．已知定义域为R 的偶函数f (x )在(－∞，0]上是减函数，且f (1)＝2，则不等式f (log 2x )>2的解集为( )A ．(2，＋∞)B ．⎝⎛⎭⎫0，12∪(2，＋∞)C ．⎝⎛⎭⎫0，22∪(2，＋∞) D ．(2，＋∞) 18．答案 B 解析 f (x )是R 上的偶函数，且在(－∞，0]上是减函数，所以f (x )在[0，＋∞)上是增函数，所以f (log 2x )>2＝f (1)⇔f (|log 2x |)>f (1)⇔|log 2x |>1⇔log 2x >1或log 2x <－1⇔x >2或0<x <12． 19．设定义在[－2，2]上的偶函数f (x )在区间[0，2]上单调递减，若f (1－m )<f (m )，则实数m 的取值范围是________．19．答案 ⎣⎡⎭⎫－1，12 解析 因为f (x )是偶函数，所以f (－x )＝f (x )＝f (|x |)．所以不等式f (1－m )<f (m )等价于f (|1－m |)<f (|m |)．又当x ∈[0，2]时，f (x )是减函数．所以⎩⎪⎨⎪⎧ |1－m |>|m |，－2≤1－m ≤2，－2≤m ≤2，解得－1≤m <12． 20．设f (x )是定义在[－2b ，3＋b ]上的偶函数，且在[－2b ，0]上为增函数，则f (x －1)≥f (3)的解集为( )A ．[－3，3]B ．[－2，4]C ．[－1，5]D ．[0，6]20．答案 B 解析 因为f (x )是定义在[－2b ，3＋b ]上的偶函数，所以有－2b ＋3＋b ＝0，解得b ＝3，由函数f (x )在[－6，0]上为增函数，得f (x )在(0，6]上为减函数．故f (x －1)≥f (3)⇒f (|x －1|)≥f (3)⇒|x －1|≤3，故－2≤x ≤4．21．已知函数y ＝f (x )是定义在R 上的偶函数，且在(－∞，0]上是增函数，若不等式f (a )≥f (x )对任意x ∈[1，2]恒成立，则实数a 的取值范围是( )A ．(－∞，1]B ．[－1，1]C ．(－∞，2]D ．[－2，2]21．答案 B 解析 因为函数f (x )为偶函数，且在(－∞，0]上是增函数，所以函数f (x )在[0，＋∞)上是减函数，则不等式f (a )≥f (x )对任意x ∈[1，2]恒成立等价于f (a )≥f (x )max ＝f (1)，所以|a |≤1，解得－1≤a ≤1，即实数a 的取值范围为[－1，1]，故选B ．22．已知f (x )是偶函数，且f (x )在[0，＋∞)上是增函数，如果f (ax ＋1)≤f (x －2)在x ∈⎣⎡⎦⎤12，1上恒成立，那么实数a 的取值范围是( )A ．[－2，1]B ．[－5，0]C ．[－5，1]D ．[－2，0]22．答案 D 解析 因为f (x )是偶函数，且f (x )在[0，＋∞)上是增函数，所以f (ax ＋1)≤f (x －2)在x ∈⎣⎡⎦⎤12，1上恒成立，即|ax ＋1|≤|x －2|，即x －2≤ax ＋1≤2－x .由ax ＋1≤2－x ，得ax ≤1－x ，a ≤1x －1，而1x－1在x ＝1时取得最小值0，故a ≤0.同理，由x －2≤ax ＋1，得a ≥－2，所以a 的取值范围是[－2，0]．考点四 解不等式(具体函数)【方法总结】函数是给定的，但解析式比较复杂，一般不把自变量代入处理．而是先研究函数的单调性与奇偶性，然后把不等式转化为f (g (x ))>f (h (x ))的形式，根据函数的单调性去掉“f ”，转化为具体的不等式(组)去解决问题．要注意奇偶性中结论8：奇函数在两个对称的区间上具有相同的单调性；偶函数在两个对称的区间上具有相反的单调性的应用．特别应用奇偶性中结论2：如果函数f (x )是偶函数，那么f (x )＝f (|x |)，可避免分类讨论．【例题选讲】[例4](1)已知函数f (x )＝sin x ＋x ，对任意的m ∈[－2，2]，f (mx －2)＋f (x )<0恒成立，则x 的取值范围是________．答案 －2<x <23解析 易知f (x )在R 上为单调递增函数，且f (x )为奇函数，故f (mx －2)＋f (x )<0等价于f (mx －2)<－f (x )＝f (－x )，则mx －2<－x ，即mx ＋x －2<0对所有m ∈[－2，2]恒成立，令h (m )＝mx ＋x －2，m∈[－2，2]，此时，只需⎩⎪⎨⎪⎧h (－2)<0，h (2)<0即可，解得－2<x <23． (2)若f (x )＝e x －a e －x 为奇函数，则满足f (x －1)>1e 2－e 2的x 的取值范围是( ) A ．(－2，＋∞) B ．(－1，＋∞) C ．(2，＋∞) D ．(3，＋∞)答案 B 解析 由f (x )＝e x －a e －x 为奇函数，得f (－x )＝－f (x )，即e －x －a e x ＝a e －x －e x ，得a ＝1，所以f (x )＝e x －e －x ，则f (x )在R 上单调递增，又f (x －1)>1e 2－e 2＝f (－2)，所以x －1>－2，解得x >－1，故选B ． (3)设函数f (x )＝ln(1＋|x |)－11＋x 2，则使得f (x )>f (2x －1)成立的x 的取值范围为______________． 答案 ⎝⎛⎭⎫13，1 解析 由已知得函数f (x )为偶函数，所以f (x )＝f (|x |)，由f (x )>f (2x －1)，可得f (|x |)>f (|2x－1|)．当x >0时，f (x )＝ln(1＋x )－11＋x 2，因为y ＝ln(1＋x )与y ＝－11＋x 2在(0，＋∞)上都单调递增，所以函数f (x )在(0，＋∞)上单调递增．由f (|x |)>f (|2x －1|)，可得|x |>|2x －1|，两边平方可得x 2>(2x －1)2，整理得3x 2－4x ＋1<0，解得13<x <1．所以符合题意的x 的取值范围为⎝⎛⎭⎫13，1． (4)已知g (x )是定义在R 上的奇函数，且当x <0时，g (x )＝－ln(1－x )，函数f (x )＝⎩⎪⎨⎪⎧x 3，x ≤0，g (x )，x >0，若f (2－x 2)>f (x )，则x 的取值范围是( )A ．(－∞，－2)∪(1，＋∞)B ．(－∞，1)∪(2，＋∞)C ．(－2，1)D ．(1，2)答案 C 解析 因为g (x )是定义在R 上的奇函数，且当x <0时，g (x )＝－ln(1－x )，所以当x >0时，－x <0，g (－x )＝－ln(1＋x )，即当x >0时，g (x )＝ln(1＋x )，因为函数f (x )＝⎩⎪⎨⎪⎧ x 3，x ≤0，g (x )，x >0，所以函数f (x )＝⎩⎪⎨⎪⎧x 3，x ≤0ln (1＋x )，x >0.函数f (x )的图象如下：可判断f (x )＝⎩⎪⎨⎪⎧x 3，x ≤0，ln (1＋x )，x >0.在(－∞，＋∞)上单调递增．因为f (2－x 2)>f (x )，所以2－x 2>x ，解得－2<x <1．故选C ．(5)已知函数f (x )＝⎩⎪⎨⎪⎧ －x 2＋2x ，x >0，0，x ＝0，x 2＋mx ，x <0是奇函数．若函数f (x )在区间[－1，a －2]上单调递增，则实数a的取值范围是____________．答案 解(1，3]析 设x <0，则－x >0，所以f (－x )＝－(－x )2＋2(－x )＝－x 2－2x ．又f (x )为奇函数，所以f (－x )＝－f (x )，于是x <0时，f (x )＝x 2＋2x ＝x 2＋mx ，所以m ＝2．要使f (x )在[－1，a －2]上单调递增，结合f (x )的图象(如图所示)知⎩⎪⎨⎪⎧ a －2>－1，a －2≤1，所以1<a ≤3，故实数a 的取值范围是(1，3]．【对点训练】23．已知函数f (x )＝x 3＋2x ，若f (1)＋f (1log a3)>0(a >0且a ≠1)，则实数a 的取值范围是____________．23．答案 (0，1)∪(3，＋∞) 解析 因为函数f (x )＝x 3＋2x 是奇函数，且在R 上是增函数，f (1)＋f (1log a3)>0，所以f (1log a 3)>－f (1)＝f (－1)，所以1log a 3>－1，所以⎩⎪⎨⎪⎧ 1a >1，0<a <3或⎩⎪⎨⎪⎧ 0<1a <1，3<a ，所以a ∈(0，1)∪(3，＋∞)．24．已知函数f (x )＝12x －2x ，则满足f (x 2－5x )＋f (6)>0的实数x 的取值范围是________． 24．答案 (2，3) 解析 根据题意，函数f (x )＝12x －2x ，f (－x )＝12－x －2－x ＝－⎝⎛⎭⎫12x －2x ＝－f (x )，即函数f (x ) 为奇函数，又由y ＝12x 在R 上为减函数，y ＝－2x 在R 上为减函数，则函数f (x )在R 上为减函数，则f (x 2－5x )＋f (6)>0⇒f (x 2－5x )>－f (6)⇒f (x 2－5x )>f (－6)⇒x 2－5x <－6，解得2<x <3，即x 的取值范围为(2，3)．25．已知定义在R 上的奇函数f (x )满足：当x >0时，f (x )＝2x －2x ，则f (x )x>0的解集为( ) A ．(－1，0)∪(0，1) B ．(－1，0)∪(1，＋∞)C ．(－∞，－1)∪(0，1)D ．(－∞，－1)∪(1，＋∞)25．答案 D 解析 因为当x >0时，函数f (x )单调递增，又f (1)＝0，所以f (x )＝2x －2x>0的解集为(1，＋ ∞)，所以f (x )x ＞0在(0，＋∞)上的解集为(1，＋∞)．因为f (x )是奇函数，所以f (x )x 是偶函数，则f (x )x>0在R 上的解集为(－∞，－1)∪(1，＋∞)．26．已知函数f (x )＝⎩⎪⎨⎪⎧x 2＋2x (x ≥0)，2x －x 2(x <0)，函数g (x )＝|f (x )|－1，若g (2－a 2)>g (a )，则实数a 的取值范围是( ) A ．(－2，1) B ．(－∞，－2)∪(2，＋∞)C ．(－2，2)D ．(－∞，－2)∪(－1，1)∪(2，＋∞)26．答案 D 解析 由题可知，f (x )为单调递增的奇函数，则g (x )为偶函数，又g (2－a 2)>g (a )，因此|2－a 2|>|a |，即(2－a 2)2>a 2，利用换元法解得a 的取值范围是(－∞，－2)∪(－1，1)∪(2，＋∞)．故选D ．。

函数的性质-单调性、奇偶性、周期性、对称性目录一、常规题型方法1题型一函数的单调性1题型二函数的奇偶性4题型三单调性与奇偶性的综合应用10题型四函数的周期性13题型五函数的对称性18题型六周期性与对称性的综合应用22二、针对性巩固练习26练习一函数的单调性26练习二函数的奇偶性28练习三单调性与奇偶性的综合应用30练习四函数的周期性32练习五函数的对称性34练习六周期性与对称性的综合应用36常规题型方法题型一函数的单调性【典例分析】典例1-1．(2020·天津·高一期末)函数f (x )=log 13-x 2+6x -5 的单调递减区间是( )A.(-∞,3]B.[3,+∞)C.(1,3]D.[3,5)【答案】C 【分析】首先由函数解析式，求其定义域，根据复合函数的单调性，结合对数函数与二次函数的单调性，可得答案.【详解】由f x =log 13-x 2+6x -5 ，则-x 2+6x -5>0，x -5 x -1 <0，解得1<x <5，即函数f x 的定义域1,5 ，由题意，令g x =log 13x ，h x =-x 2+6x -5，则f x =g h x ，易知g x 在其定义域上单调递减，要求函数f x 的单调递减区间，需求在1,5 上二次函数h x 的递增区间，由h x =-x 2+6x -5=-x -3 2+4，则在1,5 上二次函数h x 的递增区间为1,3 ，故选：C .典例1-2．(2022·湖北武汉·高一期中)若二次函数f x =ax 2+a +6 x -5在区间-∞，1 为增函数，则a 的取值范围为( )A.-2，0B.-2，0C.-2，0D.-2，0【答案】A 【分析】根据条件确定二次函数的图象应开口向下，再利用端点值和对称轴比较大小.【详解】当a <0时，-a +62a≥1，解得：a ≥-2，所以-2≤a <0，当a >0时，不满足条件，综上可知：-2≤a <0故选：A典例1-3．(浙江省台州山海协作体2022-2023学年高一上学期期中联考数学试题)已知函数f x =x 2-2ax +52a ,x ≤1ax ,x >1 是定义在R 上的减函数，则实数a 的取值范围为( )A.1,2B.1,2C.1,+∞D.0,1【答案】A 【分析】根据二次函数和反比例函数的单调性，结合分割点处函数值之间的关系，列出不等式，求解即可.【详解】解：因为函数f x =x 2-2ax +52a ,x ≤1a x,x >1 是定义在R 上的减函数，所以a ≥1a >01-2a +52a ≥a解得1≤a ≤2，即a ∈1,2 .故选：A .【方法技巧总结】1.函数单调性的判断方法有：定义法、性质法、图像法、导数法。