2014-2015-并行程序设计期末考试卷
- 格式:doc
- 大小:52.00 KB
- 文档页数:2

并行计算期末试题及答案1. 基础概念部分并行计算是一种计算模式,它使用多个处理单元同时执行计算操作,以加快计算速度。
在现代计算机系统中,我们常常使用多核处理器、图形处理器(GPU)或者分布式系统来实现并行计算。
1.1 并行计算的优势并行计算具有以下几个优势:加速计算速度:通过同时执行多个计算任务,可以极大地提高计算效率。
解决大规模问题:并行计算可以处理大规模和复杂的问题,提供更精确的结果。
降低能耗:通过合理利用处理器资源,可以降低计算任务的能耗。
应用广泛:并行计算可以应用于各个领域,如科学计算、大数据分析、机器学习等。
1.2 并行计算的分类并行计算按照任务之间的关系可以分为两类:数据并行:将数据划分为多个子集,同时在不同的处理器上进行计算,然后将计算结果汇总。
常见的应用包括矩阵运算、图像处理等。
任务并行:将任务划分为多个子任务,每个子任务由一个独立的处理器执行,最后将各个子任务的结果合并。
常见的应用包括并行搜索算法、并行排序等。
2. 并行计算的算法设计2.1 并行算法设计要点在设计并行算法时,需要考虑以下几个要点:任务划分:将计算任务划分为多个子任务,确保各个子任务之间的计算工作均衡,并保持任务之间的独立性。
任务调度:合理安排各个处理器上的任务执行顺序和时间,最大程度地减少通信开销和等待时间。
数据通信:处理器之间需要进行数据交换和通信,应选择合适的通信方式,并考虑通信延迟和带宽等因素。
数据同步:在多个处理器之间,可能需要进行数据同步操作,确保各个处理器之间的数据一致性。
2.2 并行算法实例:并行矩阵乘法并行矩阵乘法是一个常见的数据并行算法,可以有效地利用多核处理器加速大规模矩阵运算。
具体算法如下:步骤1:将输入矩阵划分为若干个小矩阵,每个小矩阵分配给一个处理器。
步骤2:每个处理器计算相应小矩阵的部分结果。
步骤3:将各个处理器计算得到的部分结果进行求和,得到最终的矩阵乘积结果。
3. 并行计算的应用举例3.1 科学计算在科学计算领域,有大量的计算任务需要处理大规模的数据和复杂的数学模型。

研究生院2014-2015学年《面向对象程序设计》考试试卷开卷一、填空(共15分,每空1分)1、编译时的多态性通过__重载__函数实现。
2、面向对象的四个基本特性是_抽象__、__多态性_、__继承性__和_封装性_。
3. 假定AB为一个类,则执行“AB a(2), b[4],*p[4];”语句时调用该类构造函数的次数为__5__。
4.要实现动态联编必须通过对象指针或引用来调用_虚函数_实现。
5.在函数前面用_ inline _保留字修饰时,则表示该函数表为内联函数。
6.如果将一个对象说明为常对象,则通过该对象只能调用它的__公有成员__函数。
7、非成员函数应声明为类的__友元___函数才能访问这个类的private成员。
8、在用class定义一个类时,数据成员和成员函数的默认访问权限是_ 私有____。
9、运算符重载函数可能是类的_友元_函数,也可以是类的_成员_函数,还可以是普通函数。
10、__转换构造函数__函数可以将一个指定的数据转换为类的对象,_类型转换函数_函数实现类的对象转换成其它类型的数据。
二、简答题(共25分,每小题5分)1、什么是类模板,类模板声明的一般形式是什么?答案:类模板是对一批仅仅成员数据类型不同的类的抽象,程序员只要为这一批类所组成的整个类家族创建一个类模板,给出一套程序代码,就可以用来生成多种具体的类,(这类可以看作是类模板的实例),从而大大提高编程的效率。
定义类模板的一般形式是:template <类型名参数名1,类型名参数名2,…>class 类名{类声明体};2、有哪几种继承方式?每种方式的派生类对基类成员的继承性如何?答案:继承方式包括:public、private、protected。
3、简述运算符重载的实现方式有哪几种?给出对应的声明语法形式。
答案:(1)类外定义的运算符重载函数格式为:friend <返回类型> operator <op>(<类型> 参数1,<类型> 参数2) { <函数体> }(2)成员运算符重载函数<返回类型> <类名>::operator <op> (<类型> 参数){ <函数体> }4、写出下面程序的输出结果#include<iostream.h>#include<string.h>class Person{}答案:第1次调用类型转换构造函数!第2次调用类型转换构造函数!调用复制构造函数!OldObjectOldObjectNewObject第1次调用析构函数!OldObject第2次调用析构函数!第3次调用析构函数!5. 写运行结果#include <iostream>using namespace std;class A{};答案:(A,B,C,D)= 31,2,3,4三、改错题(共20分,每小题4分)1. 以下程序可动态分配二维数组并释放内存,且可实现二维指针和一维指针复用,试问程序能否正常运行,如不能运行找出原因并改正之。

2014-2015第二学期《Visual Basic程序设计》期末试卷(B)1.工程文件的扩展名是()。
A.vbgB.vbpC.vbwD.vbl2以下选项中,是Visual Basic 的ActiveX控件的是()。
A.复选框控件B.定时器控件C.对话框控件D.命令按钮控件3. 文本框的默认属性是()。
A.Caption B.Text C.Top D.Name4.在下列表达式中,正确的日期型常量是_______A. "12/04/01"B. 12-04-2001C. {12/04/01}D. #12/04/01#5.表达式Not(a+b=c-d)是_______。
A.逻辑表达式B. 字符表达式C. 算术表达式D. 关系表达式6."-32768"的数据类型是_______。
A.整型常量B. 浮点型常量C. 符号常量D. 字符串型常量7. MsgBox函数的返回值的类型是______。
A.整型B. 字符串C. 逻辑值D. 日期型8.循环结构 For i = 1 To 10 Step 1.5 的执行次数是_______。
A.7B. 8C. 9D. 109.允许在菜单项的左边设置打勾标记,下面哪种论述是正确的?()A.在标题项中输入&然后打勾 B 在索引项中输入“√”C.在复选项中输入“√” D 在有效项中输入“√”10.当执行以下过程时,在窗体上将显示()。
Private Sub Commandl_Click( )Print “VB”2.铁路托运行李,从甲地到乙地,规定每张客票托运费计算方法是行李重量不超过50kg时,0.25元/kg,超过50kg而不超过100kg时,其超过部分按0.35元/kg收费,超过100kg时,其超过部分按0.45元/kg收费。
编写程序,输入行李重量,计算并输出托运的费用(写出分析步骤)。
(10分)。

XXX2014-2015学年下学期高二年级期末考试语文试卷后有答案XXX2014-2015学年下学期高二年级期末考试语文试卷后有答案本试卷满分为150分,考试时间150分钟。
第I卷50分一、基础与阅读(17分)材料一古人云“冒之以衣服,旌之以章旗,所以重其威也”,通过服饰表明贵贱在夏商时期当已形成。
我们通过《孝经》对服饰的论述片段,便能了解到古代“不僭上逼下”的着装要求。
穿错颜色,不但会受到惩罚,甚至还会招来杀身之祸。
清朝XXX 赐死年羹尧时,列举的罪状有几条就跟着装用色有关——用鹅黄色的荷包。
用黄布包裹衣服。
中国历代的服饰色彩与五行思想有着密切的关系。
从历代的服饰色彩演变中不难发现,古代服饰色彩始终以正色为尊,注重衣色之纯,五种正色白、青、黑、赤、黄源于五行金、木、水、火、土。
而历代所崇尚的颜色各异,《檀弓》有云“夏后氏尚黑,XXX尚白,XXX”,《史记·殷本纪》也记述XXX“易服色。
尚白”。
《礼记·王藻》云:“衣杂色,裳间色,非列采不入公门。
”个中的“列采”就是杂色服饰,也就是说,没有穿着杂色衣服是不能进入公门的。
作为封建社会初步的秦朝尚水德,于是黑色便成为打扮的首要颜色,“郊祀之服皆以袀玄”。
皇帝也经常是“玄衣绛裳”,即黑色上衣和深红色下衣,同样是以黑色为主调。
普通百姓单调的服色与礼制限制有关,“散民不敢服杂彩”(《春秋繁露·服制》)的描述正反映了这一现实。
《汉书·五行志》也曾记录,XXX微服私行,为了不引起人们的注意.遂穿着“白衣”。
封建社会中期当前,关于打扮颜色和等级的划定越发明确具体。
XXX虽然划定“贵贱异等,杂用五色”,但没有特别划定皇帝常服的服色。
而到了唐初,以黄袍衫等为皇帝常服,厥后逐渐用赤黄,“遂禁XXX不得以XXX为衣服杂饰”。
今后当前,黄色就成为了皇帝御用的颜色,成为皇帝王权的象征。
据《清史稿》记录:“龙袍,色用明黄。
领、袖俱石青,片金缘。

2010-2011年高二计算机专业期末考试题Ⅰ卷(共计140分)一、选择题1、variant是一种特殊的数据类型,除了( )以外,它可以包含任意一种数据。
A、固定长度字符串B、可变长度字符串C、整型D、自定义型2、数学表达式sin30o写出visual basic表达式()A、sin30B、sin(30)C、sin(30o)D、sin(30*3.14/180)3、下列语句中()语句可以用来正确地声明一个动态数组A 、private A(n)As Interger B、Dim A()As IntergerC、Dim A(,)As IntergerD、Dim A(1 to n)4、如果想在程序中反复使用一个日期数据“2011/1/11”,为了避免在编写程序时反复输入这个数据,也为了一次修改所有用到这个数据的语句,可以采用()A、将这个数据声明为字符变量,用一个变量标识符代表它B、将这个数据声明为字符常量,用一个常量标识符代表它C、将这个数据声明为日期型变量,用一个变量标识符代表它D、将这个数据声明为日期常量,用一个变量标识符代表它5.Visual Basic允许的常量有()。
(A) E7 (B) 4.8E2 (C) 2.5*10 (D) E-56.下列字符串常量中,最大的是()(A)”Abc” (B)”ABC” (C)”Therec”(D)”Therea”7.下列()是日期型常量。
(A) “2/1/02” (B) 2/1/02 (C) #2/1/02# (D) {2/1/02}8.表达式Int (8 * Sqr (36) * 10 ^ ( - 2) * 10 + 0.5) / 10的值是()(A) 0.48 (B) 0.048 (C) 0.5 (D) 0.059.下列符号常量的声明中,()是不合法的。
(A)Const a As Single=1.1 (B)Const a As Single= “12”(C)Const a As Double=Sin(1) (D)Const a = “OK”10.Visual Basic认为下面()组变量是同一个变量。

第 1 页 共 7 页5. 有输入语句:scanf(“a=%d,b=%d,c=%d ”,&a,&b,&c);为使变量 a 的值为1,b 的值为2,c 的值为3,则正确的数据输入方式是( )。
(↙表示回车) (A )123↙ (B )1,2,3↙ (C )a=1 b=2 c=3↙ (D )a=1,b=2,c=3↙6.已知字母A 的ASCII 码值为十进制的65,下面程序的输出结果是( )。
#include<stdio.h> main(){ char ch1,ch2;ch1='A'+'5'-'3'; ch2='A'+'6'-'3';printf(“%d,%c\n”,ch1,ch2); }(A )67,D (B )B,C (C )C,D (D )不确定的值 7. 为表示关系x ≥y ≥z ,应使用C 语言表达式( )。
(A )(x>=y)&&(y>=z) (B )(x>=y)AND(y>=z) (C )(x>=y>=z) (D )(x>=y) & (y>=z)8. 设有数组定义:char array[]=“China ”;则数组array 所占的存储空间为( )。
(A )4个字节 (B )5个字节 (C )6个字节 (D )7个字节 9. 以下程序的输出结果是( )。
#include<stdio.h> main(){ int x=1,a=0,b=0; switch(x){ case 0:b++;case 1:a++;case 2:a++;b++;}printf(“%d,%d”,a,b);}(A)2,1 (B)1,1 (C)1,0 (D)2,210. 若k为整型变量,则下列while循环执行的次数为()。
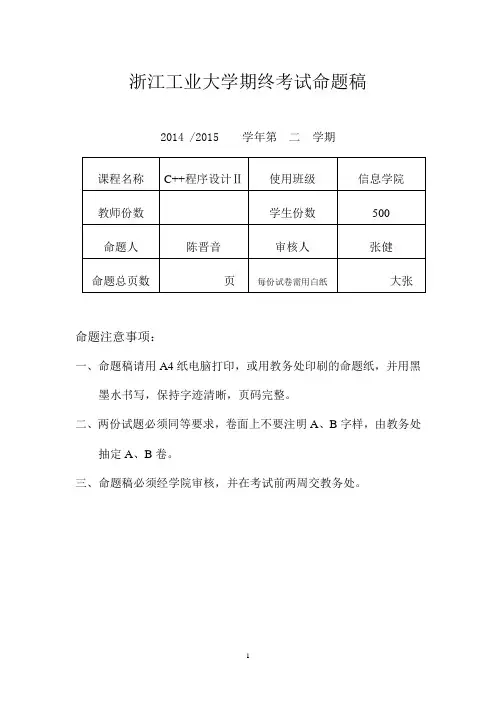

2014—2015学年第一学期初三年级期末质量抽测数学试卷2014.12学校姓名考试编号考生须知1.本试卷共6页,共五道大题,25个小题,满分120分.考试时间120分钟.2.在试卷和答题卡上认真填写学校名称、姓名和考试编号.3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效.4.考试结束,请将答题卡交回.一、选择题(共8道小题,每小题4分,共32分)下列各题均有四个选项,其中只有一个..是符合题意的.1.已知⊙O 1和⊙O 2的半径分别为3和5,如果O 1O 2= 8,那么⊙O 1和⊙O 2的位置关系是A .外切B.相交C.内切D.内含2.在不透明的布袋中装有2个白球,3个黑球,它们除颜色外完全相同,从袋中任意摸出一个球,摸出的球是白球..的概率是A .15B.13C.25D.233.如图,⊙O 的直径AB=4,点C 在⊙O 上,如果∠ABC =30°,那么AC 的长是A .1B .2C .3D .24. 在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,使它与图中阴影部分组成的新图形构成中心对称图形,该小正方形的序号是A .①B .②C .③D .④5.如图,在△ABC 中,点D E 、分别在AB AC 、边上,DE ∥BC ,若:3:4AD AB,6AE,则AC 等于A. 3B. 4C . 6D. 86.当二次函数249y xx 取最小值时,x 的值为A .2B .1C .2D .9来源学|科|网ABC30°④③②①ABCODC BAO7.课外活动小组测量学校旗杆的高度.如图,当太阳光线与地面成30°角时,测得旗杆AB 在地面上的影长BC 为24米,那么旗杆AB 的高度约是A .12米B .83米C .24米D .243米[来源:]8.已知:如图,在半径为4的⊙O 中,AB 为直径,以弦AC (非直径)为对称轴将AC折叠后与AB 相交于点D ,如果3ADDB ,那么AC 的长为A .214B .27C .42D .6二、填空题(共4道小题,每小题4分,共16分)9.如果3cos 2A,那么锐角A 的度数为.10.如果一个圆锥的母线长为4,底面半径为1,那么这个圆锥的侧面积为.11.在1×2的正方形网格格点上放三枚棋子,按图所示的位置已放置了两枚棋子,如果第三枚棋子随机放在其它格点上,那么以这三枚棋子所在的格点为顶点的三角形是直角三角形的概率为.12.在平面直角坐标系xoy 中,直线2x 和抛物线2yax 在第一象限交于点A,过A 作ABx 轴于点B .如果a 取1,2,3,,,n 时对应的△AOB 的面积为123S S S ,,,,n S ,那么1S _____;123nS S S S _____.三、解答题(共6道小题,第13题4分,第14 -18题各5分,共29分)13.如图1,正方形ABCD 是一个 6 × 6网格的示意图,其中每个小正方形的边长为1,位于AD 中点处的点P 按图2的程序移动.(1)请在图中画出点P 经过的路径;(2)求点P 经过的路径总长.绕点A 顺时针旋转90°绕点B 顺时针旋转90°绕点C 顺时针旋转90°输入点P输出点ADPxOy[来源:.Com]14.计算:3tan302cos452sin 60.15.现有三个自愿献血者,两人血型为O 型,一人血型为A 型.若在三人中随意挑选一人献血,两年以后又从此三人中随意挑选一人献血,试求两次所献血的血型均为O 型的概率(要求:用列表或画树状图的方法解答).[来源:]16. 如图,从热气球C 处测得地面A 、B 两处的俯角分别为30°、45°,如果此时热气球C处的高度CD 为100米,点A 、D 、B 在同一直线上,求AB 两处的距离.17. 已知抛物线与x 轴相交于两点A(1,0),B(-3,0),与y 轴相交于点C (0,3).(1)求此抛物线的函数表达式;(2)如果点3,2Dm 是抛物线上的一点,求△ABD 的面积.18.如图,在△ABC 中,∠AB C =2∠C ,BD 平分∠ABC ,且2AD ,22BD ,求AB 的值.BCDADCBA四、解答题(共4道小题,每小题5分,共20分)19.如图,在平面直角坐标系xoy 中,⊙A 与y 轴相切于点3(0,)2B ,与x 轴相交于M 、N 两点.如果点M 的坐标为1(,0)2,求点N 的坐标.20.(1)已知二次函数223y xx ,请你化成2()y x h k的形式,并在直角坐标系中画出223y xx 的图象;(2)如果11()A x y ,,22()B x y ,是(1)中图象上的两点,且121x x ,请直接写出1y 、2y 的大小关系;(3)利用(1)中的图象表示出方程2210xx 的根来,要求保留画图痕迹,说明结果.21.已知:如图,在△ABC 中,AB =AC ,以AC 为直径的⊙O 与BC 交于点D ,DE ⊥AB ,垂足为E ,ED 的延长线与AC 的延长线交于点F .(1)求证:DE 是⊙O 的切线;(2)若⊙O 的半径为4,BE =2,求∠F 的度数.yxO AB MNyOxEOA22.阅读下面的材料:小明遇到一个问题:如图(1),在□ABCD 中,点E 是边BC 的中点,点F 是线段AE 上一点,BF 的延长线交射线CD 于点G. 如果3AF EF,求CD CG的值.他的做法是:过点E 作EH ∥AB 交BG 于点H ,则可以得到△BAF ∽△HEF .请你回答:(1)AB 和EH 的数量关系为,CG 和EH 的数量关系为,CD CG的值为.(2)如图(2),在原题的其他条件不变的情况下,如果(0)AF a a EF,那么CD CG的值为(用含a 的代数式表示).(3)请你参考小明的方法继续探究:如图(3),在四边形ABCD 中,DC ∥AB ,点E是BC 延长线上一点,AE 和BD 相交于点 F. 如果(00)AB BC m n mnCDBE,,,那么AF EF的值为(用含m ,n 的代数式表示).H(1)ABCDE FG G FE DCBA(2)(3)AB CDEF五、解答题(共3道小题,第23题7分,第24、25题各8分,共23分)23.由于2013年第30号强台风“海燕”的侵袭,致使多个城市受到影响. 如图所示,A 市位于台风中心M 北偏东15°的方向上,距离612千米,B 市位于台风中心M 正东方向603千米处. 台风中心以每小时30千米的速度沿MF 向北偏东60°的方向移动(假设台风在移动的过程中的风速保持不变),距离台风中心60千米的圆形区域内均会受到此次强烈台风的影响.(1)A 市、B 市是否会受到此次台风的影响?说明理由.(2)如果受到此次台风影响,该城市受到台风影响的持续时间为多少小时?备用图24.已知二次函数y = x 2–kx + k – 1(k >2).(1)求证:抛物线y = x 2–kx + k- 1(k >2)与x 轴必有两个交点;(2)抛物线与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,若tan 3OAC,求抛物线的表达式;(3)以(2)中的抛物线上一点P (m,n )为圆心,1为半径作圆,直接写出:当m 取何值时,x 轴与P 相离、相切、相交.25.已知:四边形ABCD 中,AD ∥BC ,AD=AB=CD ,∠BAD =120°,点E 是射线CD 上的一个动点(与C 、D 不重合),将△ADE 绕点A 顺时针旋转120°后,得到△ABE',连接EE'.(1)如图1,∠AEE'= °;(2)如图2,如果将直线AE 绕点A 顺时针旋转30°后交直线BC 于点F ,过点E 作EM∥AD 交直线AF 于点M ,写出线段DE 、BF 、ME 之间的数量关系;(3)如图3,在(2)的条件下,如果CE =2,AE=27,求ME 的长.xyO–1–21234–1–21234E'MFEDC BAE'EDCBA图1图2E'MFEDC BA图32014—2015学年第一学期初三年级期末质量抽测数学试卷参考答案及评分标准2014.12一、选择题(共8个小题,每小题4分,共32分)题号 1 2 3 4 5 6 7 8 答案 ACDBDABA二、填空题(共4个小题,每小题4分,共16分)题号9 10 1112答案304344 ,2n(n+1)(各2分)三、解答题(共6道小题,第13题4分,第14 -18题各5分,共29分)13.解:(1)如图所示:PAB CD,,,,,,,,,,,,,,,,,,,,2分(2)由题意得,点P 经过的路径总长为:270318091802n r .,,,,,,,,,,,4分14.解:原式=323322322,,,,,,,,,,,,,,,,,,,,,,3分=113,,,,,,,,,,,,,,,,,,,,,,4分=23.,,,,,,,,,,,,,,,,,,,,,,,,,,,,5分15.解:列表如下:O 1O 2 A O 1(O 1,O 1)(O 1,O 2)(O 1,A)O 2(O 2,O 1) (O 2,O 2) (O 2,A) A(A ,O 1)(A ,O 2) (A ,A),,,,,,,,,,,,,,,,,,,,,,,4分所以,两次所献血型均为O 型的概率为49.,,,,,,,,,,,,,,,,,,,,,,5分16.解:依题意,可知:30,45,,100,CABCBACD AB D CD 于点,,,,,,,,,,,,,,,1分,CD AB 90.CDACDB ,,,,,,,,,,,,,,,,,,,,,,,,,2分Rt 100BDC BDCD 在中,,,,,,,,,,,,,,,,,,,,,,,,3分Rt tan CDADC AAD在中,.∴31003AD CD .,,,,,,,,,,,,,,,,,,,,,,,,,4分1003100ABADBD.,,,,,,,,,,,,,,,,,,,,,,,5分∴AB 两处的距离为(1003100)米.17.解:(1)∵抛物线与y 轴相交于点C (0,3),∴设抛物线的解析式为23y axbx .,,,,,,,,,,,,,,,,,1分∵抛物线与x 轴相交于两点(1,0),(3,0)A B ,∴30,9330.a b a b ,,,,,,,,,,,,,,,,,,,,,,,,,,,2分解得:1,2.a b∴抛物线的函数表达式为:232yxx .,,,,,,,,,,,,,,,,3分(2)∵点3(,)2D m 是抛物线上一点,∴2(23339)224m . ,,,,,,,,,,,,,,,,,,,,,,4分∴119942242ABDDSAB y . ,,,,,,,,,,,,,,,,,,5分18.解:∵BD 平分∠ABC ,∴∠ABC =2∠1=2∠2.∵∠ABC =2∠C ,∴∠C =∠1=∠2.,,,,,,,,,,,1分∴22CD BD . ,,,,,,,,,,,,2分∴32AC.又∵∠A=∠A,∴△ABD ∽△ACB .,,,,,,,,,,,,,,,,,,,,,,,,,,,3分∴AD AB ABAC.,,,,,,,,,,,,,,,,,,,,,,,,,,,4分∴22326AB AD AC .∴6AB(舍负).,,,,,,,,,,,,,,,,,,,,,,,,,,5分四、解答题(共4道小题,每小题5分,共20分)19.解:连接AB 、AM ,过点A 作AC ⊥MN 于点C .∵⊙A 与y 轴相切于点B(0,32),∴AB ⊥y 轴.又∵AC ⊥MN ,x 轴⊥y 轴,∴四边形BOCA 为矩形.∴AC =OB=32,OC =BA .∵AC ⊥MN ,∴∠ACM=90°,MC=CN .,,,,,,,,,,,,,,,,,,,,2分∵M(12,0),∴OM =12.在Rt △AMC 中,设AM=r.O A B MNCyx21DCBA。

2014-2015学年期末考试试卷及答案科目:高一英语第一部分:听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. When did the woman see Bob?A. At 3:00.B. At 4:00.C. At 6:00.2. What will the two speakers by next?A. A jacket.B. A handbag.C. A watch.3. What do the two speakers hope to do?A. Stop cigarette production.B. Advise people not to smoke.C. Stop young people from smoking.4. What’s the most probable relationship between the two speakers?A. Mother and son.B. Hostess and guest.C. Waitress and customer.5. Where does the man’s brother probably work now?A. At the post office.B. In a language school.C. In a publishing house.第二节(共15小题;每小题1. 5分,满分22. 5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项. 并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题给出5秒钟的作答时间。
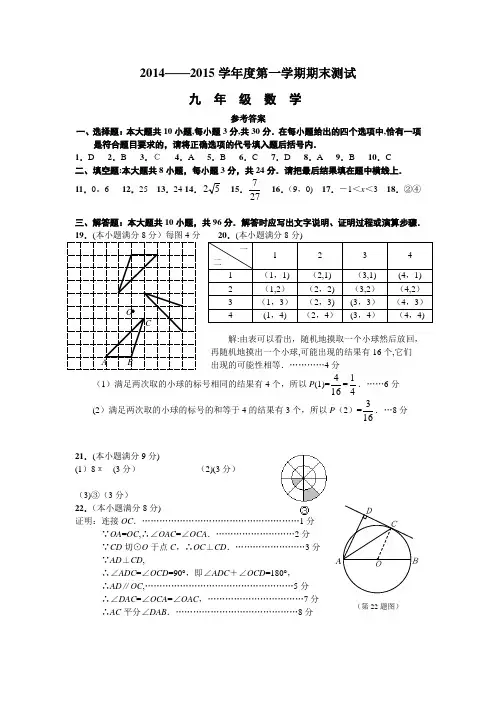
2014——2015学年度第一学期期末测试九 年 级 数 学参考答案一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,恰有一项是符合题目要求的,请将正确选项的代号填入题后括号内.1.D 2.B 3.C 4.A 5.B 6.C 7.D 8.A 9.B 10.C二、填空题:本大题共8小题,每小题3分,共24分.请把最后结果填在题中横线上. 11.0。
6 12.25 13.24 14.52 15.277 16.(9,0) 17.-1<x <3 18.②④三、解答题:本大题共10小题,共96分.解答时应写出文字说明、证明过程或演算步骤. 19.(本小题满分8分)每图4分解:由表可以看出,随机地摸取一个小球然后放回, 再随机地摸出一个小球,可能出现的结果有16个,它们出现的可能性相等.…………4分 (1)满足两次取的小球的标号相同的结果有4个,所以P (1)=164=41.……6分 (2)满足两次取的小球的标号的和等于4的结果有3个,所以P (2)=163.…8分21.(本小题满分9分)(1)8π (3分) (2)(3分)(3)③(3分)22.(本小题满分8分)证明:连接OC .………………………………………………1分∵OA =OC ,∴∠OAC =∠OCA .………………………2分∵CD 切⊙O 于点C ,∴OC ⊥CD .……………………3分∵AD ⊥CD ,∴∠ADC =∠OCD =90°,即∠ADC +∠OCD =180°,∴AD ∥OC ,……………………………………………5分∴∠DAC =∠OCA =∠OAC ,……………………………7分∴AC 平分∠DAB .……………………………………8分一 二1 2 3 4 1 (1,1) (2,1) (3,1) (4,1) 2 (1,2) (2,2) (3,2) (4,2) 3 (1,3) (2,3) (3,3) (4,3)4 (1,4) (2,4) (3,4) (4,4) A B C D O . (第22题图).O A B C解:设所围成圆锥的底面半径和高分别为r 和h .∵扇形半径为3㎝,圆心角为120°, ∴12032180r ππ⋅⋅=,……………………………………………………………………4分 ∴r =1,……………………………………………………………………………………6分∴h ==8分24.(本小题满分10分)解:(1)令y =0,得2230x x --=,………………………………………………………1分解得x 1=3,x 2=-1,………………………………………………………………3分 ∴抛物线与x 轴交点坐标为(3,0)和(-1,0).……………………………4分(2)令x =0,得y =-3,∴抛物线与y 轴交点坐标为(0,-3),…………………………………………5分 ∴将此抛物线向上平移3个单位后可以经过原点.……………………………7分 平移后抛物线解析式为22y x x =-.………………………………………10分25.(本小题满分9分)(1)证明:∵DE ∥BC ,EF ∥AB ,∴∠AED =∠ECF ,∠A =∠FEC ,……………2分∴△ADE ∽△EFC .………………………………………………………………4分(2)解:∵△ADE ∽△EFC , ∴AD DE EF FC=.…………………………5分 ∵AD =4,DE =5,EF =2, ∴FC =52.……………………………………6分 ∵DE ∥BC ,EF ∥AB ,∴四边形DEFB 是平行四边形,∴BF =DE =5,……8分∴BC =BF + FC =5+52=152.………………………………………………………9分26.(本小题满分10分)(1)证明:∵四边形ABCD 是正方形,∴∠A =∠B =90°,∴∠DEA +∠ADE =90°.…1分∵EF ⊥DE ,∴∠DEF =90°,∴∠DEA +∠FEB =90°,……………………………2分 ∴∠ADE =∠FEB ,……………………………………………………………………4分 ∴△ADE ∽△BEF .……………………………………………………………………5分(2)解:∵正方形的边长为4,AE =x ,∴BE =4-x .∵△ADE ∽△BEF , ∴DA AE EB BF =,……………………………………………7分 ∴44x x y =-, ∴2(4)144x x y x x -==-+,…………………………………10分解:(1)由题意得1060x y -=.…………………………………………………………3分 (2)由题意得1200040101)200)(1060()200(2++-=+-=+=x x x x x y z .6分 (3)由题意得)1060(201200040101202x x x y z w --++-=-= 10800421012++-=x x .…………………………………………9分 当每个房间的定价2102=-=a b x (元)时,w 有最大值,最大值是15210.………12分28.(本小题满分14分)解:(1)∵点A 坐标为(0,3),∴OA =3.∵矩形ABCO 面积为12,∴AB =4,……2分∴抛物线的对称轴为直线x =2.…………………………………………………4分(2)∵∠ADM =∠DOM ,∠AMD =∠DMO ,∴△ADM ∽△DOM , ∴MOMD MD AM =,∴MO AM MD ⋅=2.设MO=x ,则MA= x -3. ∴)3(4-=x x ,∴41=x ,12-=x ,∴MO=4,∴D 点坐标为(2,4).…6分 设抛物线的解析式为4)2(2+-=x a y . 将点A (0,3)代入得443+=a ,∴41-=a , ∴抛物线的解析式为4)2(412+--=x y .……………………………8分 (3)∵⊙P 在y 轴上截得线段长为2,OA =3, ∴P 点纵坐标为2或4.……9分在4)2(412+--=x y 中,令y=2或4得 4)2(4122+--=x 或4)2(4142+--=x ,………………………………11分 解得2221+=x ,2222-=x ,23=x ,∴P 点坐标为(222+,2)、(222-,2)或(2,4).………………14分。
中国科学技术大学2014-2015学年第一学期考试试卷考试科目:并行程序设计得分:_________学生所在系:___________ 姓名:______ 学号:___________一、分析以下3个循环中存在的依赖关系;分别通过循环交换、分布和逆转等多种方法来尝试向量化和/或并行化变换:(3×10=30分)二、假设某种MPI广播通信方案如下:将P个进程看作pp 的二维拓扑结构,并且将各个行或列进程组划分为单独的子通信域.这样,root进程可先在其行子通信域中进行广播,然后该行中的所有进程在各自的列通信子域中再广播。
给出该广播方案的MPI具体实现。
(20分)三、设有两个进程A和B,以及结构变量stu。
现在,进程A将stu发送给进程B。
请用三种不同的MPI实现来完成进程A的发送操作。
(3×10=30分)struct Student {int id; char name[10];double mark[3]; char pass;} stu;2014-2015 学年第一学期《并行程序设计》期末考试第 1 页(共 2页)四、以下是单处理器上的矩阵求逆算法:Beginfor i=1 to n do(1)a[i,i]=1/a[i,i](2)for j=1 to n do if(j≠i)then a[i,j]=a[i,j]*a[i,i]end if end for(3)for k=1 to n dofor j=1 to n doif ((k≠i and j≠i))then a[k,j]=a[k,j]-a[k,i]*a[i,j]end if end for end for(4)for k=1 to n do if (k≠i)then a[k,i]= —a[k,i]*a[i,i]end if end forend forEnd矩阵求逆的过程中,依次利用主行i(i=0,1,…,n-1)对其余各行j(j≠i)作初等行变换,由于各行计算之间没有数据相关关系,因此可以对矩阵A按行划分来实现并行计算。
姓名____________ 学号________________ 班级或选课课号______________________________ 座号_______任课教师______________
密 封 线 内 不 要 答 题 ―――――――――――――――――――密――――――――――――――――-封――――――――――――――――线――――――――――――――――――――
2014-2015学年第2学期期末考试
《课程名称全称(以人才培养方案为准)》答卷A(或B)
(供 院(系) 专业 班使用)
题 号 一 二 三 四 (请根据实际情况增减列数) 总 分
得 分 (请根据实际情况增减列数)
流水评卷人 签名
非流水评卷 签名
总分合计人(签名)________________ 评卷复核人(签名)________________
一、试题类型(共 题,每小题 分 ,共 分)
1. 2.
得分
密 封 线 内 不 要 答 题
――――――――――――――――――密――――――――――――――――-封―――――――――――――――――线――――――――――――――――――――――
二、试题类型(共 题,每小题 分 ,共 分)
1.
2.
三、试题类型(共题,每小题分,共分)
密 封 线 内 不 要 答 题
――――――――――――――――――密――――――――――――――――-封―――――――――――――――――线――――――――――――――――――――――
四、试题类型(共 题,每小题 分 ,共 分)
1.
2.。
并行计算期末考试题及答案一、选择题(每题2分,共20分)1. 并行计算中,SMP指的是什么?A. 单处理器多线程B. 单处理器多核心C. 对称多处理器D. 非对称多处理器2. MPI(Message Passing Interface)主要用于什么?A. 数据库管理B. 网络编程C. 并行编程通信D. 操作系统内核3. 在并行计算中,以下哪个不是并行算法的设计原则?A. 可分解性B. 可并行性C. 可扩展性D. 顺序性4. 下列哪个不是并行计算的硬件结构?A. 集群B. 网格C. 多核处理器D. 单核处理器5. 以下哪个算法不是并行算法?A. 快速排序B. 归并排序C. 冒泡排序D. 桶排序二、简答题(每题10分,共30分)1. 解释什么是并行计算,并简述其主要优势。
2. 描述一下并行计算中的负载均衡问题,并举例说明如何解决。
3. 什么是数据并行和任务并行?请简要比较它们的区别。
三、计算题(每题25分,共50分)1. 假设有一个需要处理的数据集大小为N,使用单核处理器处理需要T时间。
如果使用P个处理器进行并行处理,且处理器之间通信开销可以忽略不计,计算并行处理时间Tp,并讨论P对Tp的影响。
2. 给定一个并行算法,其执行时间由以下公式给出:T(P) = α +β/P,其中α是固定的启动时间,β是与问题规模相关的工作量,P 是处理器的数量。
请推导当P增加时,算法的加速比S(P)如何变化,并讨论在什么情况下算法的效率最高。
答案一、选择题1. C2. C3. D4. D5. C二、简答题1. 并行计算是指同时使用多个处理器或核心来执行计算任务,以提高计算效率和处理速度。
其主要优势包括处理大规模数据集的能力、缩短计算时间以及提高资源利用率。
2. 负载均衡问题是指在并行计算中,如何合理分配任务给各个处理器,以避免某些处理器过载而其他处理器空闲的情况。
解决这个问题的方法包括动态负载分配、任务分割等。
3. 数据并行是指将数据分割成多个小块,然后在多个处理器上同时处理这些数据块。
《java程序设计》期末复习题2014-2015第二学期《java程序设计》复习题可能题型:选择、填空、简答、判断目录练习一(两类java程序) (3)练习二(数据类型) (3)练习三(运算符与表达式) (4)练习四(条件,分支语句) (5)练习五(条件,分支语句) (7)练习六(控制结构与循环体内的跳转) (9)练习七(方法) (10)练习八(方法重载) (10)练习九(数组) (11)练习十(继承:类,属性和方法的继承,属性隐藏和方法覆盖,构造函数的继承,父类对象和子类对象的关系) (12)练习十一(多态:抽象类和抽象方法,最终类和最终方法,接口) (17) 练习十二(异常处理) (18)练习十三(杂) (20)练习十四(io) (23)练习十五(线程) (24)练习十六(网络) (26)练习十七(gui) (28)练习十八(杂) (30)练习一(两类java程序)1.Java是低级语言还是高级语言 (高级)2.Java是面向对象的程序设计语言吗 (是)3. Java是编译型的计算机语言还是解释型的计算机语言 (解释型)4. Java语言的程序设计包含哪3个步骤 (编写源程序,编译源程序,解释运行编译后形成的字节码文件)5. Java源程序文件的后缀是什么 (.java)6. Java源程序经编译后生成什么文件其后缀是什么(字节码文件,.class)7. Java程序有哪两类 (java应用程序,java小程序)8.类的定义由哪两部分组成 (类头和类体)9.方法的定义由哪两部分组成 (方法头和方法体)10.一个Java源程序中可以有多个公共类(主类)吗 (不能)11.一个Java源程序中可以有多个类吗若有多个类时,程序文件名是什么 (能,与公共类名一致)12. Java应用程序(Application)的主类的类头应如何写(public class 类名), 它的主方法的方法头应如何写(public static void main(String args[])), Application 的入口在哪(main())13.Java应用程序(Application)的主类中一定要有主方法(main)吗?是14.Java中的的字符使用什么编码 (unicode)15. 在Java语言中,将源代码翻译成____________时产生的错误称为编译错误,而将程序在运行中产生的错误称为运行错误.(字节码)16. 为了使包sos中的所有类在当前程序中可见,可以使用的语句是( A ).A)import sos.*; B)package sos.*;C)sos import; D)sos package;17. 下面关于封装性的描述中,错误的是( d )。
2014— 2015学年度第一学期期末考试八年级语文试卷(满分:100分;考试时间:120分钟)友情提示: 2.3.1. 根据拼音写汉字,(1)全桥结构y u n chan ()(),和四周景色配合得十分和谐。
()失措。
),或者是几座小山配合着 (5) 这些石刻狮子,有的母子相抱,有的交头接耳,有的像倾听水声,千态万状,惟妙惟肖( )。
(6) 日落的景象和日出同样壮观、绮 ()丽,而且神秘迷人。
2.结合句意,判断下列句子中加点词换成括号里的词恰当的一项是() ・ ・(2分)A. 他们杀孩子、老师、还有牧师,他们全是纯朴 勤劳的普通市民。
(淳朴)・ ・B. 今天,帝国居然还天真 地以为自己就是真正的物主。
(率真)・ ・C. 他们小声议论着,似乎怕惊扰那肃穆.的空气。
(严肃)D. 这些日子,家中光景很是惨淡.,一半为了丧事,一半为了父亲赋闲。
(冷 1.本试卷6页。
考生将自己的姓名、准考证号及所有答案均填写在答题卡上。
答题要求见答题卡上的“注意事项”。
一、语基(22分)或给加点字注音。
(4分)(2) 鬼子们拍打着水追过去,老头子张 hu d ng(3) 或者是重 lu d n ( )叠zh rng ( 竹子花木,全在乎设计者和匠师们生平多阅历。
(4) 因桥下多半是急流,人们到此总要 zh u ( )足欣赏飞瀑流泉。
淡)① 到处呈现一片衰草连天的景象,准备迎接风雪载途的寒冬②北雁南飞,活跃在田 间草际的昆虫销声匿迹③到了秋天,果实成熟,植物的叶子渐渐变黄,在秋风中簌簌地落了下来④在地球上温带和亚热带区域里,年年如是,周而复始。
①4.名著阅读。
(6分)(1)《钢铁是怎样炼成的》最大的成功之处在于塑造了______ 这个无 产阶级英雄形象,他在 ____________ 的影响下逐步走上革命道路。
在他的身上凝聚着那个时代最美好的精神品质,请写出两种: _______________ (4 分)(2) “两句一行,大约读了二三十行罢,他说:“给我读熟。
中 国 科 学 技 术 大 学
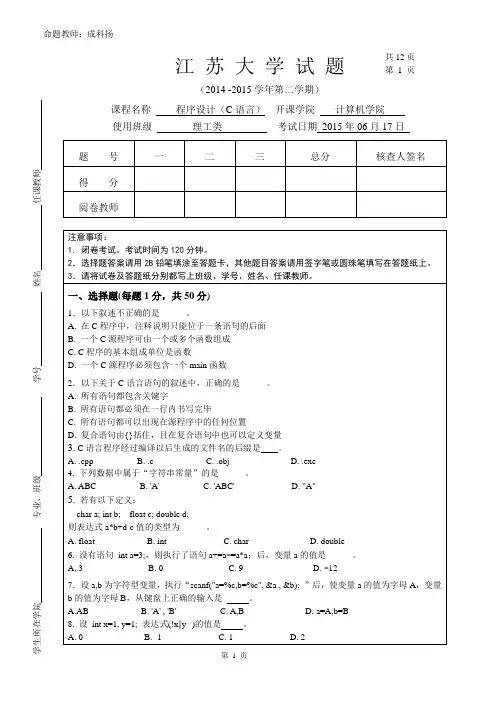
2014-2015学年第一学期考试试卷
考试科目:
并行程序设计 得分:___
______
学生所在系:______ _____ 姓名:____ _ _ 学号:_ ____ ______ 一、 分析以下3个循环中存在的依赖关系;分别通过循环交换、分布和逆转等多种方法来尝试向量化和/或并行化变换:(3×10=30分)
p 的二维拓扑结构,并且将各个行或列进程组划分为单独的子通信域。
这样,root 进程可先在其行子通信域中进行广播,然后该行中的所有进程在各自的列通信子域中再广播。
给出该广播方案的MPI 具体实现。
(20分)
三、设有两个进程A和B,以及结构变量stu。
现在,进程A将stu发
送给进程B。
请用三种不同的MPI实现来完成进程A的发送操作。
(3×10=30分)
struct Student {int id; char name[10];double mark[3]; char pass;
} stu;
四、以下是单处理器上的矩阵求逆算法:
Begin
for i=1 to n do
(1) a[i,i]=1/a[i,i]
(2)for j=1 to n do if (j≠i) then a[i,j]=a[i,j]*a[i,i] end if end for
(3)for k=1 to n do
for j=1 to n do if ((k≠i and j≠i)) then a[k,j]=a[k,j]-a[k,i]*a[i,j] end if end for end for
(4)for k=1 to n do if (k≠i) then a[k,i]= -a[k,i]*a[i,i] end if end for
end for
End
矩阵求逆的过程中,依次利用主行i(i=0,1,…,n-1)对其余各行j(j≠i)作初等行变换,由于各行计算之间没有数据相关关系,因此可以对矩阵A按行划分来实现并行计算。
考虑到在计算过程中处理器之间的负载均衡,对A采用行交叉划分:设处理器个数为p,矩阵A的阶数为n,⎡⎤p
=,对矩阵A行交叉划分后,编号为i(i=0,1,…,p-1)的处理器存有A的第i, i+p,…, i+(m-1)p n
m/
行。
在计算中,依次将第0,1,…,n-1行作为主行,将其广播给所有处理器,这实际上是各处理器轮流选出主行并广播。
发送主行数据的处理器利用主行对其主行之外的m-1行行向量做行变换,其余处理器则利用主行对其m行行向量做行变换。
请写出矩阵求逆算法的MPI并行实现。
(20分)。