当前位置：文档之家 › 南京理工大学工程流体力学基础 第2章_流体静力学

南京理工大学工程流体力学基础 第2章_流体静力学

  • 格式：ppt
  • 大小：3.74 MB
  • 文档页数：56

下载文档原格式

  / 56

合集下载

南京理工大学工程流体力学1

南京理工大学工程流体力学1

2.
4.
由于静止流体的压力沿表面的内法线方向作用，故
∫τFρdτ + ∫ pdS = 0
S
∫τFρdτ − ∫ pndS = 0
S
应用奥氏公式，有
∫τ(Fρ −∇p)dτ = 0
§1-1 静止流体的平衡方程
静止流体的平衡方程
由于体积τ是任取的，故被积函数为零
F=
1
ρ
∇p
欧拉平衡方程
1 ∂p X= ρ ∂x 1 ∂p Y= ρ ∂y 1 ∂p Z= ρ ∂z
dSz1 = dSz2 = dSz
∫
结论：浮力等于与物体同体积的液体的重量。
§1-2 重力场中不可压缩流体的静力平衡
Sz
dP = ρg∫ (h1 − h2 )dSz 阿基米德定理 = −ρgV z
Sz
第二章 流体静力学
§1-3 标准大气
§1-3 标准大气
地球大气层的结构
地球大气层厚度约为2000～3000km。分为几层： 对流层：平均11km，空气质量 约占3/4，温度随高度而降低， 各种气象变化。 平流层：对流层之上到32km， 空气质量约占1/4，空气水平流 动，20km以下为同温层。 中间层：平流层之上到80km， 空气质量约占1/3000，温度随高 度先升后降。
§1-2 重力场中不可压缩流体的静力平衡
重力场中静止液体对柱面的作用力
P = p0Sz + ρgV z
结论： p0Sz为压力p0在Sz上的作用力， 作用线通过Sz的形心； ρgV为体积V中液体的重力，作 用线通过其重心。
P = P i + Pk x z
§1-2 重力场中不可压缩流体的静力平衡
浮力问题
第二章 流体静力学

工程流体力学课件第二章 流体静力学1

工程流体力学课件第二章 流体静力学1

fx
1
p x
0
乘以dx
1 p
f y y 0
乘以dy
1 p
fz z 0
乘以dz
1 p
f xdx
dx x
0
1 p
f ydy y dy 0
1 p
fzdz z dz 0
❖三式相加，整理
( f xdx
f ydy
fzdz)
p dx x
p dy y
p dz z
39
(
f xdx
❖ 适用范围： 静止状态
0
0
实际流体、理想流体都是适用的。
2021/3/12
2
3
在什么情况下有惯性力？ 惯性坐标系：将坐标系建立在静止或匀速直线运动的
物体上 非惯性坐标系：将坐标系建立在有加速度运动的物体上 结论：
在惯性坐标系内运动的物体不考虑惯性力 在非惯性坐标系内加速运动的物体考虑惯性力
1 6
dxdydzf x
0
15
静压强两个特征（证明续）
❖ 化简得
px
pn
1 3
f xdx
0
❖ 由于等式左侧第三项为无穷小，可以略去，故得
❖ 同理可得
px pn py pn pz pn
❖ 所以
px py pz pn
❖ 结论 n的方向可以任意选择，从而证明了在静止流体 中任一点上来自各个方向的流体静压强都相等。
❖ 将质量力和表面力代入上式，则
p
1 2
p dx dydz
x
p
1 2
p dx dydz x
f x dxdydz
0
❖ 整理上式，并把各项都除以ρdxdydz，则得

工程流体力学第2章流体静力学

工程流体力学第2章流体静力学

① 沿任意方向 ② 沿外法线方向
有切向分力 流体受拉力
都将破坏流体平衡。
这与静止前提不符，故假设不成立，则原命题成立。
①
②
4
第2章 流体静力学
特性二、静止流体中任何一点上各个方向的静压力大小相等，与作用面方位无关。
证明：采用微元体分析法 ① 取微单元体
在静止流体中，在O点附近取出各边长分别 为dx、dy、dz的微小四面体OABC。相应坐标 轴为x、y、z。
第2章 流体静力学
流体静力学：研究流体在静止状态下的平衡规律及其应用。 静止：流体质点相对于参考系没有运动，质点之间也没有相对运动。 静止状态包括两种情况： 1、绝对静止：流体整体对地球没有相对运动。
2、相对静止：流体整体对地球有运动，但流体各质点之间没有相对运动。
举例：
绝对静止
等加速水平直线运动 等角速定轴转动
2
第2章 流体静力学
§2.1 流体静压力及其特性
1、静压力的概念
（1）静压力：静止流体作用在单位面积上的压力，称为静压力，或静压强。记作“p”
一点的静压力表示方法：
设静止流体中某一点m，围绕该点取一微小作用面积A，其上压力为P，则： 平均静压力： p P
A
m点的静压力：p lim P
单位：
A0 A
m
国际单位：Pa
物理单位：dyn/cm2
工程单位：kgf/m2
混合单位：1大气压（工程大气压） = 1kgf/cm2
（2）总压力：作用在某一面积上的总静压力，称为总压力。记作“P”
单位：N
3
第2章 流体静力学
2、静压力的两个重要特性
特性一、静压力方向永远沿着作用面内法线方向。

化工原理(南京理工大学)01流体流动(1)_流体静力学

化工原理(南京理工大学)01流体流动(1)_流体静力学

讨论：
a. 当将U形管一端与被测点连接、另一端与大 气相通时，可测得流体的表压或真空度；
p1
p1
pa
pa
表压
真空度
南京理工大学化工学院化学工程系
b. 指示液的选取： 指示液与被测流体不互溶，不发生化 学反应；
其密度要大于被测流体密度。
应根据被测流体的种类及压差的大小选
择指示液。
南京理工大学化工学院化学工程系
南京理工大学化工学院化学工程系
1.1.1 密度
一、定义 单位体积流体的质量，称为流体的密度。
m V
kg/m3
(1)
二、单组分流体密度
f ( p, T )
南京理工大学化工学院化学工程系
液体 密度仅随温度变化（极高压力除外），其 变化关系可从手册中查得。 气体 当压力不太高、温度不太低时，可按理想 气体状态方程计算：
质量守恒：
混合前后流体的总质量相等。
南京理工大学化工学院化学工程系
已知各组分体积分率
m 1 xV1 2 xV 2 n xVn (3)
xV1 , xV 2 , n xVn
——各组分的体积分率。
南京理工大学化工学院化学工程系
已知各组分质量分率
1 xw1 xw 2 x wn
p11
2p
2
m
b
R a a’
南京理工大学化工学院化学工程系
所以 整理得
p1 B g(m R) p2 B gm A gR
p1 p2 ( A B ) gR
若被测流体是气体， B A，则有
p1 p2 Rg A
南京理工大学化工学院化学工程系

工程流体力学第二章 流体静力学

工程流体力学第二章 流体静力学

只有重力作用下的等压面应满足的条件：
1.静止； 2.连通； 3.连通的介质为同一均质流体； 4.质量力仅有重力； 5.同一水平面。
提问:如图所示，哪个断面为等压面? 您的答案是: C-C 断面 B-B 断面
第三节 重力作用下的流体平衡
在自然界和实际工程中，经常 遇到并要研究的流体是不可压缩的 重力液体，也就是作用在液体上的 质量力只有重力的液体。
f ds f x dx f y dy f z dz 0
f
图2-4 两个矢量的数量积
两个矢量的数量积等于零，必 须f和ds互相垂直，其夹角φ等于900。 也就是说，通过静止流体中的任一点 的等压面都垂直于该点处的质量力。 例如，当质量力只有重力时，等压面 处处与重力方向正交，是一个与地球 同心的近似球面。但是，通常我们所 研究的仅是这个球面上非常小的一部 分，所以可以看成是水平面 。
一、重力作用下的静力学基本方程 在一盛有静止液体的容器上取 直角坐标系（只画出OYZ平面，Z轴 垂直向上），如图2-5所示。
P0 P2 P1 Z1 Z2
图2-5 推导静力学基本方程式用图
这时，作用在液体上的质量力 只有重力 G=mg ，其单位质量力在各 坐 标 轴 上 的 分 力 为 fx=0 ， fy=0 ， fz=-g， 代入式（2-4），得 dp gdz dp 写成 dz g 0 （2-8）
或
1 p x p n f x dx 0 3
由于等式左侧第三项为无穷小， 可以略去，故得：
（2-1）
因为n的方向完全可以任意选择， 从而证明了在静止流体中任一点上来 自各个方向的流体静压强都相等。但 是，静止流体中深度不同的点处流体 的静压强是不一样的，而流体又是连 续介质，所以流体静压强仅是空间点 坐标的连续函数，即

流体力学第2章资料

流体力学第2章资料
解 按题意，活塞底面上的压力可按静力平衡条件 来确定
pB
pa
油h1
水h2
4F
d 2
105 7840 0.5 9800 0.3 5788 4
0.42
1.53105
(N / m2)
第五节 压力的单位和压力的测量方法
一、 压力的单位
1. 应力单位－－ Pa(=N/m2)， MPa， kgf/cm2
作用在流体上的力 流体的静压力及其特性 流体的平衡微分方程式 重力场中流体静力学基本方程 压力的单位和压力的测量方法 流体的相对平衡 静止流体作用力
第一节 作用在流体上的力
作用于流体上的力按作用方式可分为表面力和质量 力两类。 一、 表面力
表面力指作用在所研究的流体表面的力。它是由所研 究流体的表面与相接触的物体的相互作用而产生的。 单位是N/m2（Pa） 。
Xdx Ydy Zdz p dx p dy p dz
x y z
dp=ρ(Xdx+Ydy+Zdz)
流体静平衡方程 式，也称压力差 公式
二、等压面
在平衡流体中，压力相等的各点所组成的面称为等 压面。
在等压面上dp=0。因流体密度ρ≠0，可得等压面微分 方程：
Xdx+Ydy+Zdz=0
(2-4)
第四节 重力场中流体静力学基本方程
在重力场中：X=0, Y=0, Z=-g
dp=ρ(Xdx+Ydy+Zdz)
dp gdz dz
dz dp 0
对于不可压缩流体，γ=常数。
z p c
z1
p1
z2
p2
c
流体静力学基 本方程式
z
p
c＝z0
p0

工程流体力学第二章

工程流体力学第二章

pxdydz pnds • sin dz 0
p y dxdz
pnds
•
cos
dz
1 2
dxdydz
g
0
所以：
px pn 0
故
py
pn
1 2
dyg
0
y b
pxdy
o
px pn py pn
pnds
G x a
p y dx
得证
微元体分析法的步骤： 1 取合适的微元体 2 受力分析 3 建立方程
F pcg A ghc A
y D
y C
J cx yA
c
常见几何形状的惯性矩（表2－2）
矩形 圆型
c
l
J cx
1 12
bl 3
b
cR
J cx
1 R4
4
¼圆
xc c yc
xc
yc
4R
3
J cx
(1 4
16
9 2
R4
) 4
例2-5 设矩形闸门的宽为6米，长10米，铰链到低水面的 距离为4米。按图示方式打开该闸门，求所需要的力 R。
z
p0
o
B
z
p0
o
B
R
(a)
pg
2
2r2
R
(b)
pg
2
2(r2
R2)
例2-4 设内装水银的U型管绕过D点的铅垂线等角速度旋 转，求旋转角速度和D点的压强。设水银密度为
13600kg/m3 且不计液面变化带来的影响。
ω
关键：
10cm 5cm
1 写出所有的体积力
20c m
z
12cm 2 根据压力差公式写出压强

工程流体力学 第二章 流体静力学201012

工程流体力学 第二章 流体静力学201012
Y = ω 2 r sin α = ω 2 y Z = −g
z ω
1.等压面方程 1.等压面方程
dp = ω 2 xdx + ω 2 ydy − gdz = 0
⇓ 积分
ω 2 x2
2 +
p0
o
m
h z
zs y
ω 2 y2
2
− gz = C
ω 2r 2
2
− gz = C
等压面是一簇绕z轴的旋转抛物面。 等压面是一簇绕z轴的旋转抛物面。 自由液面： 自由液面： x=0 z=0 C=0
z g p0
2
⇒
dp = ρ(Xdx +Ydy + Zdz)
dp = −ρgdz
p2
p1
1
⇒
dp dz + =0 ρg
z1
z2
积分得： 积分得：
p z+ =C ρg
o
p p z1 + 1 = z2 + 2 ρg ρg
基准面
x
2.物理意义 2.物理意义
z+ p =C ρg
总 势 能
3.几何意义 3.几何意义
o y
αr
y x ω2y ω2r
⇓
zs =
ω 2r 2
2g
x
ω2x
二、等角速旋转容器中液体的相对平衡
2. 静压强分布规律
dp = ρ (ω 2 xdx + ω 2 ydy − gdz )
z ω
⇓ 积分
p = ρ(
ω 2x2
2
+
ω 2 y2
2
− gz ) + C
p = ρg (
ω 2r 2

第二章.流体静力学

第二章.流体静力学

由于气体的密度很小，在高差不很大时气柱产生的压强 很小，可以忽略，则 p＝p0（即气体压强处处相等）。
流体内任二点压强的关系 已知某点的压强和两点间的深度差，即可求另外一点的压强值。
p2 p1 g h
p0
14
静力学基本方程工程应用
p p0 gh
A
1 2
A h h
平衡流体中，自由表面处压强p0 的任何变化都会等值地传递到液体中 的任意一点上。
C p0
p p0 ax gz ——等加速水平直线运动容器中静压强的分布规律
静压强不仅与垂直坐标有关系，同时还和水平坐标有关系
2.确定相对平衡液体内等压面方程
已知： X -a, Y 0，Z g
33 Xdx Ydy Zdz 0
adx gdz 0
18
测压管
二端开口的玻璃管，一端与大气相通，另一端与被测 液体想通的透明玻璃管，称为∽。 下图几种不同液面压力下测压管的情况
测压管水头处处相等
19
水平面是等压面的条件：
•同种
•均质 •连续 •连通 •质量力只有重力 •静止流体
连通容器
连通容器
连通器被隔断
二、压强的表示方法及单位
21
1、压强的表示方法 a.绝对压强:以绝对真空状态的压强为零点计量的压强：用p表示，p 0 。 b. 相对压强：以当地大气压作为零点计量的压强值。相对压强可正可负。 c.表压强（或计示压强):比当地大气压高的压强用pg表示，pg= p – pa d.真空：是指绝对压强小于一个大气压的受压状态。 真空值pv pv= pa – p
平衡有两种：
绝对平衡 ——流体相对于地球无相对运动。 相对平衡 ——流体相对于地球有相对运动，但对某物体 （或参考坐标系）无相对运动。

工程流体力学第二章

工程流体力学第二章
Z p g
位置水头 压力水头 该点压力的液柱高度
测压管水头 ——为一常量
2、物理意义
z
p g
比位能
单位重量流体所具有的位能。 单位重量流体从大气压力为基点算 起所具有的压力势能。
比压能
p z g
总势能
——为一常量
说明：
（1）静止流体中任一点的压力由两部分组成，即液面
压力p0与该点到液面间单位面积上的液柱质量。
坐标轴方向的合力均为零。
适用条件：绝对、相对静止, 可压缩与不可压缩流体。
二、方程的积分 将Euler方程分别乘以dx，dy，dz，然后相加，得
p p p dx dy dz (Xdx Ydy Zdz) x y z
因为 p＝f（x，y，z），所以上式等号左边为压强p的 全微分dp，则上式可写为
（1）
④ 等压面方程 令 所以 dp＝0， 则 adx + gdz＝0
ax gz C
a tg 1 g
结论：a.等压面是一簇平行斜平面 b.它与x轴夹角为
对于自由液面：x＝0，z＝0，C＝0 则
ax gzs 0
自由液面方程 自由液面上点的z坐标
⑤
静压力分布
p p0 U U 0
——帕斯卡（Pascal）定律
帕斯卡（Pascal）定律： 在平衡状态下的不可压缩流体中，作用在 其边界上的压力，将等值、均匀地传递到 流体的所有各点。
三、等压面 定义：同种连续静止流体中，静压力相等的点组成的 面。（p＝const） 方程：
dp ( Xdx Ydy Zdz)
（2）静止流体中，压力随深度呈线性变化。 （3）同种连续静止流体中，深度相同的点压力相同。

南京理工大学工程流体力学基础 流体静力学

南京理工大学工程流体力学基础 流体静力学

增量。
f 1 p 0
§2-2 欧拉平衡微分方程
等压面
等压面：流体中压强相等的点组成的面。
px, y, z const. dp 0
f dl fxdx f ydy fzdz 0
dp fxdx f ydy fzdz
压强差公式
重要性质：静止流体中，质量力垂直于等压面。
f 1 p 0
x
p p dx x 2
z
fx a
p p dx
o x 2
dx
y
§2-2 欧拉平衡微分方程
流体平衡微分方程
微元体在静压强和质量力的作用下平衡。 微元体上的力在x方向的平衡方程：
p
p x
dx dydz
2
p
p x
dx dydz 2
fx dxdydz 0
p p dx
化简：
fx
1
p x
0
同理：
由压强差公式
dp fxdx f ydy fzdz
dp gdz
dz dp 0
g
设不可压缩，积分 z p C
g
流体静力学 基本方程
对图中1、2点
z1
p1
g
z2
p2
g
适用条件：同一容器、同种不可 压缩重力流体。 §2-3 重力场中流体的平衡
流体静力学基本方程
物理意义
z p C
g
单位重量流体 单位重量流体 单位重量流体
第二章 流体静力学
第一节 流体静压强
流体静压强
流体平衡，则作用在流体上的应力只有法向应 力，而没有切向应力。流体作用面上负的法向 应力就是静压强。
pn
dF dA
pnn
§2-1 流体静压强

流体力学 第2章 静力学

流体力学 第2章 静力学

作用在为微元四面体上的力有：
2.1.2 表面力
1 Pz p z dAz p z dxdy 2
P n = pn dA n
Pn在x、y、z轴方向的投影分别为Pncos(n，x)、 Pncos(n，y)、Pncos(n，z)。 2）质量力 作用在微元四面体上的质量力只有重力，它在 各坐标轴方向的分量为Fx、Fy、Fz。设流体的 密度为ρ，则：
2.1.2 表面力
流体静压强的特征 流体静压强没有方向性，是一个标量。静止流体中 任意点的静压强值仅由该点的坐标位置决定，而与 该点静压力的作用方向无关。 证明 如图2.2所示，在静止流 体中的点M(x,y,z)处取 一微元四面体，其边长 分别为dx、dy、dz，斜 面的的外法线方向的
单位矢量为n,
2.1.2 表面力
解释
1）因为流体不能抵抗拉力，所以除液体自由表 面处的微弱表面张力外，在流体内部是不存 在拉力或张力的。
2）由于流体不表现出粘性，在静止流体内部也 就不存在切向摩擦力。 流体静压力是一个有大小、方向、合力作用 点的矢量，它的大小和方向都与受压面密切 相关。
2.1.2 表面力
当微元四面体的边长趋于零时，Px、Py、Pz、Pn就是 作用在 M 点各个方向的压强。因此，上式表明流体 中某一点任意方向的静压强是相等的，是位置坐标的 连续函数，即P = P(x,y,z)。
2.2 流体的平衡微分方程及其积分
2.2.1 欧拉平衡微分方程
如图2.3所示，在平 衡流体中任取一个微 元六面体 abdcc´d´b´a´，其边 长分别为dx、dy、dz， 形心点为M(x,y,z)， 该点压强为p(x,y,z)，
化简得
p dxdydz Xdxdydz 0 x

水力学（工程流体力学）流体静力学要点总结

水力学（工程流体力学）流体静力学要点总结

第二章 流体静力学•静水压强特性：（1）第一特性：静水压强的方向与作用面的内法线方向重合（2）第二特性：静止流体中某一点静水压强的大小与作用面的方位无关（只与深度位置有关）•流体平衡微分方程：⎪⎪⎪⎭⎪⎪⎪⎬⎫=∂∂⋅-=∂∂⋅-=∂∂⋅-010101z p Z y p Y x p X ρρρ流体处于平衡状态时，作用于流体上的质量力与压强递增率间的关系 用途：质量力已知时，用该式求静止流体内的压强分布规律)(Zdz Ydy Xdx dp ++=ρ dz zW dy y W dx x W dW ∂∂+∂∂+∂∂= 势函数；有势的力zW Z y W Y x W X ∂∂=∂∂=∂∂=；； dW dp ρ= 积分得：p W C ρ=+ 当某点压强0p 、力的势函数0W 已知时（即边界条件已知）得 00()p p W W ρ=+-•静水压强分布规律：〖一〗 'pC z C γγ+== 或 1212p p z z γγ+=+z ：单位重量流体具有的位能或位置水头；γp：单位重量流体具有的压能或压强水头； γp z +：单位重量流体具有的总势能或测压管水头（测压管液面相对于基准面的高度）；C p z =+γ: 表明静止流体中单位重量流体具有的总势能守恒或测压管水头为常数物理意义：静止液体中各点单位重量液体具有的总势能相等几何意义：静止液体中各点的测压管水头相等，测压管水头线是水平线从能量意义上来说：静止流体中各点的位置水头与压强水头之和都相等，或者静止流体中各点的测压管水头线为一水平线。

〖二〗边界条件：0z z =时，0p p =则0p p h γ=+•22/10132533.107601m N O mH mmHg atm ===（标准大气压）22/98070107361m N O mH mmHg at ===（工程大气压）•压强表示方法：绝对压强：绝对真空状态做为压强起始计算零点，以abs p 表示；相对压强：一个大气压做为压强起始计算零点，以p 表示；•等压面及其性质：①等压面与质量力正交②水平面是等压面的条件：由于等压面与质量力正交，静止流体中等压面是水平面。

流体力学_02_流体静力学

流体力学_02_流体静力学

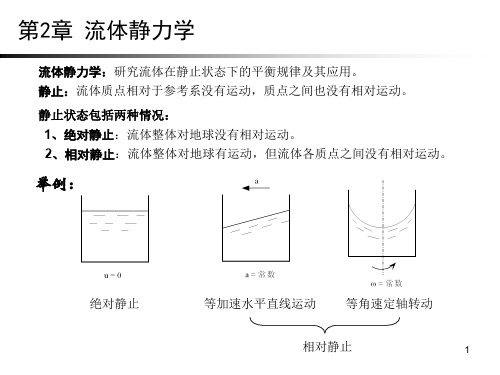
2.流体静力学流体静力学研究静止流体平衡的力学规律及其在工程技术上的应用。

静止流体的概念：流体（宏观）质点之间没有相对运动。

绝对静止：流体整体对于地球没有相对运动（一般工程的观点）。

相对静止：流体整体对于地球有相对运动，但流体质点间及流体与容器壁间无相对运动。

静止流体内不呈现粘性，故静力学讨论的问题对理想流及实际流体均适用。

2.1.流体静压强及其特性当流体处于静止状态时，流体中的压强称为静压强。

静压强的两个重要特性：1）流体静压强方向沿作用面的内法线方向（静止流体不可能存在切应力；流体内聚力很小，不能承受拉力）；2）流体静压强的数值与作用面在空间的方位无关，即任一点的压强不论来自何方均相等。

通过微小四面体证明上述第二条特性。

1）因静止流体不能承受剪切力，故作用于微小四面体表面的力均为法向力；2）流体不能承受拉力，所以法向力指向四面体内部（压应力）；3）微小四面体在四个表面力和一个体积力的作用下保持平衡。

表面力在x方向的分量为：()x p p dydzp n ABC n x,cos 2∆−()cos ,2ABC n dydzp x ∆= （在xoz 平面上的投影） ()2dydzp p n x −体积力在x 方向的分量：6x dxdydzf ρ 由力的平衡得：()062=+−x n x f dxdydzdydz p p ρ()03=+−x n x f dxp p ρ当四面体很小时，体积力项与表面力项的比值趋于零，可以忽略，由此得：n x p p =同理可证：y n p p =，z n p p =2.2. 流体平衡方程流体的平衡微分方程由Euler 于1755年首先得出，故又称为欧拉平衡微分方程。

用立方体微元推导平衡方程。

静止流场黏性作用不存在，作用于微元上的力为正压力和体积力，按Taylor 级数展开，舍弃二阶以上小量，可得平衡方程。

受力平衡：面力＋体积力＝0 x 方向的体积力：x x F x y zf =∆∆∆x 方向的表面力：x x x x x p pS p y z p x y z x y z x x ∂∂ =∆∆−+∆∆∆=−∆∆∆ ∂∂0=+x x S F0=∆∆∆∂∂−∆∆∆z y x x p zf y x xx 由此可得：1x pf x ρ∂=∂ 同理：1y pf yρ∂=∂ 1z pf zρ∂=∂ 平衡方程的物理意义：在静止流体中，作用在单位质量流体上的质量力的分量与作用在该流体表面上的表面力的分量相互平衡。

《流体力学》第二章流体静力学

《流体力学》第二章流体静力学

y
p x p y p z pn
C x
pz
f
↑
z
表 面 力 质 量 力
1 d yd z 2 1 Py p y d zd x 2 1 P p d yd x z z 2 P n pn d A P x px
A
P y P n
P x
dz
→
o dy dx
B
→ x
↑
1 Fx dxdydz X 6 1 Fy dxdydz Y 6 1 Fz dxdydz Z 6
2.2 流体平衡微分方程 相对静止的质量力包 三、等压面 括惯性力！ 液体压强相等的各点组成的平面或曲面 在等压面上处处 dp 0 等压面是等 高平行平面
dp dy dz ) f x dx ( f xydx dy ff dzf z 0 yz
f (0 ,0 gf) , f ) (dx, dy, dz ) 0 f ds (, f , 两种不相混合平衡液体交界面为等压面 x y z
2.3 重力场中的平衡流体 §2-3 重力场中的平衡流体 (均质不可压缩重力流体) 一、在重力作用下静止液体的压强分布 1. 静力学基本方程
f x 0, f y 0, f z g
压强差公式为
z 轴垂直向上
p z C g
dp ( fgdz dp x dx f y dy f z dz )
ds (dx, dy, dz )
dp ( f x dx f y dy f z dz )
压强差公式
欧拉平衡方程式综合形式
2.2 流体平衡微分方程
二、质量力的势函数
压强差公式 表明：在静止流体中，空间点的坐标增量为

《工程流体力学》第二章 流体静力学

《工程流体力学》第二章 流体静力学

20 0 2340 615
各项物理意义：
容器：封闭
液体重度：g
自由液面压强：po 小孔： 器壁上距底部z处
小孔处压强：p = po+ gh
在o处与一根抽成真空的小管相通，液体进入小管，并迅
速上升到A点： p = gh’
h ——O、B两处单位重量流体位能差 h’ ——O、A两处单位重量流体位能差
代表一种能量，称为压力能
容器旋转：绕铅直轴，角速度w
容器旋转后，液体虽未流出，但压强发生了变化，
画出过边上小孔的等压线
虚线 —— 相对压强为 0
盖板各点承受的相对压强：
或真空度： 盖板上： 在轴心处，真空度 最大： 在边缘处，真空度 最小： 离心泵和风机就是利用这个原理，使 流体不断从叶轮中心吸入。
3. 流体静压强仅是空间位置和时间的标量函数，与所取 作用面的方向无关——各向同性 证：取一五面体
(1)表面力：作用静止(或相对静止)流体上无拉力和切力， 表面力只有压力，
在左面上：pydxdz 在底面上：pzdxdy 在斜面上：pndxds 在前面上：pxdydz/2 在后面上：pxdydz/2
液面上半径r处： 液体体积：
由此可测得w值。
速很高，液面上升过高， 溢出容器，容器为封闭的，只在中间留有一小口。
容器静止时：液面离盖板Dho 容器旋转时：液面中心下降到b
求：w
(1)求R’：
(2)静止时空出体积＝旋转时下凹体积
画出等压线
讨论： 1、AA`处压强？ 2、A`B处压强？ 3、容器底部压强？
外力场作用在流体微团上的非接触力，与流体质量(或 体积)成正比， 如地球吸引力、惯性力、电磁力等。 流体力学中一般只考虑地球吸引力，惯性力。 单位质量力：单位质量流体受到的质量力。

南京理工大学工程流体力学基础 第2章_流体静力学剖析

南京理工大学工程流体力学基础 第2章_流体静力学剖析

静水头线 计示静水头线 §2-3 重力场中流体的平衡
重力场中静止液体内的静压强
对淹深为h的a点和压强为p0的自由液面列静力 学基本方程
z p z h p0
g
g
p p0 gh
表明不可压缩的重力流体处于平衡状态时：
静压强随深度线性分布； z
p0
H
静压强包括自由表面压强
h
和液重产生的压强；
a
p
§2-1 流体静压强
证明：静压强大小与作用面方向无关
任取微元四面体MABC，作用有表面力和质量 力f。
斜面ABC外法线n的方向余弦为
z
cosn, x cosn, y cosn,z
设ABC面积为dS，则
C
py M
f
px
n
pn B
ABC面 MBC面 MCA面 MAB面 dS αdS βdS γdS
§2-2 欧拉平衡微分方程
等压面
取一微元矢量 dl dx, dy, dz dp
与欧拉平衡微分方程点乘
fxdx f ydy fzdz
p dx p dy p dz x y z
dp fxdx f ydy fzdz
压强差公式
说明：质量力一定时，静压强的增量取决于坐标 增量。
f 1 p 0
第二章 流体静力学
第一节 流体静压强
流体静压强
流体平衡，则作用在流体上的应力只有法向应 力，而没有切向应力。流体作用面上负的法向 应力就是静压强。
pnLeabharlann dF dApnn§2-1 流体静压强
流体静压强的特性
特性一 流体静压强的作用方向沿作用面的内 法线方向。
特性二 流体静压强的大小与作用面在空间的 方位无关，只是坐标的函数。

南京理工大学工程流体力学基础 第2章_流体静力学

南京理工大学工程流体力学基础 第2章_流体静力学

设ABC面积为dS，则
ABC面 MBC面 MCA面 MAB面 dS αdS βdS γdS
证明：静压强大小与作用面方向无关
流体微元静力平衡 fd pxdS py dS pzdS pn dS 0
1 d hdS 3
z
py M A o y x §2-1 流体静压强 pz
1 p fx 0 x 1 p fy 0 y 1 p fz 0 z f 1

p 0
欧拉平衡 微分方程
§2-2 欧拉平衡微分方程
等压面
取一微元矢量
dl dx, dy, dz
与欧拉平衡微分方程点乘
p p p f x dx f y dy f z dz dx dy dz x y z 1 p fx 0 x 1 p fy 0 y 1 p fz 0 z f 1
x
p
p dx x 2
z
p
fx
a dx
o
p dx x 2
y
§2-2 欧拉平衡微分方程
流体平衡微分方程
微元体在静压强和质量力的作用下平衡。 微元体上的力在x方向的平衡方程：
p dx p dx p dydz p dydz f x dxdydz 0 x 2 x 2 p dx
压强差公式
说明：质量力一定时，静压强的增量取决于坐标 增量。
f 1

p 0
§2-2 欧拉平衡微分方程
等压面
等压面：流体中压强相等的点组成的面。
px, y, z const. dp 0
f dl f x dx f y dy f z dz 0
dp f x dx f y dy f z dz

工程流体力学 第二章流体静力学

工程流体力学 第二章流体静力学
工程流体力学
第二章 流体静力学
地球 惯性系 平衡或静止 非惯性系 相对平衡或相对静止
二、静压强的两个特性
1．静压强方向永远沿着作用面内法线方向（“内”—指向作用面；“法 线”—垂直作用面）。
❖ 证明：（反证法）如图，取静止流体中任意隔离体。设切割面上任一 点 m 处受力F为任意方向。则 F一定可分解为垂直于作用面的法向分 力 Fn 和平行于作用面的切向分力Fτ。
略去二阶以上高阶小量后，得：
p1
p
1 2
p x
dx
p2
p
1 2
p x
dx
3. 导出关系：
根据流体平衡的充要条件，静止流体所受的所有外力在各
个坐标轴方向上的投影之和为零，即 Fi 0 。以x方向为
例：
fx d x d y d z ( p 1 2 p x d x ) d y d z ( p 1 2 p x d x ) d y d z 0
若存在垂直于作用 面的法向作用力 Fn ，由流体不能 承受拉力的性质可 知：垂向作用力Fn 只能为压力。
F
Fn
Fτ
2 垂向作用Fn指向作用面。
m
图2-1 静止流体中的单元体
2．静止流体中任何一点上各个方向的静压强大小相等，与作用面方位无关。 即静压力各向等值。只是坐标点的连续可微函数。
一 般 流 体 力微 学元 证分 明析 思法 路
若存在平行于作用
面的切向作用力
Fτ ：流体在切向
F
力作用下必然发生
流动，这与流体静 止的前提条件相悖。
Fn
Fτ
m
1 静止流体不能承受剪切作用力Fτ
图2-1 静止流体中的单元体
二、静压强的两个特性
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
p1 pA 1 gh1 p4 p3 3 gh4 p2 p1 3 gh2 pB p4 1 g h5 h4 p3 p2 2 gh3
逐一代入，得
pB pA 1 gh1 3 gh2 2 gh3
dp f x dx f y dy f z dz dp dz 0 dp gdz g 流体静力学 p 设不可压缩，积分 基本方程 z C g
fx f y 0 f z g
对图中1、2点
p1 p2 z1 z2 g g
适用条件：同一容器、同种不可 压缩重力流体。 §2-3

p 0
欧拉平衡 微分方程
§2-2 欧拉平衡微分方程
等压面
取一微元矢量
dl dx, dy, dz
与欧拉平衡微分方程点乘
dp
p p p f x dx f y dy f z dz dx dy dz x y z
dp f x dx f y dy f z dz
绝对压强 以完全真空为基准计量的压强。 p pa gh 计示压强 以大气压为基准计量的压强，也称为 相对压强或表压强。 pe p pa gh 真空 绝对压强低于大气压时，负的计示压强。
pv pe pa p
§2-3 重力场中流体的平衡
压强的单位
单位面积上的力：
重力场中流体的平衡
流体静力学基本方程
物理意义
p z C g
单位重量流体 的压强势能 单位重量流体 的总势能
单位重量流体 的重力势能
不可压缩的重力流体处于平衡状态时，其中任 意点上的单位重量流体的总势能为常数。
§2-3 重力场中流体的平衡
流体静力学基本方程
几何意义
位置水头
p z C g
标准大气
T0 288.15K p0 101325Pa
0.0065K/m
§2-3 重力场中流体的平衡
可压缩流体中压强的变化
对于可压缩流体，密度随压强和温度变化。 p 完全气体的状态方程为
考虑大气层中对流层和同温层的情况。 T T1 标准大气同温层（11-20km）： 代入压强差公式 dp gdz
等压强 压强差 压强差
pA 1 gh pB 1 gh2 2 gh 1
p pA pB 2 1 gh
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量，测量量程较小)：
倾斜式微压计：较大的容器和带刻度的倾斜玻璃 管，内有工作液体（蒸馏水或酒精）。测量精度 较高，常用来测量微小压强或压强差。
表明不可压缩的重力流体处于平衡状态时： z p 静压强随深度线性分布； H h 静压强包括自由表面压强 a 和液重产生的压强； g z 自由表面的压强以相同大 o 帕斯卡原理 小传到液体内部任意点。
0
p
§2-3 重力场中流体的平衡
可压缩流体中压强的变化
对于可压缩流体，密度随压强和温度变化。 p 完全气体的状态方程为
1 p fx 0 x 1 p fy 0 y 1 p fz 0 z f 1

p 0
欧拉平衡 微分方程
§2-2 欧拉平衡微分方程
等压面
取一微元矢量
dl dx, dy, dz
与欧拉平衡微分方程点乘
p p p f x dx f y dy f z dz dx dy dz x y z 1 p fx 0 x 1 p fy 0 y 1 p fz 0 z f 1
计示压强 等压强
p 1 gh 2 gh2 pa 1
p pa 绝对压强
真空
p pa 2 gh2 1 gh1
pv 2 gh2 1 gh 1
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量，测量量程较小)：
U形管测压计：还可测量压强差。
1 p fy 0 y 1 p fz 0 z
欧拉平衡微分方程
流体平衡的条件
结论： 质量力有势是不可压缩流体静止的必要条件； 对于不可压缩流体，等压面与等势面重合。
§2-2 欧拉平衡微分方程
第二章 流体静力学
第三节 重力场中流体的平衡
流体静力学基本方程
质量力仅为重力 由压强差公式
fx x fy y fz z
fx
x
0
由压强差公式 dp f x dx f y dy f z dz
x dx y dy z dz d §2-2
C
f px pn B n
h→0： px py pz pn 0 分别投影到x、y、z轴上
pn p x p y pz
静压强只是空间坐标的函数
p px, y, z
第二章 流体静力学
第二节 欧拉平衡微分方程
流体平衡微分方程
在静止流体中取一微元六面体，各面平行于坐 标平面。 微元体边长：dx dy dz 中心点坐标：a(x, y, z) 中心点压强：p 单位质量力：fx fy fz 中心点压强按泰勒级数展开 可得各面中心压强。
§2-1 流体静压强
证明：静压强大小与作用面方向无关
任取微元四面体MABC，作用有表面力和质量 力f。 斜面ABC外法线n的方向余弦为
cosn, x cosn, y cosn, z
z
py M A o y x §2-1 流体静压强 pz
C
f px pn B n
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量，测量量程较小)：
测压管：玻璃管，直接连接到测量压强的容器上。
绝对压强
p pa
p pa gh
pe gh
计示压强 绝对压强
真空
p pa
p pa gh
pv gh
§2-3 重力场中流体的平衡
压强的测量
压强水头 总水头
静水头线 计示静水头线
不可压缩的重力流体 处于平衡状态时，静 水头线或计示静水头 线为平行于基准面的 水平线。
§2-3 重力场中流体的平衡
重力场中静止液体内的静压强
对淹深为h的a点和压强为p0的自由液面列静力 学基本方程
p0 p z z h g g
p p0 gh
国际单位制：N/m2（Pa） bar
工程单位制：kgf/cm2
液柱高：mH2O mmHg 大气压：工程大气压 标准大气压
§2-3 重力场中流体的平衡
压强的测量
测压计分类 金属测压计(间接测量，可测量较高压强)：
波登管测压计：利用椭圆截面的金属弯管受压变 形原理制作。 膜片式测压计：利用膜片受压变形原理制作。
x
p
p dx x 2
z
p
fx
a dx
o
p dx x 2
y
§2-2 欧拉平衡微分方程
流体平衡微分方程
微元体在静压强和质量力的作用下平衡。 微元体上的力在x方向的平衡方程：
p dx p dx p dydz p dydz f x dxdydz 0 x 2 x 2 p dx
第二章 流体静力学
第一节 流体静压强
流体静压强
流体平衡，则作用在流体上的应力只有法向应 力，而没有切向应力。流体作用面上负的法向 应力就是静压强。
dF pn pnn dA
§2-1 流体静压强
流体静压强的特性
特性一 流体静压强的作用方向沿作用面的内 法线方向。
特性二 流体静压强的大小与作用面在空间的 方位无关，只是坐标的函数。
设ABC面积为dS，则
ABC面 MBC面 MCA面 MAB面 dS αdS βdS γdS
证明：静压强大小与作用面方向无关
流体微元静力平衡 fd pxdS py dS pzdS pn dS 0
1 d hdS 3
z
py M A o y x §2-1 流体静压强 pz
1 p fx 0 x 同理： f y 1 p 0 y 1 p fz 0 z
p
化简：
f
1
x 2

p 0
z
p
fx
a dx
欧拉平衡 微分方程 x
o
p dx x 2
y
§2-2 欧拉平衡微分方程
流体平衡微分方程
物理意义：静止流体内质量力与静压强相平衡。 适用范围：理想流体 黏性流体 可压缩流体 不可压缩流体 静止 相对静止
压强差公式
重要性质：静止流体中，质量力垂直于等压面。
f 1

p 0
§2-2 欧拉平衡微分方程
流体平衡的条件
由欧拉平衡微分方程，对坐标交错求导，可得
f x f y y x f y f z z y f z f x x z
（不可压缩）
根据场论，此式表明质量力场是有势场，存在 势函数π(x, y, z)，且 1 p
p2 p1
h1 l sin
h2 l A1 A2
h h1 h2 l sin A1 A2
p p2 p1 gh g sin A1 A2 l kl
§2-3 重力场中流体的平衡
例2-3
活塞直径d=35mm，重15N，油密度ρ1=920kg/m3 ，水 银密度ρ2=13600kg/m3，h=0.7m，求Δh。 解：活塞重量造成的其底面压强为
p g z - z1 ln p1 RT1 dp gdz p RT1
标准大气
z1 11000m T1 216.7K p1 22638Pa