图形的平移习题

2024年数学五年级下册图形的平移与旋转基础练习题（含答案）试题部分一、选择题：1. 下列哪个图形不是轴对称图形？（）A. 长方形B. 正方形C. 椭圆D. 平行四边形2. 一个图形平移后，下列哪个属性不会发生改变？（）A. 形状B. 大小C. 方向D. 位置3. 下列哪个现象属于旋转现象？（）A. 拉抽屉B. 推门C. 滚动圆球D. 滑动滑板4. 将一个正方形绕着它的一个顶点旋转90度，得到的图形是？（）A. 矩形B. 菱形C. 正方形D. 平行四边形5. 在平移现象中，下面哪个说法是正确的？（）A. 平移前后图形的大小和形状会改变B. 平移前后图形的方向会改变C. 平移前后图形的位置会发生改变D. 平移前后图形的面积会改变6. 下列哪个图形可以通过平移得到另一个相同的图形？（）A. 心形B. 数字“8”C. 英文字母“Z”D. 英文字母“B”7. 一个图形绕着某一点旋转180度，得到的图形与原图形（）A. 重合B. 相似C. 全等D. 不确定8. 在平移过程中，下面哪个量是不变的？（）A. 路程B. 速度C. 时间D. 方向9. 下列哪个图形可以通过旋转90度后与原图形重合？（）A. 正三角形B. 正方形C. 长方形D. 梯形10. 一个图形平移3格，再旋转90度，平移2格，这个图形的最终位置与原来相比（）A. 向右平移了5格B. 向左平移了5格C. 向上平移了5格D. 向下平移了5格二、判断题：1. 平移是指将一个图形上的所有点按照某个方向作相同距离的移动。

（）2. 旋转是指将一个图形绕着某一点转动一个角度的图形变换。

（）3. 平移和旋转都不会改变图形的大小和形状。

（）4. 旋转180度后，图形的每个点都会与原来的点关于旋转中心对称。

（）5. 平移和旋转都是刚体变换。

（）6. 一个图形旋转360度后，会回到原来的位置。

（）7. 平移和旋转都可以改变图形的位置。

（）8. 旋转过程中，图形的大小和形状会发生改变。

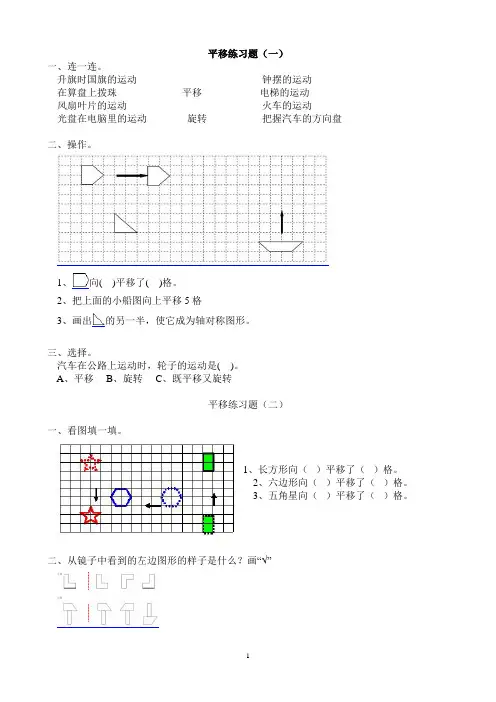
平移练习题（一）一、连一连。

升旗时国旗的运动钟摆的运动在算盘上拨珠平移电梯的运动风扇叶片的运动火车的运动光盘在电脑里的运动旋转把握汽车的方向盘二、操作。

1、向( )平移了( )格。

2、把上面的小船图向上平移5格3、画出的另一半，使它成为轴对称图形。

三、选择。

汽车在公路上运动时，轮子的运动是( )。

A、平移B、旋转C、既平移又旋转平移练习题（二）一、看图填一填。

1、长方形向（）平移了（）格。

2、六边形向（）平移了（）格。

3、五角星向（）平移了（）格。

二、从镜子中看到的左边图形的样子是什么？画“√”三、按要求操作。

1、把图中长方形向上平移2格；2、把图中三角形向右平移3格；3、把图中平行四边形向左平移5格。

四、按要求填图五、分别画出下面图形向下平移2格后再向右平移8格后得到的图形六、画出拖拉机先向左平移4格，再向下平移3格后的图形。

平移练习题（三）一、看图填一填。

1、长方形向（）平移了（）格。

2、六边形向（）平移了（）格。

3、五角星向（）平移了（）格。

二、按要求操作。

1、把图中下边的长方形向上平移2格；2、把图中左边的三角形向右平移3格；3、把图中上边的长方形向下平移4格；4、把图中右边的平行四边形向左平移5格。

5、平移后的图像什么？三、接着往下画。

四、在各图形中填上合适的数。

五、下图是按照一定规律排列起来的,请按这一规律在空格处画出适当的图形。

六、画一画。

七、在下图空格内画出合适的图形。

四年级图形平移练习题1. 平移是指将一个图形在平面上沿指定方向移动一段距离，图形的大小和形状都保持不变。

下面是一些针对四年级学生的图形平移练习题，通过解题来巩固对平移的理解和应用。

题目1：将正方形A沿向右的方向平移3个单位长度，得到新的正方形B。

请问，新的正方形B的图形是如何相对于原正方形A的位置变化的？题目2：将长方形C沿向下的方向平移2个单位长度，得到新的长方形D。

请问，新的长方形D的图形是如何相对于原长方形C的位置变化的？题目3：将三角形E沿向左的方向平移4个单位长度，得到新的三角形F。

请问，新的三角形F的图形是如何相对于原三角形E的位置变化的？题目4：将梯形G沿向上的方向平移1个单位长度，得到新的梯形H。

请问，新的梯形H的图形是如何相对于原梯形G的位置变化的？题目5：将圆形I沿向右的方向平移5个单位长度，得到新的圆形J。

请问，新的圆形J的图形是如何相对于原圆形I的位置变化的？题目6：将正方形K沿向下的方向平移3个单位长度，得到新的正方形L。

请问，新的正方形L的图形是如何相对于原正方形K的位置变化的？题目7：将长方形M沿向左的方向平移7个单位长度，得到新的长方形N。

请问，新的长方形N的图形是如何相对于原长方形M的位置变化的？题目8：将梯形O沿向上的方向平移2个单位长度，得到新的梯形P。

请问，新的梯形P的图形是如何相对于原梯形O的位置变化的？题目9：将圆形Q沿向右的方向平移6个单位长度，得到新的圆形R。

请问，新的圆形R的图形是如何相对于原圆形Q的位置变化的？题目10：将正方形S沿向下的方向平移4个单位长度，得到新的正方形T。

请问，新的正方形T的图形是如何相对于原正方形S的位置变化的？以上是一些四年级图形平移的练习题，希望能够帮助学生巩固对平移概念的理解和应用。

通过反复练习，学生将能够更加熟练地解决平移问题，并培养出准确观察和判断图形位置变化的能力。

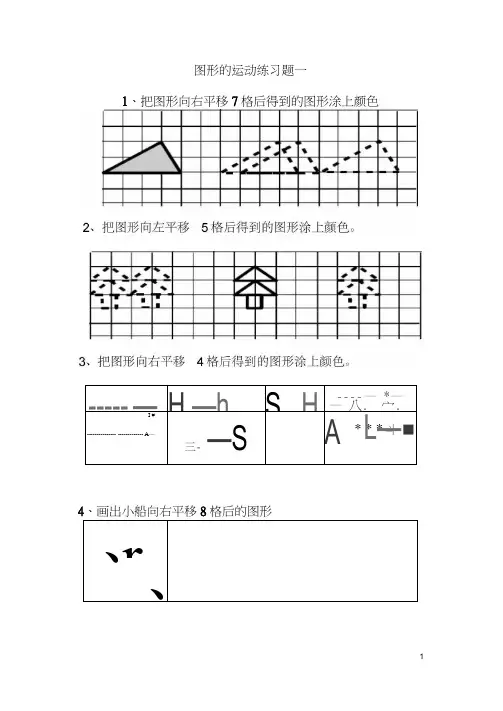
图形的运动练习题一
1、把图形向右平移7格后得到的图形涂上颜色
4、画出小船向右平移8格后的图形
二
图形的运动练习题二
1、画出向右平移6格后的图形
2、（1）小汽车
向（）平移了
（）格。

（2）小船
向（）平移
了（）格。

（3）小飞
机向（）平
移了
（）格。

3、（1）向左平移2
格
7
r\
/
/\
/
7\
（2）向右平移5格
图形的运动练习题二
4、A 图向（）平移（）格到B 图
B 图向（）平移（）格到
C 图
1、画出花瓶向上平移
2、（ 1）画出三角形向右平移6
4格后的图形，再 画出它继续向左平 移7格后的图形。

格后的图形。

3、（ 1）画出小旗向右平移
3格再向下平移2格
后的图形。

（2）分别画出将图形向上平 移3格向左平移8格的图 形。

（2）画出梯形向下平移5
格后的图形
画对称图形11、画出轴对称图形的另一边。

平移练习题1.将如图所示的图案通过平移后可以得到的图案是( )2.下列图形中，是由(1)仅通过平移得到的是( )3．下列生活中的各个现象，属于平移变换现象的是( )A ．拉开抽屉B ．用放大镜看文字C ．时钟上分针的运动D ．你和平面镜中的像 4．下列说法中正确的是（ ）A ．一个图形经过平移后，与原图形成轴对称B ．如果两个图形成轴对称，那么一个图形可由另一个图形经过平移变换得到C ．一个图形经过平移后，它的性质都发生了变化D ．图形的平移由平移的方向和距离决定5．一个图形先向右平移5个单位,再向左平移7个单位,所得到的图形,可以看作是原来位置的图形一次向 平移 个单位得到的6．如果三角形ABC 沿着北偏东300的方向移动了２cm ，那么三角形ABC 的一条边AB 边上的一点Ｐ向__________移动了______cm 。

7．在下列说法中：①△ABC 在平移过程中，对应线段一定相等；②△ABC 在平移过程中，对应线段一定平行；③△ABC 在平移过程中，周长不变；④△ABC 在平移过程中，面积不变。

其中正确的有____________________。

8．如图，△ABC 经过平移之后得△DEF ，请你在两三角形的内角中找出图中相等的线段写出图中互相平行的线段写出图中相等的角9.将长度为3cm 的线段向上平移20cm ，所得线段的长度是（ ）A ．3cmB ．23cmC ．20cmD ．17cm 10. 如图，△ABC 平移后得到了△DEF ，若∠A=400，∠E=600，那么，∠1=_________°， ∠2=________°,∠F=_______°,∠C=_________°。

11．如图a 是长方形纸带，∠DEF =20°，将纸带沿EF 折叠成图b ，再沿BF 折叠成图c ，则图c 中的∠CFE 的度数是 ．E D B CFA O12.如图，将∆ABC 沿直线AB 向右平移后到达∆BDE 的位置，若∠CAB ＝50°，∠ABC ＝100°，则∠CBE的度数为 ．12题 13题13.如图ABE ∆沿BC 方向平移到FCD ∆的位置，若有AB=4，AE=3，BC=5，则CF= ，EF= .14．如图①，两个等边△ABD 、△CBD 的边长均为1，将△ABD 沿AC 方向向右平移到△A ′B ′D ′的位置得到图②，则阴影部分的周长为________．15.如图，直角梯形ABCD 中，AD ∥BC ，AD ⊥AB ，BC=5，将直角梯形ABCD 沿AB 方向平移2个单位得到直角梯形EFGH ，HG 与BC 交于点M ，且CM=1，则图中阴影部分面积为 .15题 16题17题16.如图所示是重叠的两个直角三角形．将其中一个直角三角形沿BC 方向平移得到DEF △．如果8cm AB =，4cm BE =，3cm DH =，则图中阴影部分面积为 2cm ．17.把三张大小相同的正方形卡片A 、B 、C 叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图①摆放时，阴影部分的面积为S 1；若按图②摆放时，阴影部分的面积为S 2，则S 1________S 2(填“＞”“＜”或“＝”)．A D A CB AE A C A B AF AD AC DB E A FC G B A AE AF CB A图a图b图cC B E F DAC G HMD H18.如图，△ABC 沿着射线BM 的方向平移，请你画出当B 平移到B ′位置时的△A ′B ′C ′19.经过平移，△ABC 的边AB 移到了EF ，作出平移后的三角形．20.小镇A 和B 在一条河的两岸，现要在河上造一座桥MN ，桥造在何处才能使从A 到B 的路径AMNB 最短？（假设河两岸1l 、2l 平行,桥MN 与河岸垂直，A 到离它较近的河岸的距离大于河宽）．B MB '．．．．．ABCE F。

平移变换练习题平移变换是图形学中的一项重要概念，它可以将一个图形在平面上进行移动，而保持其形状和大小不变。

在这里，我们将介绍一些平移变换的练习题，帮助您更好地理解和应用平移变换。

练习一：平移变换的基本概念考虑一个点P(x, y)，进行平移变换时，将其坐标分别增加dx和dy，可以得到新的坐标P'(x+dx, y+dy)。

请根据此概念回答以下问题：1. 一个点A(-2, 3)进行平移变换，dx=4，dy=2，求变换后的坐标。

2. 一个点B(1, -5)进行平移变换，dx=-3，dy=8，求变换后的坐标。

练习二：平移变换与向量的关系在平移变换中，可以使用向量来表示平移的位移向量。

请使用向量表示以下平移变换：1. 图形G中的点C(3, 2)进行平移变换，位移向量为v(4, -1)，求变换后的坐标。

练习三：平移变换的性质平移变换具有一些特定的性质，请根据下列性质回答问题：1. 平移变换保持图形的形状和大小不变，只改变其位置。

True/False？2. 平移变换前后，图形的所有线段长度都不变。

True/False？3. 平移变换前后，图形的所有内角度数都不变。

True/False？练习四：多个点的平移变换考虑一个由多个点组成的图形F，进行平移变换时，每个点都按照相同的位移向量进行平移。

请根据以下题目求解：1. 图形F中的点D(1, 2)和点E(4, -1)进行平移变换，位移向量为w(2, 3)，求变换后的坐标。

练习五：平移变换的应用平移变换在图形学中有广泛的应用，例如在计算机图形学中，创建动画效果时常用到平移变换。

请根据以下题目进行应用练习：1. 平面上有一个正方形图形S，其中各顶点坐标分别为A(1, 1), B(2, 1), C(2, 2), D(1, 2)。

将图形S沿x轴平移2个单位和y轴平移3个单位，求变换后的图形S'的顶点坐标。

练习六：综合应用题请根据以下综合题目进行综合应用练习：1. 设平面上有一个三角形图形T，其中顶点坐标分别为A(1, 1), B(4, 1), C(3, 3)。

图形的平移与旋转练习题图形的平移与旋转练习题在数学中，平移与旋转是两种常见的图形变换方式。

通过平移和旋转，我们可以改变图形的位置和方向，使其更加多样化和有趣。

下面，我们将通过一些练习题来巩固和加深对图形平移与旋转的理解。

练习题一：平移1. 将一个正方形沿着x轴正方向平移3个单位，结果是什么？解答：平移是指将图形沿着指定的方向移动一定的距离。

对于正方形，沿着x轴正方向平移3个单位，意味着将正方形的每个顶点都向右移动3个单位。

因此，结果是一个新的正方形，其每个顶点的坐标都比原来的正方形的坐标大3。

2. 如果将一个长方形沿着y轴负方向平移5个单位，结果是什么？解答：这个问题和上一个问题类似，只是平移的方向和距离不同。

沿着y轴负方向平移5个单位，意味着将长方形的每个顶点都向下移动5个单位。

因此，结果是一个新的长方形，其每个顶点的y坐标都比原来的长方形的y坐标小5。

练习题二：旋转1. 将一个正方形绕原点逆时针旋转90度，结果是什么？解答：旋转是指将图形绕着指定的中心点旋转一定的角度。

对于正方形，绕原点逆时针旋转90度，意味着将正方形的每个顶点按照逆时针方向旋转90度。

因此，结果是一个新的正方形，其每个顶点的坐标都发生了变化，但是仍然是一个正方形。

2. 如果将一个长方形绕坐标轴上的一点顺时针旋转45度，结果是什么？解答：这个问题和上一个问题类似，只是旋转的方向和角度不同。

绕坐标轴上的一点顺时针旋转45度，意味着将长方形的每个顶点按照顺时针方向旋转45度。

因此，结果是一个新的长方形，其每个顶点的坐标都发生了变化，但是仍然是一个长方形。

通过以上练习题，我们可以看到平移和旋转对于图形的变化有着重要的作用。

通过平移，我们可以改变图形的位置，使其在平面上的不同位置出现；通过旋转，我们可以改变图形的方向，使其变得更加灵活和多样化。

这些变换不仅在数学中有着重要的应用，还在日常生活和工程设计中发挥着重要的作用。

总结起来，图形的平移与旋转是数学中常见的图形变换方式。

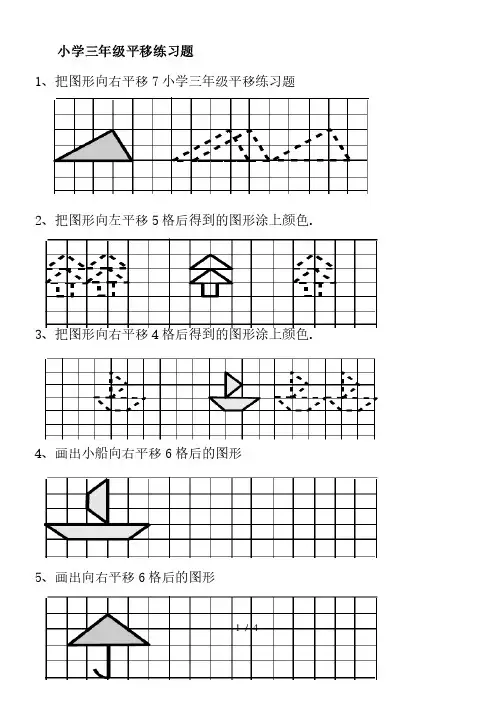
小学三年级平移练习题
1、把图形向右平移7小学三年级平移练习题
.
2、把图形向左平移5格后得到的图形涂上颜色
格后得到的图形涂上颜色.
.
3、把图形向右平移4格后得到的图形涂上颜色
格后得到的图形涂上颜色.
4、画出小船向右平移6格后的图形
5、画出向右平移6格后的图形
1 / 4
6、（1）小汽车向）小汽车向
（ ）平移了）平移了）平移了
（ ）格）格）格. .
（2）小船向）小船向
（ ）平移）平移）平移
了（了（ ）格）格）格. .
（3）小飞机向）小飞机向
（ ）平移了）平移了）平移了
（ ）格）格）格. .
7、（1）向左平移2格 （（2） 向右平移5格
8、画出花瓶向上平移、画出花瓶向上平移 9、
（1）画出三角形向右平移6 4格后的图形，再格后的图形，再
格后的图形. 画出它继续向左平画出它继续向左平 （2）画出梯形向下平移5
移7格后的图形. 格后的图形格后的图形
10、
（1）画出小旗向右平移画出小旗向右平移 （2）分别画出将图形向上平）分别画出将图形向上平 3格再向下平移2格 移3格向左平移8格的图格的图
后的图形. 形.
11、A 图向（图向（
）平移（）平移（ ）格到B 图 B 图向（图向（
）平移（）平移（ ）格到C 图.
12、
（1）向（）向（ ）平移了（）平移了（）平移了（ ）格）格）格. . （2）向（）向（ ）平移了（）平移了（）平移了（ ）格）格）格. .
A B C
（3）向（）向（ ）平移了（）平移了（）平移了（ ）格）格）格. .。

后的图形。形。
4、A图向（）平移（）格到B图
B图向（）平移（）格到C图。
画对称图形
11、画出轴对称图形的另一边。
欢迎您的下载，
资料仅供参考！
致力为企业和个人提供合同协议，策划案计划书，学习课件等等
打造全网一站式需求
（）平移了
（）格。
3、（1）向左平移2格（2）向右平移5格
图形的运动练习题三
1、画出花瓶向上平移2、（1）画出三角形向右平移6
4格后的图形，再格后的图形。
画出它继续向左平（2）画出梯形向下平移5
移7格后的图形。格后的图形
ቤተ መጻሕፍቲ ባይዱ3、（1）画出小旗向右平移（2）分别画出将图形向上平
3格再向下平移2格移3格向左平移8格的图
图形的运动练习题一
1、把图形向右平移7格后得到的图形涂上颜色。
2、把图形向左平移5格后得到的图形涂上颜色。
3、把图形向右平移4格后得到的图形涂上颜色。
4、画出小船向右平移8格后的图形
图形的运动练习题二
1、画出向右平移6格后的图形
2、（1）小汽车向
（）平移了
（）格。
（2）小船向
（）平移
了（）格。
（3）小飞机向

图形的平移与旋转练习题在几何学中，平移和旋转是两个基本的变形操作。

平移是指将图形沿着给定的方向移动一定的距离，而旋转则是指将图形绕着一个固定的点旋转一定的角度。

这两种操作在解决几何问题以及设计和建筑领域中都起着至关重要的作用。

为了更好地理解和掌握图形的平移和旋转，下面将给出一些练习题，通过实践来提高我们的技巧和思维能力。

练习题1：平移给定一个图形ABC，其中A(-1, 2)，B(2, 4)，C(4, 1)。

请将该图形沿x轴平移3个单位和沿y轴平移-1个单位，然后画出平移后的图形。

解答：首先，我们需要将原始图形ABC的坐标分别进行平移操作。

沿x轴平移3个单位后，A的坐标变为A'(-1+3, 2)，即A'(2, 2)；同理，B的坐标变为B'(2+3, 4)，即B'(5, 4)；C的坐标变为C'(4+3, 1)，即C'(7, 1)。

然后，我们将平移后的坐标连接起来，得到平移后的图形A'B'C'。

详细计算过程如下：A' = (2, 2)B' = (5, 4)C' = (7, 1)接下来，我们将平移后的图形绘制出来：(在此处绘制图形A'B'C'，具体形状可根据自己的判断和计算结果进行绘制)练习题2：旋转给定一个图形PQR，其中P(1, 1)，Q(3, 3)，R(5, 1)。

请将该图形绕点P逆时针旋转45度，并画出旋转后的图形P'Q'R'。

解答：首先，我们需要将原始图形PQR的坐标进行旋转操作。

绕点P逆时针旋转45度后，Q和R的坐标分别为：Q' = (1 + (3-1)*cos(45度) - (3-1)*sin(45度), 1 + (3-1)*cos(45度) + (3-1)*sin(45度))R' = (1 + (5-1)*cos(45度) - (1-1)*sin(45度), 1 + (5-1)*cos(45度) + (1-1)*sin(45度))计算结果如下：Q' = (1 + (3-1)*√2/2 - (3-1)*√2/2, 1 + (3-1)*√2/2 + (3-1)*√2/2)= (1, 3)R' = (1 + (5-1)*√2/2 - (1-1)*√2/2, 1 + (5-1)*√2/2 + (1-1)*√2/2)= (5, 1)然后，我们将旋转后的坐标连接起来，得到旋转后的图形P'Q'R'。

3.1 图形的平移（第一课时）1、下列几种运动属于平移的是（）（1）水平运输带上的砖的运动；（2）啤酒生产线上的啤酒通过压盖机前后的运动；（3）升降机上下做机械运动；（4）足球场上足球的运动A．一种B．两种C．三种D．四种2、如图所示，△ABC平移到△DEF，则点A、B、C的对应点分别是_____________________。

线段AB、BC、CA的对应线段分别是_________________________。

∠A、∠B、∠C的对应角分别是__________________________；3、在平面内，将一个图形_______________，这样的图形运动称为平移，平移不改变图形的________和________.平移后，对应线段______________；平移后，对应角______________；平移后，对应点的连线段______________；平移后，新图形和原图形是一对______________4、在日常生活中，你所看过的图形平移的例子有__________ (至少两例)5、如图△ABC沿着PQ的方向平移到△A′B′C′位置，则AA′∥_________∥__________；AA′=__________ = _____________；AB∥_______，AB=________，∠A=_______。

6、（1）将线段AB向右平移3cm得到线段CD，如果AB=5cm,则CD=cm。

（2）将∠ABC向上平移10cm得到∠EFG？如果∠ABC=52°，则∠EFG= °BF= cm。

（3）将面积为30(cm2)的等腰直角三角形ABC向下平移20cm，得到△MNP，则△MNP是三角形，它的面积是(cm2)。

7、经过平移，△ABC的边AB移到了EF，作出平移后的三角形，你有几种作法？8、如图，直线m∥n，它们的距离是1.5厘米，画出△ABC关于直线m对称的△A′B′C′，再做△A'B'C'关于直线n对称的△A″B″C″。

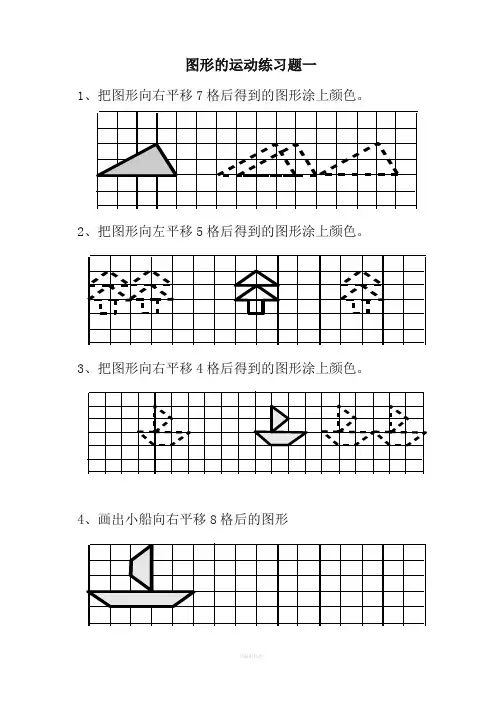
1、把图形向右平移7格后得到的图形涂上颜色。

2、把图形向左平移5格后得到的图形涂上颜色。

3、把图形向右平移4格后得到的图形涂上颜色。

4、画出小船向右平移6格后的图形
5、画出向右平移6格后的图形
6、（1）小汽车向
（）平移了
（）格。

（2）小船向
（）平移
了（）格。

（3）小飞机向
（）平移了
（）格。

7、（1）向左平移2格（2）向右平移5格
8、画出花瓶向上平移 9、（1）画出三角形向右平移6
4格后的图形，再格后的图形。

画出它继续向左平（2）画出梯形向下平移5
移7格后的图形。

格后的图形
10、（1）画出小旗向右平移（2）分别画出将图形向上平
3格再向下平移2格移3格向左平移8格的图后的图形。

形。

11、A图向（）平移（）格到B图
B图向（）平移（）格到C图。

12、（1）向（）平移了（）格。

（2）向（）平移了（）格。

（3）向（）平移了（）格。

（1）分别画出向上平移3格，向左平移8格后得到的图形。

（2）画出向上平移3格，向左平移8格后得到的图形。

（3）分别把向左平移7格和向右平移4格后的图形涂上红色、绿色。

（4）把向右平移7格后的图形涂上黄色。

（5）画出平移后的图形，再向左平移4格。

（6）这个⊿向（）平移（）格，向（）平移（）格后的图形。

（7）画出向左平移8格后的图形。

情景再现：你对以上图片熟悉吗？请你答复以下几个问题：〔1〕汽车中的乘客在乘车过程中，身高、体重改变了吗？乘客所处的地理位置改变了吗？〔2〕传送带上的物品，比方带有图标的长方体纸箱，向前移动了20米，它上面的图标移动了多少米？〔3〕以上都是我们常见的平移问题，认真想一想，你还能举一些平移的例子吗？1.如图1，面积为5平方厘米的梯形A′B′C′D′是梯形ABCD经过平移得到的且∠ABC=90°.那么梯形ABCD的面积为________，∠A′B′C =________.图12.在下面的六幅图中，〔2〕〔3〕〔4〕〔5〕〔6〕中的图案_________可以通过平移图案〔1〕得到的.图2“小鱼〞向左平移5格.图34.请欣赏下面的图形4，它是由假设干个体积相等的正方体拼成的.你能用平移分析这个图形是如何形成的吗？§图形的平移与旋转一、填空：1、如下左图，△ABC经过平移到△A′B′C′的位置，那么平移的方向是______，平移的距离是______，约厘米______.2、如下中图，线段AB是线段CD经过平移得到的，那么线段AC与BC的关系为〔〕3、如下右图，△ABC经过平移得到△DEF，请写出图中相等的线段______，互相平行的线段______，相等的角______.〔在两个三角形的内角中找〕4、如下左图，四边形ABCD平移后得到四边形EFGH，那么：①画出平移方向，平移距离是_______；〔准确到0.1cm〕②HE=_________，∠A=_______,∠A=_______.③DH=_________=_______A=_______.5、如下右图，△ABC平移后得到了△DEF，〔1〕假设∠A=28º，∠E=72º，BC=2，那么∠1=____º，∠F=____º，EF=____º；〔2〕在图中A、B、C、D、E、F六点中，选取点_______和点_______，使连结两点的线段与AE平行.6、如图，请画出△ABC向左平移4格后的△A1B1C1，然后再画出△A1B1C1向上平移3格后的△A2B2C2，假设把△A2B2C2看成是△ABC经过一次平移而得到的，那么平移的方向是______，距离是____的长度.二、选择题：7、如下左图，△ABC经过平移到△DEF的位置，那么以下说法：①AB∥DE，AD=CF=BE；②∠ACB=∠DEF；③平移的方向是点C到点E的方向；④平移距离为线段BE的长.其中说法正确的有〔〕8、如下右图，在等边△ABC中，D、E、F分别是边BC、AC、AB的中点，那么△AFE经过平移可以得到〔〕A.△DEFB.△FBDC.△EDCD.△FBD和△EDC三、探究升级：1、如图，△ABC上的点A平移到点A1，请画出平移后的图形△A1B1C1.3、△ABC经过平移后得到△DEF，这时，我们可以说△ABC与△DEF是两个全等三角形，请你说出全等三角形的一些特征，并与同伴交流.4、如以下图中，有一块长32米，宽24米的草坪，其中有两条宽2米的直道把草坪分为四块，那么草坪的面积是______.5、利用如图的图形，通过平移设计图案，并用一句诙谐、幽默的词语概括你所画的图形.§图形的平移与旋转一、填空、选择题：1、图形的旋转是由____和____决定的，在旋转过程中位置保持不动的点叫做____，任意一对对应点与旋转中心连线所成的角叫做_____.2、如以下图，如果线段MO绕点O旋转90°得到线段NO，在这个旋转过程中，旋转中心是_______，旋转角是_______，它时______°.3、如图，在以下四张图中不能看成由一个平面图形旋转而产生的是〔〕4、请你先观察图，然后确定第四张图为( )4、如下左图，△ABC绕着点O旋转后得到△DEF，那么点A的对应点是_______，线段AB 的对应线段是_____，_____的对应角是∠F. 6、如下中图，△ABC与△BDE都是等腰三角形，假设△ABC经旋转后能与△BDE重合，那么旋转中心是________，旋转了______°.7、如下右图，C是AB上一点，△ACD和△BCE 都是等边三角形，如果△ACE经过旋转后能与△DCB重合，那么旋转中心是_______，旋转了______°，点A的对应点是_______.二、解答题：8、如图11.4.7，△ABC绕顶点C旋转某一个角度后得到△A′B′C，问：〔1〕旋转中心是哪一点？〔2〕旋转角是什么？〔3〕如果点M是BC的中点，那么经过上述旋转后，点M转到了什么位置？9、观察以下图形，它可以看作是什么“根本图形〞通过怎样的旋转而得到的？三、探究升级10、如图，△ACE、△ABF都是等腰三角形，∠BAF=∠CAE=90°，那么△AFC是哪一点为旋转中心，旋转多少度之后能与另一个三角形重合？点F的对应点是什么？§图形的平移与旋转一、选择题1.平面图形的旋转一般情况下改变图形的〔 〕° ° ° °ABCD 旋转到平行四边形A ′B ′C ′D ′的位置，以下结论错误的选项是〔 〕A.AB =A ′B ′B.AB ∥A ′B ′C.∠A =∠A ′D.△ABC ≌△A ′B ′C ′ 二、填空题4.钟表上的指针随时间的变化而移动，这可以看作是数学上的_______.ABCD 绕点O 沿逆时针方向旋转到四边形D C B A '''',那么四边形D C B A ''''是________. 6.△ABC 绕一点旋转到△A ′B ′C ′，那么△ABC 和△A ′B ′C ′的关系是_______.7.钟表的时针经过20分钟，旋转了_______度. 8.图形的旋转只改变图形的_______，而不改变图形的_______. 三、解答题9.以下图中的两个正方形的边长相等，请你指出可以通过绕点O 旋转而相互得到的图形并说明旋转的角度.10.在图中，将大写字母H 绕它右上侧的顶点按逆时针方向旋转90°，请作出旋转后的图案.11.如图，菱形A ′B ′C ′D ′是菱形ABCD 绕点O 顺时针旋转90°后得到的，你能作出旋转前的图形吗？△ABC ，绕它的锐角顶点A 分别逆时针旋转90°、180°和顺时针旋转90°，〔1〕试作出Rt △ABC 旋转后的三角形； 〔2〕将所得的所有三角形看成一个图形，你将得到怎样的图形？13.如图，将右面的扇形绕点O 按顺时针方向旋转，分别作出旋转以下角度后的图形： 〔1〕90°；〔2〕180°；〔3〕270°.你能发现将扇形旋转多少度后能与原图形重合吗？14.如图，分析图中的旋转现象，并仿照此图案设计一个图案.§图形的平移与旋转看一看：以下三幅图案分别是由什么“根本图形〞经过平移或旋转而得到的？1.2.3.试一试：怎样将以下图中的甲图变成乙图？做一做：1、如图①，在正方形ABCD 中，E 是AD 的中点，F 是BA 延长线上的一点，AF =21AB ， 〔1〕△ABE ≌△ADF .吗？说明理由。

初一数学平移练习题一、选择题1. 下列图形中，经过平移后能与原图形重合的是（）A. 正方形B. 长方形C. 梯形D. 半圆A. 平移后图形的位置改变，大小不变B. 平移后图形的位置不变，大小改变C. 平移后图形的位置和大小都改变D. 平移后图形的位置和大小都不变3. 已知点A(2,3)经过平移后得到点A'(4,7)，则平移向量为（）A. (2,4)B. (4,2)C. (2,7)D. (4,7)二、填空题1. 平移前后，图形的__________不变，__________改变。

2. 已知点P(3,1)经过平移后得到点P'(1,3)，则平移向量是__________。

3. 平移向量(3,2)表示将图形向__________平移3个单位，向__________平移2个单位。

三、解答题1. 已知线段AB平移后得到线段A'B'，且A(1,2)，B(4,6)，A'(3,5)，求B'的坐标。

2. 平移向量(2,3)作用于点C(5,2)，求平移后点C'的坐标。

3. 在平面直角坐标系中，将正方形ABCD沿x轴向右平移4个单位，沿y轴向上平移3个单位，求平移后正方形A'B'C'D'的顶点坐标。

4. 已知三角形ABC的顶点坐标分别为A(0,0)，B(4,0)，C(0,3)，将三角形ABC沿x轴向右平移2个单位，沿y轴向下平移1个单位，求平移后三角形A'B'C'的顶点坐标。

5. 在平面直角坐标系中，将点P(6,8)沿x轴负方向平移5个单位，沿y轴正方向平移3个单位，求平移后点P'的坐标。

6. 已知四边形ABCD的顶点坐标分别为A(2,1)，B(1,1)，C(1,4)，D(2,4)，将四边形ABCD沿x轴向右平移3个单位，沿y轴向下平移2个单位，求平移后四边形A'B'C'D'的顶点坐标。

四年级平移旋转练习题四年级平移旋转练习题在四年级的数学学习中，平移和旋转是一个非常重要的概念。

通过平移和旋转，我们可以改变图形的位置和方向，进一步发展我们的空间想象力和几何观念。

下面，我们来看一些关于平移旋转的练习题，帮助我们更好地理解和应用这些概念。

练习题一：平移1. 将图形A向右平移3个单位，得到图形B。

请问图形B的坐标是多少？2. 将图形C向左平移5个单位，得到图形D。

请问图形D的坐标是多少？3. 将图形E向上平移2个单位，得到图形F。

请问图形F的坐标是多少？4. 将图形G向下平移4个单位，得到图形H。

请问图形H的坐标是多少？通过这些平移题目，我们可以锻炼我们对坐标系的理解和运用能力。

通过计算坐标的变化，我们可以准确地找到图形在平移后的位置。

练习题二：旋转1. 将图形A按顺时针方向旋转90度，得到图形B。

请问图形B的顶点坐标是多少？2. 将图形C按逆时针方向旋转180度，得到图形D。

请问图形D的顶点坐标是多少？3. 将图形E按顺时针方向旋转270度，得到图形F。

请问图形F的顶点坐标是多少？4. 将图形G按逆时针方向旋转360度，得到图形H。

请问图形H的顶点坐标是多少？通过这些旋转题目，我们可以进一步熟悉顺时针和逆时针旋转的概念，并且学会如何计算旋转后的坐标。

练习题三：平移和旋转的结合1. 将图形A向右平移2个单位，再按顺时针方向旋转90度，得到图形B。

请问图形B的顶点坐标是多少？2. 将图形C向左平移4个单位，再按逆时针方向旋转180度，得到图形D。

请问图形D的顶点坐标是多少？3. 将图形E向上平移3个单位，再按顺时针方向旋转270度，得到图形F。

请问图形F的顶点坐标是多少？通过这些综合题目，我们可以综合运用平移和旋转的概念，进一步加深对这两个概念的理解和应用。

通过以上的练习题，我们可以发现平移和旋转是非常有趣和实用的数学概念。

通过这些练习题的训练，我们可以提高我们的观察能力、逻辑思维和计算能力。