图形的平移练习题教学文案
- 格式:doc
- 大小:62.50 KB
- 文档页数:4

教案:平移解决问题课程目标:1. 让学生理解平移的概念,能够识别平移现象。
2. 培养学生运用平移方法解决问题的能力。
3. 培养学生的空间想象力和逻辑思维能力。
教学内容:1. 平移的概念2. 平移的性质3. 平移在实际问题中的应用教学重点:1. 平移的概念和性质2. 平移在实际问题中的应用教学难点:1. 平移的性质2. 平移在实际问题中的应用教学准备:1. 课件或黑板2. 平移教具或模型教学过程:一、导入1. 引入平移的概念,让学生观察一些平移现象,如电梯的运动、滑滑梯等。
2. 引导学生总结平移的特点,如方向、距离等。
二、新课导入1. 讲解平移的概念,强调平移不改变图形的形状和大小。
2. 讲解平移的性质,如平移前后图形对应点之间的关系、平移的距离和方向等。
3. 通过示例演示平移的过程,让学生更好地理解平移。
三、巩固练习1. 让学生完成一些平移练习题,巩固对平移的理解和应用。
2. 引导学生运用平移方法解决实际问题,如平移图形拼图、平移小动物等。
四、拓展提高1. 引导学生思考平移在实际生活中的应用,如建筑设计、机械运动等。
2. 让学生尝试运用平移方法解决一些复杂问题,如平移多个图形、平移立体图形等。
五、总结1. 让学生总结本节课所学的内容,加深对平移的理解和应用。
2. 强调平移在实际问题中的重要性和应用价值。
教学反思:本节课通过引入平移的概念和性质,让学生掌握了平移的基本知识。
通过示例演示和练习题,让学生更好地理解了平移的过程和应用。
在拓展提高环节,让学生思考平移在实际生活中的应用,培养了学生的空间想象力和逻辑思维能力。
整体来说,本节课达到了预期的教学目标,学生对平移有了更深入的理解和应用能力。
重点关注的细节:平移的性质及其在实际问题中的应用平移的性质是本节课的重点,因为它不仅帮助学生深入理解平移的概念,而且为他们在实际问题中应用平移方法奠定了基础。
以下是关于平移性质及其应用的详细补充和说明。
平移的性质:1. 平移前后图形的形状和大小不变:这意味着无论图形如何移动,它的内部角度、边长和面积都保持不变。

第01讲图形的平移【题型1生活中的平移现象】【题型2图形的平移】【题型3利用平移的性质求面积】【题型4利用平移的性质求长度】【题型5利用平移的性质求角度】【题型6利用平移解决实际问题】【题型7平移作图】考点:平移1.定义:在平面内,将一个图形整体沿某一方向由一个位置平移到另一个位置,图形的这种移动,叫做平移变换,简称平移。
2.平移三要素:图形的原来位置、平移的方向、平移的距离。
3.平移的性质(1)对应点的连线平行(或共线)且相等(2)对应线段平行(或共线)且相等;(3)对应角相等,对应角两边分别平行,且方向一致。
4.平移作图的步骤和方法:平行线法、对应点连线法、全等图形法(1)找关键点;(2)过每个关键点作平移方向的平行线,截取与之相等的距离,标出对应点(3)连接对应点。
将原图形的各个特征点按规定的方向平移,得到相应的对称点,再将各对称点进行相应连接,即得到平移后的图形【题型1生活中的平移现象】【典例1】(2023秋•道里区校级期中)在下列实例中,属于平移过程的有()①时针运行的过程;②电梯上升的过程;③地球自转的过程;④小汽车在平直的公路行驶.A.1个B.2个C.3个D.4个【变式1-1】(2023春•林州市期末)下列运动属于平移的是()A.荡秋千的小朋友B.转动的电风扇叶片C.正在上升的电梯D.行驶的自行车后轮【变式1-2】(2023春•富川县期末)一个图形,经过平移后,改变的是()A.颜色B.形状C.大小D.位置【变式1-3】(2023春•呼伦贝尔期末)在下列现象中,属于平移的是()A.小亮荡秋千运动B.升降电梯由一楼升到八楼C.时针的运行过程D.卫星绕地球运动【题型2图形的平移】【典例2】(2023春•罗山县期末)如图所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标,其中,可以看作由“基本图案”经过平移得到的是()A.B.C.D.【变式2-1】(2023春•启东市期末)“水是生命之源,滋润着世间万物”国家节水标志由水滴,手掌和地球变形而成.寓意:像对待掌上明珠一样,珍惜每一滴水!以下通过平移节水标志得到的图形是()A.B.C.D.【变式2-2】(2023春•扎赉特旗期末)如图,将图中的冰墩墩通过平移可得到图为()A.B.C.D.【变式2-3】(2023春•琼海期末)如图所示的各组图形中,表示平移关系的是()A.B.C.D.【题型3利用平移的性质求面积】【典例3】(2023春•惠城区校级期中)如图,长为50m,宽为30m的长方形地块上,有纵横交错的几条小路,宽均为1m,其它部分均种植草坪,则种植草坪的面积为()A.1344m2B.1421m2C.1431m2D.1341m2【变式3-1】(2023春•凉山州期末)如图在一块长为12m,宽为6m的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2m),则空白部分表示的草地面积是()A.70m2B.60m2C.48m2D.18m2【变式3-2】(2023春•南陵县期末)如图,小红家楼梯长3m,高2m,宽1m,若想铺上地毯,则所需地毯的面积()A.2m2B.3m2C.5m2D.6m2【变式3-3】(2023秋•滨州期中)如图,将Rt△ABC沿着点B到点C的方向平移到△DEF 的位置,平移距离为7,AB=13,DO=6,则图中阴影部分的面积为()A.70B.48C.84D.96【题型4利用平移的性质求长度】【典例4】(2022秋•芝罘区期末)如图,将△ABC沿BC方向平移3cm得到△DEF,若△ABC的周长为16cm,则四边形ABFD的周长为()A.16cm B.22cm C.20cm D.24cm【变式4-1】(2022秋•桓台县期末)如图,△ABC沿射线BC方向平移到△DEF(点E在线段BC上).若BF=10cm,EC=4cm,则平移距离为()A.3cm B.4cm C.6cm D.10cm【变式4-2】(2023春•南山区期末)如图,将直角△ABC沿边AC的方向平移到△DEF的位置,连结BE,若CD=6,AF=14,则BE的长为()A.4B.6C.8D.12【变式4-3】(2023春•唐县期末)如图,直角三角形ABC的周长为22,在其内部有5个小直角三角形,这5个小直角三角形都有一条边与BC平行,则这5个小直角三角形的周长为()A.11B.22C.33D.44【题型5利用平移的性质求角度】【典例5】(2023春•霸州市期末)如图,点B,C在直线l上,直线l外有一点A,连接AB,AC,∠BAC=45°,∠ACB是钝角,将三角形ABC沿着直线l向右平移得到三角形A1B1C1,连接AB1,在平移过程中,当∠AB1A1=2∠CAB1时,∠CAB1的度数是()A.15°B.30°C.15°或45°D.30°或45°【变式5-1】(2023春•丰满区期末)将△ABC沿AB方向平移到△EFD的位置,若∠1=31°,∠2=57°,则∠D的度数为()A.91°B.90°C.92°D.105°【变式5-2】(2023春•凤翔县期中)如图,∠1=70°,∠2=160°直线a平移后得到直线b,则∠3=()A.20°B.30°C.40°D.50°【变式5-3】(2023春•遂川县期末)如图(1),将一副直角三角板两斜边摆放在同一直线上,且点A,D重合,固定含45°角的三角板ABC,将含角的三角板DEF从图(1)的位置,沿射线BA平移至图(2)的位置,则平移过程中,根据两个三角板的摆放位置,下列钝角:100°,105°,120°,135°,150°,165°,170°,沿三角板的边缘能直接画出的有()A.1个B.2个C.3个D.4个【题型6利用平移解决实际问题】【典例6】(2023春•南宁月考)如图,粗线A→C→B和细线A→D→E→F→G→H→B是公交车从少年宫A到体育馆B的两条行驶路线.(1)比较两条线路的长短:粗线①细线②;(填“>”、“<”或“=”)(2)如果这段路程长4.7千米,小丽坐出租车从体育馆B到少年宫A,假设出租车的收费标准为:起步价为7元,3千米以后每千米1.7元,小丽身上有10元钱,够不够坐出租车从体育馆到少年宫呢?说明理由.【变式6-1】(2022秋•路北区期末)如图,有一块长为20米,宽为10米的长方形土地,现在将三面留出宽都是x米的小路,中间余下的长方形部分做草坪(阴影部分).(1)用含字母x的式子表示:草坪的长a=米,宽b=米;(2)请求出草坪的周长;(3)当小路的宽为1米时,草坪的周长是多少?【变式6-2】(2022春•婺城区校级期中)如图是某一长方形闲置空地,宽为3a米,长为b 米,为了美化环境,准备在这个长方形空地的四个顶点处分别修建一个半径为a米的扇形花圃(阴影部分),然后在花圃内种花,中间修一条长b米,宽a米的甬路,剩余部分种草.(提示:π取3)(1)甬路的面积为平方米;种花的面积为平方米.(2)当a=2,b=10时,请计算该长方形场地上种草的面积.(3)在(2)的条件下,种花的费用为每平方米30元,种草的费用为每平方米20元,甬路的费用为每平方米10元.那么美化这块空地共需要资金多少元?【变式6-3】(2023春•莱州市期末)如图,某市修建了一个大正方形休闲场所,在大正方形内规划了一个正方形活动区,连接绿地到大正方形四边的笔直小路如图所示.已知大正方形休闲场所的边长为6a米,四条小路的长与宽都为b米和米.阴影区域铺设草坪,草坪的造价为每平米30元.(1)用含a、b的代数式表示草坪(阴影)面积并化简.(2)若a=10,b=5,计算草坪的造价.【题型7平移作图】【典例7】(2022秋•蚌山区期末)已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度).(1)在图中画出平移后的△A1B1C1;(2)直接写出△A1B1C1各顶点的坐标.A1;B1;C1;(3)求出△ABC的面积.【变式7-1】(2023秋•崇左期中)如图,在平面直角坐标系中,点A(﹣1,4),B(﹣2,1),C(﹣4,1),将△ABC向右平移3个单位再向下平移2个单位得到△A1B1C1,点A、B、C的对应点分别为点A1、B1、C1.(1)在图上画出△A1B1C1,并写出点A1,B1,C1的坐标;(2)设点P(m,n)为△ABC内一点,经过平移后,请写出点P在△A1B1C1内的对应点P1的坐标.【变式7-2】(2023秋•铜陵期中)如图,在正方形网格中有一个格点三角形ABC(△ABC 的各顶点都在格点上).(1)画出△ABC中AB边上的高CD;(2)将△ABC先向上平移3格,再向右平移4格,画出平移后的△A′B′C′;(3)在图中画出一个锐角格点三角形ABP,使得其面积等于△ABC的面积,并回答满足条件的点P有多少个.【变式7-3】(2023秋•蚌山区期中)如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣2,﹣2),B(3,1),C(0,2),将△ABC先向左平移2个单位,再向上平移3个单位得到△A'B'C'.(1)在图中画出平移后的△A'B'C';(2)求△ABC的面积.一.选择题(共10小题)1.(2023春•高邮市期中)下列图形中,不能通过其中一个四边形平移得到的是()A.B.C.D.2.(2023秋•长汀县期中)小芳和小明在手工课上各自制作楼梯模型,他们用的材料如图,则()A.一样多B.小明多C.小芳多D.不能确定3.(2022春•当涂县期末)下列生活现象中,属于平移现象的是()A.急刹车时汽车在地面滑行B.足球在草地上跳动C.投影片的文字经投影转换到屏幕上D.钟摆的摆动4.(2023秋•金安区校级月考)将点P(﹣3,2)先向右平移2个单位,再向下平移4个单位,得到的点的坐标为()A.(﹣1,﹣4)B.(﹣1,﹣2)C.(﹣5,﹣4)D.(﹣5,﹣2)5.(2022•陵水县二模)如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为()A.48B.96C.84D.42 6.(2022•定海区校级模拟)如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为()A.3B.4C.5D.6 7.(2022春•甘井子区校级期末)线段CD是由线段AB平移得到的,点A(3,﹣1)的对应点C的坐标是(﹣2,5),则点B(0,4)的对应点D的坐标是()A.(5,﹣7)B.(4,3)C.(﹣5,10)D.(﹣3,7)8.(2022春•古城区期末)如图,图1与图2中的三角形相比,图2中的三角形发生的变化是()A.向左平移3个单位长度B.向左平移1个单位长度C.向上平移3个单位长度D.向下平移1个单位长度9.(2022春•淮南期末)线段CD是由线段AB平移得到的,点A(﹣2,3)的对应点为C (2,﹣1),则点B(1,1)的对应点D的坐标为()A.(﹣1,﹣3)B.(5,3)C.(5,﹣3)D.(0,3)10.(2022春•曲靖期末)如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为()A.5050m2B.5000m2C.4900m2D.4998m2二.填空题(共6小题)11.(2021•鞍山)如图,△ABC沿BC所在直线向右平移得到△DEF,已知EC=2,BF=8,则平移的距离为.12.(2022春•兴庆区期末)将点A(﹣2,﹣3)先向右平移3个单位长度再向上平移2个单位长度得到点B,则点B所在象限是第象限.13.(2020春•德州期末)某景点拟在如图的矩形荷塘上架设小桥,若荷塘中小桥的总长为100米,则荷塘周长为.14.(2022春•清河县期末)如图,把边长为3cm的正方形ABCD先向右平移1cm,再向上平移1cm,得到正方形EFGH,则阴影部分的面积为.15.(2022春•连平县校级期末)如图,长方形ABCD的边AB=6,BC=8,则图中五个小长方形的周长之和为.16.(2023春•康巴什期末)如图,将三角形ABE向右平移1cm得到三角形DCF,如果三角形ABE的周长是10cm,那么四边形ABFD的周长是.三.解答题(共3小题)17.(2022春•饶平县校级月考)宾馆重新装修后,准备在大厅的主楼梯上铺设一种红地毯,已知这种地毯每平方米售价40元,主楼梯道宽2米,其侧面如图所示,求买地毯至少需要多少元?18.(2022秋•大祥区期末)如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).(1)请在图中作出△A′B′C′;(2)写出点A′、B′、C′的坐标.19.(2022春•上海期末)如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD.;(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC=S四边形ABDC?若存在这样一点,(2)在y轴上是否存在一点P,连接PA,PB,使S△P AB求出点P的坐标;若不存在,试说明理由;(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)给出下列结论:①的值不变,②的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.。

《平移》教案一、教学目标1.经历观察、分析、操作、欣赏以及抽象、归纳等过程,以及与他人合作交流探索的过程,进一步发展空间观念,增强审美意识,学会用运动的观点分析问题.2.通过实例,认识图形平移,了解平移的特征,理解平移的含义,会进行点的平移.3.理解平移前后两个图形对应点连线平行且相等的性质,能解决简单的平移问题.二、教学重点与难点重点:图形平移的特征和作平移图形.难点:平移的性质探索和理解.三、教学过程(一)创设情境,引入新课1.感受平移,体验新知你坐过公车和搭过电梯吗?它是一种什么样的运动?这样的运动在生活中还有哪些现象?(活动1:学生讨论)2.观察图形,形成印象生活中有许多美丽的图案,他们都有着共同的特点,请同学们欣赏下面图案.观察上面图形,我们发现他们都有一个局部和其他部分重复,如果给你一个局部,你能复制他们吗?学生思考讨论,并回答问题.(1)它们有什么共同的特点?(2)能否根据其中的一部分绘制出整个图案?(活动2:师生交流.)这些美丽的图案是由若干个相同的图案组合而成的,每个图形都有“基本图形”,而“基本图形”是什么?如第一个图形是中间一个正方形,上、下有正立与倒立的正三角形,下排的左图中的“基本图形”是鸽子与橄榄枝;下排右图中的“基本图形”是上、下一对面朝右与面朝左的人头像组成的图案.3.实践探索,得出新知探究:设计一个简单的图案,利用一张半透明的纸附在上面,绘制一排形状,大小完全一样的图案如:引导学生找规律,发现平移特征,回答下面问题:1、图形经过平移后,_______图形的位置,________图形的形状,________图形的大小.(填“改变”或“不改变”)2、经过平移,每一组对应点所连成的线段________.归纳 (活动3:分组讨论)平移:(1)把一个图形整体沿某一方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同. (2)新图形中的每一点,都是由原图形中的某一个点移动后得到的,这两个点是对应点. (3)连接各组对应的线段平行且相等.图形的这种变换,叫做平移变换,简称平移简单归纳为两点:1.平移的方向. 2.平移的距离四、典例剖析,深化巩固1. 把鱼往左平移8cm.(假设每小格是1cm2)五、小结(学生回答):这节课你学了什么?知道了什么?学会了什么?六、课后作业必做题:教科书习题:3.6题《平移》习题1、决定平移的基本要素是____和____。

平移一、知识点复习知识点1:平移的定义:在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移。
知识点2:平移的要素1.平移的方向:原图上的点指向它的对应点的射线方向;2.平移的距离:连接原图与平移后图形上的一对对应点的线段的长度。
知识点3:平移的性质1.性质(1)平移只改变图形的位置,不改变图形的形状和大小。
(2)平移后的图形与原图形上对应点连成的线段,①数量关系是相等 .②位置关系是平行或在同一条直线上。
2.判断一组图形能不能通过平移得到的方法(1)看对应点连线是否平行或在同一条直线上;(2)看它的形状、大小是否发生变化,位置的变化是否由平移产生。
★★★特别注意:平移是由平移的方向和距离决定的,平移必须指明平移的方向和距离;平移是在平面内,整个图形沿着某一直线平行移动的过程,原图上的每个点都沿同一方向移动相同的距离;平移的距离不能为0;平移的方向是任意的,但就一次平移而言,只能有一个方向,一次平移完成后可以改变方向进行下一次平移。
二、典型例题题型1:生活中平移现象【例题1】(2017春•乌海期末)下列运动属于平移的是()A.荡秋千 B.推开教室的门 C.风筝在空中随风飘动 D.急刹车时,汽车在地面上的滑动【例题2】:(2016春•淮安期中)下列现象:①电梯的升降运动,②飞机在地面上沿直线滑行,③风车的转动,④冷水加热过程中气泡的上升.其中属于平移的是()A.①② B.①③ C.②③ D.③④题型2:平移的性质【例题4】:(2016春•沧州期末)在下列说法中:①△ABC在平移过程中,对应线段一定相等;②△ABC 在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长保持不变;④△ABC在平移过程中,对应边中点所连线段的长等于平移的距离;⑤△ABC在平移过程中,面积不变,其中正确的有()A.①②③④ B.①②③④⑤ C.①②③⑤ D.①③④⑤题型3:与平移有关的计算【例题5】:(2015春•石家庄期末)如图,将△ABC沿射线BC方向移动,使点B移动到点C,得到△DCE,连接AE,若△ABC的面积为2,则△ACE的面积为()A .2B .4C .8D .16【例题6】:(2017秋•兴化市期末)如图,将△ABE 向右平移2cm 得到△DCF ,AE 、DC 交于点G .如果△ABE 的周长是16cm ,那么△ADG 与△CEG 的周长之和是 cm 。

1.5 图形的平移导学案【学习目标】1.通过具体实例认识图形的平移变换.探索它的基本性质 .理解平移不改变图形的形状和大小,平移前后两个图形对应点连线平行且相等的性质.2.能按要求画出简单的平面图形平移后的图形.【课前学习,课中交流】利用 8 分钟时间认真学习书本P21-P23 的内容,完成下列问题 .1.日常生活中经常可以看到的一些现象,如下图,都给了我们平移的大致形象.哪位同学能说—说什么叫平移 ?子传人电送梯带上上的的箱车索运一的从道动个方远上正队处方好看的缆形象行在是进在平面内,我们将一个图形沿着移动,在移动的过程中,原图形上的距离,这样的图形运动叫做图形的平移 .2.做一做:下面两组图形的运动,哪一个属于平移?3.当我们如图所示的那样使用直尺与三角板画平行线时,△ABC 沿着直尺 PQ 平移到△ A'B'C ′,,就可以画出 AB 的平行线 A′B了′.我们把点 A 与点 A′叫做对应点,线段 AB 与线段 A′ B叫′做对应线段,∠ A与∠ A′叫做对应角 .此时,点 B 的对应点是点;点C的对应点是点;线段 AC 的对应线段是线段;线段BC 的对应线段是线段;∠ B的对应角是;∠ C 的对应角是.△ ABC 平移的方向就是由点 B 到点 B′的方向,平移的距离就是线段BB'的长度 .4.参考书本 P22 例题作图 .如图 ,平移三角形 ABC, 使点 A 运动到 A`,画出平移后的三角形A`B`C`.想一想:原图形与平移后所得的图形相比,哪些改变了?哪些保持不变?连接对应点的线段之间有什么关系?5.一般地,图形的平移有下面的性质:注意:要描述一个平移,必须指出平移的和.6.△ ABC 在网格中如图所示,请根据下列提示作图(1)先向上平移 2 个单位长度得△ A 1B1C1.A(2)再向右移 3 个单位长度△ A 2B2C2..B C【当堂检测】如图所示,△ ABE 沿 GH 方向平移一定距离后记为△CDF,找到图中平行且相等的线段 .HCGDF AB E【课后反思】。

第三章《图形的平移与旋转》复习学案学习目标:1.能判断实例中的平移和旋转。
2.能根据平移、旋转的基本性质解决实际问题。
3.能作出简单的平面图形平移、旋转后的图形。
4.能够运用平移、旋转、轴对称及其组合进行图案设计。
【知识整理】1. 平移的定义:在平面内将一个图形沿某个方向移动一定的距离,这种图形变换称为平移.平移变换的两个要素:________________、________________.2. 平移变换的性质:(1)平移前、后的图形_____,即:平移只改变图形的_____,不改变图形的_____________;(2)对应线段平行(或共线)且相等;(3)对应点所连的线段平行(或共线)且相等.3. 旋转的定义:在平面内,将一个图形绕一个定点沿某个方向(逆时针或顺时针)转动一定的角度,这样的图形变换叫做旋转.这个定点叫做_________,转动的角称为_________.旋转变换的三个要素:_________,_________,_________.4. 旋转变换的性质:(1)旋转前、后的图形_____;(2)对应点到旋转中心的距离_____,即:旋转中心在对应点所连线段的_____________上;(3)对应点与旋转中心所连线段的夹角等于_________.例题解析例1如图,在平面直角坐标系内有一个△ABC.(1) 在平面直角坐标系内画出△ABC向下平移4个单位得到的△A1B1C1;(2) 在平面直角坐标系内画出△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;(3) 分别写出△A1B1C1与△A2B2C2各顶点的坐标.例2 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)求证:△COD是等边三角形;(2)当a=150°时,试判断△AOD的形状,并说明理由;例3 如图,两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1,固定△ABC不动,将△DEF进行如下操作:(1) 如图(a),△DEF沿AB向右平移,连接DC、CF、FB,四边形CDBF的形状在不断的变化,问:四边形CDBF的面积是否发生变化,若有变化,请举例说明;若不变化,请求出它的面积.(注:D点在AB内,不包括A、B两点)(2) 如图(b)当D点移动到AB得中点时,请你猜想四边形CDBF的形状,并说明理由.(3) 如图(c)△DEF的D点固定在AB的中点时然后绕D点按顺时针方向旋转△DEF,使DF落在AB上,此时F点恰好与B点重合,连接AE,求AE的值.测试题1.将线段AB=2cm向右平移1cm,得到线段DE,则对应点A与D的距离为_____cm. 2. 将正六边形绕其对称中心旋转后,恰好能与原来的正六边形重合,那么旋转的角度至少是______.3.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移得到△DEF.如果AB=8cm,BE=4cm,DH=3cm,则图中阴影部分面积为______cm2.4. 如图,阴影部分为2m宽的道路,则余下的部分面积为______m2.第3题第4题第5题5. 如图,△ACE,△ABF均为等腰直角三角形,∠BAF=∠EAC=90°,那么△AFC以点A为旋转中心逆时针旋转90°之后与________重合,其中点F与点____对应,点C与点____对应.6. 如图,在直角坐标系中,AO=AB,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上,点O′、B′在x轴上. 则点B′的坐标是_______.第6题第7题第8题7. 如图,当半径为30cm的转动轮转过120°角时,传送带上的物体A平移的距离为___cm.8. 如图,将正方形ABCD中的△ABP绕点B顺时针旋转90°,使得AB与CB重合,若BP=4,则点P所走过的路径长为_____.9. 下列图案中,不能由一个图形通过旋转而构成的是( )A. B. C. D.10. 下列各组图形,可经过平移变换由一个图形得到另一个图形的是( )A. B. C. D.11. 在下列现象中,是平移现象的是( )①方向盘的转动②电梯的上下移动③保持一定姿势滑行④钟摆的运动A. ①②B. ②③C. ③④D. ①④12. 在5×5方格纸中,将图1中的图形N平移后的位置如图2中所示,那么正确的平移方法是( )A. 先向下移动1格,再向左移动1格B. 先向下移动1格,再向左移动2格C. 先向下移动2格,再向左移动1格D. 先向下移动2格,再向左移动2格13.如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向转动一个角度α到A1BC1的位置,使得点A、B、C1在同一条直线上,那么这个角度α等于( )A.120° B.90° C.60° D.30°14.在13题中,若BC的长为15cm,那么顶点A从开始到结束所经过的路径长为( )A. 10πcmB. 103πcmC. 303cmD. 20πcm15.△ABC在平面直角坐标系中的位置如图所示.(1) 将△ABC向右平移6个单位得到△A1B1C1,请画出△A1B1C1,并写出点C1的坐标;(2) 将△ABC绕点C顺时针旋转90°得到△A2B2C,请画出△A2B2C,并写出点A2的坐标.16.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),这时AB 与CD1相交于点O,与D1E1相交于点F.(1) 求∠OFE1的度数;(2) 求线段AD1的长;(3) 若把三角板D1CE1绕着点C顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.。

图形的平移和旋转教学目标:1. 理解平移和旋转的概念。
2. 学会用平移和旋转的方法来变换图形。
3. 能够判断图形是否发生了平移或旋转。
教学重点:1. 平移和旋转的定义。
2. 平移和旋转的方法。
3. 平移和旋转的性质。
教学难点:1. 理解平移和旋转的本质区别。
2. 学会用平移和旋转的方法来变换复杂图形。
教学准备:1. 教学PPT。
2. 图形卡片。
3. 练习题。
教学过程:第一章:平移的概念和性质1.1 引入平移的概念教师展示一些平移的实例,如滑滑梯、电梯等,引导学生感受平移的特点。
1.2 学习平移的性质学生通过观察和操作,发现平移不改变图形的形状和大小,只改变图形的位置。
1.3 练习平移学生分组合作,用图形卡片进行平移操作,体会平移的方法。
第二章:旋转的概念和性质2.1 引入旋转的概念教师展示一些旋转的实例,如旋转门、风车等,引导学生感受旋转的特点。
2.2 学习旋转的性质学生通过观察和操作,发现旋转不改变图形的大小,只改变图形的位置和方向。
2.3 练习旋转学生分组合作,用图形卡片进行旋转操作,体会旋转的方法。
第三章:平移和旋转的判定3.1 学习平移的判定方法学生通过观察和操作,学会判断图形是否发生了平移。
3.2 学习旋转的判定方法学生通过观察和操作,学会判断图形是否发生了旋转。
3.3 练习判断学生独立完成判断题目,巩固平移和旋转的判定方法。
第四章:平移和旋转的应用4.1 学习用平移和旋转的方法来变换图形学生通过观察和操作,学会用平移和旋转的方法来变换图形。
4.2 练习变换学生独立完成变换题目,巩固平移和旋转的变换方法。
第五章:总结与拓展5.1 总结平移和旋转的概念、性质和判定方法学生通过回顾本节课的内容,总结平移和旋转的概念、性质和判定方法。
5.2 拓展平移和旋转的应用学生分组合作,用平移和旋转的方法来创作有趣的图形图案。
教学评价:1. 通过课堂观察,评价学生对平移和旋转概念的理解程度。
2. 通过练习题,评价学生对平移和旋转性质的掌握程度。

学霸笔记—苏教版2021-2022学年苏教版数学四年级下册同步重难点讲练第一单元平移、旋转和轴对称1.1 平移教学目标1.通过观察、比较,掌握图形平移的方法,能在方格纸上将简单图形进行平移。
2.培养学生的操作能力和分析能力,发展学生的空间观念。
3.通过图形的平移,激发学生学习数学的兴趣,积累成功的体验。
教学重难点教学重点:掌握图形平移的方法,在方格纸上将简单图形进行平移。
教学难点:能对图形平移过程中的距离进行准确判断。
【重点剖析】1.在平面内,将一个图形沿着某个方向移动一定的距离,但不改变图形的形状和大小,像这样的运动现象叫平移。
2.图形的平移包括平移的方向和距离这两个关键要素。
3.判断图形平移的方向和距离的方法:根据箭头指向确定平移的方向;根据平移前后图形中一组对应线段或对应点之间的格数确定平移的距离。
【典例分析1】想一想,选一选。
(右面的哪个图形是通过平移左面的图案得到的?画“√”)(1)(2)【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。
平移后图形的位置改变,形状、大小、方向不变。
【解答】解:(1)(2)【点评】此题考查了平移的意义及在实际当中的运用。
【典例分析2】移一移,填一填。
(1)从图①到图②向右平移了4格。
(2)从图③到图④向下平移了4格。
(3)从图⑤到图⑥可以先向下平移2格,再向右平移9格。
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。
平移后图形的位置改变,形状、大小、方向不变。
据此解答即可。
【解答】解:(1)从图①到图②向右平移了4格。
(2)从图③到图④向下平移了4格。
(3)从图⑤到图⑥可以先向下平移2格,再向右平移9格。
故答案为:4,下,4,2,右。
【点评】此题考查了平移的意义及在实际当中的运用。
【题干】如图4只蝴蝶中,哪一只通过平移可以与右面方框中的蝴蝶重合?圈出来吧。
【题干】(1)小车图向上平移了4格,房子图向左平移了5格.(2)请你把小船图向左平移5格.【题干】请你用平移和旋转的方法,将图二恢复到图一的样子。
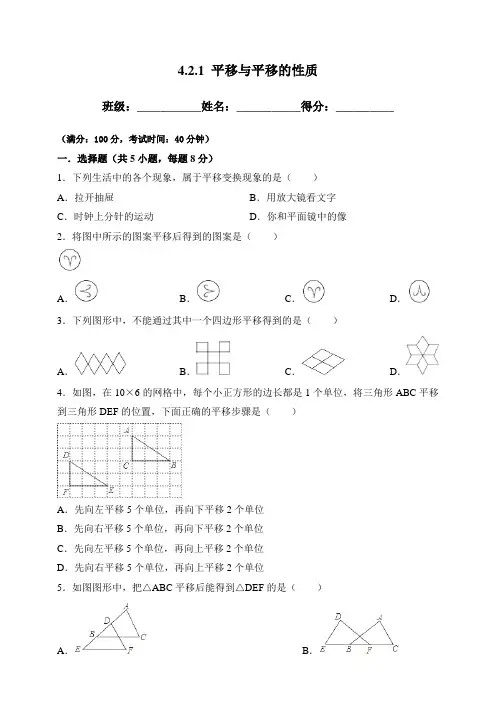
4.2.1 平移与平移的性质班级:___________姓名:___________得分:__________(满分:100分,考试时间:40分钟)一.选择题(共5小题,每题8分)1.下列生活中的各个现象,属于平移变换现象的是()A.拉开抽屉B.用放大镜看文字C.时钟上分针的运动D.你和平面镜中的像2.将图中所示的图案平移后得到的图案是()A.B.C.D.3.下列图形中,不能通过其中一个四边形平移得到的是()A.B.C.D.4.如图,在10×6的网格中,每个小正方形的边长都是1个单位,将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是()A.先向左平移5个单位,再向下平移2个单位B.先向右平移5个单位,再向下平移2个单位C.先向左平移5个单位,再向上平移2个单位D.先向右平移5个单位,再向上平移2个单位5.如图图形中,把△ABC平移后能得到△DEF的是()A.B.C.D.二.填空题(共4小题,每题5分)6.用4根木棍可拼成大写的英文字母“M”,平移其中一根木棍,你能得到另一个大写的英文字母,请写出这个英文字母.7.如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是cm.8.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3=°.9.如下图所示,图中为一块矩形ABCD的场地,AB=102m,AD=51m,从A,B两地入口的路宽都为1m,两小路汇合处的路宽为2m,其余部分种植草坪,那么草坪的面积为m2.三.解答题(共3小题,第10、12题各15分,第11题10分)10.若在方格(每小格正方形边长为1m)上沿着网格线平移,规定:沿水平方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿竖直方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.例如:点A按“平移量”{1,4}可平移至点B.(1)从点C按“平移量”{ ,}可平移到点B;(2)若点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D,①请在图中标出点D;(用黑色水笔在答题卡上作出点D)②如果每平移1m需要2.5秒,那么按此方法从点B移动至点D需要多少秒?③观察点D的位置,其实点B也可按“平移量”{ ,}直接平移至点D;观察这两种平移的“平移量”,猜想:点E依次按“平移量”{2a,3b}、{﹣5a,b}、{a,﹣5b}平移至点F,则相当于点E按“平移量”{ ,}直接平移至点F.11.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.12.张明的父亲打算在院子里种上蔬菜,已知院子是东西长为40m,南北宽为30m的长方形,为了行走方便,要修筑同样宽的三条道路(如图),东西方向两条,南北方向一条.南北方向道路垂直于东西道路,余下的部分分别种上蔬菜,若每条道路的宽为1m,求种蔬菜的土地的总面积.试题解析一.选择题1.A【分析】根据平移的定义直接判断即可.【解答】解:A、是平移;B、大小发生变化,不是平移;C、是旋转;D、你和平面镜中的像不是平移,是轴对称.故选:A.【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转而误选.2.C【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.【解答】解:通过图案平移得到必须与图案完全相同,角度也必须相同,观察图形可知C可以通过图案平移得到.故选:C.【点评】本题考查平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.3.D【分析】根据平移与旋转的性质得出.【解答】解:A、能通过其中一个四边形平移得到,错误;B、能通过其中一个四边形平移得到,错误;C、能通过其中一个四边形平移得到,错误;D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,正确.故选:D.【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,导致误选.4.A【分析】根据网格结构,可以利用一对对应点的平移关系解答.【解答】解:根据网格结构,观察对应点A、D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,所以平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位.故选:A.【点评】本题考查了坐标与图形变化﹣平移,利用对应点的平移规律确定图形的平移规律是解题的关键.5.A【分析】根据图形平移的性质对各选项进行逐一分析即可.【解答】解:A、△DEF由△ABC平移而成,故本选项正确;B、△DEF由△ABC对称而成,故本选项错误;C、△DEF由△ABC旋转而成,故本选项错误;D、△DEF由△ABC对称而成,故本选项错误.故选:A.【点评】本题考查的是平移的性质,熟知把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同是解答此题的关键.二.填空题6.W.【分析】根据平移的性质,将最左边的木棍移到右边即可得到字母W.【解答】解:如图,能得到大写英文字母W.故答案为:W.【点评】本题考查了平移的性质,比较简单,主要是英文字母M、W之间的关系.7.210cm.【分析】利用平移的性质将EF,GH,AH,分别向左和上平移即可得出平移后图形,进而求出这块垫片的周长.【解答】解:如图所示:这块垫片的周长为:50×4+FG+NH=200+10=210(cm),故答案为:210.【点评】本题考查了生活中的平移现象,利用平移的性质得出是解题关键.8.110°.【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可.【解答】解:延长直线,如图:,∵直线a平移后得到直线b,∴a∥b,∴∠5=180°﹣∠1=180°﹣70°=110°,∵∠2=∠4+∠5,∵∠3=∠4,∴∠2﹣∠3=∠5=110°,故答案为:110.【点评】此题考查平移问题,关键是根据平行线的性质和三角形的外角性质解答.9.5000m2.【分析】本题主要利用矩形的性质求出长和宽,再进行解答.【解答】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:102﹣2=100,宽为51﹣1=50.所以草坪的面积应该是长×宽=100×50=5000.故选:5000.【点评】本题考查矩形的性质及空间想象能力,有一定的思维容量.三.解答题10.【分析】(1)根据图形,点B在点C的左边2个单位,下方1个单位,再根据“平移量”的定义即可求解;(2)①根据“平移量”的定义确定出点D的位置即可;②根据“平移量”的定义求出从点B移动到点D的路程,然后乘以2.5,计算即可得解;③根据“平移量”的定义结合直接写出点B到点D的平移量即可;把从点E到点F所有平移量的横向相加,纵向相加,计算即可得解.【解答】解:(1)从C到B,向左2个单位,向下1个单位,所以,平移量为{﹣2,﹣1};(2)①点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D如图所示;②(4+3+2+1)×2.5=10×2.5=25秒;③由图可知,点B到点D,向右2个单位,向下2个单位,所以,平移量为{2,﹣2},∵2a﹣5a+a=﹣2a,3b+b﹣5b=﹣b,∴点E到F的平移量为{﹣2a,﹣b}.故答案为:(1)﹣2,﹣1;(2)③2,﹣2;﹣2a,﹣b.【点评】本题考查了平移的性质,平移量的定义,读懂题目信息,理解平移量的定义并熟练掌握网格结构是解题的关键.11.【分析】根据平移的变换只改变图形的位置不改变图形的形状与大小可得梯形ABCD 的面积等于梯形EFGH的面积,CD=HG,从而得到阴影部分的面积等于梯形DWGH的面积,再求出DW的长,然后利用梯形的面积公式列式计算即可得解.【解答】解:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,∴阴影部分的面积=梯形DWGH的面积,∵CW=6cm,∴DW=CD﹣CW=24﹣6=18cm,∴阴影部分的面积=(DW+HG)•WG=(18+24)×8=168cm2.答:阴影部分面积是168cm2.【点评】本题考查了平移的性质,根据图形判断出阴影部分的面积等于梯形DWGH的面积是解题的关键,也是本题的难点.。

第五章相交线与平行线《5.4 平移》教案【教学目标】1.通过实例了解平移的概念;2.理解并掌握平移的性质;(重点、难点)3.能按要求作出平移后的图形.(重点)【教学过程】一、情境导入如图,高铁在笔直的铁轨上向前运行,它的形状和大小发生了变化吗?二、合作探究探究点一:平移的概念【类型一】生活中的平移下面生活中的物体的运动情况可以看成平移的是( ) A.摆动的钟摆B.在笔直的公路上行驶的汽车C.随风摆动的旗帜D.汽车玻璃上雨刷的运动解析:选项A、C、D中图形的所有点不是沿同一方向运动,所以不是平移.选项B符合平移的条件.故选B.方法总结:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移.注意平移是图形整体沿某一直线方向移动.图形绕某一点的旋转不是平移.【类型二】平移的判断下列哪个图形是由左图平移得到的( )解析:选项A、B、D是由左图通过旋转得到,只有选项C是平移得到的.故选C.方法总结:本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,同学们容易混淆图形的平移与旋转或翻转,以致选错.探究点二:平移的性质如图,三角形ABC沿BC方向平移到三角形DEF的位置,若EF=7cm,CE=3cm,求平移的距离.解析:平移的距离可以看作是线段CF的长.解:观察图形可知,平移的距离可以看作是线段CF的长.因为EF=7cm,CE=3cm,所以平移的距离为CF=EF-EC=7-3=4(cm).方法总结:平移既能产生线段相等,又能产生线段平行.平移前后的两个图形中,对应角相等,对应线段平行(或在同一条直线上)且相等.如图,将周长为8的三角形ABC沿BC方向平移1个单位得到三角形DEF,则四边形ABFD的周长为( )A.6 B.8 C.10 D.12解析:根据题意,将周长为8的三角形ABC沿边BC向右平移1个单位得到三角形DEF,故AD=CF=1,DF=AC,AB+BC+AC=8,则AB+BC+CF+DF+AD =10.故四边形ABFD的周长为10.故选C.方法总结:平移不改变图形的形状和大小.平移后对应线段平行(或在同一直线上)且相等,对应角相等.探究点三:平移的作图将图中的三角形ABC向右平移6格.解析:分别作出点A 、B 、C 三点向右平移6格后的对应点A ′、B ′、C ′,再顺次连接即可.解:如图所示.方法总结:(1)平移的作图要注意两个方面:平移的方向和平移的距离;(2)作直线型图形平移后的图形,关键是作出点平移后的对应点.三、板书设计平移⎩⎪⎪⎨⎪⎪⎧平移的概念平移的性质⎩⎪⎨⎪⎧平移不改变图形的形状和大小平移不改变直线的方向一个图形和它经过平移后所得的图形中,两组对应点的连线平行(或在同一直线上)且相等平移的作图【教学反思】本节课通过生活中的实例引入平移的概念,在学习中,引导学生分析、观察、概括得出平移的性质,并通过例题和练习加深对平移性质的理解.让学生作图,自主探究.平移的作图是本节课的重点,应让学生加强训练,结合解题中的错误分析原因,举一反三第五章 相交线与平行线《5.4 平移》导学案【学习目标】:1.通过实例认识图形的平移,经历作图的操作过程,理解平移的内涵,掌握图形平移的特征,能按要求作出简单平面图形平移后的图形,提高学生的作图能力.2.通过小组探究质疑,发展学生的空间观念.3.激情投入,进一步增强数学应用意识及审美意识,培养学生对图形的欣赏意识.【重点】:理解平移是由移动的方向和移动的距离所决定的,能按要求作出简单平面图形平移后的图形.【难点】:确定图形平移的方向和距离.【自主学习】一、知识链接1.如何过直线外一点画出已知直线的平行线?2.如何用圆规和直尺画一条线段等于已知线段?二、新知预习1.图形的平移是由平移的和所决定的.2.平移后的图形与原图形的形状、大小 .三、自学自测1.如图所示的图案中,可以看作由图案自身的一部分经过平移得到的是()2.下列现象:①电梯的升降运动;②飞机在地面上沿直线滑行;③风车的转动,①汽车轮胎的转动,其中属于平移现象的是()A.②③B.②④C.①②D.①①【自主学习】要点探究探究点1:平移的相关概念问题1:如何在一张半透明的纸上,画出一排形状和大小如图的尼克呢?问题2:你还能举出生活中有关平移的例子吗?问题3:根据以上例子你能总结出平移的概念吗?问题4:图形平移的根据是什么?知识要点:平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.判一判:判断下面几组图形运动是不是平移?归纳总结:1.图形的平移不一定是水平的,也不一定是竖直的.2.图形的平移由移动的方向和距离决定.试一试:如图,平移三角形ABC,得到三角形A′B′C′.分析两个图形中的对应关系.练一练:将图中的小船向左平移6格.探究点2:平移的性质动动手:用三角板、直尺画平行线.思考:(1)线段AB与DE的位置关系与数量关系.(2)线段AC与DF的位置关系与数量关系.问题:三角形ABC沿着PQ的方向平移到三角形A`B`C`的位置,除了对应线段平行且相等外,你还发现了什么现象?要点归纳:图形平移的基本性质: 平移的两个图形形状和大小完全相同;②对应线段平行(或在同一直线上)且相等;③各对应点所连线段平行(或在同一直线上)且相等;几何符号语言:∵三角形ABC平移得到三角形DEF,∴AB∥DE,AC∥DF,BC ∥EF(或共线), AB=DE,AC=DF,BC=EF,AD∥BE∥CF(或共线),AD=BE=CF.例1.如图所示,经过平移,三角形ABC的顶点C移到了点C'.画出平移后的三角形A'B'C'的位置.并指出平移的方向和距离.练一练:在图形平移中,下面说法错误的是()A. 图形上任意点移动的方向相同B. 图形上任意点移动的距离相等C. 图形上任意两点的连线的长度改变D. 图形在平移前后形状和大小不发生改变1.如图,将字母A按箭头所指的方向平移3cm,做出平移后的图形.2.将图中的字母N沿水平方向向右平移3cm,作出平移后的图形.例3.如图是一块长方形的草地, 长为21m.宽为15m. 在草地上有两条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?如图是一块长方形的草地, 长为21米.宽为15米.在草地上有一条宽为1米的小道,长方形的草地上除小道外长满青草.求长草部分的面积为多少?【当堂检测】1.平移改变的是图形的()A.位置B.大小C.形状D.位置、大小和形状2.经过平移,对应点所连的线段()A.平行B.相等C.平行(或在同一直线上)且相等D.既不平行,又不相等3.下面 2,3,4,5 幅图中哪幅图是由1平移得到的?4.经过平移,图形上每个点都沿同一个方向移动了一段距离.下面说法正确的是()A.不同的点移动的距离不同B.不同的点移动的距离既可能相同也可能不同C.不同的点移动的距离相同D.无法确定5.如何将平行四边形ABCD平移,使点A移动到点E,画出平移后的图形.第五章相交线与平行线5.4《平移》同步练习一、单选题(共15小题)1、下列各组图形,可经平移变换由一个图形得到另一个图形的是()A、 B、 C、 D、2、如图所示,四幅汽车标志设计中,能通过平移得到的是()A、 B、 C、 D、3、线段AB经过平移得到线段CD,若CD=5cm,则AB等于()A、3cmB、4cmC、5cmD、6cm4、通过平移得到的新图形中的每一点与原图形中的对应点的连线()A、平行B、相等C、共线D、平行(或在同一条直线上)且相等5、下列运动过程属于平移的是()A、荡秋千B、摇动水井上的轱辘C、小火车在笔直的铁轨上行进D、宇宙中的行星运轨6、将字母“E” 沿垂直方向向下平移3㎝的作图中,第一步应在字母“E”上找出的关键点的个数为()A、4个B、5个C、6个D、7个7、将长度为3cm的线段向下平移2cm,则平移后的线段长度是()A、3cmB、2cmC、5cmD、1cm8、在下列说法中:①△ABC在平移过程中,对应线段一定相等;②△ABC在平移过程中,对应线段一定平行;③△ABC在平移过程中,周长保持不变;④△ABC 在平移过程中,对应边中点所连线段的长等于平移的距离;⑤△ABC在平移过程中,面积不变,其中正确的有()A、①②③B、①②④C、①③④D、①③④⑤9、如图,O是正六边形ABCDEF的中心,下列图形中可由△OBC平移得到的是()A、△OCDB、△OABC、△OAFD、△DEF10、将图形A向右平移3个单位得到图形B ,再将图形B向左平移5个单位得到图形C。

三年级数学平移和旋转教案最新文案认识平移现象,知道平移的基本特征,能正确的画出物体平移后的图形。
了解平移在生活中的重要性。
今天小编在这里整理了一些三年级数学平移和旋转教案最新文案,我们一起来看看吧!三年级数学平移和旋转教案最新文案1教学目标:1、知识与技能:感知平移和旋转的现象。
能在方格纸上画出一个简单图形沿水平方向或竖直方向平移后的图形。
2、过程与方法:能通过比较平较平移前后两个对应部分之间的距离的方法来研究一个图形平移的距离。
3、情感、态度和价值观:感受数学和日常生活之间的紧密联系,培养用数学地眼光去看问题。
教学重点:能通过比较平移前后两个对应部分之间的距离的方法来研究一个图形平移的距离。
教学难点: 1、对平移的切实感知。
2、能在方格纸上画出一个简单图形沿水平方向或竖直方向平移后的图形。
教学准备:白纸、作业纸、小纸船、小房子、小汽车、风车、闹钟。
教学过程:一、导入新课同学们,你们去过游乐园吗?你都玩过哪些项目?给大家说说你是怎么玩的?二、初步感知1、看一看,说一说(从学生生活经验出发,初步感知平移和旋转的实例)。
⑴出示小汽车师做运动说一说是怎样运动变化的,是怎么运动的,用手势比划比划。
请孩子们跟随活动的画面用自己的'动作把看到的表演出来。
你能用简单的图把它是怎么运动的画出来吗?(2)出示风车做运动说一说是怎样运动变化的,是怎么运动的,用手势比划比划。
请孩子们跟随活动的画面用自己的动作把看到的表演出来。
你能用简单的图把它是怎么运动的画出来吗?2、说一说(初步感知平移和旋转的特性)(1)以上两种运动方式相同吗? 看41页图说一说它们的运动方式看42页图说一说它们的运动方式(2)学生回答,师总结:像火车、缆车、滑梯等物体的运动,我们把它叫做平移,(板书:平移)。
像摩天轮、转椅、风车等物体的运动,我们把它叫“旋转”(板书:旋转)。
板书:平移旋转 3、辨一辨。
下面物体的运动,哪些是平移?哪些是旋转? (用手势表示) 看书43页图4、分一分先闭上眼睛静静地想一想什么是平移,什么是旋转,然后让他们站起来用自己的动作表现出来。
《平移》教案教学目的:要求学生理解“平移”的概念和平移的几何意义,并掌握平移公式,能运用公式解决有关具体问题。
(如求平移后的函数解析式)教学重点:平移公式教学难点:利用点的平移公式化简函数解析式教学方法:启发式 教学过程:一、复习引入函数图象的沿x 轴或y 轴平移 二、新课讲解:1、 平移的概念:将图形上所有点按同一方向移动同样 的长度,得到另一个图形,这个过程称做图形的平移。
(点的位置、图形的位置改变,而形状、大小没有改变, 从而导致函数的解析式也随着改变)。
(作图、讲解)2、平移公式的推导:设P (x ,y )是图形F 上的任意一点,它在平移后的图象F ′上的对应点为P ′(x ′,y ′)可以看出一个平移实质上是一个向量。
设'PP =(h ,k ),即:''PP OP +=∴(x ′,y ′)=(x ,y )+(h ,k )∴⎩⎨⎧+=+=k y y h x x ''——平移公式注意:1.它反映了平移后的新坐标与原坐标间的关系;2.知二求一 三、应用:例1、将函数y =3x 的图象l 按a =(0,3)平移到l ′,求l ′的函数解析式。
解:设P (x ,y )为l 上任一点,它在l ′上的对应点为P ′(x ′,y ′)由平移公式:⎩⎨⎧⎩⎨⎧-==⇒+=+=3''3'0'y y x x y y x x代入y =3x 得:y ′-3=3x ′即:y ′=3x ′+3按习惯,将x ′、y ′写成x 、y 得l ′的解析式:y =2x +3(实际上是图象向上平移了3个单位) 课堂练习:课本123页练习3例2、函数1)23lg(+-=x y 图象按向量平移后图象的解析式为x y 3lg =,求, 解法一:设向量a =(h ,k )P(x ,y)是函数1)23lg(+-=x y 图象上任一点,平移后函数x y 3lg =图象上的对应点为)(y x P ''',,由平移公式得⎩⎨⎧+='+='ky y h x x 将它代入x y 3lg =得,与)(lg h x k y +=+31)23lg(+-=x y 为同一函数,⎪⎩⎪⎨⎧-=-=⎩⎨⎧=--=∴132123k h k h 解得,故所求向量)(132--=,a 解法二:1323lg 1)23lg(+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=+-=x x y 即⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-=-323lg 1x y 令⎪⎩⎪⎨⎧-='-='132y y x x 则得x y '='3lg 所以将函数1)23lg(+-=x y 的图象按)(132--=, 平移后得到的解析式为x y 3lg =。
第03讲图形的平移1、通过具体实例认识平移,探索它的基本性质:一个图形和它经过平移所得的图形中,两组对应点的连线平行(或在同一条直线上)且相等。
2、利用平移设计图案,认识并欣赏平移在自然界和现实生活中的应用。
3、经历探索平移基本性质的过程,发展空间观念,增强审美意识。
一.平行线之间的距离(1)平行线之间的距离从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.(2)平行线间的距离处处相等.二.生活中的平移现象1、平移的概念在平面内,把一个图形整体沿某一的方向移动,这种图形的平行移动,叫做平移变换,简称平移.2、平移是指图形的平行移动,平移时图形中所有点移动的方向一致,并且移动的距离相等.3、确定一个图形平移的方向和距离,只需确定其中一个点平移的方向和距离.三.平移的性质(1)平移的条件平移的方向、平移的距离(2)平移的性质①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.四.作图-平移变换(1)确定平移后图形的基本要素有两个:平移方向、平移距离.(2)作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.五.利用平移设计图案确定一个基本图案按照一定的方向平移一定的距离,连续作图即可设计出美丽的图案.通过改变平移的方向和距离可使图案变得丰富多彩.一.平行线之间的距离(共3小题)1.(2023春•海港区校级期中)直线a、b、c是三条平行直线.已知a与b的距离为5厘米,b与c的距离为2厘米,求a与c的距离为( )A.2厘米B.3厘米C.7厘米D.3厘米或7厘米【分析】根据a、b、c这三条平行直线的位置不同,结合两平行线间的距离的定义,得出结果.【解答】解:分两种情况:①当直线b在直线a与c之间时,如图.+=厘米;a与c的距离为527②当直线c在直线a与b之间时,如图.-=厘米.a与c的距离为523故选:D.【点评】本题考查了两平行线间的距离的求法.得出a、b、c这三条平行直线的不同位置关系是解决此题的关键.2.(2023春•秦皇岛期末)如图,直线//AB CD,点P是直线AB上一个动点,当点P的位置发生变化时,D的面积( )PCDA.向左移动变小B.向右移动变小C.始终不变D.无法确定【分析】根据平行线间的距离处处相等可得点P到CD的距离不变,因此三角形的面积不变.【解答】解:Q直线//AB CD,点P是直线AB上一个动点,\无论点P怎么移动,点P到CD的距离不变,\D的底不变,高不变,面积也不变,PCD故选:C.【点评】本题考查平行线间的距离,掌握平行线间的距离处处相等是解题的关键.3.(2021春•宁德期末)如图,MN AB^,垂足为^,垂足为M点,MN交CD于N,过M点作MG CDEF AB,交MG于H点,其中线段GM的长度是 点M 到 的距离,线段G,EF过点N点,且//MN的长度是 到 的距离,又是 的距离,点N到直线MG的距离是 .【分析】点到直线的距离是指直线外一点到这条直线的垂线段的长度,根据这一定义结合图形进行填空即可.【解答】解:线段GM的长度是点M到直线CD的距离;线段MN的长度是点M到直线EF的距离,又是平行线AB、EF间的距离;点N到直线MG的距离是线段GN的长度.【点评】正确理解点到直线的距离的定义是解决此类问题的关键.二.生活中的平移现象(共4小题)4.(2023春•天宁区校级期中)下列现象属于平移的是( )A.下雨天雨刮刮车玻璃B.每天早上打开教室门C.每天早上打开教室窗户D.荡秋千【分析】根据平移不改变图形的形状和大小,只是改变位置解答即可.【解答】解:A.下雨天雨刮刮车玻璃是旋转现象,故不符合题意;B.每天早上打开教室门是旋转现象,故不符合题意;C .每天早上打开教室窗户是平移现象,符合题意;D .荡秋千是旋转现象,故不符合题意.故选:C .【点评】此题考查了平移的定义,熟练掌握平移不改变图形的形状和大小,只改变位置是解答本题的关键.5.(2023春•连云区校级月考)2022年,中国举办了第二十四届冬季奥林匹克运动会,如图,通过平移吉祥物“冰墩墩”可以得到的图形是( )A .B .C .D .【分析】根据平移的性质,即可解答.【解答】解:如图,通过平移吉祥物“冰墩墩”可以得到的图形.故选:D .【点评】本题考查平移的性质,掌握平移不改变图形的大小形状,只改变位置是解决问题的关键.6.(2023春•启东市期末)“水是生命之源,滋润着世间万物”国家节水标志由水滴,手掌和地球变形而成.寓意:像对待掌上明珠一样,珍惜每一滴水!以下通过平移节水标志得到的图形是( )A .B .C .D .【分析】平移是物体运动时,物体上任意两点间,从一点到另一点的方向与距离都不变的运动,据此判断即可.【解答】解:C 选项中的图:通过平移能与上面的图形重合.故选:C .【点评】本题主要考查了平移的定义,平移时移动过程中只改变图形的位置,而不改变图形的形状、大小和方向,掌握平移的定义是解题的关键.7.(2023春•盱眙县期末)如图,在一块长为11米,宽为5米的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1米就是它的右边线,这块草地的绿地面积是( )平方米.A .50B .55C .40D .44【分析】根据平移的性质,将草地面积转化为长为10米,宽为5米的长方形面积即可.【解答】解:根据平移的性质可知,草地可以看作长为11110-=米,宽为5米的长方形,因此面积为10550´=(平方米),故选:A .【点评】本题生活中的平移现象,理解平移的定义,掌握平移的性质是中正确解答的前提.三.平移的性质(共6小题)8.(2023春•建邺区期中)如图,ABC D 沿着直线BC 向右平移得到DEF D ,则①BE CF =;②//AB DE ;③AG DG =;④ACB DFE Ð=Ð,其中结论正确的是( )A .①②B .①②④C .②④D .①③④【分析】根据平移后两个三角形全等,逐一进行判断即可.【解答】解:ABC D Q 沿着直线BC 向右平移得到DEF D ,ABC DEF \D @D ,BC EF \=,B DEF Ð=Ð,ACE DFE Ð=Ð,BC CE EF CE \-=-,//AB DE ,BE FC \=,故①②④正确,条件不足,无法得到AG DG =,故③错误.故选:B .【点评】本题考查全等三角形的性质.熟练掌握平移后的两个三角形全等,是解题的关键.9.(2023春•兴化市月考)如图,4AB cm =,5BC cm =,2AC cm =,将ABC D 沿BC 方向平移a (05)cm a <<,得到DEF D ,连接AD ,则阴影部分的周长为 11 cm .【分析】根据平移的性质得到4DE AB cm ==,AD BE a ==cm ,根据周长公式计算,得到答案.【解答】解:由平移的性质可知:4DE AB cm ==,AD BE a ==cm ,(5)EC a cm \=-,\阴影部分的周长(5)2411()AD EC AC DE a a cm =+++=+-++=,故答案为:11.【点评】本题考查的是平移的性质,平移不改变图形的形状和大小、经过平移,对应点所连的线段平行且相等,对应线段平行且相等.10.(2023春•丹阳市校级期末)如图,将直角ABC D 沿AC 的方向平移得到直角DEF D ,DE 交BC 于点G .若6AB cm =,2EG cm =,3BG cm =,则图中阴影部分的面积等于( )A .212cmB .215cmC .224cmD .230cm 【分析】根据平移的性质得出6AB DE cm ==,进而得到4DG cm =,由GEFC ABGD S S =梯形梯形进行计算即可.【解答】解:由平移的性质可知,6AB DE cm ==,2EG cm =,3BG cm =,624()DG cm \=-=,()()21463152GEFC ABGD S S cm \==´+´=梯形梯形,故选:B .【点评】本题考查平移的性质,理解平移的定义,掌握平移的性质是正确解答的前提.11.(2023春•梁溪区校级期中)如图,将周长为8的ABC D 沿BC 方向向右平移2个单位长度得到DEF D ,则四边形ABFD 的周长为( )A.10B.12C.14D.16【分析】根据平移的性质可得DF AC==,然后求出四边形ABFD的周长等于ABCD的周长=、2AD CF与AD、CF的和,再求解即可.D,【解答】解:ABCDQ沿BC方向平移2个单位长度得到DEFAD CF==,\=,2DF AC=+++\四边形ABFD的周长AB BF DF AD=++++AB BC CF AC AD++ABC=D的周长AD CF=++822=.12故选:B.【点评】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.D的位置,点A、B、C 12.(2023春•洪泽区期中)如图,将ABCD沿射线AB的方向平移2个单位到DEF的对应点分别点D、E、F.(1)若3AB=,则AE= 5 .(2)若75Ð的度数.ABCÐ=°,求CFE【分析】(1)直接平移的性质得出BE的长进而得出答案;(2)利用平移的性质进而得出CFEÐ的度数.D的位置,【解答】解:(1)3AB=D沿射线AB的方向平移2个单位到DEFQ,将ABC\=,BE2则5=+=.AE BE AB故答案为:5;(2)Q由平移变换的性质得://AE CF,BC EF,//\Ð=Ð=°,75E ABC\Ð+Ð=°,180CFE E\Ð=°.CFE105【点评】此题主要考查了平移变换,正确应用平移的性质是解题关键.13.(2023春•如东县期中)如图,直线//AB CD,直线EF与AB、CD分别交于点G、H,EHD a aÐ=°<<°.小安将一个含30°角的直角三角板PMN按如图①放置,使点N、M分别在直线(090)AB、CD上,且在点G、H的右侧,90PMNÐ=°.Ð=°,60P(1)填空:PNB PMDÐ(填“>”“<”或“=”);Ð+Ð = P(2)若MNGÐ的平分线NO交直线CD于点O,如图②.①当//PM EF时,求a的度数;NO EF,//②小安将三角板PMN保持//Ð的度数(用含a的式子表示).PM EF并向左平移,在平移的过程中求MONÐ=Ð,进而可求解;【分析】(1)过P点作//Ð=Ð,PMD QPMPQ AB,根据平行线的性质可得PNB NPQ(2)①由平行线的性质可得60Ð=Ð=°,再ANO ONMÐ=Ð=°,结合角平分线的定义可得60ONM PMN利用平行线的性质可求解;②利用平行线的性质及角平分线的定义计算可求解.【解答】解:(1)过P点作//PQ AB,\Ð=Ð,PNB NPQ//Q,AB CD\,//PQ CDPMD QPM \Ð=Ð,PNB PMD NPQ QPM MPN \Ð+Ð=Ð+Ð=Ð,故答案为:=(2)①//NO EF Q ,//PM EF ,//NO PM \,ONM NMP \Ð=Ð,60PMN Ð=°Q ,60ONM PMN \Ð=Ð=°,NO Q 平分MNO Ð,60ANO ONM \Ð=Ð=°,//AB CD Q ,60NOM ANO \Ð=Ð=°,60NOM a \=Ð=°;②点N 在G 的右侧时,如图②,//PM EF Q ,EHD a Ð=,PMD a \Ð=,60NMD a \Ð=°+,//AB CD Q ,60ANM NMD a \Ð=Ð=°+,NO Q 平分ANM Ð,113022ANO ANM a \Ð=Ð=°+,//AB CD Q ,1302MON ANO a \Ð=Ð=°+,点N 在G 的左侧时,如图,//PM EF Q ,EHD a Ð=,PMD a \Ð=,60NMD a \Ð=°+,//AB CD Q ,180BNM NMO \Ð+Ð=°,BNO MON Ð=Ð,NO Q 平分MNG Ð,11[180(60)]6022BNO a a \Ð=°-°+=°-,1602MON a \Ð=°-,综上所述,MON Ð的度数为1302a °+或1602a °-.综上所述,MON Ð的度数为1302a °+或1602a °-.【点评】本题主要考查平行线的性质,角平分线的定义,分类讨论是解题的关键.四.作图-平移变换(共6小题)14.(2023春•高港区月考)画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.(1)将ABC D 向左平移8格,再向下平移1格.请在图中画出平移后的△A B C ¢¢¢;(2)利用网格在图中画出ABC D 的中线CD ,高线AE ;(3)△A B C ¢¢¢的面积为 8 ;(4)在平移过程中线段BC 所扫过的面积为 ;(5)在图中能使ABC PBC S S D D =的格点P 的个数有 个(点P 异于)A .【分析】(1)根据图形平移的性质画出平移后的△A B C ¢¢¢即可;(2)根据格点的特点ABC D 的中线CD ,高线AE 即可;(3)利用三角形的面积公式即可得出结论;(4)利用平行四边形的面积公式即可得出结论;(5)过点A 作直线BC 的平行线,此直线与格点的交点即为P 点.【解答】解:(1)如图,△A B C ¢¢¢即为所求;(2)如图,中线CD ,高线AE 即为所求;(3)14482A B C S ¢¢¢=´´=V .故答案为:8;(4)线段BC 所扫过的面积4832=´=.故答案为:32;(5)如图,共有9个点.故答案为:9.【点评】本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.15.(2023春•工业园区校级月考)在正方形网格中,小正方形的顶点称为“格点”,每个小正方形的边长均为1,ABC D 的三个顶点均在“格点”处.(1)在给定方格纸中,平移ABC D ,使点B 与点B ¢对应,请画出平移后的△A B C ¢¢¢;(2)线段AA ¢与线段CC ¢的关系是 平行且相等 ;(3)求平移过程中,线段BC 扫过的面积.【分析】(1)分别作出各点的对应点,再顺次连接即可;(2)根据图形平移的性质即可而出结论;(3)根据平行四边形的面积公式即可得出结论.【解答】解:(1)如图,△A B C ¢¢¢即为所求;(2)线段AA ¢与线段CC ¢平行且相等.故答案为:平行且相等;(3)线段BC 扫过的面积5315BCC B S ¢¢==´=平行四边形.【点评】本题考查的是作图-平移变换,熟知图形平移不变性的性质是解题的关键.16.(2023春•崇川区校级月考)按要求画图及填空:在由边长为1个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点O 及ABC D 的顶点都在格点上.(1)点A 的坐标为 (4,2)- .(2)将ABC D 先向下平移2个单位长度,再向右平移5个单位长度得到△111A B C ,画出△111A B C .(3)计算△111A B C 的面积.【分析】(1)根据点A 的位置写出坐标即可.(2)根据平移变换的性质分别作出A ,B ,C 的对应点1A ,1B ,1C 即可.(3)利用分割法求面积即可.【解答】解:(1)如图,(4,2)A -.故答案为:(4,2)-.(2)如图,△111A B C 即为所求作.(3)11111134132314 5.5222A B C S =´-´´-´´-´´=V .【点评】本题考查作图-平移变换,三角形的面积等知识,解题的关键是熟练掌握平移变换的性质,正确作出图形是解题的关键.17.(2023春•江阴市校级月考)如图,在边长为1个单位的正方形网格中,ABC D 经过平移后得到△A B C ¢¢¢,图中标出了点B 的对应点B ¢.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题:(1)画出△A B C ¢¢¢;(2)画出ABCD的高BD;(3)求ABCD的面积为 7.5 ;D的面积和ABC(4)在AB的右侧确定格点Q,使ABQD的面积相等,这样的Q点有 个.【分析】(1)根据题意分别作出A,B,C的对应点A¢,B¢,C¢即可;(2)根据格点垂直画法画出高即可;(3)利用分割法求解即可;(4)找出C关于AB对称的对应点Q,利用等高模型解决问题即可.5【解答】解:(1)如图1,根据题意,向下平移一格,再向左平移6格;(2)如图2,线段BD即为所求;(3)如图3,ABC ACN BCN S S S D D D \=+,11313422=´´+´´,1.56=+,7.5=;故答案为:7.5.(4)如图4,找出C 关于AB 对称的对应点5Q ,过5Q 作AB 平行线,与格点的交点即为所求;+故答案为:8.【点评】此题考查了作图-平移变换,三角形的面积,三角形的高等知识,解题的关键是熟练掌握基本知识.18.(2023春•天宁区校级期中)如图,图形在方格(小正方形的边长为1个单位)上沿着网格线平移,规定:若沿水平方向平移的数量为x (向右为正,向左为负,平移||x 个单位),沿竖直方向平移的数量为y (向上为正,向下为负,平移||y 个单位),则把有序数对(,)x y 叫做这一平移的“平移量”.如图,已知ABC D ,点A 按“平移量” (2,3)可平移到点B .(1)填空,点B 可看作点C 位“平移量” ( 2- , )平移得到.(2)若将ABC D 依次按“平移量” (1,1)-平移得到△A B C ¢¢¢,请在图中画出△A B C ¢¢¢.(3)将点A 按“平移量“(,)a b 平移得到点D (点D 在直线BC 上),使32ABD ABC S S D D =写出此时的平移量(,)a b .D的面积与ABCa b平移得到点P,连接AP、BP,若ABP(4)将点C按平移量”(,)D的面积相等,写出a、b满足的关系式.【分析】(1)根据“平移量”(的定义判断即可;(2)利用平移变换的性质分别作出A,B,C的对应点A¢,B¢,C¢即可;(3)判断出点D的位置,可得结论;(4)取格点T,作直线CT,当点P在直线CT上时,满足条件.【解答】解:(1)点B可看作点C位“平移量”(2,2)-平移得到.-,2;故答案为:2(2)如图,△A B C¢¢¢即为所求;(3)如图点D或D¢即为所求,-或(5,0);\平移量(1,6)(4)取格点T ,作直线CT ,当点P 在直线CT 上时,满足条件,此时23a b =.当点P 在AB 的上方直线l 上时,也满足条件,此时2223a b --=-.【点评】本题考查作图-平移变换,正数与负数,平移变换等知识,解题的关键是理解题意,灵活运用所学知识解决问题.19.(2023春•泗洪县期中)如图,在边长为1个单位长度的正方形网格中,ABC D 经过平移后得到△A B C ¢¢¢¢,图中标出了点B 的对应点B ¢.(1)画出△A B C ¢¢¢;(2)连接AA ¢、CC ¢,那么AA ¢与CC ¢的关系是 AA CC ¢=¢,//AA CC ¢¢. ;(3)线段AC 扫过的图形的面积为 .【分析】(1)利用平移变换的性质分别作出A ,B ,C 的对应点A ¢,B ¢,C ¢即可;(2)利用平移变换的性质判断即可;(3)利用分割法求出四边形面积即可.【解答】解:(1)如图,△A B C ¢¢¢即为所求;(2)AA ¢与CC ¢的关系是:AA CC ¢=¢,//AA CC ¢¢.故答案为:AA CC ¢=¢,//AA CC ¢¢;(3)线段AC 扫过的图形的面积为112102142161022´-´´´-´´´=.故答案为:10.【点评】本题考查作图-平移变换,四边形的面积等知识,解题的关键是理解题意,灵活运用所学知识解决问题.五.利用平移设计图案(共4小题)20.(2023春•宜兴市月考)下列图案中,可以利用平移来设计的图案是( )A .B .C .D .【分析】根据平移变换,轴对称变换中心对称对各选项分析判断后利用排除法求解.【解答】解:A 、是利用中心对称设计的,不合题意;B ,C 是利用轴对称设计的,不合题意;D 、是利用平移设计的,符合题意.故选:D .【点评】本题考查的是利用平移设计图案,熟知图形平移不变性的性质是解答此题的关键.21.(2023春•工业园区校级月考)下面所示的图案中,可以看成是由图案自身的一部分经过平移得到的是( )A .B .C .D .【分析】根据平移不改变图形的形状和大小,结合图案,对选项一一分析,排除错误答案.【解答】解:A 、是一个对称图形,不能由平移得到,故此选项不合题意;B 、是一个对称图形,不能由平移得到,故此选项不合题意;C 、是一个对称图形,不能由平移得到,故此选项不合题意;D 、图案自身的一部分沿着直线运动而得到,是平移,故此选项符合题意.故选:D .【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,以致选错.22.(2021春•鼓楼区校级月考)如图是由边长为1的小正方形构成的格点图形,A 、B 、C 在格点上,将三角形ABC 向右平移3个单位,再向上平移2个单位得到三角形111A B C .(1)在网格中画出三角形111A B C ;(2)求线段AB 在变换到11A B 过程中扫过的区域面积(重叠部分不重复计算).【分析】(1)将点A 、B 、C 分别向右平移3个单位,再向上平移2个单位得到对应点,再顺次连接可得;(2)根据扫过的区域面积1111A B C ABB C S S ¢=+V 平行四边形,据此列式计算可得.【解答】解:(1)如图所示,△111A B C 即为所求;(2)线段AB 在变换到11A B 过程中扫过的区域面积11111321272A B C ABB C S S ¢=+=´+´´=V 平行四边形.【点评】本题主要考查利用平移设计图案,解题的关键是掌握平移变换的定义和性质.23.(2021春•新吴区月考)请把下面的小船图案先向上平移3格,再向右平移4格.【分析】分别作出MNED和梯形ABCD向上平移3格,再向右平移4格的对应位置即可.【解答】解:如图所示:.【点评】此题主要考查了图形的平移,关键是掌握平移后图形的大小和形状不发生改变.一.选择题(共8小题)D的是( )1.(2023春•工业园区校级期中)下列图形中,把ABCD平移后,能得到DEFA.B.C.D.【分析】根据平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等解答.【解答】解:由图可知,只有A选项ABCD.D平移后,能得到DEF故选:A.【点评】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.2.(2023春•泗洪县期末)下列现象中,属于平移的是( )A.滚动的足球B.转动的电风扇叶片C.正在上升的电梯D.正在行驶的汽车后轮【分析】利用平移的定义进行判断即可.【解答】解:A.滚动的足球是旋转,故不符合题意;B.转动的电风扇叶片是旋转,故不符合题意;C.正在上升的电梯是平移,故符合题意;D.正在行驶的汽车后轮是旋转,故不符合题意;故选:C.【点评】本题考查平移的定义,掌握图形经过平移,对应线段相等,对应角相等,对应点所连的线段相等是解题的关键.3.(2023春•江阴市期中)下列各组图形,可由一个图形平移得到另一个图形的是( )A.B.C.D.【分析】根据平移的基本性质,结合图形,对选项进行一一分析即可得到答案.【解答】解:A、图形由轴对称所得到,不属于平移,故本选项不符合题意;B、图形平移前后的形状和大小没有变化,只是位置发生变化,符合平移性质,故本选项符合题意;C、图形由旋转所得到,不属于平移,故本选项不符合题意;D、图形大小不一,大小发生变化,不符合平移性质,故本选项不符合题意.故选:B.【点评】本题考查的是平移的性质,把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.4.(2023春•海安市月考)如图,ABCD的周长为20cm,D沿BC所在直线向左平移4cm得到△A B C¢¢¢,若ABC则四边形A B CA¢¢的周长为( )A.16cm B.24cm C.28cm D.32cm【分析】根据平移的性质,对应点的距离等于平移距离求出AA¢、BB¢,然后求出CB¢,再根据周长的定义解答即可.【解答】解:Q平移距离是4cm,\¢=¢=,4AA CC cmQ的周长为20cm,ABCD=++=.Q四边形A B CA¢¢的周长442028()cm故选:C.【点评】本题考查了平移的性质,熟练掌握平移的性质是解题的关键.5.(2023春•天宁区校级期中)如图,ABCD,如果四边形ABFD的周长是20cm,D向右平移2cm得到DEF那么ABCD的周长是( )A.14cm B.16cm C.18cm D.20cm【分析】根据平移的性质得到2=,根据四边形的周长公式、三角形的周长公式计==,AC DFAD CF cm算即可.【解答】解:由平移的性质可知,2=,==,AC DFAD CF cmQ四边形ABFD的周长是20cm,\+++=,20AB BF DF AD cm\++++=,AB BC CF AC AD cm20AB BC AC cm\++=,16=++=,AB BC AC cm\D的周长16ABC故选:B.【点评】本题考查的是平移的性质,①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.6.(2023春•建湖县期中)如图,ABCD以每秒2cm的速度沿着射线BC向右平移,平移2秒后所得图形是=,那么BC的长是( )AP MCPMND,如果2A .4B .6C .8D .9【分析】连接AP ,根据平移的性质可得224()AP BM cm ==´=,再由2AP MC =,可得2MC cm =,即可求解.【解答】解:如图,连接AP ,ABC D Q 以每秒2cm 的速度沿着射线BC 向右平移,平移2秒后所得图形是PMN D ,224()AP BM cm \==´=,2AP MC =Q ,2MC cm \=,6BC BM MC cm \=+=.故选:B .【点评】本题主要考查了图形的平移,熟练掌握平移的性质是解题的关键.7.(2023春•海州区校级期中)如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B 到点C 的方向平移到DEF D 的位置,90B Ð=°,7AB =,2DH =,平移距离为3,则阴影部分的面积为( )A .20B .18C .15D .26【分析】由ABC DEF S S D D =,推出ABEH S S =阴四边形即可解决问题.【解答】解:Q 平移距离为3,3BE \=,7AB =Q ,2DH =,725EH \=-=,ABC DEF S S D D =Q ,ABEH S S \=阴四边形,\阴影部分的面积为1(57)3182=´+´=.故选:B .【点评】本题考查了平移的基本性质,掌握①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等是解题的关键.8.(2023春•钟楼区校级期中)学校一长方形草地中需修建一条等宽的小路,为了达到“曲径通幽”的效果,下列四种设计方案,其中有一个方案修建小路后剩余草坪面积与其它三个方案不等,它是( )A .B .C .D .【分析】根据平移的性质得出修建小路后剩余草坪面积等于矩形的面积-小路的面积解答.【解答】解:A 、B 、D 三种方案剩余草坪面积都是:(长方形的长-小路的宽)´长方形的宽,而C 方案的小路的模块比其他三种方案多1个以小路的宽度为边长的正方形的面积,故选:C .【点评】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应线段平行且相等,对应角相等;本题判断出阴影部分的面积与梯形的面积相等是解题的关键.二.填空题(共9小题)9.(2023春•宿迁期末)如图,将ABC D 沿AC 方向平移1cm 得到DEF D ,若3DC cm =,则AF = 5cm .【分析】根据平移的性质得出1AD CF cm ==,再根据线段的和差关系进行计算即可.【解答】解:由平移的性质可知,1AD CF cm ==,所以1315()AF AD DC CF cm =++=++=,故答案为:5cm .【点评】本题考查生活中的平移现象,掌握平移的性质是正确解答的关键.10.(2023春•淮安区校级期末)如图,将ABC D 沿BC 方向平移3cm 得到DEF D ,若三角形ABC 的周长为20cm ,则四边形ABFD 的周长为 26 cm .【分析】先根据平移的性质得DF AC =,3AD CF cm ==,再由ABC D 的周长为20cm 得到20AB BC AC cm ++=,然后利用等线段代换可计算出26()AB BC CF DF AD cm ++++=,于是得到四边形ABFD的周长为26cm.【解答】解:ABCD,Q沿BC方向平移3cm得到DEFD==,AD CF cmDF AC\=,3++=,AB BC AC cmABCQ的周长为20cm,即20D\++++=++++=++=,AB BC CF DF AD AB BC AC AD CF cm203326()即四边形ABFD的周长为26cm.故答案为:26.【点评】本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.11.(2023春•盱眙县期末)如图,箭头ABCD在网格中做平行移动,当点A移到点P位置时,点C移到的位置为点 R .【分析】根据平移的基本性质,C在A左边1个单位处,经过平移,对应点位置关系不变.【解答】解:当点A移到点P位置时,点C移到的位置为点R.故答案为:R.【点评】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.12.(2023春•建邺区期中)如图,在一块长方形草坪中间,有一条处处1m宽的“曲径”,则“曲径”的面m.积为 b 2-,宽为b m的矩形,然后进行计算即可解答.a m【分析】根据平移的性质可得:草坪可看作长为(1)【解答】解:由题意得:。
平移练习题教案一、教学目标通过本节课的学习,使学生掌握平移的基本概念,能够准确理解和描述平移的过程;能够在平面直角坐标系中进行平移操作,画出平移后的图形;能够解决与平移相关的实际问题。
二、教学重点1. 平移的基本概念。
2. 平面直角坐标系的运用。
3. 平移图形的方法和步骤。
三、教学内容和步骤Step 1:导入与复习(5分钟)教师通过巩固学生对坐标系的认识,回顾上节课学习的内容,引出本节课的主题:平移。
Step 2:引入新知(10分钟)1. 教师出示一张示意图,向学生解释平移的概念,并与平移相关的日常生活中的例子进行关联,激发学生对平移的兴趣。
2. 教师给出平移的定义,并与学生一同总结平移的特点和性质。
Step 3:引导学习(15分钟)1. 教师给出一个简单的平移练习题,让学生根据题目中给出的图形和向量描述进行解答。
鼓励学生积极思考和参与讨论,找出解题的思路和方法。
2. 学生独立完成一道平移练习题,并与同桌交流答案,互相检查并改正错误。
Step 4:巩固与拓展(15分钟)1. 教师出示多个平移练习题,让学生分组完成。
每组选择一道练习题,以小组为单位展示解题过程和结果。
其他学生可以提出问题和建议。
2. 教师指导学生通过观察图形和向量的变化规律,总结平移图形的一般步骤和方法。
Step 5:练习与应用(20分钟)1. 学生独立完成一套平移练习题,巩固所学的知识和技能。
2. 学生通过解决与平移相关的实际问题,将所学知识应用到实际情境中。
四、教学反思通过本节课的教学,学生对平移的基本概念有了较为准确的理解,能够运用平面直角坐标系进行平移操作,并能够解决一些与平移相关的实际问题。
课堂上,教师注重启发学生思考,鼓励他们积极参与讨论和解题过程,提高了学生的学习兴趣和主动性。
同时,通过小组合作和展示,增强了学生的合作意识和团队精神。
在今后的教学中,应继续鼓励学生主动思考和探索,通过更多的实例引导学生深入理解和应用平移的知识。
课题名称 1.1图形的平移年级四年级下第一单元
课题目标认识图形的平移,会判断出图形是否平移
重难点把简单图形沿水平(或竖直)方向平移
知识再现订正与总结经典例题:
基础练习
4.小鱼先向()平移了()格,再向()
平移了()格,又向()平移了()格,最后向()平移了()格。
拓展延伸
一、看图填一填
(1)小树向()平移了()格。
(2)小鱼向()平移了()格。
(3)三角形向()平移了()格。
二、
(1)图1先向()平移了()格,再向()平移了()格。
(2)图2先向()平移了()格,再向()平移了()格。
三、选一选
1、平移不改变图形的()和(),只改变图形的()。
A、位置
B、大小
C、形状
2、由右图平移后得到的是()
3、下列生活中的现象,属于平移的是( )
A.抽屉的拉开
B.汽车刮雨器的运动
C.坐在秋千上人的运动
D.投影片的文字经投影变换到屏幕
4、以下现象中属于平移的是( )
①温度计中,液柱的上升或下降;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上瓶装饮料的移动.
A.①②
B.①③
C.②③
D.②④
5、下面生活中的物体的运动情况可以看成平移的是( )
A.摆动的钟摆
B.在笔直的公路上行驶的汽车
C.随风摆动的旗帜
D.汽车玻璃上雨刷的运动
评价与反思:
参考答案。
图形的平移练习题
仅供学习与交流,如有侵权请联系网站删除 谢谢
2
第一周 图形的平移练习
班级_____________ 姓名:_____________ 1.图形的平移只改变图形的________,不改变图形的_______、________。
2.图形平移的决定因素:平移的_______和_______。
3.平移的方向是图形上的某一点到它_____点的方向;平移的距离是图形上的某一点
到它对应点的连线的______。
平移的对应点所连线段 。
4.一个图形先向右平移5个单位,再向左平移7个单位,所得到的图形,可以看作是
原来位置的图形一次向 平移 个单位得到的 5.如果三角形ABC 沿着北偏东300的方向移动了2cm ,那么三角形ABC 的一条边AB
边上的一点P向__________移动了______cm 。
6.在下列说法中:①△ABC 在平移过程中,对应线段一定相等;
②△ABC 在平移过程中,对应线段一定平行;③△ABC 在平移过程中,周长不变;
④△ABC 在平移过程中,面积不变。
其中正确的有____________________。
7.下列说法中正确的是( )
A .一个图形经过平移后,与原图形成轴对称
B .如果两个图形成轴对称,那么一个图形可由另一个图形经过平移变换得到
C .一个图形经过平移后,它的性质都发生了变化
D .图形的平移由平移的方向和距离决定 8.在以下现象中,属于平移的是( )
① 在挡秋千的小朋友;② 打气筒打气时,活塞的运动;
仅供学习与交流,如有侵权请联系网站删除 谢谢3
③ 钟摆的摆动; ④ 传送带上,瓶装饮料的移动 A . ①② B . ①③ C . ②③ D . ②④ 9.如图,大矩形的长是10cm ,宽是8cm ,阴影的宽为2cm ,则空白部分的面积是( ) A.36cm 2 B.40cm 2 C.32cm 2 D.48 cm 2
10.如图,△ABC 经过平移之后得△DEF ,
请你在两三角形的内角中找出图中相等的线段
写出图中互相平行的线段
写出图中相等的角
11.如图,△ABC 经过平移后称为△A ′B ′C ′,画出平移的方向,量出平移的距离。
思路点拔:先找出一组对应点,确定平移方向,测量平移的距离.
12.(1)已知△ABC 和线段PQ ,画出△ABC 沿线段PQ 的方向平移2cm 后的图形;
E
D B
C
F
A O
仅供学习与交流,如有侵权请联系网站删除 谢谢4
13.如图,已知平行四边形ABCD ,作DE ⊥AB ,垂足为E ,把三角形AED 沿AB 方向 平移AB 长个单位. ①作出平移后的图形.
②经过这样的平移后,原来的图形变成了什么图形? 等吗?
③这两个图形的面积相
E D B
C
A。