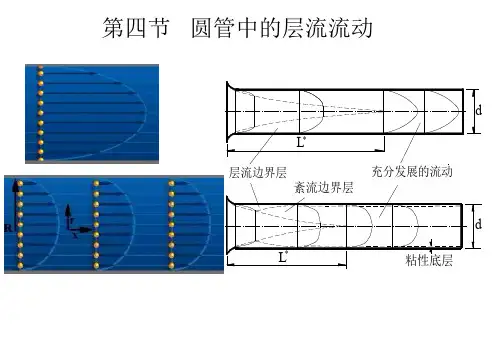
圆管中的层流流动

非牛顿流体在圆管中层流-紊流分层流动规律
非牛顿流体在圆管中的层流-紊流分层流动规律是一种复杂且有趣的现象。

在层流区域，流体运动稳定，速度和压力的分布呈现对称性，流线光滑，无旋转，流体分子之间的作用力决定了整个流场的运动；而在紊流区域，流体运动变得不规则，出现了湍流涡旋和涡流结构，速度和压力变化随时间和空间的变化而不断变化，流体分子之间的作用力失去了主导作用。

在层流和紊流之间，存在着分层流的过渡区域，其特性介于层流和紊流之间。

分层流区域的分层情况取决于流体黏度的大小和流速的剪切率，黏度越大，分层越明显，流速越快，分层趋向于消失。

非牛顿流体具有黏弹性，其黏度随着剪切应力的变化而变化，其在圆管中的层流-紊流分层流动规律的研究对于深入了解非牛顿流体的流动特性和应用具有重要的理论和实践意义。

圆管层流流动的模拟实验研究报告摘要：圆管层流流动的方式受到流体的质量流量影响，以及圆管内部阻力的影响。

在本研究中，对圆管层流流动的影响因素进行分析和模拟实验。

该实验利用定常水流模拟仪，测试圆管内安装不同型号、结构和大小的层流设备，并观察层流流动情况。

实验结果表明，通过实验法确定的层流流量的量化值与定常流模拟仪的指示值相较接近，结论认为层流流量的大小和流体的质量流量以及管内的阻力有关。

关键词：圆管层流流动；流体质量流量；模拟实验；阻力1.言随着圆管层流流动技术的发展，以及其在不同领域应用的广泛推广，对圆管层流流动的深入研究及其影响因素分析也受到国内外研究人员的长期关注。

圆管层流是一种较新型的水流控制技术，其影响流量的因素主要有：流体质量流量和管内阻力；它们影响管道层流流量和圆管层流流动质量流速的变化规律。

本研究利用定常水流模拟仪模拟不同型号、结构和大小的层流设备，观察层流流动的情况，并对层流流量的影响因素进行实验分析。

2.验设计实验以定常水流模拟仪为主要仪器，测试圆管内安装的不同型号、结构和大小的层流设备。

仪器的工作原理是：模拟水流通过圆管内不同结构的层流设备时，圆管内液力聚焦设备会产生液力聚焦，也就是水流经过不同层流设备时，其速度会变化，然后根据变化的流速来测量层流流量；仪器设置有安全阀，当压力超标时，安全阀会起到保护功能，以防止压力过高造成实验室设备的损坏，使实验结果准确可靠。

3.验结果3.1础数据分析表1为实验所用管道层流设备的参数及参数组合，包括管径、残余膨胀比、层流残余膨胀比、平均流速和层流流量。

表1验参数及参数组合|径 (mm) |余膨胀比 |流残余膨胀比 |均流速 (m/s) |流流量(L/m) || -------------- | ------------ | -------------------- | ------------------------- | ------------------------- || 113 | 0.9 | 5.6 | 0.09 | 3.2 || 115 | 0.8 | 4.5 | 0.14 | 4.5 || 117 | 0.7 | 3.7 | 0.19 | 6.2 |3.2验结果分析在表2中，给出了实验结果的数据，展示了实验法测量的层流流量与定常水流模拟仪的指示值间的差异情况，可见实验法确定的层流流量的量化值与定常水流模拟仪的指示值相比，波动范围很小，平均值可以接近指示值，表明实验结果准确可靠。

管道流量计算1）流体在水平圆管中作层流运动时，其体积流量Q与管子两端的压强差Δp，管的半径r，长度L，以及流体的粘滞系数η有以下关系：Q=π·r4·Δp/(8ηL)式中：Q-流量，单位r-管的半径，单位Δp -管两端的压力差η-流体粘度L-管的长度2）液体流速与管径、流量的关系式：Q=V·r2·3.14×3600；D=管径=2×2×；P=RL；R=(λ/D)*(ν^2*γ/2g)。

Q-流量(m3/h)；ν-流速(m/s)；r-管道半径(m)；D-管道直径(m)；P-压力(kg/m2)；R-沿程摩擦阻力(kg/m2)；L-管道长度(m)；g-重力加速度=9.8。

压力可以换算成Pa，方法如下：1帕=1/9.81(kg/m2)3）对于短管道：（局部阻力和流速水头不能忽略不计）流量Q=[(π/4)d2·√(1+λL/d+ζ)]·√(2gH)式中：Q--流量，（m3/s)；Π--圆周率；d--管内径（m)，L--管道长度（m)；g--重力加速度(m/s^2)；H--管道两端水头差（m)；Λ--管道的沿程阻力系数（无单位）；Ζ--管道的局部阻力系数（无单位，有多个的要累加）。

使中部的截面积变为原来的一半，其他条件都不变，这就相当于增加了一个局部阻力系数ζ’，流量变为：Q’=[(π/4)d^2 √(1+λL/d+ζ+ζ’)] √(2gH)。

流量比原来小了。

流量减小的程度要看增加的ζ’与原来沿程阻力和局部阻力的相对大小。

当管很长（L很大），管径很小，原来管道局部阻力很大时，流量变化就小。

相反当管很短（L很小），管径很大，原来管道局部阻力很小时，流量变化就大。

定量变化必须通过定量计算确定。

流量计算公式（1）差压式流量计差压式流量计是以伯努利方程和流体连续性方程为依据，根据节流原理，当流体流经节流件时（如标准孔板、标准喷嘴、长径喷嘴、经典文丘利嘴、文丘利喷嘴等），在其前后产生压差，此差压值与该流量的平方成正比。

简述圆管层流的速度分布特征和切应力分布特征圆管层流是指在一个圆形管道内，流体的流动是以层流方式进行的现象。

在圆管层流中，流体的速度分布特征和切应力分布特征是非常重要的。

首先，我们来看圆管层流的速度分布特征。

在层流中，流体的速度是随着管道的距离均匀分布的。

也就是说，在管道的不同位置处，流体的速度是相同的。

这是因为在层流中，流体是按照一定的轨迹和速度流动的，流线是平行且不交叉的。

这种速度分布特征使得层流具有稳定性和可预测性，对于一些需要精确控制流速的应用非常有益。

其次，圆管层流的切应力分布特征也是很重要的。

在层流中，切应力是与速度梯度成正比的。

也就是说，当速度梯度变大时，切应力也随之增大；当速度梯度变小时，切应力也随之减小。

这是因为流体的黏性导致了相邻层之间的内部摩擦，从而产生了切应力。

在层流中，切应力的分布是均匀且平稳的，不会出现剧烈的涡旋和湍流现象。

这种切应力分布特征使得层流具有较小的能量损失和较低的压降，对于一些需要节能优化的应用非常有益。

综上所述，圆管层流的速度分布特征和切应力分布特征对于流体的运动和控制具有重要意义。

速度分布特征使得层流具有稳定性和可预测性，而切应力分布特征使得层流具有较小的能量损失和较低的压降。

因此，在实际应用中，我们可以利用这些特征来设计和优化圆管流体系统，从而提高流体的运动效率和节能性能。

同时，对于液体和气体的输送和操控也有指导意义，能够使得流体的传输更加安全和可靠。

这些特征的理解和应用将有助于推动科学技术的发展和创新，为社会的可持续发展做出贡献。

圆管层流运动的沿程阻力系数λ=
圆管层流运动的沿程阻力系数λ是一个无量纲的参数，用来描述液体在圆管中流动时的阻力大小。

这个参数是通过流体力学实验和理论推导得出的。

对于圆管中的层流流动，根据流体力学理论，沿程阻力系数λ可以用以下公式表示：
λ = 64 / Re
其中，Re是雷诺数，定义为体积流率与粘性系数的比值乘以管径：
Re = (ρ * V * D) / μ
其中，ρ是液体密度，V是液体在管道中的速度，D是管道的直径，μ是液体的动力粘性系数。

需要注意的是，上述公式只适用于层流流动情况下的圆管，当流动情况变为湍流时，阻力系数的计算方法会有所不同。

此外，这个公式也是基于一些假设条件的，例如流体是牛顿流体、流动是稳定和定常的等。

总之，圆管层流运动的沿程阻力系数λ可以根据上述公式来计算，通过这个参数可以评估流体在圆管中的阻力大小和流动性质。

流体在圆管中层流流动的速度分布在物理学中，流体的运动方式可以分为层流流动和湍流流动两种。

层流流动是指流体在管道中以层状流动的状态，流速分布均匀且稳定。

而湍流流动则是指流体运动呈现旋涡、乱流的状态，流速分布不均匀且不稳定。

本文将重点介绍流体在圆管中层流流动的速度分布。

在圆管中，当流体以层状流动时，流速的分布具有一定的规律。

根据流体的连续性方程和动量守恒方程，可以得出流体在圆管中的速度分布与半径的关系。

根据流体的连续性方程，可以得到流体流速和管道截面积的关系。

流体的流速与管道截面积成反比，即流速越大，管道截面积越小。

这是因为在层流流动中，不同层次的流体速度需要相互配合才能维持流动。

根据动量守恒方程，可以得到流体的速度分布与半径的关系。

根据该方程的推导可知，流体的速度随着管道半径的变化而变化。

具体来说，当流体靠近管道内壁时，由于受到摩擦力的作用，流体速度会减小；而当流体靠近管道中心时，受到的摩擦力较小，流体速度较大。

因此，流体在圆管中的速度分布呈现出一种从管道中心到管道壁逐渐减小的趋势。

根据这一规律，可以得出流体速度与管道半径的关系。

在圆管中，流体速度随着管道半径的增大而减小。

具体来说，流体速度与管道半径的平方成反比关系。

这意味着，管道中心处的流体速度最大，而管道壁处的流体速度最小。

在实际应用中，对于层流流动的速度分布，可以利用该规律进行流体的控制和调整。

例如，在工业生产中，希望流体在管道中保持层流流动的状态，可以通过调整管道直径和流体流速来实现。

根据流体速度与管道半径平方的关系，可以控制流体在管道中的速度分布，从而保持流体的层流状态。

总而言之，流体在圆管中的层流流动速度分布遵循一定的规律。

通过了解流体速度与管道半径的关系，可以对流体在圆管中的速度分布进行预测和调整。

这对于实际应用中对流体的控制和调整具有重要的指导意义。

圆管内层流和湍流雷诺数
雷诺数（Reynolds number）是流体力学中一个无量纲参数，用来描述流体在运动过程中惯性力和粘性力的相对重要性。

雷诺数的定义如下：
Re = ρVD/μ
其中，Re为雷诺数，ρ为流体的密度，V为流体的速度，D为流体流动的特征长度（如管道的直径），μ为流体的动力粘度。

根据雷诺数的大小，流体可以分为层流和湍流两种情况：
1. 层流（Laminar flow）：当雷诺数Re较小（通常小于2000）时，流体分层流动，流线平行且稳定，粘性力起主要作用。

层流的特点是流动平稳，无乱流、涡旋和混合现象，粘性损失小，能量损失少。

2. 湍流（Turbulent flow）：当雷诺数Re较大（通常大于4000）时，流体流动变得混乱，流线交错交织，粘性力相对较小，惯性力主导。

湍流的特点是流动不稳定，存在乱流、涡旋和混合现象，粘性损失大，能量损失多。

在雷诺数介于2000和4000之间时，流体的流动既可能是层流，也可能是湍流，这个过渡区域的流动称为过渡流动。

过渡流动的特点是既有层流的稳定性，也有湍流的混乱性，流动状态较为复杂。