第七章 垄断市场(剩余理论)
- 格式:ppt
- 大小:608.00 KB
- 文档页数:57


(竞争策略)完全垄断市场与垄断竞争市场第7章完全垄断市场与垄断竞争市场7.1 考点难点归纳7.1.1 提纲挈领条件需求曲线:右下方倾斜收益曲线完全垄断市场短期均衡:MR=SMC供给曲线:不存在具有规律性的供给曲线长期均衡:MR=SMC=LMC差别定价:一级、二级、三级边际成本定价法:P=MC平均成本定价法:P=AC自然垄断和政府管制双重定价法:类似价格歧视资本回报率管制条件右下方倾斜需求曲线垄断竞争市场d需求曲线与D需求曲线短期均衡:MR=SMC长期均衡:MR=LMC=SMC,AR=LAC=SAC7.1.2 内容提要一、完全垄断市场垄断市场是指整个行业中只有惟一的一个厂商的市场组织。
具体地说,垄断市场的条件主要有这样三点:第一,市场上只有惟一的一个厂商生产和销售商品;第二,该厂商生产和销售的商品没有任何相近的替代品;第三,其他任何厂商进入该行业都极为困难或不可能。
二、垄断厂商的需求曲线和收益曲线1.需求曲线垄断厂商所面临的需求曲线就是市场的需求曲线,它是一条向右下方倾斜的曲线,即垄断厂商的销售量和市场价格成反方向变动。
这条向右下方倾斜的需求曲线表示垄断厂商可以通过改变销售量来控制市场价格:以减少销售量来抬高价格,以增加销售量来降低价格。
2.收益曲线垄断厂商的收益曲线具有以下特征:第一,厂商的平均收益AR曲线与需求曲线d重叠,它们是同一条向右下方倾斜的曲线,这表示在每一个销售量上厂商的平均收益都等于商品的价格。
第二,厂商的边际收益MR曲线也是向右下方倾斜的,且位于平均收益AR曲线的下方,这表示在每一个销售量上厂商的边际收益都小于平均收益。
之所以MR<AR,是因为只要平均量下降,边际量就总是小于平均量。
第三,厂商的总收益TR曲线是先上升,达到最高点以后再下降。
因为在每一个销售量上的MR值都是相应的TR曲线的斜率,所以当MR值为正时,TR曲线的斜率为正,即TR曲线上升;当MR为负时,TR曲线的斜率为负,即TR曲线是下降的;当MR=0时,TR 曲线的斜率为零,即TR曲线达到极大值。
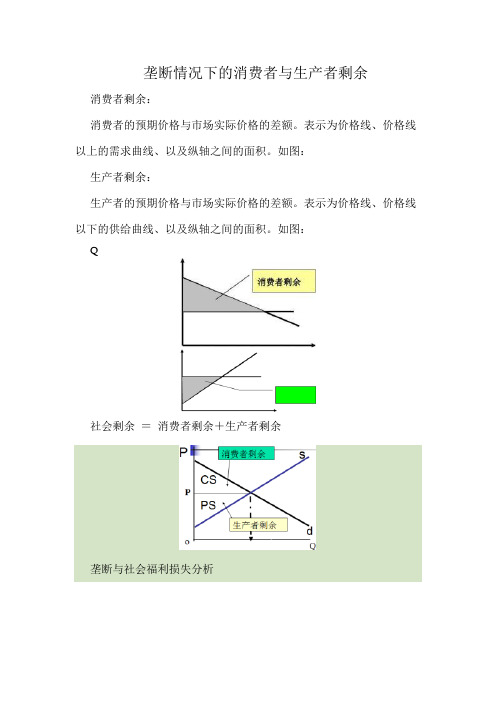
垄断情况下的消费者与生产者剩余消费者剩余:
消费者的预期价格与市场实际价格的差额。
表示为价格线、价格线以上的需求曲线、以及纵轴之间的面积。
如图:
生产者剩余:
生产者的预期价格与市场实际价格的差额。
表示为价格线、价格线以下的供给曲线、以及纵轴之间的面积。
如图:
Q
社会剩余=消费者剩余+生产者剩余
垄断与社会福利损失分析
消费者剩余是指供给需求图中位于均衡点之上与需求曲线之下的部分的面积,反映消费者本来有按比均衡价格更高的价格购买商品的意愿但是却以均衡价格购买到商品所导致消费者的盈余。
在有垄断势力存在的情况下,均衡产量减少,均衡价格提高。
消费者剩余的减少是新的均衡价格变化与
需求曲线构成的平行四边形的面积;生产者剩余增加仅是均衡价格变化形成的长方形的面积,仅仅是上述平行四边形的一部分,剩余的部分被看作社会福利的损失,也称纯损三角形,如下图阴影部分所示。
垄断会导致价格在比竞争更高的水平运行,给出了垄断势力的具体影
第2/3页响:MR=P+Q△P/△Q=P(1—1/£) (1.1)
式中MR为边际收益,P为价格,Q为产量,£为需求的价格弹性。
垄断会导致社会福利的损失是被广泛认可,供给需求曲线图上的纯损三角形被看作是垄断导致的社会福利损失。



第7章参考答案一、名词解释1.完全垄断是指没有近似替代品的产品或服务可以提供,且只有惟一的供给者的市场结构。
2.网络效应是指某种产品给消费者带来的价值或效用的大小与使用这种商品的消费者人数成正比例关系的现象。
3.成本加成定价法是这样一种定价的方法:企业不是根据MR和MC的比较来确定价格,而是根据所计算的产品平均成本,并在平均成本上加上一个固定的比例来进行定价。
4.价格歧视是指垄断者对于同样的产品收取不同价格的行为。
5.厂商的生产者剩余是所有生产单位的边际成本与产品的市场价格之间差额的总和,或者是指厂商在提供一定数量的某种产品时实际接受的总支付和意愿接受的最小总支付之间的差额。
6.一级价格歧视又称完全价格歧视,是指完全垄断厂商根据每一个消费者对买进每一单位产品意愿并能够支付的最高价格逐个确定产品卖价的行为。
7.二级价格歧视是指垄断厂商按不同的价格出售不同单位数量的同一商品,而对于每一个购买相同数量商品的消费者则收取相同的价格。
8.三级价格歧视是指垄断厂商在不同的市场对同一商品索取不同的价格,而在同一市场中则按相同的价格要价。
9.垄断利润是指垄断企业凭借对生产要素、技术专利、品牌等的排他性占有和市场势力所获得的高额利润。
垄断利润的获取一般是通过垄断价格实现的。
二、选择题三、判断题四、简答题1.假定该不完全竞争厂商的需求曲线为图7.2的 直线D ,则边际收益曲线也是一直线为图中的 MR ,则当产量为1q 时,P =P 1,1MR MR =; 当产量为2q 时,2P P =,2MR MR =,2111A A MR P =-,2122B B MR P =-,从图形直观可见,2121B B A A <。
这还可以证明如下:设需求函数为bQ a P -=,则bQ a MR 2-=,因此bQ bQ a bQ a MR P =+--=-2,b 是常数,故 bQ 随着产量 Q 增大而增大,即MR 与 P 的差距随着产量 q 的增加而越来越大。