数学建模章绍辉版作业

1. 对于不允许缺货的确定性静态库存模型，做灵敏度分析，讨论参数1p 、2p 和r 的微小变化对最优订货周期T *和最优订货量Q *的影响. 解答因为最优订货周期T *=111111(,)22p TS T p p p T***∂===∂22211(,)22p TS T p p p T***∂==-=-∂11(,)22TrS T r rr T***∂==-=-∂可见，1p 增加1%，T *增加0.5%；2p 或r 增加1%，T *都减少0.5%. 所以参数1p ，2p ，r 的微小变化对T *的影响是很小的.因为最优订货量Q *=，所以111111(,)22p QS Q p p p Q***∂===∂22211(,)22p QS Q p p p Q***∂==-=-∂11(,)22QrS Q r rr Q***∂===∂可见，1p 或r 增加1%，Q *都增加0.5%；2p 增加1%，Q *减少0.5%. 所以参数1p ，2p ，r 的微小变化对Q *的影响是很小的.2. 某配件厂为装配线生产若干种部件. 每次轮换生产不同的部件时，因更换设备要付生产准备费（与生产数量无关）. 同一部件的产量大于需求时，因积压资金、占用仓库要付库存费. 今已知某一部件的日需求量100件，生产准备费5000元，库存费每日每件1元. 如果生产能力远大于需求，并且不允许出现缺货，请制定最优生产计划.解答 依题意，每生产一次该种部件因更换设备而产生的生产准备费为15000p =元，每天每一个部件的库存费为21p =元，该种部件的日需求量为r =100件. 用EOQ 公式计算，得：最优生产周期10T *=天，每次生产1000Q *==件.3. 某商场把销售所剩的空纸皮箱压缩并打成包准备回收，每天能产生5包，在商场后院存放的费用是每包每天10元. 另一家公司负责将这些纸包运送到回收站，要收取固定费用1000元租装卸车，外加运输费每包100元. 请制定运送纸包到回收站的最优策略.解答 依题意，每运送一次纸包的固定费用为11000p =元，每天每一个纸包的库存费为210p =元，每天需要运送的纸包为r =5包. 用EOQ 公式计算，得：最优运输周期6T *=天，每次运送5630Q *=⨯=包.4. 某旅馆把毛巾送到外面的清洗店去洗. 旅馆每天有600条脏毛巾要洗，清洗店定期上门来收取这些脏毛巾，并换成洗好的干净毛巾. 清洗店清洗毛巾的标准收费每条2元，但是如果旅馆一次给清洗店至少2500条毛巾，清洗店清洗毛巾的收费为每条1.9元. 清洗店每一次取送服务都要收取上门费250元. 旅馆存放脏毛巾的费用是每天每条0.1元. 旅店应该如何使用的清洗店的取送服务呢？解答 依题意，清洗店每一次取送服务固定收取上门费1250p =元，旅馆存放脏毛巾每天每条的费用是20.1p =元，每天需要洗的脏毛巾数目为r =600条. 记旅馆每次给清洗店清洗的脏毛巾数目为Q 条，则清洗店清洗毛巾的价格（元/条）为：100022 , 25001.9, 2500p Q p p Q =<⎧=⎨=≥⎩如果2500Q≥，则取送服务的周期5TQ r =≥天. 因此，每天的总费用为11201022+, 1,2,3,42+, 52p p rT p r T T C p p rT p r T T ⎧+=⎪⎪=⎨⎪+≥⎪⎩ 用列表法及图示法，解得：每5天使用一次清洗店的取送服务，每天平均费用为1340元，达到最小值.MATLAB 脚本：p01=2; p02=1.9; p1=250; p2=0.1; r=600;f1=@(t)p01*r+p1./t+p2*r*t/2; f2=@(t)p02*r+p1./t+p2*r*t/2; c=[f1(1:4),f2(5:10)]fplot(f1,[1,4],'k'), hold onfplot(f1,[4,10],'k:'), fplot(f2,[1,5],'k:'), fplot(f2,[5,10],'k') plot(c,'ko'), hold off, axis([0,11,1300,1550])text(1.3,1450,'p_0=2元'), text(1.8,1340,'p_0=1.9元')xlabel('取送服务的周期（天）'), ylabel('每天的总费用（元）')计算结果为： c =Columns 1 through 51480 1385 1373.3 1382.5 1340 Columns 6 through 101361.7 1385.7 1411.3 1437.8 146501234567891011取送服务的周期（天）每天的总费用（元）。

数学建模课后作业第七章(总45页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第七章.多元分析实验基本实验1.线性回归；解：由题可以得出如下的R程序：> X1<-c, , , , , , , , , , 239)> X2<-c, , , , , , , , , ,> X3<-c, , , , , , , , , ,> Y<-c, , 19, , , , , ,, ,>> <-lm(Y ~ X1+X2+X3)> summary运行后可以得知；Call:lm(formula = Y ~ X1 + X2 + X3)Residuals:Min 1Q Median 3Q MaxCoefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) ***X1X2 ***X3 *---S ignif. codes: 0 ‘***’ ‘**’ ‘*’ ‘.’ ‘ ’ 1Residual standard error: on 7 degrees of freedomMultiple R-squared: , Adjusted R-squared:F-statistic: on 3 and 7 DF, p-value:则可以得出Y关于X1、X2、X3的线性回归方程；Y= X2+由上述的结果可以得知方程的常量与X2显著性为***表示十分的显著，X3显著性为*表示显著，而X2为不显著。

（2）由（1）中的数据可以得知新的分析函数anovaR程序如下：X1<-c, , , , , , , , , , 239)X2<-c, , , , , , , , , ,X3<-c, , , , , , , , , ,Y<-c, , 19, , , , , ,, ,<-lm(Y ~ X1+X2+X3, data=blood)summaryanova运行后可以得出：Min 1Q Median 3Q MaxCoefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) ***X1X2 ***X3 *---Signif. codes: 0 ‘***’ ‘**’ ‘*’ ‘.’ ‘ ’ 1Residual standard error: on 7 degrees of freedomMultiple R-squared: , Adjusted R-squared:F-statistic: on 3 and 7 DF, p-value:>> anovaAnalysis of Variance TableResponse: YDf Sum Sq Mean Sq F value Pr(>F)X1 1 ***X2 1 ***X3 1 *Residuals 7---Signif. codes: 0 ‘***’ ‘**’ ‘*’ ‘.’由此结果可以看出X1、X2、X3均能通过显著性检验，所以选择全部变量作回归方程是十分合理的。

第三章10.考虑3.4.3小节的“人口预报”案例，用前差公式计算美国人口的年增长率r k 与美国人口的数量x k 成二次函数关系，即21-10k k k k k kx x r ax bx c x +==++，k=1,2,…通过Matlab 编程并代入实际数据拟合出二项式的系数，代码如下：fun=@(a,x)a(1).*x.^2+a(2).*x+a(3);x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,... 92,106.5,123.2,131.7,150.7,179.3,204,226.5,251.4,281.4]; r=(x(2:22)-x(1:21))./(10.*x(1:21)); a=polyfit(x(1:21),r,2)输出结果为 a=7.0393e-07 -2.7030e-04 3.6840e-02即a=7.0393⨯10-7b=-2.7030⨯10-4c=3.6840⨯10-2则该假设模型为21-10()k k k k k x x x ax bx c +=++，k=1,2,…即3211010(101)k k k k x ax bx c x +=+++，k=1,2,…代入a,b,c 的值得734217.039310 2.703010 1.3684k k k k x x x x --+=⨯⨯-⨯⨯+，k=1,2,…利用Matlab 统计工具箱的非线性拟合函数nlinfit 计算参数，代码如下： M 文件fun.mfunction y=fun(a,x) SizeX=size(x); y=zeros(SizeX); y(1)=a(4);for i=2:SizeX(2)y(i)=a(1).*y(i-1).^3+a(2).*y(i-1).^2+a(3).*y(i-1);end脚本t=1790:10:2000;x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,...92,106.5,123.2,131.7,150.7,179.3,204,226.5,251.4,281.4];[b1,resd1]=nlinfit(t,x,@ fun,[7.0393e-7 -2.7030e-4 1.3684 3.9])sse1=sum(resd1.^2)x1=fun(b1,[t,2010,2020])(x1(23:24)-x1(22:23))./x1(22:23)./10.*100subplot(2,1,1);plot(t,x,'k*',t,x1(1:end-2),'ks',[2010 2020],x1(end-1:end),'kp');axis([1780,2030,0,350]);legend('统计值','模拟值','预测值',2);xlabel('年份');ylabel('人口数量x_k（百万）');title('非线性拟合美国人口增长效果图');subplot(2,1,2);plot(t,resd1,'k.',[1780 2030],[0 0],'k');axis([1780,2030,-10,10]);xlabel('年份');ylabel('模拟误差');title('非线性拟合美国人口增长模拟误差图');输出结果b1 =5.2615e-06 -0.0021 1.3239 4.9976resd1 =Columns 1 through 7-1.0976 -1.2651 -1.4034 -1.6394 -1.7244 -1.8325 -1.1541 Columns 8 through 140.3169 -0.6966 1.0726 2.2642 2.2108 3.5401 2.0489 Columns 15 through 211.6519 -7.8844 -7.8103 0.8436 4.1938 3.1885 1.0698 Column 22-1.9798sse1 =203.0297 x1 =Columns 1 through 74.9976 6.5651 8.6034 11.2394 14.6244 18.9325 24.3541 Columns 8 through 1431.0831 39.2966 49.1274 60.6358 73.7892 88.4599 104.4511 Columns 15 through 21121.5481 139.5844 158.5103 178.4564 199.8062 223.3115 250.3302 Columns 22 through 24 283.3798 327.5773 395.0407 ans =1.55972.0595即计算结果为63321 5.261510 2.110 1.3239k k k k x x x x --+=⨯⨯-⨯⨯+，且x 1=4.9976误差平方和为203.0297，预测2010年美国人口为327.5773百万，2020年美国人口为395.0407百万，经过计算得知预测2000年至2010年和2010年至2020年的年增长率分别为1.5597%和2.0595%，计算结果以及模拟效果图和模拟误差图表明（1）模拟效果基本令人满意，本模型能够很好地模拟1790年至2000年美国人口的演变过程，误差平方和不算大；（2）预测值基本合理，可能偏高，按照美国最近几十年的人口统计数据，一般推断未来20年美国人口增长率大约是1%，甚至更低，该模型得到的2000年的模拟值比实际值大 1.9798百万，预测2000年至2020年的年增长率约为 1.8096%，所以该模型对2010年和2020年的人口预报有可能偏高了一点。

第二章 习题二1.（1）按照“两秒准则”表明前后车距与车速成正比，这和“一车长度准则”是类似的。

在2.2节的基础上引入下面的符号: D ～前后车距（m ） v ～车速（m/s ）K ～按照“两秒准则”，D 与v 之间的比例系数（s ）,在“两秒准则”中，K=2 于是“两秒准则”的数学模型为（2）D K v K =⨯=而刹车距离的数学模型为212d kv k v =+ 要考虑“两秒准则”是否安全，即要比较D 与d 的大小212d D kv k v K v -=+-⨯（1） 代入k 1=0.75v ，k 2=0.082678，K=2，所以当d>D ，即刹车距离的理论大于前后车距时，认为不够安全；当d<D ，即刹车距离的理论小于前后车距时，认为足够安全。

计算得到当速度超过15.12 m/s 时，“两秒准则”就不安全了，也就是说“两秒准则”适用于车速不是很快的情况。

另外，还可以通过绘图直观解释为什么“两秒准则”不够安全，用以下程序把刹车距离实测数据与“两秒准则”都画在同一幅图中：v=(20:5:80).*0.44704;d2=[18,25,36,47,64,82,105,132,162,196,237,283,334 22,31,45,58,80,103,131,165,202,245,295,353,41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376]; d2=0.3048.*d2;k1=0.75; k2=0.082678; K=2; d1=[v;v;v].*k1;d=d1+d2;plot([0,40],[0,K*40],'k')hold onplot(0:40,polyval([k2,k1,0],0:40),':k')plot([v;v;v],d,'ok')title('比较刹车距离实测数据、理论值和两秒准则')legend('两秒准则','刹车距离理论值',...'刹车距离的最小值、平均值和最大值',2)xlabel('车速v（m/s）')ylabel('距离（m）')hold off（2）“两秒准则”的不安全性在于，其刹车距离随着车速增长的速度赶不上理论刹车距离的增长速度，为此我们提出一个“t秒准则”，通过不断增加t的值使得刹车距离总是大于理论刹车距离。

数学建模章绍辉版作业 Last revised by LE LE in 2021第四章作业第二题：针对严重的交通情况，国家质量监督检验检疫局发布的国家标准，车辆驾驶人员血液中的酒精含量大于或等于20mg/100ml,小于80mg/100ml 为饮酒驾车，血液中的酒精含量大于或等于80mg/100ml 的为醉酒驾车。

下面分别考虑大李在很短时间内和较长时间内（如2个小时）喝了三瓶啤酒，多长时间内驾车就会违反新的国家标准。

1、 问题假设大李在短时间内喝下三瓶啤酒后，酒精先从吸收室（肠胃）吸收进中心室（血液和体液），然后从中心室向体外排除，忽略喝酒的时间，根据生理学知识，假设（1） 吸收室在初始时刻t=0时，酒精量立即为032D;在任意时刻，酒精从吸收室吸收进中心室的速率（吸收室在单位时间内酒精含量的减少量）与吸收室的酒精含量成正比，比例系数为1k ；（2） 中心室的容积V 保持不变；在初始时刻t=0时，中心室的酒精含量为0；在任意时刻，酒精从中心室向体外排除的速率（中心室在单位时间内酒精含量的减少量）与中心室的酒精含量成正比，比例系数为2k ；（3） 在大李适度饮酒没有酒精中毒的前提下，假设1k 和2k 都是常量，与饮酒量无关。

2、 符号说明酒精量是指纯酒精的质量，单位是毫克；酒精含量是指纯酒精的浓度，单位是毫克/百毫升； ~t 时刻（小时）；()~x t 在时刻t 吸收室（肠胃）内的酒精量（毫克）；0~D 两瓶酒的酒精量（毫克）；(t)~c 在时刻t 吸收室（血液和体液）的酒精含量（毫克/百毫升）； 2()~c t 在时刻t 中心室（血液和体液）的酒精含量（毫克/百毫升）；~V 中心室的容积（百毫升）；1~k 酒精从吸收室吸收进中心室的速率系数（假设其为常数）；2~k 酒精从中心室向体外排除的速率系数（假设其为常数）；3~k 在短时间喝下三瓶酒的假设下是指短时间喝下的三瓶酒的酒精总量除以中心室体积，即03/2D V ；而在较长时间内（2小时内）喝下三瓶酒的假设下就特指03/4D V . 3、 模型建立和求解（1） 酒是在很短时间内喝的：记喝酒时刻为0t =（小时），设(0)0c =，可用()2113212()k t k t k k c t e e k k --=--来计算血液中的酒精含量，此时12k k 、为假设中所示的常数，而033155.792D k V ⎛⎫== ⎪⎝⎭.下面用MATLAB 程序画图展示血液中酒精含量随时间变化并且利用fzero 函数和fminbnd 函数来得到饮酒驾车醉酒驾车对应的时间段，以及血液中酒精含量最高的时刻。

甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组 甲组
学校名称 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 中山大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学 华南理工大学
省赛成绩 3 3 3 成功参赛奖 2 成功参赛奖 2 2 成功参赛奖 成功参赛奖 2 2 1 成功参赛奖 2 成功参赛奖 3 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 3 3 成功参赛奖 成功参赛奖 成功参赛奖 成功参赛奖 1 成功参赛奖 3 3 成功参赛奖 1 3 成功参赛奖 3 2 2 1 3 1 成功参赛奖 1 成功参赛奖 3 2 3 2 3 3 1 成功参赛奖 成功参赛奖
于金杨 罗剑平 辜质敏 郭浩升 欧嘉权 纪晓燕 戴育卿 黄海波 甘若迅 苏美婷 赵丽娜 陈其龙 毕瀛 谢灵玉 赵辛 张智峰 陈真佳 陈敏旋 邓小玲 何娇 张天松 姚尚君 顾龙 陈荣贵 赵必胜 曾一平 曾俊杰 王蓉 丘赟立 郑旭洲 邝永峰 李振昌 苏汉龙 程镇森 徐晓鑫 杨洁 吴劲良 黄成强 方楚逢 付神贺 黄健聪 蓝江林 于超凡 张龙光 唐南军 林兴荣 胡奕荣 王国恩 梁坚强 苏艺胜 钟顺杰 廖林文 唐光灿 黄晓敏 陈成 方菊纯

中心极限定理：当 n 时，随机变量


X 1 X 2 X n nP nP(1 P)
的分布趋向于标准正态分布 （也就是说， 当 n 充分大的时候， 随机变量 ( X1 X 2 X n ) n 的分布近似于均值为 P、方差 为 P(1 P) n 的正态分布）. 用循环语句实现以下计算：考虑试验次数 n=100、400、y Nhomakorabea0
0.1
0.2
0.3
0.4
0.5 x
0.6
0.7
0.8
0.9
1
3. 两个人玩双骰子游戏，一个人掷骰子，另一个人打赌 掷骰子者不能掷出所需点数，输赢的规则如下：如果第一次 掷出 3 或 11 点，打赌者赢；如果第一次掷出 2、7 或 12 点， 打赌者输；如果第一次掷出 4,5,6,8,9 或 10 点，记住这个点 数， 继续掷骰子， 如果不能在掷出 7 点之前再次掷出该点数， 则打赌者赢. 请模拟双骰子游戏，要求写出算法和程序，估 计打赌者赢的概率. 你能从理论上计算出打赌者赢的精确概 率吗？请问随着试验次数的增加，这些概率收敛吗？ 解答 （一）算法 输入 模拟试验的次数 n； 输出 打赌者赢的概率 p. 第 1 步 初始化计数器 k=0； 第 2 步 对 i=1,2,…,n，循环进行第 3～7 步； 第 3 步 产生两个在 1～6 这 6 个整数中机会均等地取 值的随机数， 并把这两个随机数之和赋值给 x； 第 4 步 如果 x 是 3 或 11，那么 k 加 1，进入下一步循 环；否则，做第 5 步； 第 5 步 如果 x 不是 2、7 和 12，那么做第 6～8 步；否 则，直接进入下一步循环； 第 6 步 产生两个在 1～6 这 6 个整数中机会均等地取 值的随机数， 并把这两个随机数之和赋值给 y； 第 7 步 如果 y 不等于 x，也不等于 7，重复第 6 步所 做的； 第 8 步 如果 y 等于 7，那么 k 加 1，进入下一步循环； 否则，直接进入下一步循环； 第 9 步 计算概率 p=k./n .

张明星 姜英琼 黄志祥 周玉兰 要尉鹏 郭强辉 刘挺 李亮 林波 陈芳 徐庆新 江浩 杨涛 王瑛 刘伟 刘超慧 覃健 赵亮 程亮 杨飞锋 黄华基 李玉珍 李蓉 唐卓
陈明 黄静波 陈明生 李德 王艳辉 李胜梅 彭张节 苗宇 张晖 黄厚旗 朱亚红 陈璐 孙晓 伍微 陈爽 马熠 曾艳 方程 张丽强 徐哲晟 郑顺洪 赵大 李刚 文家新
翟冰洁 林镇伟 彭志生 张凯 李小金
李峰 廖敬青 梁祖红 郑泽伟 王茜
唐海伟 梁 斌 杨春传
秦 宇 曾 毅 李作新 许 彦 郭研研 冷建全
肖伟 魏巍 雷磊 戴帅湘
杨威 弓晨 王伟民 武胜波
涂寅辉 李艳 杜雄 刘娟
吴华玉 叶 飞 任 凯 张 杨 王慧欣 孟 超 管 立 俞一凡 高 芸
宫凤强 谷霖 李振国 谢国亮
刘则毅 李宝毅 韩家楠 教练组 郝培锋 郝培锋 薛定宇 韩莉 教师组 丁永生 杜育根 数模教练组 数模教练组 数模教练组 张耀 王兵团 邢启江 王鸣 指导小组
贺祖国 贺祖国 贺祖国 贺祖国 贺祖国 汪飞星 汪飞星 指导小组 邹述超 舒慕增 马邦勤 赵凌 数模组 欧志英等 霍海峰等 张民悦等 孙海珍 宁如云等 刘启明等 数模组 数模组 秦衍 陈荣军 梅银珍
东南大学
55
东南大学
56
东南大学
57
兰州铁道学院
58
北方交通大学
59
北京大学
60
北京大学
61
北京工业大学
62
北京邮电大学
63
北京邮电大学
64
北京邮电大学
65
北京邮电大学
66
北京邮电大学
67
北京科技大学
68
北京科技大学
69
北京理工大学

习题3参考解答4. 某成功人士向学院捐献20万元设立优秀本科生奖学金，学院领导打算将这笔捐款以整存整取一年定期的形式存入银行，第二年一到期就支取，取出一部分作为当年的奖学金，剩下的继续以整存整取一年定期的形式存入银行……请你研究这个问题，并向学院领导写一份报告.解答 假设整存整取一年定期的年利率保持不变，记为r ，假设一到期就支取，取出b 元作为当年的奖学金，剩下的继续以整存整取一年定期的形式存入银行……记捐款存入银行之后第k 年一年定期到期日奖学金捐款账户余额为k x 万元，0x =20万元，则列式得1(1), 0,1,2,k k x r x b k +=+-=⋅⋅⋅.其解为()0(1), 0,1,2,k k x r x b r b r k =+-+=⋅⋅⋅ 平衡点为x b r =.因为r >0，所以如果0x b r >，即00b rx <<，k x 就会单调增加趋于无穷大，并且增加得越来越快；如果0x b r <，即0b rx >，k x 就会单调衰减（到零为止），并且减少得越来越快；如果0x b r =，即0b rx =，k x 就会保持不变，即0k x x ≡.如果取r ＝0.025，则b 的临界值为00.025200.5rx =⨯=（万元）. 进一步，可编程分别计算当b =0.4、0.5、0.6、1以及2万元时账户总额k x 的具体变化过程，并绘图.程序：r=0.025; x=[20,20,20,20,20];b=[.4,.5,.6,1,2]; n=20;for k=1:nx(k+1,:)=x(k,:).*(1+r)-b;endplot(0:n,x(:,1),'k.',0:n,x(:,2),'kx',...0:n,x(:,3),'k^',0:n,x(:,4),'ks',0:n,x(:,5),'kp')axis([-1,n+1,0,25])legend('每年用0.4万元','每年用0.5万元',...'每年用0.6万元','每年用1万元','每年用2万元',3)title('奖学金捐款账户余额的演变，年利率2.5%')xlabel('第 k 年'), ylabel('账户余额（万元）')绘得的图形：第 k 年账户余额（万元）奖学金捐款账户余额的演变，年利率2.5%（略去给学院领导的报告，该报告要用非数学语言陈述上述分析）5. 有一位老人60岁时将养老金10万元以整存零取方式（指本金一次存入，分次支取本金的一种储蓄）存入，从第一个月开始每月支取1000元，银行每月初按月利率0.3%把上月结余额孳生的利息自动存入养老金. 请你计算老人多少岁时将把养老金用完？如果想用到80岁，问60岁时应存入多少钱？解答 假设月利率保持不变，记为r ，记养老金存入银行之后第k 月末账户总额为k x 元，从第一个月开始每月支取b 元. 则列式得1(1), 0,1,2,k k x r x b k +=+-=⋅⋅⋅.解得()0(1), 0,1,2,k k x r x b r b r k =+-+=⋅⋅⋅依题意有r =0.003，b =1000，0x =100000. 因为r >0，且0x b r <，所以k x 就会单调衰减（到零为止），并且减少得越来越快；若要0k x ≤，可以解得只需要()()()0log log log 1b r b r x k r --≥+ 所以令()(){}()0log log log 1K b r b r x r ⎡⎤=--+⎢⎥（上取整），则养老金在第K 个月恰好用完. 把具体数据代入，执行以下程序，算得K =120，即10万养老金恰好10年用：x=100000; r=0.003; b=1000;K=ceil((log(b/r)-log(b/r-x))/log(1+r))也可以用条件循环语句按差分方程迭代计算，直到0k x ≤停止. 程序如下：x=100000; r=0.003; b=1000; n=0;while x(n+1)>0n=n+1;x(n+1)=(1+r).*x(n)-b;endn如果养老金想用到80岁，即240x =0，那么()()()2400240111709081b r x r r +-==+.。

序号
报名号
1
20171900100
2
肖文熙
2
20171900100
5
梁智鹏
3
20171900102
4
吕坤升
Байду номын сангаас
4
20171900106
1
张丰学
5
20171900106
8
廖晨阳
6 20171900105 王昱
本科组一等奖
获奖选手
所在院校
梅洁妍 潘珏
中山大学
梁昊
祝俊浩 中山大学
陈卓晖 周斐漩 中山大学
钟钧豪 杨斌斌 中山大学
7
孙健
21
20171900117
2
黄思集
22
20171900117
5
沙钧
23
20171900118
5
王翔宇
24
20171900122
0
陈星月
25
20171900202
5
房依璐
26
20171900206
6
马一宁
27 20171900213 张浩健
获奖选手
刘俊材 史春霓
王江寅 谭有翀
陈晓聪 江俊锋
彭劲
辛弘
2017年全国大学生数学建模竞赛广东省分赛获奖名单（初稿）
根据《广东省教育厅关于做好 2017年广东省高校大学生学科竞赛工作的通知》（粤 教高函〔2017〕39号）安排，省教育厅委托中山大学组织开展 2017年全国大学生数学 建模竞赛广东省分赛。竞赛于 9月 14日至 9月 17日分本科和高职高专两个组别进行， 全省共有 88所高校 2252支代表队伍共计 6749位选手报名参赛。

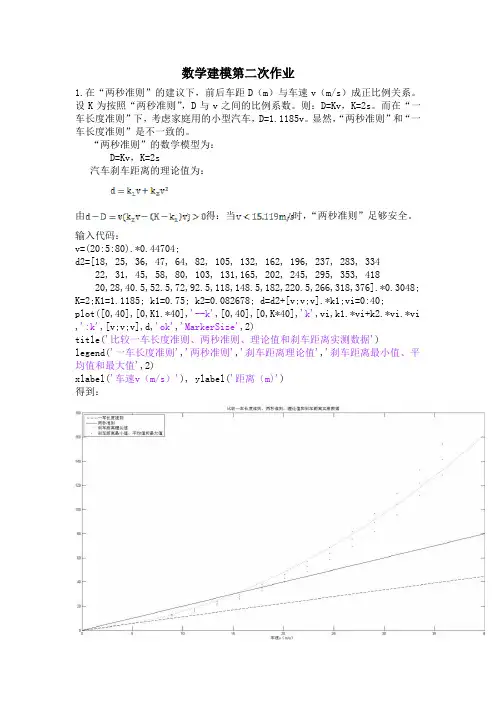
数学建模第二次作业1.在“两秒准则”的建议下，前后车距D（m）与车速v（m/s）成正比例关系。

设K为按照“两秒准则”，D与v之间的比例系数。

则：D=Kv，K=2s。

而在“一车长度准则”下，考虑家庭用的小型汽车，D=1.1185v。

显然，“两秒准则”和“一车长度准则”是不一致的。

“两秒准则”的数学模型为：D=Kv，K=2s汽车刹车距离的理论值为：由得：当时，“两秒准则”足够安全。

输入代码：v=(20:5:80).*0.44704;d2=[18, 25, 36, 47, 64, 82, 105, 132, 162, 196, 237, 283, 33422, 31, 45, 58, 80, 103, 131,165, 202, 245, 295, 353, 41820,28,40.5,52.5,72,92.5,118,148.5,182,220.5,266,318,376].*0.3048; K=2;K1=1.1185; k1=0.75; k2=0.082678; d=d2+[v;v;v].*k1;vi=0:40;plot([0,40],[0,K1.*40],'--k',[0,40],[0,K*40],'k',vi,k1.*vi+k2.*vi.*vi,':k',[v;v;v],d,'ok','MarkerSize',2)title('比较一车长度准则、两秒准则、理论值和刹车距离实测数据')legend('一车长度准则','两秒准则','刹车距离理论值','刹车距离最小值、平均值和最大值',2)xlabel('车速v（m/s）'), ylabel('距离（m)')得到：由上图也可以看出当车速超过15米每秒时，“两秒准则”不安全。

一等奖 22308
一等奖 20506
一等奖 22082
一等奖 20879
一等奖 22480
二等奖 20382
二等奖 20749
二等奖 21061
二等奖 21593
二等奖 21691
二等奖 22266
二等奖 22398
二等奖 22532
二等奖 22791
二等奖 18193
二等奖 18560
控制号 18252
20615
二等奖 22496 章绍辉
二等奖 23225 章绍辉
二等奖 23230 章绍辉
二等奖 17949 教练组
二等奖
20557
二等奖 20839 教练组
二等奖 21410 教练组
成功参赛 17929
成功参赛 23401
成功参赛 18227 李湖南
成功参赛 21730 李湖南 9 2009 数金融
队员三 黄培鸿 2010 计算机 孙淼 2010 计算机 林俊成 2009 物电 区诵宜 2011 心理 张树邦 2011 数勷勤 张俊仪 2010 光电 吴锐欢 2010 光电 吴欣 2010 数统计 黄迪 2011 物电 彭冬雨 2011 理综一 郑嘉鹏 2010 物电 尹李明 2011 物勷勤 陈祖杰 2010 物电 程志南 2010 计算机 关恩 2010 数师 史华杰 2010 数师 刘梓煊 2011 光电 萧筠儒 2011 理综一
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，通系电1，力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配，机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2，下卷而高总且中体可资配保料置障试时2卷，32调需3各控要类试在管验最路；大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷，下安要与全加过，强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中；中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整，理核或高对者中定对资值某料，些试审异卷核常弯与高扁校中度对资固图料定纸试盒，卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置，接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资，，料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气，敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术，技线以来术槽及避、系免管统不架启必等动要多方高项案中方；资式对料，整试为套卷解启突决动然高过停中程机语中。文高因电中此气资，课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试，且技合进术理行，利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。：对对在于于分调差线试动盒过保处程护，中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技，，术应作是采为指用调发金试电属人机隔员一板，变进需压行要器隔在组开事在处前发理掌生；握内同图部一纸故线资障槽料时内、，设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷，试切线验除缆报从敷告而设与采完相用毕关高，技中要术资进资料行料试检，卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

第五章作业第一题：（1） 第三种边界条件第三种边界条件要求给定三次样条s(x)在区间[x 0,x n ]的左右端点的一阶导数0'(x )S 和'(x )a S 。

我们参考了例5.1.4在210页计算出了左右端点的一阶导数，其中0'(x )S = -3.3667、'(x )a S = 2.3333MATLAB 程序如下：x=[0,1,3,6,8,9];y=[-3.3667,3,1,2,0,2,4,2.33333];pp=csape(x,y,'complete')pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4);d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3);d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2);d3s=@(t,tj,c)6.*c(1).*ones(size(t));for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c);v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c);plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold onendtitle('第三种边界条件及其一、二、三阶导函数的图像')legend('三次样条（第三种边界条件）','样条的一阶导函数','样条的二阶导函数','样条的三阶导函数')plot([0,1,3,6,8,9],[3,1,2,0,2,4],'ko'),hold off运行结果为：pp =form: 'pp'breaks: [0 1 3 6 8 9]coefs: [5x4 double]pieces: 5order: 4dim: 1ans =-0.0389 1.4056 -3.3667 3.0000-0.3514 1.2890 -0.6722 1.00000.1696 -0.8197 0.2664 2.0000-0.0848 0.7064 -0.0736 00.0678 0.1977 1.7345 2.0000所绘制的图形如下：0123456789第三种边界条件及其一、二、三阶导函数的图像结果说明：计算结果说明该三次样条的分段多项式为： S(x)= 32323232320.0389 1.4056 3.36673,010.3514(x 1) 1.289(x 1)0.6722(x 1)1,130.1696(x 3)0.8197(x 3)0.2664(x 3)2,360.0848(x 6)0.7064(x 6)0.0736(x 6),6x 80.0678(x 8)0.1977(x 8) 1.7345x x x x x x -+-+≤≤--+---+≤≤---+-+≤≤--+---≤≤-+-+(x 8)2,8x 9-+≤≤执行以下命令可以验算该三次样条在区间[0，9]的左端点x=0和右端点x=9的一阶导数分别为-3.3667和2.3333：在MATLAB 的command window 运行：[1.*pp.coefs(1,3),d1s(9,8,pp.coefs(5,:))] 运行结果为：ans =-3.3667 2.3333（2） 第四种边界条件第四种边界条件要求给定三次样条s(x)在区间[x 0,x n ]的左右端点的二阶导数0''(x )s 和''(x )n s 。

第五章1.（3）给定样条在左右端点的一阶导数的三次样条Matlab代码如下：M文件fun1_1.mx=[0,1,3,6,8,9];y=[-1,3,1,2,0,2,4,1];pp=csape(x,y,'complete'),pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4);d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3);d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2);d3s=@(t,tj,c)6.*c(1).*ones(size(t));for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c);v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c);plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold onendlegend('三次样条（给定样条在左右端点的一阶导数）','样条的一阶导函数',...'样条的二阶导函数','样条的三阶导函数');y1=[3,1,2,0,2,4];plot(x,y1,'ko'),hold off输出图像输出结果pp =form: 'pp'breaks: [0 1 3 6 8 9]coefs: [5x4 double]pieces: 5order: 4dim: 1ans =1.4903 -2.4903 -1.00003.0000-0.4879 1.9807 -1.5097 1.00000.1795 -0.9469 0.5580 2.0000-0.0157 0.6691 -0.2754 0-0.7874 0.5749 2.2126 2.0000计算结果说明该三次样条的分段多项式形式为32323232321.49032.490330.4879(1) 1.9807(1) 1.5097(1)10.1795(3)0.9469(3)0.5580(3)20.0157(6)0.6691(6)0.2754(6)0.7874(8)0.5749(8) 2.212,01,13()66,36,8x x x x x x x x x x x x x s x x x x x x --+--+---+---+-+--+-----+≤≤≤≤-+=≤≤≤≤,89(8)2x x ⎧⎪⎪⎪⎨⎪⎪⎪≤≤⎩-+ （4）给定样条在左右端点的二阶导数的三次样条 Matlab 代码如下： M 文件fun1_2.mx=[0,1,3,6,8,9];y=[0,3,1,2,0,2,4,0]; pp=csape(x,y,'second'),pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4); d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3); d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2); d3s=@(t,tj,c)6.*c(1).*ones(size(t)); for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c); v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c); plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold on endlegend('三次样条（给定样条在左右端点的二阶导数）','样条的一阶导函数',... '样条的二阶导函数','样条的三阶导函数'); y1=[3,1,2,0,2,4]; plot(x,y1,'ko'),hold off输出图像输出结果pp =form: 'pp'breaks: [0 1 3 6 8 9]coefs: [5x4 double]pieces: 5order: 4dim: 1ans =0.5134 0 -2.5134 3.0000-0.4018 1.5402 -0.9732 1.00000.1754 -0.8706 0.3661 2.0000-0.0741 0.7084 -0.1204 0 -0.0880 0.2639 1.8241 2.0000计算结果说明该三次样条的分段多项式形式为3323232320.5134 2.513430.4018(1) 1.5402(1)0.9732(1)10.1754(3)0,01,13().8706(3)0.3661(3)20.0741(6)0.7084(6)0.1204(6)0.0880(8)0.2639(8) 1.8241,36,6(8x x s x x x x x x x x x x x x x x x x x -+--+---+---+-+--+-----+-+≤≤≤≤=≤≤≤≤-,898)2x ⎧⎪⎪⎪⎨≤≤+⎪⎪⎪⎩ （5）按照非结点方法得到的三次样条 Matlab 代码如下： M 文件fun1_3.mx=[0,1,3,6,8,9];y=[3,1,2,0,2,4]; pp=csape(x,y,'not-a-knot'),pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4); d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3); d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2); d3s=@(t,tj,c)6.*c(1).*ones(size(t)); for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c); v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c); plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold on endlegend('三次样条（非结点方法）','样条的一阶导函数',... '样条的二阶导函数','样条的三阶导函数'); plot(x,y,'ko'),hold off输出图像输出结果pp =form: 'pp'breaks: [0 1 3 6 8 9]coefs: [5x4 double]pieces: 5order: 4dim: 1ans =-0.3240 2.1291 -3.8052 3.0000-0.3240 1.1573 -0.5188 1.00000.1633 -0.7864 0.2229 2.0000-0.0700 0.6833 -0.0866 0-0.0700 0.2633 1.8066 2.0000计算结果说明该三次样条的分段多项式形式为32323232320.3240 2.1291 3.805230.3240(1) 1.1573(1)0.5188(1)10.1633(3)0.7864(3)0.2229(3)20.0700(6)0.6833(6)0.0866(6)0.07,01,13(),36,600(8)0.2633(8)8x x s x x x x x x x x x x x x x x x x -++-+--+---+---+-+-≤≤≤≤=-+----+≤≤-≤≤-,81.8066(8)29x x ⎧⎪⎪⎪⎨⎪⎪⎪≤≤⎩+-+ （6）周期的三次样条 Matlab 代码如下： M 文件fun1_4.mx=[0,1,3,6,8,9];y=[3,1,2,0,2,4]; pp=csape(x,y,'periodic'),pp.coefss=@(t,tj,c)c(1).*(t-tj).^3+c(2).*(t-tj).^2+c(3).*(t-tj)+c(4); d1s=@(t,tj,c)3.*c(1).*(t-tj).^2+2.*c(2).*(t-tj)+c(3); d2s=@(t,tj,c)6.*c(1).*(t-tj)+2.*c(2); d3s=@(t,tj,c)6.*c(1).*ones(size(t)); for k=1:pp.piecesc=pp.coefs(k,:);u=x(k):.01:x(k+1);v=s(u,x(k),c); v1=d1s(u,x(k),c);v2=d2s(u,x(k),c);v3=d3s(u,x(k),c); plot(u,v,'k',u,v1,'k-.',u,v2,'k--',u,v3,'k:'),hold on endlegend('三次样条（周期的）','样条的一阶导函数',... '样条的二阶导函数','样条的三阶导函数'); plot(x,y,'ko'),hold off输出图像输出结果pp =form: 'pp'breaks: [0 1 3 6 8 9]coefs: [5x4 double]pieces: 5order: 4dim: 1ans =1.9961 -3.7833 -0.2127 3.0000-0.5296 2.2048 -1.7912 1.00000.1754 -0.9728 0.6728 2.00000.0537 0.6061 -0.4272 0-1.5706 0.9285 2.6421 2.0000计算结果说明该三次样条的分段多项式形式为32323232321.9961 3.78330.212730.5296(1) 2.2048(1) 1.7912(1)10.1754(3)0.9728(3)0.6728(3)20.0537(6)0.6061(6)0.4272(6)1.570,01,13(),36,686(8)0.9285(8)2x x x x x x x x x x x x x s x x x x x x --+--+---+---+-+-+-----+-≤≤≤≤=≤≤≤≤+,8.6421(8)92x x ⎧⎪⎪⎪⎨⎪⎪⎪≤≤⎩-+ 2.（1）多项式插值 Matlab 代码如下： M 文件polyinterp.mfunction yi=polyinterp(x,y,xi) n=length(x);m=length(xi); for k=1:m z=xi(k);s=0; for i=1:n p=1; for j=1:n if j~=ip=p*(z-x(j))/(x(i)-x(j)); end end s=p*y(i)+s; end yi(k)=s; endM 文件fun2_1.mx=[0,3,5,7,9,11,12,13,14,15];y=[0,1.8,2.2,2.7,3.0,3.1,2.9,2.5,2.0,1.6]; z=[0,1.2,1.7,2.0,2.1,2.0,1.8,1.2,1.0,1.6];xi=-1:.01:16;yi=zeros(size(xi));zi=zeros(size(xi)); figure(1) for k=1:10w=zeros(1,10);w(k)=w(k)+1; wi=polyinterp(x,w,xi); yi=yi+y(k).*wi;subplot(5,2,k),plot(x,w,'ko',xi,wi,'k'),axis([-1,16,-1,3]) end figure(2) for k=1:10w=zeros(1,10);w(k)=w(k)+1; wi=polyinterp(x,w,xi);zi=zi+z(k).*wi;subplot(5,2,k),plot(x,w,'ko',xi,wi,'k'),axis([-1,16,-1,3])endfigure(3)plot(x,y,'ko',xi,yi,'k'),hold onplot(x,z,'ko',xi,zi,'k'),hold offaxis([-1,16,-1,5])title('Lagrange插值多项式')gtext('L_16(x)=1.8*I_1+2.2*I_2+2.7*I_3+3*I_4+3.1*I_5+2.9*I_6+2.5*I_7+2*I_8+1.6*I_9'); gtext('R_16(x)=1.2*I_1+1.7*I_2+2.0*I_3+2.1*I_4+2*I_5+1.8*I_6+1.2*I_7+1*I_8+1.6*I_9');输出图像Figure 1Figure 2Figure 3由Figure 1和Figure 2可以看出多项式插值波动幅度过大，不能用来求截面面积。

1．（1） n=101;x1=linspace(-1,1,n); x2=linspace(-2,2,n);y1=[sqrt(1-x1.^2);-sqrt(1-x1.^2)];y2=[sqrt(4-x2.^2);-sqrt(4-x2.^2);sqrt(1-(x2.^2)/4);-sqrt(1-(x2.^2)/4)];plot(x1,y1) hold on; plot(x2,y2)title('椭圆x^2/4+y^2=1的内切圆和外切圆') axis equal-2.5-2-1.5-1-0.500.51 1.52 2.5-2-1.5-1-0.500.511.52椭圆x 2/4+y 2=1的内切圆和外切圆（2）x1=linspace(-2,2,101); x2=linspace(-2,8); axis equalplot(exp(x1),x1,x1,exp(x1),x2,x2)title('指数函数y=exp(x)和对数函数y=ln(x)关于y=x 对称')-2-112345678-2-1012345678指数函数y=exp(x)和对数函数y=ln(x)关于y=x 对称（3） hold onq=input('请输入一个正整数q;') for i=1:q for j=1:i if rem(j,i)plot(j/i,1/i) end end end0.10.20.30.40.50.60.70.80.9100.050.10.150.20.250.30.350.40.450.53．代码如下：n=input('请输入实验次数n=') k=0;for i=1:nx=ceil(rand*6)+ceil(rand*6); if x ==3|x==11 k=k+1; elseif x~=2&x~=7&x~=12y= ceil(rand*6)+ceil(rand*6); while y~=x&y~=7y=ceil(rand*6)+ceil(rand*6); end if y==7k=k+1; end end end从上表可看出打赌者赢的概率大约为。

f2=@(xb,t)(xb(1)).*exp(xb(2).*(t-1790)); xb0=[3.9 0.1]; xb=nlinfit(t,x,f2,xb0); x0=xb(1) r=xb(2) sseb=sum((x-f2(xb,t)).^2) %（iii) f3=@(xc,t)(xc(2)).*exp(xc(1).*(t-xc(3))); xc0=[0.1 3.9 1790]; xc=nlinfit(t,x,f3,xc0); t0=xc(3) x0=xc(2) r=xc(1) ssec=sum((x-f3(xc,t)).^2)
习题一
1. （1）Matlab命令：
hold on; x1=linspace(-1,1); y11=sqrt(1-x1.^2); y12=-sqrt(1-x1.^2); plot(x1,y11); plot(x1,y12); x2=linspace(-2,2); y21=sqrt(4-x2.^2); y22=-sqrt(4-x2.^2); plot(x2,y21); plot(x2,y22); x3=linspace(-2,2); y31=sqrt(1-x3.^2/4); y32=-sqrt(1-x3.^2/4); plot(x3,y31); plot(x3,y32);
plot(t,x,'+') xlabel('年份') ylabel('人口/百万') hold on plot(t,f2(xb,t),'ro') legend('实际值','拟合值',2) hold off
(2)对模型两边分别求对数： （1） 令，则方程（1）可化为（2）为一次线性模型，下面对方 程（2）进行线性拟合。 Matlab代码：

数学建模章绍辉答案【篇一：第三次数学建模作业】数科院105 刘镜韶 20102201092 数科院105 蔡秋荣 20102201166 数科院104 梁浩坤 201022011004、不妨令第k年取出奖学金后，继续存在银行的捐款余额为xk，且银行的整存整取的利率为r，奖学金的金额为d万元，则由已知可得：xk+1 =（1+r）xk－d 故：其解为数列：xk =(x0-d/r)+d/r,且x0=20万元；①奖学金金额d0.6万元，让存在银行的捐款余额每年逐步增加；②奖学金金额d=0.6万元，让存在银行的捐款余额每年保持不变；③奖学金金额d0.6万元，让存在银行的捐款余额每年逐步减少；故对于不同的情况，不妨通过编程对比xk的变化趋势；程序：n=20;r=[0.03,0.03,0.03];x=[20,20,20];d=[0.45,0.6,0.75]; fork=1:nx(k+1,:)=x(k,:).*(1+r)-d; enddisp(本金为20万时不同的奖学金下余额的变化)disp(年 0.45万元0.6万元0.75万元) disp([(0:n),x]);plot(0:n,x(:,1),k^,0:n,x(:,2),ko,0:n,x(:,3),kv) axis([-1,n+1,14,25]) legend(d=0.45,d=0.6,d=0.75,2)title(本金为20万时不同的奖学金下余额的变化) xlabel(第k年),ylabel(余额) 其命令窗口显示结果为：年 0.45万元0.6万元0.75万元 020.000020.000020.00001.000020.150020.000019.85002.000020.304520.000019.69553.000020.463620.000019.53644.000020.627520.000019.37255.000020.796420.000019.20366.000020.970320.000019.02977.000021.149420.000018.8506 8.000021.333920.000018.66619.000021.523920.000018.4761本金为20万时不同的奖学金下余额的变化10.000021.719620.000018.2804 11.000021.921220.000018.078812.000022.128820.000017.871213.000022.342720.000017.657314.000022.562920.000017.4371 15.000022.789820.000017.210216.000023.023520.000016.976517.000023.264220.000016.735818.000023.512220.000016.4878 19.000023.767520.000016.2325 第k年20.000024.030620.000015.9694当利率r=3%时，且以整存整取一年定期的形式来存入银行时；由上述图像可知：①奖学金金额d≤0.6万元时，可以永久持续下去，实现可持续发展，即用20万元本金所得的利息作为奖学金。