当前位置：文档之家 › 悬臂式挡土墙受力分析

悬臂式挡土墙受力分析

  • 格式：pdf
  • 大小：447.74 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

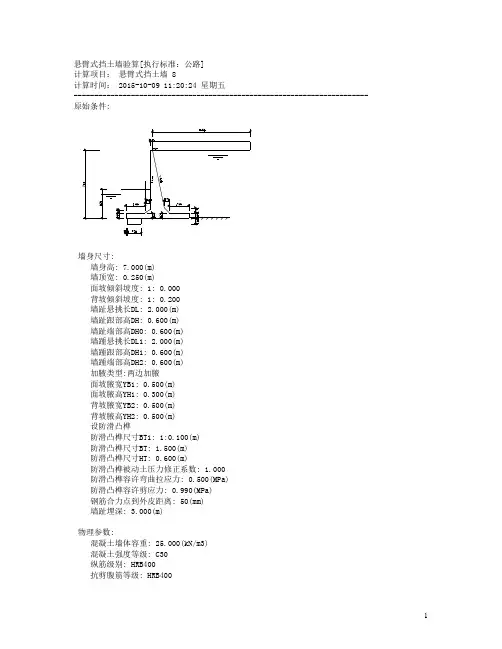
悬臂式挡土墙验算全解

悬臂式挡土墙验算全解

悬臂式挡土墙验算[执行标准：公路]计算项目：悬臂式挡土墙 8计算时间： 2015-10-09 11:20:24 星期五------------------------------------------------------------------------ 原始条件:墙身尺寸:墙身高: 7.000(m)墙顶宽: 0.250(m)面坡倾斜坡度: 1: 0.000背坡倾斜坡度: 1: 0.200墙趾悬挑长DL: 2.000(m)墙趾跟部高DH: 0.600(m)墙趾端部高DH0: 0.600(m)墙踵悬挑长DL1: 2.000(m)墙踵跟部高DH1: 0.600(m)墙踵端部高DH2: 0.600(m)加腋类型:两边加腋面坡腋宽YB1: 0.500(m)面坡腋高YH1: 0.300(m)背坡腋宽YB2: 0.500(m)背坡腋高YH2: 0.500(m)设防滑凸榫防滑凸榫尺寸BT1: 1:0.100(m)防滑凸榫尺寸BT: 1.500(m)防滑凸榫尺寸HT: 0.600(m)防滑凸榫被动土压力修正系数: 1.000防滑凸榫容许弯曲拉应力: 0.500(MPa)防滑凸榫容许剪应力: 0.990(MPa)钢筋合力点到外皮距离: 50(mm)墙趾埋深: 3.000(m)物理参数:混凝土墙体容重: 25.000(kN/m3)混凝土强度等级: C30纵筋级别: HRB400抗剪腹筋等级: HRB400裂缝计算钢筋直径: 18(mm)挡土墙类型: 浸水地区挡土墙墙后填土内摩擦角: 35.000(度)墙后填土粘聚力: 0.000(kPa)墙后填土容重: 19.000(kN/m3)墙背与墙后填土摩擦角: 17.500(度)地基土容重: 18.000(kN/m3)修正后地基土容许承载力: 232.000(kPa)地基土容许承载力提高系数:墙趾值提高系数: 1.200墙踵值提高系数: 1.300平均值提高系数: 1.000墙底摩擦系数: 0.300地基土类型: 土质地基地基土内摩擦角: 20.000(度)墙后填土浮容重: 9.000(kN/m3)地基浮力系数: 0.700土压力计算方法: 库仑坡线土柱:坡面线段数: 1折线序号水平投影长(m) 竖向投影长(m) 换算土柱数1 10.000 0.000 1第1个: 定位距离0.000(m) 挂车-80级(验算荷载)作用于墙上的附加外荷载数: 1 (作用点坐标相对于墙左上角点)荷载号 X Y P 作用角(m) (m) (kN) (度)1 -0.500 -5.167 100.000 270.000地面横坡角度: 0.000(度)墙顶标高: 0.000(m)挡墙内侧常年水位标高: -0.500(m)挡墙外侧常年水位标高: -4.500(m)浮力矩是否作为倾覆力矩加项: 是挡墙分段长度: 15.000(m)钢筋混凝土配筋计算依据:《混凝土结构设计规范》（GB 50010--2002）===================================================================== 第 1 种情况: 一般情况=============================================组合系数: 1.0001. 挡土墙结构重力分项系数 = 1.000 √2. 填土重力分项系数 = 1.000 √3. 填土侧压力分项系数 = 1.000 √4. 车辆荷载引起的土侧压力分项系数 = 1.000 √5. 计算水位的浮力分项系数 = 1.000 √6. 计算水位的静水压力分项系数 = 1.000 √7. 附加力分项系数 = 1.000 √=============================================[土压力计算] 计算高度为 7.000(m)处的库仑主动土压力无荷载时的破裂角 = 25.900(度)挂车-80级(验算荷载)路基面总宽= 10.000(m), 路肩宽=0.000(m) 安全距离=1.000(m)单车车辆外侧车轮中心到车辆边缘距离= 0.400(m), 车与车之间距离=0.600(m)经计算得，路面上横向可排列此种车辆 3列布置宽度= 7.079(m)布置宽度范围内车轮及轮重列表:第1列车:中点距全部破裂体轮号路边距离(m) 轮宽(m) 轮压(kN) 上轮压(kN)01 1.000 0.500 50.000 50.00002 1.900 0.500 50.000 50.00003 2.800 0.500 50.000 50.00004 3.700 0.500 50.000 50.00005 1.000 0.500 50.000 50.00006 1.900 0.500 50.000 50.00007 2.800 0.500 50.000 50.00008 3.700 0.500 50.000 50.00009 1.000 0.500 50.000 50.00010 1.900 0.500 50.000 50.00011 2.800 0.500 50.000 50.00012 3.700 0.500 50.000 50.00013 1.000 0.500 50.000 50.00014 1.900 0.500 50.000 50.00015 2.800 0.500 50.000 50.00016 3.700 0.500 50.000 50.000第2列车:中点距全部破裂体轮号路边距离(m) 轮宽(m) 轮压(kN) 上轮压(kN)01 5.100 0.500 50.000 50.00002 6.000 0.500 50.000 50.00003 6.900 0.500 50.000 42.90204 7.800 0.500 50.000 0.00005 5.100 0.500 50.000 50.00006 6.000 0.500 50.000 50.00007 6.900 0.500 50.000 42.90208 7.800 0.500 50.000 0.00009 5.100 0.500 50.000 50.00010 6.000 0.500 50.000 50.00011 6.900 0.500 50.000 42.90212 7.800 0.500 50.000 0.00013 5.100 0.500 50.000 50.00014 6.000 0.500 50.000 50.00015 6.900 0.500 50.000 42.90216 7.800 0.500 50.000 0.000布置宽度B0=7.079(m) 分布长度L0=10.641(m) 荷载值SG=1371.607(kN)换算土柱高度 h0 = 0.958(m)按假想墙背计算得到:第1破裂角： 27.510(度)Ea=225.762 Ex=103.435 Ey=200.673(kN) 作用点高度 Zy=2.815(m) 因为俯斜墙背，需判断第二破裂面是否存在，计算后发现第二破裂面存在：第2破裂角=27.490(度) 第1破裂角=27.500(度)Ea=223.941 Ex=103.438 Ey=198.620(kN) 作用点高度 Zy=2.815(m) 墙身截面积 = 10.629(m2) 重量 = 265.725 kN地下水作用力及合力作用点坐标(相对于墙面坡上角点)X分力(kN) Y分力(kN) Xc(m) Yc(m)墙面坡侧: 31.25 -46.75 -1.27 -6.17墙背坡侧: -211.25 -175.41 2.42 -4.83墙底面: -0.00 202.54 1.19 -7.00整个墙踵上的土重 = 60.898(kN) 重心坐标(1.781,-4.161)(相对于墙面坡上角点)整个墙踵上墙背与第二破裂面之间换算土柱重 = 0.684(kN) 重心坐标(0.269,0.000)(相对于墙面坡上角点)墙踵悬挑板上的土重 = 24.635(kN) 重心坐标(2.493,-5.319)(相对于墙面坡上角点)墙趾板上的土重 = 106.650(kN) 相对于趾点力臂=1.236(m))(一) 滑动稳定性验算基底摩擦系数 = 0.300采用防滑凸榫增强抗滑动稳定性,计算过程如下:基础底面宽度 B = 6.430 (m)墙身重力的力臂 Zw = 2.914 (m)Ey的力臂 Zx = 4.965 (m)Ex的力臂 Zy = 2.815 (m)作用于基础底的总竖向力 = 752.071(kN) 作用于墙趾下点的总弯矩=1804.617(kN-m)基础底面合力作用点距离墙趾点的距离 Zn = 2.400(m)基础底压应力: 墙趾=205.964 凸榫前沿=203.196 墙踵=27.962(kPa)凸榫前沿被动土压力=417.263(kPa)凸榫抗弯强度验算:凸榫抗弯强度验算满足: 弯曲拉应力 = 200.286 <= 500.000(kPa)凸榫抗剪强度验算:凸榫抗剪强度验算满足: 剪应力 = 166.905 <= 990.000(kPa)凸榫设计宽度为: 0.949(m)滑移力= 283.438(kN) 抗滑力= 469.841(kN)滑移验算满足: Kc = 1.658 > 1.300滑动稳定方程验算：滑动稳定方程满足: 方程值 = 33.102(kN) > 0.0(二) 倾覆稳定性验算相对于墙趾点，墙身重力的力臂 Zw = 2.914 (m)相对于墙趾点，墙踵上土重的力臂 Zw1 = 4.267 (m)相对于墙趾点，墙趾上土重的力臂 Zw2 = 1.236 (m)相对于墙趾点，Ey的力臂 Zx = 4.965 (m)相对于墙趾点，Ex的力臂 Zy = 2.815 (m)验算挡土墙绕墙趾的倾覆稳定性倾覆力矩= 549.857(kN-m) 抗倾覆力矩= 2354.474(kN-m)倾覆验算满足: K0 = 4.282 > 1.500倾覆稳定方程验算：倾覆稳定方程满足: 方程值 = 1570.958(kN-m) > 0.0(三) 地基应力及偏心距验算基础为天然地基，验算墙底偏心距及压应力作用于基础底的总竖向力 = 752.071(kN) 作用于墙趾下点的总弯矩=1804.617(kN-m)基础底面宽度 B = 6.430 (m) 偏心距 e = 0.815(m)基础底面合力作用点距离基础趾点的距离 Zn = 2.400(m)基底压应力: 趾部=205.964 踵部=27.962(kPa)最大应力与最小应力之比 = 205.964 / 27.962 = 7.366作用于基底的合力偏心距验算满足: e=0.815 <= 0.167*6.430 = 1.072(m)墙趾处地基承载力验算满足: 压应力=205.964 <= 278.400(kPa)墙踵处地基承载力验算满足: 压应力=27.962 <= 301.600(kPa)地基平均承载力验算满足: 压应力=116.963 <= 232.000(kPa)(四) 墙趾板强度计算标准值:作用于基础底的总竖向力 = 752.071(kN) 作用于墙趾下点的总弯矩=1804.617(kN-m)基础底面宽度 B = 6.430 (m) 偏心距 e = 0.815(m)基础底面合力作用点距离趾点的距离 Zn = 2.400(m)基础底压应力: 趾点=205.964 踵点=27.962(kPa)设计值:作用于基础底的总竖向力 = 752.071(kN) 作用于墙趾下点的总弯矩=1804.617(kN-m)基础底面宽度 B = 6.430 (m) 偏心距 e = 0.815(m)基础底面合力作用点距离趾点的距离 Zn = 2.400(m)基础底压应力: 趾点=205.964 踵点=27.962(kPa)[趾板根部]截面高度: H' = 0.600(m)截面剪力: Q = 240.162(kN)截面抗剪验算满足，不需要配抗剪腹筋截面弯矩: M = 258.617(kN-m)抗弯受拉筋: As = 1348(mm2)截面弯矩: M(标准值) = 258.617(kN-m)钢筋应力 = 401.03(N/mm*mm) >= fyk = 400.00 (N/mm*mm)最大裂缝宽度：鋐max= 0.723 > 鋐limit = 0.200(mm)！满足允许裂缝宽度的钢筋面积为：As = 2747.717(mm2)，对应的裂缝宽度为：0.200(mm)。

挡土墙受力分析及配筋设计

挡土墙受力分析及配筋设计
本题中， y =
2 3
b 平面上，有 σ y = − k 0 ρ 2 gx ，由于墙背光滑，故无剪应力，即 τ xy = 0 。 2
b y = − 平面上，有 σ y = 0 ，同样 τ xy = 0 。 2 x = 0 平面上，我们可利用圣维南原理，即将该面上的力和力矩进行等效替换。由于该
面上的正应力， 剪应力以及正应力对 x 轴的力矩均为 0， 因此有
-5-

x M AB = f y As (h0 − ) ，则： 2 x 0.588 × 10 6 × 10 3 = 210 × As × (465 − ) 2
……………………………（29）由式（28）
2
和 式 （ 29 ） 联 立 得 ： x = 159mm ， As = 7269mm
…………………………（17）
1 3 b4 1 b2 − k 0 x 2 ( Ab 2 − Bb + C ) + ( A − Bb3 + C1 − D1b − E1 ) = 0 2 4 32 12 4
……（18）
∫ ∫ ∫
b 2 b − 2 b 2 b − 2 b 2 b − 2
(6 A2 y + 2 B2 )dy = 0
其中， f ( y ) ， f 1 ( y ) ， f 2 ( y ) 都是待定的 y 的函数。
1.3 由相容方程求解应力函数
由艾里应力函数满足的相容方程为：
∂ 4φ ∂ 4φ ∂ 4φ + 2 + =0 ∂x 4 ∂x 2 ∂y 2 ∂y 4
将应力函数 φ 代入相容方程得：
………………………………………（7）
在这里，由于 f 2 ( y ) 中的一次项和常数项不影响应力分量，故可将其略去。 将（10）式代入（6）式得应力函数：

悬臂式和扶壁式挡土墙课件

悬臂式和扶壁式挡土墙课件

支撑板是悬臂式挡土墙的重要组成部分，主要承受墙面板传递的荷载，
并将其传递到锚杆上。支撑板的受力情况与锚杆的长度、直径和布置方
式等因素有关。
03
锚杆受力分析
锚杆是悬臂式挡土墙的关键构件之一，主要承受墙面板的拉力，并将其
传递到地基中。锚杆的受力情况与地基的承载能力和稳定性有关。
悬臂式挡土墙的设计与施工
提高挡土墙稳定性的措施
提高挡土墙的稳定性是保证工程 安全的重要措施。
在设计和施工过程中，可以通过 合理选择墙体材料、优化结构设 计、增加墙体高度或宽度等方式
来提高挡土墙的稳定性。
对于已经建成的挡土墙，可以通 过定期检查和维护来及时发现并 解决存在的安全隐患，以保障其
稳定性和安全性。
05
CATALOGUE
设计步骤
悬臂式挡土墙的设计步骤主要包括确定设计参数、进行土压 力分析、确定墙面板和支撑板的尺寸和形状、进行锚杆设计 等。在设计过程中需要考虑填方或山体滑坡等作用力的影响 ，以确保挡土墙的安全性和稳定性。
施工步骤
悬臂式挡土墙的施工步骤主要包括地基处理、安装锚杆、安 装支撑板和墙面板、填充填料等。在施工过程中需要采取相 应的安全措施和技术要求，以确保挡土墙的质量和安全性。
悬臂式和扶壁式挡 土墙课件
目 录
• 挡土墙概述 • 悬臂式挡土墙 • 扶壁式挡土墙 • 挡土墙的稳定性分析 • 工程实例
01
CATALOGUE
挡土墙概述
挡土墙的定义和作用
01
挡土墙是一种用于支撑和加固土 体的建筑物，它能够抵抗土体的 侧向压力，防止土体滑坡或坍塌 ，保障建筑物的安全和稳定。
02
工程实例
某市一条河流的护岸工程中采用了扶壁式挡土墙，有效地防止了河水的冲刷和侵蚀。

挡土墙结构设计与应力分析研究

挡土墙结构设计与应力分析研究

挡土墙结构设计与应力分析研究挡土墙是土木工程中常用的一种结构，主要用于抵抗土方的侧向土压力，确保土方的稳定性。

在挡土墙的设计和应力分析中，需要考虑挡土墙的结构形式、材料选用、抗倾覆稳定性、抗滑稳定性等方面。

本文将对挡土墙的结构设计与应力分析进行研究和探讨。

一、挡土墙的结构设计1. 结构形式选择：挡土墙的结构形式包括重力挡土墙、加筋挡土墙和悬臂挡土墙等。

根据具体工程要求和条件，选择合适的结构形式是进行挡土墙设计的首要任务。

2. 材料选用：挡土墙的结构材料应具备足够的强度、稳定性和耐久性。

常用的材料包括混凝土、钢筋混凝土和砖石等。

根据设计要求和经济性考虑，选择合适的材料是确保挡土墙结构性能的关键。

3. 坡度与坡高确定：挡土墙的坡度和坡高直接影响到挡土墙的稳定性和经济性。

通过合理地确定坡度和坡高，可以降低挡土墙的整体倾覆和滑动风险，提高挡土墙的承载能力和使用寿命。

二、挡土墙的应力分析1. 抗倾覆稳定性分析：挡土墙的抗倾覆稳定性是保证挡土墙能够抵抗土体侧向压力的关键。

应利用相关的力学理论和方法，计算和分析挡土墙的倾覆稳定性，确定是否满足设计要求。

2. 抗滑稳定性分析：挡土墙的抗滑稳定性是保证挡土墙能够抵抗土体滑动力的关键。

通过计算挡土墙的抗滑安全系数，评估其抗滑稳定性，必要时采取加筋或加大基础面积等措施提高抗滑安全系数。

3. 应力场分析：挡土墙在受到土体侧压力作用时会引起内力和应力的分布。

通过有限元分析等方法，计算和分析挡土墙内力和应力的分布，了解挡土墙结构的受力情况，为设计和改进提供依据。

三、挡土墙的工程实践1. 监测与反馈：在挡土墙的施工和使用过程中，应建立有效的监测和反馈机制，及时掌握挡土墙结构的变化和问题。

通过监测数据的分析和反馈，及时采取措施修复和加固挡土墙，确保其安全可靠。

2. 经济性评估：在挡土墙的设计过程中，除了满足结构稳定和安全性要求外，还需要综合考虑挡土墙的经济性。

以最小的投资获得最大的效益，通过经济性评估，选择合适的设计方案和材料。

悬臂式挡土墙解析PPT课件

悬臂式挡土墙解析PPT课件

悬臂式挡土墙的设计 悬臂式挡土墙的构造 3.凸榫 •为提高挡土墙抗滑稳定的能力，底 板可设置凸榫，厚度除了满足混凝 土的直剪和抗弯的要求以外，为了 便于施工，还不应小于30cm。
悬臂式挡土墙的设计 悬臂式挡土墙的构造 4.其他 •伸缩缝的间距不应大于20m。 •沉降缝、泄水孔的设置应符合重力式挡土墙的相关 要求。 •墙身混凝土强度等级不宜低于C30，受力钢筋直径 不应小于12mm。墙后填土应在墙身混凝土强度达到 设计强度的70%时方可进行。
H La
②底板配筋设计
墙踵板受力钢筋，设置在墙踵板的顶面。受力筋一端插入立臂与底板连 接 处以左不小于一个锚固长度；另一端按材料图切断，在理论切断点向外伸出一个 锚固长度。 墙趾板的受力钢筋，应设置于墙趾板的底面，该筋一端伸人墙趾板与 立臂 连接处以右不小于一个锚固长度；另一端一半延伸到墙趾，另一半在B1/2处再加 一个锚固长度处切断。
250 150 600
3000
总竖向力：
G1k G2k
1600
max
B
D
(6)结构设计 立臂与底板均采用 C20 混凝土和Ⅱ级钢筋， fck=13.4N/mm2 ， ftk=1.54N/mm2 ， fy=300N/mm2 ， Es=2× 105N/mm2； 1) 立臂设计 底截面设计弯矩：M=10× 1.5× 1.3+25.5× 1× 1.20=50.1kN· m/m； 标准弯矩： Mk=10× 1.5+25.5× 1=40.50 kN· m/m； 强度计算：取 h0=250-40=210mm，b=1000mm；
La
THANK
YOU
SUCCESS
2019/4/26
③裂缝宽度验算
悬臂式挡土墙设计实例 已知：设计一无石料地区挡土墙，墙背填土与墙前地面高 差为2.4m，填土表面水平，上有均布标准荷载， pk 10kN / m2 地基承载力设计值为 ，填土的标准重 s 17kN / m3 120kN / m2 度 ，内摩擦力 ,底板与地基摩擦 300 0.45 系数 ，由于采用钢筋混凝土挡土墙，墙背 竖直且光滑，可假定墙背与填土之间的摩擦角 0 方 。

重力式挡土墙悬臂式挡土墙

重力式挡土墙悬臂式挡土墙

05
挡土墙的设计与计算
设计原则与方法
安全可靠
挡土墙设计应确保在各种荷载 和环境条件下具有足够的稳定
性和安全性。
经济合理
在满足安全要求的前提下，应 尽可能降低工程造价，提高经 济效益。
适用性强
挡土墙设计应考虑到地质、水 文、气候等条件，确保在各种 环境下均能适用。
美观环保
挡土墙的外观应与周围环境相 协调，符合环保要求。
地质条件考虑
不同的地质条件对挡土墙 的设计和选型有不同的要 求。
工程经济性
合理的挡土墙设计能够节 省工程成本并提高工程安 全性。
挡土墙的定义与分类
定义
挡土墙是一种用于抵抗土体侧压力、 防止土体坍塌或滑坡的构筑物。
分类
根据结构形式和工作原理，挡土墙可 分为重力式挡土墙、悬臂式挡土墙、 扶壁式挡土墙等。本文将重点探讨重滤层 等，防止水分在挡土墙内部积聚。
质量控制措施
施工前质量控制
熟悉设计图纸，了解施工验收规范及质量评定标准；编制切实可行的施工方案或技术措施 ；对施工人员进行技术交底，明确施工方法和质量标准。
施工过程质量控制
加强原材料的质量控制，确保原材料符合设计要求；严格按照施工规范进行施工，确保每 个工序的质量；加强现场监督和检查，及时发现并处理质量问题。
重力式挡土墙与悬臂 式挡土墙
目录
• 引言 • 重力式挡土墙 • 悬臂式挡土墙 • 重力式挡土墙与悬臂式挡土墙的比较
目录
• 挡土墙的设计与计算 • 挡土墙的施工技术与质量控制 • 挡土墙的维护与保养
01
引言
目的和背景
01
02
03
土木工程需求
在土木工程中，挡土墙是 常见的结构物，用于防止 土壤或岩石的侧向移动。

悬臂式挡土墙

悬臂式挡土墙

冻土区路堑工程中悬臂式挡土墙的适应性摘要：根据悬臂式挡土墙自身的结构特点,结合多年冻土的物理力学特性以及其地处高原所存在的施工问题,分析了该型档墙在多年冻土区路堑边坡支档处理中的优越性,指出该型档墙是多年冻土区路堑支档结构的首选类型。

关键词:悬臂式挡土墙冻土路堑支挡结构1 引言目前,国内外在多年冻土地区厚层地下冰段修筑铁路,一般都遵循多填少挖的原则而以路堤形式通过。

所以到目前为止,在厚层地下冰地段修筑铁路路堑为数还不多,对路堑边坡挡土结构的研究也较少。

从上世纪60年代开始,中国学者在青藏高原多年冻土区进行了一些科学试验研究,分别在理论和实践方面为路堑工程的可行性建设提供了参考依据。

研究表明[1],对于多年冻土区不可避免的路堑工程建设,当路堑较深或边坡较高(H>6m)时,采用下挡上护的边坡处理方式为好。

而下挡建筑物采用柔性、轻型、预制拼装的钢筋混凝土悬臂式挡墙为宜。

为进一步探索这种挡墙在路堑工程中的实际可行性和经济合理性,本文将结合北麓河挡墙试验工程,从该型挡墙为适应冻土特性的断面形式和处理措施方面进行初步探讨和分析。

有关分析计算见其它相关文献。

2 冻土区支挡结构的受力特点及工程措施2.1 受力特点一般来说,多年冻土区挡土建筑物的修建,改变了原地面的热平衡条件,在墙背形成新的多年冻土上限。

每年夏季墙背冻土融化,形成季节融化层,这种融化土层对墙体将作用土压办。

在冬季,季节融化层冻结,在冻结过程中,由于土中水分结冰膨胀,冻结土体对挡土墙将作用冻胀力。

土压力和水平冻胀力的这种交替循环作用,是多年冻土区挡土建筑物工作的显著特点。

在无冻结的情况下,挡土墙主要承受来自墙背填土产生的主动土压力,因而,土压力是验算挡土墙稳定性的主要荷载。

在寒季,随着地温的降低,墙后土体在冻结过程当中,产生作用于墙体的水平冻胀力。

据试验测定,这种水平冻胀力往往比土压力大几倍甚至几十倍。

这时候,计算分析时,就忽略土压力的作用。

关于悬臂式挡土墙及其设计优化的讨论

关于悬臂式挡土墙及其设计优化的讨论
程 比 例 很 小 ， 此 ， 土 墙 设 置 常 被 一 些 设 计 人 员 忽 视 ， 使 因 挡 致
４． ， 宽 ３ １ｍ ， 前 基 底 以上 水 深 １５ｍ ，墙 后 水 深 距 基 ７ｍ 板 ． 墙 ． 底 ０ ５ｍ。墙 前 卸 荷 板 以 下用 碎 石 回填 ， 余 素 填 土 夯 实 ， 后 ． 其 墙 回填 土 石屑 ， 筑 凸榫 后 ， 两 侧 回 填 素 混 凝 土 垫 层 。前 墙 填 浇 其 土 表 面 布 有 人 行 道 荷 载 口１ ４ ｋ ａ和 路 面 荷 载 ｑ ＝ ０ ｋ 。 挡 ＝ Ｐ ２ ２ Ｐａ
Ｏ６ ｍ 的 凸 榫 结 构 ， 在 立 墙 上 设 卸 荷 板 ， 宽 １Ｏ ｍ ， 高 ． 并 板 ． 墙
方 向成 ：５ ＋ ／＝ ５ ＋ ５／＝ ７ 。 减 压 范 围 为 从 卸 荷 板 端 起 ４ 。 ２ ４ 。 ２ 。 ５ ． ， ２ ２ ５ 点 到 竖 向方 向的 距 离 为 Ｈ ＝ ．５ ｔ ５ ．。 １ ５ 分布 荷 载 ４ ０８ ｘ ａ ７５ ： ． ４ ｍ。 ｎ ２
ＨＩ Ｖ１ Ｖ２ ． ｎ ： 一 ＝１ ６ Ｉ Ｈ２ ＝Ｖ ２ 一Ｖ Ｏ． ｌ ３ １ ｎ Ｈ３ Ｖ Ｖ６ ． ＝ ＝ ５ 一 ＝１５ ｍ Ｈ５ ｒ － ＝０． ４６ １ ＝ Ｖｒ－ Ｈ４ ３ １ ３
Ｈ６ ＝Ｈ３ 一Ｈ７ ＝０． ６８ ｍ ＝ ９
ｅ ｌ 。 ＝１９ Ｐａ ｅ 。＝ ｌ ｇ１ ．５９ Ｍ ＝Ｋ 。 ＋ ，ｋｌ ６０６ １ ｌ。 ｑｌ ＝１ ． ０ ＭＰａ
土 墙 的 断 面 尺 寸 如 图 １所 示 。
１２ 采 用 计算 数据 ． 回 填 的 素 填 土 内 摩 擦 角 咖１ ２ ０，粘 聚 力 Ｃ１ Ｏｉ碎 石 ＝０ ＝
币２ ２ ０， ２ ０； 土 石 屑 币３ ２ ０， ３ ０； 素 混 凝 土 垫 层 咖４ ＝５ Ｃ ＝ ＝０ Ｃ ＝ －

挡土墙受力分析及配筋设计_pdf

挡土墙受力分析及配筋设计_pdf

b
b
∫ ∫ 面上的正应力，剪应力以及正应力对 x 轴的力矩均为 0，因此有
σ 2
−b
x dy
=
0，
τ2
−b
yx dy
=
0
，
2
2
b
∫ σ 2 −b
x
ydy
=
0。
2
将（12），(13),(14)式分别代入以上各边界条件中得：
k0
(1 8
Ab 3
x
+
1 4
Bb 2
x
+
1 2
Cbx
+
Dx)
=
−k0
ρ2
gx
………………………（15）
将（5）式对 x 积分得：
φ
=
1 6
k
0
x
3
f
(y) +
xf1 ( y) +
f2 (y)
…………………………………（6）
其中， f ( y) ， f1 ( y) ， f 2 ( y) 都是待定的 y 的函数。
1.3 由相容方程求解应力函数
由艾里应力函数满足的相容方程为：
∂ 4φ + 2 ∂ 4φ + ∂ 4φ = 0 ∂x 4 ∂x 2∂y 2 ∂y 4
1、弹性力学分析挡土墙受力
弹性力学是将物体作为弹性体来分析受力而建立方程的，在目前处理的挡土墙受力问题中， 绝大部分力学理论是把挡土墙当作弹性体来分析的。因此，将弹性力学方法用于挡土墙受力分 析是比较合理的。在分析完挡土墙的受力后，再对其进行配筋，便能使问题得到简化和精确。
我们来看一下具体的挡土墙问题：
Байду номын сангаас

挡土墙的抗震性能分析

挡土墙的抗震性能分析

挡土墙的抗震性能分析引言：挡土墙是一种常见的土木工程结构，用于抵御土壤压力，保护周围建筑物和土地。

而在地震灾害中，挡土墙的抗震性能显得尤为重要。

本文旨在分析挡土墙的抗震性能，并探讨提高其抗震能力的方法。

一、挡土墙的结构及工作原理挡土墙是由土壤和墙体组成的工程结构，其主要工作原理是通过阻挡并转移土壤压力，提供强大的支抗力，保持土坡的稳定。

挡土墙通常由墙体与基础组成，墙体可采用不同的结构形式，如重力式、加筋式和悬臂式。

其结构形式和材料选择，直接影响着挡土墙的抗震性能。

二、挡土墙的抗震性能评价指标1. 承载力：挡土墙在地震中承受的力量是抗震性能的重要指标。

其承载力需要满足设计要求，能够承受土壤压力和地震力的作用，不发生破坏。

2. 变形能力：挡土墙在地震中的变形能力是评价其抗震性能的关键指标。

较好的挡土墙应该具有较大的延性和韧性，能够充分吸收和分散地震能量，保持墙体的稳定。

3. 稳定性：挡土墙在地震中的稳定性是考察其抗震性能的重要指标。

稳定性包括水平稳定和垂直稳定，即挡土墙在地震作用下不会倒塌或侧倾。

三、提高挡土墙的抗震性能的方法1. 结构优化：采用适当的结构形式和合理的墙体厚度，以提高挡土墙的抗震能力。

加筋墙体可以增加其承载力和变形能力，减少破坏风险。

2. 地基加固：挡土墙的基础是其抗震性能的关键部分，通过对地基进行加固处理，可以提高挡土墙的稳定性和整体抗震性能。

常见的地基加固方法包括钢筋混凝土地基梁、地锚和土钉墙等。

3. 材料选择：选择抗震性能好、强度高、延性好的材料，以提高挡土墙的整体抗震性能。

常见的材料包括钢筋混凝土、钢板和纤维增强复合材料等。

4. 设计规范与施工质量：挡土墙的抗震性能不仅与设计规范相关，还与施工质量密切相关。

因此，需严格按照相关设计规范进行设计和施工，并加强质量监管，确保挡土墙具有良好的抗震性能。

结论：挡土墙作为一种常见的土木工程结构，在地震灾害中起着重要的作用。

为了提高挡土墙的抗震性能，我们可以通过结构优化、地基加固、材料选择以及加强设计规范与施工质量来实现。

卸荷式与悬臂式挡土墙受力分析比较

卸荷式与悬臂式挡土墙受力分析比较

“ Ｂ Ｄ 范 围内土的 自重力对 ０点产 生的弯矩为 ： ＡＣ ”
Ｍ ２ Ｂ ・ ２・ ； Ｂ ＝ Ｂ ・ ２・ ＝ Ｃ／ （ ＾ 回 Ｃ／ ＢＣ・ ）＝ ＢＣ２ ２・ ）， ｈ・ ， ／ ｈ・ ，
Ｂ Ｃ＝ｈｔ（５一声２＝ｈ ： ・ ４。 ／） ・ ｇ 。
图 １ 卸荷式挡墙断面图
３ 挡墙墙壁根部弯矩 为 ： ）
Ｍ ｏ＝Ｍ １ 一Ｍ２ １ ６ Ｈ 一 １ ２ Ｈ 。 ＭＯ 。 ＝ ／ ｙ Ｋ ／ ｙ Ｋ ≤ Ａ
１２ 普 通挡 土墙 受 力分析 （ 图 ２ ． 见 ）
＝
由此可 以看 出 ， 荷式挡墙较悬 壁式 挡墙在挡墙根 部所受弯 卸
矩要小 。
１ ２ｙ・ Ｋ ／ Ｈ２
ｈ Ｈ３√ 。 ／ ＜ 。 １ ４和 Ｍ ｏ ＞Ｍ Ｂ ， ｃ
彦 （９ ３ ， ， 程 师 ， 山钢 铁 设 计 研 究 院 有 限 公 司 ， 北 唐 山 １ ７ 一）女 工 唐 河
０３０ ６００
维普资讯
第 ３ ５期 ２０２卷 第 １ ６年 ８月 ０
。 。
式中 ： ——挡土墙墙 壁所受主动土压力 ，Ｎ； ｋ
，
４ 由于卸荷式挡墙悬 挑板 的存在 ， ） 悬挑板上土将 产生土压力 对挡墙墙壁 Ｂ点产生最大 弯矩 ＭＢ 。 Ａ
＝１ ２ｙ Ｋ。 ／ Ｈ ， ＭＢ Ａ＝ｈ／ 。 ３ ＝１ ｙ ６ ／ Ｈ 。
ｙ ——填土 的容 重 ，Ｎ ｍ ； ｋ ／ ３ Ｈ——挡 土墙 墙高 ， ｍ；
即应 当控制悬挑板 的位置 ｈ值 ：
即： Ｍｏ＞ＭＢ ， Ａ １ ｙ ６ ／ Ｈ 一１ ｒ ２ ／ ｈ ≤１６ ／ ，
对挡墙墙壁根部 ０点产生 的弯矩 为 ：
Ｍ１ ＝Ｈ／ 。 ：１ ６ｙ ３ ／ Ｈ

悬臂式挡土墙设计与分析

悬臂式挡土墙设计与分析

Ａ ＝Ｍ／ＴＪｒｈ０。
置沉降缝和伸缩缝 ：
其 中 ，Ａ，为受拉钢筋截面面积 为受拉钢筋设 计强度 ； 为
１）不 同地基土壤 的分界处 。２）挡 土墙高度 变化处 。３）所承 截面有 效高度。
受的荷载有较大变化处 。４）墙长超过 ２５ ＩＩ１时。
２．３ 地基 承载 力验 算
１．３ 基 础垫层
２）有 地下水 时。
＝ ÷［２（ｑｌＰ ）＋（ｑｌＰ ）］ｂ 。 Байду номын сангаас
ａ．地下水 位处 ： ＝ｙＨｔａｎ （４５。一 ２）。
ｂ．地下水位 以下 ：
２．５ 抗 倾覆稳 定验 算 历
扎 ‘６。。
＝ｙｈ１：［（７ 一 ）ｈ２］ｔａｎ （４５。一ｑ￣／＇２）＋ ｈ２。
２．２ 墙 身内力及配筋计算
第 ３８卷 第 １０期 · ９８ · ２ ０ １ ２ 年 ４ 月
山 西 建 筑
ＳＨＡＮＸＩ ＡＲＣＨＩＴＥＣＴＵＲＥ
Ｖｏｌ＿３８ Ｎｏ．１０ Ａｐｒ． ２０１２
文章编号 ：１００９－６８２５（２０１２）１０—００９８—０２
悬 臂 式 挡 土 墙 设 计 与 分 析
谢 俊 辉
（河北省建筑材料工业设计研究院 ，河北 石 家庄 ０５００５１）
摘 要 ：从材料 、沉降缝与伸 缩缝及基础垫层三方面介绍 了悬臂式 挡土墙的构造特 点 ，并针对 悬臂式 挡土墙 的侧压 力、墙 身 内力、
地基承载 力等计算进行 了具体阐述 ，指 出了设计过程中应注意事项 ，以期指导实践。
关键词 ：悬臂式挡土墙 ，构造特点 ，承载 力，注意事项
（景德镇市城建开发公司 ，江西 景德镇 ３３３０００）
摘 要 ：结合 自身工作实践 ，针对静压桩在 软土层施 工中出现的质量 问题进 行 了探 讨 ，分析 了天气 、地质 、施工措 施等 因素对静压

4悬臂式挡土墙解析

4悬臂式挡土墙解析

4悬臂式挡土墙解析在土木工程领域，挡土墙是一种常见的结构，用于支撑填土或山坡土体，防止土体变形失稳。

其中，悬臂式挡土墙以其独特的结构和性能特点，在许多工程中得到了广泛应用。

接下来，让我们一起深入了解一下悬臂式挡土墙。

悬臂式挡土墙通常由立壁、趾板和踵板三部分组成。

立壁就像是一面竖直的墙壁，直接承受土压力的作用；趾板位于挡土墙的前端，起到增加稳定性和分散压力的作用；踵板则位于后端，为整个结构提供支撑和平衡。

这种挡土墙的工作原理其实并不复杂。

当土体作用在立壁上时，土压力会通过立壁传递到趾板和踵板上。

由于趾板和踵板的设置，使得挡土墙能够将所承受的压力有效地分散到地基中，从而保持结构的稳定。

悬臂式挡土墙具有不少优点。

首先，它的结构相对简单，施工较为方便。

与其他复杂的挡土墙结构相比，悬臂式挡土墙不需要大量的预制构件和复杂的连接方式，这在一定程度上缩短了施工周期，降低了施工成本。

其次，它能够适应不同的地形和地质条件。

无论是在平坦的场地还是在复杂的山坡地形上，悬臂式挡土墙都可以根据实际情况进行灵活的设计和施工。

再者，它的占地面积相对较小。

在一些空间有限的场地中，悬臂式挡土墙能够充分发挥其优势，有效地利用空间。

然而，悬臂式挡土墙也并非完美无缺。

它对地基的要求相对较高。

如果地基承载力不足，就可能导致挡土墙的下沉或倾斜，从而影响其稳定性和安全性。

此外，悬臂式挡土墙的钢筋用量较大，这也在一定程度上增加了工程造价。

在设计悬臂式挡土墙时，需要考虑多个因素。

土压力的计算是至关重要的一环。

土压力的大小和分布直接影响着挡土墙的结构尺寸和配筋设计。

常用的土压力计算方法有库仑土压力理论和朗肯土压力理论。

设计师需要根据具体的工程条件选择合适的计算方法，并对计算结果进行合理的修正。

同时，挡土墙的稳定性也是设计中需要重点关注的问题。

包括抗滑移稳定性、抗倾覆稳定性和地基承载力稳定性等。

为了保证挡土墙的稳定性，设计师需要合理确定挡土墙的尺寸、配筋以及基础的形式和尺寸。

悬锚式挡土墙结构设计与分析_陈忠达

悬锚式挡土墙结构设计与分析_陈忠达
(1. Key Laboratory fo r Special Area Highway Engineering of Minist ry of Education , Chang’an U niversity , Xi’an 710064 , China ; 2. Highway Administ ration of Tianjin , Tianjin 300170 ,China)
0 引 言
随着中国高等级公路建设步伐的加快 ,特别是 高等级公路建设向中西部地区的推进 ,路基挡土墙 应用愈来愈多 。为了适应中西部地区的地形 、地质 、 土质等条件 ,满足高等级公路建设的需要 ,研究开发
新型的支挡结构具有十分重要的现实意义[1] 。 悬锚式挡土墙是利用锚定板技术与悬臂式挡土
墙组合而成的一种轻型支挡构造物 ,它是由钢筋混 凝土墙身 (指立壁和底板部分) 、锚定板 、拉杆及充填 在墙身与锚定板之间的填料构成的一种复合式结 构[2] 。它对地基承载力的要求低 ,而且由于锚定板
Abstract : The earth retaining wall is a new kind of compound supporting and retaining structure. Taking the double2layer suspended2anchor earth retaining wall as research object , based on the finite element method , the paper studies this kind of retaining wall’s design method , and put s forward it s calculation method ,which is based on Rankine active earth pressure , gives the design demand of wall structure , present s the method of designing anchor plate and drawbar , delivers the stability analysis method toward cantilever retaining wall and polygonal fracture plane stability analysis method. An example result s show that this method can be widely used in engineering design. 6 figs , 6 refs. Key words : road engineering ; suspended2ancho r eart h retaining wall ; eart h p ressure ; st ruct ure design ; stabilit y

挡土墙设计

挡土墙设计

挡土墙设计
动水压力
悬臂式挡土墙设计要点
第三章
一、挡土墙概述 二、重力式挡墙设计要点 三、悬臂式挡墙设计要点 四、扶壁式挡墙设计要点 五、加筋土挡墙设计要点
挡土墙设计
悬臂式挡土墙设计要点
一、悬臂式挡墙构造
悬臂式挡墙由立壁、底板及齿槛组成。 悬臂式挡墙由立壁、底板及齿槛组成。 立壁的顶宽不应小于20cm，立壁的外侧 立壁的顶宽不应小于 ， 表面可设1： 的仰坡。 表面可设 ：0.02～1：0.1的仰坡。前趾 ～ ： 的仰坡 板和后踵板的端部厚度不应小于30cm。 板和后踵板的端部厚度不应小于 。
挡土墙设计
总 结 与 体 会
无锡市政设计研究院有限公司 二○一○年九月
主要内容
主要内容
一、挡土墙概述 二、重力式挡墙设计要点 三、悬臂式挡墙设计要点 四、扶壁式挡墙设计要点 五、加筋土挡墙设计要点
挡土墙设计
挡土墙概述
第一章
一、挡土墙概述 二、重力式挡墙设计要点 三、悬臂式挡墙设计要点 四、扶壁式挡墙设计要点 五、加筋土挡墙设计要点
承载能力极限状态作用（或荷载） 表5.4.2-5 承载能力极限状态作用（或荷载）分项系数 综合内摩擦角 内摩擦角 重度 荷载增大对挡土墙结 荷载增大对挡土墙结 填料种类 情况 关于荷载的说明 构起不利作用时 φ0 φ kN/m3 构起有利作用时 粘性土 墙高H≤6ｍ 35～ 墙高H≤6ｍ H≤6 35～ I，II 40 III ―― I，II 即2m墙 组合 序即根据挡墙高度换算成相应的土厚；17～ III 序即根据挡墙高度换算成相应的土厚；17～18墙 墙高H＞6ｍ 30～ 墙高按10KN/m 墙高高按 H 30 0.90 ； ～35墙高按 高按20KN/m2；10m墙高按 ―― 2；1.2010m 2～ ～ 垂直恒载

《悬臂式挡土墙计算》

《悬臂式挡土墙计算》

《悬臂式挡土墙计算》Exceldocx《悬臂式挡土墙计算》悬臂式挡土墙是一种广泛应用于土木工程中的结构，它能够承受侧向土压力，保持墙体的稳定性。

在设计和建造悬臂式挡土墙时，需要进行一系列的计算和分析，以确保其具有足够的承载能力和稳定性。

下面我们将介绍悬臂式挡土墙计算的基本原理和Excel docx实现方法。

一、基本原理悬臂式挡土墙是一种利用重力作用和墙底摩阻力来保持稳定的结构，其基本原理是将挡土墙视为一个悬臂梁，通过计算其弯矩和剪力来设计挡土墙的截面尺寸和配筋。

根据弹性力学理论，悬臂梁的弯矩和剪力可由下式计算：弯矩：M(x) = ∫_{0}^{L} q(x,y)y dy剪力：Q(x) = ∫_{0}^{L} q(x,y)dx其中，q(x,y)为分布荷载，L为挡土墙的长度。

根据弯矩和剪力分布，可以计算出挡土墙的截面内力，从而确定其截面尺寸和配筋。

二、Excel docx实现方法为了方便计算和分析，我们可以使用Excel docx来实现悬臂式挡土墙的计算。

下面是一个简单的Excel docx模板，用于计算悬臂式挡土墙的弯矩和剪力分布。

1、打开Excel docx，创建一个新的工作表。

2、在第一列输入挡土墙的长度x的取值，以米为单位。

3、在第二列输入挡土墙的高度y的取值，以米为单位。

4、在第三列输入挡土墙底部的摩阻力系数μ，该系数可根据地质条件和经验数据进行调整。

5、在第四列输入挡土墙侧面的土压力强度p，该值可根据实际情况进行计算或调整。

6、使用Excel的函数SUM和∫，在第五列计算弯矩M(x)：=SUM(B2:B3)C3+∫(B4:B5)C4D2:D3从0到L对yq(x,y)进行积分。

7、使用Excel的函数SUM和∫，在第六列计算剪力Q(x)：=SUM(B2:B4)*C4+∫(B4:B6)D2:D4从0到L对xq(x,y)进行积分。

通过调整输入值，可以计算不同条件下悬臂式挡土墙的弯矩和剪力分布，从而进行截面设计和配筋分析。

挡土墙倒塌原因分析及加固处理方法

挡土墙倒塌原因分析及加固处理方法

挡土墙倒塌原因分析及加固处理方法挡土墙指为防止路基填土或山坡岩土坍塌而修筑的、抵抗土体侧压力的一种工程结构体。

挡土墙被广泛应用于交通、桥梁、建筑物基础、水利和港口等生命线工程中。

随着我国经济的高速发展，各种生命线工程的建设规模越来越大，挡土建筑物越来越多。

在使用过程中，挡土墙常存在倒塌情况。

墙体倒塌通常对行人的生命安全、过往车梁和公共财产造成重大损失，应引起足够的重视。

本文对挡土墙主要结构形式、倒塌机理及加固措施进行浅析。

为设计施工、日常使用、加固改造等提供技术依据。

1 挡土墙的结构形式挡土墙常见结构形式有重力式挡土墙、悬臂式挡土墙、扶壁式挡土墙、锚杆挡土墙、桩板式挡墙。

名称结构形式特点图例重力式挡土墙一般用块石、砖或素混凝土筑成，靠挡土墙本身所受到的重力保持稳定，通常用于较低的挡土墙。

结构简单、对地基承载力要求高。

悬臂式挡土墙多用钢筋混凝土做成，稳定性主要靠墙踵悬臂以上土体所受重力维持，悬臂部分的拉应力由钢筋承担。

截面尺寸小、施工方便、对地基承载力要求相对偏低。

扶壁式挡土墙挡土墙的墙高较高时，为增加悬臂的抗弯刚度，沿墙长纵向每隔一定距离设置一道扶壁，称为扶壁式挡土墙。

工程量小、工艺较悬臂式复杂。

锚杆挡土墙由立柱、墙面板和锚杆三部分组成的轻型支挡结构。

结构轻、柔性大，工程量小，造价低。

桩板式挡土墙由桩和混凝土挡板组成的填方边坡支挡结构。

适用于土压力较大、基础深埋的地段加筋式挡土墙由填土、填土中的拉筋条以及墙面板等三部分组成，它是通过填土与拉筋间的摩擦作用把土的侧压力削减到土体中起到稳定土体作用的。

外形美观、占地面积小，对地基适应性强2 倒塌机理分析挡土墙因抗滑移、抗倾覆、地基承载力不能满足，从而导致墙体倒塌。

（1）抗滑移不满足—挡土墙压力；—基地摩擦系数G1—每延米墙身自重；G2—每延米基底板自重；G3—每延米墙踵板在宽度内的土重（2）抗倾覆不满足Mr——抗倾覆力矩；Ms——倾覆力矩（3）地基承载力不满足fa—修正后的低级承载力特征值。

二、锚杆挡土墙

二、锚杆挡土墙
楔缝式－直径38～50mm，深度3～5m,压注水泥砂浆，防锈和提高锚 杆抗拔力－用于岩石边坡防护与加固工程
灌浆锚杆－直径100～150mm，压注水泥砂浆：如用于土层，则加压灌 浆或内部扩孔－预压锚杆或扩孔锚杆，－多用于路堑挡土墙
肋柱和墙面板≮C20。
二、锚杆挡土墙
2、可设单级墙或双级墙，每级墙高≯ 8m，多级墙间设置 宽度≮2m的平台，下两级墙的肋柱宜交错布置。
3、肋柱式间距宜为2.0～3.0m，肋柱宜垂直布置或向填土 一侧仰斜，仰斜度不应大于1：0.05。
4、每级肋柱上的锚杆层数，可设双层或多层。锚杆可按 弯距相等或支点反力相等的原则布置，向下倾斜。每 层锚杆与水平面的夹角宜控制在150～200之间，锚杆层 间距不小于2.0m。
5、肋柱受力方向的前后侧面内应配置通长受力钢筋，钢 筋直径不应小于12mm
1 2
B3tg )u
Ey
B3＝
[Kc ]Ex f Ey
f
(H
1 2
B3tg )
B2
B3由试算法求出
（3）墙胸面坡坡度1：m，胸坡修正Δ B3
B3 mH1 / 2
Kc－容许抗 滑稳定系数
2、底板宽度计算
3）墙址板宽度B1 －高墙受抗倾覆稳定性控制，一般由基底应 力或偏心距控制，并要求墙踵处的基底不应 出现拉应力。
3、底板厚度计算
1）趾板弯矩和剪力:
Q1
N1
G1
G2
B1[ 1
1 2
(1
2)
B1 B
hhpj
(h
hpj )]
M1
B12 6
[3(1
h)
( h
)(h1
2hpj ) (1
2)
B1 ] B
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

文章编号:1000-1506(2004)04-0016-03悬臂式挡土墙受力分析侯卫红1,侯永峰2(1.河北师范大学物理系,河北石家庄050014;2.北京交通大学土木建筑工程学院,北京100044)摘 要:悬臂式挡土墙是目前常用的轻型挡土墙之一,具有断面简单,施工方便,便于工场化生产等优点.通常采用朗金理论或库仑理论计算作用在挡土墙上的土压力.这里采用有限元法,在考虑挡墙与地基的相互作用的情况下,得出了悬臂式挡土墙所受到的剪力和弯矩,并与朗金法所得的结果进行了对比.关键词:悬臂式挡土墙;有限元;土压力;剪力;弯矩中图分类号:TU 413.62 文献标识码:AThe State of Stre ss of Cantilever Retaining WallH OU W ei -h o ng 1,HOU Y o ng -fe ng2(1.C olleg e of Phy sics ,H ebei Normal Univ ersity ,S hijia zh uang 050014,C hina ;2.S cho ol of Civ il En gi neer ing and Ar chite cture ,Beiji ng Jiaoto ng Unive rsity ,Beiji ng 100044,C hina )Ab s tra ct :C antile ver retainin g wall is u sed fre quentl y in d ock ,em bankment ,etc .The earth press ure is c alculated by usi ng R ankin the ory or C o lum n the ory .In this paper ,the FE M is u sed to analy sis the i nte racti o n betw e en retai ning wall an d s oi l .The she ar forc e an d ben ding mo m ent of c antilever retain -ing w all are o btained .C o mpare with the res ult thro u gh the R ankin the ory ,s o m e res ults are les s than the FE M .Ke y w ord s :c antile ver retainin g wall ;FEM ;earth pre ssure ;shear f orc e ;bend ing m oment 土压力是土与挡土结构之间相互作用的结果,其大小不仅与挡土墙的高度、填土的性质有关,而且与挡土墙的刚度和位移有关[1].《基坑工程手册》根据西南交通大学彭胤教授的研究成果,给出了不同土类、在不同的位移形式下、达到不同的应力状态时所需的不同位移量[2].梅国雄等根据土压力随挡土墙位移而变化的特点,提出了考虑变形与时间效应的土压力计算方法[3].姚辉等采用模型试验的方法,探求了刚性挡土墙主动土压力的分布规律.土压力上部呈直线分布,下部呈抛物线分布,实测土压力比库仑理论计算值小[4].岳祖润等采用离心模型试验的方法得出了相似的结论[5].刘子慧等认为地基反力直线分布法进行悬臂式挡土墙设计是偏于不安全的,弹性地基梁法计算成果较为可靠.这是因为弹性地基梁法将挡墙与地基视为耦合系统,满足底板与地基的变形协调条件,在理论上更为完备[6,7].图1(a )为姚辉等人通过模型试验得到的刚性挡墙墙背主动土压力分布,图1(b )是岳祖润等采用离心模型试验方法得到的刚性挡墙墙背主动土压力分布.这些研究成果大都是针对刚性挡土墙的,墙体本身的变形可以忽略不计.但由于刚性挡土墙的体型巨大、占地多、材料消耗多、对地基承载力要求高,在城市地区的应用受到很大的限制.因此各种轻型挡土墙,如悬臂式挡墙、锚杆挡墙、锚定板挡墙、加筋土挡墙等得到了广泛的应用.其中悬臂式挡墙由于胸坡壁立,常用于码头、站场路肩墙.其外型呈倒“T ”型,由立壁、趾板和踵板组成.踵板上回填土的重收稿日期:2003-12-02基金项目:国家自然科学基金资助项目(50208001)作者简介:侯卫红(1969—),男,河南洛阳人,讲师.email :bfxb @center .njtu .edu .cn第28卷第4期2004年8月 北 方 交 通 大 学 学 报JO URN AL OF N O RTHE RN JIA O TON G UNIVE RSITYVo l .28No .4Aug .2004(a )姚辉等人的实验(b )岳祖润等人的实验图1 挡土墙墙背主动土压力实测结果Fig .1 The m onitoring re sult o f active e arthpres sure o n ba ck of retain ing w all量有助于增加挡土墙的稳定性;趾板使抗倾覆作用力的力臂加长,力矩增大,也对稳定有利.只需根据弯矩和剪力计算,对墙身适当配筋,可实现墙身轻型化,并且断面简单,施工方便,而且便于工场化生产,是一种经济合理的结构[5].在目前的城市铁路建设中,常采用悬臂式挡土墙作为路肩墙,以节约用地.但由于轻型挡土墙的墙身在土压力的作用下会产生较大的变形,因此作用在墙背上的土压力计算更加困难,目前在设计时仍采用朗金理论,或按相同边界条件的库仑公式计算,两种方法所得的土压力相差不大.但这两种方法都不能考虑挡土墙与地基之间的相互作用,以及墙身变形等因素的影响,得出的土压力与实际情况差别较大.有限元法可以将挡土墙与墙后填土作为整体来分析,从而可以考虑墙体与填土之间的相互作用,以及由于墙身变形引起的土压力的非线性分布等问题,在理论上更为完善.1 计算模型本文作者采用有限元法,将悬臂式挡土墙简化为刚性连接的两段梁,填土与挡土墙间采用无厚度的接触面单元来模拟土与挡土墙间的摩擦.边界条件为:两侧x 方向约束,底部xz 方向约束.计算模型如图2所示.计算宽度为60m ,深度为30m ;路堤填土高度4m ,分4层填筑,每层1m ;边坡坡度为1∶1,挡墙埋深1m .挡墙基础为二灰砂砾石,宽6m ,深1.7m ;挡土墙立壁高5m ,宽30cm ;趾板宽1m ,踵板宽2m ,厚度分别取5、10、15、20、30cm 进行计算,不考虑挡墙厚度变化引起的重量变化.采用弹塑性模型、摩尔—库仑屈服准则,采用A nasy s 5.4进行计算.材料参数如表1.计算模型取自北京城铁清河段,挡墙实际厚度为30cm .图2 悬臂式挡土墙计算模型Fig .2 The c alc ulatin g m o de l of c antile ver retainin g wall表1 材料计算参数Tab .1 The c alc ulated parameters of mate rials材料名称重度/(kN ·m -3)粘聚力/kPa 内摩擦角/(°)弹性模量/MP a 泊松比初始孔隙比衰减系数回填土17.81030 200.300.80.6二灰砂砾18.510030 500.200.60.6基 底17.01520 100.350.9-挡 墙20.0--21000--2 计算结果2.1 朗金理论计算结果根据朗金理论计算得到作用在立壁上的土压力及基底应力,并考虑趾板和踵板上的土层的自重可得到立壁、趾板和踵板处的弯矩和剪力.立壁的最大弯矩为27.32kN ·m /m ,最大剪力为26.87kN /m ;趾板的最大弯矩为28.33kN ·m /m ,最大剪的力为57.92kN /m ;踵板的最大弯矩为-9.04kN ·m /m ,最大剪力为-19.05kN /m .2.2 有限元法计算结果图3为有限元计算所得的墙身变形曲线.图4为有限元计算所得的不同厚度的悬臂式挡土墙立壁的墙身剪力和墙身弯矩图.从图4中可见,按朗金理论计算所得的剪力和弯矩远小于有限元计算所得的剪力与弯矩值.这是由于墙后填土达到主要极限平衡状态所需的位移量较大,墙身的变形较小,墙后填土远不能达到主动极限平衡状态.从图371第4期 侯卫红等:悬臂式挡土墙受力分析中可见,墙身的位移在靠近墙底处是偏向填土方向的,进一步造成了墙身下部的剪力值增大.图5为趾板和踵板的剪力与弯矩图.需要注意的是踵板的最大剪力出现在远离立壁一端,而按朗金理论计算所得的最大剪力出现在靠近立壁一端.图3 不同厚度挡土墙立壁的变形图Fig .3 The h oriz ontal dis pla ce ment of c antilev erin di fferent thicknes s(a )剪力(b )弯矩图4 不同厚度挡土墙立壁的剪力与弯矩图Fi g .4 The she ar forc e an d b end ing m o ment of cantileve rin di fferent thicknes s(a )剪力(b )弯矩图5 不同厚度挡土墙趾板和踵板的剪力与弯矩图Fi g .5 The she ar forc e an d bend ing m o ment of retaini ng toe and he el of c antilever in diff erent thickness2.3 两种方法计算结果对比表2为按朗金理论和用有限元法所得的计算结果对比表,取相同位置的数值进行比较.由表2可见,两种方法所得的结果之间有很大的差别,在挡墙厚度为30cm 的情况下,按朗金理论所得的结果普遍偏小,特别是立壁和趾板的剪力和弯矩,相差2倍以上,这就必然造成结构物的安全储备不足.悬臂式挡土墙的墙身截面较小,刚度相对较弱,在荷载作用下会产生较大的变形,这就必然会造成作用在挡墙上的应力的重新分布.按传统的设计方法计算挡土墙的受力时不考虑挡土墙的变形,不考虑挡土墙与地基的相互作用,甚至不考虑立壁、趾板和踵板连接处的力矩平衡.所得的结果和实际情况必然会有很大的差别.采用有限元法进行计算可以考虑这些因素的影响,而且可以考虑由于填土、地基、挡土墙三者刚度的变化对挡土墙受力的影响.其它的一些轻型挡土墙,如扶壁式挡土墙、锚杆挡土墙、锚钉板挡土墙等均存在这一问题.表2 朗金理论和有限元法计算结果比较Tab .2 The c o m paris o n of c alcu lated res ults betw ee n FE M and Rankine theory项 目立 壁趾 板踵 板最大剪力/(kN ·m -1)最大弯矩/(kN ·m ·m -1)最大剪力/(kN ·m -1)最大弯矩/(kN ·m ·m -1)最大剪力/(kN ·m -1)最大弯矩/(kN ·m ·m -1)朗金理论26.8727.32 57.9228.33-19.05-9.04有限元法挡墙厚度/cm528.50 6.97-63.5012.60 23.30 5.701041.3022.70-82.7033.90 23.30 11.201548.6043.40-95.6055.80 9.00 12.402054.8061.30-109.3074.80 1.90 13.503076.10101.20-137.8099.50-29.00-1.70(下转第26页)81北 方 交 通 大 学 学 报 第28卷。