弹簧计算公式

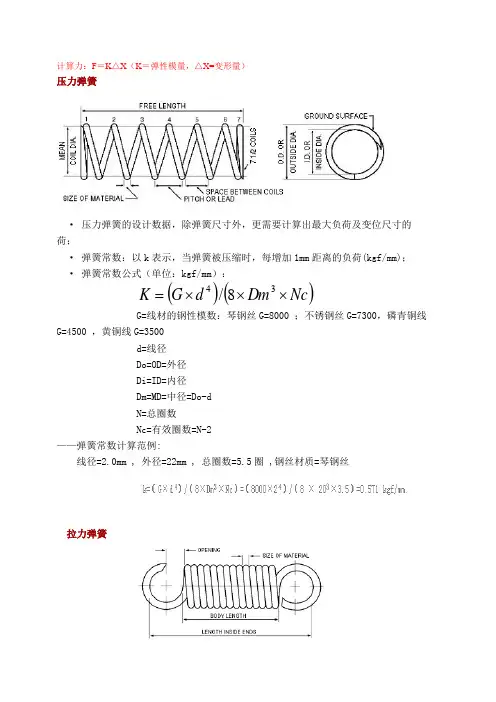
计算力：F ＝K △X （K ＝弹性模量，△X=变形量）压力弹簧· 压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的荷；· 弹簧常数：以k 表示，当弹簧被压缩时，每增加1mm 距离的负荷(kgf/mm)； · 弹簧常数公式（单位：kgf/mm ）：()()Nc Dm d G K ⨯⨯⨯=348/G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300，磷青铜线G=4500 ，黄铜线G=3500d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数Nc=有效圈数=N-2——弹簧常数计算范例:线径=2.0mm , 外径=22mm , 总圈数=5.5圈 ,钢丝材质=琴钢丝拉力弹簧拉力弹簧的 k值与压力弹簧的计算公式相同·拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

· 初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧· 弹簧常数：以 k 表示,当弹簧被扭转时，每增加1°扭转角的负荷 (kgf/mm).· 弹簧常数公式（单位：kgf/mm）:()()R4⨯⨯/=1167⨯K⨯pN⨯DmdEE=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200d=线径Do=OD=外径Di=ID=内径Dm=MD=中径=Do-dN=总圈数R=负荷作用的力臂p=3.1416。

胡克弹性定律指出，在弹性极限范围内，弹簧的弹性力f 与弹簧的长度x 成正比，即f =-kx，k 是一个物体的质量弹性系数，该系数由材料的性质决定，负号表示弹簧产生的弹性力与其延伸(或压缩)方向相反弹簧常数: 以k 表示，当弹簧被压缩时，载荷(kgf/mm)增加1mm 的距离，弹簧常数公式(单位: kgf/mm) : k = (g d4)/(8dm3 nc) g = 钢丝的刚度模量: 钢琴丝g = 8000; 不锈钢丝g = 7300; 磷青铜丝g = 4500;黄铜丝g = 3500d = 线径= 0d = 外径= id = 内径= md = 中径= do-dn = 转速总数弹簧常数的计算例子: 线径= 2.0 mm，外径= 22 mm，总匝数= 5。

5圈，钢丝材料= 钢琴钢丝k = (gxd4)/(8xdm3xnc) = (8000x24)/(8x203x3.5) = 0.571 kg f/mmpull，张力弹簧的k 值与压力弹簧的k 值相同。

张力弹簧的初始张力: 初始张力等于拉开彼此接近的弹簧所需的力，并发生在弹簧轧制成型之后。

在制作张力弹簧时，由于钢丝材质、线径、弹簧指数、静电现象、油脂、热处理、电镀等的不同，使得各张力弹簧的初始张力不均匀。

因此，在安装各种规格的张力弹簧时，应该预张力到平行弯道之间一定距离的力称为初张力。

初始张力= p-(kxf1) = 最大载荷-(弹簧常数x 拉伸长度)扭转弹簧常数: 以k 表示，当弹簧扭转时，载荷(kgf/m)增加1个扭转角。

弹簧常数(单位: kgf/mm) : k = (exd #)/(1167 xdmxpnxr) e = 钢丝的刚度模量: 钢琴线e = 21000，不锈钢线e = 19400，磷青铜线e =11200,黄铜丝e = 11200d = 线径= 0d = 外径= id = 内径= md = 中径= do-dn = 载荷作用下转臂的总长度= 3.1416。

简易的弹簧刚度计算公式
弹簧的刚度是指弹簧在单位变形时所产生的抵抗力或恢复力。

刚度通常用弹簧的切线斜率来表示，斜率越大，弹簧的刚度就越大。

弹簧的刚度可以通过以下公式进行计算：
K=(F2-F1)/(x2-x1)
其中，K是弹簧的刚度，单位是牛顿/米或N/m；F1和F2分别是弹簧在x1和x2位置施加的力，单位是牛顿；x1和x2分别是弹簧的起始位置和结束位置，单位是米。

这个简单的公式适用于线性弹簧，即在其工作范围内，变形与施加的力成正比。

对于非线性弹簧，如扭转弹簧或压缩弹簧，刚度的计算会更加复杂。

在实际应用中，弹簧的刚度也可以通过实验测量得到。

以下是一种常见的实验方法：
1.准备一根弹簧和一组质量。

2.将质量挂在弹簧上，并记录弹簧的变形量和所施加的力。

3.重复步骤2，使用不同的质量组合。

4.根据测得的弹簧变形量和所施加的力，应用上述公式计算弹簧的刚度。

需要注意的是，弹簧的刚度在真实使用中会受到多种因素的影响，如温度和弹簧的疲劳状况。

因此，在进行刚度计算时，需要考虑这些因素的影响。

此外，弹簧的刚度也可以通过有限元分析等数值模拟方法进行计算。

在这种方法中，弹簧的形状和材料性质通过建立模型进行输入，然后利用计算机模拟软件对弹簧的力学行为进行分析，从而得到刚度的准确计算结果。

综上所述，弹簧的刚度可以通过实验测量或数值模拟方法进行计算。

对于线性弹簧，可以使用简单的刚度计算公式，而对于非线性弹簧，则需要采用更为复杂的方法进行计算。

在实际应用中，还需考虑其他因素对刚度的影响。

弹簧劲度公式为: k = F / x，其中k为弹簧劲度（单位：牛/米），F为施加的力（单位：牛），x为弹簧的变形量（单位：米）。

弹簧劲度是描述弹簧刚度的物理量，用来表示弹簧在变形过程中所承受的力和变形量之间的关系。

弹簧劲度越大，说明弹簧越硬，需要施加更大的力才能产生相同的变形量；反之，弹簧劲度越小，说明弹簧越松，施加的力越小就能产生相同的变形量。

弹簧劲度的单位通常是牛/米（N/m），常用来设计和分析弹簧的性能，如弹性限制、振动消除等。

需要注意的是，弹簧劲度是一个线性量，只有在弹簧的变形量很小的情况下才能使用这个公式。

当弹簧变形量增大时，弹簧的劲度也会发生变化，这种现象被称为弹簧非线性。

如果要分析弹簧非线性的性能，需要使用非线性有限元分析或其他方法。

此外，在工程应用中，弹簧也可能会受到温度的影响，导致其劲度变化。

这种现象称为热膨胀。

热膨胀导致的劲度变化可以通过弹簧热膨胀系数来表示。

如果要考虑温度对弹簧性能的影响，需要使用带有热膨胀系数的弹簧劲度公式来计算。

弹簧力F=-KX，其中X是弹性系数，X是形状变量。

物体在外力作用下发生变形后，如果去掉外力，主体可以恢复到原来的形状，即所谓的“弹性力”。

方向与使对象变形的外力的方向相反。

由于物体变形的多样性，弹性力的形式也不同。

例如，如果把一个重物放在一个塑料板上，弯曲的塑料应该回到原来的状态，产生向上的弹性，这就是它对重物的支撑力。

把一个物体挂在弹簧上，这个物体就会拉伸弹簧。

拉长的弹簧需要回到原来的状态，产生向上的弹性力，即作用在物体上的拉力。

扩展数据：在线弹性阶段，一般虎克定律成立，即当应力σ1<σP（σP是比例极限）时，它成立。

它不一定保持在弹性范围内，σP<σ1<σe（σe是弹性极限）。

虽然在弹性范围内，广义虎克定律并不成立。

胡克弹性定律指出，弹簧的弹性力F与弹簧的伸长（或压缩）x成正比，即F=k·x。

k是材料的弹性系数，它只由特性决定，与其他因素无关。

负号表示弹簧在与其拉伸（或压缩）相反的方向上产生力。

满足虎克定律的弹性体是一种重要的物理理论模型。

它是对现实世界中复杂非线性本构关系的线性化简。

实践证明，这在一定程度上是有效的。

然而，事实上，有许多例子不符合胡克定律。

胡克定律的意义不仅在于它描述了弹性体的变形与力之间的关系，而且它创造了一种重要的研究方法：对现实世界中复杂的非线性现象进行线性化简，这在理论上在物理学中并不少见。

Fn∕S=E·（Δl∕l.）式中，FN为内力，s为FN作用的面积，L为弹性体的原始长度，ΔL为应力后的伸长率，比例系数e称为弹性模量，也称为杨氏模量，因为应变ε=ΔL/L。

因此，弹性模量和应力σ=FN/s具有相同的单位。

弹性模量是描述材料本身的物理量。

由上式可知，当应力大应变小时，弹性模量大，反之亦然。

否则，弹性模量较小。

弹性模量反映了材料对拉伸或压缩变形的抵抗力。

因为两种材料的弹性模量是不一样的，所以两者的弹性模量是不同的。

弹簧刚度计算公式：K=Gd4
8d23n
式中：
K-弹簧刚度，单位为n/m；
G-弹簧材料切变模量，钢：G=8X104MPa=8X1010Pa，青铜：G=4X104MPa=4X1010Pa；d-弹簧线径，单位为m；
d2-弹簧中经，单位为m；
n-弹簧有效圈数，无单位。

比如我们做一弹簧材料为65Mn的压簧，弹簧线径取0.8mm，弹簧中经取9mm，总圈数取6圈，有效圈数（支撑圈数）取5。

那么，这跟弹簧的刚度是：
K=Gd 4
8d23n
=8X1010X(8X10−4)4
8X(9X10−3)3X5
=84X10−6
9X10X5
=1.12X103N/m
=1.12N/mm
如果想少许提高弹簧的刚度，比如说提高25%，那可以别的参数不变，将支撑圈数改为4圈即可；如果支撑圈数改为3圈，那刚度就提高66.67%。

如果将弹簧线径由0.8mm改为1mm，别的参数都不变，那么，弹簧刚度就由原来的1.12N/mm，变为2.74N/mm，刚度提高了2.45倍！。

弹力计算公式压力弹簧初拉力计算F0=〖｛π×d3｝÷(8×D)〗×79mpaF0=｛×(5×5×5)÷(8×33)｝×79=117 kgf1.压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；2.弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；3.弹簧常数公式（单位：kgf/mm）；K=(G×d4)/(8×D3×Nc)G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，60Si2MnA钢丝G=7900，磷青铜线G=4500 ，黄铜线G=3500d=线径(钢丝直径)D=中径N=总圈数Nc=有效圈数F=运动行程(550mm)弹簧常数计算范例：线径=5.0mm , 中径=20mm , 有效圈数=圈,钢丝材质=不锈钢丝K=(G×d4)/(8×D3×Nc)=(7900×54)/(8×203×=m m×(F=100)=812 kgf拉力弹簧拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm)弹簧常数公式（单位：kgf/mm）：K=(E×d4)/(1167×D×p×N×R)E=线材之钢性模数：琴钢丝E=21000，不锈钢丝E=19400 ，磷青铜线E=11200 ，黄铜线E=11200d=线径(钢丝直径)D=中径N=总圈数R=负荷作用的力臂p=。

弹簧力F =-KX，其中X是弹性系数，X是形状变量。

在物体通过外力变形后，如果去除外力，则主体可以恢复其原始形状，这称为“弹性力”。

其方向与使物体变形的外力方向相反。

由于物体变形的多样性，弹力的形式也多种多样。

例如，如果将重物放在塑料板上，则弯曲的塑料应恢复到其原始状态并产生向上的弹力，这是其对重物的支撑力。

将一个物体挂在弹簧上，然后该物体将弹簧拉长。

需要将细长弹簧恢复到其原始状态，以产生向上的弹力，该弹力是作用在物体上的拉力。

扩展数据：在在线弹性阶段，一般的胡克定律成立，也就是说，当应力σ1 <σP（σP是比例极限）时，它成立。

它不一定保持在弹性范围内，σP <σ1 <σe（σe是弹性极限）。

尽管在弹性范围内，但广义的胡克定律不成立。

虎克的弹性定律指出，弹簧的弹力F与弹簧的伸长（或压缩）x成正比，即f = k·X。

K是材料的弹性系数，仅由特性决定材质，与其他因素无关。

负号表示弹簧在与其伸长（或压缩）相反的方向上产生力。

满足胡克定律的弹性体是重要的物理理论模型。

它是现实世界中复杂的非线性本构关系的线性简化，实践证明其在一定程度上是有效的。

但是，实际上，有许多不满足胡克定律的例子。

胡克定律的意义不仅在于它描述了弹性体的变形与力之间的关系，而且在于它创造了一种重要的研究方法：在现实世界中线性简化复杂的非线性现象，这在理论物理学中并不罕见。

Fn ∕S = E·（Δl∕l。

）其中FN是内力，s是FN作用的面积，L.是弹性体的原始长度，ΔL是应力后的伸长率，比例系数e称为弹性模量，也称为杨氏模量，因为应变ε=ΔL /L。

因此，弹性模量和应力σ= FN / s具有相同的单位。

弹性模量是描述材料本身的物理量。

从上式可以看出，如果应力大，应变小，则弹性模量大；反之，则大。

否则，弹性模量较小。

弹性模量反映了材料对拉伸或压缩变形的抵抗力。

对于某种材料，拉伸和压缩的弹性模量不同，但相差不大，因此可以将两者视为相同。

弹簧劲度系数计算公式
K=(F-x)/x
其中，F是弹簧受到的恢复力（单位是牛顿），x是弹簧的变形量（单位是米）。

实验方法是通过测量弹簧受到的力和变形量来计算劲度系数。

一种常用的实验方法是挂载一个负重于弹簧上，并测量弹簧的伸长量。

通过施加不同大小的负重，得到不同的伸长量，从而可以计算出劲度系数。

理论方法是通过弹簧的材料和几何参数来计算劲度系数。

根据材料的弹性模量和弹簧的截面积，可以计算出弹簧的刚度。

对于简单的弹簧，其劲度系数的计算可以用Hooke定律表示：
K = (Gd^4)/(8nd^3)
其中，G是弹簧材料的剪切模量，d是弹簧的直径，n是弹簧的螺旋数。

对于复杂的弹簧结构，例如扭簧和复合簧，劲度系数的计算会更加复杂。

需要考虑弹簧的几何形状、材料特性、加载方式等因素。

弹簧劲度系数的计算在工程设计和力学分析中具有重要意义。

它可以用于设计和计算弹簧系统的性能，例如弹簧片的刚度和变形量、弹簧悬挂系统的刚度和振动特性等。

在实际工程中，计算弹簧的劲度系数可以帮助工程师选择合适的弹簧材料和尺寸，以满足具体的工程要求。

总之，弹簧劲度系数是一个重要的物理量，可以通过实验或理论方法进行计算。

它在弹簧系统的设计和分析中具有重要的应用价值。

弹力计算公式压力弹簧初拉力计算F0=〖｛π3.14×d3｝÷(8×D)〗×79mpaF0=｛3.14×(5×5×5)÷(8×33)｝×79=117 kgf1.压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；2.弹簧常数：以k表示，当弹簧被压缩时，每增加1mm距离的负荷(kgf/mm)；3.弹簧常数公式（单位：kgf/mm）；K=(G×d4)/(8×D3×Nc)G=线材的钢性模数：琴钢丝G=8000 ；不锈钢丝G=7300 ，60Si2MnA钢丝G=7900，磷青铜线G=4500 ，黄铜线G=3500d=线径(钢丝直径)D=中径N=总圈数Nc=有效圈数F=运动行程(550mm)弹簧常数计算范例：线径=5.0mm , 中径=20mm , 有效圈数=9.5圈,钢丝材质=不锈钢丝K=(G×d4)/(8×D3×Nc)=(7900×54)/(8×203×9.5)=8.12kgf/m m×(F=100)=812 kgf拉力弹簧拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）扭力弹簧弹簧常数：以k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm)弹簧常数公式（单位：kgf/mm）：K=(E×d4)/(1167×D×p×N×R)E=线材之钢性模数：琴钢丝E=21000，不锈钢丝E=19400 ，磷青铜线E=11200 ，黄铜线E=11200d=线径(钢丝直径)D=中径N=总圈数R=负荷作用的力臂p=3.1416。

弹簧和重量物理公式推导
弹簧重量的计算（公斤）：
钢丝直径×钢丝直径×弹簧总圈数×弹簧中径×1.937÷100000
弹力公式
F=kx，F为弹力，k为劲度系数（或倔强系数），x为弹簧拉长（或压短）的长度。

例1：用5N力拉劲度系数为100N/m的弹簧，则弹簧被拉长5cm例2：一弹簧受大小为10N的拉力时，总长为7cm，受大小为20N的拉力时，总长为9cm，求原长和伸长3cm时受力大小？
结构分类
按受力性质，弹簧可分为拉伸弹簧、压缩弹簧、扭转弹簧和弯曲弹簧，按形状可分为碟形弹簧、环形弹簧、板弹簧、
螺旋弹簧、截锥涡卷弹簧以及扭杆弹簧等，按制作过程可以分为冷卷弹簧和热卷弹簧。

普通圆柱弹簧由于制造简单，且可根据受载情况制成各种型式，结构简单，故应用最广。

弹簧的制造材料一般来说应具有高的弹性极限、疲劳极限、冲击韧性及良好的热处理性能等，常用的有碳素弹簧钢、合金弹簧钢、不锈弹簧钢以及铜合金、镍合金和橡胶等。

弹簧的制造方法有冷卷法和热卷法。

弹簧丝直径小于8毫米的一般用冷卷法，大于8毫米的用热卷法。

有些弹簧在制成后还要进行强压或喷丸处理，可提高弹簧的承载能力。

各类弹簧弹力计算公式弹簧是一种常见的弹性元件，其具有弹力特性，用于储存和释放能量。

弹簧的弹力计算公式是根据其材料特性和几何形状来确定的。

以下是几种常见弹簧的弹力计算公式。

1.杆弹簧（线弹簧）杆弹簧是一种直线形状的弹簧，其弹力计算公式可以使用胡克定律进行描述。

胡克定律表明，弹簧的弹力与其拉伸或压缩的长度成正比，弹簧弹力的公式可以表示为：F=k*x其中，F表示弹簧的弹力，k表示弹簧的弹性系数，x表示弹簧的形变长度。

2.螺旋弹簧螺旋弹簧是一种扭转形状的弹簧，其弹力计算公式可以使用弹簧公式进行描述。

弹簧公式基于胡克定律，并考虑了螺旋形状对弹簧弹力的影响。

弹簧公式可以表示为：F=(Gd^4)/(8ND^3)其中，F表示弹簧的弹力，G表示弹簧材料的剪切模量，d表示弹簧线径，N表示弹簧的圈数，D表示弹簧的平均直径。

3.扭力弹簧扭力弹簧是一种以扭转为形变方式的弹簧，其弹力计算公式可以使用扭力弹簧公式进行描述。

扭力弹簧公式基于扭转力矩与弹簧角度的关系。

扭力弹簧公式可以表示为：T=(kφ)/L其中，T表示扭转力矩，k表示弹簧的扭力系数，φ表示弹簧的扭转角度，L表示弹簧的长度。

4.悬挂弹簧悬挂弹簧是一种用于悬挂装置的弹簧，其弹力计算公式可以根据工程需要进行设计。

常见的悬挂弹簧包括张紧弹簧和扭力挂弹簧。

对于张紧弹簧，其弹力计算公式可以表示为：F=(Gd^4)/(8Na)其中，F表示弹簧的弹力，G表示弹簧材料的剪切模量，d表示弹簧线径，N表示弹簧的圈数，a表示弹簧的平均半径。

对于扭力挂弹簧，其弹力计算公式可以表示为：F=(kφ)/R其中，F表示弹簧的弹力，k表示弹簧的扭力系数，φ表示弹簧的扭转角度，R表示弹簧的半径。

总结：以上是几种常见弹簧的弹力计算公式。

在实际设计和应用中，需要根据具体情况确定弹簧的弹性系数、形变长度、材料特性等参数，并使用相应的计算公式进行弹力计算。

扭力弹簧 弹簧常数： 以 k 表示, 当弹簧被扭 转时，每增 加1°扭转 角的负荷 (kgf/mm). 弹簧常数公 式（单位： kgf/mm）: K=(Ｅ×ｄ ４)／（１ １６７×Ｄ ｍ×ｐ×Ｎ ×Ｒ）
E=线材之钢 性模数：琴 钢丝 E=21000 , 不锈钢丝 E=19400 , 磷青铜线 E=11200,黄 铜线 E=11200 d=线径
胡克的弹性定律指出：在弹性限度内，弹簧的弹力f和弹簧的长度x成正比，即f=-kx，k是物 质的弹性系数，它由材料的性质所决定，负号表示弹簧所产生的弹力与其伸长（或压缩）的 方向相反。
压力弹簧的 设计数据， 除弹簧尺寸 外，更需要 计算出最大 负荷及变位 尺寸的负 荷；
弹簧常数： 以k表示， 当弹簧被压 缩时，每增 加1mm距离 的负荷 (kgf/mm)； 弹簧常数公 式（单位： kgf/mm）： K=(G×ｄ ４)／（８ ×Ｄｍ３× Ｎｃ）
Do=OD=外径
Di=ID=内径 Dm=MD=中径 =Do-d N=总圈数 R=负荷作用 的力臂 p=3.1416
G=线材的钢 性模数：琴 钢丝G=8000 ；不锈钢丝 G=7300；磷 青铜线 G=4500 ； 黄铜线 G=3500 d=线径
Do=OD=外径
Di=ID=内径
Dm=MD=中径 =Do-d
N=总圈数 Nc=有效圈 数=N-2 弹簧常数计 算范例:线 径=2.0mm , 外径=22mm , 总圈数 =5.5圈 ,钢 丝材质=琴 钢丝
K=(G×ｄ４) ／（８×Ｄ ｍ３×Ｎ ｃ）＝（８ ０００×２ ４）／（８ ×拉力力弹弹簧簧的 k值与压力
拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。 拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同， 使得每个拉力弹簧初始拉力产生不平均的现象。所以安装各规格的拉力弹簧时， 应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。 初张力=P（k×F1）= 最大负荷（弹簧常数 ×拉伸长 度）

弹簧变形量计算公式
弹簧是一种具有弹性的机械元件，在工程领域广泛应用。

但是，
当弹簧受到外力作用时，会发生变形。

那么，如何计算弹簧的变形量呢？
弹簧变形量与外力、材料参数和弹簧尺寸有关。

一般来说，弹簧
的变形量可以通过胡克定律进行计算。

胡克定律指出，当物体受到外
力作用时，其变形量与受力大小成正比。

对于弹簧而言，此公式可以
表示为：
ΔL = (F × L)/(k × G)
其中，ΔL表示弹簧的变形量，F表示外力大小，L表示弹簧长度，k表示弹簧劲度系数，G表示杨氏模量。

根据弹簧的劲度系数和杨氏模量，可以计算出弹簧的变形量。

但是，在计算变形量时需要注意以下几点：
1. 弹簧的劲度系数会随着材料的变化而变化，因此在计算变形量
时应该选用与实际材料相匹配的劲度系数。

2. 弹簧的变形量与长度成正比，因此在实际使用中，应该根据需
要选择适当的弹簧长度。

3. 不同类型的弹簧在计算变形量时可能需要不同的公式，因此在
实际使用中应该根据弹簧的实际情况进行计算。

总的来说，弹簧的变形量计算公式虽然简单，但其中包含了多个
参数，需要根据具体情况进行计算。

因此，在使用弹簧时，应该选择
符合实际情况的弹簧，并正确计算其变形量，以保证弹簧的正常使用。

弹簧力值计算公式表格
弹簧力值是弹簧在受力时所产生的力量大小，它是工程设计中常
用的重要参数。

为了方便大家使用和理解相关公式，本文将给出一份
弹簧力值计算公式表格，供有关人员参考使用。

（表格标题：弹簧力值计算公式）
弹簧力值计算公式
序号类型公式
1.悬臂弹簧力值F=k*x
2.压缩弹簧力值F=k*x^2
3.张紧弹簧力值F=k*ln(L0/L)
4.扭转弹簧力值F=k*θ
5.双作用弹簧力值F=k*x1*
x2/(x1+x2)
6.多级联弹簧力值F=k1*x1+ k2*x2+...+kn*xn
以上公式中，F表示弹簧力值，单位为牛顿(N)；k表示弹簧刚度
系数，单位为牛顿/米(N/m)；x表示弹簧的变形量，单位为米(m)；
x1、x2表示两个弹簧的变形量，单位为米(m)；L0表示弹簧的初始长度，单位为米(m)；L表示弹簧的变形后长度，单位为米(m)；θ表示弹簧的扭转角度，单位为弧度(rad)；xn表示第n级弹簧的变形量，单位为米(m)。

请根据实际需求选择合适的公式进行弹簧力值的计算。

在使用计
算公式时，请注意所选公式的适用范围和前提条件，避免误用导致计
算结果不准确。

以上就是弹簧力值计算公式表格的内容了。

希望这份表格能够对
您有所帮助，如果您在使用过程中遇到任何问题，欢迎随时咨询。

祝
您工作顺利！。

弹簧系数k的计算公式
弹簧系数k的计算公式是F=kx。

劲度系数，即倔强系数（弹性系数），它描述单位形变量时所产生弹力的大小，k值大，说明形变单位长度需要的力越大。

劲度系数又称刚度系数或者倔强系数。

劲度系数在数值上等于弹簧伸长（或缩短）单位长度时的弹力。

弹簧是一种利用弹性来工作的机械零件。

用弹性材料制成的零件在外力作用下发生形变，除去外力后又恢复原状。

亦作“弹簧”。

一般用弹簧钢制成。

弹簧的种类复杂多样，按形状分，主要有螺旋弹簧、涡卷弹簧、板弹簧、异型弹簧等。

F=kx，F为弹力，k为劲度系数（或倔强系数），x为弹簧拉长（或压短）的长度。

例1：用5N力拉劲度系数为100N/m的弹簧，则弹簧被拉长5cm。

按受力性质，弹簧可分为拉伸弹簧、压缩弹簧、扭转弹簧和弯曲弹簧，按形状可分为碟形弹簧、环形弹簧、板弹簧等。

1。

弹簧力F=-KX，其中X是弹性系数，X是形状变量。

物体在外力作用下发生变形后，如果去掉外力，主体可以恢复到原来的形状，这就是所谓的“弹性力”。

方向与使对象变形的外力的方向相反。

由于物体变形的多样性，弹性力的形式也不同。

例如，如果把重物放在塑料板上，弯曲的塑料应恢复到原来的状态并产生向上的弹性，这就是它对重物的支撑力。

把一个物体挂在弹簧上，然后这个物体就会拉伸弹簧。

拉长的弹簧需要恢复到其原始状态，以产生向上的弹性力，即作用于物体上的拉力。

扩展数据：在线弹性阶段，一般虎克定律成立，即当应力σ1<σP（σP是比例极限）时，它成立。

它不一定保持在弹性范围内，σP<σ1<σe（σe是弹性极限）。

虽然在弹性范围内，广义虎克定律并不成立。

胡克弹性定律指出，弹簧的弹性力F与弹簧的伸长（或压缩）x成正比，即F=k·x。

k是材料的弹性系数，它只由特性决定，与其他因素无关。

负号表示弹簧在与其拉伸（或压缩）相反的方向上产生力。

满足虎克定律的弹性体是重要的物理理论模型。

它是对现实世界中复杂非线性本构关系的线性化简，实践证明，它在一定程度上是有效的。

然而，事实上，有许多例子不符合胡克定律。

胡克定律的意义不仅在于它描述了弹性体的变形与受力之间的关系，而且它创造了一种重要的研究方法：对现实世界中复杂的非线性现象进行线性化简，这在理论物理学中并不少见。

Fn∕S=E·（Δl∕l.）式中，FN是内力，s是FN作用的面积，L是弹性体的原始长度，ΔL是应力后的伸长率，比例系数e被称为弹性模量，也称为杨氏模量，因为应变ε=ΔL/L。

因此，弹性模量和应力σ=FN/s具有相同的单位。

弹性模量是描述材料本身的物理量。

由上式可知，当应力大应变小时，弹性模量大，反之则大。

否则，弹性模量较小。

弹性模量反映了材料对拉伸或压缩变形的抵抗力。

对于某种材料，拉伸和压缩的弹性模量是不同的，但差别不大，所以可以认为两者是相同的。