(新课标)201X中考数学复习 第七章 图形与变换 第27节 图形的平移、对称与旋转(正文)
- 格式:ppt
- 大小:2.86 MB
- 文档页数:28

第七章图形与变换第二十四讲平移、旋转与对称【基础知识回顾】一、轴对称与轴对称图形:1、轴对称:把一个图形沿着某一条直线翻折过去,如果它能够与另一个图形那么就说这两个图形成轴对称,这条直线叫2、轴对称图形:如果把一个图形沿着某条直线对折,直线两旁的部分能够互相那么这个图形叫做轴对称图形3、轴对称性质:⑴关于某条直线对称的两个图形⑵对应点连接被对称轴【名师提醒:1、轴对称是指个图形的位置关系,而轴对称图形是指个具有特殊形状的图形;2、对称轴是而不是线段,轴对称图形的对称轴不一定只有一条】二、图形的平移与旋转:1、平移:⑴定义:在平面内,把某个图形沿着某个移动一定的这样的图形运动称为平移⑵性质:Ⅰ、平移不改变图形的与,即平移前后的图形Ⅱ、平移前后的图形对应点所连的线段平行且【名师提醒:平移作图的关键是确定平移的和】2、旋转:⑴定义:在平面内,将一个图形绕一个定点沿某个方向旋转一个,这样的图形运动称为旋转,这个点称为转动的称为旋转角⑵旋转的性质:Ⅰ、旋转前后的图形Ⅱ、旋转前后的两个圆形中,对应点到旋转中心的距离都,每对对应点与旋转中心的连线所成的角度都是旋转角都【名师提醒:1、旋转作用的关键是确定、和,2、一个图形旋转一定角度后如果能与自身重合,那么这个图形就是旋转对称图形】三、中心对称与中心对称图形:1、中心对称:在平面内,一个图形绕某一点旋转1800能与另一个图形就说这两个图形关于这个点成中心对称,这个点叫做2、中心对称图形:一个图形绕着某点旋转后能与自身重合,这种图形叫中心对称图形,这个点叫做3、性质:在中心对称的两个图形中,对称点的连线都经过且被平分【名师提醒:1、中心对称是指个图形的位置关系,而中心对称图形是指个具有特殊形状的图形2、常见的轴对称图形有、、、、、等,常见的中心对称图形有、、、、、等3、所有的正n边形都是对称图形,且有条对称轴,边数为偶数的正多边形,又是对称图形,4、注意圆形的各种变换在平面直角坐标系中的运用】【典型例题解析】1.已知点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),则a b的值为.2.点P(2,-1)关于x轴对称的点P′的坐标是.3.在图示的方格纸中(1)作出△ABC关于MN对称的图形△A1B1C1;(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?4.已知点P(3,2),则点P关于y轴的对称点P1的坐标是,点P关于原点O的对称点P2的坐标是5.下列图形中既是中心对称图形又是轴对称图形的是()A.B.C.D.6.点(3,2)关于x轴的对称点为()A.(3,-2)B.(-3,2)C.(-3,-2)D.(2,-3)7.在平面直角坐标系中,将点A(-2,3)向右平移3个单位长度后,那么平移后对应的点A′的坐标是()A.(-2,-3)B.(-2,6)C.(1,3)D.(-2,1)8.如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于()A.55°B.70°C.125°D.145°9.P是∠AOB内一点,分别作点P关于直线OA、OB的对称点P1、P2,连接OP1、OP2,则下列结论正确的是()A.OP1⊥OP B.OP1=OP2C.OP1⊥OP2且OP1=OP2D.OP1≠OP2 10.已知点M(3,-2),将它先向左平移4个单位,再向上平移3个单位后得到点N,则点N的坐标是.11.夏季荷花盛开,为了便于游客领略“人从桥上过,如在河中行”的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为280m,且桥宽忽略不计,则小桥总长为m.12.如图,在直角△OAB中,∠AOB=30°,将△OAB绕点O逆时针旋转100°得到△OA1B1,则∠A1OB= °.13.如图,正方形ABCD的边长为4,点P在DC边上且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为.14.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为.15.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.第二十五讲相似图形(一):【知识梳理】1.比例基本性质及运用(1)线段比的含义:如果选用同一长度单位得两条线段a、b的长度分别为m、n,那么就说这两条线段的比是a:b=m:n,或写成a m=b n,和数的一样,两条线段的比a、b中,a叫做比的前项 b叫做比的后项.注意:①针对两条线段;②两条线段的长度单位相同,但与所采用的单位无关;③其比值为一个不带单位的正数.(2)线段成比例及有关概念的意义:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段,已知四条线段a、b、c、d,如果a c=b d或a:b=c:d,那么a、b、c、d叫做成比例的项,线段a、d叫做比例外项,线段b、d叫做比例内项,线段d叫做a、b、c的第四比例项,当比例内项相同时,即a bb c=或a:b=b:c,那么线段b叫做线段a和c的比例中项.(3)比例的性质,①基本性质:如果a:b=c:d,那么ad=bc;反之亦成立。




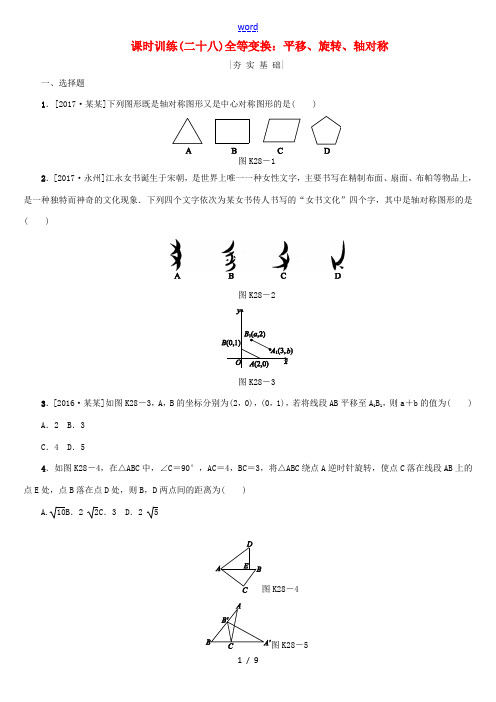
课时训练(二十八)全等变换:平移、旋转、轴对称|夯实基础|一、选择题1.[2017·某某]下列图形既是轴对称图形又是中心对称图形的是( )图K28-12.[2017·永州]江永女书诞生于宋朝,是世界上唯一一种女性文字,主要书写在精制布面、扇面、布帕等物品上,是一种独特而神奇的文化现象.下列四个文字依次为某女书传人书写的“女书文化”四个字,其中是轴对称图形的是( )图K28-2图K28-33.[2016·某某]如图K28-3,A,B的坐标分别为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( ) A.2 B.3C.4 D.54.如图K28-4,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B,D两点间的距离为( )A.10B.2 2C.3 D.2 5K28-4K28-55.[2017·聊城]如图K28-5,将△ABC绕点C顺时针旋转,使点B落在AB边上点B′处,此时,点A的对应点A′恰好落在BC的延长线上,下列结论错误的是( )A.∠BCB′=∠ACA′ B.∠ACB=2∠BC.∠B′CA=∠B′AC D.B′C平分∠BB′A′6.[2017·某某]把一X长方形纸片按如图K28-6①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则重新展开后得到的图形是( )图K28-6图K28-77.如图K28-8,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF 上点G处,并使折痕经过点A,展平纸片后∠DAG的大小为( )图K28-8A.30° B.45° C.60° D.75°二、填空题8.如图K28-9,把三角板的斜边紧靠直尺平移,一个顶点从刻度“5”平移到刻度“10”,则顶点C平移的距离CC′=________.K28-9K28-109.[2017·]如图K28-10,在平面直角坐标系xOy中,△AOB可以看作是△OCD经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△OCD得到△AOB的过程:__________________.图K28-1110.[2016·某某]将等边三角形CBA绕点C顺时针旋转∠α得到三角形CB′A′,使得B,C,A′三点在同一直线上,如图K28-11所示,则∠α的大小是________.图K28-1211.如图K28-12,已知正方形ABCD的边长为3,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D 逆时针旋转90°,得到△DCM.若AE=1,则FM的长为________.三、解答题12.[2017·某某]如图K28-13,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形;(2)画出△DEF关于直线l对称的三角形;(3)填空:∠C+∠E=________°.图K28-1313.[2017·某某]如图K28-14,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(-3,4),B(-5,2),C(-2,1).(1)画出△ABC关于y轴的对称图形△A1B1C1;(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;(3)求(2)中线段OA扫过的图形面积.图K28-1414.[2016·某某]如图K28-15,将等腰三角形ABC绕顶点B按逆时针方向旋转角α到△A1BC1的位置,AB与A1C1相交于点D,AC分别与A1C1,BC1交于点E,F.(1)求证:△BCF≌△BA1D;(2)当∠C=α时,判定四边形A1BCE的形状并说明理由.图K28-15|拓展提升|图K28-1615.[2016·某某]如图K28-16,将矩形ABCD沿GH折叠,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8,AB=6,AE=4,则△EBF的周长是________.16.在学习轴对称的时候,老师让同学们思考课本中的探究题.如图K28-17,要在燃气管道l上修建一个泵站,分别向A,B两镇供气.泵站修在管道的什么地方,可使所用的输气管线最短?图K28-17 图K28-18你可以在l上找几个点试一试,能发现什么规律?聪明的小华通过独立思考,很快得出了解决这个问题的正确方法.他把管道l看成一条直线(如图K28-18),问题就转化为要在直线l上找一点P,使AP与BP的和最小.他的做法是这样的:①作点B关于直线l的对称点B′;②连接AB′交直线l于点P,则点P即为所求.请你参考小华的做法解决下列问题.如图K28-19,在△ABC中,点D,E分别是AB,AC边的中点,BC=6,BC边上的高为4,请你在BC边上确定一点P,使△PDE的周长最小.(1)在图中作出点P(保留作图痕迹,不写作法);(2)请直接写出△PDE周长的最小值:________.图K28-19参考答案1.B2.A3.A [解析] 由B 点平移前后的纵坐标分别为1,2,可得B 点向上平移了1个单位.由A 点平移前后的横坐标分别是2,3,可得A 点向右平移了1个单位.由此可得a =1,b =1,故a +b =2.4.A [解析] 连接BD ,在Rt △ABC 中,∠C =90°,AC =4,BC =3,由勾股定理得AB =AC 2+BC 2=5.将△ABC 绕点A 逆时针旋转,使点C 落在线段AB 上的点E 处,点B 落在点D 处,则有AE =4,DE =3,∴BERt △BED 中,BD =BE 2+DE 2=10.5.C [解析] 由旋转的性质可知∠BCB′=∠ACA′,BC =B′C,∠B =∠CB′A′,∠B′A′C=∠B′AC,∠ACB =∠A ′CB ′,由BC =B′C 可得,∠B =∠CB′B,∴∠CB ′B =∠CB′A′,∴B ′C 平分∠BB′A′.又∠A′CB′=∠B +∠CB′B=2∠B ,∴∠ACB =2∠B.∴C 错误.6.C [解析] 选项A 、B 不符合以折痕所在直线为对称轴的特征,选项C 、D 四个图形都符合以折痕所在直线为对称轴的特征,但选项D 的基本图形△的位置与题意不符,只有C 与之吻合(如图),故选C.7.C [解析] 如图,根据折叠有∠1=∠2,AN =MN ,∠MGA =90°, ∴2NG =AM ,AN =NG , ∴∠2=∠4.∵EF ∥AB ,∴∠4=∠3,∴∠1=∠2=∠3=30°,∴∠DAG =60°.8.59.将△COD 绕点C 顺时针旋转90°,再向左平移2个单位长度得到△AOB(答案不唯一) 10.120° [解析] ∵三角形ABC 是等边三角形, ∴∠ACB =60°.∵等边三角形CBA 绕点C 顺时针旋转∠α得到△CB′A′,使得B ,C ,A ′三点在同一直线上, ∴∠BCA ′=180°, ∴α=180°-60°=120°.11.52 [解析] ∵△DAE 绕点D 逆时针旋转90°得到△DCM, ∴∠FCM =∠FCD+∠DCM=180°,DE =DM ,∠EDM =90°, ∴F ,C ,M 三点共线, ∠EDF +∠FDM=90°. ∵∠EDF =45°, ∴∠FDM =∠EDF=45°. 在△DEF 和△DMF 中,⎩⎪⎨⎪⎧DF =DF ,∠EDF =∠FDM,DE =DM ,∴△DEF ≌△DMF(SAS), ∴EF =MF. 设EF =MF =x ,∵AE =CM =1,且BC =3, ∴BM =BC +CM =3+1=4, ∴BF =BM -MF =4-x. 在Rt △EBF 中, EB =AB -AE =3-1=2, 由勾股定理得EB 2+BF 2=EF 2, 即22+(4-x)2=x 2, 解得x =52,∴FM =52.12.解:(1)(2)见下图.(3)4513.解:(1)如图所示,△A 1B 1C 1即为所求作的三角形. (2)如图所示,△A 2B 2C 2即为所求作的三角形.(3)线段OA 扫过的图形面积为14π·OA 2=14π·(32+42)=254π.14.解:(1)证明:∵△ABC 是等腰三角形, ∴AB =BC ,∠A =∠C.∵将等腰三角形ABC 绕顶点B 按逆时针方向旋转角α到△A 1BC 1的位置,∴A 1B =AB =BC ,∠A =∠A 1=∠C,∠A 1BD =∠CBC 1. 在△BA 1D 与△BCF 中, ⎩⎪⎨⎪⎧∠A 1=∠C,A 1B =BC ,∠A 1BD =∠CBF, ∴△BCF ≌△BA 1D(ASA).(2)四边形A 1BCE 是菱形.理由如下:∵将等腰三角形ABC 绕顶点B 按逆时针方向旋转角α到△A 1BC 1的位置, ∴∠A 1=∠A.∵∠ADE =∠A 1DB ,∴∠AED =∠A 1BD =α, ∴∠DEC =180°-α. ∵∠C=∠A=α, ∴∠A 1=∠A=α,∴∠A 1=∠C,∠A 1BC =360°-∠A 1-∠C-∠A 1EC =180°-α, ∴∠A 1BC =∠AEC,∴四边形A 1BCE 是平行四边形. 又A 1B =BC ,∴四边形A 1BCE 是菱形.15.8 [解析] 设AH =a ,则DH =AD -AH =8-a ,在Rt △AEH 中,∠EAH =90°,AE =4,AH =a ,EH =DH =8-a , 由EH 2=AE 2+AH 2,得(8-a)2=42+a 2, 解得a =3.∵∠BFE +∠BEF=90°,∠BEF +∠AEH=90°, ∴∠BFE =∠AEH.又∵∠EAH=∠FBE=90°, ∴△EBF ∽△HAE , ∴C △EBF C △HAE =BE AH =AB -AE AH =23. ∵C △HAE =AE +EH +AH =AE +AD =12, ∴C △EBF =23C △HAE =8.16.解:(1)作点D关于BC的对称点D′,连接D′E,与BC交于点P,点P即为所求(或作点E关于BC的对称点E′),如图所示.(2)如图所示,连接DE,DP,∵点D,E分别是AB,AC边的中点,∴DE为△ABC的中位线.∵BC=6,BC边上的高为4,∴DE=3,DD′=4,∴D′E=DE2+DD′2=32+42=5,∴△PDE周长的最小值为DE+D′E=3+5=8.故答案为8.。