分形几何学及应用. 上册(王兴元,孟娟著)思维导图

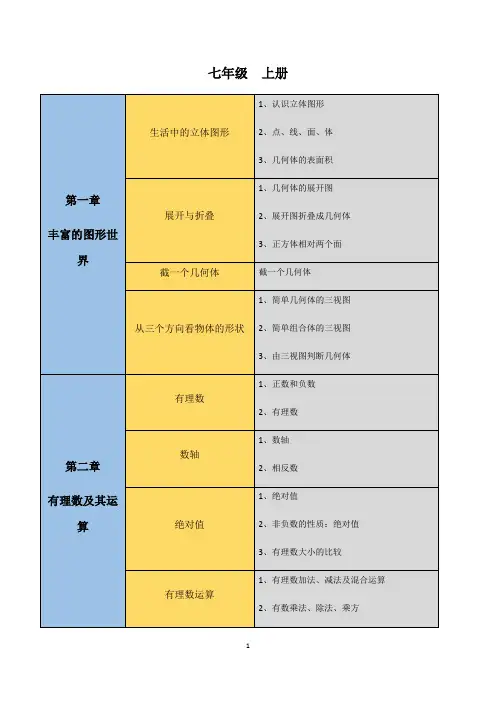
高中数学最全的思维导图小数老师2015-11-23 11:08很多同学一轮复习已经过半，但还不知道该怎么总结，小数老师给大家提个建议，要想总结，主要还是首先梳理出脉络来，提到某个知识点，那么关于这个知识点相关的所有知识你都要弄明白，这样你就成功了一半！下面是8张思维导图，先研究下看看吧！夷示方法元表、隼合之闾的关系集台「1f映射i I 函数三要妄性质表示定义定义域值域单调性周期性性质対称性基本初等函数分段国数运算：交、弃、补确定性、互异性、无序性解析达列表法使解析式有意义丿对应关采［」换元法求解析式JA连意应用函数的单调在求值域圏象法u函薮破个区圈MlWt减I与曲谒国直是秃亍区减占鱼乂耒冒：2,征阴尊讶*勒査『斷人导披追；儿麗舍弼戴的鱼调性亘塑」是乂填黄于旗点时歌氐L©社有盘文的奇證戳弋r如即）r的奇圈埶詡⑵二呻书⑹=£）最值—C环酩变拱）—f皑拦变彗）—｛棒编变箕）亘合函数二次函巍、基本不等式、打崗（耐克）函〕数、三角函数有界性、数形结台、异数.L —次、二次函数、反比例函數一幕函数指数函数对数函数三甬函埶亘台III埶的单调性：同潸异减I哦值法、典型的函数1抽象函数函数与方程函埶的应用图象V性质和应用二分注、图象迭、二次展三次方程根的分布）空间几何体liii台区梭怪梭台L囲台Sfe-正枝｛王，长方体、正方体EW.四面体、正四面体一l点在Mh±点与线纬与面一面勻面点在面內点在面外竝面岂強-直线在平窗内厂平行—相乂—f平行关系的］A 转化J i ■■-平厅J垂直曲罕的］线线1相互轉化J垂嵐L相父L平行L三视團•r直观團长对正-喜平齐卞伯隼」一刚面积.表面理体段口高—个公共点没有缺旦漫有有公扛耳------------------ 厂W T 厂直线在平面外-^―---------------- L相交亠线面- "平行「面直垂畳线面甜r-J_ -面面■乎行價耕角的畫化与糾率的变化）位臭关养相立I—C且必：-今血芒：）狂童：战距可正A可员，也可为0. J注at：栽距可正可员，也可訂oj直迭万程茹形式直迭万程茹形式两亶线的交点两亶线的交点圧意若种开式的辕化和运用范圈圧意若种开式的辕化*□运用范围不等式群三即T通项会式等比数列一1（样。

【干货】学会这8张思维导图,再复杂的知识都能轻松拿下父母在家就能指导孩子，推荐收藏。

投稿邮箱：***************你读书时候是不是有一类学生？他们学习不熬夜，考前不突击，但是门门课成绩都很好，爸妈说这叫“天资过人”。

去年同学会，我重逢那位“天资过人”的老同学，聊起对他的羡慕时他谦虚说：“大家的智商都差不多，可能我学习方法比较好。

”然后他就把当年的笔记给我看，大概是这样的——手绘思维导图示意图（图片来源于网络）后来我知道，这就是“思维导图”（Thinking Map），一种图形思维工具。

在美国新加坡思维导图已经成为小学生的必修课，近几年国内热度也上来了。

思维导图的理论是“可视化思维”（Visible Thinking）。

1967年，哈佛大学教育学院成立“零点计划”，对思维方式进行研究，其中一个明星项目就是“可视化思维”——被可视化的思维更有利于理解和记忆，现在已经是一种比较公认的高效学习方法了。

回过头再想，当年我们学习遇到困难无非就是：没兴趣、记不住、转不了弯。

使用“思维导图”的过程比传统死记硬背要主动且有趣得多，理清思路后又便于记忆，掌握原理后也减少难以融会贯通的问题。

“蓝橡树未来学校”针对1-3年级学生，订制了一个双12“思维导图探究课程礼包”，礼包包含有2节“思维导图课” 4节“社区探究主题课”，另外赠送2节“升学指导家长课”。

学生课程均为全英文外教授课！在2节思维导图课程中，学生将学到8种思维导图，这8张思维导图都是美国小学生最常使用的。

今天橡树君就根据课程内容总结这8种思维导图，如何使用？什么情况下用？一目了然。

（下文可能包含课程关键细节的透露）一、整理思路的利器：圆圈图（Circle Map）•常用指数：五颗星•使用场景：定义一件事情、展开一个主题等Circle Map是用于把一件主题，知识点，事物展开联想，或者描述细节。

它由一大一小两个圆圈构成，小圆圈里放的是你想要展开的主题，大圆圈里放的是和这个主题相关的细节和特征。

一张图读懂初中代数、几何（思维导图）很全面，值得为孩子收藏初中数学是很重要的，不论是函数还是基础对于高中的数学来说都是一个打基础的的阶段。

初中数学学得好的学生到高中无论是在数学理解能力还是在解题方面都会比其他的学生领悟性强的多。

所以初中数学需要一步步的把基础打牢，为什么要把初中数学学好呢？想要知道原因的一起来看看吧。

首先初中数学对高中数学的学习起着重要的基础作用。

初中阶段被称为培养数学运算能力的黄金期，初中的代数学习中，运算是一项重要的内容，比如有理数的运算、整式的运算、因式分解、分式的运算、根式的运算以及解方程等。

在数学的学习中经常会强调基础的重要性，而初中阶段运算能力就是数学学习中的基础内容，为进一步学习内容的深化打下良好基础。

初中三角函数部分的内容是对基本概念和定理的初步认识，在高中阶段则会进一步深入学习，如果没有掌握基础内容，则会对接下来的数学学习产生影响。

在初中数学的几何部分，主要涉及平面几何的内容，这为高中阶段难度更大的立体几何的学习做好理论基础的准备。

接下来，老师整理了初中代数、几何所有模型、知识点汇总，内容pdf格式、可下载、可打印、可编辑，有条件的家长、老师打印给孩子练练，吃透这些知识点对孩子基础知识积累、学习成绩提升有帮助。

整理不易，希望大家点赞、收藏、转发吧，感谢大家支持！需要电子版用户，请拉至文章底部↓↓↓文章篇幅较长，只展示了部分内容，完整电子版在以下内容目录中，后续将分享更多优质、精选内容，目录预览：获取以上全部word 打印版资料：1、点击头像进入主页并关注2、点击私信按钮发送资料二字即可注：极速版头条用户，找不到私信按钮，建议安装原版头条APP坚持每天整理、分享中小学语文、数学、英语各科学习辅导资料，孩子学习进步、成绩提升就是我们的目标，喜欢就多多关注吧！。

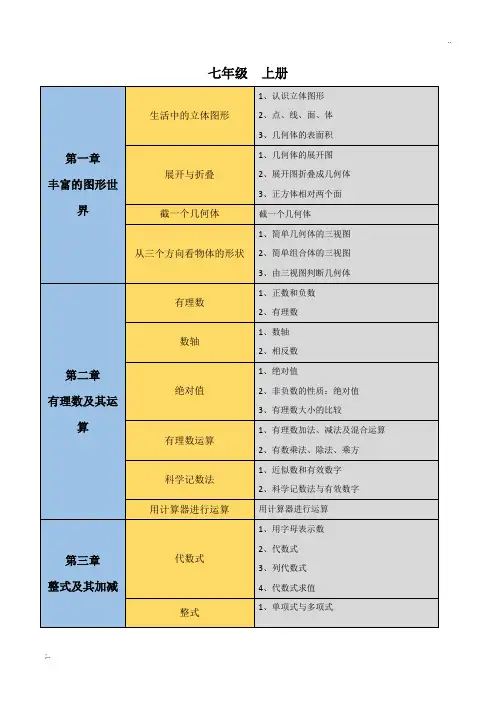
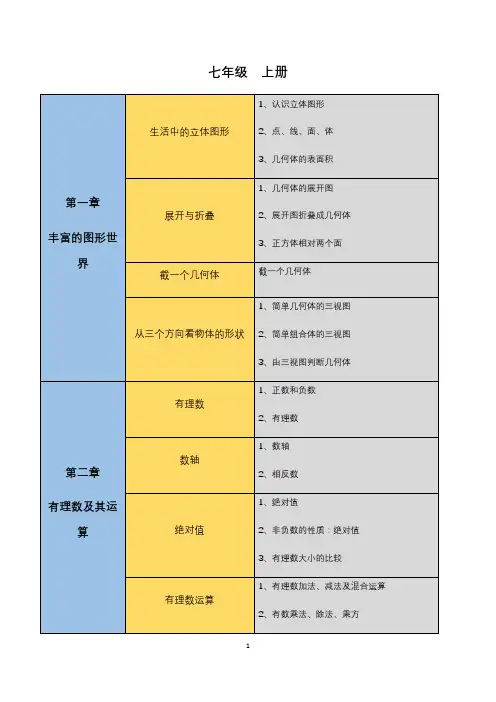
初中数学知识点思维导图（北师大版）七年级上册第一章丰富的图形世界第二章有理数及其运算第三章整式及其加减生活中的立体图形展开与折叠截一个几何体从三个方向看物体的形状有理数数轴绝对值有理数运算科学记数法用计算器进行运算代数式整式1、认识立体图形2、点、线、面、体3、几何体的表面积1、几何体的展开图2、展开图折叠成几何体3、正方体相对两个面截一个几何体1、简单几何体的三视图2、简单组合体的三视图3、由三视图判断几何体1、正数和负数2、有理数1、数轴2、相反数1、绝对值2、非负数的性质：绝对值3、有理数大小的比较1、有理数加法、减法及混合运算2、有数乘法、除法、乘方1、近似数和有效数字2、科学记数法与有效数字用计算器进行运算1、用字母表示数2、代数式3、列代数式4、代数式求值1、单项式与多项式第四章基本平面图形第五章一元一次方程整式的加减探索与表达规律线段、射线、直线比较线段的长短角角的比较多边形与圆的初步认识求解一元一次方程一元一次方程的应用1、同类项与合并同类项2、去口号与添括号3、整式的加减与化简求值数字的变化规律1、线段、射线、直线2、直线的性质：两点确定一条直线1、线段的性质：两点之间线段最短2、两点间的距离3、比较线段的长短4、尺规作图1、角的概念（钟面角、方向角）2、度分秒的换算3、作图 --基本作图1、角平分线的定义2、角的计算3、角的大小的比较1、多边形与多边形的对角线2、圆的认识（圆心角、弧、弦的关系）3、扇形面积的计算1、方程的定义2、方程的解3、等式的性质4、一元一次方程的定义1、一元一次方程的解2、解一元一次方程3、含绝对值符号的一元一次方程4、同解方程第六章数据的收集与整理数据的收集普查和抽样调查数据的表示统计图的选择1、调查收集数据的过程与方法2、统计表1、全面调查与抽样调查2、总体、个体、样本、样本容量3、用样本估计总体1、频数与频率2、频数（率）分布直方图、分布表、折现图3、统计表4、条形统计图1、扇形统计图、条形统计图、折现统计图2、统计图的选择七年级下册同底数幂的乘法同底数幂的乘法幂的乘方与积的乘方幂的乘方与积的乘方第一章整式的乘法第二章同底数幂的除法整式的乘法平方差和完全平方整式的除法两条直线的位置关系1、同底数幂的除法2、零指数幂3、负整数指数幂1、单项式乘单项式2、单项式乘多项式3、多项式乘多项式平方差公式和完全平方公式1、整式的除法2、整式的混合运算及化简求值1、相交线（对顶角、邻补角）2、垂线（垂线段最短、点到直线距离）相交线与平行线第三章变量之间的关系第四章三角形第五章生活中的轴对称探索直线平行的条件平行线的性质尺规作图用表格表示变量间的关系用关系式表示的变量间的关系用图像表示的变量间关系认识三角形图形的全等探索三角形全等的条件尺规作图全等三角形的应用轴对称现象探索轴对称的性质3、平行线1、同位角、内错角、同旁内角2、平行线的判定平行线的性质尺规作角1、常量与变量2、函数的表示方法1、函数的概念、关系式、自变量取值范围、函数值1、函数图像2、动点问题的函数图像3、分段函数1、三角形的角平分线、中线和垂线2、面积、重心、三边关系3、内角和定理4、外角性质5、直角三角形的性质1、全等图形1、三角形的稳定性2、全等三角形的判定3、全等三角形的判定与性质尺规作三角形利用三角形全等测距离1、生活中的轴对称现象2、轴对称图形1、轴对称的性质2、轴对称 --最短路径问题3、翻折变换（折叠问题）第六章概率初步简单的轴对称图形感受可能性频率的稳定性等可能事件的概率1、角平分线性质2、线段垂直平分线的性质3、等腰三角形的性质与判定4、等边三角形的性质与判定1、随机事件2、可能性的大小利用频率估计概率1、概率的意义、公式2、几何概率3、列表法与树状图法第一章勾股定理第二章实数八年级上册探索勾股定理勾股定理与证明勾股定理逆定理1、勾股定理逆定理2、勾股数勾股定理的应用1、勾股定理的应用2、平面展开 --最短路劲问题无理数无理数1、平方根平方根2、算术平方根3、非负数的性质立方根立方根估算1、实数大小的比较2、估算无理数的大小用计算器开方用计算器开方实数实数性质、数轴、运算第三章位置与坐标第四章一次函数二次根式确定位置平面直角坐标系轴对称与坐标变化函数一次函数与正比例函数一次函数的图像1、二次根式的定义2、二次根式有意义的条件3、二次根式的性质与化简4、最简二次根式5、二次根式的乘除法6、分母有理化7、同类二次根式8、二次根式的加减法9、二次根式的混合运算10、二次根式的化简求值坐标确定位置1、点的坐标2、坐标与图形性质3、两点间距离公式4、关于 x 轴、 y 轴、原点对称点的坐标轴对称与坐标变化（对称、平移、旋转）1、常量与变量2、函数概念、关系式、自变量的取值范围、函数值3、函数图像4、函数的表示方法1、一次函数、正比例函数定义2、待定系数法求一次函数与正比例函数3、一次函数与一元一次方程4、根据实际问题列一次函数关系式1、一次函数、正比例函数的图像与性质2、一次函数图像与系数的关系3、一次函数图像上点的坐标特点第五章二元一次方程组第六章数据的分析第七章平行线的证明一次函数的应用多边形与圆的初步认识认识二元一次方程组求解二元一次方程二元一次方程的应用二元一次方程与一次函数三元一次方程组平均数中位数与众数从统计图分析数据的几种趋势数据的离散程度推理论证、命题定理平行线的判定平行线的性质4、一次函数图像与几何变换一次函数的应用与综合题4、多边形与多边形的对角线5、圆的认识（圆心角、弧、弦的关系）6、扇形面积的计算1、二元一次防尘的定义、解2、解二元一次方程3、二元一次方程组的定义、解1、解二元一次方程组2、同解方程组1、鸡兔同笼2、增收节支3、里程碑1、二元一次方程（组）与一次函数2、用二元一次方程组确定一次函数表达式1、解三元一次方程组2、三元一次方程组的应用算术平均数、加权平均数中位数与众数1、扇形、条形、折线统计图及其选择2、统计量的选择1、极差、方差、标准差2、计算器 --标准差与方差推理论证、命题定理1、平行公理及推论2、平行线的判定平行线的性质三角形内角和定理三角形内角和定理八年级下册第一章三角形的证明第二章一元一次不等式（组）第三章图形的平移与等腰三角形直角三角形线段的垂直平分线角平分线不等式不等式的解集一元一次不等式一元一次不等式与一次函数一元一次不等式组图形的平移等腰三角形的性质与判定1、直角三角形全等的判定2、直角三角形的性质3、含30°角的直角三角形4、直角三角形斜边上的中线线段的垂直平分线的性质角平分线的性质1、不等关系的定义2、不等式的基本性质1、不等式的解集2、在数轴上表示不等式的解集1、一元一次不等式的定义2、解一元一次不等式3、一元一次不等式的整数解4、由实际问题抽象出一元一次不等式5、不等式的应用一元一次不等式与一次函数1、一元一次不等式组的定义2、解一元一次不等式组3、一元一次不等式组的整数解4、不等式组的应用1、生活中的平移现象2、平移的性质3、坐标与图形的变化--平移4、利用平移设计图案旋转图形的旋转中心对称简单的图案设计因式分解的意义提公因式法第四章因式分解公式法认识分式第五章分式与分式方程分式运算1、生活中的旋转现象2、旋转的性质3、旋转对称图形4、作图 --旋转变换1、中心对称图形2、关于原点对称的点的坐标1、利用旋转设计图案2、几何变换的类型因式分解的意义1、公因式2、提公因式法1、公式法2、提公因式法与公式法的综合3、分组分解法4、十字相乘法5、实数范围内分解因式6、因式分解的应用1、分式的定义2、分式有意义的条件3、分式的值为零的条件4、分式的值5、分式的基本性质6、约分7、同分8、最简分式9、最简公分母10、列代数式（分式）1、分式乘除法2、分式加减法3、分式混合运算4、分式的化简求值1、分式方程的定义域解2、解分式方程分式方程3、换元法解分式方程第六章平行四边形的性质平行四边形的判定4、分式方程的增根5、分式方程的应用1、平行四边形的性质2、等腰梯形的性质与判定平行四边形的判定与性质平行四边形三角形的中位线三角形的中位线定理1、多边形的对角线多边形内角和与外角和推理论证、命题定理2、多边形内角和外角推理论证、命题定理第七章平行线的证明平行线的判定平行线的性质3、平行公理及推论4、平行线的判定平行线的性质第一章特殊的平行四边形第二章一元二次方程三角形内角和定理三角形内角和定理九年级上册菱形的性质与判定菱形的性质与判定矩形的性质与判定矩形的性质与判定正方形的性质与判定正方形的性质与判定1、一元二次方程的定义认识一元二次方程2、一元二次方程的一般性质3、一元二次方程的解第三章概率的进一步认识第四章图形的相似第五章投影与视图第六章反比例函数配方法公式法因式分解法一元二次方程的根与系数关系一元二次方程实际应用树状图或表格求概率用频率估计概率成比例线段平行线分线段成比例三角形相似的条件利用相似三角形测高图形的位似投影视图反比例函数图像与性质1、直接开平方法2、配方法1、公式法2、根的判别式1、因式分解法2、换元法根与系数关系一元二次方程实际应用树状图或表格求概率用频率估计概率1、比例的性质2、比例线段平行线分线段成比例三角形相似的判定与性质1、相似三角形的应用2、作图 --相似变换位似变换1、平行投影、中心投影2、视点、视角和盲区1、简单几何体、组合体的三视图2、有三视图判断几何体3、作图 --三视图1、反比例函数的定义2、反比例函数的图像与对称性3、反比例函数的性质反比例函数的应用从统计图分析数据的几种趋势数据的离散程度4、系数 k 的几何意义5、反比例函数图像上点的坐标特征6、待定系数法求反比例函数解析式7、反比例函数与一次函数交点问题反比例函数的应用3、扇形、条形、折线统计图及其选择4、统计量的选择3、极差、方差、标准差4、计算器 --标准差与方差第一章直角三角形的边角关系第二章二次函数九年级下册1、锐角三角函数的定义锐角三角函数2、锐角三角函数的增减性1、同角三角函数的关系30° 45°60°角的三角函2、互余两角三角函数关系数3、特殊角的三角函数值解直角三角形解直角三角形1、三角函数的应用三角函数的应用2、坡度1、仰角俯角问题利用三角函数测高2、方向角问题1、二次函数的定义2、二次函数的图像与性质二次函数的图像与性质3、二次函数的图像与系数的关系4、二次函数图像上点的坐标特征5、二次函数图像与几何变换第三章圆确定二次函数的表达式二次函数的应用二次函数与一元二次方程圆垂径定理圆心角与圆周角的关系确定圆的条件直线与圆的位置关系切线长定理圆内接正多边形弧长与扇形面积6、二次函数的最值1、淡定系数法求二次函数解析式2、二次函数的三种形式1、二次函数的实际应用1、抛物线与x 轴的交点2、图像法求一元二次方程的近似根3、二次函数与不等式（组）1、圆的认识2、圆的对称性（圆心角、弧、弦关系）垂径定理及其应用1、圆周角定理2、圆内接四边形的性质3、相交弦定理1、点与圆的位置关系2、三角形外接圆与外心1、切线的性质2、切线的判定3、切线角定理4、切割线定理5、三角形内切圆与内心切线长定理圆内接正多边形1、弧长的计算2、扇形面积的计算。

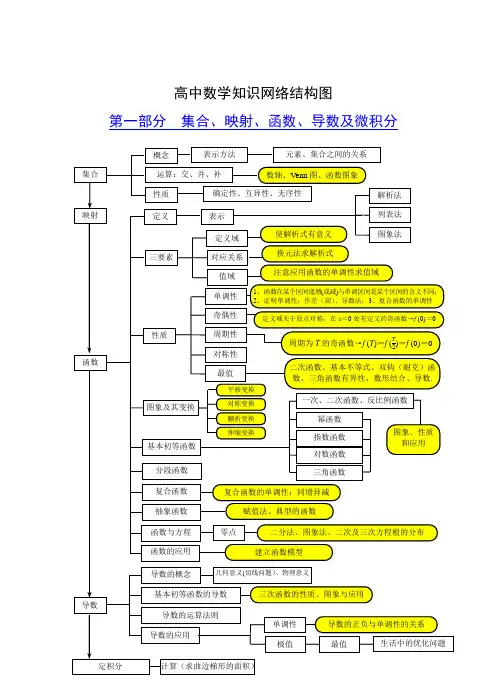
高中数学知识网络结构图第一部分 集合、映射、函数、导数及微积分集合映射 概念元素、集合之间的关系 运算：交、并、补 数轴、Venn 图、函数图象性质确定性、互异性、无序性 定义表示 解析法 列表法三要素图象法定义域对应关系值域 性质奇偶性周期性 对称性 单调性 定义域关于原点对称，在x ＝0处有定义的奇函数→f (0)＝01、函数在某个区间递增(或减)与单调区间是某个区间的含义不同；2、证明单调性：作差（商）、导数法；3、复合函数的单调性 最值二次函数、基本不等式、双钩（耐克）函数、三角函数有界性、数形结合、导数.幂函数 对数函数 三角函数基本初等函数抽象函数 复合函数 赋值法、典型的函数函数与方程 二分法、图象法、二次及三次方程根的分布 零点函数的应用 建立函数模型使解析式有意义 导数函数基本初等函数的导数导数的概念导数的运算法则导数的应用表示方法 换元法求解析式分段函数 几何意义(切线问题）、物理意义单调性导数的正负与单调性的关系生活中的优化问题注意应用函数的单调性求值域周期为T 的奇函数→f (T )＝f (T2)＝f (0)＝0 复合函数的单调性：同增异减三次函数的性质、图象与应用一次、二次函数、反比例函数指数函数图象、性质 和应用平移变换对称变换 翻折变换 伸缩变换图象及其变换最值极值第二部分 三角函数与平面向量角的概念 任意角的三角函数的定义 三角函数 弧度制 弧长公式、扇形面积公式三角函数线同角三角函数的关系 诱导公式 和角、差角公式 二倍角公式公式的变形、逆用、“1”的替换 化简、求值、证明（恒等变形）三角函数 的 图 象定义域奇偶性 单调性 周期性 最值对称轴（正切函数除外）经过函数图象的最高（或低）点且垂直x 轴的直线，对称中心是正余弦函数图象的零点，正切函数的对称中心为(k π2，0)（k ∈Z ）.正弦函数y ＝sin x= 余弦函数y ＝cos x 正切函数y ＝tan x y ＝A sin(ωx ＋ϕ)＋b①图象可由正弦曲线经过平移、伸缩得到，但要注意先平移后伸缩与先伸缩后平移不同；②图象也可以用五点作图法；③用整体代换求单调区间（注意ω的符号）； ④最小正周期T ＝2π| ω |；⑤对称轴x ＝(2k ＋1)π－2ϕ2ω，对称中心为(k π－ϕω，b )（k ∈Z ）. 平面向量 概念线性运算 基本定理 加、减、数乘几何意义坐标表示数量积几何意义模共线与垂直共线（平行）垂直 值域图象a →∥b →⇔b →＝λa → ⇔ x 1y 2－x 2y 1=0 a →⊥b →⇔b →·a →＝0 ⇔ x 1x 2＋y 1y 2=0解三角形余弦定理 面积 正弦定理 解的个数的讨论实际应用 S △＝12ah ＝12ab sin C ＝p (p －a )(p －b )(p －c )（其中p ＝a ＋b ＋c 2）投影b →在a →方向上的投影为|b →|cos θ＝a →·b→——|a →|设a →与b →夹角θ，则cos θ＝a →·b →——|a →|·|b →|对称性 |a →|＝(x 2－x 1)2＋(y 2－y 1)2夹角公式第三部分 数列与不等式概念 数列表示等差数列与等比数列的类比 解析法：a n ＝f (n )通项公式 图象法 列表法递推公式等差数列 通项公式 求和公式 性质 判断a n ＝a 1＋(n －1)d a n ＝a 1q n －1 a n ＋a m ＝a p ＋a r a n a m ＝a p a r 前n 项和 S n ＝n (a 1＋a n )2前n 项积(a n ＞0) T n ＝(a 1a n )n 常见递推类型及方法逐差累加法 逐商累积法 构造等比数列{a n ＋qp －1} 构造等差数列①a n ＋1－a n ＝f (n ) ②a n + 1a n＝f (n ) ③a n ＋1＝pa n ＋q ④pa n ＋1a n ＝a n －a n ＋1 化为a n ＋1q n =p q ·a nq n －1＋1转为③ ⑤a n + 1＝pa n ＋q n等比数列 a n ≠0，q ≠0 S n ＝⎩⎨⎧na 1，q ＝1a 1(1－q n)1－q ，q ≠1公式法：应用等差、等比数列的前n 项和公式 分组求和法 倒序相加法裂项求和法 错位相加法 常见求和方法不等式不等式的性质 一元二次不等式简单的线性规划 基本不等式：ab ≤a ＋b 2数列是特殊的函数借助二次函数的图象三个二次的关系可行域 目标函数一次函数：z ＝ax ＋by z ＝y －bx －a：构造斜率 z ＝(x －a )2＋(y －b )2：构造距离 应用题几何意义： z 是直线ax ＋by －z ＝0在x 轴截距的a 倍，y 轴上截距的b 倍.最值问题 变形 和定值，积最大；积定值，和最小 应用时注意：一正二定三相等 2aba ＋b≤ab ≤a ＋b 2≤a 2＋b 22倾斜角和斜率直线的方程位置关系直线方程的形式倾斜角的变化与斜率的变化重合平行相交垂直A1B2－A2B1＝0A1B2－A2B1≠0A1A2＋B1B2＝0点斜式：y－y0＝k(x－x0)斜截式：y＝kx＋b两点式：y－y1y2－y1＝x－x1x2－x1截距式：xa＋yb＝1一般式：Ax＋By＋C＝0注意各种形式的转化和运用范围.两直线的交点距离点到线的距离：d＝| Ax0＋By0＋C |A2＋B2，平行线间距离：d＝| C1－C2 |A2＋B2圆的方程圆的标准方程圆的一般方程直线与圆的位置关系两圆的位置关系相离相切相交∆＜0，或d＞r∆＝0，或d＝r∆＞0，或d＜r曲线与方程轨迹方程的求法：直接法、定义法、相关点法圆锥曲线椭圆双曲线抛物线定义及标准方程性质范围、对称性、顶点、焦点、长轴（实轴）、短轴（虚轴）、渐近线（双曲线）、准线（只要求抛物线）离心率对称性问题中心对称轴对称点(x1，y1) ───────→关于点(a，b)对称点(2a－x1，2b－y1)曲线f (x，y) ───────→关于点(a，b)对称曲线f (2a－x，2b－y)⎩⎪⎨⎪⎧A·x1＋x22＋B·y1＋y22＋C＝0y2－y1x2－x1·(－AB)＝－1特殊对称轴x±y＋C＝0 直接代入法截距注意：截距可正、可负，也可为0.点(x1，y1)与点(x2，y2)关于直线Ax＋By＋C＝0对称点与线空间点、 线、面的 位置关系点在直线上 点在直线外 点与面 点在面内 点在面外线与线共面直线异面直线相交平行没有公共点 只有一个公共点线与面平行相交有公共点没有公共点 直线在平面外直线在平面内面与面平行 相交平行关系的相互转化垂直关系的相互转化线线 平行线面 平行面面 平行线线 垂直线面 垂直面面 垂直空间的角异面直线所成的角 直线与平面所成的角 二面角 范围：(0︒，90︒] 范围：[0︒，90︒] 范围：[0︒，180︒]点到面的距离 直线与平面的距离 平行平面之间的距离相互之间的转化 cos θ＝|a →·b →|——|a →|·|b →|sin θ＝|a →·n →|——|a →|·|n →|cos θ＝n 1→·n 2→——|n 1→|·|n 2→|d ＝|a →·n →|——|n →|空间向量空间直角坐标系空间的距离 空间几何体柱体棱柱 圆柱 正棱柱、长方体、正方体台体 棱台 圆台 锥体 棱锥 圆锥球 三棱锥、四面体、正四面体直观图 侧面积、表面积 三视图体积长对正 高平齐 宽相等第六部分统计与概率统计随机抽样抽签法随机数表法简单随机抽样系统抽样分层抽样共同特点：抽样过程中每个个体被抽到的可能性（概率）相等用样本估计总体样本频率分布估计总体总体密度曲线频率分布表和频率分布直方图茎叶图样本数字特征估计总体众数、中位数、平均数方差、标准差变量间的相关关系两个变量的线性相关散点图回归直线正态分布列联表（2×2）独立性分析概率概率的基本性质互斥事件对立事件古典概型几何概型条件概率事件的独立性用随机模拟法求概率常用的分布及期望、方差随机变量两点分布X～B(1，p)E(X)＝p，D(X)＝p(1－p)二项分布X～B(n，p)E(X)＝np，D(X)＝np(1－p)定义概率的计算与分布列与二项分布的区别n次独立重复试验恰好发生k次的概率为P n(k)＝C k n p k(1－p)n－k超几何分布实际应用E（aX+b）=aE(X)+b2()()D aX b a D X+=P(A＋B)＝P(A)＋P(B)P(⎺A)＝1－P(A)P(A B)＝P(A)·P(B)P(B | A)＝P(A B)P(A)第七部分 其他部分内容合情推理演绎推理类比归纳 三段论 大前提，小前提，结论 两个原理分类加法计算原理和分步乘法计算原理 排列与组合 排列数：A m n ＝n !(n －m )!组合数：C m n ＝n !m !(n －m )!性质C m n ＝C n －mn C m n ＋1＝C m n ＋C m －1n计算原理二项式定理通项公式T r ＋1＝C r n a n －r b r首末两端“等距离”两项的二项式系数相等C 0n ＋C 2n ＋C 4n …＝C 1n ＋C 3n ＋C 5n …＝2n －1 C 0n ＋C 1n ＋…＋C n n ＝2n二项式系数性质 直接证明 综合法 分析法 由因导果 执果索因间接证明 反证法数学归纳法推理证明推理与证明充分非必要条件、必要非充分条件、充要条件关系条件复合命题 或：p ∨ q 且：p ∧ q 非：⌝ p应用原命题：若p 则q逆命题：若q 则p否命题：若⌝p 则⌝q逆命题：若⌝q 则⌝p互逆 互逆互否互否互为逆否 等价关系一真便真 一假则假全称量词与存在量词 简易逻辑概括性、逻辑性、有穷性、不唯一性、普遍性 顺序结构条件结构 循环结构命题算法语言算法的特征程序框图 基本算法语言算法案例 辗转相除法、更相减损术、秦九韶算法、进位制 复 数概念虚数、纯虚数、实部、虚部、实轴、虚轴、模、共轭复数 运算 加、减、乘、除、乘方几何意义与复平面内的点一一对应，其模表示到原点的距离。

文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持.
【关键字】知识
最全初中数学思维导图，7张图扫清初中三年知识点
初中数学的学习，最重要的就是建立自己的知识体系，学会全局思考的思维模式！下面这些数学知识点的思维导图，将初中重要的知识点都整理出来了，相信一定能帮助童鞋们提升数学成绩！
PS：看不清楚的地方，请打开图片，放大查看！
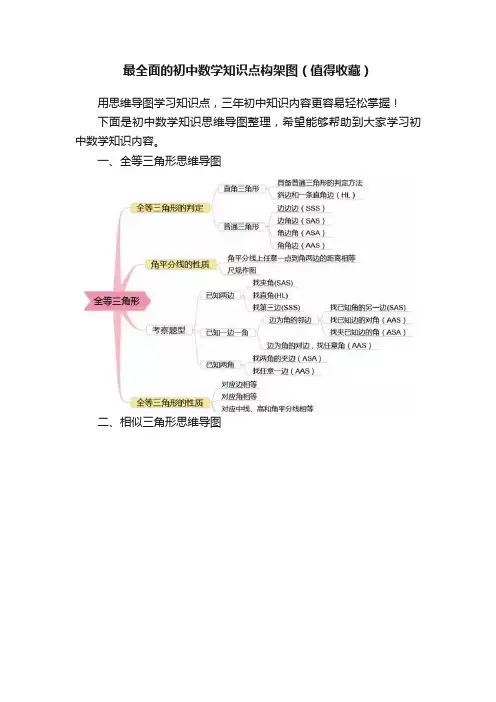
一、全等三角形
2、相似三角形
三、几何初步&三角形
四、投影与视图
五、圆
六、实数
七、代数式
此文档是由网络收集并进行重新排版整理.word可编辑版本！
1文档来源为:从网络收集整理.word版本可编辑.。