刚体力学基础 动量矩

§6、刚体的动量矩及转动动能上次课我们将质点组的两个基本动力学定理，即质心运动定理和动量矩定理:M dtd dt J d M F r v m r Fre ii i i i e ic=⨯∑=⨯∑=∑=)(,)( 应用于刚体，于是就给出了描述刚体动力学规律的基本运动微分方程。

虽然上次课已经给出刚体动力学基本方程，但是对基本方程中的动量矩的具体形式并没有给出，这次课我们仍然以质点组的动量矩和动能定义为出发点推出刚体的动量矩以及刚体的转动动能。

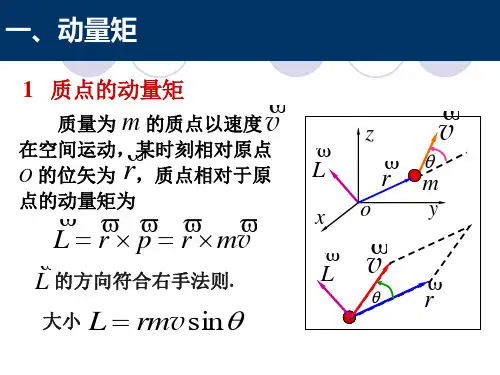
下面我们先讨论：一、 刚体定点转动的动量矩：假设刚体在某一时刻以角速度ω转动。

取刚体上任一质点p i 的质量为m i 。

它相对固定点O 点的位矢量为i r。

那么根据质点组的动量矩定义式可得整个刚体对固定点0的动量矩是：)(v m r i i i iJ⨯=∑因为，r w v ii⨯= 所以，它就等于)(r w m r iiii⨯⨯∑ 根据矢量多重叉积的基本公式：c b a b c a c b a)()()(⋅-⋅=⨯⨯ 可得[]][r r m w r m r w r w r r m rw r m iiiiiiiiiiiiiiiiIiw i J)()()(2)(⋅=-⋅=⨯=∑-∑⋅∑⨯∑由此可以看出，动量矩J 一般不与角速度ω 共线，只有0≡⋅w r时， j 与w 才是共线的。

由于角动量是个矢量，如果我们确定了坐标系，那么就可以将它写成分量形式。

如图所示，建立直角坐标系O —X 、Y 、Z(并与绕定轴转动的刚体固连在一起，坐标这样取在目前的情况下比较方便。

因为刚体上任一点的坐标（x,y,z ）不管刚体怎样运动，它们相对刚体都是不随时间改变的常数，所以取与刚体固定的动坐标系比较方便。

)则i r 和w在三正交坐标轴的分量……则：kw jw i w wk z jy ix rz yxiiii++=++=,于是可得动量矩在x 轴上的分量：wz x m wy x m wzy m xw z wy wx m wz yx m Jxiiyiixii i iziyixii xi ii i zi i )()()()()(22222∑∑∑∑∑--⎥⎦⎤⎢⎣⎡+=++-++=同理可得：wx ym w z y m wz x m J w z y m wz ym w y x m J ziiiyii xiiz ziiyi iixii y i i i i )()()()()()(2222++--=-++-=∑∑∑∑∑∑ 在这儿我们就令：)))222222(((x y m I z x m I z ym I iiizziiiyyiii xx +∑+∑+∑=== ∑∑∑======x z m IIy z m I I y x m I Iii i xzzxii i zy yzii i yxxy则动量矩在直角坐标系中的分量式就可简写为：wI w I w I J w I w I w I J w I w I w I Jzzzyzyxzxzzyzyyyxyxy zxzyxyxxxx +---=-+=--=：由这些分量式也可以看出刚体绕固定点转动的动量矩的分量与角速度的三个分量 w w w zy x ,,都有关。

§6、刚体的动量矩及转动动能上次课我们将质点组的两个基本动力学定理，即质心运动定理和动量矩定理:M dtd dt J d M F r v m r Fre ii i i i e ic=⨯∑=⨯∑=∑=)(,)( 应用于刚体，于是就给出了描述刚体动力学规律的基本运动微分方程。

虽然上次课已经给出刚体动力学基本方程，但是对基本方程中的动量矩的具体形式并没有给出，这次课我们仍然以质点组的动量矩和动能定义为出发点推出刚体的动量矩以及刚体的转动动能。

下面我们先讨论：一、 刚体定点转动的动量矩：假设刚体在某一时刻以角速度ω转动。

取刚体上任一质点p i 的质量为m i 。

它相对固定点O 点的位矢量为i r。

那么根据质点组的动量矩定义式可得整个刚体对固定点0的动量矩是：)(v m r i i i iJ⨯=∑因为，r w v ii⨯= 所以，它就等于)(r w m r i i i i⨯⨯∑ 根据矢量多重叉积的基本公 式：c b a b c a c b a)()()(⋅-⋅=⨯⨯ 可得[]][r r m w r m r w r w r r m rw r m iiiiiiiiiiiiiiiiIiw i J)()()(2)(⋅=-⋅=⨯=∑-∑⋅∑⨯∑由此可以看出，动量矩J 一般不与角速度ω 共线，只有0≡⋅w r时， j 与w 才是共线的。

由于角动量是个矢量，如果我们确定了坐标系，那么就可以将它写成分量形式。

如图所示，建立直角坐标系O —X 、Y 、Z(并与绕定轴转动的刚体固连在一起，坐标这样取在目前的情况下比较方便。

因为刚体上任一点的坐标（x,y,z ）不管刚体怎样运动，它们相对刚体都是不随时间改变的常数，所以取与刚体固定的动坐标系比较方便。

)则i r 和w在三正交坐标轴的分量……则：kw jw i w wk z jy ix rz yxiiii++=++=,于是可得动量矩在x 轴上的分量：wz x m wy x m wzy m xw z wy wx m wz yx m Jxiiyiixii i iziyixii xi ii i zi i )()()()()(22222∑∑∑∑∑--⎥⎦⎤⎢⎣⎡+=++-++=同理可得：wx ym w z y m wz x m J wz y m wz ym w y x m Jziiiyii xiiz ziiyi iixii yi i i i )()()()()()(2222++--=-++-=∑∑∑∑∑∑ 在这儿我们就令：)))222222(((x y m I z x m I z ym I iiizziiiyyiii xx +∑+∑+∑===∑∑∑======x z m II y z m I Iy x m IIii i xzzxi i i zyyzi i i yxxy则动量矩在直角坐标系中的分量式就可简写为：wI w I w I J w I w I w I J w I w I w I Jzzzyzyxzxzzyzyyyxyxy zxzyxyxxxx +---=-+=--=：由这些分量式也可以看出刚体绕固定点转动的动量矩的分量与角速度的三个分量 w w w z y x ,,都有关。

第五章 刚体力学基础 动量矩班级______________学号____________姓名________________一、选择题1、力kNj i F )53(+=，其作用点的矢径为m j i r )34(-=，则该力对坐标原点的力矩大小为 （ B ）(A)m kN ⋅-3； （B ）m kN ⋅29； (C)m kN ⋅19； (D)m kN ⋅3。

2、圆柱体以80rad /s 的角速度绕其轴线转动，它对该轴的转动惯量为24m kg ⋅。

由于恒力矩的作用，在10s 内它的角速度降为40rad /s 。

圆柱体损失的动能和所受力矩的大小为( D ) (A)80J ，80m N ⋅；(B)800J ，40m N ⋅；(C)4000J ，32m N ⋅；(D)9600J ，16m N ⋅。

3、 一匀质圆盘状飞轮质量为20kg ，半径为30cm ，当它以每分钟60转的速率旋转时，其动能为 ( D )(A)22.16π J ； (B)21.8πJ ；（C ）1.8J ； （D ）28.1πJ 。

4、如图所示，一轻绳跨过两个质量均为m 、半径均为R 的匀质圆盘状定滑轮。

绳的两端分别系着质量分别为m 和2m 的重物，不计滑轮转轴的摩擦。

将系统由静止释放，且绳与两滑轮间均无相对滑动，则两滑轮之间绳的张力。

（ D ）(A)mg ； (B)3mg /2； (C)2mg ； (D)11mg /8。

5、一根质量为m 、长度为L 的匀质细直棒，平放在水平桌面上。

若它与桌面间的滑动摩擦系数为μ，在t =0时，使该棒绕过其一端的竖直轴在水平桌面上旋转，其初始角速度为0ω，则棒停止转动所需时间为 (A )(A)μωg L 3/20； (B) μωg L 3/0； (C) μωg L 3/40； (D) μωg L 6/0。

6、关于力矩有以下几种说法，其中正确的是 ( B )（A ）内力矩会改变刚体对某个定轴的角动量（动量矩）； （B ）作用力和反作用力对同一轴的力矩之和必为零；（C ）角速度的方向一定与外力矩的方向相同；（D ）质量相等、形状和大小不同的两个刚体，在相同力矩的作用下，它们的角加速度一定相等。

第5章 刚体力学基础 动量矩5.1 选择题(1) 下列说法正确的是[CE](A)作用在定轴转动刚体上的力越大，刚体转动的角加速度越大 (B)作用在定轴转动刚体上的合力矩越大，刚体转动的角速度越大 (C)作用在定轴转动刚体上的合力矩越大，刚体转动的角加速度越大 (D)作用在定轴转动刚体上的合力矩为零，刚体转动的角速度为零 (E)作用在定轴转动刚体上的合力矩为零，刚体转动的角加速度为零(2)轮圈半径为R ，其质量M 均匀分布在轮缘上，长为R 、质量为m 的均质辐条固定在轮心和轮缘间，辐条共有2N 根。

今若将辐条数减少N 根，但保持轮对通过轮心、垂直于轮平面轴的转动惯量保持不变，则轮圈的质量为[D] (A)12N m M + (B) 6N m M + (C) 23N m M + (D) 3N m M + 解：设辐条数减少后，轮圈的质量为M ’,222211233MR N mR M R N mR '+⋅=+⋅可得13M M N m '=+⋅(3) 一质量为m 的均质杆长为l ，绕铅直轴OO ’成θ角转动，如图所示，其转动惯量为[C] (A)2112ml (B) 221sin 4ml θ (C) 221sin 3ml θ (D) 213ml 解：()222201sin sin 3lVm J r dm x dx ml l θθ==⋅=⎰⎰5.2 填空题(1)2rad/s;4.47 rad/s;30cm/s 2；(2)质量为m 的均质细杆，长为l ，以角速度ω绕过杆端点，垂直于杆的水平轴转动，细杆的动量大小为 ，绕转动轴的动能是 ，动量矩大小是 。

12ml ω；2216ml ω；213ml ω (3)均质圆盘水平面放置，可绕通过盘心的铅垂轴自由转动，圆盘对该轴的转动惯量为J 0，当其转动角速度为ω0时，有一质量为m 的质点沿铅垂方向落到圆盘上，并粘在距轴R /2处，它们共同转动的角速度为 。

2014mR J ω⎛⎫+ ⎪⎝⎭5.7某转轮直径d=40cm ，以角量表示的运动学方程为32= 3.04.0t t t θ-+，式中θ的单位为rad ，t 的单位为s 。

动量矩的单位动量矩，也称为角动量或者力矩，是物理学中重要的概念之一，它在描述物体运动和旋转时起着至关重要的作用。

在这份论述中，我们将深入探讨动量矩的概念、性质、计算方法以及其在物理学中的应用，并对动量矩的单位进行详细的阐述。

希望通过这份论述，读者能够对动量矩有一个更加清晰的了解。

一、动量矩的概念动量矩，就像其名字所表达的含义一样，是力矩和时间的乘积，通常用L来表示。

动量矩在物理学中起着至关重要的作用，特别是在描述物体的转动和旋转时。

在经典力学和量子力学中，动量矩是一个重要的物理量，它是描述物体旋转运动的必要性质之一。

在物理学中，动量矩是一个矢量，它的方向由右手定则确定。

它的大小和方向分别由以下公式给出：L = r × pL为动量矩，r为力臂长度（物体上作用力的直线距离），p为动量，×表示叉乘。

从公式可以看出，动量矩既与力臂的长度有关，也与作用力的大小和方向有关。

二、动量矩的单位在国际单位制中，动量矩的单位为牛顿·米·秒（N·m·s）。

这个单位可以通过分解来理解，即牛顿（N）是力的单位，米（m）是长度的单位，秒（s）是时间的单位。

动量矩的单位可以理解为在一个力为1牛顿的作用下，力臂长度为1米，持续作用1秒的情况下所产生的动量矩。

在实际问题中，通常也会用牛顿米（N·m）作为动量矩的单位。

这是因为动量矩的量纲为力乘以长度，而牛顿米正好满足这个量纲。

但是需要注意的是，牛顿米在国际单位制下并不是严格意义上的动量矩单位，而它的推导应该通过动能、动量以及万有引力的关系进行推导，从而可以得到动量矩的统一计量单位。

三、动量矩的计算方法动量矩可以通过作用力和力臂长度的叉乘来计算，即L = r × F。

在实际问题中，我们通常会遇到各种不同形式的作用力，包括直线力和切线力等。

对于直线力，动量矩的计算比较直接，可以直接对力臂长度与力的乘积即可得到动量矩；而对于切线力，动量矩的计算则需要更多的几何知识，需要通过向量运算来得到准确的结果。