理论力学1-01

理论力学期末考试试题1-1、自重为P=100kN的T字形钢架ABD,置于铅垂面内，载荷如图所示。

其中转矩M=20kN.m，拉力F=400kN,分布力q=20kN/m,长度l=1m。

试求固定端A的约束力。

解：取T型刚架为受力对象，画受力图.1-2 如图所示，飞机机翼上安装一台发动机，作用在机翼OA上的气动力按梯形分布：q=60kN/m，2q=40kN/m，机翼重1p=45kN，1发动机重p=20kN，发动机螺旋桨的反作用力偶矩M=18kN.m。

求2机翼处于平衡状态时，机翼根部固定端O所受的力。

解：1-3图示构件由直角弯杆EBD以及直杆AB组成，不计各杆自重，已知q=10kN/m，F=50kN，M=6kN.m，各尺寸如图。

求固定端A 处及支座C的约束力。

1-4 已知：如图所示结构，a, M=Fa, 12F F F ==, 求：A ，D 处约束力.解：1-5、平面桁架受力如图所示。

ABC为等边三角形，且AD=DB。

求杆CD的内力。

1-6、如图所示的平面桁架，A端采用铰链约束，B端采用滚动支座约束，各杆件长度为1m。

在节点E和G上分别作用载荷F=10kN，EF=7 kN。

试计算杆1、2和3的内力。

G解：2-1 图示空间力系由6根桁架构成。

在节点A上作用力F，此力在矩形ABDC平面内，且与铅直线成45º角。

ΔEAK=ΔFBM。

等腰三角形EAK，FBM和NDB在顶点A，B和D处均为直角，又EC=CK=FD=DM。

若F=10kN，求各杆的内力。

2-2 杆系由铰链连接，位于正方形的边和对角线上，如图所示。

在节点D沿对角线LD方向作用力F。

在节点C沿CH边铅直向下作用D力F。

如铰链B，L和H是固定的，杆重不计，求各杆的内力。

2-3 重为P＝980 N，半径为r =100mm的滚子A与重为2P＝4901N的板B由通过定滑轮C的柔绳相连。

已知板与斜面的静滑动摩擦因数f=0.1。

滚子A与板B间的滚阻系数为δ=0.5mm，斜面倾角αs=30º，柔绳与斜面平行，柔绳与滑轮自重不计，铰链C为光滑的。

何锃版理论⼒学部分例题及习题答案1-1-1是⾮题（正确的在括号内画√，错误在画×）。

1．作⽤于刚体上的⼒是滑动⽮量，作⽤于变形体上的⼒是定位⽮量。

（√）2．⼆⼒构件的约束反⼒是其作⽤线的⽅位沿⼆受⼒点的连线，指向可假设。

（√）3．加减平衡⼒系公理不但适⽤于刚体，还适⽤于变形体。

（×）4．若两个⼒相等，则这个⼒就等效。

（×）5．作⽤于A 点共线反向的两个⼒1F 和2F 且1F >2F ，则合⼒21F F R -=。

（×）6．⼒F 可沿其作⽤线由D 点滑移到E 点。

（×）7．两物体在光滑斜⾯m-n 处接触，不计⾃重，若⼒1F 和2F 的⼤⼩相等⽅向相反，且共线，则两个物体都处于平衡状态。

（×）1-1-2 选择题（将正确答案前⾯的序号写在括号内）1．⼆⼒平衡公理适⽤于（1）①刚体②变形体③刚体和变形体2．作⽤与反作⽤公理适⽤于（3）①刚体②变形体③刚体和变形体3．作⽤于刚体上三个相互平衡的⼒，若其中任何两上⼒的作⽤线相交于⼀点，则其余的⼀个⼒的作⽤线必定。

（2）①交于同⼀点②交于同⼀点，且三个⼒的作⽤线共⾯③不⼀定交于同⼀点4．作⽤于刚体上的平衡⼒系，如果作⽤到变形体上，则变形体（ 3 ）。

反之，作⽤于变形体上的平衡⼒系如果作⽤到刚体上，则刚体（ 1 ）。

①平衡②不平衡③不⼀定平衡5．图⽰结构中，AC 、BC ⾃重分别为P 1和P 2，各杆受⼒如图①②③④。

（3、4）1．3 画出下列指定物体的受⼒图、假定各接触处光滑，物体的重量除注明者匀均不计。

1．圆柱体O2．杆AB 3．弯杆ABC 4．刚架 5．杆AB6．杆AB 7．销钉A 8．杆AB1．4试画出下列各物系中指定物体的受⼒图。

假定各接触处光滑，物体的重量除注明者外均不计。

1．起重机构整体：轮O 、杆AB 、杆BC2．平衡构架整体：AB 部分、弯杆BC3．三铰拱整体：AB 部分、BC 部分4．A 形架整体，AB 部分、BC 部分，DE 杆及销钉B （⼒P 作⽤在销钉B上）5．⼆跨静定刚架整体、AD 部分、EC 梁。

Βιβλιοθήκη 05 功、能量与机械 能守恒
功和功率的概念及计算
功的定义
力对物体所做的功等于力的大小、 位移的大小、力与位移夹角的余 弦三者的乘积，即 $W=Flcostheta$。
功率的概念
功率是指物体在单位时间内所做的 功，即功率等于功和做功所用时间 之比，$P=W/t$。
计算方法和技巧
在计算功和功率时，需要注意力的 方向、位移的方向以及时间的对应 关系，同时要掌握一些计算技巧， 如利用动能定理等。
03 动力学基础与牛 顿定律
动力学基本概念及原理
动力学
研究物体运动与所受力 的关系，以及物体运动
状态改变的原因。
力的概念
力是物体之间的相互作 用，可以改变物体的运
动状态或形状。
惯性
物体保持静止或匀速直 线运动状态的性质，是
物体的固有属性。
动量
描述物体运动状态的物 理量，与物体的质量和
速度有关。
牛顿定律及其适用范围
典型习题解析与答案
习题一
解析物体在水平面上滑动时的受力情况，计算物体的加速度 和速度。
答案
根据牛顿第二定律，物体所受合力等于物体质量与加速度的 乘积，通过受力分析可以求出物体所受的合力，进而求出物 体的加速度和速度。
习题二
解析两个物体之间的碰撞过程，计算碰撞后的速度和能量变 化。
答案
根据动量守恒和能量守恒定律，可以求出碰撞后两个物体的 速度和能量变化。需要注意的是，碰撞过程中可能存在能量 损失，因此实际计算时需要考虑能量损失的因素。
03
题目2
04
一轻绳跨过定滑轮，两端分别系 有质量为m1和m2的物体，且 m1>m2，开始时两物体均静止， 当剪断轻绳后，求两物体的加速 度和速度变化。

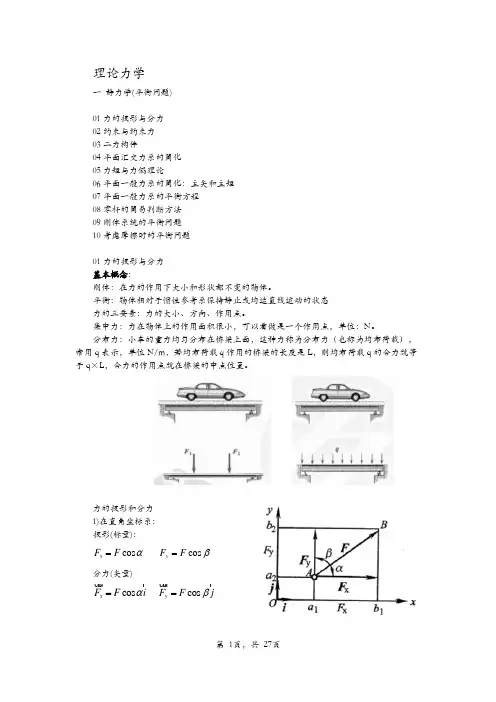
理论力学一 静力学(平衡问题)01力的投影与分力 02约束与约束力 03二力构件04平面汇交力系的简化 05力矩与力偶理论06平面一般力系的简化：主矢和主矩 07平面一般力系的平衡方程 08零杆的简易判断方法 09刚体系统的平衡问题 10考虑摩擦时的平衡问题01力的投影与分力 基本概念：刚体：在力的作用下大小和形状都不变的物体。

平衡：物体相对于惯性参考系保持静止或均速直线运动的状态 力的三要素：力的大小、方向、作用点。

集中力：力在物体上的作用面积很小，可以看做是一个作用点，单位：N 。

分布力：小车的重力均匀分布在桥梁上面，这种力称为分布力（也称为均布荷载），常用q 表示，单位N/m ，若均布荷载q 作用的桥梁的长度是L ，则均布荷载q 的合力就等于q ×L ，合力的作用点就在桥梁的中点位置。

力的投影和分力 1)在直角坐标系： 投影(标量)：cos x F F α= cos y F F β=分力(矢量)cos x F F i α=u u r r cos y F F j β=u u r r2)在斜坐标系： 投影(标量)：cos x F F α= cos()y F F ϕα=-分力(矢量)(cos sin cot )x F F F i ααϕ=-u u r rsin sin y F F j αβ=u u r r02约束与约束力约束：对于研究对象起限制作用的其他物体。

约束力方向：总是与约束所能阻止物体运动的方向相反，作用在物体和约束的接触点处。

约束力大小：通常未知，需要根据平衡条件和主动力求解。

(1)柔索约束：柔索约束：由绳索、皮带、链条等各种柔性物体所形成的约束，称为柔索约束。

特点：只能承受拉力，不能承受压力。

约束力：作用点位接触点，作用线沿拉直方向，背向约束物体。

(2)光滑面约束光滑面约束：由光滑面所形成的约束称为光滑面约束。

约束性质：只能限制物体沿接触面公法线趋向接触面的位移。

特点：只能受压不能受拉，约束力F 沿接触面公法线指向物体。

接触点处受到法向约束力的作用。
03
铰链约束
铰链约束是指两个构件通过销钉或铰链连接在一起，并能绕销钉或铰链
相对转动。这种约束只能限制物体沿垂直于销钉轴线的运动，而不能限
制物体绕销钉的转动。
平衡条件及求解方法
平面力系的平衡条件
平面任意力系平衡的充分必要条件是，力系的主矢和主矩都为零。即所有各力在x轴和y轴 上的投影的代数和分别等于零；所有各力对任意一点之矩的代数和也等于零。
汇交力系平衡条件应用
平衡条件
汇交力系平衡的充分必要条件是合力为零，即力多边形自行封闭。
应用
在静力学中，汇交力系平衡条件可应用于求解未知力、判断物体是否平衡等问题 ；在动力学中，可用于分析物体的运动状态及受力情况。
04 平面任意力系简化与平衡
平面任意力系简化方法
向一点简化
选择适当的一点，将力系中的各 力向该点平移，得到一个等效的 平面汇交力系和一个平面力偶系。
主矢和主矩
平面任意力系向作用面内任一点 简化时，一般可得到一个力和一 个力偶，这个力称为该力系的主 矢，这个力偶的矩称为该力系对
简化中心的主矩。
合力矩定理
平面任意力系的合力对作用面内 任一点之矩，等于力系中各分力
对于同一点之矩的代数和。
简化结果分析
当主矩为零时，主矢也为零
01
说明该力系本身是平衡的，或者可以合成为一个合力。
合力矩
主矩表示原力系对物体的 总体转动效应，其大小和 方向由主矩矢量确定。
平衡条件
当且仅当主矢和主矩都为 零时，空间任意力系才处 于平衡状态。
空间任意力系平衡条件应用
静力学问题
利用空间任意力系的平衡条件，可以解决各种静力学问题， 如物体的平衡、刚体的平衡等。

《理论力学》第1次作业（静力学基础）参考解答习题1-1 图中设AB=l ，在A 点受四个大小均等于F 的力1F 、2F 、3F 和4F 作用。

试分别计算每个力对B 点之矩。

【解答】：112()sin 45B M F F l l =-⋅⋅︒=⋅ 22()B M F F l F l =-⋅=-⋅332()sin 45B M F F l l =-⋅⋅︒=⋅ 4()0B M F =。

习题1-2 如图所示正平行六面体ABCD ，重为P F =100N ，边长AB=60cm ，AD=80cm 。

今将其斜放使它的底面与水平面成30ϕ=︒角，试求其重力对棱A 的力矩。

又问当ϕ等于多大时，该力矩等于零。

【解法1——直接计算法】：设AC 与BD 的交点为O ，∠BAO=α，则：cos()cos cos sin sin 33410.11965252αϕαϕαϕ+=-=⨯-⨯= 221806050cm=0.5m 2AO =+=()cos()1000.50.1196 5.98N mA P P P M F F d F AO αϕ=⋅=⨯⨯+=⨯⨯=⋅当()0A P M F =时，重力P F 的作用线必通过A 点，即90αβ+=︒，所以： 令cos()cos cos sin sin 0αϕαϕαϕ+=-=→34cos sin 055ϕϕ⨯-⨯=，得： 3tan 4ϕ=→3652ϕ'=︒。

【解法2——利用合力矩定理】：将重力P F 分解为两个正交分力1P F 和2P F ， 其中：1P F AD ，2P F AB ，则：1cos P P F F ϕ=⨯，2sin P P F F ϕ=⨯根据合力矩定理：1212()()()22cos 0.3sin 0.4311000.31000.4 5.98N m 2A P A P A P P P P P AB AD M F M F M F F F F F ϕϕ=+=⨯-⨯=⨯⨯-⨯⨯=-⨯⨯=⋅ 确定ϕ等于多大时，()0A P M F =令()0A P M F =，即：cos 0.3sin 0.40P P F F ϕϕ⨯⨯-⨯⨯= →100cos 0.3100sin 0.40ϕϕ⨯⨯-⨯⨯=→3tan 4ϕ=→3652ϕ'=︒。

物体间的相互机械作用的基本量度是力，理论力学中还广泛用到力对点之矩和力对轴之矩的概念。
物体运动的改变除与作用力有关外，还与本身的惯性有关。对于质点，惯性的量度是其质量。对于刚体，除 其总质量外，惯性还与质量在体内的分布状况有关，即与质心位置及惯性矩、惯性积有关。刚体对于三个互相垂 直的坐标轴的各惯性矩及惯性积组成刚体对该坐标系的惯性张量。
理论力学从变分法出发，最早由拉格朗日《分析力学》作为开端，引出拉格朗日力学体系、哈密顿力学体系、 哈密顿-雅克比理论等，是理论物理学的基础学科。哈密顿方法是量子力学中的正则量子化的起点，拉格朗日方法 是量子力学中路径积分量子化的起点。
发展简史
发展简史
力学是最古老的科学之一，它是社会生产和科学实践长期发展的产物。随着古代建筑技术的发展，简单机械 的应用，静力学逐渐发展完善。公元前5—前 4世纪，在中国的《墨经》中已有关于水力学的叙述。古希腊的数 学家阿基米德（公元前 3世纪）提出了杠杆平衡公式（限于平行力）及重心公式，奠定了静力学基础。荷兰学者 S.斯蒂文（16世纪）解决了非平行力情况下的杠杆问题，发现了力的平行四边形法则。他还提出了著名的“黄金 定则”，是虚位移原理的萌芽。这一原理的现代提法是瑞士学者约翰·伯努利于1717年提出的。
理论力学建立科学抽象的力学模型（如质点、刚体等）。静力学和动力学都联系运动的物理原因——力，合 称为动理学。有些文献把kinetics和dynamics看成同义词而混用，两者都可译为动力学，或把其中之一译为运动 力学。此外，把运动学和动力学合并起来，将理论力学分成静力学和动力学两部分。
理论力学依据一些基本概念和反映理想物体运动基本规律的公理、定律作为研究的出发点。例如，静力学可 由五条静力学公理演绎而成；动力学是以牛顿运动定律、万有引力定律为研究基础的。理论力学的另一特点是广 泛采用数学工具，进行数学演绎，从而导出各种以数学形式表达的普遍定理和结论 。

力矩对时间的累积等于物体角 动量的变化率。
角动量守恒的条件
系统不受外力矩或所受外力矩 的矢量和为零。
角动量守恒定律
不受外力矩作用的系统，其总 角动量保持不变。
应用领域
广泛应用于航天、航空、航海 等领域，用于分析系统的旋转
运动规律和设计。
CHAPTER 04
质点和刚体的动力学应用
质点和刚体的直线运动
理论力学的历史与发展
理论力学的起源可以追溯到古代，如阿基米德等人的贡献。 然而，真正意义上的理论力学是在牛顿发表《自然哲学的数 学原理》之后发展起来的。
随着数学和物理学的不断发展，理论力学也不断完善和深化 ，形成了多个分支。近年来，随着计算机科学的进步，理论 力学与数值计算方法的结合为解决复杂问题提供了更有效的 手段。
弹性力学的基本方程
01
02
03
平衡方程
根据牛顿第二定律，描述 了物体在力的作用下保持 平衡的状态。
几何方程
描述了物体在外力作用下 产生的变形。
物理方程
描述了物体的应力与应变 之间的关系。
弹性力学的应用实例
桥梁和建筑物的设计
材料科学的研究
通过弹性力学，可以分析桥梁和建筑 物的受力情况，从而设计出更加安全 和经济的结构。
连续性假设
物质没有空隙地连续充满所占据的空 间，或者说物质所占据空间的场内， 物质分布函数的值是连续的。
完全弹性假设
当外力撤去后，所有的变形全部恢复 ，并且不出现残余的应变。
各向同性假设
弹性性质与方向无关，也就是说，在 各个方向上，弹性模量是常数。
小变形假设
物体在外力作用下产生的变形量远远 小于物体原来的尺寸，即可以忽略不 计。
基础运动形式

05
静力学在实际问题中的应用
工程结构中的静力学问题
桥梁和建筑物的稳定性分析
静力学是评估大型工程结构稳定性的基础，通过分析受力情况和 结构响应，确保工程安全可靠。
机械设备的支撑设计
在机械设备设计中，静力学分析用于确定支撑结构的强度和刚度， 以防止过载和振动。
管道和压力容器的强度检验
静力学分析用于评估管道和压力容器在各种压力下的应力分布，确 保其正常工作并防止破裂。
静力学的基本概念
力、力矩和力的平移定理
01
02
03
力
力是一个物体对另一个物 体的作用，表示物体间的 相互作用。
力矩
力矩是力和力臂的乘积， 表示力对物体转动效应的 量度。
力的平移定理
一个力对某点的力矩等于 该力平移到另一点产生的 力矩，即力矩具有平移不 变性。
力的分类：集中力与分布力
集中力
作用在物体上的某一点，其效果 相当于作如果一个刚体只受到两个力的作用而平 衡，则这两个力大小相等、方向相反且作用在同一直线上。
详细描述
这个公理是静力学中最基本的原理之一，它告诉我们一个物 体在两个力作用下会处于平衡状态，这两个力必须等大、反 向且共线。这个公理可以用来分析各种力学问题，如确定物 体的平衡状态和支撑反作用力等。
公理三：力的平行四边形法则
总结词
力的平行四边形法则表明，作用在同一个刚 体上的两个力可以合成一个合力，这个合力 的大小和方向由这两个力和它们之间的夹角 确定。
详细描述
这个法则是静力学中重要的原理之一，它告 诉我们如何将多个力合成一个合力。具体来 说，如果将两个力画成平行四边形的两条边， 则合力的大小和方向可以通过平行四边形的 对角线来确定。这个法则可以用来分析力的 合成和分解问题，以及确定物体的运动状态。

静力学为建筑结构的优化设计提供了理论基础，通过计算和分析，确定最优的设计方案。
静力学还提供了优化设计的方法，以提高建筑结构的性能和降低成本。
03
CHAPTER
静力学在机械工程中的应用
静力学在机械零件的强度分析中发挥着重要作用，通过分析零件在不同受力情况下的应力分布和变形情况，可以评估其是否满足设计要求和使用安全。
总结词
在机械工程中，许多零件都需要承受一定的外力，如压力、拉力、弯曲力等。通过静力学分析，可以确定这些外力对零件的作用方式和影响程度，从而评估零件的强度是否足够。这有助于避免因零件强度不足而导致的断裂、变形等问题，提高机械设备的可靠性和安全性。
详细描述
机械零件的强度分析
总结词
平衡分析是静力学的一个重要应用，通过平衡分析可以确定机械系统中的各个部件是否处于稳定状态，以及是否存在潜在的失稳风险。
如杠铃、吊环、跳水板等，都需要静力学知识来保证其稳定性和安全性。
03
02
01
静力学在生活中的应用
桥梁、房屋、塔吊等建筑结构都需要利用静力学原理来设计和分析。
建筑结构
机器中的零部件，如轴承、齿轮、连杆等都需要利用静力学知识来设计和分析。
机械设计
飞机和火箭等航空航天器中的零部件，如机翼、尾翼、机身等都需要利用静力学原理来设计和分析。
静力学分析还可以用于研究推进系统的性能，如燃烧效率、燃油消耗率等，以及推力对飞行器稳定性的影响。
05
CHAPTER
静力学在交通领域的应用
车辆稳定性分析
静力学在车辆稳定性分析中发挥着重要作用。通过分析车辆在不同路面条件下的受力情况，可以评估车辆的行驶稳定性，从而优化车辆设计，提高行驶安全性。
车辆悬挂系统设计

理论力学简介
一、理论力学的研究内容 理论力学可分为下列三大部分： 静力学（第一章～第六章）
主要研究物体的平衡规律 运动学（第七章～第十章）
主要从几何的角度研究物体的机械运动 动力学（第十一章～第十五章）
主要研究物体的机械运动与作用力之间的关系
二、静力学的主要内容
1）物体的受力分析 分析物体的受力情况，并作出表明其受力情况的简图 ◆ 受力分析是解决力学问题的基础
第四节 物体的受力分析
一、受力分析的一般步骤 1）确定研究对象 2）取分离体 解除研究对象所受的全部约束，将其从周围物体中分离出来。
3）画主动力 在研究对象的分离体简图上画出主动力
4）画约束力 在研究对象的分离体简图上画出约束力
[例1] 重力为 P 的球体，在 A 处用绳索系在墙上，试画出球体的 受力图。
工程中的约束通常可分为下列五大类：
一、柔性约束·柔索
约束力： 一个拉力
◆ 柔性约束属于单面约束
二、光滑接触面约束
P
约束力： 一个法向力，指向被约束物体
◆ 光滑接触面约束属于单面约束 P
FT
P P
FN
三、光滑铰链约束 特性：只限制物体间的相对移动，而不限制物体间的相对转动。 1. 圆柱铰链（铰链） 圆柱铰链简称铰链，它是由圆柱销钉插入两构件的圆孔而构成。
O
FD D
P1 H
O C D P1 H
FH
P2 FAy
FH
A
FAx
E O
H D P1
A
（三）研究板 AB 取分离体 画主动力 画约束力
B
C P2
B E
O H
O
P1 H
FH
FD D
C D P1 P2

边界条件：描述物体表 面受力情况的方程，根 据外力条件建立。
通过学习和掌握这些基 本概念、应力与应变的 关系以及基本方程，可 以对弹性力学有更深入 的理解，为后续的学习 和应用打下坚实的基础 。
06
理论力学应用案例
机械结构设计中的理论力学应用
强度分析
利用理论力学原理，对机械设备的零部件进行应力、应变 和位移分析，确保其在工作条件下不发生破坏或塑性变形 。
析物体的稳定性等。
03
运动学基础
点的运动学
01
02
03
矢量法
通过矢量来描述点的运动 ，包括位移、速度和加速 度的矢量表示和计算。
直角坐标法
在直角坐标系中研究点的 运动，通过位移、速度和 加速度的分量来表示点的 运动状态。
自然法
借助自然坐标系研究点的 运动，用切向加速度和法 向加速度描述点的曲线运 动。
力对点的矩
力对某点的矩等于力的大小与力 臂（力作用线到该点的垂直距离 ）的乘积，表示力使物体绕该点
转动的效应。
合力矩定理
在平面汇交力系中，各力对某点 的矩的代数和等于该力系的合力 对同一点的矩。该定理可用于求
解物体的平衡问题。
矩的应用
利用矩的概念和合力矩定理，可 以方便地解决物体在平面内的平 衡问题，如确定物体的重心、分
刚度分析
通过对机械结构进行刚度分析，可以确定结构在受力时的 变形程度，为设计提供优化建议，保证机械设备的精度和 稳定性。
动力学设计
理论力学可用于研究机械设备的动态特性，如振动、冲击 等，以合理设计机械设备的动力学性能，降低噪音，提高 使用寿命。
航空航天领域中的理论力学应用
飞行器结构设计
运用理论力学方法，对飞行器的机翼、机身等结构进行强度、刚度 和稳定性分析，确保飞行器在不同飞行条件下的安全性。

Δl AC ΔlCB
l C FA A FP
2l
B
FB
第二，关于变形协调的概念 C FP A C A C FP B FP B FP
Δl AB Δl AC 0 Δl AB ΔlCB 0 Δl AC ΔlCB
FP /2
FP A B 在这三种情形下，AB杆的总变形量都不等于零，即不满足变形协调的要求， 所以是不正确的。


Analysis of Internal Forces
=
+


T: The component of the resultant couple that tends to twist (rotate) the bar is called the twisting moment or torque. T: 合力偶的分量，具有扭转（旋转）杆的趋势，称 为扭矩.

Introduction
Statics and dynamics are devoted primarily to the study of the external effects upon rigid bodies--that is, bodies for which the change in shape (deformation) can be neglected. 静力学和动力学主要研究作用在刚体上的外 力—就是说忽略物体的形状改变（变形）.

Introduction
In contrast, mechanics of materials deals with the internal effects and deformations that are caused by the applied loads. 形成对照, 材料力学研究由外力引起的内部效 果和变形.

理论力学
46
理论力学
47
（3）止推轴承（圆锥轴承）
约束特点：止推轴承比径向轴承多一个轴向的位移限制。 约束力：比径向轴承多一个轴向的约束力，亦有三个正
交分力FAx， FAy ，FAz 。
理论力学
FAz
A
FAy FAx
48
理论力学
49
§1-3 物体的受力分析和受力图
一、受力分析
解决力学问题时，首先要选定需要进行研究的物 体，即选择研究对象，然后根据已知条件，约束类型 并结合基本概念和公理分析它的受力情况，这个过程 称为物体的受力分析。
F1 二力构件
F1 二力杆
F2 F2
注意：二力构件是不计自重的。
公理3 加减平衡力系原理
在已知的任意力系上加上或减去任意一个平衡力系， 并不改变原力系对刚体的作用。
理论力学
12
[证] ∵F1，F2，F3 为平衡力系，
F1 F12
F2
∴ F12 ，F3也为平衡力系。 又∵ 二力平衡必等值、反向、共线，
动力学：研究受力物体的运动与作用力之间的关系。
理论力学
2
二、理论力学的任务
1、理论力学是一门理论性较强的技术基础课
基础课
技术基础课
专业课
2、理论力学是很多专业课程的重要基础 例如：材料力学、机械原理、机械零件、结构力学、
弹性力学 、流体力学 、机械振动等一系列后续课程的重 要基础。
理论力学
3
引言
载荷集度
荷 线载荷：载荷作用在整个长度上。
物体单位体积、单位面积、单位长度上所承受的载荷。
dFR
dFR
dFR
dV
dS
dL

(x i y j z k ) vr
r xi yj zk
vx i v y j vz k
0 i jk
i j k av x y z i y j z k vx r xi yj zk
加速度是描述速度 v 大小和方向 变化率的物理量， 是矢量。 其 方向为 v 的极限方向(指向轨迹 曲线的内凹)。
z (天 )


W
o
A
x (东)

y (北)
第一章 点的运动学
（1）点运动描述的矢量法和直角坐标法 （2）自然坐标法（难点） （3）极坐标法 （4）联合应用例题
(1) 点于其 位置矢量随时间的变化规律内。 点的运动方程（矢量形式）
位矢端图
r f (t ) xi yj zk
( BP d )
再求导得 P 点的加速度 a xi yj 2 r
x 2 (2l d ) cos(t ) y 2d sin(t )
P的轨迹方程为椭圆：
(
x 2 y 2 ) ( ) 1 2l d d
点运动中，其位置矢量首 端描绘的曲线为位矢端图 位矢端图即点的运动轨迹
点运动的一般情形 为三维变速曲线运动
点运动方程的直角坐标形式
x f1 ( t ) y f 2 (t ) z f (t ) 3
点的运动速度: 点在微小时间内其位 置矢径在单位时间内的变化率，即位 置矢量对时间的导数。
v A rAB vB rAB
v A rAB vB rAB
2
2016/9/11
例 曲柄-连杆-滑块机构
已知 曲柄滑块机构中 OA 的半 径R、角速率 。 求 图示瞬时(位置)的 vB , 。 解：由速度投影定理

注 :v 沿轨道切线方向 求证： v t = s ˙
●
速率： v t =∣v t ∣
v
●
v t t
加速度：
v d v a = lim ≡ ≡v ˙ dt t 0 t
特点 : 指向轨道的凹侧
v v t t v t
d r 求证： a = 2 ≡ r ¨ dt
a沿速端曲线切线方向并指向v沿速端曲线运动的前方12质点运动的坐标表示11中矢量形式的定义不依赖于坐标系为了研究问题的方便我们通常取合适的坐标系来表示这些运动学量在不同坐标系中运动学量的表现形式可能非常不同但是它们对应的运动学行为是相同的轨道轨迹运动学方程
第一部分
运动学
基本公设
●
机械运动发生于空间和时间之中 存在绝对空间，它是三维均匀各向同性 的欧氏空间
θ
er
cos k
O'
'
eφ
y
er
eθ'
−sin k
φ P
er ' eθ'
r
r
侧视图
eθ
eθ
e r ' =sin cos i sin j
x
e ' =cos cos i sin j
俯视图
e r =sin cos i sin sin j cos k
a =− 4 2 R [ cos t 0 e sin t 0 e ]
直角坐标和极坐标结果比较
不同坐标表示下 , r,v,a 表达式不 t = 2 R cos t 0 运动 x t = R cos 2 t 2 0 同 , 但它们对描 方程 y t = R sin 2 t 2 0 t = t 0 述 P 点运动是等 v x=− 2 R sin 2 t 2 0 v =−2 R sin t 0 v v =2 R cos 2 t 2 v = 2 R cos t 价的 ; r 对应的轨 y 0 0 道、 v,a 的大小和 2 2 a x =− 4 R cos 2 t 2 0 a =− 4 R cos t 0 方向是唯一的 ! a 2 2 直角坐标 极坐标