导数的应用—单调性与极值的习题课

导数的应用一单调性与极值的习题课【复习目标】1. 理解导数在研究函数的单调性和极值中的作用；2. 理解导数在解决有关不等式、方程的根、曲线交点个数等问题中有广泛的应用。

3. 结合实例，借助几何直观探索并了解函数的单调性与导数的关系；能利用导数研究函数的 单调性，会求不超过三次的多项式函数的单调区间；4. 结合函数的图像，了解函数在某点取得极值的必要条件和充分条件；会用导数求不超过三次的多项式函数的极大值、极小值，体会导数方法在研究函数性质中的一般性和有效性。

【重点难点】①利用导数求函数的极值；②利用导数求函数的单调区间；④利用导数证明函数的单调性； ⑤数在实际中的应用；⑥导数与函数、不等式等知识相融合的问题； 【基础过关】1.函数的单调性⑴ 函数y = f(x)在某个区间内可导，若f(X)> 0,则f (X)为 ______________ 为 .(逆命题不成立)⑵ 如果在某个区间内恒有 f(x)9，则f(x)_.注：连续函数在开区间和与之相应的闭区间上的单调性是一致的.(3)求可导函数单调区间的一般步骤和方法：确定函数f(x)的 __________ ；求f (x)，令 _________ ，解此方程，求出它在定义区间内的一切实根;③ 序排列起来，然后用这些点把函数 f(x)的定义区间分成若干个小区间;那么函数y = f(x)在这个根处取得 ___________ ;如果在根的左侧附近为负，右侧为正，那么函 数y = f(x)在这个根处取得 .【基础训练】例1•如果函数y = f(X)的图像如右图，那么导函数y =f ,(x)的图像可能是(；若 f ・(x) < 0 ,则 f(X) 把函数f(x)的间断点(即f(x)的无定义点)的横坐标和上面的各个实根按由小到大的顺 ④确定f (x)在各小开区间内的 间内的增减性. 2.可导函数的极值⑴极值的概念 设函数f(X)在点X 0附近有定义，且对 X 0附近的所有点都有 _f (x o )为函数的一个极大(小)值.称X 0为极大(小)值点.求可导函数极值的步骤： 求导数f (x)；求方程f (x) = 0的__________ ； 检验f(x)在方程f (x) = 0的根左右的符号，如果在根的左侧附近为正，右侧附近为负， ,根据f(X)的符号判定函数f(X)在各个相应小开区(或 )，则称⑵ ① ② ③)20 X2例2.曲线y=x _21 nx 的单调减区间是()A. (0,1];B.[1,+^); C.(二,1]及(0,1] ； D.[—1,0)及(0,1];2例3.若函数f(x)= —a在x=1处取极值，则a =x +1例4.函数f (x)的定义域为开区间(a, b)，导函数f '(X)在(a, b)内 的图象如图所示，则函数 f (X)在开区间(a,b)内有极小值点例5.若f(X)= X 3 +3ax 2+3(a+2)x 中1有极值，则a 的取值范围是【典型例题】1(2011浙江五校联考)已知函数f(x) = X 3+ ax 2 + bx + c(x € [ —1,2])，且函数f(x)在x = 1和x = 2—2处都取得极值. 3 (1)求a ，b 的值;(2)求函数f(x)的单调递增区间.解 (1) T f(x) = x '+ ax ? + bx + c ,.・.f' (x) = 3x 2+ 2ax + b.f ' L 2L 0 L = — 1 由题易知，V < 3丿，解得$ 2^ f (1 = 0, [b =- 2.2(2)由(1)知，f ' (x)= 3x — X — 2= (3x + 2)(x — 1), T 当 xC [— 1，— 2)寸，f' (X)>0；当 xC (— 3, 1)寸，f' (X) V 0； 当 x € (1,2]时，f '(X)> 0.2.设函数 f(X)=x 3 —3ax+b(a H0).(I)若曲线y = f(x)在点(2, f (x))处与直线y =8相切，求a,b 的值;(n)求函数f (x)的单调区间与极值点.••• f(x)的单调递增区间为 -1，— 2加(1,2].(川)若b = -1且f(x)在x = -1处取得极值，直线y=m与y = f(x)的图象有三个不同的交点，求m的取值范围。

导数与函数的单调性、极值、最值问题高考定位 高考对本内容的考查主要有：(1)导数的运算是导数应用的基础，要求是B 级，熟练掌握导数的四则运算法则、常用导数公式，一般不单独设置试题，是解决导数应用的第一步；(2)利用导数研究函数的单调性与极值是导数的核心内容，要求是B 级，对应用导数研究函数的单调性与极值要达到相等的高度.真 题 感 悟1.(2017·江苏卷)已知函数f (x )＝x 3－2x ＋e x －1e x ，其中e 是自然对数的底数，若f (a －1)＋f (2a 2)≤0，则实数a 的取值范围是________. 解析 f ′(x )＝3x 2－2＋e x ＋1e x ≥3x 2－2＋2e x ·1ex ＝3x 2≥0且f ′(x )不恒为0，所以f (x )为单调递增函数. 又f (－x )＝－x 3＋2x ＋e －x －e x ＝－(x 3－2x ＋e x－1ex )＝－f (x )，故f (x )为奇函数，由f (a －1)＋f (2a 2)≤0，得f (2a 2)≤f (1－a )， ∴2a 2≤1－a ，解之得－1≤a ≤12，故实数a 的取值范围是⎣⎢⎡⎦⎥⎤－1，12.答案 ⎣⎢⎡⎦⎥⎤－1，122.(2017·江苏卷)已知函数f (x )＝x 3＋ax 2＋bx ＋1(a >0，b ∈R)有极值，且导函数f ′(x )的极值点是f (x )的零点.(极值点是指函数取极值时对应的自变量的值)(1)求b 关于a 的函数关系式，并写出定义域；(2)证明：b 2>3a ；(3)若f (x )，f ′(x )这两个函数的所有极值之和不小于－72，求a 的取值范围.(1)解 由f (x )＝x 3＋ax 2＋bx ＋1，得f ′(x )＝3x 2＋2ax ＋b ＝3⎝⎛⎭⎪⎫x ＋a 32＋b －a 23.当x ＝－a 3时，f ′(x )有极小值b －a 23.因为f ′(x )的极值点是f (x )的零点，所以f ⎝ ⎛⎭⎪⎫－a 3＝－a 327＋a 39－ab 3＋1＝0，又a >0，故b ＝2a 29＋3a.因为f (x )有极值，故f ′(x )＝0有实根， 从而b －a 23＝19a (27－a 3)≤0，即a ≥3.当a ＝3时，f ′(x )>0(x ≠－1)，故f (x )在R 上是增函数，f (x )没有极值； 当a >3时，f ′(x )＝0有两个相异的实根 x 1＝－a －a 2－3b 3，x 2＝－a ＋a 2－3b 3.列表如下：故f (x )的极值点是x 1，x 2.从而a >3. 因此b ＝2a 29＋3a，定义域为(3，＋∞).(2)证明 由(1)知，b a ＝2a a 9＋3a a.设g (t )＝2t 9＋3t ，则g ′(t )＝29－3t 2＝2t 2－279t 2.当t ∈⎝ ⎛⎭⎪⎫362，＋∞时，g ′(t )>0，从而g (t )在⎝ ⎛⎭⎪⎫362，＋∞上单调递增.因为a >3，所以a a >33，故g (a a )>g (33)＝3，即ba > 3.因此b 2>3a .(3)解 由(1)知，f (x )的极值点是x 1，x 2， 且x 1＋x 2＝－23a ，x 21＋x 22＝4a 2－6b 9.从而f (x 1)＋f (x 2)＝x 31＋ax 21＋bx 1＋1＋x 32＋ax 22＋bx 2＋1＝x 13(3x 21＋2ax 1＋b )＋x 23(3x 22＋2ax 2＋b )＋13a (x 21＋x 22)＋23b (x 1＋x 2)＋2＝4a 3－6ab 27－4ab 9＋2＝0. 记f (x )，f ′(x )所有极值之和为h (a )， 因为f ′(x )的极值为b －a 23＝－19a 2＋3a ，所以h (a )＝－19a 2＋3a ，a >3.因为h ′(a )＝－29a －3a 2<0，于是h (a )在(3，＋∞)上单调递减.因为h (6)＝－72，于是h (a )≥h (6)，故a ≤6.因此a的取值范围为(3，6].考点整合1.导数与函数的单调性(1)函数单调性的判定方法：设函数y＝f (x)在某个区间内可导，如果f ′(x)＞0，则y＝f (x)在该区间为增函数；如果f ′(x)＜0，则y＝f (x)在该区间为减函数.(2)函数单调性问题包括：①求函数的单调区间，常常通过求导，转化为解方程或不等式，常用到分类讨论思想；②利用单调性证明不等式或比较大小，常用构造函数法.2.极值的判别方法当函数f (x)在点x0处连续时，如果在x0附近的左侧f′(x)＞0，右侧f ′(x)＜0，那么f (x0)是极大值；如果在x0附近的左侧f ′(x)＜0，右侧f ′(x)＞0，那么f (x0)是极小值.也就是说x0是极值点的充分条件是点x0两侧导数异号，而不是f ′(x)＝0.此外，函数不可导的点也可能是函数的极值点，而且极值是一个局部概念，极值的大小关系是不确定的，即有可能极大值比极小值小.3.闭区间上函数的最值在闭区间上连续的函数，一定有最大值和最小值，其最大值是区间的端点处的函数值和在这个区间内函数的所有极大值中的最大者，最小值是区间端点处的函数值和在这个区间内函数的所有极小值中的最小者.热点一利用导数研究函数的单调性[命题角度1] 求解含参函数的单调区间【例1－1】(2017·全国Ⅰ卷改编)已知函数f (x)＝e x(e x－a)－a2x，其中参数a≤0.(1)讨论f (x)的单调性；(2)若f (x)≥0，求a的取值范围.解 (1)函数f (x )的定义域为(－∞，＋∞)，且a ≤0.f ′(x )＝2e 2x －a e x －a 2＝(2e x ＋a )(e x －a ).①若a ＝0，则f (x )＝e 2x ，在(－∞，＋∞)上单调递增. ②若a <0，则由f ′(x )＝0，得x ＝ln ⎝ ⎛⎭⎪⎫－a 2.当x ∈⎝ ⎛⎭⎪⎫－∞，ln ⎝ ⎛⎭⎪⎫－a 2时，f ′(x )<0；当x ∈⎝ ⎛⎭⎪⎫ln ⎝ ⎛⎭⎪⎫－a 2，＋∞时，f ′(x )>0.故f (x )在⎝ ⎛⎭⎪⎫－∞，ln ⎝ ⎛⎭⎪⎫－a 2上单调递减，在区间⎝ ⎛⎭⎪⎫ln ⎝ ⎛⎭⎪⎫－a 2，＋∞上单调递增.(2)①当a ＝0时，f (x )＝e 2x ≥0恒成立.②若a <0，则由(1)得，当x ＝ln ⎝ ⎛⎭⎪⎫－a 2时，f (x )取得最小值，最小值为 f⎝ ⎛⎭⎪⎫ln ⎝ ⎛⎭⎪⎫－a 2＝a 2⎣⎢⎡⎦⎥⎤34－ln ⎝ ⎛⎭⎪⎫－a 2，故当且仅当a 2⎣⎢⎡⎦⎥⎤34－ln ⎝ ⎛⎭⎪⎫－a 2≥0，即a ≥－2e 34时，f (x )≥0.综上，a 的取值范围是[－2e 34，0].探究提高 讨论函数的单调性其实质就是讨论不等式的解集的情况.大多数情况下，这类问题可以归结为一个含有参数的一元二次不等式的解集的讨论，常需依据以下标准分类讨论：(1)二次项系数为0、为正、为负，目的是讨论开口方向；(2)判别式的正负，目的是讨论对应二次方程是否有解；(3)讨论两根差的正负，目的是比较根的大小；(4)讨论两根与定义域的关系，目的是根是否在定义域内.另外，需优先判断能否利用因式分解法求出根. [命题角度2] 已知函数的单调区间求参数范围【例1－2】 已知a ∈R ，函数f (x )＝(－x 2＋ax )e x (x ∈R ，e 为自然对数的底数).(1)当a ＝2时，求函数f (x )的单调递增区间；(2)若函数f (x )在(－1，1)上单调递增，求a 的取值范围；(3)函数f (x )能否为R 上的单调函数？若能，求出a 的取值范围？若不能，请说明理由.解 (1)当a ＝2时，f (x )＝(－x 2＋2x )·e x ，所以f ′(x )＝(－2x ＋2)e x ＋(－x 2＋2x )e x ＝(－x 2＋2)e x . 令f ′(x )＞0，即(－x 2＋2)e x ＞0，因为e x ＞0，所以－x 2＋2＞0，解得－2＜x ＜ 2. 所以函数f (x )的单调递增区间是(－2，2). (2)因为函数f (x )在(－1，1)上单调递增， 所以f ′(x )≥0对x ∈(－1，1)都成立. 因为f ′(x )＝(－2x ＋a )e x ＋(－x 2＋ax )e x ＝[－x 2＋(a －2)x ＋a ]e x ，所以[－x 2＋(a －2)x ＋a ]e x ≥0对x ∈(－1，1)都成立.因为e x＞0，所以－x 2＋(a －2)x ＋a ≥0对x ∈(－1，1)都成立，即a ≥x 2＋2xx ＋1＝（x ＋1）2－1x ＋1＝(x ＋1)－1x ＋1对x ∈(－1，1)都成立.令g (x )＝(x ＋1)－1x ＋1，则g ′(x )＝1＋1（x ＋1）2＞0. 所以g (x )＝(x ＋1)－1x ＋1在(－1，1)上单调递增. 所以g (x )＜g (1)＝(1＋1)－11＋1＝32.所以a 的取值范围是⎣⎢⎡⎭⎪⎫32，＋∞.(3)若函数f (x )在R 上单调递减，则f ′(x )≤0对x ∈R 都成立，即[－x 2＋(a －2)x ＋a ]e x ≤0对x ∈R 都成立.因为e x ＞0，所以x 2－(a －2)x －a ≥0对x ∈R 都成立.所以Δ＝(a －2)2＋4a ≤0，即a 2＋4≤0，这是不可能的.故函数f (x )不可能在R 上单调递减.若函数f (x )在R 上单调递增，则f ′(x )≥0对x ∈R 都成立，即[－x 2＋(a －2)x ＋a ]e x ≥0对x ∈R 都成立，因为e x ＞0，所以x 2－(a －2)x －a ≤0对x ∈R 都成立.而Δ＝(a －2)2＋4a ＝a 2＋4＞0，故函数f (x )不可能在R 上单调递增. 综上，可知函数f (x )不可能是R 上的单调函数.探究提高 (1)已知函数的单调性，求参数的取值范围，应用条件f ′(x )≥0(或f ′(x )≤0)，x ∈(a ，b )恒成立，解出参数的取值范围(一般可用不等式恒成立的理论求解)，应注意参数的取值是f ′(x )不恒等于0的参数的范围. (2)可导函数f (x )在某个区间D 内单调递增(或递减)，转化为恒成立问题时，常忽视等号这一条件，导致与正确的解法擦肩而过，注意，这里“＝”一定不能省略.【训练1】 (2017·南京、盐城模拟)设函数f (x )＝ln x ，g (x )＝ax ＋a －1x－3(a ∈R).(1)当a ＝2时，解关于x 的方程g (e x )＝0(其中e 为自然对数的底数)； (2)求函数φ(x )＝f (x )＋g (x )的单调递增区间. 解 (1)当a ＝2时，方程g (e x )＝0，即2e x ＋1e x －3＝0，去分母，得2(e x )2－3e x ＋1＝0，解得e x ＝1或e x ＝12.故所求方程的根为x ＝0或x ＝－ln 2. (2)因为φ(x )＝f (x )＋g (x )＝ln x ＋ax ＋a －1x－3(x >0)， 所以φ′(x )＝1x ＋a －a －1x 2＝ax 2＋x －（a －1）x 2＝[ax －（a －1）]（x ＋1）x2(x >0)， 当a <0时，由φ′(x )>0，解得0<x <a －1a；当a ＝0时，由φ′(x )>0，解得x >0； 当0<a <1时，由φ′(x )>0，解得x >0； 当a ＝1时，由φ′(x )>0，解得x >0； 当a >1时，由φ′(x )>0，解得x >a －1a. 综上所述，当a <0时，φ(x )的单调递增区间为⎝ ⎛⎭⎪⎫0，a －1a ； 当0≤a ≤1时，φ(x )的单调递增区间为(0，＋∞)； 当a >1时，φ(x )的单调递增区间为⎝ ⎛⎭⎪⎫a －1a ，＋∞. 热点二 利用导数研究函数的极值【例2】 (2017·南通调研)设函数f (x )＝x －2e x －k (x －2ln x )(k 为实常数，e ＝2.718 28…是自然对数的底数). (1)当k ＝1时，求函数f (x )的最小值；(2)若函数f (x )在(0，4)内存在三个极值点，求k 的取值范围. 解 (1)当k ＝1时，函数f (x )＝e xx2－(x －2ln x )(x ＞0)，则f ′(x )＝（x －2）（e x －x 2）x3(x ＞0). 当x ＞0时，e x ＞x 2，理由如下：要使当x ＞0时，e x ＞x 2，只需使x ＞2ln x ， 设φ(x )＝x －2ln x ，则φ′(x )＝1－2x ＝x －2x，所以当0＜x ＜2时，φ′(x )＜0；当x ＞2时，φ′(x )＞0， 所以φ(x )＝x －2ln x 在x ＝2处取得最小值φ(2)＝2－2ln 2＞0， 所以当x ＞0时，x ＞2ln x ， 所以e x －x 2＞0，所以当0＜x ＜2时，f ′(x )＜0；当x ＞2时，f ′(x )＞0，即函数f (x )在(0，2)上为减函数，在(2，＋ ∞)上为增函数， 所以f (x )在x ＝2处取得最小值f (2)＝e 24－2＋2ln 2.(2)因为f ′(x )＝（x －2）（e x －kx 2）x 3＝（x －2）⎝ ⎛⎭⎪⎫e xx 2－k x，当k ≤0时，e xx2－k ＞0，所以f (x )在(0，2)上单调递减，在(2，4)上单调递增，不存在三个极值点，所以k ＞0. 令g (x )＝e xx 2，得g ′(x )＝e x ·（x －2）x 3，则g (x )在(0，2)上单调递减，在(2，＋∞)上单调递增，在x ＝2处取得最小值为g (2)＝e 24，且g (4)＝e 416，于是可得y ＝k 与g (x )＝e xx 2在(0，4)内有两个不同的交点的条件是k ∈⎝ ⎛⎭⎪⎫e 24，e 416.设y ＝k 与g (x )＝e xx2在(0，4)内的两个不同交点的横坐标分别为x 1，x 2，且0＜x 1＜2＜x 2＜4，导函数f ′(x )及原函数f (x )的变化情况如下：所以 f (x )在(0，x 1)上单调递减，在(x 1，2)上单调递增，在(2，x 2)上单调递减，在(x 2，4)上单调递增，所以f (x )在(0，4)上存在三个极值点.即函数f (x )在(0，4)内存在三个极值点的k 的取值范围是⎝ ⎛⎭⎪⎫e 24，e 416.探究提高极值点的个数，一般是使f ′(x)＝0方程根的个数，一般情况下导函数若可以化成二次函数，我们可以利用判别式研究，若不是，我们可以借助导函数的性质及图象研究.【训练2】(2017·苏、锡、常、镇调研节选)已知函数f (x)＝ax2＋cos x(a ∈R)，记f (x)的导函数为g(x).(1)证明：当a＝12时，g(x)在R上单调递增；(2)若f (x)在x＝0处取得极小值，求a的取值范围.(1)证明当a＝12时，f (x)＝12x2＋cos x，所以f ′(x)＝x－sin x，令g(x)＝x－sin x，所以g′(x)＝1－cos x≥0，所以g(x)在R上单调递增.(2)解因为g(x)＝f ′(x)＝2ax－sin x，所以g′(x)＝2a－cos x.①当a≥12时，g′(x)≥1－cos x≥0，所以函数f ′(x)在R上单调递增.当x>0时，则f ′(x)>f ′(0)＝0；当x<0时，则f ′(x)<f ′(0)＝0；所以f (x)的单调递增区间是(0，＋∞)，单调递减区间是(－∞，0)，所以f (x)在x＝0处取得极小值，符合题意.②当a≤－12时，g′(x)≤－1－cos x≤0，所以函数f ′(x)在R上单调递减.当x>0时，则f ′(x)<f ′(0)＝0；当x<0时，则f ′(x)>f ′(0)＝0，所以f (x)的单调递减区间是(0，＋∞)，单调递增区间是(－∞，0)，所以f (x)在x＝0处取得极大值，不符合题意.③当－12<a <12时，∃x 0∈(0，π)，使得cos x 0＝2a ，即g ′(x 0)＝0，但当x ∈(0，x 0)时，cos x >2a ，即g ′(x )<0， 所以函数f ′(x )在(0，x 0)上单调递减， 所以f ′(x )<f ′(0)＝0，即函数f (x )在(0，x 0)上单调递减，不符合题意. 综上所述，实数a 的取值范围是⎣⎢⎡⎭⎪⎫12，＋∞.热点三 利用导数研究函数的最值【例3】 (2017·浙江卷)已知函数f (x )＝(x －2x －1)e －x ⎝ ⎛⎭⎪⎫x ≥12.(1)求f (x )的导函数；(2)求f (x )在区间⎣⎢⎡⎭⎪⎫12，＋∞上的取值范围.解 (1)f ′(x )＝(x －2x －1)′e －x ＋(x －2x －1)(e －x )′ ＝⎝⎛⎭⎪⎫1－12x －1e －x －(x －2x －1)e －x ＝⎝ ⎛⎭⎪⎫1－12x －1－x ＋2x －1e －x ＝(1－x )⎝⎛⎭⎪⎫1－22x －1e －x ⎝ ⎛⎭⎪⎫x ＞12. (2)令f ′(x )＝(1－x )⎝ ⎛⎭⎪⎫1－22x －1e －x ＝0， 解得x ＝1或52.当x 变化时，f (x )，f ′(x )的变化如下表：又f ⎝ ⎛⎭⎪⎫12＝12e －12，f (1)＝0，f ⎝ ⎛⎭⎪⎫52＝12e －52，则f (x )在区间⎣⎢⎡⎭⎪⎫12，＋∞上的最大值为12e －12.又f (x )＝(x －2x －1)e －x ＝12(2x －1－1)2e －x ≥0.综上，f (x )在区间⎣⎢⎡⎭⎪⎫12，＋∞上的取值范围是⎣⎢⎡⎦⎥⎤0，12e －12. 探究提高 含参数的函数的极值(最值)问题常在以下情况下需要分类讨论： (1)导数为零时自变量的大小不确定需要讨论；(2)导数为零的自变量是否在给定的区间内不确定需要讨论；(3)端点处的函数值和极值大小不确定需要讨论；(4)参数的取值范围不同导致函数在所给区间上的单调性的变化不确定需要讨论.【训练3】 已知函数f (x )＝x ln x . (1)求函数f (x )的单调区间和最小值； (2)若函数F (x )＝f （x ）－a x 在[1，e]上的最小值为32，求a 的值. 解 (1)因为f ′(x )＝ln x ＋1(x ＞0)， 令f ′(x )≥0，即ln x ≥－1＝ln e －1， 所以x ≥e －1＝1e ，所以x ∈⎣⎢⎡⎭⎪⎫1e ，＋∞. 同理令f ′(x )≤0，可得x ∈⎝ ⎛⎦⎥⎤0，1e .所以 f (x )的单调递增区间为⎣⎢⎡⎭⎪⎫1e ，＋∞，单调递减区间为⎝ ⎛⎦⎥⎤0，1e .由此可知 f(x )min ＝f ⎝ ⎛⎭⎪⎫1e ＝－1e .(2)由F (x )＝x ln x －a x ，得F ′(x )＝x ＋ax 2，当a ≥0时，F ′(x )＞0，F (x )在[1，e]上单调递增，F (x )min ＝F (1)＝－a ＝32， 所以a ＝－32∉[0，＋∞)，舍去.当a ＜0时，f (x )在(0，－a )上单调递减，在(－a ，＋∞)上单调递增. ①当a ∈(－1，0)，F (x )在[1，e]上单调递增， F (x )min ＝F (1)＝－a ＝32，所以a ＝－32∉(－1，0)，舍去.②若a ∈[－e ，－1]，F (x )在[1，－a ]上单调递减， 在[－a ，e]上单调递增，所以F (x )min ＝F (－a )＝ln(－a )＋1＝32，a ＝－e ∈[－e ，－1]；③若a ∈(－∞，－e)，F (x )在[1，e]上单调递减，F (x )min ＝F (e)＝1－a e＝32，所以a ＝－e2∉(－∞，－e)，舍去.综上所述，a ＝－ e.1.如果一个函数具有相同单调性的区间不止一个，这些单调区间不能用“∪”连接，而只能用逗号或“和”字隔开.2.可导函数在闭区间[a，b]上的最值，就是函数在该区间上的极值及端点值中的最大值与最小值.3.可导函数极值的理解(1)函数在定义域上的极大值与极小值的大小关系不确定，也有可能极小值大于极大值；(2)对于可导函数f (x)，“f (x)在x＝x0处的导数f ′(x0)＝0”是“f (x)在x＝x处取得极值”的必要不充分条件；(3)注意导函数的图象与原函数图象的关系，导函数由正变负的零点是原函数的极大值点，导函数由负变正的零点是原函数的极小值点.4.求函数的单调区间时，若函数的导函数中含有带参数的有理因式，因式根的个数、大小、根是否在定义域内可能都与参数有关，则需对参数进行分类讨论.5.求函数的极值、最值问题，一般需要求导，借助函数的单调性，转化为方程或不等式问题来解决，有正向思维——直接求函数的极值或最值；也有逆向思维——已知函数的极值或最值，求参数的值或范围，常常用到分类讨论、数形结合的思想.一、填空题1.已知函数f (x)＝4ln x＋ax2－6x＋b(a，b为常数)，且x＝2为f (x)的一个极值点，则a的值为________.解析由题意知，函数f (x)的定义域为(0，＋∞)，∵f ′(x)＝4x＋2ax－6，∴f ′(2)＝2＋4a－6＝0，即a＝1，经验证符合题意. 答案 12.(2017·苏州调研)函数f (x)＝12x2－ln x的单调递减区间为________.解析 由题意知，函数的定义域为(0，＋∞)，又由f ′(x )＝x －1x<0，解得0＜x <1，所以函数f (x )的单调递减区间为(0，1). 答案 (0，1)3.已知函数f (x )＝x 3＋ax 2＋bx －a 2－7a 在x ＝1处取得极大值10，则ab的值为________.解析 由题意知f ′(x )＝3x 2＋2ax ＋b ，f ′(1)＝0，f (1)＝10， 即⎩⎨⎧3＋2a ＋b ＝0，1＋a ＋b －a 2－7a ＝10，解得⎩⎨⎧a ＝－2，b ＝1或 ⎩⎨⎧a ＝－6，b ＝9，经检验⎩⎨⎧a ＝－6，b ＝9满足题意，故a b ＝－23.答案 －234.(2017·南京模拟)若函数f (x )＝e x (－x 2＋2x ＋a )在区间[a ，a ＋1]上单调递增，则实数a 的最大值为________.解析 由f (x )在区间[a ，a ＋1]上单调递增，得f ′(x )＝e x (－x 2＋a ＋2)≥0，x ∈[a ，a ＋1]恒成立，即(－x 2＋a ＋2)min ≥0，x ∈[a ，a ＋1].当a ≤－12时，－a 2＋a ＋2≥0，则－1≤a ≤－12；当a >－12时，－(a ＋1)2＋a ＋2≥0，则－12<a ≤－1＋52，所以实数a 的取值范围是－1≤a ≤－1＋52，a 的最大值是－1＋52. 答案－1＋525.(2017·浙江卷改编)函数y ＝f (x )的导函数y ＝f ′(x )的图象如图所示，则函数y ＝f (x )的图象可能是________(填序号).解析 利用导数与函数的单调性进行验证.f ′(x )＞0的解集对应y ＝f (x )的增区间，f ′(x )＜0的解集对应y ＝f (x )的减区间，验证只有④符合. 答案 ④6.(2017·泰州期末)函数f (x )＝x 3－3ax －a 在(0，1)内有最小值，则a 的取值范围是________.解析 f ′(x )＝3x 2－3a ＝3(x 2－a ).当a ≤0时，f ′(x )＞0， ∴f (x )在(0，1)内单调递增，无最小值. 当a ＞0时，f ′(x )＝3(x －a )(x ＋a ).当x ∈(－∞，－a )和(a ，＋∞)时，f (x )单调递增； 当x ∈(－a ，a )时，f (x )单调递减，所以当a ＜1，即0＜a ＜1时，f (x )在(0，1)内有最小值. 答案 (0，1)7.已知函数f (x )＝13x 3＋ax 2＋3x ＋1有两个极值点，则实数a 的取值范围是________.解析 f ′(x )＝x 2＋2ax ＋3.由题意知方程f ′(x )＝0有两个不相等的实数根， 所以Δ＝4a 2－12＞0， 解得a ＞3或a ＜－ 3.答案 (－∞，－3)∪(3，＋∞)8.(2016·北京卷)设函数f (x )＝⎩⎨⎧x 3－3x ，x ≤a ，－2x ，x ＞a .(1)若a ＝0，则f (x )的最大值为________；(2)若f (x )无最大值，则实数a 的取值范围是________. 解析 (1)当a ＝0时，f (x )＝⎩⎨⎧x 3－3x ，x ≤0，－2x ，x ＞0.若x ≤0，f ′(x )＝3x 2－3＝3(x 2－1). 由f ′(x )＞0得x ＜－1， 由f ′(x )＜0得－1＜x ≤0.∴f (x )在(－∞，－1)上单调递增，在(－1，0]上单调递减， ∴f (x )最大值为f (－1)＝2.若x ＞0，f (x )＝－2x 单调递减，所以f (x )＜f (0)＝0. 综上，f (x )最大值为2.(2)函数y ＝x 3－3x 与y ＝－2x 的图象如图.由(1)知，当a ≥－1时，f (x )取得最大值2.当a ＜－1时，y ＝－2x 在x ＞a 时无最大值.且－2a ＞2. 所以a ＜－1.答案 (1)2 (2)(－∞，－1) 二、解答题9.(2017·北京卷)已知函数f (x )＝e x cos x －x . (1)求曲线y ＝f (x )在点(0，f (0))处的切线方程； (2)求函数f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值.解 (1)∵f (x )＝e x ·cos x －x ，∴f (0)＝1，f ′(x )＝e x (cos x －sin x )－1，∴f ′(0)＝0，∴y ＝f (x )在(0，f (0))处的切线方程为y －1＝0·(x －0)，即y ＝1. (2)f ′(x )＝e x (cos x －sin x )－1，令g (x )＝f ′(x )， 则g ′(x )＝－2sin x ·e x≤0在⎣⎢⎡⎦⎥⎤0，π2上恒成立， ∴g (x )在⎣⎢⎡⎦⎥⎤0，π2上单调递减，∴g (x )≤g (0)＝0，∴f ′(x )≤0且仅在x ＝0处等号成立， ∴f (x )在⎣⎢⎡⎦⎥⎤0，π2上单调递减，∴f (x )max ＝f (0)＝1，f (x )min ＝f ⎝ ⎛⎭⎪⎫π2＝－π2.10.(2016·全国Ⅱ卷)(1)讨论函数f (x )＝x －2x ＋2e x的单调性，并证明当x >0时，(x －2)e x ＋x ＋2>0；(2)证明：当a ∈[0，1)时，函数g (x )＝e x －ax －ax 2(x >0)有最小值.设g (x )的最小值为h (a )，求函数h (a )的值域.(1)解 f (x )的定义域为(－∞，－2)∪(－2，＋∞). f ′(x )＝（x －1）（x ＋2）e x －（x －2）e x （x ＋2）2＝x 2e x（x ＋2）2≥0，且仅当x ＝0时，f ′(x )＝0，所以f (x )在(－∞，－2)，(－2，＋∞)上单调递增. 因此当x ∈(0，＋∞)时，f (x )>f (0)＝－1. 所以(x －2)e x >－(x ＋2)，即(x －2)e x ＋x ＋2>0. (2)证明 g ′(x )＝（x －2）e x ＋a （x ＋2）x3＝x ＋2x 3(f (x )＋a ). 由(1)知f (x )＋a 单调递增，对任意a ∈[0，1)，f (0)＋a ＝a －1<0，f (2)＋a ＝a ≥0. 因此，存在唯一x a ∈( 0，2]， 使得f (x a )＋a ＝0，即g ′(x a )＝0.当0<x <x a 时，f (x )＋a <0，g ′(x )<0，g (x )单调递减； 当x >x a 时，f (x )＋a >0，g ′(x )>0，g (x )单调递增. 因此g (x )在x ＝x a 处取得最小值，最小值为g (x a )＝ e x a －a （x a ＋1）x 2a＝e x a ＋f （x a ）（x a ＋1）x 2a＝e x ax a ＋2.于是h (a )＝e xax a ＋2，由⎝ ⎛⎭⎪⎫e xx ＋2′＝（x ＋1）e x （x ＋2）2>0，e x x ＋2单调递增.所以，由x a ∈(0，2]，得12＝e 00＋2<h (a )＝e x a x a ＋2≤e 22＋2＝e 24. 因为e x x ＋2单调递增，对任意λ∈⎝ ⎛⎦⎥⎤12，e 24，存在唯一的x a ∈(0，2]，a ＝－f (x a )∈[0，1)，使得h (a )＝λ.所以h (a )的值域是⎝ ⎛⎦⎥⎤12，e 24.综上，当a ∈[0，1)时，g (x )有最小值h (a )，h (a )的值域是⎝ ⎛⎦⎥⎤12，e 24.11.设函数f (x )＝e xx 2－k ⎝ ⎛⎭⎪⎫2x ＋ln x (k 为常数，e ＝2.718 28…是自然对数的底数).(1)当k ≤0时，求函数f (x )的单调区间；(2)若函数f (x )在(0，2)内存在两个极值点，求k 的取值范围. 解 (1)函数y ＝f (x )的定义域为(0，＋∞).f ′(x )＝x 2e x －2x e x x 4－k ⎝ ⎛⎭⎪⎫－2x 2＋1x＝x e x －2e x x 3－k （x －2）x 2＝（x －2）（e x －kx ）x 3.由k ≤0可得e x －kx ＞0，所以当x ∈(0，2)时，f ′(x )＜0，函数y ＝f (x )单调递减，x ∈(2，＋∞)时，f ′(x )＞0，函数y ＝f (x )单调递增.所以f (x )的单调递减区间为(0，2)，单调递增区间为(2，＋∞). (2)由(1)知，k ≤0时，函数f (x )在(0，2)内单调递减，故f (x )在(0，2)内不存在极值点；当k ＞0时，设函数g (x )＝e x －kx ，x ∈[0，＋∞). 因为g ′(x )＝e x －k ＝e x －e ln k ，当0＜k ≤1时， 当x ∈(0，2)时，g ′(x )＝e x －k ＞0，y ＝g (x )单调递增. 故f (x )在(0，2)内不存在两个极值点；当k ＞1时，得x ∈(0，ln k )时，g ′(x )＜0，函数y ＝g (x )单调递减.x ∈(ln k ，＋∞)时，g ′(x )＞0，函数y ＝g (x )单调递增. 所以函数y ＝g (x )的最小值为g (ln k )＝k (1－ln k ).函数f (x )在(0，2)内存在两个极值点当且仅当⎩⎨⎧g （0）＞0，g （ln k ）＜0，g （2）＞0，0＜ln k ＜2，解得e ＜k ＜e 22， 综上所述，函数f (x )在(0，2)内存在两个极值点时，k 的取值范围为⎝⎛⎭⎪⎫e ，e 22.。

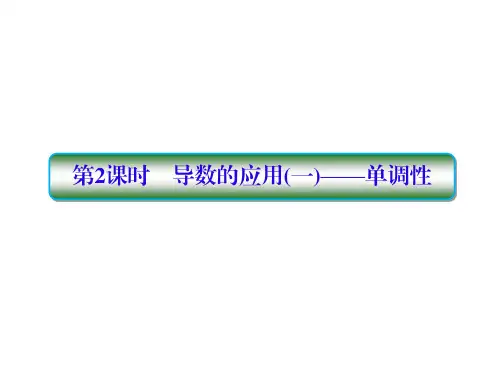
第十三讲 利用导数求函数的单调性、极值、最值一．函数的单调性在某个区间(a ，b )内，如果f ′(x )>0，那么函数y ＝f (x )在这个区间内单调递增；如果f ′(x )<0，那么函数y ＝f (x )在这个区间内单调递减． 二．函数的极值(1)一般地，求函数y ＝f (x )的极值的方法 解方程f ′(x )＝0，当f ′(x 0)＝0时：①如果在x 0附近的左侧f ′(x )>0，右侧f ′(x )<0，那么f (x 0)是极大值； ②如果在x 0附近的左侧f ′(x )<0，右侧f ′(x )>0，那么f (x 0)是极小值． (2)求可导函数极值的步骤 ①求f ′(x )；②求方程f ′(x )＝0的根；③考查f ′(x )在方程f ′(x )＝0的根附近的左右两侧导数值的符号．如果左正右负，那么f (x )在这个根处取得极大值；如果左负右正，那么f (x )在这个根处取得极小值． 三．函数的最值(1)在闭区间[a ，b ]上连续的函数f (x )在[a ，b ]上必有最大值与最小值．(2)若函数f (x )在[a ，b ]上单调递增，则f (a )为函数的最小值，f (b )为函数的最大值；若函数f (x )在[a ，b ]上单调递减，则f (a )为函数的最大值，f (b )为函数的最小值．考向一单调区间【例1】求下列函数的单调区间：（1）3()23f x x x =-；（2）2()ln f x x x =-. （3）)f (x )＝2x －x 2.【答案】见解析【解析】（1）由题意得2()63f x x '=-. 令2()630f x x '=->，解得2x <-或2x >. 当(,2x ∈-∞-时，函数为增函数；当,)2x ∈+∞时，函数也为增函数.令2()630f x x '=-<，解得22x -<<当()22x ∈-时，函数为减函数. 故函数3()23f x x x =-的单调递增区间为(,2-∞-和()2+∞，单调递减区间为(,22-. （2）函数2()ln f x x x =-的定义域为(0,)+∞.11)()2f x x x x-+'=-=. 令()0f x '>，解得x >；令()0f x '<，解得0x <<. 故函数2()ln f x x x =-的单调递增区间为)+∞，单调递减区间为. (3)要使函数f (x )＝2x －x 2有意义，必须2x －x 2≥0，即0≤x ≤2.∴函数的定义域为[0,2]．f ′(x )＝(2x －x 2)′＝12(2x －x 2)－12·(2x －x 2)′＝1－x2x －x2.令f ′(x )＞0，则1－x 2x －x2＞0.即⎩⎪⎨⎪⎧1－x ＞0，2x －x 2＞0，∴0＜x ＜1.∴函数的单调递增区间为(0,1)． 令f ′(x )＜0，则1－x2x －x 2＜0，即⎩⎪⎨⎪⎧1－x ＜0，2x －x 2＞0，∴1＜x ＜2.∴函数的单调递减区间为(1,2)．【举一反三】【套路总结】用导数研究函数的单调性 （1）用导数证明函数的单调性证明函数单调递增（减），只需证明在函数的定义域内'()f x ≥（≤）0（2）用导数求函数的单调区间 ①求函数的定义域D ②求导'()f x③解不等式'()f x ＞()<0得解集P④求DP ,得函数的单调递增（减）区间。

第二节 导数在研究函数中的应用第1课时 系统知识牢基础——导数与函数的单调性、极值与最值知识点一 利用导数研究函数的单调性1．函数f (x )在某个区间(a ，b )内的单调性与f ′(x )的关系 (1)若f ′(x )>0，则f (x )在这个区间上单调递增． (2)若f ′(x )<0，则f (x )在这个区间上单调递减． (3)若f ′(x )＝0，则f (x )在这个区间上是常数． 2．利用导数判断函数单调性的一般步骤 (1)求f ′(x )．(2)在定义域内解不等式f ′(x )>0或f ′(x )<0. (3)根据结果确定f (x )的单调性及单调区间．[提醒] (1)讨论函数的单调性或求函数的单调区间的实质是解不等式，求解时，要坚持“定义域优先”原则．(2)有相同单调性的单调区间不止一个时，用“，”隔开或用“和”连接，不能用“∪”连接． (3)若函数y ＝f (x )在区间(a ，b )上单调递增，则f ′(x )≥0，且在(a ，b )的任意子区间，等号不恒成立；若函数y ＝f (x )在区间(a ，b )上单调递减，则f ′(x )≤0，且在(a ，b )的任意子区间，等号不恒成立．[重温经典]1.(多选·教材改编题)如图是函数y ＝f (x )的导函数y ＝f ′(x )的图象，则下列判断正确的是( ) A ．在区间(－2,1)上f (x )是增函数 B ．在区间(2,3)上f (x )是减函数 C ．在区间(4,5)上f (x )是增函数 D ．当x ＝2时，f (x )取到极大值 答案：BCD2．(教材改编题)函数y ＝x 4－2x 2＋5的单调递减区间为( ) A ．(－∞，－1)和(0,1) B ．[－1,0]和[1，＋∞) C ．[－1,1] D ．(－∞，－1]和[1，＋∞)答案：A3．(易错题)若函数y ＝x 3＋x 2＋mx ＋1是R 上的单调函数，则实数m 的取值范围是( ) A.⎝⎛⎭⎫13，＋∞ B ．⎝⎛⎦⎤－∞，13C.⎣⎡⎭⎫13，＋∞ D ．⎝⎛⎭⎫－∞，13 解析：选C y ′＝3x 2＋2x ＋m ，由条件知y ′≥0在R 上恒成立，∴Δ＝4－12m ≤0，∴m ≥13.4．若函数f (x )＝kx －ln x 在区间(1，＋∞)单调递增，则k 的取值范围是( ) A ．(－∞，－2] B ．(－∞，－1] C ．[2，＋∞)D ．[1，＋∞)解析：选D 因为f (x )＝kx －ln x ，所以f ′(x )＝k －1x .因为f (x )在区间(1，＋∞)上单调递增，所以当x >1时，f ′(x )＝k －1x ≥0恒成立，即k ≥1x 在区间(1，＋∞)上恒成立．因为x >1，所以0<1x <1，所以k ≥1.故选D.5．若函数y ＝－43x 3＋ax 有三个单调区间，则a 的取值范围是________．解析：∵y ′＝－4x 2＋a ，且y 有三个单调区间，∴方程y ′＝－4x 2＋a ＝0有两个不等的实根，∴Δ＝02－4×(－4)×a >0，∴a >0. 答案：(0，＋∞)6．设函数f (x )在(a ，b )上的导函数为f ′(x )，f ′(x )在(a ，b )上的导函数为f ″(x )，若在(a ，b )上，f ″(x )<0恒成立，则称函数f (x )在(a ，b )上为“凸函数”．已知f (x )＝x 44－t 3x 3＋32x 2在(1,4)上为“凸函数”，则实数t 的取值范围是________．解析：由f (x )＝x 44－t 3x 3＋32x 2可得f ′(x )＝x 3－tx 2＋3x ，f ″(x )＝3x 2－2tx ＋3，∵f (x )在(1,4)上为“凸函数”，∴x ∈(1,4)时，3x 2－2tx ＋3<0恒成立，∴t >32⎝⎛⎭⎫x ＋1x 恒成立． 令g (x )＝32⎝⎛⎭⎫x ＋1x ，∵g (x )在(1,4)上单调递增， ∴t ≥g (4)＝518.∴实数t 的取值范围是⎣⎡⎭⎫518，＋∞. 答案：⎣⎡⎭⎫518，＋∞知识点二 利用导数研究函数的极值 1．函数的极大值在包含x 0的一个区间(a ，b )内，函数y ＝f (x )在任何一点的函数值都小于x 0点的函数值，称点x 0为函数y ＝f (x )的极大值点，其函数值f (x 0)为函数的极大值． 2．函数的极小值在包含x 0的一个区间(a ，b )内，函数y ＝f (x )在任何一点的函数值都大于x 0点的函数值，称点x 0为函数y ＝f (x )的极小值点，其函数值f (x 0)为函数的极小值．极大值与极小值统称为极值，极大值点与极小值点统称为极值点．[提醒] (1)极值点不是点，若函数f (x )在x 1处取得极大值，则x 1为极大值点，极大值为f (x 1)；在x 2处取得极小值，则x 2为极小值点，极小值为f (x 2)．极大值与极小值之间无确定的大小关系．(2)极值一定在区间内部取得，有极值的函数一定不是单调函数．(3)f ′(x 0)＝0是x 0为f (x )的极值点的必要而非充分条件．例如，f (x )＝x 3，f ′(0)＝0，但x ＝0不是极值点．[重温经典]1．(多选)(2021·福州模拟)下列函数中，存在极值点的是( ) A ．y ＝x －1xB ．y ＝2|x |C ．y ＝－2x 3－xD ．y ＝x ln x解析：选BD 由题意函数y ＝x －1x ，则y ′＝1＋1x2＞0，所以函数y ＝x －1x 在(－∞，0)，(0，＋∞)内单调递增，没有极值点；函数y ＝2|x |＝⎩⎪⎨⎪⎧2x ，x ≥0，2－x ，x ＜0，根据指数函数的图象与性质可得，当x ＜0时，函数y ＝2|x |单调递减，当x ＞0时，函数y ＝2|x |单调递增，所以函数y ＝2|x |在x ＝0处取得极小值；函数y ＝－2x 3－x ，则y ′＝－6x 2－1＜0，所以函数y ＝－2x 3－x 在R 上单调递减，没有极值点；函数y ＝x ln x ，则y ′＝ln x ＋1，当x ∈⎝⎛⎭⎫0，1e 时，y ′＜0，函数单调递减，当x ∈⎝⎛⎭⎫1e ，＋∞时，y ′＞0，函数单调递增，当x ＝1e 时，函数取得极小值，故选B 、D.2．(教材改编题)如图是f (x )的导函数f ′(x )的图象，则f (x )的极小值点的个数为( ) A ．1 B ．2 C ．3D ．4解析：选A 由图象及极值点的定义知，f (x )只有一个极小值点．3．(教材改编题)若函数f (x )＝x 3＋ax 2＋3x －9在x ＝－3时取得极值，则a 的值为( ) A ．2 B ．3 C ．4D ．5解析：选D f ′(x )＝3x 2＋2ax ＋3，由题意知f ′(－3)＝0，即3×(－3)2＋2a ×(－3)＋3＝0，解得a ＝5.4．(多选)材料：函数是描述客观世界变化规律的重要数学模型，在现行的高等数学与数学分析教材中，对“初等函数”给出了确切的定义，即由常数和基本初等函数经过有限次的四则运算及有限次的复合步骤所构成的，且能用一个式子表示的，如函数f(x)＝x x(x＞0)，我们可以作变形：f(x)＝x x＝eln x x＝e x ln x＝e t(t＝x ln x)，所以f(x)可看作是由函数f(t)＝e t和g(x)＝x ln x复合而成的，即f(x)＝x x(x＞0)为初等函数．根据以上材料，对于初等函数h(x)＝x 1x(x＞0)的说法正确的是()A．无极小值B．有极小值1C．无极大值D．有极大值e 1 e解析：选AD根据材料知：h(x)＝x 1x＝e1ln xx＝e1ln xx，所以h′(x)＝e 1ln xx·⎝⎛⎭⎫1x ln x′＝e1ln xx·⎝⎛⎭⎫－1x2ln x＋1x2＝1x2e1ln xx(1－ln x)，令h′(x)＝0得x＝e，当0＜x＜e时，h′(x)＞0，此时函数h(x)单调递增；当x＞e时，h′(x)＜0，此时函数h(x)单调递减．所以h(x)有极大值且为h(e)＝e 1e，无极小值．5．若x＝－2是函数f(x)＝(x2＋ax－1)e x的极值点，则f′(－2)＝________，f(x)的极小值为________．解析：由函数f(x)＝(x2＋ax－1)e x可得f′(x)＝(2x＋a)e x＋(x2＋ax－1)e x，因为x＝－2是函数f(x)的极值点，所以f′(－2)＝(－4＋a)e－2＋(4－2a－1)e－2＝0，即－4＋a＋3－2a＝0，解得a＝－1.所以f′(x)＝(x2＋x－2)e x.令f′(x)＝0可得x＝－2或x＝1.当x<－2或x>1时，f′(x)>0，此时函数f(x)为增函数，当－2<x<1时，f′(x)<0，此时函数f(x)为减函数，所以当x＝1时函数f(x)取得极小值，极小值为f(1)＝(12－1－1)×e1＝－e.答案：0－e6．设x1，x2是函数f(x)＝x3－2ax2＋a2x的两个极值点，若x1<2<x2，则实数a的取值范围是________．解析：由题意得f′(x)＝3x2－4ax＋a2的两个零点x1，x2满足x1<2<x2，所以f′(2)＝12－8a＋a2<0，解得2<a<6.答案：(2,6)知识点三 函数的最值1．在闭区间[a ，b ]上连续的函数f (x )在[a ，b ]上必有最大值与最小值．2．若函数f (x )在[a ，b ]上单调递增，则f (a )为函数的最小值，f (b )为函数的最大值；若函数f (x )在[a ，b ]上单调递减，则f (a )为函数的最大值，f (b )为函数的最小值．[提醒] 求函数最值时，易误认为极值点就是最值点，不通过比较就下结论，这种做法是错误的．[重温经典]1．(教材改编题)函数f (x )＝ln x －x 在区间(0，e]上的最大值为( ) A ．1－e B ．－1 C ．－eD ．0解析：选B 因为f ′(x )＝1x －1＝1－x x ，当x ∈(0,1)时，f ′(x )＞0；当x ∈(1，e]时，f ′(x )＜0，所以f (x )的单调递增区间是(0,1)，单调递减区间是(1，e]，所以当x ＝1时，f (x )取得最大值f (1)＝ln 1－1＝－1.2．(教材改编题)函数f (x )＝x 4－4x (|x |<1)( ) A ．有最大值，无最小值 B ．有最大值，也有最小值 C ．无最大值，有最小值D ．既无最大值，也无最小值解析：选D f ′(x )＝4x 3－4＝4(x －1)(x 2＋x ＋1)．令f ′(x )＝0，得x ＝1.又x ∈(－1,1)且1∉(－1,1)，∴该方程无解，故函数f (x )在(－1,1)上既无极值也无最值．故选D. 3．(教材改编题)函数y ＝x ＋2cos x 在区间⎣⎡⎦⎤0，π2上的最大值是________． 答案：3＋π64．(易错题)已知f (x )＝－x 2＋mx ＋1在区间[－2，－1]上的最大值就是函数f (x )的极大值，则m 的取值范围是________． 答案：(－4，－2)5．函数f (x )＝x e －x ，x ∈[0,4]的最小值为________． 解析：f ′(x )＝e －x －x e －x ＝e －x (1－x )． 令f ′(x )＝0，得x ＝1(e －x >0)， 又f (1)＝1e >0，f (0)＝0，f (4)＝4e 4>0，所以f (x )的最小值为0. 答案：06．已知函数f (x )＝2sin x ＋sin 2x ，则f (x )的最小值是________．解析：f ′(x )＝2cos x ＋2cos 2x ＝2cos x ＋2(2cos 2x －1) ＝2(2cos 2x ＋cos x －1)＝2(2cos x －1)(cos x ＋1)．∵cos x ＋1≥0，∴当cos x <12时，f ′(x )<0，f (x )单调递减；当cos x >12时，f ′(x )>0，f (x )单调递增．∴当cos x ＝12时，f (x )有最小值．又f (x )＝2sin x ＋sin 2x ＝2sin x (1＋cos x )， ∴当sin x ＝－32时，f (x )有最小值， 即f (x )min ＝2×⎝⎛⎭⎫－32×⎝⎛⎭⎫1＋12＝－332.答案：－332。

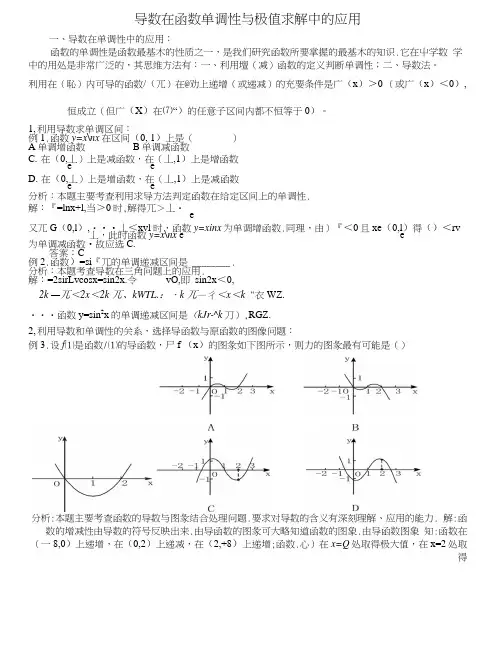
导数在函数单调性与极值求解中的应用一、导数在单调性中的应用：函数的单调性是函数最基木的性质之一，是我们研究函数所要掌握的最基木的知识.它在屮学数学中的用处是非常广泛的，其思维方法有：一、利用壇（减）函数的定义判断单调性；二、导数法。

利用在（恥）内可导的函数/（兀）在@劝上递增（或递减）的充要条件是广（x）＞0 （或广（x）＜0）,恒成立（但广（X）在⑺“）的任意子区间内都不恒等于0）。

1,利用导数求单调区间：例1.函数y=x\nx在区间（0, 1）上是（）A单调增函数B单调减函数C.在（0,丄）上是减函数，在（丄,1）上是增函数e eD.在（0,丄）上是增函数，在（丄,1）上是减函数e e分析：本题主要考查利用求导方法判定函数在给定区间上的单调性.解：『=lnx+l,当＞0时,解得兀＞丄・e又兀G（0,l）,・••丄＜xvl时，函数y=xinx为单调增函数.同理，由）『＜0且xe（0,l）得（）＜rv 丄，此时函数y=x\nx e e为单调减函数•故应选C.答案：C例2.函数）=si『兀的单调递减区间是 ________ .分析：本题考查导数在三角问题上的应用.解：=2sirLvcosx=sin2x.令vO,即sin2x＜0,2k —兀＜2x＜2k 兀、kWTL.：・k 兀—彳＜x＜k "衣WZ.・・・函数y=sin2x的单调递减区间是（kJr-^k刀）,RGZ.2,利用导数和单调性的关系，选择导函数与原函数的图像问题：例3.设f⑴是函数/⑴的导函数，尸f （x）的图彖如下图所示，则力的图彖最有可能是（）分析:本题主要考查函数的导数与图彖结合处理问题.要求对导数的含义有深刻理解、应用的能力. 解:函数的增减性由导数的符号反映出来.由导函数的图彖可大略知道函数的图象.由导函数图象知:函数在（一8,0）上递增，在（0,2）上递减，在（2,+8）上递增;函数.心）在x=Q处取得极大值，在x=2处取得极小值.答案:c例4.已知函数y = xf'M 的图象如右图所示（其中广（X ）是函数/（X ）的导函数），下面四个图象中 y = /（%）的图象大致是（ ）解析:由y = xfXx ）图象可知:y = f\x ）在［-1,1］上小于等于零,故原函数在［-1,1］ ±为减函数,故选评注：函数y = xf\x ）图象捉供了很多信息，但要抓住关键特点，如导数为零的点、导数为正值或 负值的区间等.3, 利用导数和单调性的关系判断方程解的个数：例5、方程?-6X 2+9X -10 = 0的实根的个数是 （ ）A 、3B 、2C 、1 D. 0分析：此题是一个三次方程，不易猜根。

导数在函数的单调性、极值中的应用一、知识梳理1．函数的单调性与导数在区间(a，b)内，函数的单调性与其导数的正负有如下关系：如果f_′(x)>0，那么函数y＝f(x)在这个区间内单调递增；如果f_′(x)<0，那么函数y＝f(x)在这个区间内单调递减；如果f_′(x)＝0，那么f(x)在这个区间内为常数．问题探究1：若函数f(x)在(a，b)内单调递增，那么一定有f ′(x)>0吗？f ′(x)>0是否是f(x)在(a，b)内单调递增的充要条件？提示：函数f(x)在(a，b)内单调递增，则f ′(x)≥0，f ′(x)>0是f(x)在(a，b)内单调递增的充分不必要条件．2．函数的极值与导数(1)函数的极小值函数y＝f(x)在点x＝a的函数值f(a)比它在x＝a附近其他点的函数值都小，f ′(a)＝0，而且在点x＝a附近的左侧f_′(x)<0，右侧f_′(x)>0，则点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．(2)函数的极大值函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近的其他点的函数值都大，f ′(b)＝0，而且在点x＝b附近，左侧f_′(x)>0，右侧f_′(x)<0，则点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．极小值点，极大值点统称为极值点，极大值和极小值统称为极值．问题探究2：若f ′(x0)＝0，则x0一定是f(x)的极值点吗？提示：不一定．可导函数在一点的导数值为0是函数在这点取得极值的必要条件，而不是充分条件，如函数f(x)＝x3，在x＝0时，有f ′(x)＝0，但x＝0不是函数f(x)＝x3的极值点．二、自主检测1．函数y＝x－lnx的单调减区间是( )A．(－∞，1) B．(0,1)C．(1，＋∞) D．(0,2)2．函数f(x)＝x3－3x2＋3x的极值点的个数是( )A．0 B．1C．2 D．33．函数f(x)＝x3＋ax－2在区间(1，＋∞)上是增函数，则实数a的取值范围是( ) A．[3，＋∞) B．[－3，＋∞)C．(－3，＋∞) D．(－∞，－3)4．(2012年山东诸城高三月考)已知函数y＝f(x)，其导函数y＝f ′(x)的图象如图所示，则y＝f(x)( )A．在(－∞，0)上为减函数B．在x＝0处取极小值C．在(4，＋∞)上为减函数D．在x＝2处取极大值5．若函数f(x)＝x3＋ax2＋3x－9在x＝－3时取得极值，则a＝( )A．2 B．3C．4 D．56．(1)函数f(x)在x＝x0处可导，则“f ′(x0)＝0”是“x0是函数f(x)极值点”的________条件．(2)函数f(x)在(a，b)上可导，则“f ′(x)>0”是“f(x)在(a，b)上单调递增”的________条件．(3)函数f(x)在(a，b)上可导，则“f ′(x)≥0”是“f(x)在(a，b)上单调递增”的________条件．三、考向指导考点1 求函数的单调区间1.求可导函数单调区间的一般步骤和方法(1)确定函数f(x)的定义域；(2)求 f ′(x)，令f ′(x)＝0，求出它在定义域内的一切实根；(3)把函数f(x)的间断点(即f(x)的无定义点)的横坐标和上面的各实数根按由小到大的顺序排列起来，然后用这些点把函数f(x)的定义区间分成若干个小区间；(4)确定f ′(x)在各个开区间内的符号，根据f ′(x)的符号判定函数f(x)在每个相应小开区间内的增减性．2．证明可导函数f(x)在(a，b)内的单调性的步骤(1)求 f ′(x)．(2)确认 f ′(x)在(a，b)内的符号．(3)作出结论： f ′(x)>0时，f(x)为增函数； f ′(x)<0时，f(x)为减函数．例1 (2010年全国)已知函数f(x)＝x3－3ax2＋3x＋1.(1)设a＝2，求f(x)的单调区间；(2)设f(x)在区间(2,3)中至少有一个极值点，求a的取值范围．课堂过手练习：设函数f(x)＝x3＋ax2－9x－1(a<0)．若曲线y＝f(x)的斜率最小的切线与直线12x＋y＝6平行，求：(1)a的值；(2)函数y＝f(x)的单调区间．考点2 由函数的单调性求参数的取值范围已知函数的单调性，求参数的取值范围，应注意函数f(x)在(a，b)上递增(或递减)的充要条件应是 f ′(x)≥0(或 f ′(x)≤0)，x∈(a，b)恒成立，且 f ′(x)在(a，b)的任意子区间内都不恒等于0，这就是说，函数f(x)在区间上的增减性并不排斥在区间内个别点处有 f ′(x0)＝0，甚至可以在无穷多个点处 f ′(x0)＝0，只要这样的点不能充满所给区间的任何一个子区间．例2 已知函数f(x)＝x3－ax－1，在实数集R上y＝f(x)单调递增，求实数a的取值范围．课堂过手练习：已知f(x)＝ex－ax－1.(1)求f(x)的单调增区间；(2)若f(x)在定义域R 内单调递增，求a 的取值范围；(3)是否存在a ，使f(x)在(－∞，0]上单调递减，在[0，＋∞)上单调递增？若存在，求出a 的值；若不存在，说明理由．考点3 求已知函数的极值运用导数求可导函数 y ＝f(x)极值的步骤：(1)先求函数的定义域，再求函数 y ＝f(x)的导数 f ′(x)；(2)求方程 f ′(x)＝0的根；(3)检查 f ′(x)在方程根的左右的值的符号，如果左正右负，那么f(x)在这个根处取得极大值．如果左负右正，那么 f(x)在这个根处取得极小值．例3 设f(x)＝ex1＋ax 2，其中a 为正实数．(1)当a ＝43时，求f(x)的极值点；(2)若f(x)为R 上的单调函数，求a 的取值范围．课堂过手练习：函数f(x)＝x3－3x2＋1在x ＝________处取得极小值．考点4 利用极值求参数已知函数解析式，可利用导数及极值的定义求出其极大值与极小值；反过来，如果已知某函数的极值点或极值，也可利用导数及极值的必要条件建立参数方程或方程组，从而解出参数，求出函数解析式．例4 设x＝1与x＝2是函数f(x)＝alnx＋bx2＋x的两个极值点．(1)试确定常数a和b的值；(2)试判断x＝1，x＝2是函数f(x)的极大值点还是极小值点，并说明理由．课堂过手练习：设函数f(x)＝(x－a)2lnx，a∈R.若x＝e为y＝f(x)的极值点，求实数a.易错点求参数取值时出现典例：已知函数f(x)＝ax3＋3x2－x＋1在R上是减函数，求a的取值范围．(1)当函数在某个区间内恒有f ′(x)＝0，则f(x)为常数，函数不具有单调性．∴f (x)≥0是f(x)为增函数的必要不充分条件．在解题中误将必要条件作充分条件或将既不充分与不必要条件误作充要条件使用而导致的错误还很多，在学习过程中注意思维的严密性．(2)函数极值是一个局部性概念，函数的极值可以有多个，并且极大值与极小值的大小关系不确定．要强化用导数处理单调性、极值、最值、方程的根及不等式的证明等数学问题的意识．(3)如果一个函数在给定定义域上的单调区间不止一个，这些区间之间一般不能用并集符号“∪”连接，只能用“，”或“和”字隔开．纠错课堂练习：已知函数f(x)＝x3＋ax2＋bx＋c在x＝1处取极值－2.(1)试用c表示a，b；(2)求f(x)的单调递减区间．1．与函数的单调性有关的问题(1)利用导数求函数的单调区间，可通过f ′(x)>0或f ′(x)<0来进行，至于区间的端点是否包含，取决于函数在端点处是否有意义，若有意义，则端点包含与不包含均可；若无意义，则必不能包含端点．(2)若函数f(x)在(a，b)上递增(或递减)，则在(a，b)上f ′(x)≥0(或f ′(x)≤0)恒成立，若该不等式中含有参数，我们可利用上述结论求参数的范围，它蕴涵了恒成立思想．利用上述方法求得参数的范围后，要注意检验该参数的端点值能否使f ′(x)＝0恒成立．若能，则去掉该端点值；否则，即为所求．2．与函数的极值有关的问题(1)求函数的极值点，可通过f ′(x)＝0来求得，但同时还要注意检验在其两侧附近的导函数值是否异号．(2)若函数f(x)在x＝x0处有极值，则一定有f ′(x0)＝0，我们可利用上述结论求参数的值．。

导数的应用一(单调性与极值)专题训练真题再现1.已知a 是函数f (x )＝x 3－12x 的极小值点，则a ＝( ) A.－4 B.－2 C.4 D.22.(若函数f (x )＝x －13sin 2x ＋a sin x 在(－∞，＋∞)单调递增，则a 的取值范围是( )A.[－1，1]B.⎣⎢⎡⎦⎥⎤－1，13C.⎣⎢⎡⎦⎥⎤－13，13D.⎣⎢⎡⎦⎥⎤－1，－133.设f (x )＝x ln x －ax 2＋(2a －1)x ，a ∈R. (1)令g (x )＝f ′(x )，求g (x )的单调区间；(2)已知f (x )在x ＝1处取得极大值.求实数a 的取值范围.提高演练考点1 判断函数的单调性1.若定义在R 上的函数f (x )满足f (0)＝－1，其导函数f ′(x )满足f ′(x )＞k ＞1，则下列结论中一定错误的是( )A.f ⎝ ⎛⎭⎪⎫1k ＜1kB.f ⎝ ⎛⎭⎪⎫1k ＞1k －1C.f ⎝ ⎛⎭⎪⎫1k －1＜1k －1D.f ⎝ ⎛⎭⎪⎫1k －1＞k k －12.设函数f ′(x )是奇函数f (x )(x ∈R)的导函数，f (－1)＝0，当x >0时，xf ′(x )－f (x )＜0，则使得f (x )>0成立的x 的取值范围是( )A.(－∞，－1)∪(0，1)B.(－1，0)∪(1，＋∞)C.(－∞，－1)∪(－1，0)D.(0，1)∪(1，＋∞)3.若函数f (x )＝kx －ln x 在区间(1，＋∞)上单调递增，则k 的取值范围是( )A.(－∞，－2]B.(－∞，－1]C.[2，＋∞)D.[1，＋∞)4.已知函数f (x )＝ax 3－3x 2＋1，若f (x )存在唯一的零点x 0，且x 0＞0，则a 的取值范围是( ) A.(2，＋∞)B.(1，＋∞)C.(－∞，－2)D.(－∞，－1)5.已知函数f (x )＝ax 3＋x 2(a ∈R)在x ＝－43处取得极值.(1)确定a 的值；(2)若g (x )＝f (x )e x ，讨论g (x )的单调性.考点2 应用导数研究函数的极值6.对二次函数f (x )＝ax 2＋bx ＋c (a 为非零整数)，四位同学分别给出下列结论，其中有且只有一个结论是错误的，则错误的结论是( )A.－1是f (x )的零点B.1是f (x )的极值点C.3是f (x )的极值D.点(2，8)在曲线y ＝f (x )上7.函数f (x )在x ＝x 0处导数存在.若p ：f ′(x 0)＝0；q ：x ＝x 0是f (x )的极值点，则( ) A.p 是q 的充分必要条件 B.p 是q 的充分条件，但不是q 的必要条件 C.p 是q 的必要条件，但不是q 的充分条件 D.p 既不是q 的充分条件，也不是q 的必要条件 8.知函数f (x )＝ax（x ＋r ）2(a >0，r >0).(1)求f (x )的定义域，并讨论f (x )的单调性； (2)若a r＝400，求f (x )在(0，＋∞)内的极值.9.已知函数f (x )＝(x 2＋bx ＋b )·1－2x (b ∈R). (1)当b ＝4时，求f (x )的极值；(2)若f (x )在区间⎝ ⎛⎭⎪⎫0，13上单调递增，求b 的取值范围.1.已知函数f (x )＝sin x －cos x ，且f ′(x )＝12f (x )，则tan 2x 的值是( )A.－23B.－43C.43D.342.如图是函数f (x )＝x 2＋ax ＋b 的部分图象，则函数g (x )＝ln x ＋f ′(x )的零点所在的区间是()A.⎝ ⎛⎭⎪⎫14，12 B.(1，2) C.⎝ ⎛⎭⎪⎫12，1D.(2，3)3.设f 0(x )＝sin x ，f 1(x )＝f 0′(x )，f 2(x )＝f 1′(x )，…，f n (x )＝f n －1′(x )，n ∈N ，则f 2 015(x )＝( )A.sin xB.－sin xC.cos xD.－cos x 4.函数f (x )＝e x cos x 的图象在点(0，f (0))处的切线方程是( ) A.x ＋y ＋1＝0B.x ＋y －1＝0C.x －y ＋1＝0D.x －y －1＝05.设函数f ′(x )是函数f (x )(x ∈R)的导函数，f (0)＝1，且3f (x )＝f ′(x )－3，则4f (x )>f ′(x )的解集为( )A.⎝ ⎛⎭⎪⎫ln 43，＋∞B.⎝ ⎛⎭⎪⎫ln 23，＋∞ C.⎝ ⎛⎭⎪⎫32，＋∞ D.⎝ ⎛⎭⎪⎫e 2，＋∞ 6.已知函数y ＝f (x －1)的图象关于直线x ＝1对称，且当x ∈(－∞，0)时，f (x )＋xf ′(x )＜0成立，若a ＝20.2f (20.2)，b ＝(ln 2)f (ln 2)，c ＝⎝ ⎛⎭⎪⎫log 1214f⎝ ⎛⎭⎪⎫log 1214，则a ，b ，c 的大小关系是( ) A.a ＞b ＞cB.b ＞a ＞cC.c ＞a ＞bD.a ＞c ＞b7.已知定义域为R 的奇函数y ＝f (x )的导函数为y ＝f ′(x )，当x ≠0时，f ′(x )＋f （x ）x＞0，若a ＝12f ⎝ ⎛⎭⎪⎫12，b ＝－2f (－2)，c ＝⎝ ⎛⎭⎪⎫ln 12f ⎝ ⎛⎭⎪⎫ln 12，则a ，b ，c 的大小关系正确的是( )A.a ＜c ＜bB.b ＜c ＜aC.a ＜b ＜cD.c ＜a ＜b8.对于三次函数f (x )＝ax 3＋bx 2＋cx ＋d (a ≠0)，定义：设f ″(x )是函数y ＝f (x )的导数y ＝f ′(x )的导数，若方程f ″(x )＝0有实数解x 0，则称点(x 0，f (x 0))为函数y ＝f (x )的“拐点”.有同学发现“任何一个三次函数都有“拐点”；任何一个三次函数都有对称中心；且“拐点”就是对称中心.”请你根据这一发现，函数f (x )＝x 3－3x 2＋3x ＋1对称中心为________. 9.已知函数f (x )＝x e x ，记f 0(x )＝f ′(x )，f 1(x )＝f ′(x 0)，…，f n (x )＝f n －1′(x )且x 2＞x 1，对于下列命题：①函数f (x )存在平行于x 轴的切线；②f （x 1）－f （x 2）x 1－x 2＞0；③f 2 012′(x )＝x e x ＋2 014e x ；④f (x 1)＋x 2＜f (x 2)＋x 1.其中正确的命题序号是________(写出所有满足题目条件的序号). 10.已知函数y ＝f (x )对任意的x ∈⎝ ⎛⎭⎪⎫－π2，π2满足f ′(x )·cos x ＋f (x )sin x >0(其中f ′(x )是函数f (x )的导函数)，则下列不等式成立的是( )A.2f ⎝ ⎛⎭⎪⎫－π3<f ⎝ ⎛⎭⎪⎫－π4B.2f ⎝ ⎛⎭⎪⎫π3<f ⎝ ⎛⎭⎪⎫π4C.f (0)>2f ⎝ ⎛⎭⎪⎫π3D.f (0)>2f ⎝ ⎛⎭⎪⎫π411.已知函数f (x )＝kx ，g (x )＝ln xx ，若x i ∈⎣⎢⎡⎦⎥⎤1e ，e ，(i ＝1，2)使得f (x i )＝g (x i )，(i ＝1，2)，则实数k 的取值范围是( ) A.⎣⎢⎡⎭⎪⎫1e 2，12e B.⎝ ⎛⎦⎥⎤12e ，1e C.⎝ ⎛⎭⎪⎫0，1e 2 D.⎝ ⎛⎭⎪⎫1e ，＋∞12.已知函数f (x )＝a e x ＋x 2，g (x )＝sin πx2＋bx ，直线l 与曲线y ＝f (x )切于点(0，f (0))且与曲线y ＝g (x )切于点(1，g (1)). (1)求a ，b 的值和直线l 的方程. (2)证明：f (x )＞g (x ).13.已知函数f(x)＝x4＋ax－ln x－32，其中a∈R.(1)若曲线y＝f(x)在点(1，f(1))处的切线垂直于直线y＝12x，求a的值.(2)讨论函数f(x)的单调区间.导数的应用一(单调性与极值)专题训练答案真题再现1.D [∵f(x)＝x3－12x，∴f′(x)＝3x2－12，令f′(x)＝0，则x1＝－2，x2＝2. 当x∈(－∞，－2)，(2，＋∞)时，f′(x)>0，则f(x)单调递增；当x∈(－2，2)时，f′(x)<0，则f(x)单调递减，∴f(x)的极小值点为a＝2.]2.C [法一(特殊值法)：不妨取a＝－1，则f(x)＝x－13sin 2x－sin x，f′(x)＝1－23cos 2x－cos x，但f′(0)＝1－23－1＝－23<0，不具备在(－∞，＋∞)单调递增，排除A，B，D.故选C.法二(综合法)：∵函数f(x)＝x－13sin 2x＋a sin x在(－∞，＋∞)单调递增，∴f′(x)＝1－23cos 2x＋a cos x＝1－23(2cos2x－1)＋a cos x＝－43cos2x＋a cos x＋53≥0，即a cos x≥43cos2x－53在(－∞，＋∞)恒成立.当cos x＝0时，恒有0≥－53，得a∈R；当0<cos x≤1时，得a≥43cos x－53cos x，令t＝cos x，f(t)＝43t－53t在(0，1]上为增函数，得a≥f(1)＝－1 3；当－1≤cos x<0时，得a≤43cos x－53cos x，令t＝cos x，f(t)＝43t－53t在[－1，0)上为增函数，得a≤f(－1)＝13.综上，可得a的取值范围是⎣⎢⎡⎦⎥⎤－13，13，故选C.]3.解(1)由f′(x)＝ln x－2ax＋2a.可得g(x)＝ln x－2ax＋2a，x∈(0，＋∞)，则g ′(x )＝1x －2a ＝1－2axx.当a ≤0时，x ∈(0，＋∞)时，g ′(x )＞0，函数g (x )单调递增；当a ＞0时，x ∈⎝ ⎛⎭⎪⎫0，12a 时，g ′(x )＞0时，函数g (x )单调递增，x ∈⎝ ⎛⎭⎪⎫12a ，＋∞时，g ′(x )＜0，函数g (x )单调递减.所以当a ≤0时，g (x )的单调递增区间为(0，＋∞)；当a ＞0时，g (x )的单调增区间为⎝⎛⎭⎪⎫0，12a ，单调减区间为⎝ ⎛⎭⎪⎫12a ，＋∞. (2)由(1)知，f ′(1)＝0. ①当a ≤0时，f ′(x )单调递增，所以当x ∈(0，1)时，f ′(x )＜0，f (x )单调递减， 当x ∈(1，＋∞)时，f ′(x )＞0，f (x )单调递增， 所以f (x )在x ＝1处取得极小值，不合题意.②当0＜a ＜12时，12a ＞1，由(1)知f ′(x )在⎝ ⎛⎭⎪⎫0，12a 内单调递增.可得当x ∈(0，1)时，f ′(x )＜0，x ∈⎝ ⎛⎭⎪⎫1，12a 时，f ′(x )＞0. 所以f (x )在(0，1)内单调递减，在⎝ ⎛⎭⎪⎫1，12a 内单调递增.所以f (x )在x ＝1处取得极小值，不合题意. ③当a ＝12时，12a ＝1，f ′(x )在(0，1)内单调递增，在(1，＋∞)内单调递减.所以当x ∈(0，＋∞)时，f ′(x )≤0，f (x )单调递减，不合题意. ④当a ＞12时，0＜12a ＜1，当x ∈⎝ ⎛⎭⎪⎫12a ，1时，f ′(x )＞0，f (x )单调递增，当x ∈(1，＋∞)时，f ′(x )＜0，f (x )单调递减. 所以f (x )在x ＝1处取极大值，合题意 . 综上可知，实数a 的取值范围为a ＞12.提高演练1.C [∵导函数f ′(x )满足f ′(x )＞k ＞1，∴f ′(x )－k ＞0，k －1＞0，1k －1＞0，可构造函数g (x )＝f (x )－kx ，可得g ′(x )＞0，故g (x )在R 上为增函数，∵f (0)＝－1，∴g (0)＝－1，∴g ⎝⎛⎭⎪⎫1k －1＞g (0)， ∴f ⎝ ⎛⎭⎪⎫1k －1－k k －1＞－1，∴f ⎝ ⎛⎭⎪⎫1k －1＞1k －1，∴选项C 错误，故选C.] 2.A [因为f (x )(x ∈R)为奇函数，f (－1)＝0，所以f (1)＝－f (－1)＝0.当x ≠0时，令g (x )＝f （x ）x ，则g (x )为偶函数，且g (1)＝g (－1)＝0.则当x ＞0时，g ′(x )＝⎝⎛⎭⎪⎫f （x ）x ′＝xf ′（x ）－f （x ）x 2＜0，故g (x )在(0，＋∞)上为减函数，在(－∞，0)上为增函数.所以在(0，＋∞)上，当0＜x ＜1时，g (x )＞g (1)＝0⇔f （x ）x＞0⇔f (x )＞0； 在(－∞，0)上，当x ＜－1时，g (x )＜g (－1)＝0⇔f （x ）x ＜0⇔f (x )＞0.综上，得使得f (x )＞0成立的x 的取值范围是(－∞，－1)∪(0，1)，选A.] 3.D4.C [由题意知f ′(x )＝3ax 2－6x ＝3x (ax －2)，当a ＝0时，不满足题意.当a ≠0时，令f ′(x )＝0，解得x ＝0或x ＝2a ，当a ＞0时，f (x )在(－∞，0)，⎝ ⎛⎭⎪⎫2a ，＋∞上单调递增，在 ⎝ ⎛⎭⎪⎫0，2a上单调递减.又f (0)＝1，此时f (x )在(－∞，0)上存在零点，不满足题意；当a ＜0时，f (x )在⎝ ⎛⎭⎪⎫－∞，2a ，(0，＋∞)上单调递减，在⎝ ⎛⎭⎪⎫2a ，0上单调递增，要使f (x )存在唯一的零点x 0，且x 0＞0，则需f ⎝ ⎛⎭⎪⎫2a ＞0，即a ×⎝ ⎛⎭⎪⎫2a 3－3×⎝ ⎛⎭⎪⎫2a 2＋1＞0，解得a ＜－2，故选C.]5.解 (1)对f (x )求导得f ′(x )＝3ax 2＋2x ，因为f (x )在x ＝－43处取得极值，所以f ′⎝ ⎛⎭⎪⎫－43＝0，即3a ·169＋2·⎝ ⎛⎭⎪⎫－43＝16a 3－83＝0，解得a ＝12.(2)由(1)得g (x )＝⎝ ⎛⎭⎪⎫12x 3＋x 2e x ，故g ′(x )＝⎝ ⎛⎭⎪⎫32x 2＋2x e x ＋⎝ ⎛⎭⎪⎫12x 3＋x 2e x＝⎝ ⎛⎭⎪⎫12x 3＋52x 2＋2x e x＝12x (x ＋1)(x ＋4)e x . 令g ′(x )＝0，解得x ＝0，x ＝－1或x ＝－4. 当x ＜－4时，g ′(x )＜0，故g (x )为减函数； 当－4＜x ＜－1时，g ′(x )＞0，故g (x )为增函数； 当－1＜x ＜0时，g ′(x )＜0，故g (x )为减函数； 当x ＞0时，g ′(x )＞0，故g (x )为增函数.综上知g (x )在(－∞，－4)和(－1，0)内为减函数，在(－4，－1)和(0，＋∞)内为增函数. 6.A [A 正确等价于a －b ＋c ＝0，① B 正确等价于b ＝－2a ，② C 正确等价于4ac －b 24a ＝3，③D 正确等价于4a ＋2b ＋c ＝8.④ 下面分情况验证，若A 错，由②、③、④组成的方程组的解为⎩⎨⎧a ＝5，b ＝－10，c ＝8.符合题意；若B 错，由①、③、④组成的方程组消元转化为关于a 的方程后无实数解； 若C 错，由①、②、④组成方程组，经验证a 无整数解； 若D 错，由①、②、③组成的方程组a 的解为－34也不是整数.综上，故选A.]7.C [设f (x )＝x 3，f ′(0)＝0，但是f (x )是单调增函数，在x ＝0处不存在极值，故若p 则q 是一个假命题，由极值的定义可得若q 则p 是一个真命题.故选C.] 8.解 (1)由题意知x ≠－r ，所求的定义域为(－∞，－r )∪(－r ，＋∞).f (x )＝ax （x ＋r ）2＝axx 2＋2rx ＋r 2，f ′(x )＝a （x 2＋2rx ＋r 2）－ax （2x ＋2r ）（x 2＋2rx ＋r 2）2＝a （r －x ）（x ＋r ）（x ＋r ）4. 所以当x <－r 或x >r 时，f ′(x )<0， 当－r <x <r 时，f ′(x )>0.因此，f (x )的单调递减区间为(－∞，－r )，(r ，＋∞)；f (x )的单调递增区间为(－r ，r ).(2)由(1)的解答可知f ′(r )＝0，f (x )在(0，r )上单调递增，在(r ，＋∞)上单调递减.因此，x ＝r 是f (x )的极大值点，所以f (x )在(0，＋∞)内的极大值为f (r )＝ar （2r ）2＝a 4r ＝4004＝100. 9.解 (1)当b ＝4时，f ′(x )＝－5x （x ＋2）1－2x，由f ′(x )＝0得x ＝－2或x ＝0.当x ∈(－∞，－2)时，f ′(x )<0，f (x )单调递减； 当x ∈(－2，0)时，f ′(x )>0，f (x )单调递增；当x ∈⎝ ⎛⎭⎪⎫0，12时，f ′(x )<0，f (x )单调递减，故f (x )在x ＝－2处取极小值f (－2)＝0，在x＝0处取极大值f (0)＝4.(2)f ′(x )＝－x [5x ＋（3b －2）]1－2x ，因为当x ∈⎝ ⎛⎭⎪⎫0，13时，－x 1－2x <0，依题意，当x ∈⎝⎛⎭⎪⎫0，13时，有5x ＋(3b －2)≤0， 从而53＋(3b －2)≤0.所以b 的取值范围为⎝⎛⎦⎥⎤－∞，19.【两年模拟试题精练】1.D [因为f ′(x )＝cos x ＋sin x ＝12sin x ＝12cos x ，所以tan x ＝－3，所以tan 2x ＝2tan x1－tan 2x ＝－61－9＝34，故选D.] 2.C [函数f (x )＝x 2＋ax ＋b 的部分图象得0＜b ＜1，f (1)＝0，从而－2＜a ＜－1，而g (x )＝ln x ＋f ′(x )在定义域内单调递增，g ⎝ ⎛⎭⎪⎫12＝ln 12＋1＋a ＜0，g (1)＝ln 1＋2＋a ＝2＋a ＞0，∴函数g (x )＝ln x ＋f ′(x )的零点所在的区间是⎝ ⎛⎭⎪⎫12，1；故选C.] 3.D [f 0(x )＝sin xf 1(x )＝f 0′(x )＝cos x f 2(x )＝f 1′(x )＝－sin x f 3(x )＝f 2′(x )＝－cos x f 4(x )＝f 3′(x )＝sin x …由上面可以看出，以4为周期进行循环. 所以f 2 015(x )＝f 3(x )＝－cos x ，故选D.]4.C [依题意，f (0)＝e 0cos 0＝1，因为f ′(x )＝e x cos x －e x sin x ，所以f ′(0)＝1，所以切线方程为y －1＝x －0，即x －y ＋1＝0，故选C.]5.B [不妨设f (x )＝2e 3x －1，则f ′(x )＝6e 3x ＝3(2e 3x －1)＋3，满足3f (x )＝f ′(x )－3，而4f (x )>f ′(x )，即f (x )>3，∴有2e 3x－1>3，即e 3x>2，解得x >ln 23.故选B.]6.B [∵函数y ＝f (x －1)的图象关于直线x ＝1对称，∴函数y ＝f (x )的图象关于y 轴对称，是偶函数.令g (x )＝xf (x )，g (x )为奇函数则当x ∈(－∞，0)时，g ′(x )＝f (x )＋xf ′(x )＜0，∴函数g (x )在x ∈(－∞，0)上为减函数.因此函数g (x )在(0，＋∞)上单调递减.∵log 1214＝2＞20.2＞1＞ln 2＞0. ∴c ＜a ＜b .故选B.] 7.A [设h (x )＝xf (x )， ∴h ′(x )＝f (x )＋x ·f ′(x )，∵y ＝f (x )是定义在实数集R 上的奇函数， ∴h (x )是定义在实数集R 上的偶函数， 当x ＞0时，h ′(x )＝f (x )＋x ·f ′(x )＞0， ∴此时函数h (x )单调递增.∵a ＝12f ⎝ ⎛⎭⎪⎫12＝h ⎝ ⎛⎭⎪⎫12，b ＝－2f (－2)＝2f (2)＝h (2)，c ＝⎝ ⎛⎭⎪⎫ln 12f ⎝ ⎛⎭⎪⎫ln 12＝h ⎝⎛⎭⎪⎫ln 12＝h (－ln 2)＝h (ln 2)，又2＞ln 2＞12，∴b ＞c ＞a .故选A.]8.(1，2) [∵函数f (x )＝x 3－3x 2＋3x ＋1，∴f ′(x )＝3x 2－6x ＋3，∴f ″(x )＝6x －6.令f ″(x )＝6x －6＝0，解得x ＝1，且f (1)＝2，故函数f (x )＝x 3－3x 2＋3x 对称中心为(1，2)，故答案为(1，2).] 9.①③10.A [令h (x )＝f （x ）cos x ，则h ′(x )＝f ′（x ）cos x ＋f （x ）sin xcos 2x>0，∴函数h (x )是⎝ ⎛⎭⎪⎫－π2，π2上的增函数，∴h ⎝ ⎛⎭⎪⎫－π3<h ⎝ ⎛⎭⎪⎫－π4，即f ⎝⎛⎭⎪⎫－π3cos ⎝ ⎛⎭⎪⎫－π3<f ⎝ ⎛⎭⎪⎫－π4cos ⎝ ⎛⎭⎪⎫－π4⇒f ⎝ ⎛⎭⎪⎫－π312<f ⎝ ⎛⎭⎪⎫－π422⇒2f ⎝ ⎛⎭⎪⎫－π3<f ⎝ ⎛⎭⎪⎫－π4，故选A.] 11.A [由f (x )＝g (x )得k ＝ln xx 2，令t (x )＝ln xx 2，由t ′(x )＝1－2ln xx 3＝0得x ＝e ，得函数t (x )在⎣⎢⎡⎦⎥⎤1e ，e 上单调递增，在[e ，e]上单调递减，又t (e)＝12e ，t ⎝ ⎛⎭⎪⎫1e ＝－e 2，t (e)＝1e 2，所以∃x i ∈⎣⎢⎡⎦⎥⎤1e ，e ，(i ＝1，2)使得f (x i )＝g (x i )，(i ＝1，2)，则实数k 的取值范围是⎣⎢⎡⎭⎪⎫1e 2，12e ，故选A.]12.(1)解 f ′(x )＝a e x＋2x ，g ′(x )＝π2cos πx 2＋b ， f (0)＝a ，f ′(0)＝a ，g (1)＝1＋b ，g ′(1)＝b ， 曲线y ＝f (x )在点(0，f (0))处的切线为y ＝ax ＋a ， 曲线y ＝g (x )在点(1，g (1))处的切线为y ＝b (x －1)＋1＋b ，即y ＝bx ＋1.依题意，有a ＝b ＝1，直线l 方程为y ＝x ＋1. (2)证明 由(1)知f (x )＝e x ＋x 2，g (x )＝sinπx2＋x . 设F (x )＝f (x )－(x ＋1)＝e x ＋x 2－x －1，则F ′(x )＝e x ＋2x －1， 当x ∈(－∞，0)时，F ′(x )＜F ′(0)＝0； 当x ∈(0，＋∞)时，F ′(x )＞F ′(0)＝0.F (x )在(－∞，0)上单调递减，在(0，＋∞)上单调递增， 故F (x )≥F (0)＝0.设G (x )＝x ＋1－g (x )＝1－sin πx2，则G (x )≥0，当且仅当x ＝4k ＋1(k ∈Z)时等号成立. 由上可知，f (x )≥x ＋1≥g (x )，且两个等号不同时成立， 因此f (x )＞g (x ).13.解 (1)对f (x )求导得f ′(x )＝14－a x 2－1x ，由f (x )在点(1，f (1))处的切线垂直于直线y ＝12x 知f ′(1)＝－34－a ＝－2，解得a ＝54.(2)函数f (x )的定义域为(0，＋∞)，由(1)知f ′(x )＝x 2－4x －4a4x 2令g (x )＝x 2－4x －4a ，由于Δ＝16＋16a ＝16(a ＋1)，当a ＝－1时，Δ＝0，g (x )≥0，f ′(x )≥0恒成立，函数f (x )在(0，＋∞)上单调递增； 当a ＜－1时，Δ＜0，g (x )＞0，f ′(x )＞0恒成立，函数f (x )在(0，＋∞)上单调递增； 当a ＞－1时，Δ＞0.设x 1，x 2(x 1＜x 2)是函数g (x )的两个零点， 则x 1＝2－2a ＋1，x 2＝2＋2a ＋1.若－1＜a＜0时，x1＝2－2a＋1＞0，x2＞0.所以，x∈(0，x1)时，g(x)＞0，f(x)＞0，函数f(x)单调递增，x∈(x1，x2)时，g(x)＜0，f′(x)＜0，函数f(x)单调递减，x∈(x2，＋∞)时，g(x)＞0，f′(x)＞0，函数f(x)单调递增. 若a≥0时，x1＝2－2a＋1≤0，x2＞0.所以，x∈(0，x2)时，g(x)＜0，f′(x)＜0，函数f(x)单调递减，x∈(x，＋∞)时，g(x)＞0，f(x)＞0，函数f(x)单调递增.2综上可得，当a≤－1时，函数f(x)在(0，＋∞)上单调递增；当－1＜a＜0时，函数f(x)在(0，2－2a＋1)上单调递增，在(2－2a＋1，2＋2a＋1)上单调递减，在(2＋2a＋1，＋∞)上单调递增；当a≥0时，函数f(x)在(0，2＋2a＋1)上单调递减，在(2＋2a＋1，＋∞)上单调递增.。

y顼（x）的图象大致是（A. ( —, +8)B. (0, —)C. (0, +3) a aD. (0, a)A4. y = x2 - e~x（x > 0）的单调递增区间为B5.A6.1 0如果函数y = -x2+\nx-ax在定义域上为增函数，则a的取值范围是求函数y =上亍一m工的单调区间。

【学习目标】1、明确利用导函数研究原函数性质（如单调性、极值、最值）的方法；2、总结恒成立问题的求解思路：（1）转化为最值问题（2）分离参数。

［学法指导】运用导数研究函数的性质，题型丰富多样，在处理问题中应抓住以下几点：（1）抓住基本思路：即导函数的正负决定原函数的增减；要求函数在某段闭区间上的最值，先求极值和端点函数值再比较。

（2）对于复杂问题，要善于转化，将所给问题转化为研究某个函数的某个性质，再借助导函数模拟原函数的图像，数形结合分析、处理问题（3）以三次函数为载体，熟悉借助导数研究函数性质的方法。

考点一、导函数与单调性A1.已知函数y = VV）的图象如图［其中广⑴是函数f（x）的导函数1，下面四个图象中)函数f(x)=lnx-ax(a>0)的单调递增区间为( )2 gC7.已知函数f(x) = -x-(x2-3ax一一)(♦ c R),若函数f(x)在(1, 2)内是增函数，求3 2a的取值范围。

小结:(1)求函数/(X)的单调区间即解不等式,对于定义域不是R的函数在求单调区间时要先注意；(2)己知可导函数了0)在区间(",/?)单调递增，则Pxgb),都有r(i)Oo考点二、函数的极值和最值7A1.设函数/(x) = - + ln%,则( )xA. x=L为f(x)的极大值点B. x=L为f(x)的极小值点2 2C. x=2为f(x)的极大值点D. x=2为f(x)的极小值点A2.已知函数f(x)=2x3-6x2+a在［.2, 2］上有最小值.37,求a的值，并求f(x)在［.2, 2］上的最大值。

第4讲利用导数研究函数的单调性、极值与最值问题【题型精讲】题型一：利用导数研究函数的单调性1、讨论函数的单调性（或区间）1．（2021·广东·深圳市福田区福田中学高三月考）已知函数211()(1)ln (,0)22f x x a x a a =-+-∈≠R ．（1）讨论函数的单调性；【答案】（1）答案见解析；（2）0a ≤.【详解】解：（1）由已知定义域为()0,∞+，()211'()x a a f x x x x-++=-=当10a +≤，即1a ≤-时，()'0f x >恒成立，则()f x 在()0,∞+上单调递增；当10a +>，即1a >-时，x =或x =所以()f x 在(上单调递减，在)+∞上单调递增.所以1a ≤-时，()f x 在()0,∞+上单调递增；1a >-时，()f x 在(上单调递减，在)+∞上单调递增.（2）由（1）可知，当1a ≤-时，()f x 在()1,+∞上单调递增，若()0f x ≥对任意的[1,)x ∈+∞恒成立，只需(1)0f ≥，而(1)0f =恒成立，所以1a ≤-成立；当1a >-1，即10a -<≤，则()f x 在()1,+∞上单调递增，又(1)0f =，所以10a -<≤成立；若0a >，则()f x 在(上单调递减，在)+∞上单调递增，又(1)0f =，所以(0x ∃∈，()0()10f x f <=，不满足()0f x ≥对任意的[1,)x ∈+∞恒成立.所以综上所述：0a ≤.2．（2021·安徽·芜湖一中高三月考（理））已知函数32()f x x x mx =+-.（1）若函数()f x 在2x =处取到极值，求曲线()y f x =在(1,())f x 处的切线方程；（2）讨论函数()f x 的单调性.【答案】（1）113y x =--；（2）()f x 在⎛⎫-∞ ⎪ ⎪⎝⎭和⎫+∞⎪⎪⎝⎭上单调递增，在11,33⎛-- ⎝⎭上单调递减.【详解】（1）依题意，2()32f x x x m '=+-，(2)1240f m '=+-=，解得16m =，经检验，16m =符合题意；故32()16f x x x x =+-，2()3216f x x x '=+-，故(1)21614f =-=-，(1)11f '=-，故所求切线方程为1411(1)y x +=--，即113y x =--；（2）依题意2()32f x x x m '=+-，412m ∆=+，若0∆，即13m - 时，()0f x ' ，()f x 在R 上单调递增；若0∆>，即13m >-时，令()0,f x x '==令12x x =故当()1,x x ∈-∞时，()0f x '>，当()12,x x x ∈时，()0f x '<，当()2,x x ∈+∞时，()0f x '>，故函数()f x 在⎛⎫-∞ ⎪ ⎪⎝⎭和⎫+∞⎪⎪⎝⎭上单调递增，在⎝⎭上单调递减.3．（2021·宁夏·青铜峡市高级中学高三月考（文））已知函数()ln af x x x=+（a 为常数）（1）讨论函数()f x 的单调性；【答案】（1）0a ≤时，(0,)+∞递增，0a >时，在(0,)a 递减，(,)a +∞递增；【详解】（1）函数定义域是(0,)+∞，221()a x a f x x x x-'=-=，0a ≤时，()0f x '>恒成立，()f x 在(0,)+∞上是增函数；0a <时，0x a <<时，()0f x '<，()f x 递减，x a >时，()0f x '>，()f x 递增．2、根据函数的单调性求参数的取值范围1．（2021·重庆市清华中学校高三月考）已知函数321()23f x ax x x =+-+，其中a R ∈.（1）若函数()f x 恰好有三个单调区间，求实数a 的取值范围；【答案】（1）()()1,00,a ∈-+∞ ；【详解】（1）由321()23f x ax x x =+-+，得2()21f x ax x '=+-.∵()f x 存在三个单调区间∴()0f x '=有两个不相等的实数根，即2210ax x +-=.∴00a ≠⎧⎨∆>⎩，即0440a a ≠⎧⎨+>⎩，故()()1,00,a ∈-+∞ .2．（2021·山西省新绛中学校高三月考（文））已知函数()321f x x ax =++，a R ∈.（1）讨论函数()f x 的单调区间；（2）若函数()f x 在区间2,03⎛⎫- ⎪⎝⎭内是减函数，求a 的取值范围；（3）若函数()f x 的单调减区间是2,03⎛⎫- ⎪⎝⎭，求a 的值.【答案】（1）答案见解析（2）[)1,+∞（3）1（1）由题意知，22()323()3a f x x ax x x '=+=+，当0a =时，2()30f x x '=≥恒成立，所以()f x 的单调递增区间是()-∞+∞，；当0a >时，令2()0()(0)3a f x x '>⇒∈-∞-+∞ ，，，令2()0(0)3af x x '<⇒∈-，所以()f x 的单调递增区间为2(),(0)3a -∞-+∞，，，单调递减区间为2(0)3a -，当0a <时，令2()0(0)()3a f x x '>⇒∈-∞-+∞ ，，令2()0(03af x x '<⇒∈-，，所以()f x 的单调递增区间为2(0)()3a -∞-+∞，，，，单调递减区间为2(0)3a -，；（2）由(1)知，当0a >时，有22(0)(0)33a -⊆-，，所以2233a -≤-，解得1a ≥，即a 的取值范围为[1)+∞，；（3）由(1)知，当0a >时，有22(0)(0)33a -=-，，，所以2233a -=-，解得1a =.3．（2021·河南·新蔡县第一高级中学高三月考（文））已知函数()3f x x ax =-+，a R∈（1）若()f x 在)1,⎡+∞⎣上为单调减函数，求实数a 取值范围；【答案】（1）3a ≤；（2）最大值为0，最小值为16-．【详解】解：（1）因为()3f x x ax =-+，则()'23f x x a =-+．依题意得()'230f x x a =-+≤在[)1,x ∈+∞恒成立，∴23a x ≤在[)1,x ∈+∞恒成立．因为当1≥x 时，233x ≥，所以3a ≤．（2）当12a =时，()312f x x x =-+，()()()'2312322f x x x x =-+=-+-，令()'0f x =得[]123,0x =∉-，22x =-，所以当32x -<<-时，()'0f x <，()f x 单调递减，当20x -<<时，()'>0f x ，()f x 单调递增，又()327369f -=-=-，()282416f -=-=-，()00f =．∴()f x 在[]3,0-上最大值为0，最小值为16-．题型二：利用导数研究函数的极值、最值1．（2021·天津·大钟庄高中高三月考）设函数()32f x x ax bx c =-+++的导数()f x '满足()10f '-=，()29f '=.（1）求()f x 的单调区间；（2）()f x 在区间[]22-,上的最大值为20，求c 的值.（3）若函数()f x 的图象与x 轴有三个交点，求c 的范围.【答案】（1）递增区间为()1,3-，递减区间为(),1-∞-，()3,+∞（2）2-（3）()27,5-（1）由()32f x x ax bx c =-+++可得()232x x x b f a '=-++，因为()10f '-=，()29f '=，所以3201249a b a b --+=⎧⎨-++=⎩，解得：3a =，9b =，所以()3239f x x x x c =-+++，()()22369323x x f x x x =-++=---'，由()0f x '>即2230x x --<可得：13x -<<，由()0f x '<即2230x x -->可得：1x <-或3x >，所以()f x 的单调递增区间为()1,3-，单减区间为(),1-∞-和()3,+∞.（2）由（1）知，()f x 在()2,1--上单调递减，在()1,2-上单调递增，所以当1x =-时，()f x 取得极小值()()()()321131915f c c -=--+⨯-+⨯-+=-，()()()()322232922f c c -=--+⨯-+⨯-+=+，()3222329222f c c =-+⨯+⨯+=+，则()f x 在区间[]22-,上的最大值为()22220f c =+=，所以2c =-.（3）由（1）知当1x =-时，()f x 取得极小值()()()()321131915f c c -=--+⨯-+⨯-+=-，当3x =时，()f x 取得极大值()3233339327f c c =-+⨯+⨯+=+，若函数()f x 的图象与x 轴有三个交点，则(1)50(3)270f c f c -=-<⎧⎨=+>⎩得527c c <⎧⎨>-⎩，解得275c -<<，即c 的范围是()27,5-.2．（2021·陕西·西安中学高三期中）已知函数()ln 2f x x x =-.（1）求函数()f x 在()()1,1f 处的切线方程；（2）求函数()f x 的单调区间和极值.【答案】（1）30x y --=（2）单调递增区间是1e ⎛⎫+∞ ⎪⎝⎭，，单调减区间是()10e ，，极小值12e --，无极大值（1）()f x 的定义域为()0,∞+，由()ln 2f x x x =-可得()ln 1f x x '=+，所以()11f '=，()12f =-，切点为()1,2-，所以所求切线方程为21y x +=-，即30x y --=.（2）由()ln 10f x x '=+=，得ln 1x =-解得：1ex =，当10e x <<时，()0f x '<，()f x 递减，当1ex >时，()0f x '>，()f x 递增，所以()f x 的单调递增区间是1e ⎛⎫+∞ ⎪⎝⎭，单调减区间是()10e ，；当1e x =时，函数()f x 取得极小值112e e f ⎛⎫=-- ⎪⎝⎭，无极大值.3．（2021·四川资阳·高三月考（理））已知函数()322133f x x ax a x =+-．（1）当1a =时，求函数()f x 在x ∈[]0,2时的最大值和最小值；（2）若函数()f x 在区间()1,2存在极小值，求a 的取值范围．【答案】（1）最大值为23，最小值为53-（2）()21,313,2⎛⎫⋃-- ⎪⎝⎭（1）当1a =时，()32133f x x x x =+-，则()()()22331f x x x x x '=+-=+-，由()0f x '>，可得3x <-或1x >，由()0f x '<，可得31x -<<，所以()f x 在()0,1上()f x 单调递减，在()1,2上单调递增；()00f =，()1511333f =+-=-，()122843233f =⨯+-⨯=，所以函数()f x 在x ∈[]0,2时的最大值为23，最小值为53-.（2）()()()22233f x x ax a x a x a '=+-=+-，当0a =时，知()f x 单调递增，函数()f x 没有极值；当0a >时，3x a <-时，()0f x '>，()f x 单调递增；3a x a -<<时，()0f x '<，()f x 单调递减；x a >时，()0f x '>，()f x 单调递增，则()f x 在3x a =-取得极大值，在x a =取得极小值，若函数()f x 在区间()1,2存在极小值，则12a <<，当0a <时x a <时，()0f x '>，()f x 单调递增，3a x a <<-时，()0f x '<，()f x 单调递减，3x a >-时，()0f x '>，()f x 单调递增，则()f x 在x a =取得极大值，在3x a =-取得极小值，若函数()f x 在区间()1,2存在极小值，则132a <-<可得：2133a -<<-．综上所述：实数a 的取值范围是()21,313,2⎛⎫⋃-- ⎪⎝⎭．4．（2021·河南南阳·高三期中（理））已知函数2()(2)21x f x x e x ax =---+，a ∈R .（1）当1a =-时，求()f x 的单调区间；（2）若函数()f x 不存在极值点，求证：1a <-.【答案】（1）增区间是(,ln 2)-∞和(1,)+∞，减区间是(ln 2,1)（2）证明见解析（1）解：当1a =-时，2()(2)21x f x x e x x =--++，则()()(1)2(1)(1)2x xf x x e x x e '=---=--令()0f x ¢>得：1x >或ln 2x <令()0f x ¢<得：ln 21x <<所以()f x 的单调增区间是(,ln 2)-∞和(1,)+∞，单调减区间是(ln 2,1)（2）解：()(1)22xf x x e x a '=---，因为函数()f x 无极值点，故()f x ¢无变号零点，，令()(1)22x g x x e x a =---，则2()x g x xe =-'，当(,0)x ∈-∞时，恒有()0g x '<，当[0,)x ∈+∞时，显然()'g x 是单调增加的，又因为(0)2g '=-，(1)20g e '=->，故0(0,1)x ∃∈，使得()00g x '=，即002xx e =，故()g x 在()0,x -∞上单调递减，在()0,x +∞上单调递增，则()0()min g x g x =，所以()00g x ≥，即000(1)220x x e x a ---≥，又002xx e =可得0011a x x ⎛⎫≤-+ ⎪⎝⎭，又因为0(0,1)x ∈，所以0012x x +>故1a <-5．（2021·广东顺德·高三月考）已知函数()32f x ax bx cx d =+++的两个极值点为1-，2，且在0x =处的切线方程为210x y +-=．（1）求函数()f x 的表达式；（2）当1,33x ⎡⎤∈-⎢⎥⎣⎦时，()56f x kx >+恒成立，求实数k 的取值范围．【答案】（1）()32112132f x x x x =--+（2）62,227⎛⎫-- ⎪⎝⎭（1）由()32f x ax bx cx d =+++可得()232f x ax bx c '=++，则1-，2是方程()2320f x ax bx c '=++=的两根，所以()()132021240f a b c f a b c ⎧-=-+=⎪⎨=++=''⎪⎩，（*）因为又因为0x =处的切线方程为210x y +-=故()01f d ==，()02f c '==-代入（*）式解得13a =，12b =-故()32112132f x x x x =--+（2）由（1）知：()32112132f x x x x =--+，①当0x =时，()56f x kx >+即516>恒成立，此时R k ∈，②当(]0,3x ∈时，由()56f x kx >+即3211521326x x x kx --+>+，分离参数k 可得：21112326k x x x<--+，设()21112326g x x x x=--+，则()min k g x <，()()()23222214121143132666x x x x x g x x x x x -++--'=--==，故()g x 在(),0-∞上单调递减，()0,1上单调递减，()1,+∞上单调递增，故当(]0,3x ∈时，()g x 在()0,1上单调递减，()1,3上单调递增，所以()g x 的最小值为()()2min 11111231226g x g =⨯-⨯-+==-，所以2k <-，③当1,03x ⎡⎫∈-⎪⎢⎣⎭时，由()56f x kx >+分离参数可得21112326k x x x >--+设()21112326g x x x x=--+，则()max k g x >，由②过程知()g x 在1,03⎡⎫-⎪⎢⎣⎭上单调递减，故()2max1111116221333232763g x g ⎛⎫⎛⎫⎛⎫=-=--⨯--+=-⎪ ⎪ ⎪⎛⎫⎝⎭⎝⎭⎝⎭⨯- ⎪⎝⎭，所以6227k >-，综上所述：k 的取值范围为62,227⎛⎫-- ⎪⎝⎭.6．（2021·福建·福清西山学校高三期中）已知函数()()1ln 0f x a x a x=+>.（1）求函数()f x 的极值；（2）是否存在实数a ，使得函数()f x 在区间[]1,e 上的最小值为2e？若存在，求出a 的值；若不存在，请说明理由.【答案】（1）极小值ln a a a -，无极大值；（2）存在，1a e=.【详解】（1）函数()1ln f x a x x =+定义域为()0,∞+，()21-='ax f x x，其中0a >，由()0f x '>，得1x a >；由()0f x '<，得10x a<<.所以函数()f x 的单调递增区间为1,a ⎛⎫+∞ ⎪⎝⎭，单调递减区间为10,a ⎛⎫⎪⎝⎭，所以，函数()f x 的极小值为11ln ln f a a a a a a a ⎛⎫=+=- ⎪⎝⎭，无极大值；（2）①当101a<≤时，即1a ≥时，函数()f x 在[]1,e 上为增函数，故函数()f x 的最小值为()11f =，显然21e≠，故不满足条件；②当11e a <<时，即11a e <<时，函数()f x 在11,a ⎡⎤⎢⎥⎣⎦上为减函数，在1,e a ⎛⎤⎥⎝⎦上为增函数，故函数()f x 的最小值为11ln ln f a a a a a a a ⎛⎫=+=- ⎪⎝⎭，令()ln g a a a a =-，1,1a e ⎛⎫∈ ⎪⎝⎭，则12g e e⎛⎫= ⎪⎝⎭，其导函数()ln 0g a a =->'，可知()g a 在1,1e ⎛⎫⎪⎝⎭单调递增，因为()min 2f x e =，有2ln a a a e -=，可得1a e=不符合题意；③当1e a ≥时，即10a e<≤时，函数()f x 在[]1,e 上为减函数，故函数()f x 的最小值为()11ln f e a e a e e =+=+，由12a e e +=，得1a e =满足条件.综上所述：存在1a e=符合题意.【课后精练】1．（2021·黑龙江·模拟预测（文））已知函数()2(2)2,2xa f x x e x ax a R =--++∈.（1）当1a =时，求()f x 的单调区间；（2）当0x ≥时，恒有()0f x ≥，求实数a 的最小值.【答案】（1）增区间：(,0)-∞，(1,)+∞，减区间：(0,1)（2）24e -（1）当1a =时，2()(2)22xx f x x e x =--++，()(1)(1)x f x x e '=--，令()00'>⇒<f x x 或1x >，()001f x x <⇒<<'，()f x ∴的增区间：(,0)-∞，(1,)+∞，减区间：(0,1)；（2）()(1)()x f x x e a '=--①当1a ≤时：0x e a -≥，(0,1)x ∴∈时：()0,()f x f x '<单调递减()(0)0f x f ⇒<=，不符合题意.②当1a >时：令12()01,ln f x x x a '=⇒==，若1a e <<，则12x x >，令()00ln f x x a '>⇒<<或1x >，()0ln 1f x a x '<⇒<<，所以()f x 在(0,ln )a 单调递增，在(ln ,1)a 单调递减，在(1,)+∞单调递增，又(0)0f = ，∴只需(1)024f a e ≥⇒≥-，综上，a 的最小值为24e -.2．（2021·山东·滕州市第一中学新校高三期中）已知函数()()2xf x x mx m e =--.（1）求()f x 的单调区间；（2）当1m ≤时，求证：对()0,x ∀∈+∞，()0f x e +≥.【答案】（1）答案见解析（2）证明见解析（1）解:()()()2,x f x e x x m ¢=+-当m 2=-时，()()220x f x e x ¢=+³，所以()f x 的单调增区间是()-∞+∞，；当2m >-时，由()0f x '>，得2x <-或x m >，所以()f x 的增区间是()()2m ，，，-¥-+¥，减区间是()2m ，-；当2m <-时，由()0f x '>，得x m <或2x >-，所以()f x 的增区间是()()m 2，，，-¥-+¥，减区间是()2m ，-；（2）当m 1≤时，()0,10x x >-+<，则()()()2-1x f x e h m x m x e e ⎡⎤+==++⎣⎦在1m £上单调递减，()()()()211x h m h x x e e g x ≥=--+=，()()()()2x =221x x g e x x e x x +-=+-，当()'x 0g >时，1x >，当()'x 0g <时，01x <<，所以()g x 在()0,1上递减，在()1+∞，上递增，所以()()g x g 1=0.≥所以当1m £时，对()0,x ∀∈+∞，()0f x e +≥.3．（2021·山西吕梁·高三月考（理））已知函数()2xf x ae x =-，a R ∈.（1）讨论函数()f x 的单调性；（2）当1a =时，求证：()221108f x x x +-+>.【答案】（1）当0a ≤时，()f x 在R 上单调递减；当0a >时，()f x 在2,ln a ⎛⎫-∞ ⎪⎝⎭上单调递减，在2ln ,a ⎛⎫+∞ ⎪⎝⎭上单调递增.（2）答案见详解（1）∵()'2xf x ae =-，当0a ≤时，20x ae -<恒成立，()f x 单调递减.当0a >时，当20x ae -<，2xe a<，2ln x a <时，()f x 单调递减；当2ln x a >时，()f x 单调递增.∴函数()f x 的单调性为：当0a ≤时，()f x 在R 上单调递减；当0a >时，()f x 在2,ln a ⎛⎫-∞ ⎪⎝⎭上单调递减，在2ln ,a ⎛⎫+∞ ⎪⎝⎭上单调递增.（2）当1a =时，()2xf x e x =-.设()222212137()1211888x x g x f x x x e x x x e x x =+-+=-+-+=+-+，则'37()28xg x e x =+-，令'37()()28xh x g x e x ==+-则'()20x h x e =+>，所以()h x 在R 上单调递增，又∵(0)0h <，(1)0h >∴存在唯一零点()00,1x ∈，且0037208xe x +-=①()0,x x ∈-∞时，()0h x <，即'()0g x <，()g x 单调递减，()0,x x ∈+∞时，()0h x >，即'()0g x >，()g x 单调递增，故()g x 在0x x =处取得极小值，也是最小值.()02000min 37()18x g x g x e x x ==+-+，将①式代入，则()22000000min 373745()21885838g x g x x x x x x ==-+-+=-+∵二次函数2534588y x x =-+在()0,1上单调递减，∴在1x =时，y 有最小值2min 54510838y =-+=∴()min 0g x >∴()221108f x x x +-+>4．（2021·山东德州·高三期中）已知函数()2(1)x f x xe a x =++(其中常数e 2.718= 是自然对数的底数).（1）当0a <时，讨论函数()f x 的单调性；（2）证明：对任意1a ≤，当0x >时，()()23231f x ex a x x x -≥-++.【答案】（1）答案见解析（2）证明见解析（1）由()()()()12(1)12x xf x x e a x x e a =+++=++，令()0f x '=，解得1x =-，()ln 2x a =-，①当102a e-<<，由()0f x '>，解得()ln 2x a <-或1x >-，由()0f x '<，解得()ln 21a x -<<-，故()f x 在()(),ln 2a -∞-，()1,-+∞上单调递增；在()()ln 2,1a --上单调递减，②当12a e=-，()0f x '≥，()f x 在R 上单调递增;③当12a e<-，由()0f x '>，解得1x <-或()ln 2x a >-，由()0f x '<，解得()1ln 2x a -<<-故()f x 在(),1-∞-，()()ln 2,a -+∞上单调递增；在()()1,ln 2a --上单调递减，综上所述，当102a e-<<时，()f x 在()(),ln 2a -∞-，()1,-+∞上单调递增；在()()ln 2,1a --上单调递减，当12a e=-，()f x 在R 上单调递增;当12a e<-，()f x 在(),1-∞-，()()ln 2,a -+∞上单调递增；在()()1,ln 2a --上单调递减.（2）证明：对任意1a ≤，当0x >时，要证()()23231f x ex a x x x --++≥，需证，20x e aa ax e x x +---≥，令()2x e ag x a ax e x x=+---，则()()()21x x e ax a g x x ---'=，令()xh x e ax a =--，则()xh x e a '=-，因为0x >，1a ≤，所以()0x h x e a '=->，所以()()010h x h a >=-≥，所以()0,1x ∈时，()0g x '<，()g x 单调递减，当()1,x ∈+∞时，()0g x '>，()g x 单调递增，所以()()10g x g ≥=，即20x e aa ax e x x+---≥，原不等式成立.5．（2021·河南三门峡·高三月考（文））已知函数()2ln f x ax x =--，12a >-且0a ≠.（1）当1a =时，求函数()f x 的单调区间与极大值；（2）当1x >时，()()20g x f x ax =+<恒成立，求实数a 的取值范围.【答案】（1）增区间为10,2⎛⎫ ⎪⎝⎭，减区间为1,2⎛⎫+∞ ⎪⎝⎭，极大值13ln 224f ⎛⎫=-- ⎪⎝⎭（2）(]0,1（1）解：当1a =时，函数()2ln f x x x x =--，()0,x ∈+∞可得()()()212112121x x x x f x x x x x+-+-'=--=-=-，令()0f x '>，解得102x <<，()f x 单调递增；令()0f x '<，可得12x >，()f x 单调递减；所以函数()f x 的单调增区间为10,2⎛⎫ ⎪⎝⎭，单调减区间为1,2⎛⎫+∞ ⎪⎝⎭，当12x =时，函数()f x 取极大值13ln 224f ⎛⎫=-- ⎪⎝⎭.（2）解：由题意，函数()()()22ln 21g x f x ax x ax a x =+=-+-，()1,x ∈+∞可得()()()()2111221ax x g x ax a x x+-'=-+-=-，①当102a -<<，11,2x a ⎛⎫∈- ⎪⎝⎭时，()0g x '<；1,2x a ⎛⎫∈-+∞ ⎪⎝⎭时，()0g x '>恒成立，所以()g x 在11,2a ⎛⎫- ⎪⎝⎭上单调递减，在1,2a ⎛⎫-+∞ ⎪⎝⎭上是增函数，所以()1,2g x g a ⎛⎫⎛⎫∈-+∞ ⎪ ⎪⎝⎭⎝⎭，不符合题意；②当0a >时，()1,x ∈+∞时恒有()0g x '<，故()g x 在()1,+∞上是减函数，所以()0g x <对任意()1,x ∈+∞都成立，只需()10g ≤，即210a a -+-≤，解得1a ≤，故01a <≤.综上所述：a 的取值范围是(]0,1.6．（2021·江西赣州·高三期中（文））已知函数()e x f x ax =-，且函数()f x 在(1,(1))f 处的切线为(e 2)=-+y x b ．（1）求a ，b 的值并分析函数()f x 单调性；（2）若函数()(),[1,1]g x f x m x =-∈-恰有两个零点，求实数m 的取值范围．【答案】（1）2,0a b ==；函数()f x 在(,ln 2)-∞上单调递减，在(ln 2,)+∞上单调递增（2）(22ln 2,e 2]∈--m （1）解：由()e x f x ax =-得()e '=-x f x a ，由题意知(1)e 2='-f ，即e e 2-=-a ，解得2a =，又(1)e 2f =-，而切点(1,(1))f 在切线(e 2)=-+y x b 上，所以e 2e 2-=-+b ，解得0b =，则()e 2x f x '=-，令()0f x '>，得ln 2x >，令()0f x '>，得ln 2x <，故函数()f x 在(,ln 2)-∞上单调递减，在(ln 2,)+∞上单调递增；（2）由（1）知()()e 2,[1,1]=-=--∈-x g x f x m x m x ，且函数()g x 在[1,ln 2)-上递减，在(]ln 2,1上单调递增，而因为函数()g x 恰有两个零点，所以函数()g x 在区间[)(]1,ln 2ln 2,1-、各有一个零点，由零点存在性定理得(1)0(ln 2)0(1)0g g g ≥⎧⎪<⎨⎪-≥⎩，即e 2022ln 20120em m m ⎧⎪--≥⎪--<⎨⎪⎪+-≥⎩，解得22ln 2e 2-<≤-m ；∴(22ln 2,e 2]∈--m ．7．（2021·天津市第二十一中学高三期中）已知函数2()(21)ln f x ax a x x =+--．（1）当12a =时，求函数()f x 的单调区间和极值；（2）讨论函数()f x 单调性．【答案】（1）单减区间()0,1，单增区间()1,+∞，()f x 极小值=()112f =，无极大值；（2）见解析.（1）当12a =时，()21()ln 02f x x x x =->，所以()()111()x x f x x x x+-'=-=.故当()0,1x ∈时，()0f x '<，()f x 为减函数；当()1,x ∈+∞时，()0f x '>，()f x 为增函数.所以当x =1时，()f x 极小值=()112f =，无极大值.（2）由()2()(21)ln ,0f x ax a x x x =+-->可得：()21(21)2(21)1()x ax ax a x f x x x+-+--'==.①当a ≤0时，()0f x '<，()f x 在()0,∞+为减函数；②当a >0时，10,2x a ⎛⎫∈ ⎪⎝⎭时()0f x '<，故()f x 为减函数；1,2x a ⎛⎫∈+∞ ⎪⎝⎭时，()0f x '>，故()f x 为增函数.8．（2021·全国·高三月考（文））已知函数2()(21)ln f x ax a x x =-++.（1）当1a =时，求()f x 的单调区间与极值；（2）若()0f x <恒成立，求a 的取值范围.【答案】（1）单调递增区间为10,2⎛⎫ ⎪⎝⎭，(1,)+∞，单调递减区间为1,12⎛⎫⎪⎝⎭，极大值15ln 224f ⎛⎫=-- ⎪⎝⎭，极小值(1)2f =-（2）(1,0]-（1）当1a =时，函数2()3ln =-+f x x x x ，定义域为(0,)+∞，()21231(21)(1)23x x x x f x x x x x-+--'=-+==.当()0f x '>时，102x <<或1x >，当()0f x '<时，112x <<，所以函数()f x 的单调递增区间为10,2⎛⎫ ⎪⎝⎭，(1,)+∞，单调递减区间为1,12⎛⎫⎪⎝⎭，所以当12x =时，函数()f x 取得极大值15ln 224f ⎛⎫=-- ⎪⎝⎭，当1x =时，函数()f x 取得极小值(1)2f =-.（2）()1(21)(1)2(21)ax x f x ax a x x--'=-++=.①当0a >时，2()(21)ln f x ax a x x =-++，(0,)x ∈+∞，令2(21)0ax a x -+>，解得12x a>+，则当01(2,)x a∈++∞时，200(21)0ax a x -+>，且0ln ln 20x >>，所以函数2()(21)ln 0f x ax a x x =-++>恒成立，不符合题意，舍去；②当0a ≤时，令()0f x '>，解得01x <<，令()0f x '<，解得1x >，则函数()f x 在(0,1)上为增函数，在(1,)+∞上为减函数，所以函数()f x 在1x =处取得极大值，也是最大值，要使得()0f x <恒成立，则只需(1)(21)0f a a =-+<，解得1a >-，故10a -<≤.综上，a 的取值范围是(1,0]-.9．（2021·山西太原·高三期中）已知函数2()e x f x ax x =+-.（1）若12a =，讨论()f x 的单调性；（2）若()1f x ≤恒成立，求实数a 的取值范围.【答案】（1）()f x 为R 上的单调递减函数（2）(],0-∞（1）解：当12a =时，21()e 2xf x x x =+-，所以'()1e x f x x =+-，令()'()1e x g x f x x ==+-，则()'1e xg x =-，所以当0x >时，()'0g x <，()g x 单调递减，当0x <时，()'0g x >，()g x 单调递增，所以()()00g x g ≤=，即'()0f x ≤，所以函数()f x 为R 上的单调递减函数.（2）解：若()1f x ≤恒成立，即21e x ax x +-≤恒成立，显然，当0x =时成立，当0x ≠时，不等式等价于21e x x a x-+≤恒成立，令()21e x x h x x -+=，则()()()32e 1'x h x xx +=-，当()'0h x >时，得0x <或2x >，即函数()h x 在(),0-∞和()2,+∞上单调递增，当()'0h x <时，得02x <<，即函数()h x 在()0,2上单调递减，由于x →-∞时，()h x 由正数趋近于0，当2x =时，()21204e h -=>所以函数()h x 的草图如图，所以21e x x a x -+≤恒成立，只需0a ≤所以实数a 的取值范围是(],0-∞10．（2021·陕西·西安中学高三期中（文））己知函数e ()(0)xa f x a x=≠．（1）讨论函数()f x 的单调区间；（2）当(0,)x ∈+∞时，若()1f x ≥恒成立，求a 的取值范围．【答案】（1）答案见解析．（2）1[,)e+∞（1）解：函数定义域是{|0}x x ≠，2e (1)()x a x f x x -'=，0a >时，01x <<或0x <时，()0f x '<，1x >时，()0f x '>，()f x 的增区间是(1,)+∞，减区间是(,0)-∞和(0,1)．同理可得0a <时，()f x 的减区间是(1,)+∞，增区间是(,0)-∞和(0,1)．（2）由（1）知，若0a >，则1x =时，min ()(1)e f x f a ==，()1f x ≥恒成立，则e 1a ≥，1ea ≥，若0a <，0x >时，()0f x <，不合题意．综上，a 的取值范围是1[,)e+∞．。

3.2导数在函数单调性、极值中的应用(理-测试)限时作业15 导数在函数单调性、极值中的应用一、选择题1.函数f(x)=的单调递减区间是( ).A.[e,+∞)B.[1,+∞)C.[0,e]D.[0,1]2.(2011福建高考,文10)若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( ).A.2B.3C.6D.93.设f(x)=kx--2ln x,若f(x)在其定义域内为单调增函数,则k的取值范围是( ).A.(-∞,1]B.[1,+∞)C.(-∞,-1]D.[-1,+∞)4.(2012天津模拟)定义在R上的函数y=f(x),满足f(3-x)=f(x),f'(x)<0,若x1<x2,且x1+x2>3,则有( ).7.已知函数f(x)=(m-2)x2+(m2-4)x+m是偶函数,函数g(x)=-x3+2x2+mx+5在(-∞,+∞)内单调递减,则实数m的值为.8.已知函数f(x)=x3+ax2+bx+a2在x=1处取得极值10,则f(2)= .9.已知某质点的运动方程为s(t)=t3+bt2+ct+d,如图所示是其运动轨迹的一部分,若t∈时,s(t)<3d2恒成立,则d的取值范围为.三、解答题10.(2011江西高考,理19)设f(x)=-x3+x2+2ax. (1)若f(x)在(,+∞)上存在单调递增区间,求a的取值范围;(2)当0<a<2时,f(x)在[1,4]上的最小值为-,求f(x)在该区间上的最大值.11.已知x=3是函数f(x)=aln(1+x)+x2-10x的一个极值点.(1)求a的值;(2)求函数f(x)的单调区间;(3)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.12.(2011辽宁高考,理21)已知函数f(x)=lnx-ax2+(2-a)x.(1)讨论f(x)的单调性;(2)设a>0,证明:当0<x<时,f>f;(3)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f'(x)<0.参考答案一、选择题1.B2.A3.D4.D5.C6.C 解析:依题意,当a≤1时, S(a)=+2a=-a2+3a;当1<a≤2时,S(a)=+2a;当2<a≤3时,S(a)=+2+a=a+;当a>3时,S(a)=+2+3=,于是S(a)=由解析式可知选C.二、填空题7.6.5 8.赔14元9.2 000 解析:设树苗放置在距一端距离为x 米的树坑旁边,则0≤x≤190,且∈Z,设距离之和为2f(x),由题意易知:f(x)=|x|+|x-10|+|x-20|+…+|x-x|+|x-(x+10 )|+|x-(x+20)|+…+|x-180|+|x-190|=x+(x-10)+(x -20)+…+10+0+10+20+…+(180-x)+(190-x) =+==.x∈[0,190],且∈Z,∴当且仅当x=90或x=100时,f(x)取最小值,∴最小距离之和为2f(x)=2f(90)=2f(100)=2min000.三、解答题10.解:(1)当甲户的用水量不超过4吨时,即x≤,乙户的用水量也不超过4吨,y=(5x+3x)×1.8=14.4x;当甲户的用水量超过4吨,乙户的用水量不超过4吨时,即<x≤,y=4×1.8+3x×1.8+3×(5x-4)=20.4x-4.8,当乙户的用水量超过4吨时,即x>,y=8×1.8+3×(8x-8)=24x-9.6,所以y=(2)由(1)可知y=f(x)在各段区间上均为单调递增,当x∈时,y≤f=11.52<26.4;当x∈时,y≤f=22.4<26.4;当x∈时,令24x-9.6=26.4,解得x=1.5,所以甲户用水量为5x=7.5吨,付费S1=4×1.8+3.5×3=17.70(元);乙户用水量为3x=4.5吨,付费S2=4×1.8+0.5×3=8.70(元).11.解:(1)由题意知,E移动时单位时间内的淋雨量为|v-c|+,故y==(3|v-c|+10).(2)由(1)知,当0<v≤c时,y=(3c-3v+10)=-15;当c<v≤10时,y=(3v-3c+10)=+15;故y=①当0<c≤时,y是关于v的减函数.故当v=10时,ymin=20-.②当<c≤5时,在(0,c]上,y是关于v的减函数;在(c,10]上,y是关于v的增函数.故当v=c时,ymin=.12.解:(1)设0≤t1<t2,∵g(t)为常数,∴g(t1)=g(t2),即·(-)=0,∴g(0)=.即湖水污染的初始质量分数为.(2)证明:设0≤t1<t2,则g(t1)-g(t2)=·(-) =·,∵g(0)-<0,t1<t2,∴g(t1)-g(t2)<0.∴g(t1)<g(t2).故湖泊污染质量分数随时间变化而增加,污染越来越严重.(3)污染源停止,即p=0,此时g(t)=g(0)·.设要经过t天能使湖水的污染水平下降到开始时污染水平的5%.即g(t)=5%·g(0),即有5%·g(0)=g(0)·.由实际意义知g(0)≠0,∴=.∴t=ln 20(天),即需要ln 20天时间.一、选择题1.A2.A3.B4.D5.A6.A 解析:设点P的横坐标是m,则曲线在点P=2m+2,由于该切线的倾斜处的切线的斜率等于y'|x=m角的取值范围为,因此有0≤2m+2≤1,由此解得-1≤m≤-.二、填空题7. 8.69.4 解析:设切线的斜率为k,则k=y'=3x2+6x+a,又∵k=tan θ,θ∈,∴k∈[1,+∞).又k=3(x+1)2+a-3,∴当x=-1时,k取最小值为a-3=1.∴a=4.三、解答题10.解:(1)设u=3-x, 则y=,u=3-x.y'=f'u ·u'x=()'(3-x)'=(-1)=-=-.(2)y'='+'+'=(x-1)'+(2x-2)'+(x-3)' =-x-2-4x-3-3x-4=---.(3)y'='==.(4)令y=loga u,u=sin x,y'=logae·cosx=·logae=.11.解:y=x3+,则y'=x2.(1)由题意可知点P(4,2)为切点,y'|x=2=22=4,所以曲线在点P(2,4)处的切线方程为y-4=4(x-2),即4x-y-4=0.(2)由题意可知点P(2,4)不一定为切点,故设切点为,y'=,曲线过点P(2,4)的切线方程为y-=(x-x), 所以4-=(2-x0),-3+4=0⇔(+1)-3(-1)=0⇔(x+1)(-4x+4)=0.解得x0=-1或x=2,即切点为(-1,1)或(2,4).所以曲线过点P(2,4)的切线方程为x-y+2=0或4x-y-4=0.12.解:(1)因为切点在切线上,所以将点M代入切线方程解得f()=.由f'(x)=a-,根据题意,得关于a,b的方程组解得所以f(x)的解析式为f(x)=x+.(2)由f'(x)=1-(x≠0),令f'(x)<0,解得-1<x<0或0<x<1.所以f(x)的单调递减区间为(-1,0),(0,1).(3)证明:设P(x0,y)为曲线上任一点,由y'=1-知曲线在点P(x0,y)处的切线方程为y-y0=(x-x),即y-=(x-x).令x=0,得y=,从而得切线与直线x=0的交点坐标为.令y=x,得y=x=2x,从而得切线与直线y=x的交点坐标为(2x0,2x).所以点P(x0,y)处的切线与直线x=0,y=x所围成的三角形面积为|2x|=2.一、选择题1.A2.D3.B4.A5.A6.B 解析:易得f'(x)=x2+|a|x+a·b,函数f(x)=x3+|a|x2+a·bx在R上单调递增时,方程x2+|a|x+a·b=0的判别式Δ=|a|2-4a·b≤0,设a,b的夹角为θ,则|a|2-4|a||b|cos θ≤0,将|a|=2|b|≠0代入上式得1-2cos θ≤0,即cos θ≥,又0≤θ≤π,故0≤θ≤.二、填空题7.-2 8.189.d>或d<-1 解析:∵质点的运动方程为s(t)=t3+bt2+ct+d,∴s'(t)=3t2+2bt+c.由图可知,s(t)在t=1和t=3处取得极值.则s'(1)=0,s'(3)=0,即∴∴s'(t)=3t2-12t+9=3(t-1)(t-3).当t∈时,s'(t)>0;当t∈(1,3)时,s'(t)<0;当t∈(3,4)时,s'(t)>0,∴当t=1时,s(t)取得极大值4+d.又∵s(4)=4+d,∴当t∈时,s(t)的最大值为4+d.∵当t∈时,s(t)<3d2恒成立,∴4+d<3d2,即d>或d<-1.三、解答题10.解:(1)由f'(x)=-x2+x+2a=-++2a,当x∈[,+∞)时,f'(x)的最大值为f'=+2a;令+2a>0,得a>-,所以,当a>-时,f(x)在上存在单调递增区间.(2)令f'(x)=0,得两根x1=,x2=.所以f(x)在(-∞,x1),(x2,+∞)上单调递减,在(x1,x2)上单调递增.当0<a<2时,有x1<1<x2<4,所以f(x)在[1,4]上的最大值为f(x2).又f(4)-f(1)=-+6a<0,即f(4)<f(1),所以f(x)在[1,4]上的最小值为f(4)=8a-=-,得a=1,x=2,从而f(x)在[1,4]上的最大值为2f(2)=.11.解:(1)因为f'(x)=+2x-10,所以f'(3)=+6-10=0,因此a=16.(2)由(1),知f(x)=16ln(1+x)+x2-10x,x∈(-1,+∞),f'(x)=.当x∈(-1,1)和x∈(3,+∞)时,f'(x)>0;当x∈(1,3)时,f'(x)<0.所以f(x)的单调递增区间是(-1,1),(3,+∞);f(x)的单调递减区间是(1,3).(3)由(2)知,f(x)在(-1,1)内单调递增,在(1,3)内单调递减,在(3,+∞)上单调递增,且当x=1或x=3时,f'(x)=0.所以f(x)的极大值为f(1)=16ln 2-9,极小值为f(3)=32ln 2-21.因为f(16)>162-10×16>16ln 2-9=f(1),f(e-2-1)<-32+11=-21<f(3),所以在f(x)的三个单调区间(-1,1),(1,3),(3,+∞)上,直线y=b与y=f(x)的图象各有一个交点,当且仅当f(3)<b<f(1).因此,b的取值范围为(32ln 2-21,16ln 2-9).12.(1)解:f(x)的定义域为(0,+∞),f'(x)=-2ax+(2-a)=-.①若a≤0,则f'(x)>0,所以f(x)在(0,+∞)上单调增加.②若a>0,则由f'(x)=0得x=,且当x∈时,f'(x)>0,当x>时,f'(x)<0,所以f(x)在上单调增加,在上单调减少.(2)证明:设函数g(x)=f-f,则g(x)=ln (1+ax)-ln (1-ax)-2ax,g'(x)=+-2a=当0<x<时,g'(x)>0,而g(0)=0,所以g(x)>0.故当0<x<时,f>f.(3)由(1)可得,当a≤0时,函数y=f(x)的图象与x轴至多有一个交点,故a>0,从而f(x)的最大值为f,且f>0.不妨设A(x1,0),B(x2,0),0<x1<x2,则0<x1<<x2.由(2)得f =f>f(x1)=0.从而x2>-x1,于是x=>.由(1)知,f'(x)<0.。

导数及其应用-单调性和极值一、选择题：1.设函数1()21(0),f x x x x =+-< 则()f x （ ） A ．有最大值 B ．有最小值 C ．是增函数 D ．是减函数2．．设曲线2ax y =在点（1，a ）处的切线与直线062=--y x 平行，则=a （ ）A ．1B ．12C ．12- D ．1- 3．如果函数()y f x =的图像如右图,那么导函数,()y f x =的图像可能是 （ ）4、设()ln f x x x =，若0'()2f x =，则0x = （ ）A. 2eB. eC.ln 22D. ln 2 5．曲线324y x x =-+在点(13)，处的切线的倾斜角为 （ ） A ．30°B ．45°C ．60°D ．120° 6．设曲线11x y x +=-在点(32)，处的切线与直线10ax y ++=垂直，则a = （ ） A ．2 B ．12 C ．12- D ．2- 7．.直线12y x b =+是曲线()ln 0y x x =>的一条切线，则实数b ＝ ． 8．设R a ∈，若函数ax e y x +=，R x ∈有大于零的极值点，则 （ ）A ．1-<a B. 1->a C. e a 1-> D. ea 1-< 9．设P 为曲线C ：223y x x =++上的点，且曲线C 在点P 处切线 倾斜角的取值范围为04π⎡⎤⎢⎥⎣⎦，，则点P 横坐标的取值范围为 （ ） A ．112⎡⎤--⎢⎥⎣⎦， B ．[]10-， C ．[]01， D ．112⎡⎤⎢⎥⎣⎦， 10.若f(x)=21ln(2)2x b x -++∞在(-1,+)上是减函数，则b 的取值范围是 （ ） A.[-1，+∞] B.（-1，+∞） C.（-∞，-1） D.（-∞，-1）二、解答题：1.已知函数32()3(0),()()2f x x ax bx c b g x f x =+++≠=-且是奇函数.（Ⅰ）求a ,c 的值； （Ⅱ）求函数f (x )的单调区间.练习：已知函数32()2f x x mx nx =++-的图像过点（-1，-6），且函数()'()6g x f x x =+的图像关于y 轴对称。

卜人入州八九几市潮王学校高三数学导数的应用(一)单调性与极值例题解析一.本周教学内容：导数的应用〔一〕单调性与极值 1.函数的单调性 一般地，设函数)(x f y =在某个区间内可导，假设0)(>'x f ，那么)(x f 为增函数；假设0)(<'x f ，那么)(x f 为减函数，假设在某个区间内恒有0)(='x f ，那么)(x f 为常数。

2.函数的极值一般地，设函数)(x f 在点0x 附近有定义，假设对0x 附近的所有点，都有)()(0x f x f <，就称)(0x f 是函数)(x f 的一个极大值，记作极大值y )(0x f =；假设对0x 附近的所有的点，都有)()(0x f x f >就称)(0x f 是函数)(x f 的一个极小值，记作)(0x f y =极小值。

极大值和极小值统称为极值。

判别)(0x f 是极大〔小〕值的方法是：〔1〕假设在0x 附近的左侧0)(>'x f ，右侧0)(<'x f ，那么)(0x f 是极大值； 〔2〕假设在0x 附近的左侧0)(<'x f ，右侧)(x f '0>，那么)(0x f 是极小值。

导数为0的点不一定是极值点，例如函数3)(x x f =，0=x 处的导数是0，但非极值点。

求可导函数)(x f 的极值的步骤如下： 〔1〕求导数)(x f '〔2〕求出方程0)(='x f 的根〔3〕检查0)(='x f 在方程根左右的值的符号，假设左正右负，那么)(x f 在这个根处获得极大值；假设左负右正，那么)(x f 在这个根处获得极小值，假设左右符号一样，那么这个根不是极值点。

【典型例题】 [例1]确定函数762)(23+-=x x x f 在哪个区间内是增函数，哪个区间内是减函数？解：x x x f 126)(2-='令01262>-x x ，解得2>x 或者0<x 令01262<-x x，解得20<<x故函数)(x f 在)0,(-∞∈x 和),2(∞+∈x 为增函数，在)2,0(∈x 为减函数 [例2]研究函数ax x x f +=3)(的单调性。