当前位置：文档之家 › 精选数学物理方法第四版梁昆淼期末总结讲义

精选数学物理方法第四版梁昆淼期末总结讲义

  • 格式：ppt
  • 大小：2.61 MB
  • 文档页数：84

下载文档原格式

  / 84

合集下载

数学物理方法第一章

数学物理方法第一章

存在，并且与 z 0 的方式无关，则称函数 w=f(z) 在 z 点可导(或单演)，此(有限的)极限称为函数 f(z) 在 z 的导数
(或微商)，以 f '(z) 或 df/dz 表示
讨论：
1、从形式上看，复变函数导数的定义与实变函数的定义相同，
因而实变函数论中关于导数的规则和公式往往可以适用于实变 函数。
则
x cos y sin

z (cos i sin )
z e
i

指数式
讨论：i)复数的辐角不能唯一地确定。如果 0 是其中一个辐角， 则
0 2k (k 0,1,2,) 也是其辐角，把属于 [0,2 ) 的辐角称为主值辐角，记为arg z .
存在，且连续，并
且满足柯西-黎曼条件。 证明：由于这些偏导数连续，二元函数 u 和 v 的增量可分别写为
各 个
，于是有
根据柯西-黎曼条件，上式即
这一极限是与 z 0 无关的有限值。证毕。
讨论：复变函数与实变函数的导数有本质上的差别，复变函数 可微，不但要求复变函数的实部与虚部可微，而且还要求其实 部与虚部满足柯西-黎曼条件。
单连通区域：在区域 B 做任何简单的闭曲线，曲线包围 的点全属于 B。否则为多连通区域。
三、复变函数例
多项式
a0 a1 z a2 z an z
2
n
n 为正整数
有理分式
a0 a1 z a2 z 2 an z n b0 b1 z b2 z 2 bm z m
ii)当 1时，z cos i sin ei 称为单位复数。
iii)复数 z 的共轭复数
z x iy (cos isin ) e
数学物理方法(梁昆淼)chapt7

数学物理方法(梁昆淼)chapt7

ut t 0 ( x)
x0
x0
( x)
1 1 x at u ( x, t ) [ ( x at ) ( x at )] ( )d 2 2a x at
x (t ) a
1 1 x at 1 at x u ( x, t ) [ ( x at ) (at x)] ( )d ( )d 2 2a 0 2a 0
n
xl
f (t )
u f (t ) (Ys ) x x l
ux
k
x l
ux
二齐
x l
f (t ) Ys
若为自由振动 f (t ) 0 例2 细杆导热问题
f (t )
xl
0
流出 流入
u f (t ) x x l u k f (t ) x x l
端点绝热 f (t ) 0
utt a2uxx 0在x0无意义
u1x ( x0 ) u2 x ( x0 )
例 均匀细杆长为 l ， x 0 固定，
（1）另一端受着沿杆方向的力 Q ，如果开始的一瞬间 t 0 突然停止力的作用，求杆纵振动的定解条件。
振动方向
t0
x0 xl
t 0 时， Q 沿杆长方向加于杆的另一 （2）处于静止状态中， 端，写出定解条件 力从 t 0 开始作用在 x l
x (t ) a
4
utt a uxx 0
2
(0 x , t 0)
半无界区间内的一维自由振动
u x0 f (t )
u t 0 ( x)
ut t 0 ( x)
非奇非 偶延拓
一非齐
(0 x )
梁昆淼教材《数学物理方法》第00章 绪论

梁昆淼教材《数学物理方法》第00章 绪论


机动1 机动1课时
第二篇 数学物理方程
（共30课时） 30课时） 课时 第七章 数学物理定解问题 课时） （5课时） 课时 分离变数（傅立叶级数） 第八章 分离变数（傅立叶级数）法 课时） （6课时） 课时 第九章 二阶常微分方程级数解法 本征值问题 课时） （4课时） 课时 第十章 球函数 课时） （5课时） 课时 第十一章 柱函数 课时） （4课时） 课时 第十二章 Green函数 解的积分公式 函数 课时） （3课时） 课时 第十三章 积分变换法 课时） （3课时） 课时
《数学物理方法》 数学物理方法》
数学物理方法课程的学习方法
一、对于复变函数部分，学习时注意以下问题： 对于复变函数部分，学习时注意以下问题： 1、注意对定理的理解与实际应用； 注意对定理的理解与实际应用； 2、注意描述的数学内容与物理内容上的对应与联系； 注意描述的数学内容与物理内容上的对应与联系； 二、对于数学物理方程部分，注意以下几点： 对于数学物理方程部分，注意以下几点： 1、注意考虑物理系统中涉及到的物理定理、定律以及偏微 注意考虑物理系统中涉及到的物理定理、 考虑物理系统中涉及到的物理定理 分方程 ； 2、注意研究将偏微分方程转化为常微分方程的方法，或能 、注意研究将偏微分方程转化为常微分方程的方法， 够利用已有的常微分方程知识进行求解的方法； 够利用已有的常微分方程知识进行求解的方法； 3、注意将解出的结果进行讨论，给予其物理意义的解释。 、注意将解出的结果进行讨论，给予其物理意义的解释。
《数学物理方法》 数学物理方法》
Methods of Mathematical Physics
（第三版） 第三版）
梁昆淼 编 刘 法 缪国庆 修订
高等教育出版社
《数学物理方法》 数学物理方法》
精选数学物理方法第四版梁昆淼期末总结讲义

精选数学物理方法第四版梁昆淼期末总结讲义

一、留数定理：——P52
设函数 f(z)在回路 l 所围区域 B上除有限个孤
立奇点b1，b2，…，bn外解析，在闭区域 B 上除b1，
b2，…，bn外连续，则f(z)沿l正向积分 l f (z)dz 之值
等于f(z)在l所围区域内各奇点的留数和的2 i倍.
n
l
f
( z )dz
2 i
Re sf
j 1
1 cos 2 2
u v 1 sin sin
2 2
22
第14页，共84页。
u 1 cos 2 2
u sin 2 2
将上面第二式对 积分， 视作参数，有
u
u
d
R(
)
sin d R()
22
2
sin
2
d
R(
)
2 cos R()
2
其中 R() 为 的任意函数。 将上式两边对 求导，
0 arg z 2 ,
辐角：Argz arg z 2k (k 0,1,2,)
共轭复数: z x iy z* x iy
第2页，共84页。
2、复数的运算: 加、减、乘、除、乘方、开方 (1)、加法和减法
z1 x1 iy1 z2 x2 iy2
z1 z2 (x1 x2 ) i( y1 y2 ) (2)、乘法和除法
2kπ n
i sin
2kπ n
i 2k
n e n
( k 0, 1, 2, , n 1 )
复数的乘、除、乘方和开方运算，采用三角式
或指数式往往比代数式来得方便。
第5页，共84页。
二、六种初等复变函数：
1. 幂函数 w z n
2 .指数函数 w e z
梁昆淼 第12章 数学物理方法

梁昆淼 第12章 数学物理方法



T
T
vu dS vudV vudV

T
T
上述两式相减得到


(u
v n

v
u )dS n


T
(uv

vu)dV
第二格林公式
表示沿边界
n
的外方向求导数
6
三 泊松方程的解用点源函数与边界条件表示——解出积分公式 1. 泊松方程的求解：
T K
T K
9
[G(r , r0 )u u(r )G(r , r0)]dV G(r, r0) f (r )dV
T K
T K
应用第二类格林
公式将左边的体 积分化为面积分


(u
v n

v
u )dS n


T
(uv

vu)dV
(G u u G)dS (G u u G)dS Gf dV (3)
u(r )乘以 G(r , r0 ) (r r0 ) u(r )G(r , r0 ) u(r ) (r r0 ) (2)
8
(1)—(2)式
G(r , r0 )u u(r )G(r , r0 ) G(r , r0 ) f (r ) u(r ) (r r0)
第十二章 格林函数法 (Method of Green Function)
Introduction
行波法
无界空间波动问题，有局限性
分离变量法 格林函数法
各种定解问题（有界）， 其解为无穷级数
直接求特解，各种定解问题， 解一个含有格林函数的有限积分
1
格林（Green）函数：又称为点源影响函数，是数学物理中的
数学物理方法讲义

数学物理方法讲义

《数学物理方法》（Methods of MathematicalPhysics）《数学物理方法》是物理类及光电子类本科专业学生必修的重要基础课，是在《高等数学》课程基础上的一门重要的应用数学类课程，为专业课程的深入学习提供所需的数学方法及工具。

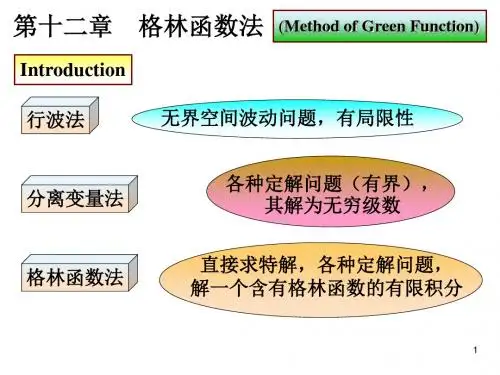
课程内容：复变函数（18学时），付氏变换（20学时），数理方程（26学时）第一篇复变函数（38学时）绪论第一章复变函数基本知识4学时第二章复变函数微分4学时第三章复变函数积分4学时第四章幂级数4学时第五章留数定理及应用简介2学时第六章付里叶级数第七章付里叶变换第八章拉普拉斯变换第二篇数学物理方程（26学时）第九章数理方程的预备知识第十章偏微分方程常见形式第十一章偏微分方程的应用绪 论含 义使用数学的物理——（数学）物理 物理学中的数学——（应用）数学Mathematical Physics方 程1=x{222111c y b x a c y b x a =+=+()t a dtdx= ⎰=)(t a xdt常微分方程0222=⎪⎪⎭⎫ ⎝⎛+x dt x d ω ()C t A x +=ωcos偏微分方程——数学物理方程0222222=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂z y x ψψψ ()z y x ,,ψψ=12=x()ψψψψψz y x U zy x m h t h i ,,22222222+⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂-=∂∂()t z y x ,,,ψψ=复 数1. 数的概念的扩充正整数（自然数） 1，2，…运算规则 ＋，－，×，÷，()2，－ 121-=-负 数 0，-1，-2，…整 数 …，-2，-1，0，1，2，…÷ 5.021= 333.031=有理数（分数） 整数、有限小数、无限循环小数414.12=无理数 无限不循环小数 实 数 有理数、无理数i =-1 虚 数y i复 数 实数、虚数、实数＋虚数 yi x y x +,,2. 负数的运算符号12-=xi x ±=i 虚数单位，作为运算符号。

梁昆淼 数学物理方法教学大纲

梁昆淼 数学物理方法教学大纲

《数学物理方法》教学大纲（供物理专业试用）前言一、课程概述1．《数学物理方法》是物理教育专业本科的一门重要的基础课，它是前导课程《高等数学》的延伸，为后继开设的《电动力学》、《量子力学》和《电子技术》等课程提供必需的数学理论知识和计算工具。

本课程在本科物理教育专业中占有重要的地位，本专业学生必须掌握它们的基本内容，否则对后继课的学习将会带来很大困难。

在物理教育专业的所有课程中，本课程是相对难学的一门课，学生应以认真的态度来学好本课程。

2．本课程的主要内容包括复变函数、傅立叶级数、数学物理方程、特殊函数等。

理论力学中常用的变分法，量子力学中用到的群论以及现代物理中用到的非线性微分方程理论等，虽然也属于《数学物理方法》的内容，但在本大纲中不作要求。

可以在后续的选修课中加以介绍。

3．本课程的内容为数学课程，注重逻辑推理和具有一定的系统性和严谨性。

但是，它与其它的数学课有所不同。

本课程内容有很深广的物理背景，实用性很强。

因此，在这门课的教学过程中，不能单纯地追求理论上的完美、严谨，而忽视其应用。

学生在学习时，不必过分地追求一些定理的严格证明、复杂公式的精确推导，更不能死记硬背，而应重视其应用技巧和处理方法。

4．本课程的内容是几代数学家与物理学家进行长期创造性研究的成果，几乎处处都闪耀创新精神的光芒。

教师应当提示学生注意在概念建立、定理提出的过程中所用的创新思维方法，在课堂教学中应尽可能地体现历史上的创造过程，提高学生的创造性思维能力。

二、目的要求1．本课程要求学生对规定的内容有一个总体了解。

掌握其中的基本概念，熟悉一些重要的理论及公式，并使所学到的知识在头脑中形成合理的结构。

2．本课程要求学生能运用学到的基本数学方法解决一类常见的物理问题，能较顺利地学习本专业后继的物理课程。

3．本课程要求学生能熟悉在数学物理方法的创立过程中用过的创新思维方法，如类比、推广、猜想及模型化等，为写出有特色的学年论文和/或毕业论文创造条件。

数学物理方法第四版梁昆淼期末总结86页PPT

数学物理方法第四版梁昆淼期末总结86页PPT

23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ，而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
数学物理方法第四版梁昆淼 期末总结
41、实际上，我们想要的不是针对犯 罪的法 律公民，就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律，法律受制于情 理。— —托·富 勒
数学物理方法第(梁昆淼)部分知识点

数学物理方法第(梁昆淼)部分知识点

数学物理方法第（梁昆淼）部分知识点
1.复变函数 .................................................................................................................................................................. 2 1.1 复数与复数运算 ........................................................................................................................................... 2 1.2 复变函数 ....................................................................................................................................................... 2 1.3 导数 ............................................................................................................................................................... 2 1.4 解析函数 ..........................................................................................................................
数学物理方法教学Chapt3

数学物理方法教学Chapt3


对于与点z0紧邻z而言，Iz-z0I很小，上式中以am最为重要，则
这意味着F1-F2不可能在α上处处为零.这样，在α上处处为零，势必 使得在β上也处处为零，这与原来的假定矛盾！解析延拓唯一得证！
第三章 幂级数展开
3.1 复数项级数 3.2 幂级数 3.3 泰勒级数展开 3.4 解析延拓 3.5 洛朗级数展开 3.6 孤立奇点分类
两个级数和的乘积.
函数项级数收敛：如果函数项级数wk，
在某个区域B(或某根曲线l)上所有的点z都收敛，则称级数在B(或l)上 收敛.
复数项级数
函数项级数一致收敛：如果函数项级数wk在B(或l)上各点z，对于任
一给定的小正数ε，必有N(z)存在，使得n>N(z)时，
式中p为任意正整数.若N跟z无关，则称级数在B(或l)上一致收敛.
解析延拓就是解析函数定义域的扩大!
B F(z) b f(z)
解析延拓
解析延拓的方法
1. 利用泰勒级数展开：选取区域b的任一内点z0， 在z0的邻域上将解析函数f(z)展开为泰勒级数.如果泰勒 级数的收敛圆有一部分超出b之外，解析函数f(z)的定义 域就扩大一步;
2. 利用一些特殊方法.
解析延拓的唯一性证明
一给定的小正数ε，必有N存在，使得n>N时，
式中p为任意正整数.
绝对收敛：若复数项无穷级数wk各项的模组成的级数
收敛，则级数wk绝对收敛.
复数项级数
绝对收敛级数性质：
1.绝对收敛级数必是收敛的； 2.绝对收敛级数各项先后顺序可以任意改变，其和不变；
3.两个绝对收敛级数各项相乘得到的级数也是绝对收敛的，其和等于
数学物理方法梁昆淼编刘法缪国庆修订梁昆淼编刘法缪国庆修订讲演者徐卫青xuwq412mailustceducn数理系物理教研室第三章幂级数展开第三章幂级数展开31复数项级数31复数项级数32幂级数32幂级数33泰勒级数展开34解析延拓35洛朗级数展开36孤立奇点分类33泰勒级数展开34解析延拓35洛朗级数展开36孤立奇点分类第三章幂级数展开第三章幂级数展开31复数项级数31复数项级数32幂级数32幂级数33泰勒级数展开34解析延拓35洛朗级数展开36孤立奇点分类33泰勒级数展开34解析延拓35洛朗级数展开36孤立奇点分类复数项级数表达式设有复数项的无穷级数它的每一项都可分为实部和虚部复数项级数它的每项都可分为实部和虚部它的每项都可分为实部和虚部那么wk的前n1项的和可以写为从而复数项无穷级数wk的收敛性问题归结为两个实数项级数的收敛性问题
数学物理方法期末总结

数学物理方法期末总结

数学物理方法期末总结目录一、基本概念与理论 (3)1. 数学物理方法概述 (4)1.1 定义与重要性 (5)1.2 历史发展 (6)2. 微积分的应用 (8)2.1 微分在物理学中的应用 (9)2.2 积分在物理学中的应用 (9)3. 线性代数 (10)3.1 向量与矩阵 (12)3.2 线性方程组 (13)3.3 特征值与特征向量 (13)4. 微分方程 (15)4.1 常微分方程 (16)4.2 偏微分方程 (17)二、数值方法与计算 (18)1. 数值分析基础 (19)1.1 误差分析 (21)1.2 置信区间与假设检验 (22)2. 求解方法 (22)2.1 直接法 (23)2.2 迭代法 (25)2.3 分裂法 (25)3. 计算机模拟 (27)3.1 数值实验步骤 (28)3.2 实验数据分析 (29)三、专题研究 (30)1. 波动理论 (31)1.1 波的传播 (32)1.2 驻波与干涉 (34)2. 量子力学基础 (35)2.1 波粒二象性 (36)2.2 薛定谔方程 (37)3. 统计物理 (38)3.1 随机过程 (40)3.2 熵与热力学第二定律 (40)四、课程总结与展望 (41)1. 重点回顾 (42)1.1 核心知识点总结 (43)1.2 学习难点解析 (44)2. 未来发展趋势 (45)2.1 数学物理方法的进步方向 (46)2.2 在现代物理学的应用前景 (47)3. 个人学习体会 (48)3.1 学习过程中的收获 (49)3.2 对未来学习的展望 (51)一、基本概念与理论数学物理方法是将数学工具应用于物理学问题的过程，它包括了数学分析、微分方程、复变函数、概率论等数学分支。

数学物理方法的基本目标是建立物理现象与数学模型之间的联系，通过求解数学模型来揭示物理现象的本质规律。

微分方程是描述自然界中运动变化的数学工具，它将偏微分方程和常微分方程两种形式结合在一起，可以用于求解各种类型的物理问题。

数学物理方法

物理学院本科生课程教案单位：物理学院学年度：2017——2018课程名称：数学物理方法课程类型：B使用教材名称：数学物理方法作（译）者：梁昆淼出版社/年度：高等教育出版社/第四版适用专业：物理学、光信息科学与技术、材料物理、应用物理学授课教师：缪炎刚教授考试方式（比重）：平时作业20%，期末考试80%物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

每次三课时的可按三课时为一个教案单元。

物理学院本科生课程教案注：一般的每两个课时为一个教案单元。

数学物理方法讲义

《数学物理方法》（Methods of MathematicalPhysics）《数学物理方法》是物理类及光电子类本科专业学生必修的重要基础课，是在《高等数学》课程基础上的一门重要的应用数学类课程，为专业课程的深入学习提供所需的数学方法及工具。

课程内容：复变函数（18学时），付氏变换（20学时），数理方程（26学时）第一篇复变函数（38学时）绪论第一章复变函数基本知识4学时第二章复变函数微分4学时第三章复变函数积分4学时第四章幂级数4学时第五章留数定理及应用简介2学时第六章付里叶级数第七章付里叶变换第八章拉普拉斯变换第二篇数学物理方程（26学时）第九章数理方程的预备知识第十章偏微分方程常见形式第十一章偏微分方程的应用绪 论含 义使用数学的物理——（数学）物理 物理学中的数学——（应用）数学Mathematical Physics方 程1=x{222111c y b x a c y b x a =+=+()t a dtdx= ⎰=)(t a xdt常微分方程0222=⎪⎪⎭⎫ ⎝⎛+x dt x d ω ()C t A x +=ωcos偏微分方程——数学物理方程0222222=⎪⎪⎭⎫ ⎝⎛∂∂+∂∂+∂∂z y x ψψψ ()z y x ,,ψψ=12=x()ψψψψψz y x U zy x m h t h i ,,22222222+⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂-=∂∂()t z y x ,,,ψψ=复 数1. 数的概念的扩充正整数（自然数） 1，2，…运算规则 ＋，－，×，÷，()2，－ 121-=-负 数 0，-1，-2，…整 数 …，-2，-1，0，1，2，…÷ 5.021= 333.031=有理数（分数） 整数、有限小数、无限循环小数414.12=无理数 无限不循环小数 实 数 有理数、无理数i =-1 虚 数y i复 数 实数、虚数、实数＋虚数 yi x y x +,,2. 负数的运算符号12-=xi x ±=i 虚数单位，作为运算符号。

数学物理方法第一章


1.1 复数与复数运算
（一）复数的基本概念
复数定义：复数——形如 z=x+iy 的数 （x,y 为实数，i2 =−1，i：虚数单位，一种记号约定）
将有争议的虚数合法化： 一维实数 二维实数
复数的本质：有序实数对 (大x家, 好y)
11
复数 ：i2 = −1，为什么？
简单概念的引入可 解决世界性的难题 高斯：正十七边形作图
定义了虚数单位 i＝(0, 1)
i 2＝－1
复数 z 可记为 zxiy xRe z
特殊的复数：0
y I mz
(x, y) +(0, 0) ＝ (x, y) 大家(好x, y) (0, 0) ＝ (0, 0)
13
复数的共轭： z* x iy 与 z x iy 互为共轭 (xiy)(xiy)x2y2
f (x)
n0
f (n)(0) xn n!
例
f
(x)
e1/
x2
0
（满足泰勒展开条件）
x 0 在x0各阶导数均存在, x 0 在x=0各阶导数均存在,其值为0
f(x)
f(n)(0)xn 0
n0 n!
大家好
f (x)
4
复变函数论（theory of complex functions）： 研究自变量是复数的函数的基本理论及应用的数学分支，
生了一些信心。在18世纪,尽管一些数学家已较为广泛地使用复
数,但无论欧拉还是别的数学家大对家这好 些数都还不甚清楚。
8
Euler 认为复数仅在想象中存在， 1777年，Euler采用 i 代表 1
4 复数真正被接受主要归功于德国数学家高斯 (C.F.Gauss,1777-1855), 1799年，他把复数的 思想融入到对代数学基本定理的证明中。

梁昆淼 第12章 数学物理方法

界空间的电势为：
1
G0 4 | r r0 |
所以，可以给出无界空间格林函数
G0 (r , r0 )
4
|
1 r
r0
|
在二维极坐标系下，可以给出
下面具体推导一下:
G0 (r , r0 )
1
2
ln
|
r
1 r0
|
23
第二十三页，共47页。
三维球对称
对于三维球对称情形，先选取 r0 0 即点源位于坐标原点处
对于拉普拉斯方程 f (r0 ) 0
第一边值问题的解为
u(r )
(r0
)
G(r , n0
r0
)
dS0
(12.1.21)
第三边值问题的解为
u(r ) 1
G(r , r0 )(r0 )dS0
(12.1.22)
21
第二十一页，共47页。
§12.2 用电像法求格林函数
一 无界区域的格林函数
1 一般边值问题的格林函数G的处理：
两者之一。因此，还不能利用上式解决三类边值问题。
怎样解决？让Green函数受边界条件的影响
12
第十二页，共47页。
四 泊松方程解的简化：
——具有实际意义的解
令格林函数满足一定的边界条件
(1) G(r , r0 )满足第一类齐次边界条件：
G 0
u(r ) f (r )
u
|
(r
)
相应的格林函数 G(r , r0 )是下列问题的解：
G(r , r0 )(r0 )dS0
(12.1.20)
20
第二十页，共47页。
对于泊松方程
u(r )
T

数学物理方法第四版梁昆淼期末总结共86页PPT


▪
26、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情，化为上进的力量，才是成功的保证。——罗曼·罗兰
1、不要轻言放弃，否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人，常是愿意 去做，并愿意去冒险的人。“稳妥”之船，从未能从岸边走远。-戴尔．卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡，喝起来是苦涩的，回味起来却有 久久不会退去的余香。
数学物理方法第四版梁昆淼期末总结 4、守业的最好办法就是不断的发展。 5、当爱不能完美，我宁愿选择无悔，不管来生多么美丽，我不愿失 去今生对你的记忆，我不求天长地久的美景，我只要生生世世的轮 回里有你。
▪
28、知之者不如好之者，好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
▪
30、意志是一个强壮的盲人，倚靠在明眼的跛子肩上。——叔本华
ቤተ መጻሕፍቲ ባይዱ
谢谢！
86
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

)
2 cos R()
2
其中 R( ) 为 的任意函数。 将上式两边对 求导，
u 1 cos R() 2 2
1 cos 2 2
u 1 cos R() 2 2
1 cos 2 2
R() 0 R() C
u 2 cos C
2
f (z)
2
cos
C
i
2 sin
2
2
2 (cos i sin ) C
2
2
1
2 (cos i sin )2 C
1
2[(cos i sin)]2 C
2z C
第二章 复变函数积分
一、复变函数积分的性质： ——P23
二、计算复变函数回路积分
1、单通区域柯西定理：P24 2、复通区域柯西定理：P25
x y
y x
v
v x
dx
(
y)
(2
y
x)dx
(
y)
2பைடு நூலகம்
xy
1 2
x
2
(
y)
v
v x
dx
(
y)
(2
y
x)dx
(
y)
2
xy
1 2
x2
(
y)
v 2x ( y)
y
( y) y
( y) 1 y2 C
2 v 2xy 1 ( y2 x2 ) C
2
f (z) u iv x2 y2 xy i[2xy 1 ( y2 x2 )] iC 2
22 2 2
u
1
v
1
u
v
u 1 v 1
cos
22
1 cos 2 2
u v 1 sin sin
2 2
22
u
1
cos
2 2
u sin 2 2
将上面第二式对 积分， 视作参数，有
u
u
d
R(
)
sin d R()
22
2
sin
2
d
R(
n
z
1
n
cos
2kπ n
i sin
2kπ n
i
2k
n e n
( k 0, 1, 2, , n 1 )
复数的乘、除、乘方和开方运算，采用三角式 或指数式往往比代数式来得方便。
二、六种初等复变函数：
1. 幂函数 w z n
2 .指数函数 w e z
周期为2i，
3. 三角函数
cos z eiz eiz , 2
v y v
y x
2、解析函数性质
：
u
极坐标系：
1
v
1
u
v
(1)、若 f (z) u(x, y) iv(x, y) 是解析函数，则u v 0 。
(2)、若函数 f (z) u iv 在区域 B上解析，则 u和v 必为B上的相互共轭调和函数。
3、构建解析函数：
给出一个二元调和函数作为解析函数的实部 或虚部，通过C—R条件求出该解析函数的虚部或 实部，从而写出这个解析函数。
(x iy)2 i 1 (x iy)2 iC 2
z2 i 1 z2 iC 2
v 2y x, x v 2x y y
f (0) 0 C 0
f (z) z2 i 1 z2 2
例4：已知解析函数 f (z)的虚部 v(x, y) x x 2 y 2 ，
求实部 u(x, y)和这个解析函数 f (z) 。
（优选）数学物理方法第四版 梁昆淼期末总结
第一章 复变函数
一、复数
1、复数的定义
z x iy ——代数式
z (cos i sin) ——三角式
z ei ——指数式
*复数三种表示式之间的转换
实部：x Re z 虚部：y Im z
模： z x2 y2
主辐角：arg
z
arctg(
y x
例1：已知 z 2 3i ，则 zz 13
。
zz 2 x2 y2 13
例2：复数ez 的模为 ex ，辐角为 y 2k , k 0, 1, 2,
.
ez exiy exeiy
三、解析函数 f (z) u(x, y) iv(x, y) 1、柯西-黎曼方程
u
直角坐标系：
x u
2 ) i sin(1
2 )]
e 1 i(12 ) 2
两复数相除就是把模数相除, 辐角相减。
(3) 复数的乘方和开方
z n (ei )n
n ein
( n为正整数的情况)
或 n (cos n i sin n)
棣莫弗公式： (cos i sin)n cos n i sin n
提示：当给定的 u 或 v 中含有因子x2+y2，这种情 况下采用极坐标处理比较方便，即令 2 x 2 y 2 。
解： v cos 2
cos
(1 cos)
2sin 2
2
2 sin
2
v 2 sin
2
v
2
sin
1
1 2
1 sin
22
2 2
v 2 cos 1 cos
① 算偏导
③ 求积分
② u或v 的全微分
④ 表成 f (z)
例 3：已知解析函数 f (z) 的实部u(x, y) x2 y2 xy, f (0) 0 ， 求虚部和这个解析函数。
解：
u 2x y, u x 2 y
x
y
根据C-R条件，
v u 2 y x, v u 2x y
周期为2
eiz eiz
sin z
,
2i
4、双曲函数
shz e z ez 2
5、根式函数
chz e z ez 2
z ei
2k i
w n e n
k 0,1,2,(n 1)
周期为2i
6、对数函数
w ln z ln z iArgz
Argz arg z 2k k 0,1,
x22 y22
(2)、乘法和除法
z1 1(cos1 i sin1) 1ei1 z2 2 (cos2 i sin2 ) 2ei2
z1z2 12[cos(1 2 ) i sin(1 2 )]
ei(12 ) 12
• 两复数相乘就是把模数相乘, 辐角相加;
z1 z2
1 2
[c
os(1
(2)、乘法和除法
z1z2 (x1 iy1 )( x2 iy2 )
(x1x2 y1 y2 ) i(x1 y2 x2 y1 )
z1 z2
z1
z
* 2
z2
z
* 2
(x1 iy1 )( x2 iy2 )
x
2 2
y
2 2
x1x2 y1 y2 i x2 y1 x1 y2
x22
y
2 2
)
0 arg z 2 ,
辐角：Argz arg z 2k (k 0,1,2,)
共轭复数: z x iy z* x iy
2、复数的运算: 加、减、乘、除、乘方、开方 (1)、加法和减法
z1 x1 iy1 z2 x2 iy2
z1 z2 (x1 x2 ) i( y1 y2 )