2019-2020学年人教版数学七年级上册 4.3.3 余角和补角 测试题及答案

4.3 角4.3.3 余角和补角基础稳固1.（知识点 1）以下图形中互为补角的两个角是（）A.①和②B.①和③C.①和④D.②和④2.（题型二）假如从甲船看乙船，乙船在甲船的北偏东30°方向，那么从乙船看甲船，甲船在乙船的（）A.南偏西30°方向B.南偏西60°方向C.南偏东30°方向D.南偏东60°方向3.（题型三）以下选项是将一副三角尺按不一样地点摆放的，∠α与∠β互余的是（）4.（题型二）一艘海上搜救船借助雷达探测仪找寻到事故船的地点，雷达表示图如图 4-3.3-1，搜救船位于图中圆心 O 处，事故船位于距点O 40 海里的 A 处，雷达操作员要用方向角把事故船相关于搜救船的地点报告给船长，以便调整航向，以下四种表述方式正确的选项是（）图 4-3.3-1A.事故船在搜救船的北偏东60°方向B.事故船在搜救船的北偏东30°方向C.事故船在搜救船的北偏西60°方向D.事故船在搜救船的南偏东30°方向5.（题型三）如图 4-3.3-2，∠AOC=∠BOD=90°，四位同学察看图形后分别说了自己的看法 .甲：∠ AOB=∠COD；乙：∠ BOC+∠AOD=180°；丙：∠ AOB+∠COD=90°；丁：图中小于平角的角有 6 个.此中看法正确的选项是（）图 4-3.3-2A. 甲、乙、丙B.甲、丙、丁C.乙、丙、丁D.甲、乙、丁6.（题型一）已知∠ A=35°10′48″，则∠ A 的补角是 _____.7.（题型一）如图 4-3.3-3， A， B，C 三点在同一条直线上，若∠ECD=90°，∠ 1=23°30′，则∠ 2 的度数是 ______°.图 4-3.3-38.（题型一）若∠ 1 和∠ 2 互为余角，则∠ 1 和∠ 2 的补角之和是 ______.9.（题型一）一个角的补角加上 10°后，等于这个角的余角的 3 倍，求这个角以及它的余角和补角的度数 .能力提高10.（题型二）如图 4-3.3-4，货轮 O 在航行过程中，发现灯塔 A 在它南偏东 60°的方向上，同时，在它北偏东 30°、西北（即北偏西 45°）方向上又分别发现了客轮 B 和海岛 C.（1）模仿表示灯塔方向的方法，分别画出表示客轮 B 和海岛 C 方向的射线 OB，OC（不写作法）；（2）若图中有一艘渔船 D，且∠ AOD 的补角是它的余角的 3 倍，画出表示渔船 D 方向的射线 OD，则渔船 D 在货轮 O 的 ______方向上 .（写出方向角）图 4-3.3-411.（题型三）如图 4-3.3-5，O 为直线 AB 上一点，过点 O 作射线OC 使∠ BOC=120°，将有一 30°角的直角三角尺的直角极点放在点处，一边 OM 在射线 OB 上，另一边ON 在直线 AB 的下方 .（中∠OMN=30°，∠ NOM=90°）（1）（2）（3）图 4-3.3-5（1）将图 4-3.3-5（1）中的三角尺绕点 O 逆时针旋转至图 4-3.3-5（2），使 OM 在∠ BOC 的内部，且恰巧均分∠ BOC.问：直线 ON能否均分∠ AOC？请说明原因 .（2）将图 4-3.3-5（1）中的三角尺绕点 O 按每秒 6°的速度沿逆时针方向旋转一周，在旋转的过程中，第t 秒时，直线 ON 恰巧均分∠AOC，求 t.（3）将图 4-3.3-5（1）中的三角尺绕点 O 顺时针旋转至图 4-3.3-5（3），使 ON 在∠ AOC 的内部 .请研究：∠ AOM 与∠ NOC 之间的数目关系，并说明原因 .答案基础稳固1.C 分析：由于①和④两个角的和为 180°，因此①和④互为补角 .应选 C.2.A 分析：由图 D4-3.3-1 可知，∠1=30°.由于从甲船看乙船，乙船在甲船的北偏东30°方向，因此从乙船看甲船，甲船在乙船的南偏西30°方向 .应选 A.图 D4-3.3-123.A 分析： A.∠α与∠ β互余，故此选项切合题意； B.∠α=∠β，故此选项不切合题意； C.∠α=∠β，故此选项不切合题意； D.∠α与∠β互补，故此选项不切合题意 .应选 A.4.B 分析：由题图可知，事故船在搜救船的北偏东30°方向 .应选B.5. D分析：由于∠AOC=∠BOD=90°，因此∠AOC-∠BOC=∠BOD-∠BOC，即∠AOB= ∠COD，因此甲同学的看法正确；由于∠BOC+∠AOD= ∠ AOC+ ∠ COD+ ∠ BOC= ∠ AOC+ ∠ BOD=90 ° +90 °=180°，因此乙同学的看法正确；由于∠AOB+ ∠BOC= ∠AOC=90°，∠B OC 和∠ COD 不必定相等，因此丙同学的看法不正确；由于图中小于平角的角有∠ AOB，∠AOC，∠AOD，∠BOC，∠BOD，∠COD，共 6 个，因此丁同学的看法正确.应选 D.6.144°49′12″分析：由于∠ A=35°10′48″，因此∠ A 的补角为180°-35°10′48″=144°49′12″.7.66.5 分析：由于∠ ECD=90°，∠ACB=180°，因此∠ 2+∠1=90°. 由于∠ 1=23°30′，因此∠ 2=90°-23°30′=66°30′=66.5°.8. 270°分析：设∠ 2=x，则∠ 1=90°-x.由题意，得180°-（90°-x）+180°-x=270°.9.解：设这个角为 x° .由题意，得 180-x+10=3（90-x），解得 x=40.即这个角是 40°，它的余角是50°，补角是 140°.能力提高10. 解：（1）如图 D4-3.3-2.图 D4-3.3-2图 D4-3.3-3（2）由∠ AOD 的补角是它的余角的 3 倍，得180°-∠AOD=3（90°-∠AOD），解得∠ AOD=45°.如图 D4-3.3-3，故渔船 D 在货轮 O 南偏东 15°或北偏东 75°方向上 .11.解：（1）直线ON 均分∠AOC.原因以下：设 ON 的反向延伸线为 OD.由于 OM 均分∠ BOC，∠ BOC=120°，因此∠ MOC=∠MOB= 1∠BOC=60°. 2又由于∠ MON=90°，因此∠ BON=30°，因此∠ CON=120°+30°=150°，因此∠ COD=30°.又由于∠ AOC=180° - ∠ BOC=60 °，因此∠ DOA= ∠ AOC- ∠COD=30°，因此∠ COD=∠AOD，因此 OD 均分∠ AOC，即直线 ON 均分∠ AOC.（2）由（1）可知，当ON 绕点O 沿逆时针方向旋转60°时，直线ON 均分∠ AOC，当 ON 绕点 O 沿逆时针方向旋转 240°［即（ 1）中OD 的地点］时，直线 ON 均分∠ AOC.由题意，得 6t=60 或 6t=240，解得 t=10 或 t=40.（3）由于∠ MON=90°，∠ AOC=60°，因此∠ AOM=90°-∠AON，∠ NOC=60°-∠ AON，因此∠ AOM-∠NOC=（90°-∠AON）-（60°-∠AON）=30°.。

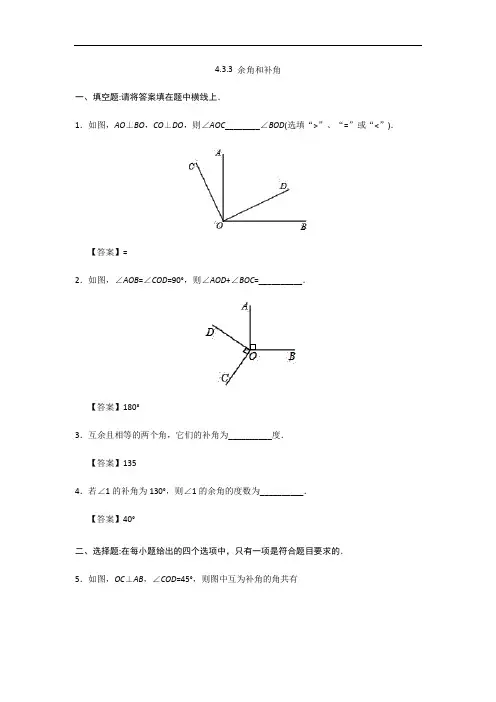
4.3.3 余角和补角一、填空题:请将答案填在题中横线上．1．如图，AO⊥BO，CO⊥DO，则∠AOC________∠BOD(选填“>”、“=”或“<”)．【答案】=2．如图，∠AOB=∠COD=90°，则∠AOD+∠BOC=__________．【答案】180°3．互余且相等的两个角，它们的补角为__________度．【答案】1354．若∠1的补角为130°，则∠1的余角的度数为__________．【答案】40°二、选择题:在每小题给出的四个选项中，只有一项是符合题目要求的．5．如图，OC⊥AB，∠COD=45°，则图中互为补角的角共有A．1对B．2对C．3对D．4对【答案】C6．下列说法正确的是A．锐角的补角一定是钝角B．锐角和钝角的和一定是平角C．互补的两个角可以都是锐角D．互余的两个角可以都是钝角【答案】A7．如果∠1+∠2=90°，∠2+∠3=90°，那么∠1与∠3的关系是A．∠1+∠3=90°B．∠1+∠3=180°C．∠1=∠3 D．不能确定【答案】C8．已知∠1+∠2=90°，∠3+∠4=180°，下列说法正确的是A．∠1是余角B．∠3是补角C．∠1是∠2的余角D．∠3和∠4都是补角【答案】C三、解答题:解答应写出文字说明、证明过程或演算步骤．10．若一个角的补角与它余角的2倍的差是平角的14．求这个角的度数．【解析】设这个角的度数为x，根据题意得(180°–x)–2(90°–x)=14×180°，解得x=45°，即这个角为45°．11．如图所示，AOB是一条直线，OC是一条射线，∠AOC=2∠AOF，∠BOC=2∠BOE．(1)∠1与∠2互余吗？(2)指出图中所有互余和互补的角．【解析】(1)互余(2)互余的角:∠1与∠2，∠1与∠BOE，∠2与∠AOF，∠AOF与∠BOE互补的角:∠AOF与∠BOF，∠1与∠BOF，∠AOC与∠BOC，∠BOE与∠AOE，∠2与∠AOE12．如图，已知∠AOC=∠BOD=90°，∠DOC=55°．求∠AOD和∠BOC的度数．【解析】∠AOD=35O ∠BOC=35O。

人教新版七年级上学期《4.3.3 余角和补角》同步练习卷一．选择题（共15小题）1．一个角的余角是这个角的补角的，则这个角的度数是（）A．30°B．45°C．60°D．70°2．如图，在△ABC中，∠C=90°，点D，E分别在边AC，AB上．若∠B=∠ADE，则下列结论正确的是（）A．∠A和∠B互为补角B．∠B和∠ADE互为补角C．∠A和∠ADE互为余角D．∠AED和∠DEB互为余角3．如果∠α和∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③（∠α+∠β）；④（∠α﹣∠β）．正确的有（）A．4个B．3个C．2个D．1个4．若∠A=34°，则∠A的补角为（）A．56°B．146°C．156°D．166°5．下列各图中，∠1与∠2互为余角的是（）A．B．C．D．6．如图，将一副三角尺按不同的位置摆放，下列方式中∠α与∠β互余的是（）A．图①B．图②C．图③D．图④7．如图所示，∠β＞∠α，且∠α与（∠β﹣∠α）关系为（）A．互补B．互余C．和为45°D．和为22.5°8．如果∠1与∠2互补，∠2与∠3互余，则∠1与∠3的关系是（）A．∠1=∠3B．∠1=180°﹣∠3C．∠1=90°+∠3D．以上都不对9．如图，O为直线AB上一点，∠AOC=α，∠BOC=β，则β的余角可表示为（）A．（α+β）B．αC．（α﹣β）D．β10．设一个锐角与这个角的补角的差的绝对值为α，则（）A．0°＜α＜90°B．0°＜α≤90°C．0°＜α＜90°或90°＜α＜180°D．0°＜α＜180°11．已知∠α与∠β互为补角，∠α=120°30′，则∠β的余角是（）A．29°30′B．30°30′C．31°30′D．59°30′12．若∠A，∠B互为补角，且∠A＜∠B，则∠A的余角是（）A．（∠A+∠B）B．∠B C．（∠B﹣∠A）D．∠A 13．如图，△ABC是直角三角形，AB⊥CD，图中与∠CAB互余的角有（）A．1个B．2个C．3个D．4个14．一副三角板按如图所示的方式摆放，且∠1比∠2大50°，则∠2的度数为（）A．20°B．50°C．70°D．30°15．一个锐角的余角加上90°，就等于（）A．这个锐角的两倍数B．这个锐角的余角C．这个锐角的补角D．这个锐角加上90°二．填空题（共4小题）16．一个角的余角比这个角的补角的一半小40°，则这个角为度．17．一个角的余角是54°38′，则这个角的补角是．18．若∠α补角是∠α余角的3倍，则∠α=．19．已知∠A与∠B互余，若∠A=20°15′，则∠B的度数为．三．解答题（共8小题）20．如图，OD平分∠BOC，OE平分∠AOC．若∠BOC=70°，∠AOC=50°．（1）求出∠AOB及其补角的度数；（2）请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由．21．一个角的余角比它的补角的大15°，求这个角的度数．22．计算：（1）62.56°的余角等于°′″；（2）140°11′24″的补角等于°．23．一个角的补角与这个角的余角的和是平角的还多1°，求这个角．24．如图，已知∠AOB=155°，∠AOC=∠BOD=90°．（1）写出与∠COD互余的角；（2）求∠COD的度数；（3）图中是否有互补的角？若有，请写出来．25．如图，将一副直角三角尺的直角顶点C叠放在一起．（1）如图1，若CE恰好是∠ACD的角平分线，则CD是∠ECB的；（2）如图2，若∠ECD=α，CD在∠BCE的内部，请你猜想∠ACE与∠DCB是否相等？并简述理由；（3）在（2）的条件下，请问∠ECD与∠ACB的和是多少？并简述理由．26．如图，已知直线AB与CD相交于点O，OE、OF分别是∠BOD、∠AOD的平分线．（1）∠DOE的补角是；（2）若∠BOD=62°，求∠AOE和∠DOF的度数；（3）判断射线OE与OF之间有怎样的位置关系？并说明理由．27．把一副三角板的直角顶点O重叠在一起．（1）如图（1），当OB平分∠COD时，则∠AOD与∠BOC的和是多少度？（2）如图（2），当OB不平分∠COD时，则∠AOD和∠BOC的和是多少度？（3）当∠BOC的余角的4倍等于∠AOD，则∠BOC多少度？人教新版七年级上学期《4.3.3 余角和补角》同步练习卷参考答案与试题解析一．选择题（共15小题）1．一个角的余角是这个角的补角的，则这个角的度数是（）A．30°B．45°C．60°D．70°【分析】设这个角的度数为x，则它的余角为90°﹣x，补角为180°﹣x，再根据题意列出方程，求出x的值即可．【解答】解：设这个角的度数为x，则它的余角为90°﹣x，补角为180°﹣x，依题意得：90°﹣x=（180°﹣x），解得x=45°．故选：B．【点评】本题考查的是余角及补角的定义，能根据题意列出关于x的方程是解答此题的关键．2．如图，在△ABC中，∠C=90°，点D，E分别在边AC，AB上．若∠B=∠ADE，则下列结论正确的是（）A．∠A和∠B互为补角B．∠B和∠ADE互为补角C．∠A和∠ADE互为余角D．∠AED和∠DEB互为余角【分析】根据余角的定义，即可解答．【解答】解：∵∠C=90°，∴∠A+∠B=90°，∵∠B=∠ADE，∴∠A+∠ADE=90°，∴∠A和∠ADE互为余角．故选：C．【点评】本题考查了余角和补角，解决本题的关键是熟记余角的定义．3．如果∠α和∠β互补，且∠α＞∠β，则下列表示∠β的余角的式子中：①90°﹣∠β；②∠α﹣90°；③（∠α+∠β）；④（∠α﹣∠β）．正确的有（）A．4个B．3个C．2个D．1个【分析】根据角的性质，互补两角之和为180°，互余两角之和为90°，可将，①②③④中的式子化为含有∠α+∠β的式子，再将∠α+∠β=180°代入即可解出此题．【解答】解：∵∠α和∠β互补，∴∠α+∠β=180°．因为90°﹣∠β+∠β=90°，所以①正确；又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°，②也正确；（∠α+∠β）+∠β=×180°+∠β=90°+∠β≠90°，所以③错误；（∠α﹣∠β）+∠β=（∠α+∠β）=×180°=90°，所以④正确．综上可知，①②④均正确．故选：B．【点评】本题考查了角之间互补与互余的关系，互补两角之和为180°，互余两角之和为90°．4．若∠A=34°，则∠A的补角为（）A．56°B．146°C．156°D．166°【分析】根据互补的两角之和为180°，可得出答案．【解答】解：∵∠A=34°，∴∠A的补角=180°﹣34°=146°．故选：B．【点评】本题考查了余角和补角的知识，解答本题的关键是掌握互补的两角之和为180°．5．下列各图中，∠1与∠2互为余角的是（）A．B．C．D．【分析】如果两个角的和等于90°（直角），就说这两个角互为余角．依此定义结合图形即可求解．【解答】解：∵三角形的内角和为180°，∴选项B中，∠1+∠2=90°，即∠1与∠2互为余角，故选：B．【点评】本题考查了余角的定义，掌握定义并且准确识图是解题的关键．6．如图，将一副三角尺按不同的位置摆放，下列方式中∠α与∠β互余的是（）A．图①B．图②C．图③D．图④【分析】根据平角的定义，同角的余角相等，等角的补角相等和邻补角的定义对各小题分析判断即可得解．【解答】解：图①，∠α+∠β=180°﹣90°，互余；图②，根据同角的余角相等，∠α=∠β；图③，根据等角的补角相等∠α=∠β；图④，∠α+∠β=180°，互补．故选：A．【点评】本题考查了余角和补角，是基础题，熟记概念与性质是解题的关键．7．如图所示，∠β＞∠α，且∠α与（∠β﹣∠α）关系为（）A．互补B．互余C．和为45°D．和为22.5°【分析】首先根据图形可得∠α+∠β=180°，再表示出∠α，然后再把等式变形即可．【解答】解：观察图形可知，∠α+∠β=180°，则∠α=180°﹣∠β，∵180°﹣∠β+（∠β﹣∠α）=180°﹣（∠β+∠α）=180°﹣90°=90°．故∠α与（∠β﹣∠α）关系为互余．故选：B．【点评】此题主要考查了余角和补角，关键是掌握余角和补角的定义．8．如果∠1与∠2互补，∠2与∠3互余，则∠1与∠3的关系是（）A．∠1=∠3B．∠1=180°﹣∠3C．∠1=90°+∠3D．以上都不对【分析】根据∠1与∠2互补，∠2与∠3互余，先把∠1、∠3都用∠2来表示，再进行运算．【解答】解：∵∠1+∠2=180°∴∠1=180°﹣∠2又∵∠2+∠3=90°∴∠3=90°﹣∠2∴∠1﹣∠3=90°，即∠1=90°+∠3．故选：C．【点评】此题主要记住互为余角的两个角的和为90°，互为补角的两个角的和为180度．9．如图，O为直线AB上一点，∠AOC=α，∠BOC=β，则β的余角可表示为（）A．（α+β）B．αC．（α﹣β）D．β【分析】根据补角的性质，余角的性质，可得答案．【解答】解：由邻补角的定义，得∠α+∠β=180°，两边都除以2，得（α+β）=90°，β的余角是（α+β）﹣β=（α﹣β），故选：C．【点评】本题考查了余角和补角，利用余角、补角的定义是解题关键．10．设一个锐角与这个角的补角的差的绝对值为α，则（）A．0°＜α＜90°B．0°＜α≤90°C．0°＜α＜90°或90°＜α＜180°D．0°＜α＜180°【分析】根据补角的定义来求．【解答】解：设这个角的为x且0＜x＜90°，根据题意可知180°﹣x﹣x=α，∴α=180°﹣2x，∴180°﹣2×90°＜α＜180°﹣2×0°，0°＜α＜180°．故选：D．【点评】主要考查了余角和补角的概念．互为余角的两角的和为90°，互为补角的两角之和为180°．解此题的关键是能准确的从题意中找出这两个角之间的数量关系，从而判断出两角之间的关系．11．已知∠α与∠β互为补角，∠α=120°30′，则∠β的余角是（）A．29°30′B．30°30′C．31°30′D．59°30′【分析】互补即两角的和为180°，互余的两个角的和等于90°．【解答】解：∵∠α与∠β互为补角，∠α=120°30′，∴∠β=180°﹣120°30′=59°30′，∴∠β的余角=90°﹣59°30′=30°30′．故选：B．【点评】根据余角和补角的关系进行计算．12．若∠A，∠B互为补角，且∠A＜∠B，则∠A的余角是（）A．（∠A+∠B）B．∠B C．（∠B﹣∠A）D．∠A【分析】根据互为补角的和得到∠A，∠B的关系式，再根据互为余角的和等于90°表示出∠A的余角，然后把常数消掉整理即可得解．【解答】解：根据题意得，∠A+∠B=180°，∴∠A的余角为：90°﹣∠A=﹣∠A，=（∠A+∠B）﹣∠A，=（∠B﹣∠A）．故选：C．【点评】本题主要考查了互为补角的和等于180°，互为余角的和等于90°的性质，利用消掉常数整理是解题的关键．13．如图，△ABC是直角三角形，AB⊥CD，图中与∠CAB互余的角有（）A．1个B．2个C．3个D．4个【分析】根据互余的两个角的和等于90°写出与∠A的和等于90°的角即可．【解答】解：∵CD是Rt△ABC斜边上的高，∴∠A+∠B=90°，∠A+∠ACD=90°，∴与∠A互余的角有∠B和∠ACD共2个．故选：B．【点评】本题主要考查了余角的定义，根据直角三角形的性质找出与∠A相加等于90°的角是解题的关键．14．一副三角板按如图所示的方式摆放，且∠1比∠2大50°，则∠2的度数为（）A．20°B．50°C．70°D．30°【分析】根据图形得出∠1+∠2=90°，然后根据∠1的度数比∠2的度数大50°列出方程求解即可．【解答】解：由图可知∠1+∠2=180°﹣90°=90°，所以∠2=90°﹣∠1，又因为∠1﹣∠2=∠1﹣（90°﹣∠1）=50°，解得∠1=70°．故选：A．【点评】本题考查了余角和补角，准确识图，用∠1表示出∠2，然后列出方程是解题的关键．15．一个锐角的余角加上90°，就等于（）A．这个锐角的两倍数B．这个锐角的余角C．这个锐角的补角D．这个锐角加上90°【分析】相加等于90°的两角互为余角，相加等于180度的两角互为补角，因而可以设这个锐角是x度，再用含x的代数式表示出所求的量，从而得出结果．【解答】解：设这个锐角是x度，则它的余角是（90﹣x）度．那么90﹣x+90=180﹣x．而x+（180﹣x）=180．故选：C．【点评】本题主要考查补角，余角的定义，是一个基础的题目．二．填空题（共4小题）16．一个角的余角比这个角的补角的一半小40°，则这个角为80度．【分析】设这个角为x，根据互为余角的两个角的和等于90°，互为补角的两个角的和等于180°表示出它的余角和补角，然后列出方程求解即可．【解答】解：设这个角为x，则它的余角为（90°﹣x），补角为（180°﹣x），由题意得，（180°﹣x）﹣（90°﹣x）=40°，解得x=80°．故答案为：80．【点评】本题考查了余角和补角的概念，是基础题，熟记概念并列出方程是解题的关键．17．一个角的余角是54°38′，则这个角的补角是144°38′．【分析】根据余角是两个角的和为90°，这两个角互为余角，两个角的和为180°，这两个角互为补角，可得答案．【解答】解：∵一个角的余角是54°38′∴这个角为：90°﹣54°38′=35°22′，∴这个角的补角为：180°﹣35°22′=144°38′．故答案为：144°38′．【点评】本题考查余角和补角，通过它们的定义来解答即可．18．若∠α补角是∠α余角的3倍，则∠α=45°．【分析】分别表示出∠α补角和∠α余角，然后根据题目所给的等量关系，列方程求出∠α的度数．【解答】解：∠α的补角=180°﹣α，∠α的余角=90°﹣α，则有：180°﹣α=3（90°﹣α），解得：α=45°．故答案为：45°．【点评】本题考查了余角和补角的知识，解答本题的关键是掌握互余两角之和为90°，互补两角之和为180°．19．已知∠A与∠B互余，若∠A=20°15′，则∠B的度数为69.75°．【分析】根据余角定义：若两个角的和为90°，则这两个角互余，直接解答，然后化为用度表示即可．【解答】解：∵∠A与∠B互余，∠A=20°15′，∴∠B=90°﹣20°15′=69°45′=69.75°．故答案为：69.75°．【点评】本题考查互余角的数量关系．理解互余的概念是解题的关键，根据余角的定义：若两个角的和为90°，则这两个角互余列式计算．三．解答题（共8小题）20．如图，OD平分∠BOC，OE平分∠AOC．若∠BOC=70°，∠AOC=50°．（1）求出∠AOB及其补角的度数；（2）请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由．【分析】（1）∠AOB的度数等于已知两角的和，再根据补角的定义求解；（2）根据角平分线把角分成两个相等的角，求出度数后即可判断．【解答】解：（1）∠AOB=∠BOC+∠AOC=70°+50°=120°，其补角为180°﹣∠AOB=180°﹣120°=60°；（2）∠DOC=×∠BOC=×70°=35°∠AOE=×∠AOC=×50°=25°．∠DOE与∠AOB互补，理由：∵∠DOE=∠DOC+∠COE=35°+25°=60°，∴∠DOE+∠AOB=60°+120°=180°，故∠DOE与∠AOB互补．【点评】本题主要考查角平分线的定义和补角的定义，需要熟练掌握．21．一个角的余角比它的补角的大15°，求这个角的度数．【分析】设这个角为x°，则它的余角为（90°﹣x），补角为（180°﹣x），再根据题中给出的等量关系列方程即可求解．【解答】解：设这个角的度数为x，则它的余角为（90°﹣x），补角为（180°﹣x），依题意，得：（90﹣x）﹣（180﹣x）=15，解得x=40．答：这个角是40°．【点评】本题主要考查了余角、补角的定义以及一元一次方程的应用．解题的关键是能准确地从题中找出各个量之间的数量关系，列出方程，从而计算出结果．互为余角的两角的和为90°，互为补角的两角的和为180°．22．计算：（1）62.56°的余角等于27°26′24″；（2）140°11′24″的补角等于39.81°．【分析】（1）根据余角的含义，用90°减去62.56°，求出62.56°的余角等于多少即可．（2）根据补角的含义，用180°减去140°11′24″，求出140°11′24″的补角等于多少即可．【解答】解：（1）∵90°﹣62.56°=27.44°=27° 26′24″，∴62.56°的余角等于27°26′24″．（2）∵180°﹣140°11′24″=180°﹣140.19°=39.81°，∴140°11′24″的补角等于39.81°．故答案为：27、26、24；39.81．【点评】（1）此题主要考查了余角和补角的含义和运算，要熟练掌握，解答此题的关键是要明确：①余角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．②补角：如果两个角的和等于180°（平角），就说这两个角互为补角．即其中一个角是另一个角的补角．③性质：等角的补角相等．等角的余角相等．（2）此题还考查了度分秒的换算，要熟练掌握，解答此题的关键是要明确：1度=60分，即1°=60′，1分=60秒，即1′=60″．23．一个角的补角与这个角的余角的和是平角的还多1°，求这个角．【分析】首先根据余角与补角的定义，设这个角为x，则它的余角为（90°﹣x），补角为（180°﹣x），再根据题中给出的等量关系列方程即可求解．【解答】解：设这个角为x，则它的余角为（90°﹣x），补角为（180°﹣x），则（90°﹣x+180°﹣x）﹣×180°=1，x=67°．答：这个角为67°【点评】此题综合考查余角与补角，属于基础题中较难的题，解答此类题一般先用未知数表示所求角的度数，再根据一个角的余角和补角列出代数式和方程求解．24．如图，已知∠AOB=155°，∠AOC=∠BOD=90°．（1）写出与∠COD互余的角；（2）求∠COD的度数；（3）图中是否有互补的角？若有，请写出来．【分析】根据余角和补角的概念进行计算即可．【解答】解：（1）∵∠AOC=∠BOD=90°，∴∠COD+∠AOD=90°，∠COD+∠BOC=90°，∴与∠COD互余的角是∠AOD和∠BOC；（2）∠BOC=∠AOB﹣∠AOC=65°，∴∠COD=∠BOD﹣∠BOC=25°；（3）∠COD与∠AOB、∠AOC与∠BOD互补．【点评】本题考查的是余角和补角，如果两个角的和等于90°，就说这两个角互为余角，如果两个角的和等于180°，就说这两个角互为补角．25．如图，将一副直角三角尺的直角顶点C叠放在一起．（1）如图1，若CE恰好是∠ACD的角平分线，则CD是∠ECB的角平分线；（2）如图2，若∠ECD=α，CD在∠BCE的内部，请你猜想∠ACE与∠DCB是否相等？并简述理由；（3）在（2）的条件下，请问∠ECD与∠ACB的和是多少？并简述理由．【分析】（1）是，首先根据直角三角板的特点得到∠ACD=90°，∠ECB=90°，再根据角平分线的定义计算出∠ECD和∠DCB的度数即可；（2）∠ACE与∠DCB相等；根据等角的余角相等即可得到答案；（3）根据角的和差关系进行等量代换即可．【解答】解：（1）是，∵∠ACD=90°，CE恰好是∠ACD的角平分线，∴∠ECD=45°，∵∠ECB=90°，∴∠DCB=90°﹣45°=45°，∴∠ECD=∠DCB，∴此时CD是∠ECB的角平分线；故答案为：角平分线．（2）∠ACE=∠DCB，∵∠ACD=90°，∠BCE=90°，∠ECD=α，∴∠ACE=90°﹣α，∠DCB=90°﹣α，∴∠ACE=∠DCB．（3）∠ECD+∠ACB=180°．理由如下：∠ECD+∠ACB=∠ECD+∠ACE+∠ECB=∠ACD+∠ECB=90°+90°=180°．【点评】此题主要考查了角的计算，关键是根据图形分清角之间的和差关系．26．如图，已知直线AB与CD相交于点O，OE、OF分别是∠BOD、∠AOD的平分线．（1）∠DOE的补角是∠AOE或∠COE；（2）若∠BOD=62°，求∠AOE和∠DOF的度数；（3）判断射线OE与OF之间有怎样的位置关系？并说明理由．【分析】（1）根据角平分线的定义可得∠DOE=∠BOE，再根据补角的定义结合图形找出即可；（2）根据角平分线的定义计算即可求出∠BOE，然后根据补角的和等于180°列式计算即可求出∠AOE，先求出∠AOD，再根据角平分线的定义解答；（3）计算出∠EOF的度数是90°，然后判断位置关系为垂直．【解答】解：（1）∵OE是∠BOD的平分线，∴∠DOE=∠BOE，又∵∠BOE+∠AOE=180°，∠DOE+∠COE=180°，∴∠DOE的补角是∠AOE或∠COE；（2）∵OE是∠BOD的平分线，∠BOD=62°，∴∠BOE=∠BOD=31°，∴∠AOE=180°﹣31°=149°，∵∠BOD=62°，∴∠AOD=180°﹣62°=118°，∵OF是∠AOD的平分线，∴∠DOF=×118°=59°；（3）OE与OF的位置关系是：OE⊥OF．理由如下：∵OE、OF分别是∠BOD、∠AOD的平分线，∴∠DOE=∠BOD，∠DOF=∠AOD，∵∠BOD+∠AOD=180°，∴∠EOF=∠DOE+∠DOF=（∠BOD+∠AOD）=90°，∴OE⊥OF．【点评】本题考查余角与补角，角平分线的定义，角度的计算，是基础题，熟记性质并准确识图，找出图中各角之间的关系是解题的关键．27．把一副三角板的直角顶点O重叠在一起．（1）如图（1），当OB平分∠COD时，则∠AOD与∠BOC的和是多少度？（2）如图（2），当OB不平分∠COD时，则∠AOD和∠BOC的和是多少度？（3）当∠BOC的余角的4倍等于∠AOD，则∠BOC多少度？【分析】（1）根据角平分线的性质可得∠BOC=∠BOD=45°，根据角的和差可得∠AOC=90°﹣45°=45°，再根据角的和差可得∠AOD+∠BOC的和是多少度；（2）根据角的和差关系可得∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC=（∠AOC+∠BOC）+（∠BOD+∠BOC），依此即可求解；（3）可得方程∠AOD+∠BOC=180°，∠AOD=180°﹣∠BOC，联立即可求解．【解答】解：（1）当OB平分∠COD时，有∠BOC=∠BOD=45°，于是∠AOC=90°﹣45°=45°，所以∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°；（2）当OB不平分∠COD时，有∠AOB=∠AOC+∠BOC=90°，∠COD=∠BOD+∠BOC=90°，于是∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC，所以∠AOD+∠BOC=90°+90°=180°．（3）由上得∠AOD+∠BOC=180°，有∠AOD=180°﹣∠BOC，180°﹣∠BOC=4（90°﹣∠BOC），所以∠BOC=60°．【点评】考查了角平分线的定义，角度的计算．根据角平分线定义得出所求角与已知角的关系转化求解．注意一副三角板的直角顶点O重叠在一起时角的关系．。

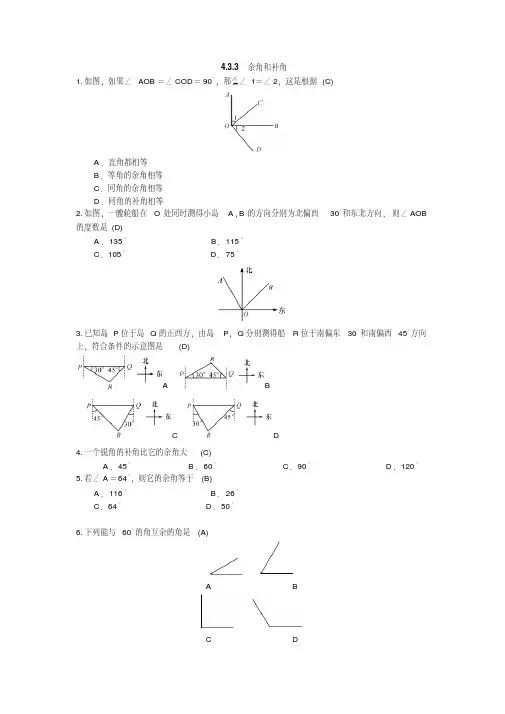
4.3.3余角和补角1.如图，如果∠AOB＝∠COD＝90°，那么∠1＝∠2，这是根据(C)A．直角都相等B．等角的余角相等C．同角的余角相等D．同角的补角相等2.如图，一艘轮船在O处同时测得小岛A，B的方向分别为北偏西30°和东北方向，则∠AOB 的度数是(D)A．135°B．115°C．105°D．75°3.已知岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，符合条件的示意图是(D)A BC D4.一个锐角的补角比它的余角大(C)A．45°B．60°C．90°D．120°5.若∠A＝64°，则它的余角等于(B)A．116°B．26°C．64°D．50°6.下列能与60°的角互余的角是(A)A BC D7.如图所示，∠1>∠2，那么∠2与12(∠1－∠2)之间的关系是(B)A．互补B．互余C．和为45°D．和为22.5°8.已知∠A＝60°，则它的补角的度数是120°.9.若∠1＝∠2，且∠1与∠2互余，则∠1＝∠2＝45°．10.已知∠α＝59°20′，若∠α与∠β互余，且∠β与∠γ互余，则∠γ的度数为59°20′．11.若∠α＝∠β，且∠α＋∠1＝180°，∠β＋∠2＝180°，则∠1与∠2的大小关系是相等．12.一个角的余角比它的补角的13还少20°，则这个角的大小是75°．13.如图，根据点A、B、C、D、E在图中的位置填空．(1)射线OA表示东北方向；(2)射线OB表示北偏西30°；(3)射线OC表示南偏西60°；(4)射线OD表示正南方向；(5)射线OE表示南偏东50°．14.如图，∠AOB＝124°，OC是∠AOB的平分线，∠1与∠2互余，求∠1和∠BOD的度数．解：因为∠AOB＝124°，OC是∠AOB的平分线，所以∠BOC＝∠2＝12∠AOB＝62°.因为∠1与∠2互余，所以∠1＋∠2＝90°.所以∠1＝90°－∠2＝28°.所以∠BOD＝∠BOC－∠1＝34°.15.如图，O点是学校所在位置，A村位于学校南偏东42°方向，B村位于学校北偏东25°方向，C村位于学校北偏西65°方向，在B村和C村间的公路OE(射线)平分∠BOC.(1)求∠AOE的度数；(2)公路OE上的车站D相对于学校O的方位是什么？(以正北、正南方向为基准)解：(1)如图所示：因为A村位于学校南偏东42°方向，所以∠1＝42°.因为B村位于学校北偏东25°方向，所以∠4＝25°.所以∠AOB＝180°－∠1－∠4＝113°.因为C村位于学校北偏西65°方向，所以∠COM＝65°.所以∠BOC＝∠COM＋∠4＝90°.因为OE平分∠BOC，所以∠COE＝∠BOE＝45°.所以∠AOE＝∠AOB＋∠BOE＝113°＋45°＝158°.(2)∠EOM＝∠BOE－∠4＝20°，所以车站D相对于学校O的方位是北偏西20°.16.如图1所示，将一副三角尺的直角顶点重合在点O处．(1)①∠AOD和∠BOC相等吗？说明理由；②∠AOC和∠BOD在数量上有何关系？说明理由；(2)若将等腰的三角尺绕点O旋转到如图2的位置．①∠AOD和∠BOC相等吗？说明理由；②∠AOC和∠BOD的以上关系还成立吗？说明理由．解：(1)①∠AOD＝∠BOC.理由略．②∠AOC和∠BOD互补．理由略．(2)①∠AOD＝∠BOC.理由略．②∠AOC和∠BOD互补．理由略．。

4.3.3余角和补角1.如果α与β互为余角，那么( )A.α＋β＝180°B.α－β＝180°C.α－β＝90°D.α＋β＝90°2.已知∠A＝55°，则它的余角是( )A.25°B.35°C.45°D.55°3.如图，直线a与直线c相交于点O，∠1的余角的度数是( )A.60°B.50°C.40°D.30°4.若∠α＝35°，则∠α的补角为 .5.一个角是70°39′，则它的余角的度数是 .6.(1)已知一个角是它的余角的一半，求这个角的度数；(2)如图，∠AOB＝114°，OD是∠AOB的平分线，∠1与∠2互余，求∠1的度数.7.已知∠1＋∠2＝180°，∠3＋∠4＝180°，如果∠1＝∠3，那么∠2＝∠4，依据是( )A.同角的余角相等B.同角的补角相等C.等角的余角相等D.等角的补角相等8.已知∠A与∠B互余，∠B与∠C互余，则∠A与∠C( )A.互余B.相等C.互补D.差为90°9.如图，射线OA的方向是北偏西60°，射线OB的方向是南偏东25°，则∠AOB的度数为( )A.120°B.145°C.115°D.130°10.如图，指出OA是表示什么方向的一条射线？仿照这条射线画出表示下列方向的射线：(1)南偏东60°；(2)北偏西70°；(3)西南方向(即南偏西45°).11.已知岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，符合条件的示意图是 ( )A BC D12.一个锐角的补角比它的余角大( )A.45°B.60°C.90°D.120°13.将一副三角板按如图所示位置摆放，其中∠α与∠β一定互余的是( )14.若∠1与∠2互余，∠2与∠3互补，∠1＋∠3＝150°，则∠2＝ .15.一个角的补角加上10°后等于这个角的余角的3倍，求这个角的度数.16.如图，OD平分∠BOC，OE平分∠AOC，∠BOC＝70°，∠AOC＝50°.(1)求出∠AOB及其补角的度数；(2)请求出∠DOC和∠AOE的度数，并判断∠DOE与∠AOB是否互补，并说明理由.17.如图1所示，∠AOB，∠COD都是直角.(1)试猜想∠AOD与∠COB在数量上是相等，互余，还是互补的关系，并用推理的方法说明你的猜想是合理的；(2)当∠COD绕着点O旋转到图2所示位置时，你在(1)中的猜想还成立吗？请证明你的结论.参考答案：1.D2.B3.A4. 145°.5. 19°21′.6.解：(1)设这个角的度数是x°，根据题意，得x ＝12(90－x). 解得x ＝30.所以这个角的度数是30°.(2)因为OD 平分∠AOB，所以∠2＝12∠AOB＝12×114°＝57°. 又因为∠1和∠2互余，所以∠1＝90°－∠2＝90°－57°＝33°.7.D8.B9.B10.解：OA 表示北偏东40°.(1)(2)(3)画图略.11.D12.C13.C14.60°.15.解：设这个角为x°，则它的余角为90°－x°，补角为180°－x°，根据题意，得 180°－x°＋10°＝3×(90°－x°).解得x ＝40.答：这个角为40°.16.解：(1)∠AOB＝∠BOC＋∠AOC＝70°＋50°＝120°，其补角为180°－∠AOB＝180°－120°＝60°.(2)∠DOC＝12∠BOC＝12×70°＝35°， ∠AOE＝12∠AOC＝12×50°＝25°. ∠DOE 与∠AOB 互补.理由：因为∠DOE＝∠DOC＋∠COE＝35°＋25°＝60°，所以∠DOE＋∠AOB＝60°＋120°＝180°.故∠DOE 与∠AOB 互补.17.解：(1)∠AOD 与∠COB 互补.理由：因为∠AOB、∠COD 都是直角，所以∠AOB＝∠COD＝90°.所以∠BOD＝∠AOD－∠AOB＝∠AOD－90°，∠BOD＝∠COD－∠COB＝90°－∠COB.所以∠AOD－90°＝90°－∠COB.所以∠AOD＋∠COB＝180°.所以∠AOD 与∠COB 互补.(2)成立.证明：因为∠AOB，∠COD 都是直角，所以∠AOB＝∠COD＝90°.因为∠AOB＋∠BOC＋∠COD＋∠AOD＝360°，所以∠AOD＋∠COB＝180°.所以∠AOD 与∠COB 互补.。

如果别人思考数学的真理像我一样深入持久，他也会找到我的发现。

——高斯2020年人教版七年级数学上册课时训练：4.3.3《余角和补角》一．选择题1．25°的补角是（）A．155°B．145°C．55°D．65°2．一个角的余角是44°，这个角的补角是（）A．134°B．136°C．156°D．146°3．若∠A与∠B互为补角，∠A＝40°，则∠B＝（）A．50°B．40°C．140°D．60°4．已知∠1和∠2互为余角，且∠2与∠3互补，∠1＝60°，则∠3为（）A．120°B．60°C．30°D．150°5．如果一个角的余角是50°，那么这个角的补角的度数是（）A．130°B．40°C．90°D．140°6．如果∠1与∠2互补，∠2与∠3互余，则∠1与∠3的关系是（）A．∠1＝∠3B．∠1＝180°﹣∠3C．∠1＝90°+∠3D．以上都不对7．如图，∠AOB＝∠COD＝90°，那么∠AOC＝∠BOD，这是根据（）A．直角都相等B．同角的余角相等C．同角的补角相等D．互为余角的两个角相等8．如图，一副三角尺按不同的位置摆放，下列摆放方式中∠α与∠β互余的是（）A．B．C．D．9．一个角的余角是它的补角的，这个角的补角是（）A．30°B．60°C．120°D．150°10．如图，点A、O、B在一条直线上，∠1是锐角，则∠1的余角是（）A．∠2﹣∠1B．∠2﹣∠1C．（∠2﹣∠1）D．（∠1+∠2）二．填空题11．一个角的度数是30°，则它的补角的度数为．12．如图，∠BOC＝90°，∠COD＝45°，则图中互为补角的角共有对．13．如果一个角的补角是它余角的3倍少10°，则这个角是．14．一个角的余角比这个角的补角的一半少42°，则这个角的度数是．15．如图所示，A，O，B三点在同一条直线上，∠AOC与∠AOD互余，已知∠BOC＝110°，则∠AOD＝°．16．若两个角互补，且度数之比为3：2，求较大角度数为．三．解答题17．一个角的余角比这个角少20°，则这个角的补角为多少度．18．已知∠1与∠2互余，且∠1的补角比∠2的2倍多25°，求∠1的大小．19．如图，点O是直线AB上一点，OC为任一条射线，OD平分∠AOC，OE平分∠BOC．（1）分别写出图中∠AOD和∠AOC的补角；（2）求∠DOE的度数．20．如图，已知∠AOB和∠COD都是∠BOC的余角，OE、OF分别为∠AOB和∠COD的角平分线，如果∠AOD＝130°，（1）求∠BOC的度数；（2）求∠EOF的度数．21．如图，已知射线OB平分∠AOC，∠AOC的余角比∠BOC小42°．（1）求∠AOB的度数：（2）过点O作射线OD，使得∠AOC＝4∠AOD，请你求出∠COD的度数．（3）在（2）的条件下，画∠AOD的角平分线OE，则∠BOE＝．22．如图所示，已知O是直线AB上一点，∠BOE＝∠FOD＝90°，OB平分∠COD．（1）图中与∠DOE互余的角是．（2）图中是否有与∠DOE互补的角？如果有，直接写出全部结果；如果没有，说明理由．（3）如果∠EOD：∠EOF＝3：2，求长∠AOC的度数．参考答案一．选择题1．解：25°的补角是：180°﹣25°＝155°．故选：A．2．解：∵一个角的余角是44°，∴这个角的度数是：90°﹣44°＝46°，∴这个角的补角是：180°﹣46°＝134°．故选：A．3．解：∵∠A与∠B互为补角，∴∠A+∠B＝180°，∵∠A＝40°，∴∠B＝180°﹣40°＝140°．故选：C．4．解：∵∠1和∠2互为余角，∠1＝60°，∴∠2＝90°﹣∠1＝90°﹣60°＝30°，∵∠2与∠3互补，∴∠3＝180°﹣∠2＝180°﹣30°＝150°．故选：D．5．解：∵一个角的余角是50°，则这个角为40°，∴这个角的补角的度数是180°﹣40°＝140°．故选：D．6．解：∵∠1+∠2＝180°∴∠1＝180°﹣∠2又∵∠2+∠3＝90°∴∠3＝90°﹣∠2∴∠1﹣∠3＝90°，即∠1＝90°+∠3．故选：C．7．解：∵∠AOC+∠BOC＝∠BOD+∠BOC＝90°，∠AOC和∠BOD都与∠BOC互余，故同角的余角相等，故选：B．8．解：A、图中∠α+∠β＝180°﹣90°＝90°，∠α与∠β互余，故本选项正确；B、图中∠α＝∠β，不一定互余，故本选项错误；C、图中∠α+∠β＝180°﹣45°+180°﹣45°＝270°，不是互余关系，故本选项错误；D、图中∠α+∠β＝180°，互为补角，故本选项错误．故选：A．9．解：设这个角的度数为x，则它的余角为（90°﹣x），补角为（180°﹣x），依题意，得90°﹣x＝（180°﹣x）解得x＝30°．∴这个角的补角是：180°﹣30°＝150°．故选：D．10．解：由图知：∠1+∠2＝180°；∴（∠1+∠2）＝90°；∴90°﹣∠1＝（∠1+∠2）﹣∠1＝（∠2﹣∠1）．故选：C．二．填空题11．解：这个角的补角＝180°﹣30°＝150°．故答案为：150°．12．解：∵∠BOC＝90°，∴∠AOC＝∠BOC＝90°，∴∠AOC与∠BOC互为补角；∵∠BOD+∠AOD＝180°，∴∠AOD与∠BOD互为补角；∵∠COD＝45°，∴∠BOD＝45°，∴∠AOD与∠COD互为补角；∴图中互为补角的角共有3对，故答案为：3．13．解：设这个角为∠A，则根据题意得：180°﹣∠A＝3（90°﹣∠A）﹣10°，解得：∠A＝40°，故答案为：40°．14．解：设这个角的度数是x°，则它的余角为（90﹣x）°，补角为（180﹣x）°．依题意得：90﹣x＝（180﹣x）﹣42，解得x＝84．∴这个角的度数是84°．故答案为：84°．15．解：∵∠BOC＝110°，∴∠AOC＝180°﹣∠BOC＝70°，∵∠AOC与∠AOD互余，∴∠AOD＝90°﹣∠AOC＝20°．故答案为：2016．解：因为两个角的度数之比为3：2，所以设这两个角的度数分别为（3x）°和（2x）°．根据题意，列方程，得3x+2x＝180，解这个方程，得x＝36，所以3x＝108．即较大角度数为108°．故答案为108°．三．解答题17．解：设这个角的度数为x度，则x﹣（90﹣x）＝20，解得：x＝55，即这个角的度数为55°，所以这个角的补角为180°﹣55°＝125°．18．解：设∠1＝x°，则∠2＝（90﹣x）°，根据题意得：180﹣x＝2（90﹣x）+25，解得x＝25，∴∠1＝25°．19．解：（1）∠AOD的补角是：∠BOD；∠AOC的补角是∠BOC；（2）∵OD平分∠AOC，OE平分∠BOC∴，，∴∠DOE＝∠COD+∠COE＝＝＝＝90°．20．解：∵∠AOB和∠COD都是∠BOC的余角，∴∠AOB+∠BOC＝90°，∠COD+∠BOC＝90°，∴（∠AOB+∠BOC）+（∠COD+∠BOC）＝180°，∴∠BOC＝180°﹣∠AOD＝180°﹣130°＝50°；（2）解：∵∠AOB与∠COD都是∠BOC的余角，∠BOC＝50°，∴∠AOB＝90°﹣50°＝40°，∠COD＝90°﹣50°＝40°，∵OE、OF分别是∠AOB、∠COD的平分线，∴∠AOE＝∠AOB＝×40°＝20°，∠DOF＝∠COD＝×40°＝20°，∴∠EOF＝∠AOD﹣∠AOE﹣∠DOF＝130°﹣20°﹣20°＝90°．21．解：（1）由射线OB平分∠AOC可得∠AOC＝2∠BOC，依题意列方程90°﹣2x＝x﹣42°，解得：x＝44°，即∠AOB＝44°．（2）由（1）得，∠AOC＝88°，①当射线OD在∠AOC内部时，∠AOD＝22°，则∠COD＝∠AOC﹣∠AOD＝66°；②当射线OD在∠AOC外部时，∠AOD＝22°则∠COD＝∠AOC+∠AOD＝110°；（3）∵OE平分∠AOD，∴∠AOE＝，当射线OD在∠AOC内部时，∠BOE＝∠AOB﹣∠AOE＝44°﹣11°＝33°；当射线OD在∠AOC外部时，∠BOE＝∠AOB+∠AOE＝44°+11°＝55°．∴∠BOE度数为33°或55°．故答案为：33°或55°22．解：（1）图中与∠DOE互余的角有：∠EOF，∠BOD，∠BOC，故答案为：∠EOF，∠BOD，∠BOC；（2）与∠DOE互补的角有∠BOF，∠COE；（3）∵∠EOD：∠EOF＝3：2，∴∠EOD＝3x，则∠EOF＝2x，∵∠FOD＝90°，∴3x+2x＝90°，x＝18°，∴∠EOF＝36°，∵∠BOE＝∠FOD＝90°，∴∠DOE+∠EOF＝90°，∠DOE+∠DOB＝90°，∴∠EOF＝∠DOB＝36°，∵OB平分∠COD，∵∠AOC+∠COB＝180°，∴∠AOC＝180°﹣∠COB＝144°．。

人教版数学(七上)第4章 4.3.3 余角和补角同步练习一、选择题1. 若一个角为65°，则它的补角的度数为()A．25° B．36° C．115° D．125°2.若一个角为75°，则它的余角的度数为()A．285° B．105° C．75° D．15°3. 下列说法正确的是()A．90°角是余角B．如果一个角有补角，那么它一定有余角C．若∠1＋∠2＋∠3＝180°，则∠1，∠2，∠3互补D．66°角的余角是24°4. 如图，直线AB，CD交于点O，因为∠1＋∠3＝180°，∠2＋∠3＝180°，所以∠1＝∠2的依据是()A．同角的余角相等B．等角的余角相等C．同角的补角相等D．等角的补角相等5. 如图，下列说法中不正确的是()A．射线OA表示北偏东25°B．射线OB表示西北方向C．射线OC表示西偏南80°D．射线OD表示南偏东70°6. 如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA夹角为90°，则OB的方位角是()A．北偏西30° B．北偏西60°C．东偏北30° D．东偏北60°7. 已知：岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，以下符合条件的示意图是()A BC D8. 已知M，N，P，Q四点的位置如图所示，下列结论中，正确的是()A．∠NOQ＝42°B．∠NOP＝132°C．∠PON比∠MOQ大D．∠MOQ与∠MOP互补9. 将一副三角尺按不同的位置摆放，下列摆放方式中∠α与∠β互余的是()A B C D二、填空题10. (1)若∠α＝35°，则∠α的补角为____，∠α的余角为____，∠α的补角与余角的差为____；(2)若∠α的补角为76°28′，则∠α＝____．(3)一个角是70°39′，则它的余角的度数是____．11. 如图，∠1＝32°，则∠2＝____，∠AOD＝____．12. 一个角的余角比这个角的补角的一半小40°，则这个角为____°.13. 南偏西15°与北偏东25°的两条射线组成的小于平角的角等于____．三、解答题14. 如图，已知∠AOC＝∠BOD＝90°.(1)若∠DOC＝55°，求∠AOD和∠BOC的度数；(2)试说明：∠AOD＝∠BOC.15. 如图，直线AB，CD相交于点O，OF平分∠AOE，∠DOF＝90°.(1)写出图中所有与∠AOD互补的角；(2)若∠AOE＝120°，求∠BOD的度数．16. 如图，点O是直线AB上任一点，射线OD和射线OE分别平分∠AOC和∠BOC．（1）填空：与∠AOE互补的角有；（2）若∠COD=30°，求∠DOE的度数；（3）当∠AOD=α°时，请直接写出∠DOE的度数．参考答案一、选择题1. 若一个角为65°，则它的补角的度数为()A．25° B．36° C．115° D．125°【答案】C2.若一个角为75°，则它的余角的度数为()A．285° B．105° C．75° D．15°【答案】D3. 下列说法正确的是()A．90°角是余角B．如果一个角有补角，那么它一定有余角C．若∠1＋∠2＋∠3＝180°，则∠1，∠2，∠3互补D．66°角的余角是24°【答案】D4. 如图，直线AB，CD交于点O，因为∠1＋∠3＝180°，∠2＋∠3＝180°，所以∠1＝∠2的依据是()A．同角的余角相等B．等角的余角相等C．同角的补角相等D．等角的补角相等【答案】C5. 如图，下列说法中不正确的是()A．射线OA表示北偏东25°B．射线OB表示西北方向C．射线OC表示西偏南80°D．射线OD表示南偏东70°【答案】C6. 如图，OA是北偏东30°方向的一条射线，若射线OB与射线OA夹角为90°，则OB的方位角是()A．北偏西30° B．北偏西60°C．东偏北30° D．东偏北60°【答案】B7. 已知：岛P位于岛Q的正西方，由岛P，Q分别测得船R位于南偏东30°和南偏西45°方向上，以下符合条件的示意图是()A BC D【答案】D8. 已知M，N，P，Q四点的位置如图所示，下列结论中，正确的是()A．∠NOQ＝42°B．∠NOP＝132°C．∠PON比∠MOQ大D．∠MOQ与∠MOP互补【答案】C【解析】如图所示：∠NOQ＝138°，故选项A错误；∠NOP＝48°，故选项B错误；∠PON＝48°，∠MOQ＝42°，故∠PON比∠MOQ大，故选项C正确；∵∠MOQ＝42°，∠MOP＝132°，∠MOQ＋∠MOP≠180°，∴∠MOQ与∠MOP 不互补，选项D错误．故选C.9. 将一副三角尺按不同的位置摆放，下列摆放方式中∠α与∠β互余的是()A B C D【答案】A【解析】 A 中∠α与∠β互余，B 中∠α＝∠β，C 中∠α＝∠β，D 中∠α与∠β互补．故选A.二、填空题10. (1)若∠α＝35°，则∠α的补角为____，∠α的余角为____，∠α的补角与余角的差为____；(2)若∠α的补角为76°28′，则∠α＝____． (3)一个角是70°39′，则它的余角的度数是____． 【答案】(1) 145°; 55°; 90°(2) 103°32′;(3) 19°21′11. 如图，∠1＝32°，则∠2＝____，∠AOD ＝____．【答案】32°; 148°12. 一个角的余角比这个角的补角的一半小40°，则这个角为____°. 【答案】80【解析】 设这个角为x ，则它的余角为(90°－x )，补角为(180°－x )．根据题意，得12(180°－x )－(90°－x )＝40°，解得x ＝80°.13. 南偏西15°与北偏东25°的两条射线组成的小于平角的角等于____． 【答案】170°【解析】 依题意画图如答图，则90°＋15°＋90°－25°＝170°.三、解答题14. 如图，已知∠AOC＝∠BOD＝90°.(1)若∠DOC＝55°，求∠AOD和∠BOC的度数；(2)试说明：∠AOD＝∠BOC.【答案】解：(1)∵∠AOC＝∠BOD＝90°，∠DOC＝55°，∴∠AOD＝∠AOC－∠DOC＝90°－55°＝35°，∠BOC＝∠BOD－∠DOC＝90°－55°＝35°；(2)∵∠AOD＋∠DOC＝90°，∠BOC＋∠DOC＝90°，∴∠AOD＝∠BOC(同角的余角相等)．15. 如图，直线AB，CD相交于点O，OF平分∠AOE，∠DOF＝90°.(1)写出图中所有与∠AOD互补的角；(2)若∠AOE＝120°，求∠BOD的度数．【答案】解：(1)∵直线AB，CD相交于点O，∴∠AOC和∠BOD与∠AOD互补．∵OF平分∠AOE，∴∠AOF＝∠EOF，∵∠DOF＝90°，∴∠COF＝90°，则∠DOE＝∠AOC(等角的余角相等)，∴∠DOE也是∠AOD的补角．综上，与∠AOD互补的角有∠AOC，∠BOD，∠DOE；(2)由(1)知∠AOC＝∠BOD＝∠DOE，又∵∠AOC＋∠AOE＋∠DOE＝180°，∴∠BOD＝∠AOC＝180°－120°2＝30°.16. 如图，点O是直线AB上任一点，射线OD和射线OE分别平分∠AOC和∠BOC．（1）填空：与∠AOE互补的角有；（2）若∠COD=30°，求∠DOE的度数；（3）当∠AOD=α°时，请直接写出∠DOE的度数．【答案】解：（1）∵OE平分∠BOC，∴∠BOE=∠COE；∵∠AOE+∠BOE=180°，∴∠AOE+∠COE=180°，∴与∠AOE互补的角是∠BOE、∠COE；故答案为∠BOE、∠COE；（2）∵OD、OE分别平分∠AOC、∠BOC，∴∠COD=∠AOD=30°，∠COE=∠BOE=∠BOC，∴∠AOC=2×30°=60°，∴∠BOC=180°﹣60°=120°，∴∠CO E=∠BOC=60°，∴∠DOE=∠COD+∠COE=90°；（3）当∠AOD=α°时，∠DOE=90°．。

东D FAEB2019-2020学年七年级数学上册 4.3.3 余角和补角同步练习 新人教版一、选择题：1、下列说法错误的是 （ ） A 、同角或等角的余角相等 B 、同角或等角的补角相等 C 、两个锐角的余角相等 D 、两个直角的补角相等2、一个角的补角是 （ ） A 、锐角 B 、直角 C 、钝角 D 、以上三种情况都有可能3、一个锐角的补角比这个角的余角大 （ ） A 、30º B 、45º C 、60º D 、90º4、如图，∠AOD =∠DOB=∠COE=90º，其中共有互余的角( ） A 、2对 B 、3对 C 、4对 D 、6对5、若∠1与∠2互补，∠3与∠1互余，∠2+∠3=240º，由∠2是∠1的 （ ） A 、251倍 B 、5倍 C 、11倍 D 、无法确定倍数 6、若∠1与∠2互为补角，且∠1<∠2，则∠1的余角是 （ ） A 、∠1 B 、∠1+∠2 C 、21（∠1+∠2） D 、21（∠2-∠1） 7.如图,甲从A 点出发向北偏东70°方向走50m 至点B,乙从A 出发向南偏西15°方向走80m 至点C,则∠BAC 的度数是( )A.85°B.160°C.125°D.105°8.如图,长方形ABCD 沿AE 折叠,使D 点落在BC 边上的F 点处, 如果∠BAF=60°,则∠DAE 等于( ) A.15° B.30° C.45° D.60°二、填空题9、如果两个锐角的和是 ，则这两个角互为余角，如果两个角的和是 ，则这两个角互为补角。

10、若∠α=50º，则它的余角是 ，它的补角是 。

OEDCBA11、若∠β=110º，则它的补角是 ，它的补角的余角是 。

12、如图，∠ACB=∠CDB=90º，图中∠ACD 的余角有 。

4.3.3余角和补角同步练习一．选择题1．若∠A与∠B互为补角，∠A＝40°，则∠B＝（）A．50°B．40°C．140°D．60°2．下列叙述正确的是（）A．一个钝角和一个锐角一定互为补角B．每一个锐角都有余角C．两个锐角一定互为余角D．一个钝角的余角是锐角3．如图，∠AOB＝∠COD＝90°，∠AOD＝146°，则∠BOC的度数为（）A．43°B．34°C．56°D．50°4．下列说法中，正确的是（）①已知∠A＝40°，则∠A的余角是50°．②若∠1+∠2＝90°，则∠1和∠2互为余角．③若∠1+∠2+∠3＝180°，则∠1、∠2和∠3互为补角．④一个角的补角必为钝角．A．①，②B．①，②，③C．③，④，②D．③，④5．已知锐角α，那么∠α的补角与∠α的余角的差是（）A．90°B．120°C．60°+αD．180°﹣α6．若α＝27°25'，则α的余角等于（）A．62°25'B．62°35'C．152°25'D．152°35'7．如果∠1与∠2互补，∠2与∠3互余，那么∠1与∠3的关系是（）A．∠1＝90°+∠3B．∠3＝90°+∠1C．∠1＝∠3D．∠1＝180°﹣∠3 8．如图，∠AOC和∠BOD都是直角．如果∠DOC＝58°，则下列判断错误的是（）A．∠AOD＝∠BOCB．∠AOB＝132°C．∠AOB+∠DOC＝180°D．若∠DOC变小，则∠AOB变大9．将一副三角尺按不同位置摆放，下列摆放中∠1与∠2互为余角的是（）A．B．C．D．10．如图，点A，O，B在一条直线上，OE⊥AB于点O，如果∠1与∠2互余，那么图中相等的角有（）A．5对B．4对C．3对D．2对二．填空题11．若两个角互补，且度数之比为3：2，求较大角度数为．12．一个角的补角与它的余角的3倍的差是40°，则这个角为．13．已知：如图，在△ABC中，∠ACB＝90°，CD⊥AD，垂足为点D，图形中相等的角有对，互余的角有对．14．若一个角的补角与这个角的余角之和为200°，则这个角的度数为度．15．如图，将一副三角尺的直角顶点O重合在一起．若∠COB与∠DOA的比是5：13，OE 平分∠DOA，则∠EOC＝度．三．解答题16．如图，已知∠AOB＝128°，OC平分∠AOB，请你在∠COB内部画射线OD，使∠COD 和∠AOC互余，并求∠COD的度数．17．如图，在直线AD上任取一点O，过点O做射线OB，OE平分∠DOB，OC平分∠AOB，∠BOC＝26°时，求∠BOE的度数．18．如图①，点O为直线AB上一点，过点O作射线OC，使∠BOC＝60°，将一直角三角板的直角顶点放在点O处，一边ON在射线OB上，另一边OM在直线AB的上方．（1）在图①中，∠COM＝度；（2）将图①中的三角板绕点O按逆时针方向旋转，使得ON在∠BOC的内部，如图②，若∠NOC＝∠MOA，求∠BON的度数；（3）将图①中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周，在旋转的过程中，当直线ON恰好平分锐角∠BOC时，旋转的时间是秒．（直接写出结果）参考答案一．选择题1．解：∵∠A与∠B互为补角，∴∠A+∠B＝180°，∵∠A＝40°，∴∠B＝180°﹣40°＝140°．故选：C．2．解：A．一个锐角与一个钝角不一定互为补角，故本选项错误；B．每一个锐角都有余角，故本选项正确；C．只有两个锐角的和为90°时，这两个角才互余，故原说法错误；D．钝角的没有余角，故此选项错误；故选：B．3．解：∠AOB＝∠COD＝90°，∠AOD＝146°则∠BOC＝360°﹣2×90°﹣146°＝34°则∠BOC＝34°．故选：B．4．解：①已知∠A＝40°，则∠A的余角是50°，原说法正确；②若∠1+∠2＝90°，则∠1和∠2互为余角，原说法正确；③若∠1+∠2+∠3＝180°，则∠1、∠2和∠3不能互为补角，原说法错误；④一个角的补角不一定是钝角，原说法错误．说法正确的是①②，故选：A．5．解：（180°﹣∠α）﹣（90°﹣∠α）＝180°﹣∠α﹣90°+∠α＝90°．故选：A．6．解：α的余角＝90°﹣α＝90°﹣27°25'＝62°35'．故选：B．7．解：∵∠1+∠2＝180°∴∠1＝180°﹣∠2又∵∠2+∠3＝90°∴∠3＝90°﹣∠2∴∠1﹣∠3＝90°，即∠1＝90°+∠3．故选：A．8．解：A、∵∠AOC和∠BOD都是直角，∴∠AOD+∠DOC＝∠DOC+∠BOC＝90°，∴∠AOD＝∠BOC，故A正确，不符合题意；B、∵∠DOC＝58°，∴∠AOD＝32°，∴∠AOB＝32°+90°＝122°，故B错误，符合题意，C、∵∠AOD+∠DOC＝∠DOC+∠BOC＝90°，∴∠AOD+∠DOC+∠DOC+∠BOC＝180°，∴∠AOB+∠DOC＝180°，故C正确，不符合题意；D、∵∠AOD+∠DOC+∠DOC+∠BOC＝180°，∴∠AOB+∠DOC＝180°，∴∠DOC变小，则∠AOB变大，故D正确，不符合题意．故选：B．9．解：A、∠1与∠2不互余，故本选项错误；B、∠1与∠2不互余，故本选项错误；C、∠1与∠2不互余，故本选项错误；D、∠1与∠2互余，故本选项正确．故选：D．10．解：∵OE⊥AB，∴∠AOE＝∠BOE＝90°，∵∠1与∠2互余，∴∠1+∠2＝90°，∴∠1＝∠AOC，∠2＝∠BOD，∠AOE＝∠COD，∴图中相等的角有5对．故选：A．二．填空题11．解：因为两个角的度数之比为3：2，所以设这两个角的度数分别为（3x）°和（2x）°．根据题意，列方程，得3x+2x＝180，解这个方程，得x＝36，所以3x＝108．即较大角度数为108°．故答案为108°．12．解：设这个角为x°，则其余角为（90﹣x）°，补角为（180﹣x）°，依题意有180﹣x﹣3（90﹣x）＝40，解得x＝65．故这个角是65°．故答案为：65°．13．解：图形中相等的角有∠A＝∠BCD，∠B＝∠ACD，∠ACB＝∠BDC，∠ACB＝∠CDA，∠BDC＝∠CDA，一共5对，互余的角有∠A和∠B，∠A和∠ACD，∠B和∠BCD，∠ACD和∠BCD，一共4对．故答案为：5；4．14．解：设这个角为x°，由题意得：90﹣x+180﹣x＝200，解得：x＝35，故答案为：35．15．解：∵∠COB+∠DOA＝∠COB+∠COA+∠COB+∠DOB＝∠AOB+∠COD＝180°，又∵∠COB与∠DOA的比是5：13，∴∠DOA＝180°×＝130°，∵OE平分∠DOA，∴∠DOE＝65°，故答案为：25．三．解答题16．解：作OD⊥OA，则∠COD和∠AOC互余，如图所示．∵∠AOB＝128°，OC平分∠AOB，∴∠AOC＝∠AOB＝64°，∵∠COD和∠AOC互余，∴∠COD＝90°﹣∠AOC＝26°．17．解：∵OC平分∠AOB，∠BOC＝26°，∴∠AOB＝2∠BOC＝52°．∴∠BOD＝180°﹣52°＝128°．∵OE平分∠DOB，∴∠BOE＝∠DOB＝×128°＝64°．18．解：（1）∵将一直角三角板的直角顶点放在点O处，一边ON在射线OB上，另一边OM在直线AB的上方，∴∠MON＝90°，∴∠COM＝∠MON﹣∠BOC＝90°﹣60°＝30°，故答案为：30（2）设∠NOC＝x，那么∠MOA＝6x，∠BON＝60°﹣x．由题意，可知6x+90°+60°﹣x＝180°，即5x＝180°﹣90°﹣60°，即5x＝30°，所以x＝6°．所以∠BON＝60°﹣x＝60°﹣6°＝54°．（3）∵直线ON平分∠BOC，∠BOC＝60°，∴∠BON＝30°或∠BON＝210°，∵三角板绕点O以每秒10°的速度沿逆时针方向旋转一周，∴直线ON平分∠BOC时，旋转的时间是3或21秒，故答案为：3或21。

数学：4.3.3《余角和补角（1）》学案（人教版七年级上）【学习目标】在具体的现实情境中，认识一个角的余角和补角； 【重点难点】正确求出一个角的余角和补角。

【导学指导】 一、知识链接 思考：（1） 在一副三角板中同一块三角板的两个锐角和等于多少度？ （2） 如图1，已知∠1=61°，∠2=29°，那么∠1+∠2= 。

（3） 如 图 2，已知点A 、O 、B 在一直线上 ，∠COD=90°，那么∠1+∠2= 。

二、自主探究1.互为余角的定义： 思考：（1） 如图3，已知∠1=62°,∠2=118°,那么 ∠1+∠2＝（2） 如图4，A 、O 、B 在同一直线上，∠1+∠2=2.互为补角的定义：2图 190°12图 212Ａ Ｏ Ｂ图 412图 3 CODOEDCBA问题1：以上定义中的“互为”是什么意思？问题2：若 ∠1+∠2 +∠3 =180° ，那么∠1、∠2、∠3互为补角吗？ 3.新知应用：例1:若一个角的补角等于它的余角4倍，求这个角的度数。

例2：如图，∠AOC ＝∠COB ＝90°，∠DOE ＝90°，A 、O 、B 三点在一直线上 （1）写出∠COE 的余角，∠AOE 的补角； （2）找出图中一对相等的角，并说明理由；【课堂练习】：课本141页练习1、2、3；【要点归纳】：【拓展训练】：1、一个角的余角比它的补角的31还少︒20，求这个角的度数。

2、若α∠和β∠互余，且α∠：β∠=7：2，求α∠、β∠的度数。

【总结反思】：2019-2020学年七年级数学上学期期末模拟试卷一、选择题1．如图，若延长线段AB 到点C ，使BC=AB ，D 为AC 的中点，DC=5cm ，则线段AB 的长度是（ ）A.10cmB.8cmC.6cmD.4cm2．若∠β=25°31'，则∠β的余角等于（ ） A.64°29'B.64°69'C.154°29'D.154°69'3．如图，两块直角三角板的直顶角O 重合在一起，若∠BOC=15∠AOD ，则∠BOC 的度数为（ ）A ．30° B. 45° C．54° D．60° 4．下列解方程去分母正确的是( ) A.由，得2x ﹣1＝3﹣3x B.由，得2x ﹣2﹣x ＝﹣4 C.由，得2y-15=3yD.由，得3(y+1)＝2y+65．甲、乙两工程队开挖一条水渠各需10天、15天，两队合作2天后，甲有其他任务，剩下的工作由乙队单独做，还需多少天能完成任务？设还需x 天，可得方程（ ）A.11()21101515x+⨯+= B.11015x x+= C.2211015x ++= D.2211015x ++= 6．中国古代问题：有甲、乙两个牧童，甲对乙说：“把你的羊给我一只，我的羊数就是你的羊数的2倍”．乙回答说：“最好还是把你的羊给我一只，我们羊数就一样了”．若设甲有x 只羊，则下列方程正确的是（ ） A.x+1=2（x ﹣2） B.x+3=2（x ﹣1） C.x+1=2（x ﹣3）D.1112x x +-=+ 7．已知一个多项式与3x 2+9x 的和等于3x 2+4x ﹣1,则这个多项式是（ ） A ．﹣5x ﹣1B ．5x+1C ．﹣13x ﹣1D ．13x+18．定义一种正整数n “F ”的运算：①当n 是奇数时，()31F n n =+；②当n 是偶数时，()2kn F n =(其中k 是使得2k n为奇数的正整数......，)两种运算交替重复运行.例如，取24n =，则： 243105F F F −−−→−−−→−−−→⋅⋅⋅⋅⋅⋅第一次第二次第三次②①②，若13n =，则第2019次“F ”运算的结果是( ) A.1B.4C.2019D.201949．下列判断正确的是（ ） A ．-a 不一定是负数 B ．|a|是一个正数C ．若|a|=a ，则a ＞0；若|a|=-a ，则a ＜0D ．只有负数的绝对值是它的相反数10．现有五种说法：①-a 表示负数；②绝对值最小的有理数是0；③3×102x 2y 是5次单项式；④5x y-是多项式．其中正确的是（ ） A.①③B.②④C.②③D.①④11．如果水位升高1米记为+1米，那么水位下降2米应记为（ ） A.﹣1米B.+1米C.﹣2米D.+2米12．已知a ，b ，c 是有理数，且a+b+c=0，abc （乘积）是负数，则||||||b c a c a b a b c +++++的值是（ ）A.3B.﹣3C.1D.﹣1二、填空题13．如果∠A 的余角是26°，那么∠A 的补角为_______°．14．如图，在灯塔O 处观测到轮船A 位于北偏西54°的方向，同时轮船B 在南偏东15°的方向，那么∠AOB=_______°．15．关于x 的方程ax ﹣2x ﹣5＝0(a≠2)的解是_____． 16．已知关于x 的一元一次方程2019x +5＝2019x+m 的解为x ＝2018，那么关于y 的一元一次方程52019y-﹣5＝2019（5﹣y ）﹣m 的解为_____．17．如图所示，若三角形纸片内有100个点，连同三角形的顶点共103个点，其中任意三点都不共线.现以这些点为顶点作三角形，并把纸片剪成小三角形，这样的小三角形的个数是______.18．观察下列图形，它是把一个三角形分别连接这个三角形三边的中点，构成4个小三角形，挖去中间的一个小三角形(如图1)；对剩下的三个小三角形再分别重复以上做法，…将这种做法继续下去(如图2，图3…)，则图5中挖去三角形的个数为______19．若a,b 是整数，且ab ＝12，|a|＜|b|，则a+b=________ . 20．与原点的距离为 2 个单位的点所表示的有理数是________． 三、解答题21．如图，长方形ABCD 中，AB ＝4cm ，BC ＝8cm ．点P 从点A 出发，沿AB 匀速运动；点Q 从点C 出发，沿C→B→A→D→C 的路径匀速运动．两点同时出发，在B 点处首次相遇后，点P 的运动速度每秒提高了3cm ，并沿B→C→D→A 的路径匀速运动；点Q 保持速度不变，继续沿原路径匀速运动，3s 后两点在长方形ABCD 某一边上的E 点处第二次相遇后停止运动．设点P 原来的速度为xcm/s ． （1）点Q 的速度为 cm/s （用含x 的代数式表示）； （2）求点P 原来的速度．（3）判断E 点的位置并求线段DE 的长．22．已知，O 是直线AB 上的一点，COD ∠是直角，OE 平分BOC ∠．()1如图1，若AOC 30∠=，求DOE ∠的度数；()2在图1中，若AOC a ∠=，直接写出DOE ∠的度数(用含a 的代数式表示)； ()3将图1中的DOC ∠绕顶点O 顺时针旋转至图2的位置．①探究AOC ∠和DOE ∠的度数之间的关系，写出你的结论，并说明理由；②在AOC ∠的内部有一条射线OF ，满足：AOC 4AOF 2BOE AOF ∠∠∠∠-=+，试确定AOF ∠与DOE ∠的度数之间的关系，说明理由．23．如图所示，一幅地图上有A ，B ，C 三地，地图被墨迹污染，C 地具体位置看不清楚了，但知道C 地在A 地的北偏东30°方向，在B 地的南偏东45°方向，你能确定C 地位置吗？24．先化简，再求值：22113122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭，其中x=-1，y=23. 25．先化简，再求值：-2x 2•4x 4+（x 4）2÷x 2-（-3x 3）2，其中x 3=12． 26．现从小欣作业中摘抄了下面一道题的解题过程：计算：24÷（13-18-16）； 解：24÷（13-18-16）=24÷13-24÷18-24÷16=72-192-144 =-264；观察以上解答过程，请问是否正确？若不正确，请写出正确的解答． 27．观察下列等式： 第一个等式：122211a 132222121==-+⨯+⨯++ 第二个等式：2222223211a 1322(2)2121==-+⨯+⨯++第三个等式：3333234211a 1322(2)2121==-+⨯+⨯++ 第四个等式：4444245211a 1322(2)2121==-+⨯+⨯++按上述规律，回答下列问题：()1请写出第六个等式：6a =______=______；()2用含n 的代数式表示第n 个等式：n a =______=______； ()1234563a a a a a a +++++=______(得出最简结果)； ()4计算：12n a a a ++⋯+．28．学校准备添置一批课桌椅，原计划订购60套，每套100元，店方表示：如果多购，可以优惠．结果校方实际订购了72套，每套减价3元，但商店获得了同样多的利润．（1）求每套课桌椅的成本；（2）求商店获得的利润．【参考答案】***一、选择题1．B2．A3．A4．D5．A6．C7．A8．B9．A10．B11．C12．D二、填空题13．116°14．14115． SKIPIF 1 < 0解析：52 a-16．2023 17．201 18．121 19．7，8，13 20．±2三、解答题21．（1）2x；（2）点P原来的速度为53cm/s．（3）此时点E在AD边上，且DE=2.22．（1）15°；（2）12α；（3）①∠AOC＝2∠DOE；②4∠DOE－5∠AOF＝180°.23．画图见解析.24．-3x+y2，31 925．-4.26．错误，正确的解法见解析. 27．（1）()6266213222+⨯+⨯，6121+-7121+；（2）()2213222nn n +⨯+⨯，121n +-1121n ++；（3）1443；（4）()1122321n n ++-+.28．（1）每套课桌椅的成本为82元．（2）商店获得的利润为1080元．2019-2020学年七年级数学上学期期末模拟试卷一、选择题1．如图，点A 、B 在线段EF 上，点M 、N 分别是线段EA 、BF 的中点，EA ：AB ：BF ＝1：2：3，若MN ＝8cm ，则线段EF 的长是（ ）A.10 cmB.11 cmC.12 cmD.13 cm2．如果一个角α的度数为13°14'，那么关于x 的方程21803x x α-=︒-的解为（ ） A.76°46'B.76°86'C.86°56'D.166°46'3．如图，直线l 是一条河，P ，Q 是两个村庄。

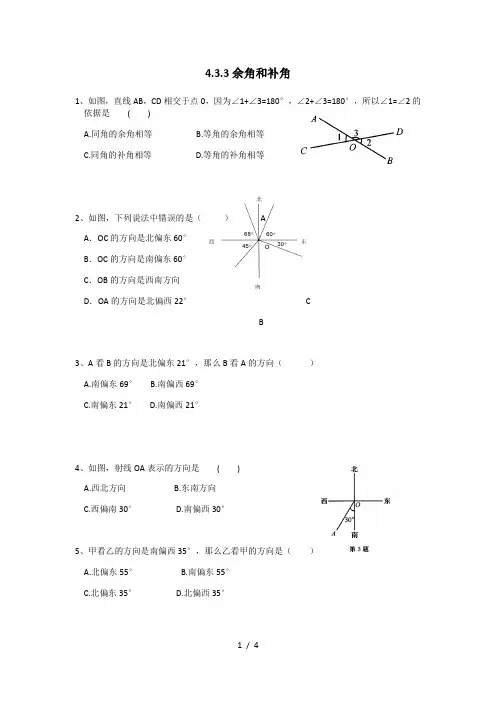
4.3.3余角和补角1、如图，直线AB，CD相交于点0，因为∠1+∠3=180°，∠2+∠3=180°，所以∠1=∠2的依据是( )A.同角的余角相等B.等角的余角相等C.同角的补角相等D.等角的补角相等2、如图，下列说法中错误的是（）AA．OC的方向是北偏东60°B．OC的方向是南偏东60°C．OB的方向是西南方向D．OA的方向是北偏西22°CB3、A看B的方向是北偏东21°，那么B看A的方向（）A.南偏东69°B.南偏西69°C.南偏东21°D.南偏西21°4、如图，射线OA表示的方向是( )A.西北方向B.东南方向C.西偏南30°D.南偏西30°5、甲看乙的方向是南偏西35°，那么乙看甲的方向是（）A.北偏东55°B.南偏东55°C.北偏东35°D.北偏西35°O EDCB6、一艘轮船从点A出发，沿南偏西60°方向航行到B点，再从B点出发沿北偏东15°方向航行到C点，则∠ABC等于（）A.45°B.75°C.105°D.135°7、如果∠1+∠2=180°，∠2+∠3=180°，则∠1___∠3（填＞、=或＜），理由是__________；8、如果∠1+∠2=90°，∠3+∠4=90°，∠1=∠4，则∠2___∠3，理由是____________.9、目标A在点C的北偏东60°方向，目标B在点C的南偏西20°方向，则∠ACB= 。

10、如图，直线AE上有一点O，∠AOC=90°，∠BOD=90°，有哪些相等的角？有哪些互余的角？有哪些互补的角？11、灯塔A在灯塔B的南偏东74°，轮船C在灯塔B的正东，在灯塔A的北偏西40°，画图确定轮船C的位置。

余角和补角单元检测班级：姓名：成绩：1、下列说法：①锐角的补角一定是钝角；②一个角的补角一定大于这个角；③如果两个角是同一个角的余角，那么它们相等；④锐角和钝角互补．其中，正确的说法有( )A．1个 B．2个 C．3个 D．4个2、如图所示，点A位于点O的__________方向上．（）A. 南偏东25°B. 北偏西65°C. 南偏东65°D. 南偏西65°第2题第3题第4题3、如图所示，∠AOB是直角，∠COD也是直角，∠AOC=α，则∠BOD等于CA. 90°+αB. α+180°C. 180°-αD. 90°-α4、如图所示，将一副三角板折叠放在一起，使直角的顶点重合于点O，则∠AOC+∠DO 的值= （）A.小于180°B.等于180 °C.大于180°D.不能确定5、南偏东40°与北偏东70°方向的两条射线所夹角是____ °6、若∠α与∠β互余，且∠α=15°，则∠β的补角的度数为________7、若∠1+∠2=90°，∠3+∠2=90°，则∠3____∠1，依据是________8、一个角的补角是它的余角的3倍，这个角是____________9、如图，AB是直线，O是AB上一点，∠AOE是直角，∠FOD=90°，OB平分∠DOC，则图中与∠DOE互余的角有哪些？与∠DOE互补的角有哪些？10、已知锐角α，那么α的补角与α的余角的差是（）A.60°+αB.90°C.120°D.180°-α11、如果∠α和∠β互补，且α<β,则下列表示β的余角的式子中正确的是（）：①90°-∠β；②∠α-90°；③180°-∠α；④（∠α-∠β），正确的是：A.①②③④B.①②④C.①②③D.①②12、小明有一张地图，如图所示，上面标有A、B、C三地，由于被墨迹污染，C地的具体位置看不清楚了，但知道C地在A地的北偏东30°，在B地的东南方向，A地在B地的东偏南70°．（1）请你在图中画一画，试着帮他确定C地在地图上的位置；（2）求∠ABC的大小．参考答案1、B2、B3、D4、B5、706、105°7、= 同角的余角相等8、45°9、与∠DOE互余的角有:∠FOE, ∠DOB, ∠COB;与∠DOE互补的角有：∠FOB, ∠EOC,10、B 11、B12、解：（1）如图所示，射线BC与AC的交点即为C点；（2）∵∠ABX=70°，∠CBX=45°，∴∠ABC=70°-45°=25°．故答案为：25°．。

第四章几何图形的初步余角和补角优选练习答案基础篇一 .选择题（共10小题)90°﹣∠ α；②∠β﹣ 90°；③ （∠β+∠ α）；④ （∠β1．假如∠ α和∠β互补，且∠α＜∠β，以下表达式：①﹣∠ α）中，等于∠ α的余角的式子有（）A．1 个B．2 个C．3 个D．4 个【答案】 C【详解】∵∠α和∠ β互补，且∠ α＜∠ β，∴∠ β=180°﹣∠ α，∠ α的余角是 90°﹣α，∠ β﹣ 90°=180°﹣∠ α﹣ 90°=90°﹣∠ α，（∠β+∠ α） = （ 180°﹣∠ α+∠ α） =90°，（∠β﹣∠ α）= （ 180°﹣∠ α﹣∠ α） =90°﹣∠ α，即①②④， 3 个，应选 C．2．（ 2018 ·南宁市期末）以下图形中，∠1 和∠ 2 互为余角的是()A．B．C．D．【答案】 D【详解】依据余角的定义，两角之和为90°，这两个角互余．D 中∠ 1 和∠ 2 之和为 90°，互为余角．应选： D．3．（ 2018 ·卢龙县期中）假如与互补，与互余，则与的关系是（）A．B．C．D．以上都不对【答案】 C【详解】∵∠ 1+∠ 2=180°∴∠ 1=180°-∠ 2又∵∠ 2+∠3=90°∴∠ 3=90°-∠ 2∴∠ 1-∠3=90°，即∠ 1=90°+∠ 3．应选 C．4．（ 2018 ·宁海县期末）如图，点O 在直线 DB 上，已知∠ 1=15 °，∠ AOC=90°，则∠ 2 的度数为（）A．B．C．D．【答案】 B【详解】解：∵∠ 1=15°，∠ AOC=90°，∴∠ COB=75°，∴∠ 2=180°-∠ COB=105°．应选： B．5．已知∠ α与∠ β互补，且∠ α＞∠ β，则∠ β的余角能够表示为（）A．B．C．D．【答案】 C【详解】∵∠ α与∠ β互补，∴∠ α+∠β=180°，∵∠ α＞∠ β，∴∠ β=180°-∠ α，∴∠ β的余角为： 90°-（ 180°-∠ α）=∠ α-90 °=∠ α- （∠α+∠ β） = ∠ α-∠ β=（∠ α-∠β），应选： C．6．如图， O 为直线 AB 上一点，∠ AOC=α，∠ BOC=β，则β的余角可表示为（）A．（α +β）B．αC．（α﹣β）D．β【答案】 C【详解】由邻补角的定义，得∠ α+∠ β=180°，两边都除以2，得（α +β） =90 °，β的余角是（α +β）-β= （α-β），应选 C．7．已知∠ 1 与∠ 2 互余，∠ 2 与∠ 3 互补，∠ 1=58 °，则∠ 3=（）A．58°B．148 °C．158 °D． 32°【答案】 B【详解】解：∵∠ 1 与∠ 2 互余，∠ 1=58°，∴∠ 2=90°﹣∠ 1=32°，又∵∠ 2 与∠ 3 互补，∴∠ 3=180°﹣∠ 2=180°﹣32°=148°.应选： B.8．（ 2018 ·海口市期末）如图∠BCA=90，CD⊥AB，则图中互余的角有（）对.A．1B．2C． 3D． 4【答案】 D【详解】∵∠ BCA=90， CD⊥ AB，∴互余的角有：∠ A 与∠ B，∠ A 与∠ ACD，∠ ACD与∠ BCD，∠ BCD与∠ B，共 4 对．应选： D．9．（ 2018 ·武汉市期末）如图，点 B 在点 A 的方向是（）A．南偏东 43°B．北偏西47°C．西偏北 47°D．东偏南47°【答案】 B【详解】解：如图，由余角的定义，得∠CAB=90o-43o=47o，∴点 B 在点 A 的北偏西47o.应选 B.10．（ 2018 ·惠州市实验中学初一期末）一个角的补角为158 °，那么这个角的余角是（）A．22°B．52°C． 58°D．68°【答案】 C【详解】详解：设原角为∠ α，所求角为∠β，则∠α=180°-158 °=22°，∠ β=90°-∠ α=68°．应选 C．提升篇二. 填空题（共5小题)11．（ 2018 ·兴化市期末）如图，射线OA⊥ OC，射线 OB⊥ OD，若∠ AOB＝ 40°，则∠ COD＝____ °.【答案】40【详解】解：∵OA⊥ OC， OB⊥ OD，∴∠ AOC=90°，∠ BOD=90°，∴∠ AOB 与∠ BOC互余，∠ COD 与∠ BOC互余，∴∠ AOB=∠ COD =40°，故答案为：40°．12．（ 2019 ·顺义区期末）如图，订交于点，均分AOD ，若，则的度数是_____________.【答案】 150°【详解】∵∠ BOC＝，∴∠ AOD＝∠ BOC＝.∴∠ AOC＝-＝，∵OE 均分∠ AOD∴∠ AOE＝∠ AOD＝×.∴∠ AOC＋，故答案为：.13．（ 2018 ·北京北方交大附中第二分校初一期末）一个角的余角比它的补角的多 1°，则这个角的度数为______ 度．【答案】 63【详解】设这个角为x°，则它的余角为（90﹣ x）°，补角为（ 180﹣x）°，依据题意有：（ 90﹣ x） = （180 ﹣x） +1，解得x=63，故答案为： 63．14．（ 2019 ·南山区期末）如图，直线AB， CD 订交于点O， EO⊥ AB 于点 O，∠ EOD=50°，则∠ BOC的度数为_____．【答案】 140°【分析】详解：∵直线AB，CD 订交于点 O， EO⊥AB 于点 O，∴∠ EOB=90°，∵∠ EOD=50°，∴∠ BOD=40°，则∠ BOC的度数为： 180°-40 °=140°．故答案为： 140°．15．（ 2018 ·长兴县期末）一个角的余角比这个角的补角的一半小40°，则这个角为 _____度．【答案】 80【分析】试题分析：设这个角为x，则它的余角为补角为由题意得，解得故答案为：80.三 .解答题（共2小题)16．（ 2017 ·扬州中学教育公司树人学校初一期末）如图，直线AB，CD 订交于点O，OE 均分，，图中的余角是______把切合条件的角都填出来；假如，那么依据______可得______ 度；假如，求和的度数．【答案】（1）∠ BOC、∠ AOD（2）对顶角相等， 160（ 3） 26°【分析】试题剖析：（ 1）依据互余两角和为90°，联合图形找出即可；（2）从图形中可知∠ AOC 和∠ DOB 为对顶角，直接可求解；（3）依据角均分线可求∠ AOD 的度数，而后依据对顶角和邻补角可求解.试题分析：（ 1）图中∠ AOF的余角是∠ BOC、∠ AOD（把切合条件的角都填出来）；（ 2）假如∠ AOC=160°，那么依据对顶角相等可得∠BOD=160 度；（3）∵ OE 均分∠ AOD，∴∠AOD=2∠ 1=64°，∴∠ 2=∠ AOD=64°，∠ 3=90°﹣ 64°=26°．17．（ 2017 ·弥勒市江边中学初一期末）如图，O 是直线 AC上一点， OB 是一条射线， OD 均分∠ AOB，OE在∠BOC内部，∠ BOE＝∠ EOC，∠ DOE＝ 70°，求∠ EOC的度数．【答案】 80°【分析】设∠ BOE=x°，则∠ EOC=2x°，由∠ DOE=70°，OD 均分∠ AOB 知，∠ AOD=∠DOB=70°﹣ x°，再依据∠ AOD+∠DOB+∠BOE+∠EOC=180°，列出对于 x 的方程求解即可．解：如图，设∠ BOE=x°，∵∠ BOE= ∠ EOC，∴∠ EOC=2x°，∵OD 均分∠ AOB，∴∠ AOD=∠ DOB=70°﹣ x°，∵∠ AOD+∠ DOB+∠ BOE+∠ EOC=180°，∴70°﹣ x°+70°﹣ x°+x°+2x°=180°，∴x°=40°，∴∠ EOC=80°．18．（ 2018 ·扬州市期末）如图，直线AB、 CD 订交于点O， OE均分∠ BOD．（1）若∠ AOC=68°，∠ DOF=90°，求∠ EOF 的度数．（2）若 OF均分∠ COE，∠ BOF=30°，求∠ AOC的度数．【答案】（1） 56°；（ 2） 80°．【剖析】(1) 依据对顶角相等和角均分线的定义计算即可;(2)设∠ AOC=x, 依据对顶角相等和角均分线的定义用x 表示出∠ BOE 和∠ EOF, 依据题意列方程 , 解方程即可 .【详解】（1）∵直线 AB、 CD 订交于点 O，∴∠ BOD=∠ AOC=68°，∵ OE 均分∠ BOD，∴∠ DOE= ∠ BOD=34°，∴∠ EOF=∠ DOF﹣∠ DOE=56°；（2）设∠ AOC=x，则∠ BOD=x，∵ OE 均分∠ BOD，∴∠ BOE=∠ DOE= x，∵ OF 均分∠ COE，∴∠ EOF=（ 180°﹣ x），由题意得，（ 180°﹣ x）﹣ x=30°，解得， x=80°，∴∠ AOC=80°．。

2019-2020 学年七年级数学上册第四章《余角和补角》练习新人教版一、选择题题号12345678910答案1．以下说法中正确的选项是( )A．一个角的补角只有一个B．一个角的补角必大于这个角C．若不相等的两个角互补，则这两个角一个是锐角，一个是钝角D．互余的两个角必然相等2．若是一个角等于360，那么它的余角等于( )A. 64 0B. 540C. 1440D. 360※ 3．以下结论中，正确的个数有( )(1)一个角的补角比这个角的余角大900(2) 互余的两个角的比是4:6 ，这两个角分别是360和 540(3)小于平角的角是钝角(4)两个角互补，必然一个锐角，另一个钝角．A． 0 个 B ． 1 个 C ． 2 个 D ． 3 个4．∠=∠，且∠与∠互余，则( )A. ∠=900B.∠=450C.∠=600D.∠=3005．以下说法正确的选项是()A ．一个锐角的余角是一个锐角B．一个锐角的补角是一个锐角C ．一个锐角的补角不是一个钝角D．一个锐角的余角是一个直角※ 6． A 看 B 的方向是北偏东190，那么 B 看 A 的方向是()A ．南偏东 710B ．南偏西 710C ．南偏东 190D ．南偏西 1907．一个锐角的余角加上900，就等于()A ．这个锐角的余角B．这个锐角的补角C ．这个锐角的 2 倍D．这个锐角的 3 倍8．一个角的余角比它自己小，这个角是( )A ．大于 450B．小于 450C ．大于 00小于 450D．大于450小于 9009．如图，已知∠ ACB= 900，∠ l= ∠ B，∠ 2=∠ A，那么以下说法错误的选项是( )A ．∠ l 与∠ 2 是互为余角B．∠ A 与∠B 不是互为余角C ．∠ 1 与∠ A 是互为余角D．∠ 2 与∠ B 是互为余角10. OA 表示南偏西400方向的一条射线，则OA的方向还可以表示为( )A．北偏西 400 B ．西偏南 500 C ．西偏南 400 D ．北偏东 400二、填空题11. 若∠与∠都是 _______角，则∠与∠互补，若∠与∠互补，∠是锐角，则∠是 ______角．12. 如图， OA与 OB的夹角为 ______0， OC的方向为 ________ ．000013．如图，直线 AB、CD订交于 O，∠ BOE=90，若∠ 3=45 ，则∠ 1=______，∠ 4=_____ .∠ 1 和∠ 2 叫做互为 ____角，∠ 3 和∠ 4 互为 _____角．14.一个角的补角是这个角的 5 倍，则这个角的余角为 _______015.一个角的余角是 55047/ 25//, 则这个角是 __________.16．如图，∠ AOC=∠COB=90， OE均分∠ AOC， OD均分∠ COB，则∠ COD的余角有_________ 个，是 _________________________.第 12 题图第13题图第16题图17．若两角之和是1800，我们说这两个角互补．∠ 1与∠ 2互补，∠ 3与∠ 4互补，若是∠ l=∠ 2，则∠ 2=____0，∠1+∠ 2+∠3+∠ 4=_______0.18．互补两角之比是2： 3，则这两个角分别是______________.19．（南通）已知∠ a= 35 019/，则∠ a 的余角等于 ________.20．（内江）一个角的余角比它的补角的1少200，则这个角为______0 2三、解答题21．如图，已知AOB为直线， OC均分∠ AOD，∠ BOD=30，求∠ AOC的度数．22．一个角的余角的 3 倍等于它的补角，求这个角，23．已知一个角的余角比这个角的补角的一半还少40，求这个角的度数．24．如图，在一个五边形的边AB上有一点O，将 O与五边形的极点C、 D、 E 相连，∠COB =360，∠ DOE= 540， OC、 OE分别是∠ DOB、∠ AOD的均分线。

∠1与∠3互补,∠2与∠3的和等于周角的1,则∠1,∠2,∠33C.3个D.4角的三角板的60°角的顶点与另一个三角板的直角顶点重合( )C.58°19'倍少20°,则这个角的度数是C.40°B.OB的方向是北偏西D.OD的方向是南偏东C.3对D.4方向走到点B,乙从点 C.120° 如果一个角的余角与它的补角度数之比为2∶5,则这个角等于 互为余角,∠α=38°24',则∠β= 互为余角,∠A=60°,则∠B的度数是 A,B,O,在小岛O处观测到小岛若∠AOC+∠BOD=90°,则∠BOC= 2倍还大45°,则这个角的度数为 方向,点B在点O的北偏东点重合摆放在桌等于这个角的余角的3倍,求这个角的度数22.(1)如图1所示,一副直角三角尺的直角顶点重合在点O处.①∠AOC与∠BOD相等吗?说明理由;②∠AOD与∠BOC数量上有什么关系?说明理由;(2)若将这副直角三角尺按图2所示的方式摆放,直角顶点重合在点O处,不添加字母,分析图中已标注字母所表示的角.①找出图中相等的角;②找出图中互补的角,并说明理由.的补角,∴∠DOH=∠BOF=40°,∴∠AOB+∠BOC=∠DOC+∠BOC,即∠AOC=∠BOD.②∠AOD+∠BOC=180°.理由如下:∵∠AOD+∠BOC+∠COD+∠AOB=360°,∠AOB=∠COD=90°,∴∠AOD+∠BOC=180°.(2)①∠AOB=∠COD,∠AOC=∠BOD.②∠AOB与∠COD互补,∠AOD与∠BOC互补.理由如下:∵∠AOB=∠COD=90°,∴∠AOB+∠COD=180°,即∠AOB与∠COD互补. ∵∠AOD=∠AOB+∠BOD=90°+∠BOD,∠BOC=∠COD-∠BOD=90°-∠BOD,∴∠AOD+∠BOC=90°+∠BOD+90°-∠BOD=180°,∴∠AOD与∠BOC互补.。

2020-2021学年人教版七年级数学上学期《4.3.3 余角和补角》测试卷一．选择题（共10小题）1．若α＝29°45′，则α的余角等于（）A．60°55′B．60°15′C．150°55′D．150°15′2．与30°的角互为余角的角的度数是（）A．30°B．60°C．70°D．90°3．已知∠α＝60°32′，则∠α的余角是（）A．29°28′B．29°68′C．119°28′D．119°68′4．如果∠1和∠2互补，且∠1＞∠2，则下列表示∠2的余角的式子中：①90°﹣∠1；②∠1﹣90°；③（∠1+∠2）；④（∠1﹣∠2）．正确的有（）A．1个B．2个C．3个D．4个5．下列说法：①射线AB和射线BA是同一条射线；②锐角和钝角互补；③若一个角是钝角，则它的一半是锐角；④一个锐角的补角比这个角的余角大90度．其中正确的个数是（）A．1个B．2个C．3个D．4个6．如果∠1与∠2互余，∠2与∠3互余，那么∠1与∠3的关系为（）A．互余B．互补C．相等D．无法确定7．如果∠1的余角是∠2，并且∠1＝2∠2，则∠1的补角为（）A．30°B．60°C．120°D．150°8．如图，在△ABC中，∠BAC＝90°，点D，E分别在BC，CA边的延长线上，EH⊥BC 于点H，EH与AB交于点F．则∠1与∠2的数量关系是（）A．∠1＝∠2B．∠1与∠2互余C．∠1与∠2互补D．∠1+∠2＝100°9．∠1、∠2互为补角，且∠1＞∠2，则∠2的余角是（）A．∠1+∠2B．∠1﹣∠2C．∠1﹣90°D．90°﹣∠1 10．如图，一副三角板按不同的位置摆放，摆放位置中∠1≠∠2的是（）A．B．C．D．二．填空题（共9小题）11．如果∠α＝35°，那么∠α的余角等于°．12．如图，∠AOB与∠BOD互为余角，OB是∠AOC的平分线，∠AOB＝25°，则∠COD 的度数是．13．已知∠α和∠β互为余角，且∠β比∠α大40°，则∠β＝°．14．一个角的余角的度数为30°，则这个角的补角的度数为．15．如图，∠AOC与∠BOD都是直角，且∠AOD：∠AOB＝7：2，则∠AOB等于度．16．已知∠α+∠β＝90°，且∠α＝35°41′，则∠β＝．17．如图，将一副直角三角尺的直角顶点C叠放在一起，若∠ECD比∠ACB的小6°，则∠BCD的度数为．18．如图将一副三角板的直角顶点重合，摆放在桌面上，若∠AOC＝110°，则∠BOD。