五年级奥数专题组合图形面积

组合图形的面积一、已知右面的两个正方形边长分别为6分米和4分米，求图中阴影部分的面积。

分析：S阴影=6*6+4*4－4*10÷2－6*6÷2=14平方分米二、右图是两个相同的直角三角形叠在一起，求阴影部分的面积。

（单位：厘米）分析：S阴影=（7+10）*2÷2=17平方厘米三、如图，这个长方形的长是9厘米，宽是8厘米，A和B是宽的中点，求长方形内阴影部分的面积。

分析：S阴影=4*H1÷2+4*H2÷2=2*（H1+ H2）=2*9=18平方厘米四、在右图中，三角形EDF的面积比三角形ABE的面积大6平方厘米，已知长方形ABDC的长和宽分别为6厘米、4厘米，DF的长是多少厘米？分析：S ACF=S ACDE+S EDF S ABCD= S ACDE+S ABES ACF－S ABCD= S ACDE+S EDF －（S ACDE+S ABE）= S EDF－S ABE=6平方厘米S ACF=（4+DF）*6÷2 S ABCD =4*6=24平方厘米S ACF－S ABCD=（4+DF）*6÷2－24=6；求得DF=6厘米五、右图是一块长方形公园绿地，绿地长24米，宽16米，中间有一条宽为2米的道路，求草地（阴影部分）的面积。

分析：S阴影=24*16－（24+16）*2+4*2*2=512平方米六、如图，三角形ABC的面积是24平方厘米，且DC=2AD，E、F分别是AF、BC的中点，那么阴影部分的面积是多少？分析：因为F是中点，S ABF与S AFC面积相等；S ABC=S ABF+S AFC故S ABF与S AFC面积为12平方厘米，同理E是中点，S ABE与S BEF面积相等；S ABE与S BEF面积为6平方厘米，DC=2AD；故S BCD=2S ABDS ABC=S BCD+ S ABD；S ABD面积为8平方厘米，S BCD面积为16平方厘米S阴影=S BCD－S BEF=16－6=10平方厘米七、如图，三角形ABC的面积是90平方厘米，EF平行于BC，AB=3AE，那么三角形甲、乙、丙的面积各是多少平方厘米？分析：BE=2AE，故S BEC=2S ACE；S ABC=S BEC+ S ACE；S BEC面积为60平方厘米，S ACE面积为30平方厘米EF平行于BC，CF=2AF，故S CEF=2S AEF；S ACE =S CEF+ S AEF；S CEF面积为20平方厘米，S AEF面积为10平方厘米甲面积为10平方厘米；乙面积为20平方厘米；丙面积为60平方厘米八、如图长方形，长18厘米，宽12厘米，AE、AF两条线段把长方形面积三等分，求三角形AEF的面积。

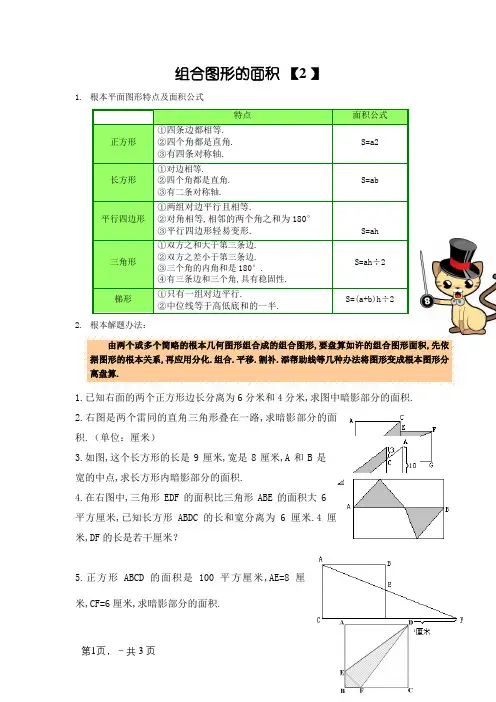
组合图形的面积【2 】1.根本平面图形特点及面积公式特点面积公式正方形①四条边都相等.②四个角都是直角.③有四条对称轴.S=a2长方形①对边相等.②四个角都是直角.③有二条对称轴.S=ab平行四边形①两组对边平行且相等.②对角相等,相邻的两个角之和为180°③平行四边形轻易变形.S=ah三角形①双方之和大于第三条边.②双方之差小于第三条边.③三个角的内角和是180°.④有三条边和三个角,具有稳固性.S=ah÷2梯形①只有一组对边平行.②中位线等于高低底和的一半.S=(a+b)h÷22.根本解题办法：由两个或多个简略的根本几何图形组合成的组合图形,要盘算如许的组合图形面积,先依据图形的根本关系,再应用分化.组合.平移.割补.添帮助线等几种办法将图形变成根本图形分离盘算.1.已知右面的两个正方形边长分离为6分米和4分米,求图中暗影部分的面积.2.右图是两个雷同的直角三角形叠在一路,求暗影部分的面积.（单位：厘米）3.如图,这个长方形的长是9厘米,宽是8厘米,A和B是宽的中点,求长方形内暗影部分的面积.4.在右图中,三角形EDF的面积比三角形ABE的面积大6平方厘米,已知长方形ABDC的长和宽分离为6厘米.4厘米,DF的长是若干厘米？5.正方形ABCD的面积是100平方厘米,AE=8厘米,CF=6厘米,求暗影部分的面积.6.右图是一块长方形公园绿地,绿地长24米,宽16米,中央有一条宽为2米的道路,求草地（暗影部分）的面积.7.如图,三角形ABC的面积是24平方厘米,且DC=2AD,E.F分离是AF.BC的中点,那么暗影部分的面积是若干？8.如下图,是一块长方形草地,长方形的长是16米,宽是10米,中央有两条宽2米的道路,一条是长方形,一条是平行四边形,那么有草部分（暗影部分）的面积有多大？9.如图,一个三角形的底长5米,假如底延伸1米,那么面积就增长2平方米.问本来的三角形的面积是若干平方米?1米组合图形的面积功课1.在右图中,三角形EDF的面积比三角形ABE的面积大75平方厘米,已知正方形ABCD的边长为15厘米,DF的长是若干厘米？2.如图,ABCD是一个长12厘米,宽5厘米的长方形,求暗影部分三角形ACE的面积.3.已知正方形乙的边长是8厘米,正方形甲的面积是36平方厘米,那么图中暗影部分的面积是若干？4.如图,A.B两点是长方形长和宽的中点,那么暗影部分占长方形的面积是若干？5.如图,在平行四边形ABCD中,E.F分离是AC.BC的三等分点,且平行四边形的.面积为54平方厘米,求S△BEF6.盘算右边图形的面积.（至罕用3种办法）（单位：米）。

人教版五年级奥数教案：组合图形的面积
专题知识点详解：
在组合图形中，三角形的面积出现的机会很多，解题时我们还可以记住下面三点：
1，两个三角形等底、等高，其面积相等；
2，两个三角形底相等，高成倍数关系，面积也成倍数关系；
3，两个三角形高相等，底成倍数关系，面积也成倍数关系。

例题如图，ABCD是直角梯形，求阴影部分的面积和。

（单位：厘米）
分析按照一般解法，首先要求出梯形的面积，然后减去空白部分的面积即得所求面积。

其实，只要连接AC，显然三角形AEC与三角形DEC同底等高其面积相等，这样，我们把两个阴影部分合成了一个三角形ABC。

面积是：6×3÷2=9平方厘米。

第1 页共1 页。

第18讲组合图形面积（一）一、知识要点组合图形是由两个或两个以上的简单的几何图形组合而成的。

组合的形式分为两种：一是拼合组合，二是重叠组合。

由于组合图形具有条件相等的特点，往往使得问题的解决无从下手。

要正确解答组合图形的面积，应该注意以下几点：1.切实掌握有关简单图形的概念、公式，牢固建立空间观念；2.仔细观察，认真思考，看清所求图形是由哪几个基本图形组合而成的；3.适当采用增加辅助线等方法帮助解题；4，采用割、补、分解、代换等方法，可将复杂问题变得简单。

二、精讲精练【例题1】一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？练习1：1.求四边形ABCD的面积。

（单位：厘米）2.已知正方形ABCD的边长是7厘米，求正方形EFGH的面积。

3.有一个梯形，它的上底是5厘米，下底7厘米。

如果只把上底增加3厘米，那么面积就增加4.5平方厘米。

求原来梯形的面积。

【例题2】正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

练习2：1.（如下图）已知大正方形的边长是12厘米，求中间最小正方形的面积。

2.正图长方形ABCD的面积是16平方厘米，E、F都是所在边的中点，求三角形AEF的面积。

3.求下图（上右图）长方形ABCD的面积（单位：厘米）。

【例题3】四边形ABCD和四边形DEFG都是正方形，已知三角形AFH的面积是7平方厘米。

三角形CDH的面积是多少平方厘米？练习3：1.图中两个正方形的边长分别是6厘米和4厘米，求阴影部分的面积。

2.下图中两个完全一样的三角形重叠在一起，求阴影部分的面积。

（单位：厘米）3.下图中，甲三角形的面积比乙三角形的面积大多少平方厘米？【例题4】下图中正方形的边长为8厘米，CE为20厘米，梯形BCDF的面积是多少平方厘米？练习4：1.如下图，正方形ABCD中，AB=4厘米，EC=10厘米，求阴影部分的面积。

【小学五年级奥数讲义】组合图形面积（一）一、知识重点组合图形是由两个或两个以上的简单的几何图形组合而成的。

组合的形式分为两种：一是拼合组合，二是重叠组合。

因为组合图形拥有条件相等的特色，常常使得问题的解决无从下手。

要正确解答组合图形的面积，应当注意以下几点：1.确实掌握相关简单图形的观点、公式，坚固成立空间观点；2.认真察看，认真思虑，看清所求图形是由哪几个基本图形组合而成的；3.适合采纳增添协助线等方法帮助解题；4，采纳割、补、分解、代换等方法，可将复杂问题变得简单。

二、精讲精练【例题 1】一个等腰直角三角形，最长的边是 12 厘米，这个三角形的面积是多少平方厘米？练习 1：1. 求四边形 ABCD的面积。

（单位：厘米）2.已知正方形 ABCD的边长是 7 厘米，求正方形 EFGH的面积。

3.有一个梯形，它的上底是 5 厘米，下底 7 厘米。

假如只把上底增添 3 厘米，那么面积就增添4.5 平方厘米。

求本来梯形的面积。

【例题 2】正图正方形中套着一个长方形，正方形的边长是12 厘米，长方形的四个角的极点把正方形的四条边各分红两段，此中长的一段是短的 2 倍。

求中间长方形的面积。

练习 2：1. （以下列图）已知大正方形的边长是12 厘米，求中间最小正方形的面积。

2.正图长方形 ABCD的面积是 16 平方厘米， E、F 都是所在边的中点，求三角形AEF的面积。

3.求下列图（上右图）长方形 ABCD的面积（单位：厘米）。

【例题 3】四边形 ABCD和四边形 DEFG都是正方形，已知三角形AFH的面积是7 平方厘米。

三角形CDH的面积是多少平方厘米？练习 3：1. 图中两个正方形的边长分别是 6 厘米和 4 厘米，求暗影部分的面积。

2.下列图中两个完整同样的三角形重叠在一同，求暗影部分的面积。

（单位：厘米）3.下列图中，甲三角形的面积比乙三角形的面积大多少平方厘米？【例题 4】下列图中正方形的边长为 8 厘米， CE为 20 厘米，梯形 BCDF的面积是多少平方厘米？练习 4：1. 以下列图，正方形ABCD中， AB=4厘米， EC=10厘米，求暗影部分的面积。

组合图形面积（一）专题简析：组合图形是由两个或两个以上的简单的几何图形组合而成的。

组合的形式分为两种：一是拼合组合，二是重叠组合。

由于组合图形具有条件相等的特点，往往使得问题的解决无从下手。

要正确解答组合图形的面积，应该注意以下几点：1，切实掌握有关简单图形的概念、公式，牢固建立空间观念；2，仔细观察，认真思考，看清所求图形是由哪几个基本图形组合而成的；3，适当采用增加辅助线等方法帮助解题；4，采用割、补、分解、代换等方法，可将复杂问题变得简单。

例1 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？分析与解答由于此三角形中只知道最长的边是12厘米，所以，不能用三角形的面积公式来计算它的面积。

我们可以假设有4个这样的三角形，且拼成了下图正方形。

显然，这个正方形的面积是12×12，那么，一个三角形的面积就是12×12÷4=36平方厘米。

练习一1，求四边形ABCD的面积。

（单位：厘米）2，已知正方形ABCD的边长是7厘米，求正方形EFGH的面积。

例2 右图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

分析与解答图中的两个小三角形平移后可拼得一个小正方形，两个大三角形平移后可拼得一个大正方形。

这两个正方形的边长分别是12÷（1＋2）=4（厘米）和4×2=8（厘米）。

中间长方形的面积只要用总面积减去这两个拼起来的正方形的面积就可以得到。

即：12×12－（4×4＋8×8）=64（平方厘米）1，（如下图）已知大正方形的边长是12厘米，求中间最小正方形的面积。

2，如下图长方形ABCD的面积是16平方厘米，E、F都是所在边的中点，求三角形AEF的面积。

例3 四边形ABCD和四边形DEFG都是正方形，已知三角形AFH 的面积是7平方厘米。

【五年级奥数举一反三—全国通用】测评卷24《组合图形的面积》试卷满分：100分考试时间：100分钟姓名：_________班级：_________得分：_________ 一．选择题（共8小题，满分16分，每小题2分）1．（2分）如图中长方形的面积相等，则图中阴影部分面积相比较，()A．甲的面积大B．乙的面积大C．甲和乙的面积相等D．无法确定【解答】解：甲的面积=长方形的长⨯长方形的宽2÷；乙的面积=长方形的长⨯长方形的宽2÷；即：甲乙的面积都是长方形面积的一半，它们的面积一样大．故选：C。

2．（2分）在图中，平行线间的三个图形，它们的面积()A．平行四边形最大B．三角形最大C．梯形最大D．一样大【解答】解：设他们的高为h，平行四边形的面积4h=三角形的面积184 2h h =⨯⨯=梯形面积(26)24h h=+⨯÷=所以它们的面积相比，都相等；故选：D。

3．（2分）甲长方形包含16个小正方形，乙长方形包含12个小正方形．甲长方形与乙长方形的面积相比，结果是什么？()A．甲的面积大B．乙的面积大C．无法确定【解答】解：因为不能确定甲、乙长方形包含的小正方形的面积是否相等，所以无法比较甲长方形与乙长方形面积的大小；故选：C．4．（2分）如图所示，把一个长方形分成一个梯形和一个三角形．已知梯形的面积比三角形的面积大18厘米2，那么梯形的上底长为()厘米．A．2 B．3 C．4 D．6【解答】解：设梯形的上底为a厘米，那么三角形的底为(12)a-厘米，根据题意可得：+⨯÷--⨯÷=(12)62(12)6218a a+⨯--⨯=a a(12)3(12)318+-+=a a33636318a=618a=3答：梯形的上底是3厘米．故选：B．5．（2分）如图，甲、乙两个平行四边形中阴影部分面积的大小为()A．甲>乙B．甲=乙C．甲<乙D．无法确定【解答】解：如图：甲+丙=乙+丙，丙是公共部分，所以甲=乙，答：甲的面积等于乙的面积．故选：B ．6．（2分）如图的长方形中有三个三角形，它们面积间的关系是( )A ．123S S S +=B ．13S S =C ．23S S =D ．321S S S =-【解答】解：由图可知：2S 的面积是长方形形面积的一半，3S 和1S 的面积和也是长方形面积的一半，由此可得：132S S S +=，即：321S S S =-．故选：D ．7．（2分）图中，直线//a b ，比较三角形ADC 和三角形ABD 面积的大小，结果是( )A ．三角形ADC 面积大B ．三角形ABD 面积大C ．它们的面积相等D ．无法比较【解答】解：由题意可知：三角形ADC 和三角形ABD 等底等高，所以角形ADC 和三角形ABD 面积相等． 故选：C ．8．（2分）如图ABCD 是长方形，已知4AB =厘米，6BC =厘米，三角形EFD 的面积比三角形ABF 的面积大6平方厘米，求(ED = )厘米．A ．9B ．7C ．8D ．6【解答】解：长方形ABCD 的面积：4624⨯=（平方厘米）；三角形EBC的面积：+=（平方厘米）；24630⨯÷=（厘米）；CE的长：302610DE的长：1046-=（厘米）．故选：D．二．填空题（共9小题，满分18分，每小题2分）9．（2分）如图，图中2=，阴影部分的面积是6平方厘米，求梯形ABCD的面积是27平方厘米．BO DO【解答】解：因为2=，BO DO所以三角形CDO的面积=三角形BCO面积的一半，即三角形CDO的面积3=平方厘米；三角形BCD与三角形ACD同底等高，所以三角形BCD与三角形ACD的面积相等，三角形AOD的面积=三角形BCO的面积，即三角形AOD的面积6=平方厘米；=，三角形ABO的面积是三角形AOD面积的2倍，BO DO2即三角形AOB的面积12=平方厘米；梯形ABCD的面积为：6361227+++=（平方厘米），答：梯形ABCD的面积为27平方厘米．故答案为：27．10．（2分）如图涂色部分的面积是322cm．【解答】解：8866⨯+⨯=+6436=（平方厘米）100(86)62882+⨯÷+⨯÷=+423274=（平方厘米）⨯-÷6(86)2=⨯÷6226=（平方厘米）-+100746=+266=（平方厘米）32答：涂色部分的面积是232cm．故答案为：32．11．（2分）如图，它是由两个正方形拼成的，小正方形的边长为2厘米，大正方形的边长为4厘米，阴影部分的面积为6平方厘米．【解答】解：(24)22+⨯÷=⨯÷622=（平方厘米）6答：阴影部分的面积是6平方厘米．故答案为：6．12．（2分）六个等腰三角形如图摆放，那么四个空白三角形的面积和是两个阴影三角形的面积和的6倍．【解答】解：如下图：把这六个等腰直角三角形从小到大分别编号为①②③④⑤⑥，设①号三角形的面积为1，则②号的面积为2，③号的面积为4，④号的面积为8，⑤号的面积为16，⑥号的面积为32，+++÷+(241632)(18)=÷5496=答：四个空白三角形的面积和是两个阴影三角形的面积和的6倍．故答案为：6．13．（2分）如图，梯形的面积是18．【解答】解：如图：已知45BAC∠=︒，90ABC∠=︒，所以180904545ACB∠=︒-︒-︒=︒，所以AB BC=；因为90ACE∠=︒，所以180904545ECD∠=︒-︒-︒=︒，则45DEC∠=︒，所以DE CD=，梯形的面积()62DE AB=+⨯÷()62BC CD=+⨯÷662=⨯÷18=．故答案为：18．14．（2分）如图：ABCD是一个面积为36平方厘米的长方形，E为BC中点，则阴影部分的面积是15平方厘米．【解答】解：据分析可知：三角形ABE的面积为13694⨯=（平方厘米）；三角形DHC的面积和三角形ADH的面积比是1:2，而三角形ADC的面积是36218÷=（平方厘米），所以三角形DHC 的面积为18(12)6÷+=（平方厘米），则三角形AHE 的面积也是6平方厘米．所以阴影部分的面积是9615+=（平方厘米）．答：阴影部分的面积是15平方厘米．故答案为：15．15．（2分）如图，ABCD 是直角梯形，5AD =厘米，3DC =厘米，三角形DOC 的面积是1.5平方厘米，则阴影部分的面积是 6 平方厘米．【解答】解：352 1.5⨯÷-，7.5 1.5=-，6=（平方厘米）； 答：阴影部分的面积是6平方厘米．故答案为：6．16．（2分）图中直角三角形里有3个正方形，已知25AD cm =，100BD cm =，阴影部分的面积是 10754 2cm ．【解答】解：100:25100254=÷=4BC AB =4(25100)=⨯+500=（厘米）设最小正方形的边长为x 厘米4()1005004x x x x ++++= 6.25100500x ++=6.25100100500100x +-=-6.25400x =6.25 6.25400 6.25x ÷=÷64x =中正方形的边长：4x x + 64644=+6416=+80=（厘米）500(25100)2(10010080806464)⨯+÷-⨯+⨯+⨯5001252(1000064004096)=⨯÷-++3125020496=-10754=（平方厘米）答：阴影部分的面积是10754平方厘米．故答案为：10754．17．（2分）如图，已知正方形ABCD 的周长是40厘米， 6.4DE =厘米，阴影部分的面积是 32 平方厘米．【解答】解：由分析可知阴影部分的面积为：6.4(404)2⨯÷÷6.4102=⨯÷642=÷32=（平方厘米）； 答：阴影部分的面积是32平方厘米．故答案为：32．三．计算题（共3小题，满分18分，每小题6分）18．（6分）求阴影部分面积．【解答】解：（1）222+=，空白三角形是一个直角三角形，304050空白三角形的面积：30402⨯÷=÷12002=（平方分米）600斜边上的高：⨯÷600250=÷120050=（分米）24+⨯÷(4050)242=⨯÷90242=（平方分米）1080-=（平方分米）1080600480答：阴影部分的面积是480平方分米．（2）40403030⨯+⨯=+1600900=（平方分米）2500⨯÷=（平方分米）40402800+⨯÷(4030)302=⨯÷70302=÷21002=（平方分米）1050--25008001050=-17001050=（平方分米）650答：阴影部分的面积是650平方分米．19．（6分）平行四边形ABCD的边BC长10厘米，直角三角形的直角边EC长8厘米．已知阴影部分的面积比三角形EGF的面积大9平方厘米．求CF的长．【解答】解：设EF长为x厘米，则CF就是8x-厘米，根据题干分析可得方程：x⨯-=⨯÷+10(8)10829-=801049xx=1031x=3.1-=（厘米）；8 3.1 4.9答：CF长为4.9厘米．20．（6分）求图中阴影部分的面积．【解答】解：6644662(64)42⨯+⨯-⨯÷-+⨯÷3616181042=+--⨯÷=+--36161820=（平方厘米）14答：阴影部分的面积是14平方厘米．四．应用题（共5小题，满分29分）21．（5分）如图是一幢楼房占地的平面图，算一算它的占地面积有多大？（单位：)m你能想出几种算法？【解答】解：方法一如图：⨯+-⨯-÷6048(6030)(7248)2=+⨯÷288030242=+28803603240=（平方米）方法二如图：⨯-+⨯-÷7260(6030)(7248)2432090242=-⨯÷=-43201080=（平方米）3240答：它的占地面积有3240平方米。

五年级组合图形面积专题简析：组合图形是由两个或两个以上的简单的几何图形组合而成的。

组合的形式分为两种：一是拼合组合，二是重叠组合。

由于组合图形具有条件相等的特点，往往使得问题的解决无从下手。

要正确解答组合图形的面积，应该注意以下几点：1．切实掌握有关简单图形的概念、公式，牢固建立空间观念；2．仔细观察，认真思考，看清所求图形是由哪几个基本图形组合而成的；3．适当采用增加辅助线等方法帮助解题；4．采用割、补、分解、代换等方法，可将复杂问题变得简单。

例1 一个等腰直角三角形，最长的边是12厘米，这个三角形的面积是多少平方厘米？分析与解答由于此三角形中只知道最长的边是12厘米，所以，不能用三角形的面积公式来计算它的面积。

我们可以假设有4个这样的三角形，且拼成了下图正方形。

显然，这个正方形的面积是12×12，那么，一个三角形的面积就是12×12÷4=36平方厘米。

练习一1．求四边形ABCD的面积。

（单位：厘米）2．已知正方形ABCD的边长是7厘米，求正方形EFGH的面积。

3．有一个梯形，它的上底是5厘米，下底7厘米。

如果只把上底增加3厘米，那么面积就增加4.5平方厘米。

求原来梯形的面积。

例2 正图正方形中套着一个长方形，正方形的边长是12厘米，长方形的四个角的顶点把正方形的四条边各分成两段，其中长的一段是短的2倍。

求中间长方形的面积。

分析与解答图中的两个小三角形平移后可拼得一个小正方形，两个大三角形平移后可拼得一个大正方形。

这两个正方形的边长分别是12÷（1＋2）=4（厘米）和4×2=8（厘米）。

中间长方形的面积只要用总面积减去这两个拼起来的正方形的面积就可以得到。

即：12×12－（4×4＋8×8）=64（平方厘米）练习二1．（如下图）已知大正方形的边长是12厘米，求中间最小正方形的面积。

2．正图长方形ABCD的面积是16平方厘米，E、F都是所在边的中点，求三角形AEF的面积。

第19讲组合图形的面积（二）一、知识要点在组合图形中，三角形的面积出现的机会很多，解题时我们还可以记住下面三点：1.两个三角形等底、等高，其面积相等；2.两个三角形底相等，高成倍数关系，面积也成倍数关系；3.两个三角形高相等，底成倍数关系，面积也成倍数关系。

二、精讲精练【例题1】如图，ABCD是直角梯形，求阴影部分的面积和。

（单位：厘米）练习1：1.求下图中阴影部分的面积。

2.求图中阴影部分的面积。

（单位：厘米）3.下图的长方形是一块草坪，中间有两条宽1米的走道，求植草的面积。

【例题2】下图中，边长为10和15的两个正方体并放在一起，求三角形ABC （阴影部分）的面积。

练习2：1.下图中，三角形ABC的面积是36平方厘米，三角形ABE与三角形AEC的面积相等，如果AB=9厘米，FB=FE，求三角形AFE的面积。

2.图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。

3.图中三角形ABC的面积是36平方厘米，AC长8厘米，DE长3厘米，求阴影部分的面积（ADFC不是正方形）。

【例题3】两条对角线把梯形ABCD分割成四个三角形。

已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？（单位：平方厘米）练习3：1.如下图，图中BO=2DO，阴影部分的面积是4平方厘米，求梯形ABCD的面积是多少平方厘米？2.下图的梯形ABCD中，下底是上底的2倍，E是AB的中点。

那么梯形ABCD的面积是三角形BDE面积的多少倍？3.下图梯形ABCD中，AD=7厘米，BC=12厘米，梯形高8厘米，求三角形BOC的面积比三角形AOD的面积大多少平方厘米？【例题4】在三角形ABC中，DC=2BD，CE=3AE，阴影部分的面积是20平方厘米，求三角形ABC的面积。

练习4：1.把下图三角形的底边BC四等分，在下面括号里填上“＞”、“＜”或“=”。

甲的面积（）乙的面积。

2.如图，在三角形ABC中，D是BC的中点，E、F是AC的三等分点。

五年级奥数之组合图形的面积组合图形的面积1，如图，ABCD是直角梯形，求阴影部分的面积和。

（单位：厘米）2，求下图中阴影部分的面积。

3，求图中阴影部分的面积。

（单位：厘米）4，下图的长方形是一块草坪，中间有两条宽1米的走道，求植草的面积。

5，下图中，边长为10和15的两个正方体并放在一起，求三角形ABC（阴影部分）的面积。

6，下图中，三角形ABC的面积是36平方厘米，三角形ABE与三角形AEC的面积相等，如果AB=9厘米，FB=FE，求三角形AFE的面积。

7，图中两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积。

8，图中三角形ABC的面积是36平方厘米，AC长8厘米，DE长3厘米，求阴影部分的面积（ADFC不是正方形）。

9，两条对角线把梯形ABCD分割成四个三角形。

已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？（单位：平方厘米）10，如下图，图中BO=2DO，阴影部分的面积是4平方厘米，求梯形ABCD的面积是多少平方厘米？11，下图的梯形ABCD中，下底是上底的2倍，E是AB 的中点。

那么梯形ABCD的面积是三角形BDE面积的多少倍？12，下图梯形ABCD中，AD=7厘米，BC=12厘米，梯形高8厘米，求三角形BOC的面积比三角形AOD的面积大多少平方厘米？13，在三角形ABC中，DC=2BD，CE=3AE，阴影部分的面积是20平方厘米，求三角形ABC的面积。

14，把下图三角形的底边BC四等分，在下面括号里填上“＞”、“＜”或“=”。

甲的面积（）乙的面积。

15，如图，在三角形ABC中，D是BC的中点，E、F是AC的三等分点。

已知三角形的面积是108平方厘米，求三角形CDE的面积。

16，下图中，BD=2厘米，DE=4厘米，EC=2厘米，F是AE的中点，三角形ABC的BC边上的高是4厘米，阴影面积是多少平方厘米？17，边长是9厘米的正三角形的面积是边长为3厘米的正三角形面积的多少倍？18，边长是8厘米的正三角形的面积是边长为2厘米的正三角形面积的多少倍？19，一个梯形与一个三角形等高，梯形下底的长是上底的2倍，梯形上底的长又是三角形底长的2倍。