九年级数学综合训练一

2021-2022学年北师大版九年级数学第一学期期末复习综合训练题1（附答案）1．若一元二次方程（k﹣1）x2+3x+k2﹣1＝0的一个根为0，则k的值为（）A．k＝0B．k＝1C．k＝﹣1D．k＝1或k＝﹣1 2．菱形ABCD的周长是8cm，∠ABC＝60°，那么这个菱形的对角线BD的长是（）A．cm B．2cm C．1cm D．2cm3．如图，在菱形ABCD中，P是对角线AC上一动点，过点P作PE⊥BC于点E．PF⊥AB 于点F．若菱形ABCD的周长为24，面积为24，则PE+PF的值为（）A．4B．C．6D．4．在一个不透明的袋子里，装有6枚白色棋子和若干枚黑色棋子，这些棋子除颜色外都相同．将袋子里的棋子摇匀，随机摸出一枚棋子，记下它的颜色后再放回袋子里．不断重复这一过程，统计发现，摸到白色棋子的频率稳定在0.1，由此估计袋子里黑色棋子的个数为（）A．60B．56C．54D．525．已知反比例函数y＝（k≠0）与正比例函数y＝﹣2x没有交点，且双曲线图象上有三点A（﹣1，a）、B（﹣3，b）、C（4，c），则a、b、c的大小关系为（）A．a＞b＞c B．b＞a＞c C．c＞b＞a D．c＞a＞b6．某广场有一块正方形的空地正中间修建一个圆形喷泉，在四个角修建四个四分之一圆形的水池，其余部分种植花草．若喷泉和水池的半径都相同，喷泉边缘到空地边界的距离为3m，种植花草的区域的面积为100m2，设水池半径为xm，可列出方程（）A．（2x+3）2﹣πx2＝100B．（x+6）2﹣πx2＝100C．（2x+3）2﹣2x2＝100D．（2x+6）2﹣2πx2＝1007．如图，已知AB∥CD∥EF，它们依次交直线l1，l2于点A、D、F和点B、C、E，如果AD：DF＝3：1，BE＝12，那么CE等于（）A．9B．4C．6D．38．矩形的正投影不可能是（）A．矩形B．梯形C．正方形D．线段9．下列四个三角形，与图中的三角形相似的是（）A．B．C．D．10．把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为（）A．6B．24C．26D．1211．下列关于比例线段和相似的叙述，不正确的是（）A．若a：b＝c：d，则ac＝bdB．相似三角形的面积比等于相似比的平方C．点C是线段AB的黄金分割点，且AC＞BC，则D．经过位似多边形对应顶点的直线一定交于同一点12．一个长方体的三视图如图所示，若其俯视图为正方形，则这个长方体的体积为（）A．48cm3B．72cm3C．144cm3D．288cm313．x2＝﹣x方程的根是．14．如图，在△ABC中，AB＝6，AC＝4，D是AB边上的一点，当AD＝时，△ABC ∽△ACD．15．点（m+3，2）和点（3，）是同一个反比例函数图象上的点，则m的值为．16．如图，在边长为4cm的正方形ABCD中，点Q是边CD的中点，点P是边BC上的一点，连接AP，PQ，且∠APQ＝∠P AD，则线段PQ的长为cm．17．如图，利用一面墙（墙长25米），用总长度49米的栅栏（图中实线部分）围成一个矩形围栏ABCD，且中间共留两个1米的小门，设栅栏BC长为x米．（1）若矩形围栏ABCD面积为210平方米，求栅栏BC的长；（2）矩形围栏ABCD面积是否有可能达到240平方米？若有可能，求出相应x的值，若不可能，请说明理由．18．新冠肺炎疫情期间，口罩需求量大幅上升．某工厂接到任务紧急生产一批口罩，下面是每时生产口罩的数量与完成任务总共需要的时间的关系．每时生产口罩的数量/万只2346时间/时72483624（1）每时生产口罩的数量与时间有什么关系？（2）如果每时生产8万只口罩，那么完成这项任务一共需要多少时？19．如图，转盘黑色扇形和白色扇形的圆心角分别为120°和240°．（1）让转盘自由转动一次，指针落在白色区域的概率是多少？（2）让转盘自由转动两次，请用树状图或者列表法求出两次指针都落在白色区域的概率．（注：当指针恰好指在分界线上时，无效重转）20．如图，在△ABC中，AB＝AC，点D是BC中点，点E是AD中点，延长BE至F，使EF＝BE，连接AF，CF，BF与AC交于点G．（1）求证：四边形ADCF是矩形．（2）若AB＝5，BC＝6，线段CG的长为．21．某一广告墙PQ旁有两根直立的木杆AB和CD，某一时刻在太阳光下，木杆CD的影子刚好不落在广告墙PQ上，（1）你在图中画出此时的太阳光线CE及木杆AB的影子BF；（2）若AB＝6米，CD＝3米，CD到PQ的距离DQ的长为4米，求此时木杆AB的影长．22．如图，在正方形ABCD中，E是边AD上的点，点F在边CD上，且CF＝3FD，∠BEF ＝90°．（1）求证：△ABE∽△DEF；（2）若AB＝6，延长EF交BC的延长线于点G，求CG的长．23．如图，在平面直角坐标系中，点B在x轴上，∠ABO＝90°，AB＝BO，直线y＝kx﹣4与反比例函数y＝（x＞0）的图象交于点A，与y轴分别交于点C．（1）求k的值；（2）点D与点O关于AB对称，连接AD，CD．证明：△ACD是直角三角形；（3）在（2）的条件下，点E在反比例函数的图象上，若S△ECD＝S△OCD，直接写出点E 的坐标．参考答案1．解：把x＝0代入一元二次方程（k﹣1）x2+3x+k2﹣1＝0，得k2﹣1＝0，解得k＝﹣1或1；又k﹣1≠0，即k≠1；所以k＝﹣1．故选：C．2．解：∵菱形ABCD的周长为8cm，∴AB＝BC＝2（cm），OA＝OC，OB＝OD，AC⊥BD，∵∠ABC＝60°，∴△ABC是等边三角形，∴AC＝AB＝2cm，∴OA＝1（cm），在Rt△AOB中，由勾股定理得：OB＝＝＝（cm），∴BD＝2OB＝2（cm），故选：B．3．解：连接BP，如图，∵四边形ABCD为菱形，菱形ABCD的周长为24，面积为24，∴BA＝BC＝6，S△ABC＝S菱形ABCD＝12，∵S△ABC＝S△P AB+S△PBC，∴×6×PE+×6×PF＝12，∴PE+PF＝4，故选：A．4．解：设袋子里黑色棋子的个数为x个，根据题意得：＝0.1，解得：x＝54，经检验：x＝54是分式方程的解，估计袋子里黑色棋子的个数为54个．故选：C．5．解：∵反比例函数y＝（k≠0）与正比例函数y＝﹣2x没有交点，∴函数y＝﹣2x在二、四象限，则反比例函数y＝（k≠0）图象在一、三象限，∵﹣3＜﹣1＜0，∴点A（﹣1，a）、B（﹣3，b）在第三象限，∴a＜b＜0，∵4＞0，∴C（4，c）在第一象限，∴c＞0，∴a、b、c的大小关系是c＞b＞a，故选：C．6．解：设水池半径为xm，则正方形的边长为（2x+6）m，根据题意得：（2x+6）2﹣2πx2＝100，故选：D．7．解：∵AB∥CD∥EF，∴＝3，∴BC＝3CE，∵BC+CE＝BE，∴3CE+CE＝12，∴CE＝3．故选：D．8．解：用平行光线对矩形从不同的方向，不同的角度正投影，可以得到矩形、正方形、线段，不可能是梯形，故选：B．9．解：根据勾股定理，所给图形的两直角边为＝，＝2，所以，夹直角的两边的比为＝，观各选项，只有B选项三角形符合，与所给图形的三角形相似．故选：B．10．解：设图1中分成的直角三角形的长直角边为a，短直角边为b，，得，∴图1中菱形的面积为：×4＝12，故选：D．11．解：若a：b＝c：d，则ad＝bc，A不正确；相似三角形的面积比等于相似比的平方，B正确；点C是线段AB的黄金分割点，且AC＞BC，则，C正确；经过位似多边形对应顶点的直线一定交于同一点，D正确．故选：A．12．解：∵俯视图为正方形，根据主视图可得：正方形对角线为6cm，长方体的高为8cm，∴长方体的体积为：6×6÷2×8＝144（cm3）．故选：C．13．解：x2＝﹣x，x2+x＝0，x（x+1）＝0，∴x＝0或x+1＝0，∴x1＝0，x2＝﹣1．14．解：∵△ABC∽△ACD，AB＝6，AC＝4，∴，即，解得AD＝．故答案为：．15．解：∵点（m+3，2）和点（3，）是同一个反比例函数图象上的点，∴2（m+3）＝3×，∴m＝﹣6．故答案为：﹣6．16．解：如图，延长AD，PQ交于点H，设PC＝xcm，∵四边形ABCD是正方形，∴AD＝CD＝BC＝4cm，AD∥BC，∵点Q是边CD的中点，∴DQ＝CQ＝2cm，∵AD∥BC，∴∠H＝∠QPC，又∵∠DQH＝∠CQP，∴△DQH≌△CQP（AAS），∴PC＝DH＝xcm，PQ＝QH，∴AH＝AD+DH＝（4+x）cm，∵∠APQ＝∠P AD，∴AH＝PH＝（4+x）cm，∴PQ＝QH＝（）cm，∵PQ2＝CQ2+PC2，∴（）2＝4+x2，∴x＝或x＝0（舍），∴PQ＝cm，故答案为：．17．解：若设BC＝x米，则AB＝（49+1+1﹣3x）＝（51﹣3x）米．（1）依题意得：x（51﹣3x）＝210，整理得：x2﹣17x+70＝0，解得：x1＝7，x2＝10．当x＝7时，51﹣3x＝51﹣3×7＝30＞25，不合题意，舍去；当x＝10时，51﹣3x＝51﹣3×10＝21＜25，符合题意．答：栅栏BC的长为10米．（2）矩形围栏ABCD的面积不可能达到240平方米，理由如下：依题意得：x（51﹣3x）＝240，整理得：x2﹣17x+80＝0．∵Δ＝（﹣17）2﹣4×1×80＝﹣31＜0，∴原方程没有实数根，∴矩形围栏ABCD的面积不可能达到240平方米．18．解：（1）因为每时生产口罩的数量与时间的积一定，所以每时生产口罩的数量与时间成反比例；（2）设反比例函数解析式为：y＝，把（2，72）代入得：k＝144，故反比例函数解析式为：y＝，∴y＝＝18（时），答：完成这项任务一共需要18小时．19．解：（1）∵转盘黑色扇形和白色扇形的圆心角分别为120°和240°，∴白色扇形是黑色扇形的2倍，∴让转盘自由转动一次，指针落在白色区域的概率是；（2）画树状图如下：共有9种等可能的结果，两次指针都落在白色区域的结果有4种，∴两次指针都落在白色区域的概率为．20．（1）证明：∵点E是AD中点，∴AE＝DE，在△AEF和△DEB中，，∴△AEF≌△DEB（SAS），∴AF＝DB，∠AFE＝∠DBE，∴AF∥DB，∵AB＝AC，点D是BC中点，∴DB＝DC，AD⊥BC，∴AF＝DC，∠ADC＝90°，∴四边形ADCF是平行四边形，∵∠ADC＝90°，∴平行四边形ADCF是矩形；（2）解：过G作GH⊥CD于H，如图所示：则GH∥AD，∵AB＝AC＝5，点D是BC中点，∴AD⊥BC，BD＝CD＝BC＝3，∴AD＝＝＝4，由（1）得：AF＝DC＝BD＝3＝BC，AF∥BC，∴△AGF∽△CGB，∴＝＝，∴AG＝CG，∴AG＝AC＝，∴CG＝AC﹣AG＝5﹣＝，故答案为：．21．解：（1）如图所示：（2）设木杆AB的影长BF为x米，由题意，得＝，解得x＝8．答：木杆AB的影长是8米．22．（1）证明：∵四边形ABCD是正方形，∴∠A＝∠D＝90°，∵∠BEF＝90°，∴∠AEB+∠DEF＝90°，又∵∠ABE+∠AEB＝90°，∴∠ABE＝∠DEF，∴△ABE∽△DEF；（2）解：∵四边形ABCD是正方形，∴AB＝AD＝CD＝6，AD∥BG，∵CF＝3FD，∴DF＝1.5，设DE＝x，∵△ABE∽△DEF，∴，即，解得x＝3，∴DE＝3，∵DE∥CG，∴△DEF∽△CGF，∴，∵CF＝3FD，∴，∴CG＝9，23．（1）解：令AB＝BO＝m，∵∠ABO＝90°，∴AB⊥x轴，则设点A的坐标为（m，m），∵反比例函数y＝（x＞0）的图象交于点A，∴＝m，解得m＝±2，∵m＞0，∴m＝2，∵点A（2，2）在直线y＝kx﹣4上，∴2＝2k﹣4，∴k＝3；（2）证明：由（1）可知B（2，0），AB＝2，∵AB⊥BO，点D与点O关于AB对称，∴D（4，0），BD＝2，∴AD2＝AB2+BD2＝22+22＝8，过点A作AE⊥y轴，垂足为E，则点E（0，2），AE＝2，∵直线y＝3x﹣4与y轴交于点C，∴C（0，﹣4）则CE＝6，∴AC2＝AE2+CE2＝22+62＝40，∵∠OCD＝90°，OD＝4，OC＝4，∴CD2＝OD2+OC2＝42+42＝32，∵8+32＝40，∴AD2+CD2＝AC2，∴△ACD是直角三角形；（3）解：①当点E在CD上方时，如下图，过点O、A作直线m，由点O、A的坐标知，直线OA的表达式为y＝x，由点C、D的坐标知，直线CD的表达式为y＝x﹣4，则直线CD∥m，即OA∥CD，∵S△ECD＝S△OCD，即两个三角形同底，则点E与点A重合，故点E的坐标为（2，2）；②当点E（E′）在CD下方时，在y轴负半轴取CH＝OC＝4，则点H（0，﹣8），∵则S△ECD＝S△OCD，∴过点H作直线m′∥CD，则直线m′与反比例函数的交点即为点E，∴直线m′的表达式为y＝x﹣8，联立y＝x﹣8和y＝并解得（不合题意值已舍去），故点E的坐标为（4+2，2﹣4），综上，点E的坐标为（4+2，2﹣4）或（2，2）．。

2021年九年级数学中考复习知识点综合专题训练：一次函数与几何变换1（附答案）1．在平面直角坐标系中，把直线y＝﹣2x+3沿y轴向上平移两个单位长度后．得到的直线的函数关系式为（）A．y＝﹣2x+5B．y＝﹣2x﹣5C．y＝﹣2x+1D．y＝﹣2x+72．如图，直线l：与y轴交于点A，将直线l绕点A顺时针旋转75°后，所得直线的解析式为（）A．y＝x+B．y＝x﹣C．y＝﹣x+D．y＝x+3．在平面直角坐标系中，将直线y＝﹣2x+2关于平行于y轴的一条直线对称后得到直线AB，若直线AB恰好过点（6，2），则直线AB的表达式为（）A．y＝2x﹣10B．y＝﹣2x+14C．y＝2x+2D．y＝﹣x+54．将直线y＝﹣3x沿着x轴向右平移2个单位，所得直线的表达式为（）A．y＝﹣3x+6B．y＝﹣3x﹣6C．y＝﹣3x+2D．y＝﹣3x﹣25．将直线y＝﹣2x+1向上平移2个单位长度，所得到的直线解析式为（）A．y＝2x+1B．y＝﹣2x﹣1C．y＝2x+3D．y＝﹣2x+36．将直线y＝﹣2x+1向下平移2个单位，平移后的直线表达式为（）A．y＝﹣2x﹣5B．y＝﹣2x﹣3C．y＝﹣2x﹣1D．y＝﹣2x+37．将直线y＝x平移，使得它经过点（﹣2，0），则平移后的直线为（）A．y＝x﹣2B．y＝x+1C．y＝﹣x﹣2D．y＝x+28．将一次函数y＝3x向左平移后所得直线与坐标轴围成的三角形面积是24，则平移距离（）A．4B．6C．6D．129．把直线y＝2x﹣1向下平移1个单位，平移后直线的关系式为（）A．y＝2x﹣2B．y＝2x+1C．y＝2x D．y＝2x+210．将直线y＝﹣2x﹣1向上平移两个单位，平移后的直线所对应的函数关系式为（）A．y＝﹣2x﹣5B．y＝﹣2x﹣3C．y＝﹣2x+1D．y＝﹣2x+3 11．将直线y＝3x沿y轴向下平移1个单位长度后得到的直线解析式为（）A．y＝3x+1B．y＝3x﹣1C．y＝x+1D．y＝x﹣112．在平面直角坐标系中，把直线y＝2x﹣3沿y轴向上平移2个单位后，得到的直线的函数表达式为（）A．y＝2x+2B．y＝2x﹣5C．y＝2x+1D．y＝2x﹣113．将直线y＝2x+1向上平移3个单位后得到的解析式为．14．如果将直线y＝3x平移，使其经过点（0，﹣1），那么平移后的直线表达式是．15．把直线y＝2x﹣1向左平移1个单位长度，再向上平移2个单位长度，则平移后所得直线的解析式为．16．将直线y＝2x﹣5向上平移3个单位长度，所得直线的解析式为．17．把直线y＝﹣2x+5向下平移2个单位，得到的直线解析式是．18．在平面直角坐标系xOy中，将函数y＝3x+3图象向右平移5个单位长度，则平移后的图象与x轴、y轴分别交于A、B两点，则△AOB的面积为．19．将直线y＝2x﹣3沿y轴向上平移2个单位后，所得直线的解析式是．20．将直线y＝﹣2x+3向下平移5个单位，得到直线．21．将直线y＝2x向上平移2个单位后得到的直线解析式为．22．在平面直角坐标系中，把直线y＝x沿y轴向上平移后得到直线AB，如果点P（m，n）是直线AB上的一点，且m﹣n+8＝0，那么直线AB的函数表达式为．23．在平面直角坐标系中，已知A，B两点的坐标分别（2，4），（﹣3，1）．（1）在平面直角坐标系中，描出点A；（2）若函数y＝mx的图象经过点A，求m的值；（3）若一次函数y＝kx+b的图象由（2）中函数y＝mx的图象经过平移，且经过点B得到，求这个一次函数的表达式，并在直角坐标系中画出该函数对应的图象．24．已知一次函数y＝kx﹣4，当x＝2时，y＝﹣3．（1）求一次函数的解析式；（2）将该函数的图象向上平移6个单位长度，求平移后的图象与x轴交点的坐标；（3）在（2）的条件下，直接写出y＞0时，x的取值范围．25．在一次函数学习中，我们经历了列表、描点、连线画函数图象，结合图象研究函数性质并对其性质进行应用的过程．小红对函数y＝的图象和性质进行了如下探究，请同学们认真阅读探究过程并解答：（1）小红列出了如下表格，请同学们把下列表格补充完整，并在平面直角坐标系中画出该函数的图象：x…﹣10123456…y……（2）根据函数图象，以下判断该函数性质的说法，正确的有（填正确答案的序号）．①函数图象关于y轴对称；②此函数无最小值；③当x＜3时，y随x的增大而增大；当x≥3时，y的值不变．（3）若直线y＝x+b与函数y＝的图象只有一个交点，求b的值．26．已知一次函数y＝kx+b（k，b是常数，且k≠0）的图象过A，B两点．（1）在图中画出该一次函数并求其表达式；（2）若点（a﹣3，﹣a）在该一次函数图象上，求a的值；（3）把y＝kx+b的图象向下平移3个单位后得到新的一次函数图象，在图中画出新函数图形，并直接写出新函数图象对应的表达式．27．有这样一个问题：探究函数y＝|x+1|的图象与性质．小明根据学习一次函数的经验，对函数y＝|x+1|的图象与性质进行了探究．下面是小明的探究过程，请补充完整：（1）函数y＝|x+1|的自变量x的取值范围是；（2）如表是x与y的几组对应值．x…﹣5﹣4﹣3﹣2﹣10123…y…432m01234…m的值为；（3）在如图网格中，建立平面直角坐标系xOy，描出表中各对对应值为坐标的点，并画出该函数的图象；（4）小明根据画出的函数图象，得出了如下几条结论：①函数有最小值为0；②当x＞﹣1时，y随x的增大而增大；③图象关于过点（﹣1，0）且垂直于x轴的直线对称．小明得出的结论中正确的是．（只填序号）28．已知正比例函数的图象经过点A（2，3）；（1）求出此正比例函数表达式；（2）该直线向上平移3个单位，写出平移后所得直线的表达式，并画出它的图象．29．一次函数y＝2x+a的图象与x轴交与点（2，0），（1）求出a的值；（2）将该一次函数的图象向上平移5个单位长度，求平移后的函数解析式．30．表格中的两组对应值满足一次函数y＝kx+b，现画出了它的图象为直线l，如图．而某同学为观察k，b对图象的影响，将上面函数中的k与b交换位置后得另一个一次函数，设其图象为直线l'．x﹣10y﹣21（1）求直线l的解析式；（2）请在图上画出直线l'（不要求列表计算），并求直线l'被直线l和y轴所截线段的长；（3）设直线y＝a与直线l，l′及y轴有三个不同的交点，且其中两点关于第三点对称，直接写出a的值．31．已知一次函数y＝kx+b（k，b是常数，且k≠0）的图象过A（3，5）与B（﹣2，﹣5）两点．（1）求一次函数的解析式；（2）若点（a﹣3，﹣a）在该一次函数图象上，求a的值；（3）把y＝kx+b的图象向下平移3个单位后得到新的一次函数图象，在图中画出新函数图象，并直接写出新函数图象对应的解析式．32．如图，在平面直角坐标系xOy中，直线y＝﹣x+8与x、y轴分别相交于点A、B，此直线向下平移后与y轴相交于点C、与x轴相交于点D，四边形ABCD的面积为18．（1）求直线CD的表达式；（2）如果点E在直线CD上，四边形ABED是等腰梯形，求点E的坐标．参考答案1．解：直线y＝﹣2x+3沿y轴向上平移2个单位，则平移后直线解析式为：y＝﹣2x+3+2＝﹣2x+5，故选：A．2．解：由直线l：可知，直线与x轴的夹角为60°，∴与y轴的夹角为30°，∴直线l绕点A顺时针旋转75°后的直线与y轴的夹角为45°，∴旋转后的直线的斜率为1，∵直线l：与y轴交于点A，∴A（0，）．∴旋转后的直线解析式为：y＝x+，故选：D．3．解：由题意得，直线AB的解析式为y＝2x+b，∵直线AB恰好过点（6，2），∴2＝2×6+b，解得b＝﹣10，∴直线AB的表达式为y＝2x﹣10，故选：A．4．解：根据题意，得直线向右平移2个单位，即对应点的纵坐标不变，横坐标减2，所以得到的解析式是y＝﹣3（x﹣2）＝﹣3x+6．故选：A．5．解：由“上加下减”的原则可知，把直线y＝﹣2x+1上平移2个单位长度后所得直线的解析式为：y＝﹣2x+1+2，即y＝﹣2x+3故选：D．6．解：由题意得：平移后的解析式为：y＝﹣2x+1﹣2＝﹣2x﹣1，即．所得直线的表达式是y＝﹣2x﹣1．故选：C．7．解：设平移后直线的解析式为y＝x+b．把（﹣2，0）代入直线解析式得0＝﹣2+b解得b＝2所以平移后直线的解析式为y＝x+2．故选：D．8．解：设平移的距离为k（k＞0），则将一次函数y＝3x向左平移后所得直线解析式为：y ＝3（x+k）＝3x+3k．易求得新直线与坐标轴的交点为（﹣k，0）、（0，3k）所以，新直线与坐标轴所围成的三角形的面积为：•3k＝24，解得k＝4或﹣4（舍去）．故选：A．9．解：根据题意，把直线y＝2x﹣1向下平移1个单位后得到的直线解析式为：y＝2x﹣1﹣1，即y＝2x﹣2，故选：A．10．解：直线y＝﹣2x﹣1向上平移两个单位，所得的直线是y＝﹣2x+1，故选：C．11．解：由“上加下减”的原则可知：将直线y＝3x沿y轴向下平移1个单位长度后，其直线解析式为y＝3x﹣1．故选：B．12．解：由题意得：平移后的解析式为：y＝2x﹣3+2，即y＝2x﹣1．故选：D．13．解：由“上加下减”的原则可知，把直线y＝2x+1上平移3个单位长度后所得直线的解析式为：y＝2x+1+3，即y＝2x+4，故答案为：y＝2x+4．14．解：设平移后直线的解析式为y＝3x+b，把（0，﹣1）代入直线解析式得﹣1＝b，解得b＝﹣1．所以平移后直线的解析式为y＝3x﹣1．故答案为：y＝3x﹣1．15．解：把直线y＝2x﹣1向左平移1个单位长度，得到y＝2（x+1）﹣1＝2x+1，再向上平移2个单位长度，得到y＝2x+3．故答案为：y＝2x+3．16．解：由“上加下减”的原则可知，将函数y＝2x﹣5向上平移3个单位所得函数的解析式为y＝2x﹣5+3，即y＝2x﹣2．故答案为：y＝2x﹣2．17．解：由“上加下减”的原则可知，把直线y＝﹣2x+5向下平移2个单位后所得直线的解析式为：y＝﹣2x+5﹣2，即y＝﹣2x+3．故答案为：y＝﹣2x+3．18．解：根据题意知，平移后直线方程为y＝3（x﹣5）+3＝3x﹣12．所以A（4，0），B（0，﹣12）．故OA＝4，OB＝12．所以S△AOB＝OA•OB＝＝24．故答案是：24．19．解：由“上加下减”的原则可知，直线y＝2x﹣3沿y轴向上平移2个单位，所得直线的函数关系式为y＝2x﹣3+2，即y＝2x﹣1；故答案为y＝2x﹣1．20．解：原直线的k＝﹣2，b＝3．向下平移5个单位长度得到了新直线，那么新直线的k＝﹣2，b＝3﹣5＝﹣2．∴新直线的解析式为y＝﹣2x﹣2．故答案为：y＝﹣2x﹣2．21．解：直线y＝2x向上平移2个单位后得到的直线解析式为y＝2x+2．故答案为y＝2x+2．22．解：设直线AB的解析式为y＝x+b．将（m，n）代入y＝x+b，得m+b＝n，则m﹣n+8＝0，∴b＝8，∴直线AB的解析式为y＝x+8．故答案为y＝x+8．23．解：（1）点A（2，4），如图所示：（2）∵函数y＝mx的图象经过点A，∴4＝2m，∴m＝2；（3）由（2）可得经过点A的函数为y＝2x，∵一次函数y＝kx+b的图象由函数y＝2x经过平移，且经过点B，∴，解得，∴这个一次函数的表达式为y＝2x+7，依题意画出图象如图所示；24．解：（1）当x＝2时，y＝﹣3，∴﹣3＝2k﹣4，则，∴，（2）图象向上平移6个单位长度，∴，当y＝0时，x＝﹣4，∴平移后的图象与x轴交点的坐标为（﹣4，0），（3）y＞0时，x的取值范围为x＞﹣4．25．解：（1）补充表格：x…﹣10123456…y…﹣2﹣1012222…画出函数图象如图所示：（2）由图象可知，正确的性质为②此函数无最小值；③当x＜3时，y随x的增大而增大；当x≥3时，y的值不变．故答案为②③；（3）直线y＝x+b与函数y＝的图象只有一个交点，根据图象直线y＝+b经过点（3，2），∴2＝+b，∴b＝．26．解：（1）∵一次函数y＝kx+b（k，b是常数，k≠0）的图象过A（1，5），B（﹣1，﹣1）两点，∴，得，即该一次函数的表达式是y＝3x+2；（2）点（a﹣3，﹣a）在该一次函数y＝3x+2的图象上，∴﹣a＝3（a﹣3）+2，解得，a＝，即a的值是；（3）把y＝3x+2向下平移3个单位后可得：y＝3x+2﹣3＝3x﹣1，图象如图：27．解：（1）在函数y＝|x+1|中，自变量x的取值范围是x为任意实数，故答案为：x为任意实数；（2）当x＝﹣2时，m＝|﹣2+1|＝1，故答案为1；（3）画出函数的图象如图：；（4）由函数图象可知，①函数有最小值为0，正确；②当x＞﹣1时，y随x的增大而增大，正确；③图象关于过点（﹣1，0）且垂直于x轴的直线对称，正确；．故答案为：①②③．28．解：（1）设正比例函数的解析式为y＝kx，把A（2，3），代入得到k＝，∴正比例函数的解析式为y＝x．（2）将直线y＝x向上平移3个单位，得直线y＝x+3，如图；29．解：（1）∵一次函数y＝2x+a的图象与x轴交与点（2，0），∴4+a＝0，解得a＝﹣4；（2）将一次函数y＝2x﹣4的图象向上平移5个单位长度，得到y＝2x﹣4+5，即y＝2x+1，故平移后的函数解析式为y＝2x+1．30．解：（1）∵直线l：y＝kx+b中，当x＝﹣1时，y＝﹣2；当x＝0时，y＝1，∴，解得，∴直线l的解析式为y＝3x+1；（2）依题意可得直线l′的解析式为y＝x+3如图，解得，∴两直线的交点为A（1，4），∵直线l′：y＝x+3与y轴的交点为B（0，3），∴直线l'被直线l和y轴所截线段的长为：AB＝＝；（3）把y＝a代入y＝3x+1得，a＝3x+1，解得x＝；把y＝a代入y＝x+3得，a＝x+3，解得x＝a﹣3；分三种情况：①当第三点在y轴上时，a﹣3+＝0，解得a＝；②当第三点在直l上时，2×＝a﹣3，解得a＝7；③当第三点在直线l'上时，2×（a﹣3）＝，解得a＝；∴直线y＝a与直线l，l′及y轴有三个不同的交点，且其中两点关于第三点对称，则a 的值为或7或．31．解：（1）∵一次函数y＝kx+b（k，b是常数，且k≠0）的图象过A（3，5）与B（﹣2，﹣5）两点，∴，解得，即该一次函数的表达式是y＝2x﹣1；（2）点（a﹣3，﹣a）在该一次函数y＝2x﹣1的图象上，∴﹣a＝2（a﹣3）﹣1，解得，a＝，即a的值是；（3）把y＝2x﹣1向下平移3个单位后可得：y＝2x﹣1﹣3＝2x﹣4，图象如图：32．解：（1）∵直线y＝﹣x+8与x、y轴分别相交于点A、B，∴A（6，0）B（0，8），∴OA＝6，OB＝8，∴AB＝＝＝10，∴S△AOB＝＝24，四边形ABCD的面积为18．∴S△COD＝24﹣18＝6，∵AB∥CD，∴△COD∽△BOA，∴＝（）2，即＝，∴OC＝4，∴C（0，4），∴直线CD的解析式为：y＝﹣x+4；（2）作DM⊥AB于M，EN⊥AB于N，∵四边形ABED是等腰梯形，∴AD＝BE，∠DAB＝∠EBA，∵∠DMA＝∠ENB＝90°，∴△ADM≌△BEN（AAS），∴AM＝BN，∵直线CD的解析式为：y＝﹣x+4，∴D（3，0），∴OD＝3，∴AD＝6﹣3＝3，∵∠AMD＝∠AOB，∠DAM＝∠BAO，∴△ADM∽△ABO，∴＝，即，∴AM＝，∴BN＝AM＝，∴MN＝10﹣2×＝，∴ED＝MN＝，∵OD＝3，OC＝4，∴CD＝＝5，∴CE＝DE﹣CD＝﹣5＝，作EH⊥x轴于H，则EH∥OC，∴，即＝，∴OH＝，∴E的横坐标为﹣，把x＝﹣代入直线CD：y＝﹣x+4得y＝，∴点E的坐标为（﹣，）．。

九年级数学竞赛综合训练题(1)（满分120分，考试时间120分）学校 班级 姓名一、选择题:（每小题5分，共30分）1．过点P （-1，3）作直线，使它与两坐标轴围成的三角形面积为5，这样的直线可以作（ ）条 （A ）4 （B ）3 （C ）2 （D ）1 2．方程13++x x －y=0的整数解有（ ）组 （A ）1 （B ）2 （C ）3 （D ）4 3．如图，若将图（a ）的正方形剪成四块，恰能拼成图(b)的矩形，设a=1，则这个正方形的面积为（ ）（A ）2537+ （B ）253+（C ）251+ （D ）21(+)24．关于x 的不等式组255332x x x x a +⎧>-⎪⎪⎨+⎪<+⎪⎩只有5个整数解，则a 的取值范围是（ ）（A ）－6＜a ＜－211 （B ）－6≤a ＜－211 （C ）－6＜a ≤－211 （D ）－6≤a ≤－2115．已知四边形ABCD ，从下列条件：（1）AB ∥CD （2）BC ∥AD （3）AB ＝CD （4）BC ＝AD （5）∠A ＝∠C （6）∠B ＝∠D中任取其中两个，可以得出“四边形ABCD 是平行四边形”这一结论的情况有（ ）种（A ）4 （B ）9 （C ）13 （D ）15 6．已知x 、y 、z 都是实数，且x 2+y 2+z 2=1，则m=xy+yz+zx （ ）(A)只有最大值 （B ）只有最小值 （C ）既有最大值又有最小值 （D ）既无最大值又无最小值 二、填空题:（每小题5分，共30分）jab a b ⅠⅡⅢⅣⅣⅢⅡⅠ(b)(a)ba7．已知x=1313+-，y=1313-+, 则x 4+y 4等于 .8．甲、乙两商店某种铅笔标价都是1元，一天，让学生小王欲购这种铅笔，发现甲、乙两商店都让利优惠：甲店实行每买5枝送1枝（不足5枝不送）；乙店实行买4枝或4枝以上打8.5折，小王买了13枝这种铅笔，最少需要花 元.9．若1≤p ≤20， 1≤q ≤10，且方程4x 2－px+q=0的两根均为奇数，则此方程的根为 . 10．在1、2、……，2003中有些正整数n ，使得x 2+x －n 能分解为两个整系数一次式的乘积，则这样的n 共有 个.11．已知如图所示，∠MON=40°，P 为∠MON 内一点，A 为OM 上一点，B 为ON 上一点，则当△PAB 的周长取最小值时，∠APB 的度数为 .12．若关于x 的方程rx 2－(2r+7)x+r+7=0的根是正整数，则整数r 的值可以是 .三、解答题:（每小题15分，共60分）13．已知a 、b 、c满足方程组2848a b ab c +=⎧⎪⎨-+=⎪⎩, 试求方程bx 2+cx-a=0的根.PNMBOA14．已知两个二次函数y1 和y2，当x=a（a＞0）时，y1取得最大值5，且y2=25. 又y2的最小值为-2，y1+y2=x2+16x+13. 求a的值及二次函数y1、y2的解析式.15．如图所示，正方形ABCD的边长为1，点M、N分别在BC、CD上，使得△CMN的周长为2.求：（1）∠MAN的大小;（2）△MAN面积的最小值.ND CMAB16．如图所示，四边形ABCD 是矩形，甲、乙两人分别从A 、B 同时出发，沿矩形按逆时针方向前进，即按A →B →C →D →……顺序前进，已知甲的速度为每分钟65米，乙的速度为每分钟74米，问乙至少在跑第几圈时才有可能第一次追上甲？又乙至多在跑第几圈时一定能追上甲？请说明理由。

备战2022最新年九年级中考数学考点训练——几何专题：《圆的综合》（一）1．对于平面内⊙C和⊙C外一点P，若过点P的直线l与⊙C有两个不同的公共点M，N，点Q为直线l上的另一点，且满足（如图1所示），则称点Q是点P关于⊙O的密切点．已知在平面直角坐标系xOy中，⊙O的半径为2，点P（4，0）．（1）在点D（﹣2，1），E（1，0），F（3，）中，是点P关于⊙O的密切点的为．（2）设直线l方程为y＝kx+b，如图2所示，①k＝﹣时，求出点P关于O的密切点Q的坐标；②⊙T的圆心为T（t，0），半径为2，若⊙T上存在点P关于⊙O 的密切点，直接写出t的取值范围．2．A，B是⊙C上的两个点，点P在⊙C的内部．若∠APB为直角，则称∠APB为AB关于⊙C的内直角，特别地，当圆心C在∠APB 边（含顶点）上时，称∠APB为AB关于⊙C的最佳内直角．如图1，∠AMB是AB关于⊙C的内直角，∠ANB是AB关于⊙C的最佳内直角．在平面直角坐标系xOy中．（1）如图2，⊙O的半径为5，A（0，﹣5），B（4，3）是⊙O 上两点．①已知P1（1，0），P2（0，3），P3（﹣2，1），在∠AP1B，∠AP2B，∠AP3B，中，是AB关于⊙O的内直角的是；②若在直线y＝2x+b上存在一点P，使得∠APB是AB关于⊙O的内直角，求b的取值范围．（2）点E是以T（t，0）为圆心，4为半径的圆上一个动点，⊙T 与x轴交于点D（点D在点T的右边）．现有点M（1，0），N（0，n），对于线段MN上每一点H，都存在点T，使∠DHE是DE关于⊙T的最佳内直角，请直接写出n的最大值，以及n取得最大值时t的取值范围．3．定义：三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到该边所对顶点连线的平方，则称这个点为三角形该边的“好点”．如图1，△ABC中，点D是BC边上一点，连结AD，若AD2＝BD•CD，则称点D是△ABC中BC边上的“好点”．（1）如图2，△ABC的顶点是4×3网格图的格点，请仅用直尺画出AB边上的一个“好点”．（2）△ABC中，BC＝9，tanB＝，tanC＝，点D是BC边上的“好点”，求线段BD的长．（3）如图3，△ABC是⊙O的内接三角形，OH⊥AB于点H，连结CH并延长交⊙O于点D．①求证：点H是△BCD中CD边上的“好点”．②若⊙O的半径为9，∠ABD＝90°，OH＝6，请直接写出的值．4．如图，⊙O是△ABD的外接圆，AB为直径，点C是弧AD的中点，连接OC，BC分别交AD于点F，E．（1）求证：∠ABD＝2∠C．（2）若AB＝10，BC＝8，求BD的长．5．如图，在平面直角坐标系xOy中，A（0，8），B（6，0），C（0，3），点D从点A运动到点B停止，连接CD，以CD长为直径作⊙P．（1）若△ACD∽△AOB，求⊙P的半径；（2）当⊙P与AB相切时，求△POB的面积；（3）连接AP、BP，在整个运动过程中，△PAB的面积是否为定值，如果是，请直接写出面积的定值，如果不是，请说明理由．6．如图，已知Rt△ABC中，∠A＝30°，AC＝6．边长为4的等边△DEF沿射线AC运动（A、D、E、C四点共线）．当等边△DEF的边DF、EF与Rt△ABC的边AB分别相交于点M、N（M、N不与A、B重合）时，设AD＝x．（1）则△FMN的形状是，△ADM的形状是；（2）△ABC与△DEF重叠部分的面积为y，求y关于x的函数解析式，并写出的取值范围；（3）若以点M为圆心，MN为半径的圆与边AC、EF同时相切，求此时MN的长．7．如图，以点O为圆心，OE为半径作优弧EF，连接OE，OF，且OE＝3，∠EOF＝120°，在弧EF上任意取点A，B（点B在点A 的顺时针方向）且使AB＝2，以AB为边向弧内作正三角形ABC．（1）发现：不论点A在弧上什么位置，点C与点O的距离不变，点C与点O的距离是；点C到直线EF的最大距离是．（2）思考：当点B在直线OE上时，求点C到OE的距离，在备用图1中画出示意图，并写出计算过程．（3）探究：当BC与OE垂直或平行时，直接写出点C到OE的距离．8．如图，在平面直角坐标系中，点A的坐标为（6，0），点B的坐标为（0，2），点M从点A出发沿x轴负方向以每秒3cm的速度移动，同时点N从原点出发沿y轴正方向以每秒1cm的速度移动．设移动的时间为t秒．（1）若点M在线段OA上，试问当t为何值时，△ABO与以点O、M、N为顶点的三角形相似？（2）若直线y＝x与△OMN外接圆的另一个交点是点C．①试说明：当0＜t＜2时，OM、ON、OC在移动过程满足OM+ON ＝OC；②试探究：当t＞2时，OM、ON、OC之间的数量关系是否发生变化，并说明理由．9．如图，将一副斜边相等的直角三角板按斜边重合摆放在同一平面内，其中∠CAB＝30°，∠DAB＝45°，点O为斜边AB的中点，连接CD交AB于点E．（1）求证：A，B，C，D四个点在以点O为圆心的同一个圆上；（2）求证：CD平分∠ACB；（3）过点D作DF∥BC交AB于点F，求证：BO2+OF2＝EF•BF．10．如图，在△ABC中，∠BAC＝90°，∠B＝60°，AB＝2．AD⊥BC 于D．E为边BC上的一个（不与B、C重合）点，且AE⊥EF于E，∠EAF＝∠B，AF相交于点F．（1）填空：AC＝；∠F＝．（2）当BD＝DE时，证明：△ABC≌△EAF．（3）△EAF面积的最小值是．（4）当△EAF的内心在△ABC的外部时，直接写出AE的范围．参考答案1．解：（1）当圆心在坐标原点时，直线l为y＝0时，∵⊙O的半径为2，点P（4，0）．∴M（2，0），N（﹣2，0），PM＝2，PN＝6，＝，∵，∴＝，设Q点坐标为（x，y），则QM＝|2﹣x|，QN＝|x﹣（﹣2）|＝|x+2|，∴＝，∴|2+x|＝3|2﹣x|，∴2+x＝6﹣3x，或2+x＝3x﹣6，∴x＝1，或x＝4，∴E（1，0）是点P关于⊙O的密切点．故答案为：E．（2）①依题意直线l：y＝kx+b过定点P（4，0），∵k＝﹣∴将P（4，0）代入y＝﹣x+b得：0＝﹣×4+b，∴b＝，∴y＝﹣x+．如图，作MA⊥x轴于点A，NB垂直x轴于点B，设M（x，﹣x+），由OM＝2得：x2+＝4，∴5x2﹣4x﹣10＝0，则M，N两点的横坐标xM，xN是方程5x2﹣4x﹣10＝0的两根，解得xM＝，xN＝，∴AB＝，PA＝，PB＝，∵，∴＝，＝，∴＝，∴HA＝，∴OH＝OA﹣HA＝﹣＝1，∴Q（1，1）．②点P关于⊙O的密切点的轨迹为切点弦ST（不含端点），如图所示：∴﹣1≤t＜0或2＜t≤3．2．解：（1）如图1，∵P1（1，0），A（0，﹣5），B（4，3），∴AB＝＝4，P1A＝＝，P1B＝＝3，∴P1不在以AB为直径的圆弧上，故∠AP1B不是AB关于⊙O的内直角，∵P2（0，3），A（0，﹣5），B（4，3），∴P2A＝8，AB＝4，P2B＝4，∴P2A2+P2B2＝AB2，∴∠AP2B＝90°，∴∠AP2B是AB关于⊙O的内直角，同理可得，P3B2+P3A2＝AB2，∴∠AP3B是AB关于⊙O的内直角，故答案为：∠AP2B，∠AP3B；（2）∵∠APB是AB关于⊙O的内直角，∴∠APB＝90°，且点P在⊙O的内部，∴满足条件的点P形成的图形为如图2中的半圆H（点A，B均不能取到），过点B作BD⊥y轴于点D，∵A（0，﹣5），B（4，3），∴BD＝4，AD＝8，并可求出直线AB的解析式为y＝2x﹣5，∴当直线y＝2x+b过直径AB时，b＝﹣5，连接OB，作直线OH交半圆于点E，过点E作直线EF∥AB，交y 轴于点F，∵OA＝OB，AH＝BH，∴EH⊥AB，∴EH⊥EF，∴EF是半圆H的切线．∵∠OAH＝∠OAH，∠OHB＝∠BDA＝90°，∴△OAH∽△BAD，∴，∴OH＝AH＝EH，∴OH＝EO，∵∠EOF＝∠AOH，∠FEO＝∠AHO＝90°，∴△EOF≌△HOA（ASA），∴OF＝OA＝5，∵EF∥AB，直线AB的解析式为y＝2x﹣5，∴直线EF的解析式为y＝2x+5，此时b＝5，∴b的取值范围是﹣5＜b≤5．（3）∵对于线段MN上每一个点H，都存在点T，使∠DHE是DE 关于⊙T的最佳内直角，∴点T一定在∠DHE的边上，∵TD＝4，∠DHT＝90°，线段MN上任意一点（不包含点M）都必须在以TD为直径的圆上，该圆的半径为2，∴当点N在该圆的最高点时，n有最大值，即n的最大值为2．分两种情况：①若点H不与点M重合，那么点T必须在边HE上，此时∠DHT ＝90°，∴点H在以DT为直径的圆上，如图3，当⊙G与MN相切时，GH⊥MN，∵OM＝1，ON＝2，∴MN＝＝，∵∠GMH＝∠OMN，∠GHM＝∠NOM，ON＝GH＝2，∴△GHM≌△NOM（ASA），∴MN＝GM＝，∴OG＝﹣1，∴OT＝+1，当T与M重合时，t＝1，∴此时t的取值范围是﹣﹣1≤t＜1，②若点H与点M重合时，临界位置有两个，一个是当点T与M重合时，t＝1，另一个是当TM＝4时，t＝5，∴此时t的取值范围是1≤t＜5，综合以上可得，t的取值范围是﹣﹣1≤t＜5．3．解：（1）如答图1，当CD⊥AB或点D是AB的中点是，CD2＝AD•BD；（2）作AE⊥BC于点E，由，可设AE＝4x，则BE＝3x，CE＝6x，∴BC＝9x＝9，∴x＝1，∴BE＝3，CE＝6，AE＝4，设DE＝a，①如答图2，若点D在点E左侧，由点D是BC边上的“好点”知，AD2＝BD•CD，∴a2+42＝（3﹣a）（6+a），即2a2+3a﹣2＝0，解得，a2＝﹣2（舍去），∴．②如答图3，若点D在点E右侧，由点D是BC边上的“好点”知，AD2＝BD•CD，∴a2+42＝（3+a）（6﹣a），即2a2﹣3a﹣2＝0，解得a1＝2，（舍去）∴BD＝3+a＝3+2＝5．∴或5．（3）①如答图4，连接AD，BD，∵∠CHA＝∠BHD，∠ACH＝∠DBH∴△AHC∽△DHB，∴，即AH•BH＝CH•DH，∵OH⊥AB，∴AH＝BH，∴BH2＝CH•DH∴点H是△BCD中CD边上的“好点”．②．理由如下：如答图4，∵∠ABD＝90°，∴AD是直径，∴AD＝18．又∵OH⊥AB，∴OH∥BD．∵点O是线段AD的中点，∴OH是△ABD的中位线，∴BD＝2OH＝12．在直角△ABD中，由勾股定理知：AB＝＝＝6．∴由垂径定理得到：BH＝AB＝3．在直角△BDH中，由勾股定理知：DH＝＝＝3．又由①知，BH2＝CH•DH，即45＝3CH，则CH＝．∴＝＝，即．4．（1）证明：∵C是的中点，∴＝，∴∠ABC＝∠CBD，∵OB＝OC，∴∠ABC＝∠C，∴∠ABC＝∠CBD＝∠C，∴∠ABD＝∠ABC+CBD＝2∠C；（2）解：连接AC，∵AB为⊙O的直径，∴∠ACB＝90°，∴AC＝＝6，∵C是的中点，∴OC⊥AD，∴OA2﹣OF2＝AF2＝AC2﹣CF2，∴52﹣OF2＝62﹣（5﹣OF）2，∴OF＝1.4，又∵O是AB的中点，∴BD＝2OF＝2.8．5．解：（1）如图1，∵A（0，8），B（6，0），C（0，3），∴OA＝8，OB＝6，OC＝3，∴AC＝5，∵△ACD∽△AOB，∴，∴∴CD的＝，∴⊙P的半径为；（2）在Rt△AOB中，OA＝8，OB＝6，∴＝＝10，如图2，当⊙P与AB相切时，CD⊥AB，∴∠ADC＝∠AOB＝90°，∠CAD＝∠BAO，∴△ACD∽△ABO，∴，即，∴AD＝4，CD＝3，∵CD为⊙P的直径，∴CP＝，过点P作PE⊥AO于点E，∵∠PEC＝∠ADC＝90°，∠PCE＝∠ACD，∴△CPE∽△CAD，∴，即，∴，∴，∴△POB的面积＝＝；（3）①如图3，若⊙P与AB只有一个交点，则⊙P与AB相切，由（2）可知PD⊥AB，PD＝，∴△PAB的面积＝．②如图4，若⊙P与AB有两个交点，设另一个交点为F，连接CF，可得∠CFD＝90°，由（2）可得CF＝3，过点P作PG⊥AB于点G，则DG＝，则PG为△DCF的中位线，PG＝，∴△PAB的面积＝＝．综上所述，在整个运动过程中，△PAB的面积是定值，定值为．6．解：（1）如图1，∵△DEF是等边三角形，∴∠FDE＝∠F＝60°．∵∠A＝30°，∴∠AMD＝∠FDE﹣∠A＝30°，∴∠FMN＝∠AMD＝30°，∴∠MNF＝90°，即△FMN是直角三角形，∵∠FDE＝60°，∴∠AMD＝∠FDE﹣∠A＝30°，∴∠AMD＝∠A，∴DM＝DA，∴△ADM是等腰三角形；故答案为：直角三角形，等腰三角形；（2）如图2，△ADM是等腰三角形，∴DM＝AD＝x，FM＝4﹣x，又∵∠FED＝60°，∠A＝30°，∴∠FNM＝90°，∴MN＝MF•sinF＝（4﹣x），FN＝，∴y＝＝，＝．当0＜x≤2时，∴y＝S四边形DENM＝S△FDE﹣S△FMN＝4，当2≤x＜4时，CD＝6﹣x，∵∠BCE＝90°，∠PDC＝60°，∴PC＝（6﹣x），∴，＝．（3）如图3，点M作MG⊥AC于点G，由（2）得DM＝x，∵∠MDG＝60°，∴MG＝，MNF＝90°∴MN⊥FC要使以点M为圆心，MN长为半径的圆与边AC、EF相切，则有MG＝MN，∴，解得：x＝2，∴圆的半径MN＝．7．解：（1）如图1，连接OA、OB、OC，延长OC交AB于点G，在正三角形ABC中，AB＝BC＝AC＝2，∵OA＝OB，AC＝BC，∴OC垂直平分AB，∴AG＝AB＝1，∴在Rt△AGC中，由勾股定理得：CG＝＝＝，在Rt△AGO中，由勾股定理得：OG＝＝＝2，∴OC＝2﹣；如图2，延长CO交EF于点H，当CO⊥EF时，点C到直线EF的距离最大，最大距离为CH的长，∵OE＝OF，CO⊥EF，∴CO平分∠EOF，∵∠EOF＝120°，∴∠EOH＝∠EOF＝60°，在Rt△EOH中，cos∠EOH＝，∴cos60°＝＝，∴OH＝，∴CH＝CO+OH＝，∴点C到直线EF的最大距离是．故答案为：2﹣；．（2）如图3，当点B在直线OE上时，由OA＝OB，CA＝CB可知，点O，C都在线段AB的垂直平分线上，过点C作AB的垂线，垂足为G，则G为AB中点，直线CG过点O．∴由∠COM＝∠BOG，∠CMO＝∠BGO∴△OCM∽△OBG，∴＝，∴＝，∴CM＝，∴点C到OE的距离为．（3）如图4，当BC⊥OE时，设垂足为点M，∵∠EOF＝120°，∴∠COM＝180°﹣120°＝60°，∴在Rt△COM中，sin∠COM＝，∴sin60°＝＝，∴CM＝CO＝（2﹣）＝﹣；如图5，当BC∥OE时，过点C作CN⊥OE，垂足为N，∵BC∥OE，∴∠CON＝∠GCB＝30°，∴在Rt△CON中，sin∠CON＝，∴sin30°＝＝，∴CN＝CO＝（2﹣）＝﹣；综上所述，当BC与OE垂直或平行时，点C到OE的距离为﹣或﹣．8．解：（1）由题意，得OA＝6，OB＝2．当0＜t＜2时，OM＝6﹣3t，ON＝t．若△ABO∽△MNO，则＝，即＝，解得t＝1．若△ABO∽△NMO，则＝，即＝，解得t＝1.8．综上，当t为1或1.8时，△ABO与以点O、M、N为顶点的三角形相似．（2）①当0＜t＜2时，在ON的延长线的截取ND＝OM，连接CD、CN、CM，如图所示：∵直线y＝x与x轴的夹角为450，∴OC平分∠AOB．∴∠AOC＝∠BOC．∴CN＝CM．又∵在⊙O中∠CNO+∠CMO＝180°，∠DNC+∠CNO＝180°，∴∠CND＝∠CMO．∴△CND≌△CMO（SAS）．∴CD＝CO，∠DCN＝∠OCM．又∵∠AOB＝90°，∴MN为⊙O的直径，∴∠MCN＝90°．∴∠OCM+∠OCN＝90°．∴∠DCN+∠OCN＝90°．∴∠OCD＝90°．又∵CD＝CO，∴OD＝OC．∴ON+ND＝OC．∴OM+ON＝OC．②当t＞2时，过点C作CD⊥OC交ON于点D，连接CM、CN，如图所示：∵∠COD＝45°，∴△CDO为等腰直角三角形，∴OD＝OC．∵MN为⊙O的直径，∴∠MCN＝90°．又∵在⊙O中，∠CMN＝∠CNM＝45°，∴MC＝NC．又∵∠OCD＝∠MCN＝90°，∴∠DCN＝∠OCM．∴△CDN≌△COM（SAS）．∴DN＝OM．又∵OD＝OC，∴ON﹣DN＝OC．∴ON﹣OM＝OC．9．证明：（1）如图，连接OD，OC，在Rt△ABC中，∠ACB＝90°，点O是AB的中点，在Rt△ABD中，∠ADB＝90°，点O是AB的中点，∴OD＝OA＝OB，∴OA＝OB＝OC＝OD，∴A，B，C，D四个点在以点O为圆心的同一个圆上；（2）由（1）知，A，B，C，D四个点在以点O为圆心的同一个圆上，且AD＝BD，∴，∴CD平分∠ACB；（3）由（2）知，∠BCD＝45°，∵∠ABC＝60°，∴∠BEC＝75°，∴∠AED＝75°，∵DF∥BC，∴∠BFD＝∠ABC＝60°，∵∠ABD＝45°，∴∠BDF＝180°﹣∠BFD﹣∠ABD＝75°＝∠AED，∵∠DFE＝∠BFD，∴△DEF∽△BDF，∴，连接OD，则∠BOD＝90°，OB＝OD，在Rt△DOF中，根据勾股定理得，OD2+OF2＝DF2，∴OB2+OF2＝BF•EF，即BO2+OF2＝EF•BF．10．解：（1）∵∠BAC＝90°，∠B＝60°，AB＝2，tanB＝，∴AC＝AB•tanB＝2tan60°＝2；∵AE⊥EF，∴∠AEF＝90°，∵∠EAF＝∠B＝60°，∴∠F＝90°﹣∠EAF＝90°﹣60°＝30°．故答案为：2，30°；（2）证明：当BD＝DE时，∵AD⊥BC于D，∴AB＝AE，∵∠AEF＝90°，∠BAC＝90°，∴∠AEF＝∠BAC，又∠EAF＝∠B，∴△ABC≌△EAF（ASA）；（3）∵∠AEF＝90°，∠EAF＝60°，tan∠EAF＝，∴EF＝AE•tan∠EAF＝AE•tan60°＝AE，∴S△EAF＝AE•EF＝AE×AE＝AE2，当AE⊥BC时，AE最短，S△EAF最小，此时∠AEB＝90°，sinB＝，∴AE＝AB•sinB＝2sin60°＝2×＝，S△EAF＝AE2＝×3＝，∴△EAF面积的最小值是，故答案为：；（4）当△EAF内心恰好落在AC上时，设△EAF的内心为N，连接EN，如图：∵N是△EAF的内心，∴AN平分∠EAF，EN平分∠AEF，∴∠EAC＝∠AEF＝×60°＝30°，∵∠BAC＝90°，∴∠BAE＝∠BAC﹣∠EAC＝90°﹣30°＝60°，又∵∠B＝60°，∴△ABE是等边三角形，∴AE＝AB＝2，∵E为BC上的一点，不与B、C重合，由（1）可知AC＝2，∴当△EAF的内心在△ABC的外部时，．故答案为：．。

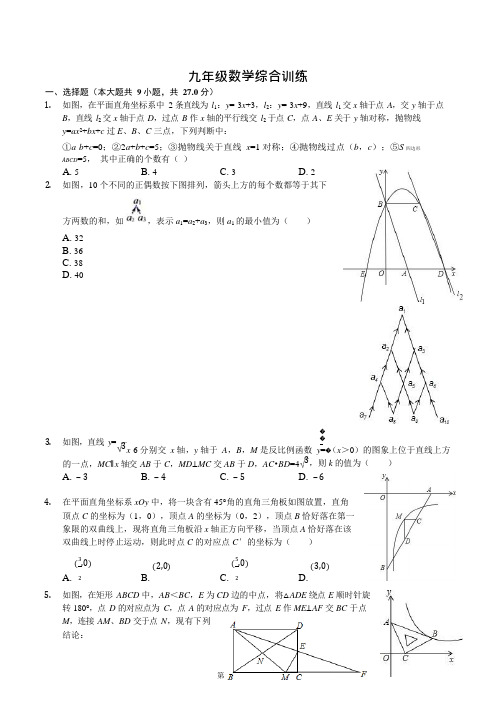
九年级数学综合训练一、选择题（本大题共9 小题，共27.0 分）1.如图，在平面直角坐标系中2 条直线为l1：y=-3x+3，l2：y=-3x+9，直线l1交x 轴于点A，交y 轴于点B，直线l2交x 轴于点D，过点B 作x 轴的平行线交l2于点C，点A、E 关于y 轴对称，抛物线y=ax2+bx+c 过E、B、C 三点，下列判断中：①a-b+c=0；②2a+b+c=5；③抛物线关于直线x=1 对称；④抛物线过点（b，c）；⑤S 四边形ABCD=5，其中正确的个数有（）A. 5B. 4C. 3D. 22.如图，10 个不同的正偶数按下图排列，箭头上方的每个数都等于其下方两数的和，如，表示a1=a2+a3，则a1的最小值为（）A.32B.36C.38D.403.如图，直线y= ��x -6 分别交x 轴，y 轴于A，B，M 是反比例函数y=�（x＞0）的图象上位于直线上方的一点，MC∥x 轴交AB 于C，MD⊥MC 交AB 于D，AC•BD=43，则k 的值为（）A. ‒ 3B. ‒ 4C. ‒ 5D. ‒ 64.在平面直角坐标系xOy 中，将一块含有45°角的直角三角板如图放置，直角顶点C 的坐标为（1，0），顶点A 的坐标为（0，2），顶点B 恰好落在第一象限的双曲线上，现将直角三角板沿x 轴正方向平移，当顶点A 恰好落在该双曲线上时停止运动，则此时点C 的对应点C′的坐标为（）(3,0) (2,0) (5,0) (3,0)A. 2B.C. 2D.5.如图，在矩形ABCD 中，AB＜BC，E 为CD 边的中点，将△ADE 绕点E 顺时针旋转180°，点D 的对应点为C，点A 的对应点为F，过点E 作ME⊥AF 交BC 于点M，连接AM、BD 交于点N，现有下列结论：35 ①AM =AD +MC ；②AM =DE +BM ；③DE 2=AD •CM ；④点 N 为△ABM 的外心． 其中正确的个数为（）A. 1 个B. 2 个C. 3 个D. 4 个6. 规定：如果关于 x 的一元二次方程 ax 2+bx +c =0（a ≠0）有两个实数根，且其中一个根是另一个根的 2倍，则称这样的方程为“倍根方程”．现有下列结论：①方程 x 2+2x -8=0 是倍根方程；②若关于 x 的方程 x 2+ax +2=0 是倍根方程，则 a =±3；③若关于 x 的方程 ax 2-6ax +c =0（a ≠0）是倍根方程，则抛物线 y =ax 2-6ax +c 与 x 轴的公共点的坐标是 （2，0）和（4，0）； 4 ④若点（m ，n ）在反比例函数 y =x 的图象上，则关于 x 的方程 mx 2+5x +n =0 是倍根方程． 上述结论中正确的有（ ）A. ①②B. ③④C. ②③D. ②④7. 如图，六边形 ABCDEF 的内角都相等，∠DAB =60°，AB =DE ，则下列结论成立的个数是（） ①AB ∥DE ；②EF ∥AD ∥BC ；③AF =CD ；④四边形 ACDF 是平行四边形；⑤六边形 ABCDEF 既是中心对称图形，又是轴对称图形．A. 2B. 3C. 4D. 58. 如图，在 Rt △ABC 中，∠C =90°，以△ABC 的一边为边画等腰三角形，使得它的第三个顶点在△ABC 的其他边上，则可以画出的不同的等腰三角形的个数最多为（ ）A. 4B. 5C. 6D. 79. 如图，矩形 ABCD 中，AE ⊥BD 于点 E ，CF 平分∠BCD ，交 EA 的延长线于点 F ，且 BC =4，CD =2，给出下列结论：①∠BAE =∠CAD ；4②∠DBC =30°；③AE =5 5；④AF =2 ，其中正确结论的个数有（ ）A. 1 个B. 2 个C. 3 个D. 4 个二、填空题（本大题共 10 小题，共 30.0 分）10.如图，在Rt△ABC 中，∠BAC=30°，以直角边AB 为直径作半圆交AC 于点D，以AD 为边作等边△ADE，延长ED 交BC 于点F，BC=2 3，则图中阴影部分的面积为．（结果不取近似值）11.如图，在6×6 的网格内填入1 至6 的数字后，使每行、每列、每个小粗线宫中的数字不重复，则a×c=．12.如图，正方形ABCD 中，BE=EF=FC，CG=2GD，BG 分别交AE，AF 于M，N．下列结论：4 �M 3 1①AF⊥BG；②BN=3NF；③M G=8；④S 四边形CGNF=2S 四边形ANGD．其中正确的结论的序号是．13.已知：如图，在△AOB 中，∠AOB=90°，AO=3cm，BO=4cm．将△AOB 绕顶点O，按顺时针方向旋转到△A1OB1处，此时线段OB1与AB 的交点D 恰好为AB 的中点，则线段B1D= cm．14.如图，边长为4 的正六边形ABCDEF 的中心与坐标原点O 重合，AF∥x 轴，将正六边形ABCDEF 绕原点O 顺时针旋转n 次，每次旋转60°．当n=2017 时，顶点A 的坐标为．15.如图，在Rt△ABC 中，BC=2，∠BAC=30°，斜边AB 的两个端点分别在相互垂直的射线OM、ON 上滑动，下列结论：①若C、O 两点关于AB 对称，则OA=2 3；②C、O 两点距离的最大值为4；③若AB 平分CO，则AB⊥CO；�④斜边AB 的中点D 运动路径的长为2；其中正确的是（把你认为正确结论的序号都填上）．16.如图，∠AOB 的边OB 与x 轴正半轴重合，点P 是OA 上的一动点，点N（3，0）是OB 上的一定点，点M 是ON 的中点，∠AOB=30°，要使PM+PN 最小，则点P 的坐标为．17.在一条笔直的公路上有A、B、C 三地，C 地位于A、B 两地之间，甲车从A地沿这条公路匀速驶向C 地，乙车从B 地沿这条公路匀速驶向A 地，在甲车出发至甲车到达C 地的过程中，甲、乙两车各自与C 地的距离y（km）与甲车行驶时间t（h）之间的函数关系如图所示．下列结论：①甲车出发2h 时，两车相遇；②乙车出发1.5h 时，两车相距170km；③乙车出5发27h 时，两车相遇；④甲车到达C 地时，两车相距40km．其中正确的是（填写所有正确结论的序号）．�18.如图，在平面直角坐标系中，OA=AB，∠OAB=90°，反比例函数y=x（x＞0）的图象经过A，B 两点．若点A 的坐标为（n，1），则k 的值为．19.如图，在平面直角坐标系中，△ABC 的顶点坐标分别为A（-1，1），B（0，-2），C（1，0），点P（0，2）绕点A 旋转180°得到点P1，点P1绕点B 旋转180°得到点P2，点P2绕点C 旋转180°得到点P3，点P3绕点A 旋转180°得到点P4，…，按此作法进行下去，则点P2017的坐标为．答案和解析1.【答案】C【解析】解：∵直线l1：y=-3x+3 交x 轴于点A，交y 轴于点B，∴A（1，0），B（0，3），∵点A、E 关于y 轴对称，∴E（-1，0）．∵直线l2：y=-3x+9 交x 轴于点D，过点B 作x 轴的平行线交l2 于点C，∴D（3，0），C 点纵坐标与B 点纵坐标相同都是3，把y=3 代入y=-3x+9，得3=-3x+9，解得x=2，∴C（2，3）．∵抛物线y=ax2+bx+c 过E、B、C 三点，∴，解得，∴y=-x2+2x+3．①∵抛物线y=ax2+bx+c 过E（-1，0），∴a-b+c=0，故①正确；②∵a=-1，b=2，c=3，∴2a+b+c=-2+2+3=3≠5，故②错误；③∵抛物线过B（0，3），C（2，3）两点，∴对称轴是直线x=1，∴抛物线关于直线x=1 对称，故③正确；④∵b=2，c=3，抛物线过C（2，3）点，∴抛物线过点（b，c），故④正确；⑤∵直线l1∥l2，即AB∥CD，又BC∥AD，∴四边形ABCD 是平行四边形，∴S 四边形ABCD=BC•OB=2×3=6≠5，故⑤错误．综上可知，正确的结论有3个．故选：C．根据直线l1的解析式求出A（1，0），B（0，3），根据关于y 轴对称的两点坐标特征求出E（- 1，0）．根据平行于x 轴的直线上任意两点纵坐标相同得出C 点纵坐标与B 点纵坐标相同都是3，再根据二次函数图象上点的坐标特征求出C（2，3）．利用待定系数法求出抛物线的解析式为y=-x2+2x+3，进而判断各选项即可．本题考查了抛物线与x 轴的交点，一次函数、二次函数图象上点的坐标特征，关于y 轴对称的两点坐标特征，平行于x 轴的直线上任意两点坐标特征，待定系数法求抛物线的解析式，平行四边形的判定及面积公式，综合性较强，求出抛物线的解析式是解题的关键．2.【答案】D【解析】解：∵a1=a2+a3=a4+a5+a5+a6=a7+a8+a8+a9+a8+a9+a9+a10=a7+3（a8+a9）+a10，∴要使a1 取得最小值，则a8+a9 应尽可能的小，取a8=2、a9=4，∵a5=a8+a9=6，则a7、a10 中不能有6，若a7=8、a10=10，则a4=10=a10，不符合题意，舍去；若a7=10、a10=8，则a4=12、a6=4+8=12，不符合题意，舍去；若a7=10、a10=12，则a4=10+2=12、a6=4+12=16、a2=12+6=18、a3=6+16=22、a1=18+22=40，符合题意；综上，a1的最小值为40，故选：D．由a1=a7+3（a8+a9）+a10 知要使a1 取得最小值，则a8+a9 应尽可能的小，取a8=2、a9=4，根据a5=a8+a9=6，则a7、a10 中不能有6，据此对于a7、a8，分别取8、10、12 检验可得，从而得出答案．本题主要考查数字的变化类，根据题目要求得出a1取得最小值的切入点是解题的关键．3.【答案】A【解析】解：过点D 作DE⊥y 轴于点E，过点C 作CF⊥x 轴于点F，令x=0 代入y= x-6，∴y=-6，∴B（0，-6），∴OB=6，令y=0 代入y= x-6，∴x=2 ，∴（2 ，0），∴OA=2 ，∴勾股定理可知：AB=4 ，∴sin∠OAB= = ，cos∠OAB= =设M（x，y），∴CF=-y，ED=x，∴sin∠OAB= ，∴AC=- y，∵cos∠OAB=cos∠EDB= ，∴BD=2x，∵AC•BD=4，∴- y×2x=4 ，∴xy=-3，∵M 在反比例函数的图象上，∴k=xy=-3，故选（A）过点D 作DE⊥y 轴于点E，过点C 作CF⊥x 轴于点F，然后求出OA 与OB 的长度，即可求出∠OAB 的正弦值与余弦值，再设M（x，y），从而可表示出BD 与AC 的长度，根据AC•BD=4列出即可求出k 的值．本题考查反比例函数与一次函数的综合问题，解题的关键是根据∠OAB 的锐角三角函数值求出BD、AC，本题属于中等题型．4.【答案】C【解析】解：过点B 作BD⊥x 轴于点D，∵∠ACO+∠BCD=90°，∠OAC+∠ACO=90°，∴∠OAC=∠BCD，在△ACO 与△BCD 中，∴△ACO➴△BCD（AAS）∴OC=BD，OA=CD，∵A（0，2），C（1，0）∴OD=3，BD=1，∴B（3，1），∴设反比例函数的解析式为y= ，将B（3，1）代入y= ，∴k=3，∴y= ，∴把y=2 代入y= ，∴x= ，当顶点A 恰好落在该双曲线上时，此时点A 移动了个单位长度，∴C 也移动了个单位长度，此时点C 的对应点C′的坐标为（，0）故选：C．过点B 作BD⊥x 轴于点D，易证△ACO➴△BCD（AAS），从而可求出B 的坐标，进而可求出反比例函数的解析式，根据解析式与 A 的坐标即可得知平移的单位长度，从而求出 C 的对应点．本题考查反比例函数的综合问题，涉及全等三角形的性质与判定，反比例函数的解析式，平移的性质等知识，综合程度较高，属于中等题型．5.【答案】B【解析】解：∵E 为CD 边的中点，∴DE=CE，又∵∠D=∠ECF=90°，∠AED=∠FEC，∴△ADE➴△FCE，∴AD=CF，AE=FE，又∵ME⊥AF，∴ME 垂直平分AF，∴AM=MF=MC+CF，∴AM=MC+AD，故①正确；如图，延长CB 至G，使得∠BAG=∠DAE，由AM=MF，AD∥BF，可得∠DAE=∠F=∠EAM，可设∠BAG=∠DAE=∠EAM=α，∠BAM=β，则∠AED=∠EAB=∠GAM=α+β，由∠BAG=∠DAE，∠ABG=∠ADE=90°，可得△ABG∽△ADE，∴∠G=∠AED=α+β，∴∠G=∠GAM，∴AM=GM=BG+BM，由△ABG∽△ADE，可得= ，而AB＜BC=AD，∴BG＜DE，∴BG+BM＜DE+BM，即AM＜DE+BM，∴AM=DE+BM 不成立，故②错误；∵ME⊥FF，EC⊥MF，∴EC2=CM×CF，又∵EC=DE，AD=CF，∴DE2=AD•CM，故③正确；∵∠ABM=90°，∴AM 是△ABM 的❧➓圆的直径，∵BM＜AD，∴当BM∥AD 时，= ＜1，∴N 不是AM 的中点，∴点N 不是△ABM 的❧心，故④错误．综上所述，正确的结论有2 个，故选：B．根据全等三角形的性质以及线段垂直平分线的性质，即可得出AM=MC+AD；根据△ABG∽△ ADE，且AB＜BC，即可得出BG＜DE，再根据AM=GM=BG+BM，即可得出AM=DE+BM 不成立；根据ME⊥FF，EC⊥MF，运用射影定理即可得出EC2=CM×CF，据此可得DE2=AD•CM 成立；根据N 不是AM 的中点，可得点N 不是△ABM 的❧心．本题主要考查了相似三角形的判定与性质，全等三角形的判定与性质，矩形的性质以及旋转的性质的综合应用，解决问题的关键是运用全等三角形的对应边相等以及相似三角形的对应边成比例进行推导，解题时注意：三角形❧➓圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的❧心，故❧心到三角形三个顶点的距离相等．6.【答案】C【解析】解：①由x2-2x-8=0，得（x-4）（x+2）=0，解得x1=4，x2=-2，∵x1≠2x2，或x2≠2x1，1 1 ∴方程 x 2-2x-8=0 不是倍根方程． 故①错误；②关于 x 的方程 x 2+ax+2=0 是倍根方程，∴设 x 2=2x 1，∴x 1•x 2=2x 2=2，∴x 1=±1，当 x 1=1 时 ，x 2=2，当 x 1=-1 时 ，x 2=-2，∴x 1+x 2=-a=±3，∴a=±3，故②正确；③关于 x 的方程 ax 2-6ax+c=0（a≠0）是倍根方程，∴x 2=2x 1，∵抛物线 y=ax 2-6ax+c 的对称轴是直线 x=3，∴抛物线 y=ax 2-6ax+c 与 x 轴的交点的坐标是（2，0）和（4，0），故③正确；④∵点（m ，n ）在反比例函数 y= 的图象上，∴mn=4，解 mx 2+5x+n=0 得 x 1=- ，x 2=- ，∴x 2=4x 1，∴关于 x 的方程 mx 2+5x+n=0 不是倍根方程；故选：C ．①通过解方程得到该方程的根，结合“倍根方程”的定义进行判断；②设 x 2=2x 1，得到 x 1•x 2=2x 2=2，得到当 x 1=1 时，x 2=2，当 x 1=-1 时，x 2=-2，于是得到结论；③根据“倍根方程”的定义即可得到结论；④若点（m，n）在反比例函数y= 的图象上，得到mn=4，然后解方程mx2+5x+n=0 即可得到正确的结论；本题考查了反比例函数图象上点的坐标特征，根与系数的关系，正确的理解倍根方程的定义是解题的关键．7.【答案】D【解析】解：∵六边形ABCDEF 的内角都相等，∴∠EFA=∠FED=∠FAB=∠ABC=120°，∵∠DAB=60°，∴∠DAF=60°，∴∠EFA+∠DAF=180°，∠DAB+∠ABC=180°，∴AD∥EF∥CB，故②正确，∴∠FED+∠EDA=180°，∴∠EDA=∠ADC=60°，∴∠EDA=∠DAB，∴AB∥DE，故①正确，∵∠FAD=∠EDA，∠CDA=∠BAD，EF∥AD∥BC，∴四边形EFAD，四边形BCDA 是等腰梯形，∴AF=DE，AB=CD，∵AB=DE，∴AF=CD，故③正确，连➓CF 与AD 交于点O，连➓DF、AC、AE、DB、BE．∵∠CDA=∠DAF，∴AF∥CD，AF=CD，∴四边形AFDC 是平行四边形，故④正确，同法可证四边形AEDB 是平行四边形，∴AD 与CF，AD 与BE 互相平分，∴OF=OC，OE=OB，OA=OD，∴六边形ABCDEF 既是中心对称图形，故⑤正确，故选D．根据六边形ABCDEF 的内角都相等，∠DAB=60°，平行线的判定，平行四边形的判定，中心对称图形的定义一一判断即可．本题考查平行四边形的判定和性质、平行线的判定和性质、轴对称图形、中心对称图形等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．8.【答案】D【解析】解：如图：故选：D．①以B 为圆心，BC 长为半径画弧，交AB 于点D，△BCD 就是等腰三角形；②以A 为圆心，AC 长为半径画弧，交AB 于点E，△ACE 就是等腰三角形；③以C 为圆心，BC 长为半径画弧，交AC 于点F，△BCF 就是等腰三角形；④以C 为圆心，BC 长为半径画弧，交AB 于点K，△BCK 就是等腰三角形；⑤作AB 的垂直平分线交AC 于G，则△AGB 是等腰三角形；➅作BC 的垂直平分线交AB 于I，则△BCI 和△ACI 是等腰三角形．本题考查了等腰三角形的判定的应用，主要考查学生的理解能力和动手操作能力．9.【答案】C【解析】解：在矩形ABCD 中，∵∠BAD=90°，∵AE⊥BD，∴∠AED=90°，∴∠ADE+∠DAE=∠DAE+∠BAE=90°，∴∠BAE=∠ADB，∵∠CAD=∠ADB，∴∠BAE=∠CAD，故①正确；∵BC=4，CD=2，∴tan∠DBC= = ，∴∠DBC≠30°，故②错误；∵BD= =2 ，∵AB=CD=2，AD=BC=4，∵△ABE∽△DBA，∴，即，∴AE= ；故③正确；∵CF 平分∠BCD，∴∠BCF=45°，∴∠ACF=45°-∠ACB，∵AD∥BC，∴∠DAC=∠BAE=∠ACB，∴∠EAC=90°-2∠ACB，∴∠EAC=2∠ACF，∵∠EAC=∠ACF+∠F，∴∠ACF=∠F，∴AF=AC，∵AC=BD=2 ，∴AF=2 ，故④正确；故选C．根据余角的性质得到∠BAE=∠ADB，等量代换得到∠BAE=∠CAD，故①正确；根据三角函数的定义得到tan∠DBC= = ，于是得到∠DBC≠30°，故②错误；由勾股定理得到BD==2 ，根据相似三角形的性质得到AE= ；故③正确；根据角平分线的定义得到∠BCF=45°，求得∠ACF=45°-∠ACB，推出∠EAC=2∠ACF，根据❧角的性质得到∠EAC=∠ACF+∠F，得到∠ACF=∠F，根据等腰三角形的判定得到AF=AC，于是得到AF=2 ，故④正确．本题考查了矩形的性质，相似三角形的判定和性质，三角形的❧角的性质，角平分线的定义，熟练掌握相似三角形的判定和性质是解题的关键．10.【答案】3【解析】3 3-2π解：如图所示：设半圆的圆心为O，连➓DO，过D 作DG⊥AB 于点G，过D 作DN⊥CB 于点N，∵在Rt△ABC 中，∠BAC=30°，∴∠ACB=60°，∠ABC=90°，∵以AD 为边作等边△ADE，∴∠EAD=60°，∴∠EAB=60°+30°=90°，可得：AE∥BC，则△ADE∽△CDF，∴△CDF 是等边三角形，∵在Rt△ABC 中，∠BAC=30°，BC=2 ，∴AC=4 ，AB=6，∠DOG=60°，则AO=BO=3，故DG=DO•sin60°=，则AD=3 ，DC=AC-AD= ，故DN=DC•sin60°=×= ，则S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF= ×2 ×6- ×3×- - × ×=3 - π．故答案为：3 - π．根据题意结合等边三角形的性质分别得出AB，AC，AD，DC 的长，进而利用S 阴影=S△ABC-S△AOD-S 扇形DOB-S△DCF 求出答案．此题主要考查了扇形面积求法以及等边三角形的性质和锐角三角函数关系等知识，正确分割图形是解题关键．11.【答案】2【解析】解：对各个小宫格编号如下：先看己：已经有了数字3、5、6，缺少1、2、4；观察发现：4 不能在第四列，2 不能在第五列，而2 不能在第六列；所以2 只能在第六行第四列，即a=2；则b 和c 有一个是1，有一个是4，不确定，如下：观察上图发现：第四列已经有数字2、3、4、6，缺少1 和5，由于5 不能在第二行，所以5 在第四行，那么1 在第二行；如下：再看乙部分：已经有了数字1、2、3，缺少数字4、5、6，观察上图发现：5 不能在第六列，所以5在第五列的第一行；4 和6 在第六列的第一行和第二行，不确定，分两种情况：①当4 在第一行时，6 在第二行；那么第二行第二列就是4，如下：再看甲部分：已经有了数字1、3、4、5，缺少数字2、6，观察上图发现：2 不能在第三列，所以2 在第二列，则6 在第三列的第一行，如下：观察上图可知：第三列少1 和4，4 不能在第三行，所以4 在第五行，则1 在第三行，如下：观察上图可知：第五行缺少1 和2，1 不能在第1 列，所以1 在第五列，则2 在第一列，即c=1，所以b=4，如下：观察上图可知：第六列缺少1 和2，1 不能在第三行，则在第四行，所以2 在第三行，如下：再看戊部分：已经有了数字2、3、4、5，缺少数字1、6，观察上图发现：1 不能在第一列，所以1 在第二列，则6 在第一列，如下：观察上图可知：第一列缺少3 和4，4 不能在第三行，所以4 在第四行，则3 在第三行，如下：观察上图可知：第二列缺少5 和6，5 不能在第四行，所以5 在第三行，则6 在第四行，如下：观察上图可知：第三行第五列少6，第四行第五列少3，如下：所以，a=2，c=1，ac=2；②当6 在第一行，4 在第二行时，那么第二行第二列就是6，如下：再看甲部分：已经有了数字1、3、5、6，缺少数字2、4，观察上图发现：2 不能在第三列，所以2 在第2 列，4 在第三列，如下：观察上图可知：第三列缺少数字1 和6，6 不能在第五行，所以6 在第三行，则1 在第五行，所以c=4，b=1，如下：观察上图可知：第五列缺少数字3 和6，6 不能在第三行，所以6 在第四行，则3 在第三行，如下：观察上图可知：第六列缺少数字1 和2，2 不能在第四行，所以2 在第三行，则1 在第四行，如下：观察上图可知：第三行缺少数字1 和5，1 和5 都不能在第一列，所以此种情况不成立；综上所述：a=2，c=1，a×c=2；故答案为：2．粗线把这个数独分成了6 块，为了便于解答，对各部分进行编号：甲、乙、丙、丁、戊、己，先从各部分中数字最多的己出发，找出其各个小方格里面的数，再根据每行、每列、每小宫格都不出现重复的数字进行推算．本题是六阶数独，比较复杂，关键是找出突破口，先推算出一个区域或者一行、一列，再逐步的进行推算．12.【答案】①③【解析】解：①∵四边形ABCD 为正方形，∴AB=BC=CD，∵BE=EF=FC，CG=2GD，∴BF=CG，∵在△ABF 和△BCG 中，，∴△ABF➴△BCG，∴∠BAF=∠CBG，∵∠BAF+∠BFA=90°，∴∠CBG+∠BFA=90°，即AF⊥BG；①正确；②∵在△BNF 和△BCG 中，，∴△BNF∽△BCG，∴ = = ，∴BN= NF；②错误；③作EH⊥AF，令AB=3，则BF=2，BE=EF=CF=1，AF= = ，∵S△ABF= AF•BN=AB•BF，∴BN= ，NF= BN= ，∴AN=AF-NF= ，∵E 是BF 中点，∴EH 是△BFN 的中位线，∴EH= ，NH= ，BN∥EH，∴AH= ， = ，解得：MN= ，∴BM=BN-MN= ，MG=BG-BM= ，∴ = ；③正确；④连➓AG，FG，根据③中结论，则NG=BG-BN= ，∵S 四边形CGNF=S△CFG+S△GNF= CG•CF+NF•NG=1+= ，S 四边形ANGD=S△ANG+S△ADG= AN•GN+AD•DG= + = ，∴S 四边形CGNF≠S 四边形ANGD，④错误；故答案为①③．①易证△ABF➴△BCG，即可解题；②易证△BNF∽△BCG，即可求得的值，即可解题；③作EH⊥AF，令AB=3，即可求得MN，BM 的值，即可解题；④连➓AG，FG，根据③中结论即可求得S 四边形CGNF 和S 四边形ANGD，即可解题．本题考查了全等三角形的判定和性质，考查了相似三角形的判定和对应边成比例的性质，本题中令AB=3 求得AN，BN，NG，NF 的值是解题的关键．13.【答案】1.5【解析】解：∵在△AOB 中，∠AOB=90°，AO=3cm，BO=4cm，∴AB= =5cm，∵点D 为AB 的中点，∴OD= AB=2.5cm．∵将△AOB 绕顶点O，按顺时针方向旋转到△A1OB1 处，∴OB1=OB=4cm，∴B1D=OB1-OD=1.5cm．故答案为1.5．先在直角△AOB 中利用勾股定理求出AB= =5cm，再利用直角三角形斜边上的中线等于斜边的一半得出OD= AB=2.5cm．然后根据旋转的性质得到OB1=OB=4cm，那么B1D=OB1-OD=1.5cm．本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了直角三角形斜边上的中线等于斜边的一半的性质以及勾股定理．14.【答案】（2，2 3）【解析】解：2017×60°÷360°=336…1，即与正六边形ABCDEF 绕原点O 顺时针旋转1 次时点A 的坐标是一样的．当点A 按顺时针旋转60°时，与原F 点重合．连➓OF，过点F 作FH⊥x 轴，垂足为H；由已知EF=4，∠FOE=60°（正六边形的性质），∴△OEF 是等边三角形，∴OF=EF=4，∴F（2，2 ），即旋转2017 后点A 的坐标是（2，2 ），故答案是：（2，2 ）．将正六边形ABCDEF 绕原点O 顺时针旋转2017 次时，点A 所在的位置就是原F 点所在的位置．此题主要考查了正六边形的性质，坐标与图形的性质-旋转．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．15.【答案】①②③【解析】解：在Rt△ABC 中，∵BC=2，∠BAC=30°，∴AB=4，AC= =2 ，①若C、O 两点关于AB 对称，如图1，∴AB 是OC 的垂直平分线，则OA=AC=2 ；所以①正确；②如图1，取AB 的中点为E，连➓OE、CE，∵∠AOB=∠ACB=90°，∴OE=CE= AB=2，当OC 经过点E 时，OC 最大，则C、O 两点距离的最大值为4；所以②正确；③如图2，同理取AB 的中点E，则OE=CE，∵AB 平分CO，∴OF=CF，∴AB⊥OC，所以③正确；④如图3，斜边AB 的中点D 运动路径是：以O 为圆心，以2 为半径的圆周的，则：=π．所以④不正确；综上所述，本题正确的有：①②③；故答案为：①②③．①先根据直角三角形30°的性质和勾股定理分别求AC 和AB，由对称的性质可知：AB 是OC 的垂直平分线，所以OA=AC；②当OC 经过AB 的中点E 时，OC 最大，则C、O 两点距离的最大值为4；③如图2，根据等腰三角形三线合一可知：AB⊥OC；④如图3，半径为2，圆心角为90°，根据弧长公式进行计算即可．本题是三角形的综合题，考查了直角三角形30°的性质、直角三角形斜边中线的性质、等腰三角形的性质、轴对称的性质、线段垂直平分线的性质、动点运动路径问题、弧长公式，熟练掌握直角三角形斜边中线等于斜边一半是本题的关键，难度适中．3 316.【答案】（2， 2 ）【解析】解：作N 关于OA 的对称点N′，连➓N′M 交OA 于P，则此时，PM+PN 最小，∵OA 垂直平分NN′，∴ON=ON′，∠N′ON=2∠AON=60°，∴△NON′是等边三角形，∵点M 是ON 的中点，∴N′M⊥ON，∵点N（3，0），∴ON=3，∵点M 是ON 的中点，∴OM=1.5，∴PM= ，∴P（，）．故答案为：（，）．作N 关于OA 的对称点N′，连➓N′M 交OA 于P，则此时，PM+PN 最小，由作图得到ON=ON′，∠N′ON=2∠AON=60°，求得△NON′是等边三角形，根据等边三角形的性质得到N′M⊥ON，解直角三角形即可得到结论．本题考查了轴对称-最短路线问题，等边三角形的判定和性质，解直角三角形，关键是确定P 的位置．17.【答案】②③④【解析】解：①观察函数图象可知，当t=2 时，两函数图象相交，∵C 地位于A、B 两地之间，∴交点代表了两车离C 地的距离相等，并不是两车相遇，结论①错误；②甲车的速度为240÷4=60（km/h），乙车的速度为200÷（3.5-1）=80（km/h），∵（240+200-60-170）÷（60+80）=1.5（h），∴乙车出发1.5h 时，两车相距170km，结论②正确；③∵（240+200-60）÷（60+80）=2 （h），∴乙车出发2 h 时，两车相遇，结论③正确；④∵80×（4-3.5）=40（km），∴甲车到达C 地时，两车相距40km，结论④正确．综上所述，正确的结论有：②③④．故答案为：②③④．①观察函数图象可知，当t=2 时，两函数图象相交，结合交点代表的意义，即可得出结论①错误；②根据速度=路程÷时间分别求出甲、乙两车的速度，再根据时间=路程÷速度和可求出乙车出发1.5h 时，两车相距170km，结论②正确；③根据时间=路程÷速度和可求出乙车出发2 h 时，两车相遇，结论③正确；④结合函数图象可知当甲到C 地时，乙车离开C 地0.5 小时，根据路程=速度×时间，即可得出结论④正确．综上即可得出结论．本题考查了一次函数的应用，根据函数图象逐一分析四条结论的正误是解题的关键．18.【答案】【解析】5 ‒ 1 2解：作AE⊥x 轴于E，BF⊥x 轴于F，过B 点作BC⊥y 轴于C，交AE 于G，如图所示：则AG⊥BC，∵∠OAB=90°，∴∠OAE+∠BAG=90°，∵∠OAE+∠AOE=90°，∴∠AOE=∠GAB ，在△AOE 和△BAG 中，，∴△AOE ➴△BAG （AAS ），∴OE=AG ，AE=BG ，∵点 A （n ，1），∴AG=OE=n ，BG=AE=1，∴B （n+1，1-n ），∴k=n×1=（n+1）（1-n ），整理得：n 2+n-1=0，解得：n= ∴n=，（负值舍去）， ∴k=故答案为： ；．作 AE ⊥x 轴于 E ，BF ⊥x 轴于 F ，过 B 点作 BC ⊥y 轴于 C ，交 AE 于 G ，则 AG ⊥BC ，先求得△ AOE ➴△BAG ，得出 AG=OE=n ，BG=AE=1，从而求得 B （n+1，1-n ），根据 k=n×1=（n+1）（1-n ）得出方程，解方程即可．本题考查了全等三角形的判定与性质、反比例函数图象上点的坐标特征、解方程等知识；熟练掌握反比例函数图象上点的坐标特征，证明三角形全等是解决问题的关键．19.【答案】（-2，0）【解析】解：如图所示，P 1（-2，0），P 2（2，-4），P 3（0，4），P 4（-2，-2），P 5（2，-2），P 6（0，2），发现 6 次一个循环，∵2017÷6=336…1，∴点 P 2017 的坐标与 P 1 的坐标相同，即 P 2017（-2，0），故答案为（-2，0）．画出P1～P6，寻找规律后即可解决问题．本题考查坐标与图形的性质、点的坐标等知识，解题的关键是循环探究问题的方法，属于中考常考题型．“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

选择、填空综合训练(时间：40分钟分值：54分)一、选择题：本大题共10小题，每小题3分，共30分．每小题只有一个正确选项．1.√（−8）33的立方根是( )A．8 B．－8 C．2 D．－22.下列计算结果是x5的为( C )A．x10÷x2B．x6－x1C．－x2·(－x)3D．(－x)3·(－x)2 3.一个物体的三视图如图所示，根据图中的数据，可求这个物体的表面积为( )第3题图A．60π cm2B．48π cm2C．96π cm2D．80π cm2 4.一组数据3，5，5，7，若添加一个数据5，则发生变化的统计量是( )A．平均数B．中位数C．方差D．众数5.满足下列条件的三条线段a，b，c能构成三角形的是( )A．a∶b∶c＝1∶2∶3 B．a＋b＝4，a＋b＋c＝9C．a＝3，b＝4，c＝5 D．a∶b∶c＝1∶1∶26.如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部(阴影)区域的概率为( )第6题图A.34B.13C.12D.147.如图所示，在正五边形ABCDE中，过顶点A作AF⊥CD，垂足为点F，连接对角线AC，则∠CAF的度数是( )第7题图A．16° B．18° C．24° D．28°8.如图，在长为62米、宽为42米的矩形草地上修同样宽的路，余下部分种植草坪．要使草坪的面积为2400平方米，设道路的宽为x米，则可列方程为( )第8题图A．(62－x)(42－x)＝2400 B．(62－x)(42－x)＋x2＝2400C．62×42－62x－42x＝2400 D．62x＋42x＝24009.已知二次函数y＝－14x2＋bx＋c的图象如图，则一次函数y＝－14x－2b与反比例函数y＝cx在同一平面直角坐标系中的图象大致是( )第9题图10.如图1，点P为矩形ABCD边上的一个动点，运动路线是A→B→C→D→A.设点P运动的路径长为x，△ABP的面积S△ABP＝y，图2是y随x变化的函数图象，则矩形ABCD的对角线BD的长是( )第10题图A.34B.41 C．8 D．10二、填空题：本大题共8小题，每小题3分，共24分．11.比较大小：－3－22(填“＞”“＜”或“＝”)．12.要使式子x＋3x－1＋(x－2)0有意义，则x的取值范围为.13.如果在解关于x的分式方程xx－1＋k1－x＝2时出现了增根x＝1，那么常数k的值为.14.如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作MN∥BC，分别交AB，AC于点M，N.若AB＝8，AC＝10，则△AMN的周长为.第14题图15.《九章算术》第九章“勾股”问题十九：“今有邑方(正方形小城)不知大小，各开中门．出北门三十步有木，出西门七百五十步见木．问：邑方几何(小城的边长)？”根据描述如图所示，其中E表示西门，F表示北门，G，H处是木(E，F 分别是所在边的中点)．则邑的边长为步．第15题图16.如图，在Rt△ABC中，∠B＝90°，点O在边AB上，以点O为圆心，OA为半径的圆经过点C，过点C作直线MN，使∠BCM＝2∠A.若OA＝4，∠BCM＝60°，则图中阴影部分的面积为 .第16题图17.如图，点O是▱ABCD的对称中心，AD＞AB，E，F是边AB上的点，且EF＝12 AB，G，H是BC边上的点，且GH＝13BC，若S1，S2分别表示△EOF和△GOH的面积，则S 1与S2之间的等量关系是.第17题图18.如图，等腰Rt△ABC中，∠ACB＝90°，AC＝BC＝1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①，可得到点P1，此时AP1＝2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2＝1＋2；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3＝2＋2；….按此规律继续旋转，直至得到点P2020为止，则AP2020＝.第18题图选择、填空综合训练(时间：40分钟分值：54分)一、选择题：本大题共10小题，每小题3分，共30分．每小题只有一个正确选项．1.√（−8）33的立方根是( D )A．8 B．－8 C．2 D．－22.下列计算结果是x5的为( C )A．x10÷x2B．x6－x1C．－x2·(－x)3D．(－x)3·(－x)2 3.一个物体的三视图如图所示，根据图中的数据，可求这个物体的表面积为( C )第3题图A．60π cm2B．48π cm2C．96π cm2D．80π cm2 4.一组数据3，5，5，7，若添加一个数据5，则发生变化的统计量是( C )A．平均数B．中位数C．方差D．众数5.满足下列条件的三条线段a，b，c能构成三角形的是( C )A．a∶b∶c＝1∶2∶3 B．a＋b＝4，a＋b＋c＝9C．a＝3，b＝4，c＝5 D．a∶b∶c＝1∶1∶26.如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部(阴影)区域的概率为( C )第6题图A.34B.13C.12D.147.如图所示，在正五边形ABCDE中，过顶点A作AF⊥CD，垂足为点F，连接对角线AC，则∠CAF的度数是( B )第7题图A．16° B．18° C．24° D．28°8.如图，在长为62米、宽为42米的矩形草地上修同样宽的路，余下部分种植草坪．要使草坪的面积为2400平方米，设道路的宽为x米，则可列方程为( A )第8题图A．(62－x)(42－x)＝2400 B．(62－x)(42－x)＋x2＝2400C．62×42－62x－42x＝2400 D．62x＋42x＝24009.已知二次函数y＝－14x2＋bx＋c的图象如图，则一次函数y＝－14x－2b与反比例函数y＝cx在同一平面直角坐标系中的图象大致是( C )第9题图10.如图1，点P为矩形ABCD边上的一个动点，运动路线是A→B→C→D→A.设点P运动的路径长为x，△ABP的面积S△ABP＝y，图2是y随x变化的函数图象，则矩形ABCD的对角线BD的长是( B )第10题图A.34B.41 C．8 D．10二、填空题：本大题共8小题，每小题3分，共24分．11.比较大小：－3＜－22(填“＞”“＜”或“＝”)．12.要使式子x＋3x－1＋(x－2)0有意义，则x的取值范围为 x≥－3且x≠1且x≠2.13.如果在解关于x的分式方程xx－1＋k1－x＝2时出现了增根x＝1，那么常数k的值为 1 .14.如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作MN∥BC，分别交AB，AC于点M，N.若AB＝8，AC＝10，则△AMN的周长为 18 .第14题图15.《九章算术》第九章“勾股”问题十九：“今有邑方(正方形小城)不知大小，各开中门．出北门三十步有木，出西门七百五十步见木．问：邑方几何(小城的边长)？”根据描述如图所示，其中E表示西门，F表示北门，G，H处是木(E，F 分别是所在边的中点)．则邑的边长为 300 步．第15题图16.如图，在Rt△ABC中，∠B＝90°，点O在边AB上，以点O为圆心，OA为半径的圆经过点C，过点C作直线MN，使∠BCM＝2∠A.若OA＝4，∠BCM＝60°，则图中阴影部分的面积为16π3－4 3 .第16题图17.如图，点O是▱ABCD的对称中心，AD＞AB，E，F是边AB上的点，且EF＝12 AB，G，H是BC边上的点，且GH＝13BC，若S1，S2分别表示△EOF和△GOH的面积，则S 1与S2之间的等量关系是 S1＝32S2.第17题图18.如图，等腰Rt△ABC中，∠ACB＝90°，AC＝BC＝1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①，可得到点P1，此时AP1＝2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2＝1＋2；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3＝2＋2；….按此规律继续旋转，直至得到点P2020为止，则AP2020＝ 1346＋674 2 .第18题图。

2021北师大版九年级数学上册《第1章特殊平行四边形》单元训练1．▱ABCD中，AC、BD交于点O，再添加一个条件，不一能判定四边形ABCD是菱形的是（）A．AB＝AD B．AC⊥BD C．AC＝BD D．AC平分∠BAD 2．四边形ABCD的对角线AC、BD相交于点O，从以下四个条件：①OA＝OC，OB＝OD；②AB∥CD，AD＝BC；③AB＝BC；④AB⊥BC中选两个，能推出四边形ABCD是矩形的是（）A．①②B．②③C．①④D．①③3．下列说法正确的是（）A．矩形的对角线相等垂直B．菱形的对角线相等C．正方形的对角线相等D．菱形的四个角都是直角4．如图，在矩形ABCD中，AD＝10，点E是边BC上一点，sin∠AEB＝，若ED平分∠AEC，则CE的长为（）A．2B．4C．6D．85．如图，四边形ABCD是菱形，其中A，B两点的坐标为A（0，3），B（4，0），则点D的坐标为（）A．（0，1）B．（0，﹣1）C．（0，2）D．（0，﹣2）6．如图，菱形ABCD的对角线AC、BD相交于点O，AC＝10，BD＝4，EF为过点O的一条直线，则图中阴影部分的面积为（）A．5B．6C．8D．127．如图，矩形ABCD中，对角线AC，BD交于点O，点E是边AB上一点，且OE⊥AC．设∠AOD＝α，∠AEO＝β，则α与β间的关系正确的是（）A．α＝βB．α+β＝180°C．2α+β＝180°D．α+2β＝180°8．在平面直角坐标系xOy中，A（﹣2，2），B（0，4），C（2，2），则正方形ABCD的顶点D的坐标是（）A．（﹣2，4）B．（2，4）C．（0，0）D．（0，﹣2）9．如图，点E，F在菱形ABCD的对角线AC上，∠ADC＝120°，∠BEC＝∠CBF＝50°，ED与BF的延长线交于点M．则对于以下结论：①∠BME＝30°；②△ADE≌△ABE；③EM＝BC；④AE+BM＝EM．其中正确结论的个数是（）A．1个B．2个C．3个D．4个10．如图，在平面直角坐标系中，矩形ABCD的边AB＝4，BC＝6．若不改变矩形ABCD的形状和大小，当矩形顶点A在x轴的正半轴上左右移动时，矩形的另一个顶点D始终在y轴的正半轴上随之上下移动．当点A移动到某一位置时，点C到点O的距离有最大值，则此时点A的横坐标为．11．如图，矩形ABCD中，AD＝，F是DA延长线上一点，G是CF上一点，且∠ACG ＝∠AGC，∠GAF＝∠F＝20°，则AB＝．12．如果一条直线把一个平面图形的面积分成相等的两部分，那么我们把这条直线叫做这个平面图形的面积等分线．已知在菱形ABCD中，AB＝6，∠B＝60°，点E在边AD上，且AE＝2，过点E的面积等分线与菱形的另一条边交于点F，那么线段EF的长为．13．如图，在正方形ABCD外取一点E，连接AE，BE，DE，过点A作AE的垂线交DE于点P．若AE＝AP＝1，PB＝，下列结论：①EB⊥ED；②点B到直线AE的距离为；③S△APD+S△APB＝；④S正方形ABCD＝5+2．其中正确的序号是．14．如图，在菱形ABCD中，AB＝5，AC＝6．过点D作BA的垂线，交BA的延长线于点E，则线段DE的长为．15．如图，O为坐标原点，四边形OABC为矩形，A（20，0），C（0，8），点D是OA的中点，点P在边BC上运动，当△ODP是以OD为腰的等腰三角形时，则P点的坐标为．16．如图，矩形ABCD中，对角线AC的垂直平分线交AD、BC于点E、F，AC与EF交于点O，连接AF、CE．（1）求证：四边形AFCE是菱形；（2）若AB＝3，AD＝4，求菱形AFCE的边长．17．如图，矩形ABCD的对角线AC、BD相交于点O，点E与点O关于CD对称．（1）连接CE、DE，求证：四边形CEDO是菱形；（2）若AB＝2，∠AOB＝60°，求点E、O之间的距离．18．如图，在长方形ABCD中，AB＝4cm，BE＝5cm，点E是AD边上的一点，AE、DE分别长acm、bcm，满足（a﹣3）2+|2a+b﹣9|＝0．动点P从B点出发，以2cm/s的速度沿B→C→D运动，最终到达点D．设运动时间为ts．（1）a＝cm，b＝cm；（2）t为何值时，EP把四边形BCDE的周长平分？（3）另有一点Q从点E出发，按照E→D→C的路径运动，且速度为1cm/s，若P、Q 两点同时出发，当其中一点到达终点时，另一点随之停止运动．求t为何值时，△BPQ 的面积等于6cm2．19．如图，在矩形ABCD中，∠BAD的平分线交BC于点E，EF⊥AD于点F，DG⊥AE于点G，DG与EF交于点O．（1）求证：四边形ABEF是正方形；（2）若AD＝AE，求证：AB＝AG；（3）在（2）的条件下，已知AB＝1，求OD的长．20．如图，△ABC中，点P在边AB上，过P分别作PE⊥AC，PF⊥BC垂足分别为E、F，如果AB＝13，AC＝12，BC＝5．（1）求证：四边形PECF是矩形；（2）若P为AB中点，连接CP，求CP的长．参考答案1．解：A、∵▱ABCD中，AB＝AD，∴▱ABCD是菱形，故选项A不符合题意；B、∵▱ABCD中，AC⊥BD，∴▱ABCD是菱形，故选项B不符合题意；C、∵▱ABCD中，AC＝BD，∴▱ABCD是矩形，故选项C符合题意；D、∵▱ABCD中，AD∥BC，∴∠DAC＝∠ACB，∵AC平分∠BAD，∴∠DAC＝∠BAC，∴∠ACB＝∠BAC，∴AB＝CB，∴▱ABCD是菱形，故选项D不符合题意；故选：C．2．解：A、∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形，再由AB∥CD，AD＝BC无法判断四边形ABCD是矩形，故选项A不符合题意；B、由②AB∥CD，AD＝BC；③AB＝BC无法判断四边形ABCD是矩形，故选项A不符合题意；C∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形，∵AB⊥BC，∴∠ABC＝90°，∴平行四边形ABCD是矩形，故选项C符合题意；D、∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形，又∵AB＝BC，∴平行四边形ABCD是菱形，故选项D不符合题意；故选：C．3．解：A、矩形的对角线相等且平分，选项错误，不符合题意；B、菱形的对角线垂直且平分，选项错误，不符合题意；C、正方形的对角线相等，选项正确，符合题意；D、矩形的四个角都是直角，而菱形的四个角不是直角，选项错误，不符合题意；故选：C．4．解：∵四边形ABCD是矩形，∴∠DEC＝∠ADE，又∵∠DEC＝∠AED，∴∠ADE＝∠AED，∴AE＝AD＝10，在直角△ABE中，∴AB＝6，BE＝＝＝8，∴CE＝BC﹣BE＝AD﹣BE＝10﹣8＝2．故选：A．5．解：∵A（0，3），B（4，0），∴OA＝3，OB＝4，∴AB＝＝＝5，∵四边形ABCD是菱形，∴DA＝AB＝5，∴OD＝2，∴点D（0，﹣2），故选：D．6．解：∵四边形ABCD是菱形，∴AC⊥BD，AO＝CO，AD∥BC，∴∠DAO＝∠BCO，在△AEO和△CFO中，，∴△AEO≌△CFO（ASA），∴S△AEO＝S△CFO，∴图中阴影部分的面积＝S△BOC＝S菱形ABCD＝×＝5，故选：A．7．解：∵四边形ABCD是矩形，∴∠OAD＝∠ODA，∵∠AOD＝α，∴∠OAD＝（180°﹣α），∵OE⊥AC，∴∠AOE＝90°，∵∠AEO＝β，∠DAE＝90°，∴∠OAD＝∠AEO，∴（180°﹣α）＝β，∴α+2β＝180°．故选：D．8．解：结合正方形对边平行且相等的性质，A（﹣2，2）向右平移2个单位、向上平移2个单位可得到B（0，4），同理：C（2，2）向左平移2个单位、向下平移2个单位可得到D，∴D的坐标为（0，0），故选：C．9．解：∵四边形ABD是菱形，∠ADC＝120°，∴AD＝AB＝BC＝CD，∠BAD＝∠BCD＝60°，∠DAE＝∠BAE，∠DCE＝∠BCE＝∠BCD＝30°，∵∠BFE＝∠BCE+∠CBF＝30°+50°＝80°，∴∠EBF＝180°﹣∠BEC﹣∠BFE＝180°﹣50°﹣80°＝50°，在△CDE和△CBE中，，∴△CDE≌△CBE（SAS），∴∠DEC＝∠BEC＝50°，∴∠BEM＝∠DEC+∠BEC＝100°，∴∠BME＝180°﹣∠BEM﹣∠EBF＝180°﹣100°﹣50°＝30°，故①正确；在△ADE和△ABE中，，∴△ADE≌△ABE（SAS），故②正确；∵∠EBC＝∠EBF+∠CBF＝100°，∴∠BEM＝∠EBC，在△BEM和△EBC中，，∴△BEM≌△EBC（AAS），∴BM＝EC，EM＝BC，故③正确；连接BD交AC于O，如图所示：∵四边形ABCD是菱形，∴OA＝OC，AC⊥BD，∵∠DCO＝30°，∴OD＝CD＝BC，OC＝OD，∴OC＝BC，∴AC＝2OC＝BC，∵BM＝EC，EM＝BC，∴AE+BM＝AE+EC＝AC＝BC＝EM，故④正确，正确结论的个数是4个，故选：D．10．解：如图，取AD的中点M，连接MC，OM，过点O作ON⊥AD，如图所示：∵矩形ABCD的边AB＝4，BC＝6，M为AD的中点，∴DC＝AB＝4，DM＝AM＝AD＝BC＝3，∴在Rt△CDM中，由勾股定理得CM＝5，在Rt△AOD中，OM＝AD＝3，∵当OC不过点M时，OM+CM＞OC∴当O、C、M共线时，点C到点O的距离有最大值，最大值为8．∵当O、C、M共线时，∠DMC＝∠NMO，∠CDM＝∠OMN＝90°，∴MN＝，ON＝，∴在Rt△OAN中，OA＝＝＝．∴此时点A的横坐标为．故答案为：．11．解：由三角形的外角性质得，∠AGC＝∠GAF+∠F＝20°+20°＝40°，∵∠ACG＝∠AGC，∴∠CAG＝180°﹣∠ACG﹣∠AGC＝180°﹣2×40°＝100°，∴∠CAF＝∠CAG+∠GAF＝100°+20°＝120°，∴∠BAC＝∠CAF﹣∠BAF＝120°﹣90°＝30°，在Rt△ABC中，AC＝2BC＝2AD＝2，由勾股定理，AB＝＝＝．故答案为：．12．解：如图，过点A和点E作AG⊥BC，EH⊥BC于点G和H，得矩形AGHE，∴GH＝AE＝2，∵在菱形ABCD中，AB＝6，∠B＝60°，∴BG＝3，AG＝3＝EH，∴HC＝BC﹣BG﹣GH＝6﹣3﹣2＝1，∵EF平分菱形面积，EF经过菱形对角线交点，∴FC＝AE＝2，∴FH＝FC﹣HC＝2﹣1＝1，在Rt△EFH中，根据勾股定理，得EF＝＝＝2．故答案为：2．13．解：∵AE⊥AP，AE＝AP＝1，∴∠AEP＝∠APE＝45°，∠EAB＝90°﹣∠BAP，∵四边形ABCD是正方形，∴AB＝AD，∠P AD＝90°﹣∠BAP，∴∠EAB＝∠P AD，在△AEB和△APD中，，∴△AEB≌△APD（SAS），∴∠AEB＝∠APD，∵∠APD＝180°﹣∠APE＝135°，∴∠AEB＝135°，∴∠BEP＝∠AEB﹣∠AEP＝135°﹣45°＝90°，∴EB⊥ED，①正确；Rt△AEP中，PE＝＝，Rt△BEP中，BE＝＝2，过B作BF⊥AE于F，如图：∵∠BEF＝180°﹣∠BEP﹣∠AEP＝45°，∴△BEF是等腰直角三角形，∴BF＝＝，故②正确；∵△AEB≌△APD，∴S△APD+S△APB＝S△AEB+S△APB＝S四边形AEBP＝S△AEP+S△BEP＝AE•AP+EP•BE＝+，故③不正确；∵△BEF是等腰直角三角形，∴EF＝BF＝，∴AF＝AE+EF＝1+，Rt△ABF中，AB2＝AF2+BF2，∴AB2＝（1+）2+（）2＝5+2，∴S正方形ABCD＝5+2，故④正确；故答案为：①②④．14．解：∵四边形ABCD是菱形，AB＝5，AC＝6．∴AB＝BC＝CD＝DA＝5，AC⊥BD，OA＝OC＝3，∴OB＝＝＝4，∴BD＝2OB＝8，∵，∴＝5DE，解得，DE＝，故答案为：．15．解：OD是等腰三角形的一条腰时：①若点O是顶角顶点时，P点就是以点O为圆心，以10为半径的弧与CB的交点，在直角△OPC中，CP＝＝6，则P的坐标是（6，8）．②若D是顶角顶点时，P点就是以点D为圆心，以10为半径的弧与CB的交点，过D作DM⊥BC于点M，在直角△PDM中，PM＝＝6，当P在M的左边时，CP＝10﹣6＝4，则P的坐标是（4，8）；当P在M的右侧时，CP＝5+3＝8，则P的坐标是（16，8）．故P的坐标为：（6，8）或（4，8）或（16，8）．故答案为：（6，8）或（4，8）或（16，8）．16．（1）证明：∵四边形ABCD是矩形，∴AD∥BC，AD＝BC，∴∠EAO＝∠FCO，∵EF是AC的垂直平分线，∴AO＝CO，∠EOA＝∠FOC＝90°，在△AEO和△CFO中，，∴△AEO≌△CFO（ASA），∴AE＝CF，∴四边形AFCE是平行四边形，又∵AC⊥EF，∴四边形AFCE是菱形；（2）解：∵四边形AFCE是菱形，∴AF＝CF，设AF＝CF＝x，则BF＝4﹣x，在Rt△ABF中，AF2＝AB2+BF2，即x2＝32+（4﹣x）2，解得x＝，∴菱形AFCE的边长为．17．（1）证明：如图，连接OE交DC于点F，∵四边形ABCD是矩形，∴AC＝BD，OC＝AC，OD＝BD，∴OC＝OD，∵点E与点O关于CD对称．∴CD垂直平分OE，∴DO＝DE，CO＝CE，∴DO＝DE＝CO＝CE，∴四边形CEDO是菱形；（2）∵四边形ABCD是矩形，∴AB＝CD＝2，∵OD＝OC，∴△ODC是等腰三角形，∵∠AOB＝∠COD＝60°，∴△ODC是等边三角形，∴∠ODC＝60°，∴∠DOE＝30°，∴OD＝DC＝2，∵CD垂直平分OE，∴DF＝1，∴OF＝∴OE＝2OF＝2，∴点E、O之间的距离为2．18．解：（1）∵（a﹣3）2+|2a+b﹣9|＝0，∴a﹣3＝0，2a+b﹣9＝0，∴a＝3，b＝3；故答案为：3，3；（2）∵AE＝3cm，DE＝3cm，∴AD＝6cm＝BC，∴C四边形BCDE＝BC+CD+DE+EB＝18cm，∵EP把四边形BCDE的周长平分，∴BE+BP＝9cm，∴点P在BC上，BP＝4cm，∴t＝＝2s；（3）解：①点P在BC上（0＜t≤3），∵S△BPQ＝×2t×4＝6，∴t＝；②相遇前，点P在CD上（3＜t≤），∵S△BPQ＝×[（4﹣（t﹣3）﹣（2t﹣6）]×6＝6，∴t＝；③相遇后，点P在CD上（＜t≤5），∵S△BPQ＝×[（t﹣3）+（2t﹣6）﹣4]×6＝6，∴t＝5；∴综上所述，当t＝s或s或5s时，△BPQ的面积等于6cm2．19．（1）证明：∵矩形ABCD，∴∠BAF＝∠ABE＝90°，∵EF⊥AD，∴四边形ABEF是矩形，∵AE平分∠BAD，∴EF＝EB，∴四边形ABEF是正方形；（2）∵AE平分∠BAD，∴∠DAG＝∠BAE，在△AGD和△ABE中，，∴△AGD≌△ABE（AAS），∴AB＝AG；（3）∵四边形ABEF是正方形，∴AB＝AF＝1，∵△AGD≌△ABE，∴DG＝AB＝AF＝AG＝1，∵AD＝AE，∴AD﹣AF＝AE﹣AG，即DF＝EG，在△DFO和△EGO中，，∴△DFO≌△EGO（AAS），∴FO＝GO，FD＝EG∵∠DAE＝∠AEF＝45°，∠AFE＝∠AGD＝90°，∴DF＝FO＝OG＝EG，∴DO＝OF＝OG，∴DG＝DO+OG＝OG+OG＝1，∴OG＝＝﹣1，∴OD＝（﹣1）＝2﹣．20．（1）证明：∵AB＝13，AC＝12，BC＝5，∴AC2+BC2＝122+52＝169，AB2＝132＝169，∴AC2+BC2＝AB2，∴△ABC是直角三角形，∠ACB＝90°，∵PE⊥AC，PF⊥BC，∴∠PEC＝∠PFC＝90°，∴四边形PECF是矩形；（2）解：由（1）得：∠ACB＝90°，∵P为AB中点，∴PC＝。

2022-2023学年浙教版九年级数学上册第二次阶段性（第1—4章）综合训练题（附答案）一．选择题（共10小题，每题3分，满分30分）1．若＝，则的值为（）A．B．C．D．2．已知一个扇形的弧长为π，半径是3，则这个扇形的面积为（）A．πB．C．D．3π3．如图，在△ABC中，点D，E分别在边AB，AC上，且＝＝，则三角形ADE 周长与三角形ABC的周长比是（）A．1：B．1：2C．1：3D．1：44．数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB＝c，一条直角边BC＝a．小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（）A．勾股定理B．直径所对的圆周角是直角C．勾股定理的逆定理D．90°的圆周角所对的弦是直径5．如图，在正五边形ABCDE中，记∠BCD＝x°，∠ACB＝y°，则等于（）A．B．2C．3D．46．若点A（﹣1，y1），B（2，y2），C（3，y3）在二次函数y＝（x﹣2）2+3的图象上，则y1、y2、y3的大小关系是（）A．y3＜y2＜y1B．y2＜y3＜y1C．y1＜y3＜y2D．y1＜y2＜y3 7．校园里一片小小的树叶，也蕴含着“黄金分割”，如图，P为AB的黄金分割点（AP＞PB），如果AB的长度为10cm，那么AP的长度为（）cm．A．﹣1B．2﹣2C．5﹣5D．10﹣10 8．已知二次函数y＝ax2+bx+c（a≠0）图象上部分点的坐标（x，y）的对应值如表所示：x…04…y…0.37﹣10.37…则方程ax2+bx+1.37＝0的根是（）A．0或4B．或4﹣C．1或5D．无实根9．如图，由边长为1的正方形组成的6×5网格中，一块含45°的三角板ABC的斜边AB 始终经过格点N，AC始终经过格点M，点A在MN下方运动，格点P到A的距离最小值为（）A．1B．C．﹣1D．2﹣210．如图，△ABC中，点D为边BC上的点，点E、F分别是边AB、AC上两点，且EF∥BC，若AE：EB＝m，BD：DC＝n，则（）A．m＞1，n＞1，则2S△AEF＞S△ABD B．m＜1，n＜1，则2S△AEF＞S△ABDC．m＞1，n＜1，则2S△AEF＜S△ABD D．m＜1，n＞1，则2S△AEF＜S△ABD二．填空题。

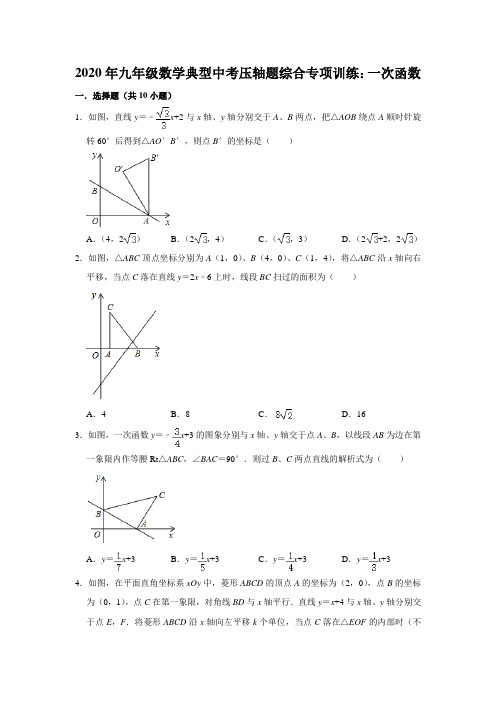
2020年九年级数学典型中考压轴题综合专项训练：一次函数一．选择题（共10小题）1．如图，直线y＝﹣x+2与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转60°后得到△AO′B′，则点B′的坐标是（）A．（4，2）B．（2，4）C．（，3）D．（2+2，2）2．如图，△ABC顶点坐标分别为A（1，0）、B（4，0）、C（1，4），将△ABC沿x轴向右平移，当点C落在直线y＝2x﹣6上时，线段BC扫过的面积为（）A．4B．8C．D．163．如图，一次函数y＝﹣x+3的图象分别与x轴、y轴交于点A、B，以线段AB为边在第一象限内作等腰Rt△ABC，∠BAC＝90°．则过B、C两点直线的解析式为（）A．y＝x+3B．y＝x+3C．y＝x+3D．y＝x+34．如图，在平面直角坐标系xOy中，菱形ABCD的顶点A的坐标为（2，0），点B的坐标为（0，1），点C在第一象限，对角线BD与x轴平行．直线y＝x+4与x轴、y轴分别交于点E，F．将菱形ABCD沿x轴向左平移k个单位，当点C落在△EOF的内部时（不包括三角形的边），k的值可能是（）A．2B．3C．4D．55．如图，点B，C分别在直线y＝2x和直线y＝kx上，A，D是x轴上两点，若四边形ABCD 是长方形，且AB：AD＝1：2，则k的值是（）A．B．C．D．6．如图，在平面直角坐标系中，点C的坐标为（0，4），动点A以每秒1个单位长的速度，从点O出发沿x轴的正方向运动，M是线段AC的中点．将线段AM以点A为中心，沿顺时针方向旋转90°，得到线段AB．过点B作x轴的垂线，垂足为E，过点C作y轴的垂线，交直线BE于点D，运动时间为t秒．当S△BCD＝时，t的值为（）A．2或2+3B．2或2+3C．3或3+5D．3或3+57．八个边长为1的正方形如图摆放在平面直角坐标系中，经过P点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（）A．y＝x+B．y＝x+C．y＝x+D．y＝x+8．如图，点M（﹣3，4），点P从O点出发，沿射线OM方向1个单位/秒匀速运动，运动的过程中以P为对称中心，O为一个顶点作正方形OABC，当正方形面积为128时，点A 坐标是（）A．（，）B．（，11）C．（2，2）D．（，）9．如图，直线AB：y＝﹣x+9交y轴于A，交x轴于B，x轴上一点C（﹣1，0），D为y 轴上一动点，把线段BD绕B点逆时针旋转120°得到线段BE，连接CE，CD，则当CE 长度最小时，线段CD的长为（）A．B．C．2D．510．如图，直角坐标系xOy中，A（0，5），直线x＝﹣5与x轴交于点D，直线y＝﹣x﹣与x轴及直线x＝﹣5分别交于点C，E，点B，E关于x轴对称，连接AB．①C（﹣13，0），E（﹣5，﹣3）；②直线AB的解析式为：y＝x+5；③设面积的和S＝S△CDE+S四边形ABDO，则S＝32；④在求面积的和S＝S△CDE+S四边形ABDO时，琪琪有个想法：“将△CDE沿x轴翻折到△CDB的位置，而△CDB与四边形ABDO拼接后可看成△AOC，即S＝S△CDE+S四边形ABDO ＝S△AOC”．其中正确的结论个数是（）A．1个B．2个C．3个D．4个二．填空题（共10小题）11．已知平面直角坐标系中，O为坐标原点，点A坐标为（0，8），点B坐标为（4，0），点E是直线y＝x+4上的一个动点，若∠EAB＝∠ABO，则点E的坐标为．12．如图，点M是直线y＝2x+3上的动点，过点M作MN垂直于x轴于点N，y轴上是否存在点P，使△MNP为等腰直角三角形，请写出符合条件的点P的坐标．13．如图，一次函数y＝﹣x+1的图象与x轴，y轴分别交于点A，B，点C在y轴的正半轴上，且OC＝3．在直线AB上有一点P，若满足∠CPB＞∠ACB，则点P横坐标x的取值范围是．14．如图，在平面直角坐标系中，四边形ABCO是正方形，点B的坐标为（4，4），直线y ＝mx﹣2恰好把正方形ABCO的面积分成相等的两部分，则m＝．15．如图，平面直角坐标系中，已知点P（2，2），C为y轴正半轴上一点，连接PC，线段PC绕点P顺时针旋转90°至线段PD，过点D作直线AB⊥x轴，垂足为B，直线AB与直线OP交于点A，且BD＝4AD，直线CD与直线OP交于点Q，则点Q的坐标为．16．如图，在平面直角坐标系中，点A的坐标是（0，2），点B的坐标是（2，0），连结AB，点P是线段AB上的一个动点（包括两端点），直线y＝﹣x上有一动点Q，连结OP，PQ，已知△OPQ的面积为，则点Q的坐标为．17．如图，点A、B的坐标分别为（0，2），（3，4），点P为x轴上的一点，若点B关于直线AP的对称点B′恰好落在x轴上，则点P的坐标为．18．平面直角坐标系中，直线y＝﹣x﹣1与x轴和y轴分别交于B、C两点，与直线x＝4交于点D，直线x＝4与x轴交于点A，点M（3，0），点E为直线x＝4上一动点，点F 为直线y＝﹣x﹣1上一动点，ME+EF最小值为，此时点F的坐标为．19．如图，平面直角坐标系中，已知直线y＝x上一点P（1，1），C为y轴上一点，连接PC，以PC为边做等腰直角三角形PCD，∠CPD＝90°，PC＝PD，过点D作线段AB⊥x轴，垂足为B，直线AB与直线y＝x交于点A，且BD＝2AD，连接CD，直线CD与直线y＝x交于点Q，则Q点的坐标是．20．如图，将一块等腰直角三角板ABC放置在平面直角坐标系中，∠ACB＝90°，AC＝BC，点A在y轴的正半轴上，点C在x轴的负半轴上，点B在第二象限，AC所在直线的函数表达式是y＝2x+4，若保持AC的长不变，当点A在y轴的正半轴滑动，点C随之在x 轴的负半轴上滑动，则在滑动过程中，点B与原点O的最大距离是．三．解答题（共10小题）21．如图，直线l与x轴、y轴分别交于点A（3，0）、点B（0，2），以线段AB为直角边在第一象限内作等腰直角三角形ABC，∠BAC＝90°，点P（1，a）为坐标系中的一个动点．（1）请直接写出直线l的表达式；（2）求出△ABC的面积；（3）当△ABC与△ABP面积相等时，求实数a的值．22．如图，在平面直角坐标系中，直线AB分别交x轴、y轴于点A（a，0）点，B（0，b），且a、b满足a2﹣4a+4+|2a﹣b|＝0，点P在直线AB的左侧，且∠APB＝45°．（1）求a、b的值；（2）若点P在x轴上，求点P的坐标；（3）若△ABP为直角三角形，求点P的坐标．23．在平面直角坐标系中，直线AB与x轴交于点A，与y轴交于点B，与直线OC：y1＝x 交于点C．（1）当直线AB解析式为y2＝﹣x+10时，如图1．①求点C的坐标；②根据图象求出当x满足什么条件时﹣x+10＜x．（2）如图2，作∠AOC的平分线ON，若AB⊥ON，垂足为E，△OAC的面积为9，且OA＝6．P，Q分别为线段OA、OE上的动点，连接AQ与PQ，试探索AQ+PQ是否存在最小值？若存在，求出这个最小值：若不存在，说明理由．24．如图1，已知直线y＝2x+4与y轴，x轴分别交于A，B两点，以B为直角顶点在第二象限作等腰Rt△ABC（1）求点C的坐标，并求出直线AC的关系式；（2）如图2，直线CB交y轴于E，在直线CB上取一点D，连接AD，若AD＝AC，求证BE＝DE；（3）如图3，在（1）的条件下，直线AC交x轴于点M，P（﹣，a）是线段BC上一点，在x轴上是否存在一点N，使△BPN面积等于△BCM面积的一半？若存在，请求出点N的坐标；若不存在，请说明理由．25．如图（a），直线l1：y＝kx+b经过点A、B，OA＝OB＝3，直线12：y＝x﹣2交y轴于点C，且与直线l1交于点D，连接OD．（1）求直线11的表达式；（2）求△OCD的面积；（3）如图（b），点P是直线11上的一动点；连接CP交线段OD于点E，当△COE与△DEP的面积相等时，求点P的坐标．26．如图，在平面直角坐标系中，直线y＝﹣x+8与x轴和y轴分别交于点B和点C，与直线OA相交于点A（3，4）．（1）求点B和点C的坐标；（2）求△OAC的面积；（3）在线段OA或射线AC上是否存在点M，使△OMC的面积是△OAC的面积的？若存在，求出点M的坐标，若不存在，说明理由；（4）若点N是线段OC上一点，若将△BCN沿直线BN折叠，点C恰好落在x轴负半轴上的点D处，求BN所在直线的函数关系式．27．如图，直线y＝kx+b与x轴，y轴分别交于点A，点B，点A的坐标为（﹣2，0），且2OA＝OB．（1）求直线AB解析式；（2）如图，将△AOB向右平移6个单位长度，得到△A1O1B1，求线段OB1的长；（3）求（2）中△AOB扫过的面积．28．定义：在平面直角坐标系中，对于任意两点A（a，b），B（c，d），若点T（x，y）满足x＝，y＝，那么称点T是点A和B的融合点．例如：M（﹣1，8），N（4，﹣2），则点T（1，2）是点M和N的融合点．如图，已知点D（3，0），点E是直线y ＝x+2上任意一点，点T（x，y）是点D和E的融合点．（1）若点E的纵坐标是6，则点T的坐标为；（2）求点T（x，y）的纵坐标y与横坐标x的函数关系式：（3）若直线ET交x轴于点H，当△DTH为直角三角形时，求点E的坐标．29．如图1，在平面直角坐标系xOy中，直线y＝kx+8分别交x轴，y轴于A、B两点，已知A点坐标（6，0），点C在直线AB上，横坐标为3，点D是x轴正半轴上的一个动点，连结CD，以CD为直角边在右侧构造一个等腰Rt△CDE，且∠CDE＝90°．（1）求直线AB的解析式以及C点坐标；（2）设点D的横坐标为m，试用含m的代数式表示点E的坐标；（3）如图2，连结OC，OE，请直接写出使得△OCE周长最小时，点E的坐标．30．在平面直角坐标系xOy中，直线l1：y＝k1x+6与x轴、y轴分别交于A、B两点，且OB ＝OA，直线l2：y＝k2x+b经过点C（，1），与x轴、y轴、直线AB分别交于点E、F、D三点．（1）求直线l1的解析式；（2）如图1，连接CB，当CD⊥AB时，求点D的坐标和△BCD的面积；（3）如图2，当点D在直线AB上运动时，在坐标轴上是否存在点Q，使△QCD是以CD为底边的等腰直角三角形？若存在，请直接写出点Q的坐标，若不存在，请说明理由．参考答案一．选择题（共10小题）1．【解答】解：在y＝﹣x+2中令x＝0，解得：y＝2；令y＝0，解得：x＝2．则OA＝2，OB＝2．∴在直角△ABO中，AB＝＝4，∠BAO＝30°，又∵∠BAB′＝60°，∴∠OAB′＝90°，∴B′的坐标是（2，4）．故选：B．2．【解答】解：如图所示，当△ABC向右平移到△DEF位置时，四边形BCFE为平行四边形，C点与F点重合，此时C在直线y＝2x﹣6上，∵C（1，4），∴FD＝CA＝4，将y＝4代入y＝2x﹣6中得：x＝5，即OD＝5，∵A（1，0），即OA＝1，∴AD＝CF＝OD﹣OA＝5﹣1＝4，则线段BC扫过的面积S＝S平行四边形BCFE＝CF•FD＝16．故选：D．3．【解答】解：∵一次函数y＝﹣x+3中，令x＝0得：y＝3；令y＝0，解得x＝4，∴B的坐标是（0，3），A的坐标是（4，0）．如图，作CD⊥x轴于点D．∵∠BAC＝90°，∴∠OAB+∠CAD＝90°，又∵∠CAD+∠ACD＝90°，∴∠ACD＝∠BAO．在△ABO与△CAD中，，∴△ABO≌△CAD（AAS），∴OB＝AD＝3，OA＝CD＝4，OD＝OA+AD＝7．则C的坐标是（7，4）．设直线BC的解析式是y＝kx+b，根据题意得：，解得，∴直线BC的解析式是y＝x+3．故选：A．4．【解答】解：连接AC，BD，交于点Q，过C作y轴垂线，交y轴于点M，交直线EF于点N，如图所示，∵菱形ABCD的顶点A的坐标为（2，0），点B的坐标为（0，1），点C在第一象限，对角线BD与x轴平行，∴CQ＝AQ＝1，CM＝2，即AC＝2AQ＝2，∴C（2，2），当C与M重合时，k＝CM＝2；当C与N重合时，把y＝2代入y＝x+4中得：x＝﹣2，即k＝CN＝CM+MN＝4，∴当点C落在△EOF的内部时（不包括三角形的边），k的范围为2＜k＜4，则k的值可能是3，故选：B．5．【解答】解：设长方形的AB边的长为a，则BC边的长度为2a，B点的纵坐标是a，把点B的纵坐标代入直线y＝2x的解析式得：x＝，则点B的坐标为（，a），点C的坐标为（+2a，a），把点C的坐标代入y＝kx中得，a＝k（+2a），解得：k＝．故选：B．6．【解答】解：根据题意得：∠BAC＝90°，∴∠CAO+∠BAE＝90°，∵BE⊥x轴，∴∠AEB＝90°＝∠AOC，∴∠ABE+∠BAE＝90°，∴∠CAO＝∠ABE．∴△CAO∽△ABE．∴＝，∵M是AC的中点，AB＝AM，∴CA＝2AB，∴＝，∴BE＝t，AE＝2．分两种情况：①当0＜t＜8时，如图1所示：S＝CD•BD＝（2+t）（4﹣）＝解得：t1＝t2＝3．②当t＞8时，如图2所示，S＝CD•BD＝（2+t）（﹣4）＝．解得：t1＝3+5，t2＝3﹣5（不合题意，舍去）．综上所述：当t＝3或3+5时，S＝；故选：D．7．【解答】解：直线l和八个正方形的最上面交点为P，过P作PB⊥OB于B，过P作PC ⊥OC于C，∵正方形的边长为1，∴OB＝3，∵经过P点的一条直线l将这八个正方形分成面积相等的两部分，∴三角形ABP面积是8÷2+1＝5，∴BP•AB＝5，∴AB＝2.5，∴OA＝3﹣2.5＝0.5，由此可知直线l经过（0，0.5），（4，3）设直线方程为y＝kx+b，则，解得．∴直线l解析式为y＝x+．故选：A．8．【解答】解：作AD⊥x轴于D，CE⊥x轴于E，设直线OM的解析式为y＝kx，直线AC的解析式为y＝k′x+b，∵点M（﹣3，4），∴4＝﹣3k，∴k＝﹣，∵四边形ABCO是正方形，∴直线AC⊥直线OM，∴k′为，∵四边形ABCO是正方形，∴OA＝OC，∠AOC＝90°，∴∠AOD+∠COE＝90°，∵∠AOD+∠OAD＝90°∴∠COE＝∠OAD，在△COE和△OAD中，∴△COE≌△OAD（AAS），∴CE＝OD，OE＝AD，设A（a，b），则C（﹣b，a），设直线AC的解析式为y＝mx+n，∴解得m＝，∴＝，整理得，b＝7a，∵正方形面积为128，∴OA2＝128，在RT△AOD中，AD2+OD2＝OA2，即（7a）2+a2＝128，解得，a＝，∴b＝7a＝7×＝，∴A（，），故选：D．9．【解答】解：如图，设D（0，m）．由题意：B（5，0）．在BD的下方作等边三角形△BDQ，延长DQ到M，使得QM＝DQ，连接BM，DE，DE 交BQ于点N，作MH⊥x轴于H．∵△BDQ是等边三角形，∴∠DQB＝∠DBQ＝60°，∵QM＝BQ，∴∠QMB＝∠QBM，∵∠DQB＝∠QMB+∠BQM，∴∠QMB＝∠QBM＝30°，∴∠DBM＝90°，∴BM＝BD，∵∠DBO+∠ODB＝90°，∠DBO+∠MBH＝90°，∴∠MBH＝∠BDO，∵∠DOB＝∠MHB＝90°，∴△DOB∽△BHM，∴＝＝＝，∵OD＝m，OB＝5，∴BH＝m，MH＝5，∴M（5﹣m，﹣5），∵MQ＝DQ，∴Q（，），∵∠DBE＝120°，∴∠DBN＝∠EBN＝60°，∴DE⊥BQ，DN＝NE，QN＝BN，∴N（，），E（，），∴CE2＝（）2+（）2＝m2﹣6m+91，∴当m＝﹣＝3时，CE的值最小，此时D（0，3），∴CD＝＝2，故选：C．10．【解答】解：∵在直线y＝﹣x﹣中，令y＝0，则有0＝﹣x﹣，∴x＝﹣13，∴C（﹣13，0），令x＝﹣5，则有y＝﹣×（﹣5）﹣＝﹣3，∴E（﹣5，﹣3），故①正确；∵点B，E关于x轴对称，∴B（﹣5，3），∵A（0，5），∴设直线AB的解析式为y＝kx+5，∴﹣5k+5＝3，∴k＝，∴直线AB的解析式为y＝x+5．故②错误；由①知，E（﹣5，﹣3），∴DE＝3，∵C（﹣13，0），∴CD＝﹣5﹣（﹣13）＝8，∴S△CDE＝CD×DE＝12，由题意知，OA＝5，OD＝5，BD＝3，∴S四边形ABDO＝（BD+OA）×OD＝20，∴S＝S△CDE+S四边形ABDO＝12+20＝32，故③正确；④由③知，S＝32，在△AOC中，OA＝5，OC＝13，∴S△AOC＝OA×OC＝32.5，∴S△CDE+S四边形ABDO＝12+20≠S△AOC．故④错误．综上所述，正确的结论有2个．故选：B．二．填空题（共10小题）11．【解答】解：当点E在y轴右侧时，如图1，连接AE，∵∠EAB＝∠ABO，∴AE∥OB，∵A（0，8），∴E点纵坐标为8，又E点在直线y＝x+4上，把y＝8代入可求得x＝4，∴E点坐标为（4，8）；当点E在y轴左侧时，过A、E作直线交x轴于点C，如图2，设E点坐标为（a，a+4），设直线AE的解析式为y＝kx+b，把A、E坐标代入可得，解得，∴直线AE的解析式为y＝x+8，令y＝0可得x+8＝0，解得x＝，∴C点坐标为（，0），∴AC2＝OC2+OA2，即AC2＝（）2+82，∵B（4，0），∴BC2＝（4﹣）2＝（）2﹣+16，∵∠EAB＝∠ABO，∴AC＝BC，∴AC2＝BC2，即（）2+82＝（）2﹣+16，解得a＝﹣12，则a+4＝﹣8，∴E点坐标为（﹣12，﹣8）．方法二：设C（m，0），∵∠ACB＝∠CBA，∴AC＝BC，∴（4﹣m）2＝m2+82，解得m＝﹣6，∴直线AE的解析式为y＝x+8，由，解得．∴E（﹣12，﹣8）．综上可知，E点坐标为（4，8）或（﹣12，﹣8）．故答案为：（4，8）或（﹣12，﹣8）．12．【解答】解：当M运动到（﹣1，1）时，ON＝1，MN＝1，∵MN⊥x轴，所以由ON＝MN可知，（0，0）和（0，1）就是符合条件的两个P点；又∵当M运动到第三象限时，要MN＝MP，且PM⊥MN，设点M（x，2x+3），则有﹣x＝﹣（2x+3），解得x＝﹣3，所以点P坐标为（0，﹣3）．如若MN为斜边时，则∠ONP＝45°，所以ON＝OP，设点M（x，2x+3），则有﹣x＝﹣（2x+3），化简得﹣2x＝﹣2x﹣3，这方程无解，所以这时不存在符合条件的P点；又∵当点M′在第二象限，M′N′为斜边时，这时N′P＝M′P，∠M′N′P＝45°，设点M′（x，2x+3），则OP＝ON′，而OP＝M′N′，∴有﹣x＝（2x+3），解得x＝﹣，这时点P的坐标为（0，）．综上，符合条件的点P坐标是（0，0），（0，），（0，﹣3），（0，1）．故答案为：（0，0），（0，1），（0，），（0，﹣3）．13．【解答】解：如图所示：过点P1作P1E⊥x轴于点E，∵一次函数y＝﹣x+1的图象与x轴，y轴分别交于点A，B，点C在y轴的正半轴上，且OC＝3，∴AO＝BO＝1，则BC＝2，AC＝，AB＝，当∠CP1B＝∠ACB时，又∵∠CAB＝∠CAP1，∴△CAB∽△P1AC，∴＝，则＝，解得：AP1＝5，则AE＝P1E＝5，故P1（﹣4，5），当∠CPB＞∠ACB时，则点P横坐标x满足：﹣4＜x，同理可得：当∠CP2B＝∠ACB时，又∵∠ABC＝∠P2BC，∴△CAB∽△P2CB，∴＝，则＝，解得：BP2＝2，可得P2（2，﹣1），故当∠CPB＞∠ACB时，则点P横坐标x满足：2＞x，综上所述：﹣4＜x＜2且x≠0．故答案为：﹣4＜x＜2且x≠0．14．【解答】解：∵直线y＝mx﹣2恰好把正方形ABCO的面积分成相等的两部分∴直线必经过正方形的中心∵点B的坐标为（4，4）∴中心为（2，2），代入直线中得：2＝2m﹣2，m＝215．【解答】解：过点P作PE⊥OC于E，EP的延长线交AB于F．∵AB⊥OB，∴∠OBF＝∠EOB＝∠FEO＝90°，∴四边形EOBF是矩形，∵P（2，2），∴OE＝PE＝BF＝2，∵∠CPD＝90°，∴∠CPE+∠DPF＝90°，∠ECP+∠CPE＝90°，∴∠ECP＝∠DPF，在△CPE和△PDF中，，∴△CPE≌△PDF（AAS），∴DF＝PE＝2，∴BD＝BF+DF＝4，∵BD＝4AD，∴AD＝1，AB＝OB＝5，∴CE＝PF＝3，∴D（5，4），C（0，5），设直线CD的解析式为y＝kx+b则有，解得，∴直线CD的解析式为y＝﹣x+5，由解得，∴点Q的坐标为（，）．故答案为（，）．16．【解答】解：方法一：∵点Q在直线y＝﹣x上，∴设点Q的坐标为（m，﹣m）．∵点A的坐标是（0，2），点B的坐标是（2，0），∴△AOB为等腰直角三角形，点O（0，0）到AB的距离h＝OA＝．设直线AB的解析式为y＝kx+b，∵点A（0，2），点B（2，0）在直线AB上，∴有，解得．即直线AB的解析式为y＝﹣x+2，∵直线y＝﹣x+2与y＝﹣x平行，∴点P到底OQ的距离为（平行线间距离处处相等）．∵△OPQ的面积S△OPQ＝OQ•h＝OQ＝，∴OQ＝2．由两点间的距离公式可知OQ＝＝2，解得：m＝±，∴点Q的坐标为（，﹣）或（﹣，）．故答案为：（，﹣）或（﹣，）．方法二：当P点与A重合时，则△OPQ底OP为2，∵△OPQ的面积为，∴△OPQ的高为，即点Q的横坐标为﹣，∵点Q在直线y＝﹣x上，∴点Q的坐标为（﹣，）；当P点与B重合时，同理可求出点Q的坐标为（，﹣）．综上即可得出点Q的坐标为（，﹣）或（﹣，）．17．【解答】方法一：解：设直线AB的解析式为：y＝kx+b，把A（0，2），B（3，4）代入得：，解得：k＝，b＝2，∴直线AB的解析式为：y＝x+2；∵点B与B′关于直线AP对称，设B′坐标为（a，0）∴线段BB′的中点坐标为（，2）∵线段BB′的中点在直线AP上，且A点坐标为（0，2）∴A点为线段BB′的中点，即A、B、B′三点共线∴AP⊥AB，∴设直线AP的解析式为：y＝﹣x+c，把点A（0，2）代入得：c＝2，∴直线AP的解析式为：y＝﹣x+2，当y＝0时，﹣x+2＝0，解得：x＝，∴点P的坐标为：（）；故答案为：（）．方法二：解：如图，连接AB、AB′∵A（0，2），B（3，4）∴AB＝＝∵点B与B′关于直线AP对称∴AB′＝AB＝，在Rt△AOB′中，B′O＝＝3∴B′点坐标为（﹣3，0）设直线BB′方程为y＝kx+b将B（3，4），B′（﹣3，0）代入得：，解得k＝，b＝2∴直线BB′的解析式为：y＝x+2，∴直线AP的解析式为：y＝﹣x+2，当y AP＝0时，﹣x+2＝0，解得：x＝，∴点P的坐标为：（）；故答案为：（）．18．【解答】解：①如图，作M点关于直线x＝4的对称点M′，然后作M′F⊥直线y＝﹣x﹣1于F，交直线x ＝4于E，此时ME+EF有最小值，最小值为M′F；∵y＝﹣x﹣1与x轴和y轴分别交于B、C两点，令x＝0，可得y＝﹣1，令y＝0，可得x＝﹣2，∴B（﹣2，0），C（0，﹣1），∴OB＝2，OC＝1，∴BC＝＝，∵M（3，0），∴M′（5，0），∴BM′＝5+2＝7，∵M′F⊥直线BC，∴∠BFM′＝90°＝∠BOC，∵∠OBC＝∠FBM′∴△BOC∽△BFM′，∴，即，解得：M′F＝，∴ME+EF的最小值为；②∵直线M′F与直线y＝﹣x﹣1互相垂直，∴直线M′F与直线y＝﹣x﹣1的k互为负倒数，∴设直线M′F的关系式为：y＝2x+b，将M′（5，0），代入y＝2x+b，可得：b＝﹣10，∴直线M′F的关系式为：y＝2x﹣10，将直线y＝2x﹣10与直线y＝﹣x﹣1联立方程组得：，解得：，∴点F的坐标为（，﹣）．故答案为：；（，﹣）．19．【解答】解：解：过P作MN⊥y轴，交y轴于M，交AB于N，过D作DH⊥y轴，交y轴于H，∠CMP＝∠DNP＝∠CPD＝90°，∴∠MCP+∠CPM＝90°，∠MPC+∠DPN＝90°，∴∠MCP＝∠DPN，∵P（1，1），∴OM＝BN＝1，PM＝1，在△MCP和△NPD中，∴△MCP≌△NPD（AAS），∴DN＝PM，PN＝CM，∵BD＝2AD，∴设AD＝a，BD＝2a，∵P（1，1），∴BN＝2a﹣1，则2a﹣1＝1，∴a＝1，即BD＝2．∵直线y＝x，∴AB＝OB＝3，∴点D（3，2）∴PC＝PD＝＝＝，在Rt△MCP中，由勾股定理得：CM＝＝＝2，则C的坐标是（0，3），设直线CD的解析式是y＝kx+3，把D（3，2）代入得：k＝﹣，即直线CD的解析式是y＝﹣x+3，∴组成方程组解得：∴点Q（，），故答案为：（，）．20．【解答】解：当x＝0时，y＝2x+4＝4，∴A（0，4）；当y＝2x+4＝0时，x＝﹣2，∴C（﹣2，0）．∴OA＝4，OC＝2，∴AC＝＝2．如图所示．过点B作BD⊥x轴于点D．∵∠ACO+∠ACB+∠BCD＝180°，∠ACO+∠CAO＝90°，∠ACB＝90°，∴∠CAO＝∠BCD．在△AOC和△CDB中，，∴△AOC≌△CDB（AAS），∴CD＝AO＝4，DB＝OC＝2，OD＝OC+CD＝6，∴点B的坐标为（﹣6，2）．如图所示．取AC的中点E，连接BE，OE，OB，∵∠AOC＝90°，AC＝2，∴OE＝CE＝AC＝，∵BC⊥AC，BC＝2，∴BE＝＝5，若点O，E，B不在一条直线上，则OB＜OE+BE＝5+．若点O，E，B在一条直线上，则OB＝OE+BE＝5+，∴当O，E，B三点在一条直线上时，OB取得最大值，最大值为5+，故答案为：5+．三．解答题（共10小题）21．【解答】解：（1）将点A、B的坐标代入一次函数表达式：y＝kx+b得：，解得：，故直线l的表达式为：；（2）在Rt△ABC中，由勾股定理得：AB2＝OA2+OB2＝32+22＝13∵△ABC为等腰直角三角形，∴S△ABC＝AB2＝；（3）连接BP，PO，P A，则：①若点P在第一象限时，如图1：∵S△ABO＝3，S△APO＝a，S△BOP＝1，∴S△ABP＝S△BOP+S△APO﹣S△ABO＝，即，解得；②若点P在第四象限时，如图2：∵S△ABO＝3，S△APO＝﹣a，S△BOP＝1，∴S△ABP＝S△BOP+S△APO﹣S△ABO＝，即，解得a＝﹣3；故：当△ABC与△ABP面积相等时，实数a的值为或﹣3．22．【解答】解：（1）∵a2﹣4a+4+|2a+b|＝0，∴（a﹣2）2+|2a+b|＝0，∴a＝2，b＝4．（2）由（1）知，b＝4，∴B（0，4）．∴OB＝4．∵点P在直线AB的左侧，且在x轴上，∠APB＝45°∴OP＝OB＝4，∴B（4，0）．（3）由（1）知a＝﹣2，b＝4，∴A（2，0），B（0，4）∴OA＝2，OB＝4，∵△ABP是直角三角形，且∠APB＝45°，∴只有∠ABP＝90°或∠BAP＝90°，如图，①当∠ABP＝90°时，∵∠BAP＝45°，∴∠APB＝∠BAP＝45°．∴AB＝PB．过点P作PC⊥OB于C，∴∠BPC+∠CBP＝90°，∵∠CBP+∠ABO＝90°，∴∠ABO＝∠BPC．在△AOB和△BCP中，∠AOB＝∠BCP＝90°，∠ABO＝∠BPC，AB＝PB，∴△AOB≌△BCP（AAS）．∴PC＝OB＝4，BC＝OA＝2．∴OC＝OB﹣BC＝2．∴P（﹣4，2）．②当∠BAP＝90°时，过点P'作P'D⊥OA于D，同①的方法得，△ADP'≌△BOA（AAS）．∴DP'＝OA＝2，AD＝OB＝4．∴OD＝AD﹣OA＝2．∴P'（﹣2，2））．即：满足条件的点P（﹣4，2）或（﹣2，﹣2）．23．【解答】解：（1）①由題意，，解得：，所以C（4，4）．②观察图象可知x＞4时，直线AB位于直线OC的下方，即x＞4时，﹣x+10＜x．（2）由题意，在OC上截取OM＝OP，连结MQ，∵ON平分∠AOC，∴∠AOQ＝∠COQ，又OQ＝OQ．∴△POQ≌△MOQ（SAS），∴PQ＝MQ，∴AQ+PQ＝AQ+MQ，当A、Q、M在同一直銭上，且AM⊥OC吋，AQ+MQ最小，即AQ+PQ存在最小値；∴AB⊥ON，∴∠AEO＝∠CEO，∴△AEO≌△CEO（ASA），∴OC＝OA＝6，∵△OAC的面积为9，∴OC•AM＝9，∴AM＝3，∴AQ+PQ存在最小值，最小值为3．24．【解答】解：（1）如图1，作CQ⊥x轴，垂足为Q，∵∠OBA+∠OAB＝90°，∠OBA+∠QBC＝90°，∴∠OAB＝∠QBC，又∵AB＝BC，∠AOB＝∠Q＝90°，∴△ABO≌△BCQ（AAS），∴BQ＝AO＝4，OQ＝BQ+BO＝6，CQ＝OB＝2，∴C（﹣6，2），由A（0，4），C（﹣6，2）可知，直线AC：y＝x+4；（2）如图2，作CH⊥x轴于H，DF⊥x轴于F，DG⊥y轴于G，∵AC＝AD，AB⊥CB，∴BC＝BD，∴△BCH≌△BDF（AAS），∴BF＝BH＝4，∴OF＝OB＝2，∴DG＝OB，∴△BOE≌△DGE（AAS），∴BE＝DE；（3）如图3，直线BC：y＝﹣x﹣1，P（﹣，k）是线段BC上一点，∴P（﹣，），由y＝x+4知M（﹣12，0），∴BM＝10，则S△BCM＝10．设点N（n，0），则BN＝|n+2|，假设存在点N使直线PN平分△BCM的面积，则BN•y C＝×10，n＝或﹣，故点N的坐标为：（，0）或（﹣，0）．25．【解答】解：（1）OA＝OB＝3，则点A、B的坐标分别为：（3，0）、（0，3），将点A、B的坐标代入一次函数表达式：y＝kx+b得：，解得：，故直线11的表达式为：y＝﹣x+3…①；（2）联立l1、l2的表达式得：，解得：，故点D（2，1）；△OCD的面积＝×OA•y D＝3×1＝；（3）△COE与△DEP的面积相等，则S△CDO＝S△CDE+S△OCE＝S△PED+S△CED＝S△PCD，则点P、O到CD的距离相等，故OP所在的直线与CD平行，则直线OP的表达式为：y＝x…②，联立①②并解得：x＝，则点P（，）．26．【解答】解：（1）设y＝0，则x＝6；设点x＝0，则y＝6，故点B的坐标为（6，0），点C的坐标为（0，8）；（2）S△OAC＝×CO×x A＝×8×3＝12；（3）存在点M使S△OMC＝S△OAC，设M的坐标为（x，y）；OA的解析式是y＝mx，则3m＝4，解得：，则直线OA的解析式是：，∵当S△OMC＝S△OAC时，即，又∵OC＝8，∴，当M在线段OA上时，x＞0，所以时，y＝1，则M的坐标是；当M在射线上时，则y＝7，则M的坐标是；则y＝9，则M的坐标是，综上所述：M的坐标是：或或；（4）在Rt△OBC中，∠COB＝90°，OB＝6，OC＝8，∴，∵△BCN沿直线BN折叠后，所得三角形为△BDN，∴CN＝DN，BD＝BC＝10，∴OD＝4在Rt△ODN中，设ON＝x，则DN＝8﹣x，∴42+x2＝（8﹣x）2∴x＝3，故点N（0，3），设直线AM的解析式为y＝kx+b（k≠0）代入A（6，0），N（0，3）得：，解得，∴直线AM的解析式为．27．【解答】解：（1）∵点A的坐标为（﹣2，0），∴OA＝2，∵OB＝2OA＝4，∴B（0，4），把A（﹣2，0）和B（0，4）代入y＝kx+b中得：，解得：，∴直线AB解析式为：y＝2x+4；（2）∵∠AOB＝90°，∴∠AO1B1＝90°，由平移得：OO1＝6，O1B1＝OB＝4，由勾股定理得：OB1＝＝2，即线段OB1的长是2；（3）△AOB扫过的面积＝+4×6＝28．28．【解答】解：（1）∵点E是直线y＝x+2上一点，点E的纵坐标是6，∴x+2＝6，解得，x＝4，∴点E的坐标是（4，6），∵点T（x，y）是点D和E的融合点，∴x＝＝，y＝＝2，∴点T的坐标为（，2），故答案为：（，2）；（2）设点E的坐标为（a，a+2），∵点T（x，y）是点D和E的融合点，∴x＝，y＝，解得，a＝3x﹣3，a＝3y﹣2，∴3x﹣3＝3y﹣2，整理得，y＝x﹣；（3）设点E的坐标为（a，a+2），则点T的坐标为（，），当∠THD＝90°时，点E与点T的横坐标相同，∴＝a，解得，a＝，此时点E的坐标为（，），当∠TDH＝90°时，点T与点D的横坐标相同，∴＝3，解得，a＝6，此时点E的坐标为（6，8），当∠DTH＝90°时，该情况不存在，综上所述，当△DTH为直角三角形时，点E的坐标为（，）或（6，8）．29．【解答】解：（1）把A（6，0）代入y＝kx+8中，得6k+8＝0，解得：，∴，把x＝3代入，得y＝4，∴C（3，4）；（2）作CF⊥x轴于点F，EG⊥x轴于点G，∵△CDE是等腰直角三角形，∴CD＝DE，∠CDE＝90°，∴∠CDF＝90°﹣∠EDG＝∠DEG，且∠CFD＝∠DGE＝90°，∴△CDF≌△DEG（AAS）∴CF＝DG＝4，DF＝EG＝3﹣m，∴OG＝4+m，∴E（4+m，m﹣3）；（3）点E（4+m，m﹣3），则点E在直线l：y＝x﹣7上，设：直线l交y轴于点H（0，﹣7），过点O作直线l的对称点O′，∵直线l的倾斜角为45°，则HO′∥x轴，则点O′（7，﹣7），连接CO′交直线l于点E′，则点E′为所求点，OC是常数，△OCE周长＝OC+CE+OE＝OC+OE′+CE′＝OC+CE′+O′E′＝OC+CO′为最小，由点C、O′的坐标得，直线CO′的表达式为：y＝﹣x+联立，解得：，故：．30．【解答】解：（1）y＝k1x+6，当x＝0时，y＝6，∴OB＝6，∵OB＝OA，∴OA＝2，∴A（﹣2，0），把A（﹣2，0）代入：y＝k1x+6中得：﹣2k1+6＝0，k1＝，∴直线l1的解析式为：y＝x+6；（2）如图1，过C作CH⊥x轴于H，∵C（，1），∴OH＝，CH＝1，Rt△ABO中，AB＝＝4，∴AB＝2OA，∴∠OBA＝30°，∠OAB＝60°，∵CD⊥AB，∴∠ADE＝90°，∴∠AED＝30°，∴EH＝，∴OE＝OH+EH＝2，∴E（2，0），把E（2，0）和C（，1）代入y＝k2x+b中得：，解得：，∴直线l2：y＝﹣x+2，∴F（0，2）即BF＝6﹣2＝4，则，解得，∴D（﹣，3），∴S△BCD＝BF（x C﹣x D）＝＝4；（3）分四种情况：①当Q在y轴的正半轴上时，如图2，过D作DM⊥y轴于M，过C作CN⊥y轴于N，∵△QCD是以CD为底边的等腰直角三角形，∴∠CQD＝90°，CQ＝DQ，∴∠DMQ＝∠CNQ＝90°，∴∠MDQ＝∠CQN，∴△DMQ≌△QNC（AAS），∴DM＝QN，QM＝CN＝，设D（m，m+6）（m＜0），则Q（0，﹣m+1），∴OQ＝QN+ON＝OM+QM，即﹣m+1＝m+6+，m＝＝1﹣2，∴Q（0，2）；②当Q在x轴的负半轴上时，如图3，过D作DM⊥x轴于M，过C作CN⊥x轴于N，同理得：△DMQ≌△QNC（AAS），∴DM＝QN，QM＝CN＝1，设D（m，m+6）（m＜0），则Q（m+1，0），∴OQ＝QN﹣ON＝OM﹣QM，即m+6﹣＝﹣m﹣1，m＝5﹣4，∴Q（6﹣4，0）；③当Q在x轴的负半轴上时，如图4，过D作DM⊥x轴于M，过C作CN⊥x轴于N，同理得：△DMQ≌△QNC（AAS），∴DM＝QN，QM＝CN＝1，设D（m，m+6）（m＜0），则Q（m﹣1，0），∴OQ＝QN﹣ON＝OM+QM，即﹣m﹣6﹣＝﹣m+1，m＝﹣4﹣5，∴Q（﹣4﹣6，0）；④当Q在y轴的负半轴上时，如图5，过D作DM⊥y轴于M，过C作CN⊥y轴于N，同理得：△DMQ≌△QNC（AAS），∴DM＝QN，QM＝CN＝，设D（m，m+6）（m＜0），则Q（0，m+1），∴OQ＝QN﹣ON＝OM+QM，即﹣m﹣6+＝﹣m﹣1，m＝﹣2﹣1，∴Q（0，﹣2）；综上，存在点Q，使△QCD是以CD为底边的等腰直角三角形，点Q的坐标是（0，±2）或（6﹣4，0）或（﹣4﹣6，0）．。

2021年九年级数学中考复习知识点综合专题训练：一次函数与一元一次不等式1（附答案）1．直线l1：y＝k1x+b与直线l2：y＝k2x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k2x＞k1x+b的解集为（）A．x＞3B．x＜3C．x＞﹣1D．x＜﹣12．如图，已知直线y1＝x+a与y2＝kx+b相交于点P（﹣2，2），则关于x的不等式x+a＞kx+b 的解集是（）A．x＜﹣2B．x＞﹣2C．x＜2D．x＞23．如图，已知函数y＝kx+b图象如图所示，则不等式kx+b＜0的解集为（）A．x＞5B．x＜5C．x＞4D．x＜44．一次函数y＝kx+b（k，b为常数）的图象如图所示，则不等式kx+b＜1的解集是（）A．x＜﹣2B．x＜1C．x＞﹣2D．x＜05．如图，直线l1：y1＝ax（a≠0）与直线l2：y2＝x+b（b≠0）交于点P，有四个结论：①a＜0②a＞0③当x＞0时，y1＞0④当x＜﹣2时，y1＞y2，其中正确的是（）A．①②B．①③C．①④D．②③6．已知一次函数y＝kx+b的图象如图所示，则关于x的不等式kx+b＜0的解集是（）A．x＞0B．x＜0C．x＞2D．x＜27．一次函数y1＝kx+b与y2＝mx+n的图象如图所示，则以下结论：①k＞0；②b＞0；③m ＞0；④n＞0；⑤当x＝3时：y1＞y2．正确的个数是（）A．1个B．2个C．3个D．4个8．如图，已知一次函数y1＝x+b与正比例函数y2＝kx的图象交于点P．四个结论：①k＞0；②b＞0；③当x＜0时，y2＞0；④当x＜﹣2时，kx＜x+b．其中正确的是（）A．①③B．②③C．③④D．①④9．如图，直线y＝﹣x+m与y＝nx+4n（n≠0）的交点的横坐标为﹣2，则关于x的不等式﹣x+m＞nx+4n＞0的整数解为（）A．﹣1B．﹣3C．﹣4D．﹣510．一次函数y＝kx+b（k≠0）的图象经过点B（﹣6，0），且与正比例函数y＝x的图象交于点A（m，﹣3），若kx﹣x＞﹣b，则（）A．x＞0B．x＞﹣3C．x＞﹣6D．x＞﹣911．直线y＝kx+b（k＞0）与x轴的交点坐标为（2，0），则关于x的不等式kx+b＞0的解集是（）A．x＜1B．x＜2C．x＞0D．x＞212．在平面直角坐标系中，正比例函数y＝2x的图象与直线y＝kx+b交于A（﹣1，﹣2）．直线y＝kx+b，还经过点（﹣2，0）．则不等式2x＜kx+b＜0的解集为（）A．x＜﹣2B．﹣2＜x＜0C．﹣2＜x＜﹣1D．﹣1＜x＜0 13．若一次函数y＝（m﹣1）x﹣m+4的图象与y轴的交点在x轴的上方，则m的取值范围是．14．如图，直线y1＝x+b与y2＝kx﹣1相交于点P，则关于x的不等式x+b＞kx﹣1的解集为．15．一次函数y＝ax+b与正比例函数y＝kx在同一平面直角坐标系的图象如图所示，则关于x的不等式ax+b≥kx的解集为．16．如图，一次函数y＝kx+b的图象经过点（4，﹣3），则关于x的不等式kx+b＜﹣3的解集为．17．一次函数y＝kx+b的图象如图所示，则关于x的不等式kx﹣m+b＞0的解集是．18．函数y＝2x和y＝ax+4的图象相交于点A（m，2），则不等式2x﹣4≤ax的解集．19．若函数y＝kx﹣b的图象如图所示，则关于x的不等式k（x﹣1）﹣b＞0的解集为．20．已知直线y1＝2x与直线y2＝﹣2x+4相交于A，有以下结论：①A的坐标为（1，2）；②当x＝1时，两个函数值相等；③当x＜1时，y1＜y2；④y1，y2在平面直角坐标系中的位置关系是平行，其中正确的是．21．如图，直线y1＝k1x+b和直线y2＝k2x+b交于y轴上一点，则不等式k1x+b＞k2x+b的解集为．22．在平面直角坐标系xOy中，一次函数y＝ax和y＝kx+7的图象如图所示，则关于x的一元一次不等式ax＞kx+7的解集是．23．已知一次函数y＝kx+b经过点A（3，0），B（0，3）．（1）求k，b的值．（2）在平面直角坐标系xOy中，画出函数图象；（3）结合图象直接写出不等式kx+b＞0的解集．24．在给出的网格中画出一次函数y＝2x﹣3的图象，并结合图象求：（1）方程2x﹣3＝0的解；（2）不等式2x﹣3＞0的解集；（3）不等式﹣1＜2x﹣3＜5的解集．25．在初中阶段的函数学习中，我们经历了“确定函数的表达式﹣﹣利用函数图象研究其性质﹣﹣运用函数解决问题”的学习过程．在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象．同时，我们也学习了绝对值的意义|a|＝结合上面经历的学习过程，现在来解决下面的问题：在函数y＝||（k＞0）中，当x＝﹣4时，y＝1．（1）求这个函数的表达式；（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质；（3）已知函数y＝x||x 的解集．26．在平面直角坐标系中，直线y＝2x向右平移1个单位长度得到直线y1．（1）直接写出直线y1的解析式；（2）直线y1分别交x轴，y轴于点A，B，交y2＝kx于点C，若A为BC的中点．①请画图并求k的值；②当0＜y1＜y2时，请直接写出x的取值范围．27．在学习一元一次不等式与一次函数中，小明在同一个坐标系中分别作出了一次函数y＝k1x+b1和y＝kx+b的图象，分别与x轴交于点A、B，两直线交于点C．已知点A（﹣1，0），B（2，0），观察图象并回答下列问题：（1）关于x的方程k1x+b1＝0的解是；关于x的不等式kx+b＜0的解集是；（2）直接写出关于x的不等式组的解集；（3）若点C（1，3），求关于x的不等式k1x+b1＞kx+b的解集和△ABC的面积．28．如图，直线l1：y＝x+与y轴的交点为A，直线l1与直线l2：y＝kx的交点M的坐标为M（3，a）．（1）求a和k的值；（2）直接写出关于x的不等式x+＜kx的解集；（3）若点B在x轴上，MB＝MA，直接写出点B的坐标．29．如图，过点C（0，﹣2）的直线l1：y1＝kx+b（k≠0）与直线l2：y2＝x+1交于点P（2，m），且直线l1与x轴交于点B，直线l2与x轴交于点A．（1）直接写出使得y1＜y2的x的取值范围；（2）求点P的坐标和直线l1的解析式；（3）若点M在x轴的正半轴上运动，点M运动到何处时△ABP与△BPM面积相等？求出此时△BPM面积．30．如图，函数y1＝2x和y2＝kx+4（k为常数，且k≠0）的图象都经过点A（m，3）．（1）求点A的坐标及k的值；（2）结合图象直接写出）y2≥y1时x的取值范围．31．已知：如图，一次函数y1＝﹣x﹣2与y2＝x﹣4的图象相交于点A．（1）求点A的坐标．（2）若一次函数y1与y2的图象与x轴分别相交于点B、C，求△ABC的面积．（3）结合图象，直接写出y1≤y2时x的取值范围．32．设函数f（x）＝|x+2|﹣|x﹣1|．（1）画出函数y＝f（x）的图象；（2）若关于x的不等式f（x）+4≥|1﹣2m|有解，求实数m的取值范围．参考答案1．解：当x＜﹣1时，k2x＞k1x+b，所以不等式k2x＞k1x+b的解集为x＜﹣1．故选：D．2．解：因为直线y1＝x+a与y2＝kx+b相交于点P（﹣2，2），当x＞﹣2时，x+a＞kx+b，所以不等式x+a＞kx+b的解集为x＞﹣2．故选：B．3．解：∵从图象可知：一次函数图象和x轴的交点坐标为（4，0），y随x的增大而减小，∴不等式kx+b＜0的解集是x＞4，故选：C．4．解：从图象得知一次函数y＝kx+b（k，b是常数，k≠0）的图象经过点（0，1），并且函数值y随x的增大而增大，因而则不等式kx+b＜1的解集是x＜0．故选：D．5．解：∵直线l1：y1＝ax（a≠0）从左往右呈下降趋势，∴a＜0，故①正确，②错误；由函数图象可得当x＞0时，y1＜0，故③错误；∵两函数图象交于P，∴x＜﹣2时，y1＞y2，故④正确，故选：C．6．解：由图可知：当x＞2时，y＜0，即kx+b＜0；故关于x的不等式kx+b＜0的解集为x＞2．故选：C．7．解：∵一次函数y1＝kx+b的图象经过第一、三象限，∴k＞0，所以①正确；∵一次函数y1＝kx+b的图象与y轴的交点在y轴的负半轴上，∴b＜0，所以②错误；∵一次函数y2＝mx+n的图象经过第二、四象限，∴m＜0，所以③错误；∵一次函数y2＝mx+n的图象与y轴的交点在y轴的正半轴上，∴n＞0，所以④正确；∵x＞2时，y1＞y2，∴当x＝3时：y1＞y2．所以⑤正确．故选：C．8．解：∵直线y2＝kx经过第二、四象限，∴k＜0，故①错误；∵y1＝x+b与y轴交点在正半轴，∴b＞0，故②正确；∵正比例函数y2＝kx经过原点，且y随x的增大而减小，∴当x＜0时，y2＞0；故③正确；当x＜﹣2时，正比例函数y2＝kx在一次函数y1＝x+b图象的上方，即kx＞x+b，故④错误．故选：B．9．解：当y＝0时，nx+4n＝0，解得x＝﹣4，所以直线y＝nx+4n与x轴的交点坐标为（﹣4，0），当x＞﹣4时，nx+4n＞0；当x＜﹣2时，﹣x+m＞nx+4n，所以当﹣4＜x＜﹣2时，﹣x+m＞nx+4n＞0，所以不等式组﹣x+m＞nx+4n＞0的整数解为x＝﹣3．故选：B．10．解：把A（m，﹣3）代入y＝x得m＝﹣3，解得m＝﹣9，所以当x＞﹣9时，kx+b＞x，即kx﹣x＞﹣b的解集为x＞﹣9．故选：D．11．解：∵直线y＝kx+b（k＞0）与x轴的交点为（2，0），∴y随x的增大而增大，当x＞2时，y＞0，即kx+b＞0．故选：D．12．解：画出函数y＝2x与y＝kx+b如图，由图象可知：正比例函数y＝2x和一次函数y＝kx+b的图象的交点是A（﹣1，﹣2），∴不等式2x＜kx+b的解集是x＜﹣1，∵一次函数y＝kx+b的图象与x轴的交点坐标是B（﹣2，0），∴不等式kx+b＜0的解集是x＞﹣2，∴不等式2x＜kx+b＜0的解集是﹣2＜x＜﹣1，故选：C．13．解：一次函数y＝（m﹣1）x﹣m+4中，令x＝0，解得：y＝﹣m+4，与y轴的交点在x轴的上方，则有﹣m+4＞0，解得：m＜4．故本题答案为：m＜4且m≠1．14．解：当x＞﹣1，函数y＝x+b的图象在函数y＝kx﹣1图象的上方，所以关于x的不等式x+b＞kx﹣1的解集为x＞﹣1．故答案为x＞﹣1．15．解：从图象可看出当x≥﹣1，直线l2的图象在直线l1的上方，不等式ax+b＞kx．故答案为：x≥﹣1．16．解：∵一次函数y＝kx+b的图象经过（4，﹣3），∴x＝4时，kx+b＝﹣3，又y随x的增大而减小，∴关于x的不等式kx+b＜﹣3的解集是x＞4．故答案是：x＞4．17．解：当x＜﹣3时，y＝kx+b＞m，所以关于x的不等式kx﹣m+b＞0的解集为x＜﹣3．故答案为：x＜﹣3．18．解：∵函数y＝2x的图象经过点A（m，2），∴2m＝2，解得：m＝1，∴点A（1，2），当x≤1时，2x≤ax+4，即不等式2x﹣4≤ax的解集为x≤1．故答案为x≤1．19．解：把（3，0）代入y＝kx+b得3k﹣b＝0，则b＝3k，所以k（x﹣1）﹣b＞0化为k（x﹣1）﹣3k＞0，即kx﹣4k＞0，因为k＜0，所以x＜4，故答案为：x＜4．20．解：解方程组得，∴两直线的交点坐标为（1，2），所以①②正确；当y1＜y2，即2x＜﹣2x+4，解得x＜1，即当x＜1时，y1＜y2；所以③正确；∵直线y1＝2x与直线y2＝﹣2x+4相交于A，∴y1，y2在平面直角坐标系中不平行，所以④错误．故答案为：①②③．21．解：∵直线y1＝k1x+b和直线y2＝k2x+b交于y轴上一点，∴交点的横坐标为0∵从图象看，当x＞0时，直线y1＝k1x+b的图象位于直线y2＝k2x+b的上方；当x＜0时，直线y1＝k1x+b的图象位于直线y2＝k2x+b的下方∴当x＞0时，k1x+b＞k2x+b故答案为：x＞0．22．解：因为当x＞2时，ax＞kx+7，所以关于x的一元一次不等式ax＞kx+7的解集为x＞2．故答案为x＞2．23．解：（1）∵一次函数y＝kx+b经过点A（3，0），B（0，3）．∴，解得；（2）函数图象如图：；（3）不等式kx+b＞0的解集为：x＜3．24．解：（1）由图象可知，方程2x﹣3＝0的解是x＝，（2）由图象可知，不等式2x﹣3＞0的解集是x＞；（3）由图象可知，不等式﹣1＜2x﹣3＜5的解集是：1＜x＜4．25．解：（1）∵在函数y＝||（k＞0）中，当x＝﹣4时，y＝1，||1，解得k＝4，∴这个函数的表达式是y＝||；（2）∵y＝||，∴y＝，列表：x﹣4﹣2﹣1123y124421…描点、连线，画出该函数的图象如图所示：由图象可知，函数的图象关于y轴对称；（3）由函数图象可得，||x的解集是0＜x≤2或x＜0．26．解：（1）由“左加右减”的原则可知：把直线y＝2x向右平移1个单位长度后，其直线解析式为y＝2（x﹣1），即y＝2x﹣2．故直线y1的为y＝2x﹣2；（2）①如图，由直线y1的为y＝2x﹣2可知A（1，0），B（0，﹣2），∵A为BC的中点，∴C（2，2），把C（2，2）代入y2＝kx得，2＝2k，∴k＝1；②当0＜y1＜y2时，x的取值范围是1＜x＜2．故答案为1＜x＜2．27．解：（1）∵一次函数y＝k1x+b1和y＝kx+b的图象，分别与x轴交于点A（﹣1，0）、B （2，0），∴关于x的方程k1x+b1＝0的解是x＝﹣1，关于x的不等式kx+b＜0的解集，为x＞2，故答案为x＝﹣1，x＞2；（2）根据图象可以得到关于x的不等式组的解集﹣1＜x＜2；（3）∵点C（1，3），∴由图象可知，不等式k1x+b1＞kx+b的解集是x＞1，∵AB＝3，∴S△ABC＝•y C＝＝．28．解：（1）∵直线l1与直线l2的交点为M（3，a），∴M（3，a）在直线y＝x+上，也在直线y＝kx上，∴a＝×3+＝3，∴M（3，3），∴3＝3k，解得k＝1；（2）不等式x+＜kx的解集为x＞3；（3）作MN⊥x轴于N，∵直线l1：y＝x+与y轴的交点为A，∴A（0，），∵M（3，3），∴AM2＝（3﹣0）2+（3﹣）2＝，∵MN＝3，MB＝MA，∴BN＝＝，∴B（，0）或B（，0）．29．解：（1）当x＜2时，y1＜y2；（2）把点P（2，m）代入y2＝x+1中，得m＝2+1＝3，∴点P的坐标为（2，3）．把点C（0，﹣2）、P（2，3）分别代入y1＝kx+b中，得，解得，∴直线l1的解析式为y1＝x﹣2；（3）由（2）得点P的坐标为（2，3），∵△ABP与△BPM有相同的高，即h＝3．要使△ABP与△BPM面积相等，且点M在x 轴正半轴上．∴在x轴上取点M，当AB＝BM时，△ABP与△BPM面积相等．∵在直线中，当y＝0时，，即点B的坐标是（，0），∴AB＝1+＝，BM＝OM﹣OB＝，∴OM＝，则点M运动到（0，）时△ABP与△BPM面积相等．∴S△BPM＝．30．解：（1）把A（m，3）代入y1＝2x得2m＝3，解得m＝，∴A（，3），把A（，3）代入y2＝kx+4得3＝k+4，解得k＝﹣；（2）当x≤时，y2≥y1．31．解：（1）联立两函数解析式可得方程组，解得：，∴点A的坐标为（1，﹣3）；（2）当y1＝0时，﹣x﹣2＝0，解得：x＝﹣2，∴B（﹣2，0），当y2＝0时，x﹣4＝0，解得：x＝4，∴C（4，0），∴CB＝6，∴△ABC的面积为：6×3＝9；（3）由图象可得：y1≤y2时x的取值范围是x≥1．32．解：（1）函数f（x）＝，所以其图象如图：（2）若关于x的不等式f（x）+4≥|1﹣2m|有解，即（|x+2|﹣|x﹣1|+4）的最大值≥|1﹣2m|，故|x+2|﹣|x﹣1|+4的最大值大于或等于|1﹣2m|，利用绝对值的意义可得|x+2|﹣|x﹣1|+4的最小值为3+4＝7，∴|1﹣2m|≤7，解得﹣3≤m≤4。

2021年中考数学九年级复习课时训练：《圆的综合》（一）一．选择题1．下列语句中不正确的有（）①相等的圆心角所对的弧相等；②平分弦的直径垂直于弦；③圆是轴对称图形，任何一条直径都是它的对称轴；④半圆是弧．A．1个B．2个C．3个D．4个2．如图，在半径为的⊙O中，弦AB与CD交于点E，∠DEB＝75°，AB＝6，AE＝1，则CD的长是（）A．2B．2C．2D．43．如图，在平台上用直径为100mm的两根圆钢棒嵌在大型工件的两侧，测量大的圆形工件的直径D，测得两根圆钢棒与地的两个接触点之间的距离为400mm，则工件直径D（mm）用科学记数法可表示为（）mm．A．4×104B．0.4×105C．20000 D．4×1024．在圆中，与半径相等的弦所对的圆心角的度数为（）A．30°B．45°C．60°D．90°5．如图，在⊙O中，AB为直径，∠AOC＝80°．点D为弦AC的中点，点E为上任意一点．则∠CED的大小可能是（）A．10°B．20°C．30°D．40°6．如图，四边形ABCD内接于⊙O，连接BD．若，∠BDC＝50°，则∠ADC的度数是（）A．125°B．130°C．135°D．140°7．圆内两弦相交，一弦长为8cm，且被交点平分，另一弦被交点分成的两段的比是1：4，那么另一弦长是（）A．16cm B．10cm C．8cm D．2cm8．如图，直线AB经过⊙O的圆心，与⊙O相交于A、B两点，点C在⊙O上，且∠AOC＝30度．点E是直线AB上的一个动点（与点O不重合），直线EC交⊙O于D，则使DE＝DO 的点E共有（）A．1个B．2个C．3个D．4个9．如图的矩形ABCD中，E为的中点，有一圆过C、D、E三点，且此圆分别与、相交于P、Q两点．甲、乙两人想找到此圆的圆心O，其作法如下：（甲）作∠DEC的角平分线L，作的中垂线，交L于O点，则O即为所求；（乙）连接、，两线段交于一点O，则O即为所求对于甲、乙两人的作法，下列判断何者正确？（）A．两人皆正确B．两人皆错误C．甲正确，乙错误D．甲错误，乙正确10．如图，△ABC是⊙O的内接三角形，AB＝BC，∠BAC＝30°，AD是直径，AD＝8，则AC 的长为（）A．4 B．4C．D．211．在平面直角坐标系xOy中，直线l经过点A（﹣3，0），点B（0，），点P的坐标为（1，0），⊙P与y轴相切于点O．若将⊙P沿x轴向左平移，平移后得到⊙P′（点P 的对应点为点P′），当⊙P′与直线l相交时，横坐标为整数的点P′共有（）A．1个B．2个C．3个D．4个12．如图，AB为⊙O的切线，切点为A，连接AO、BO，BO与⊙O交于点C，延长BO与⊙O 交于点D，连接AD．若∠ABO＝36°，则∠ADC的度数为（）A．54°B．36°C．32°D．27°二．填空题13．如图，A是硬币圆周上一点，硬币与数轴相切于原点O（A与O点重合）．假设硬币的直径为1个单位长度，若将硬币沿数轴正方向滚动一周，点A恰好与数轴上点A′重合，则点A′对应的实数是．14．AB是⊙O的弦，OM⊥AB，垂足为M，连接OA．若△AOM中有一个角是30°，OM＝2，则弦AB的长为．15．《九章算术》是我国古代数学成就的杰出代表作，其中《方田》章计算弧田面积所用的经验公式是：弧田面积＝（弦×矢+矢2）．弧田是由圆弧和其所对的弦围成（如图中的阴影部分），公式中“弦”指圆弧所对弦长，“矢”等于半径长与圆心到弦的距离之差，运用垂径定理（当半径OC⊥弦AB时，OC平分AB）可以求解．现已知弦AB＝8米，半径等于5米的弧田，按照上述公式计算出弧田的面积为平方米．16．如图，⊙O的半径为1cm，弦AB、CD的长度分别为cm，1cm，则弦AC、BD所夹的锐角α＝度．17．如图，A，B，C，D是⊙O上的四点，且点B是的中点，BD交OC于点E，∠AOC＝100°，∠OCD＝35°，那么∠OED＝．18．如图，点A，B，C，D在⊙O上，＝，∠CAD＝30°，∠ACD＝50°，则∠ADB＝．三．解答题19．如图，圆心为点M的三个半圆的直径都在x轴上，所有标注A的图形面积都是S A，所有标注B的图形面积都是S B．（1）求标注C的图形面积S C；（2）求S A：S B．20．如图，已知△ABC内接于⊙O，且AB＝AC，直径AD交BC于点E，F是OE上的一点，使CF∥BD．（1）求证：BE＝CE；（2）试判断四边形BFCD的形状，并说明理由；（3）若BC＝8，AD＝10，求CD的长．21．如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在圆的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，求小桥所在圆的半径．22．如图，⊙O中，弦AB与CD相交于点E，AB＝CD，连接AD、BC．求证：（1）＝；（2）AE＝CE．23．如图，在⊙O中，点P为的中点，弦AD、PC互相垂直，垂足为M，BC分别与AD、PD 相交于点E、N，连接BD、MN．（1）求证：N为BE的中点．（2）若⊙O的半径为8，的度数为90°，求线段MN的长．24．如图，四边形ABCD内接于圆，∠ABC＝60°，对角线BD平分∠ADC．（1）求证：△ABC是等边三角形；（2）过点B作BE∥CD交DA的延长线于点E，若AD＝2，DC＝3，求△BDE的面积．25．已知，如图，PA切⊙O于点A，割线PD交⊙O于点C、D，∠P＝45°，弦AB⊥PD，垂足为E，且BE＝2CE，DE＝6，CF⊥PC，交DA的延长线于点F．求tan∠CFE的值．参考答案一．选择题1．解：①、要强调在同圆或等圆中相等的圆心角所对的弧相等；故错误．②、平分弦的直径垂直于弦，其中被平分的弦不能是直径，若是直径则错误．③、对称轴是直线，而直径是线段，故错误．④、正确．故选：C．2．解：过点O作OF⊥CD于点F，OG⊥AB于G，连接OB、OD、OE，如图所示：则DF＝CF，AG＝BG＝AB＝3，∴EG＝AG﹣AE＝2，在Rt△BOG中，OG＝＝＝2，∴EG＝OG，∴△EOG是等腰直角三角形，∴∠OEG＝45°，OE＝OG＝2，∵∠DEB＝75°，∴∠OEF＝30°，∴OF＝OE＝，在Rt△ODF中，DF＝＝＝，∴CD＝2DF＝2；故选：C．3．解：根据图形可知，两圆相切，过点O作OP垂直O1O2于P，则：PO1＝PO2＝200PO＝R﹣50根据勾股定理可得：2002+（R﹣50）2＝（R+50）2解得：R＝200∴D＝2R＝400＝4×102．故选：D．4．解：如图，∵OA＝OB＝AB，∴△OAB是等边三角形，∴∠AOB＝60°．故选：C．5．解：连接OD、OE，∵OC＝OA，∴△OAC是等腰三角形，∵点D为弦AC的中点，∴∠DOC＝40°，∠BOC＝100°，设∠BOE＝x，则∠COE＝100°﹣x，∠DOE＝100°﹣x+40°，∵OC＝OE，∠COE＝100°﹣x，∴∠OEC＝∠OCE＝40°+x，∵OD＜OE，∠DOE＝100°﹣x+40°＝140°﹣x，∴∠OED＜20°+x，∴∠CED＝∠OEC﹣∠OED＞（40°+x）﹣（20°+x）＝20°，∵∠CED＜∠ABC＝40°，∴20°＜∠CED＜40°故选：C．6．解：连接OA，OB，OC，∵∠BDC＝50°，∴∠BOC＝2∠BDC＝100°，∵，∴∠BOC＝∠AOC＝100°，∴∠ABC＝∠AOC＝50°，∴∠ADC＝180°﹣∠ABC＝130°．故选：B．7．解：设另一条弦分成的两段CP＝x，DP＝4x，由题意得：AP＝BP＝4cm则由相交弦定理得：AP×BP＝CP×DP，则4×4＝x•4x，x＝2，则CD＝x+4x＝10（cm），故选：B．8．解：如图所示，点E的位置有3个．当是E1时，∠CE1O＝10°；当是E2时，则∠CE20＝110°；当是E3时，则∠CE3O＝50°．故选：C．9．解：甲，∵＝，∴△DEC为等腰三角形，∴L为之中垂线，∴O为两中垂线之交点，即O为△CDE的外心，∴O为此圆圆心．乙，∵∠ADC＝90°，∠DCB＝90°，∴、为此圆直径，∴与的交点O为此圆圆心，因此甲、乙两人皆正确．故选：A．10．解：连接CD，∵AB＝BC，∠BAC＝30°，∴∠ACB＝∠BAC＝30°，∴∠B＝180°﹣30°﹣30°＝120°，∴∠D＝180°﹣∠B＝60°，∵AD是直径，∴∠ACD＝90°，∵∠CAD＝30°，AD＝8，∴CD＝AD＝4，∴AC＝＝＝4，故选：B．11．解：如图所示，∵点P的坐标为（1，0），⊙P与y轴相切于点O，∴⊙P的半径是1，若⊙P与AB相切时，设切点为D，由点A（﹣3，0），点B（0，），∴OA＝3，OB＝，由勾股定理得：AB＝2，∠DAM＝30°，设平移后圆与直线AB第一次相切时圆心为M（即对应的P′），∴MD⊥AB，MD＝1，又因为∠DAM＝30°，∴AM＝2，M点的坐标为（﹣1，0），即对应的P′点的坐标为（﹣1，0），同理可得圆与直线第二次相切时圆心N的坐标为（﹣5，0），所以当⊙P′与直线l相交时，横坐标为整数的点P′的横坐标可以是﹣2，﹣3，﹣4共三个．故选：C．12．解：∵AB为⊙O的切线，∴∠OAB＝90°，∵∠ABO＝36°，∴∠AOB＝90°﹣∠ABO＝54°，∵OA＝OD，∴∠ADC＝∠OAD，∵∠AOB＝∠ADC+∠OAD，∴∠ADC＝∠AOB＝27°；故选：D．二．填空题（共6小题）13．解：将硬币沿数轴正方向滚动一周，点A恰好与数轴上点A'重合，则转过的距离是圆的周长是π，因而点A'对应的实数是π．故答案为：π．14．解：∵OM⊥AB，∴AM＝BM，若∠OAM＝30°，则tan∠OAM＝，∴AM＝6，∴AB＝2AM＝12；若∠AOM＝30°，则tan∠AOM＝，∴AM＝2，∴AB＝2AM＝4．故答案为：12或4．15．解：∵弦AB＝8米，半径OC⊥弦AB，∴AD＝4，∴OD＝＝3，∴OA﹣OD＝2，∴弧田面积＝（弦×矢+矢2）＝×（8×2+22）＝10，故答案为：10．16．解：连接OA、OB、OC、OD，∵OA＝OB＝OC＝OD＝1，AB＝，CD＝1，∴OA2+OB2＝AB2，∴△AOB是等腰直角三角形，△COD是等边三角形，∴∠OAB＝∠OBA＝45°，∠ODC＝∠OCD＝60°，∵∠CDB＝∠CAB，∠ODB＝∠OBD，∴α＝180°﹣∠CAB﹣∠OBA﹣∠OBD＝180°﹣∠OBA﹣（∠CDB+∠ODB）＝180°﹣45°﹣60°＝75°．17．解：连接OB．∵＝，∴∠AOB＝∠BOC＝50°，∴∠BDC＝∠BOC＝25°，∵∠OED＝∠ECD+∠CDB，∠ECD＝35°，∴∠OED＝60°，故答案为60°．18．解：∵＝，∠CAD＝30°，∴∠CAD＝∠CAB＝30°，∴∠DBC＝∠DAC＝30°，∵∠ACD＝50°，∴∠ABD＝50°，∴∠ADB＝∠ACB＝180°﹣∠CAB﹣∠ABC＝180°﹣50°﹣30°﹣30°＝70°．故答案为：70°．三．解答题（共7小题）19．解：（1）由题意得到圆M的半径为（6﹣4）÷2＝1，则．（1分）（2）∴（3分）∵∴（5分）∴即S A：S B＝5：6（6分）20．（1）证明：∵AD是⊙O的直径，∴∠ABD＝∠ACD＝90°，在Rt△ABD和Rt△ACD中，，∴Rt△ABD≌Rt△ACD（HL），∴∠BAD＝∠CAD，∵AB＝AC，∴BE＝CE；（2）四边形BFCD是菱形．证明：∵AD是直径，AB＝AC，∴AD⊥BC，BE＝CE，∵CF∥BD，∴∠FCE＝∠DBE，在△BED和△CEF中，，∴△BED≌△CEF（ASA），∴CF＝BD，∴四边形BFCD是平行四边形，∵∠BAD＝∠CAD，∴BD＝CD，∴四边形BFCD是菱形；（3）解：∵AD是直径，AD⊥BC，BE＝CE，∵∠AEC＝∠CED，∠CAE＝∠ECD，∴△AEC∽△CED，∴＝，∴CE2＝DE•AE，设DE＝x，∵BC＝8，AD＝10，∴42＝x（10﹣x），解得：x＝2或x＝8（舍去）在Rt△CED中，CD＝＝＝2．21．解：∵小刚身高1.6米，测得其影长为2.4米，∴8米高旗杆DE的影子为：12m，∵测得EG的长为3米，HF的长为1米，∴GH＝12﹣3﹣1＝8（m），∴GM＝MH＝4m．如图，设小桥的圆心为O，连接OM、OG．设小桥所在圆的半径为r，∵MN＝2m，∴OM＝（r﹣2）m．在Rt△OGM中，由勾股定理得：∴OG2＝OM2+42，∴r2＝（r﹣2）2+16，解得：r＝5，答：小桥所在圆的半径为5m．22．证明（1）∵AB＝CD，∴＝，即+＝+，∴＝；（2）由（1）知＝，∴AD＝BC，∵＝，＝，∴∠ADE＝∠CBE，∠DAE＝∠BCE，∴△ADE≌△CBE（ASA），∴AE＝CE．23．（1）证明：∵AD⊥PC，∴∠EMC＝90°，∵点P为的中点，∴，∴∠ADP＝∠BCP，∵∠CEM＝∠DEN，∴∠DNE＝∠EMC＝90°＝∠DNB，∵，∴∠BDP＝∠ADP，∴∠DEN＝∠DBN，∴DE＝DB，∴EN＝BN，∴N为BE的中点；（2）解：连接OA，OB，AB，AC，∵的度数为90°，∴∠AOB＝90°，∵OA＝OB＝8，∴AB＝8，由（1）同理得：AM＝EM，∵EN＝BN，∴MN是△AEB的中位线，∴MN＝AB＝4．24．（1）证明：∵四边形ABCD内接于圆．∴∠ABC+∠ADC＝180°，∵∠ABC＝60°，∴∠ADC＝120°，∵DB平分∠ADC，∴∠ADB＝∠CDB＝60°，∴∠ACB＝∠ADB＝60°，∠BAC＝∠CDB＝60°，∴∠ABC＝∠BCA＝∠BAC，∴△ABC是等边三角形．（2）过点A作AM⊥CD，垂足为点M，过点B作BN⊥AC，垂足为点N．∴∠AMD＝90°，∵∠ADC＝120°，∴∠ADM＝60°，∴∠DAM＝30°，∴DM＝AD＝1，AM＝＝＝，∵CD＝3，∴CM＝CD+DM＝1+3＝4，∴S＝CD•AM＝×＝，△ACDRt△AMC中，∠AMD＝90°，∴AC＝＝＝，∵△ABC是等边三角形，∴AB＝BC＝AC＝，∴BN＝BC＝，∴S＝×＝，△ABC∴四边形ABCD的面积＝+＝，∵BE∥CD，∴∠E+∠ADC＝180°，∵∠ADC＝120°，∴∠E＝60°，∴∠E＝∠BDC，∵四边形ABCD内接于⊙O，∴∠EAB＝∠BCD，在△EAB和△DCB中，，∴△EAB≌△DCB（AAS），∴△BDE的面积＝四边形ABCD的面积＝．25．解：由相交弦定理，得AE•BE＝DE•CE又∵BE＝2CE∴AE•2CE＝6CE∴AE＝3∵AB⊥PD∴∠AEP＝90°又∵∠P＝45°∴∠EAP＝∠P＝45°∴PE＝AE＝3在Rt△AEP中，由勾股定理，得：PA＝＝＝∵PA切⊙O于点A∴PA2＝PC•PD∴PC＝∴CE＝PE﹣PC＝3﹣2＝1∵FC⊥PD∴∠FCE＝90°又∵∠AED＝90°∴∠AED＝∠FCE∴AE∥FC∴＝∴FC＝＝＝∴tan∠CFE＝＝＝．。

沪科版数学九年级上册综合训练50题含答案（填空、解答题）一、填空题1．如图，小明抛投一个沙包，沙包被抛出后距离地面的高度h （米）和飞行时间t （秒）近似满足函数关系式()216510h t =--+，则沙包在飞行过程中距离地面的最大高度是________米．2．如图，在△ABC 中，点D ，E 分别在AB ，AC 上，DE ∥BC ，若AD =1，AB =4，则DEBC=_____．14DE AD AB，3．点B 是线段AC 的黄金分割点，且AB BC <．若4AC =，则BC 的长为______．4．如图，抛物线2y ax bx c =++与x 轴相交于A ，B ()10t +，两点，与y 轴相交于点C ，点D 在该抛物线上，且坐标为()t c ，，则点A 的横坐标是_______．【答案】1-【分析】先求出点C 的坐标为()0c ，，进而得到点C 与点D 关于抛物线对称轴对称，据此求出抛物线对称轴即可求出点A 的坐标．【详解】解：∥抛物线2y ax bx c =++与y 轴相交于点C ， ∥点C 的坐标为()0c ，，5．如图，点P 在反比例函数ky x=的图象上，P A ∥x 轴于点A ，PB ∥y 轴于点B ，且△APB 的面积为2，则k 等于______．6．若抛物线2(2)2y x m x m =---的顶点在y 轴上，则m =_______． 【答案】2【分析】根据题意可知抛物线对称轴为0x =，然后可求得m 的值． 【详解】解：∥抛物线2(2)2y x m x m =---的顶点在y 轴上，7．如图，无人机与亮亮的水平距离是15米，当他抬头仰视无人机时，仰角恰好为30°，若亮亮身高1.70米，则无人机距离地面的高度为____米．（结果带根号即可）【答案】()1.7##(1.7+【分析】根据特殊角三角函数值求出AB的长，再由矩形的判定和性质，得出BE的【点睛】本题考查了矩形的判定和性质以及利用特殊三角函数值求边长，理解题意，作出相应辅助线，利用三角函数求解是解题关键.8．抛物线y ＝a(x －h)2＋k 经过(－1，0)，(5，0)两点，则关于x 的一元二次方程－a(x+h －2)2－k ＝0的解是__________． 【答案】x 1=3，x 2=－3【分析】将(－1，0)，(5，0)代入到二次函数解析式中，即可得出两个等式，然后对照一元二次方程与两个等式的关系即可得出结论． 【详解】解：将(－1，0)，(5，0)代入到解析式中，得 0＝a(-1－h)2＋k∥ 0= a(5－h)2＋k∥将∥变形，得-a(1＋h)2-k=0∥ 将∥变形，得-a(-5＋h)2-k=0∥∥关于x 的一元二次方程－a(x+h －2)2－k ＝0的解应满足x+h －2=1＋h 或x+h －2=-5＋h解得：x 1=3，x 2=－3 故答案为x 1=3，x 2=－3．【点睛】此题考查的是根据二次函数与x 轴的交点坐标，求一元二次方程的解，掌握二次函数与x 轴的交点坐标与一元二次方程的解的关系是解决此题的关键．9．关于x 的函数()()2211y a x a =+-+（a 为实数）的函数上两点()12,A y 、2(3,)B y -，则1y ________2y （填>、＜、＝号） 【答案】<【分析】根据二次函数的对称性，可利用对称性，找出点A 的对称点'A ，再利用二次函数的增减性可判断y 值的大小．【详解】解：∵该函数的解析式为：()()2211y a x a =+-+∴对称轴为：1x =∴点()12,A y 关于对称轴的对称点坐标()1'0A y ， ∵210a +>∴该二次函数开口向上，在对称轴左边y 随x 的增大而减小 ∥0＞-3 ∴12y y < 故答案为：12y y <【点睛】本题考查了二次函数图象上点的坐标特征和二次函数的性质，掌握二次函数图象的增减性是解题的关键． 10．如果反比例函数my x=过A(2，-3)，则m=_______．11．某校有航模组设计制作的火箭，它的升空高度()h m 与飞行时间()t s 满足函数关系式2261h t t =-++，则该火箭升高的最大高度是________m ． 【答案】170【分析】直接利用配方法将二次函数写成顶点式，进而求出即可． 【详解】由题意可得： h =-t 2+26t +1 =-（t 2-26t ）+1 =-（t -13）2+170，故火箭点火后13秒降落伞将打开，这时火箭的最大高度是170米， 故答案为170．【点睛】此题主要考查了二次函数的应用，正确配方求出是解题关键，难度不大． 12．若反比例函数ky x=的图象经过点(3，2)，则此函数在每一个象限内随的增大而_______． 【答案】减小．【详解】试题分析：图象经过点（3，2），先求出k 值，再根据反比例函数的性质解答．试题解析：∥图象经过点（3，2），13．如图，DE 与ABC 的边AB ，AC 分别相交于D ，E 两点，且DE BC ∥．若2,3DE cm BC cm ==，23AE cm =，则AC ＝________cm ．14．如图，正比例函数2y x =-与反比例函数()80y x x=-<的图象有一个交点A ，直线BC OA ∥，交反比例函数的图象于点B ，交y 轴于点C ，若2BC OA =，则直线BC 的解析式为______．【答案】26y x =--##62y x =--的横坐标，根据定义求得点B 的横坐标，然后求得点B 的坐标，将点B 的坐标代入15．如图是二次函数2y ax bx c =++的图象的一部分，图象过点()3,0A -，对称轴是直线1x =-，给出五个结论：①24b ac >；②20a b -=；③0c <；④0a b c ++=；⑤0a b c -+<．其中正确的是________（把你认为正确的序号都填上，答案格式如：“1234”）．16．已知线段AB=2cm，点C是线段AB的黄金分割点，则线段AC等于__________cm【点睛】本题考查的是黄金分割，掌握黄金比值是解题的关键． 17．如图，AB ，CD 都与x 轴垂直，垂足分别为B ，D ，点C 在双曲线ky x=上．若∥AOC =90°，8AOB S =△，:2:1OA OC =，则k 的值是____．CODS =CODS =122k =4k =，18．函数22y x x =-()03x ≤≤有最大值，也有最小值，则最小值是___________． 【答案】1-【分析】把函数22y x x =-变成顶点式，()211y x =--，结合x 的范围，即可求得． 【详解】把函数22y x x =-变成顶点式， ()211y x =--，对称轴为1x =，开口向上， 在03x ≤≤，对称轴1x =取最小值， 最小值：1y =-， 故答案为：1-．【点睛】本题考查了二次函数得图像和性质，解决本题的关键是把二次函数化为顶点式．19．如图，两根竖直的电线杆AB 长为12，CD 长为4，AD 交BC 于点E ，则点E 到地面的距离EF 的长是__________．故答案为3．【点睛】此题主要考查了相似三角形的判定与性质，正确找出相似比是解题的关键．20．在ABC中，D为AB边上一点，E为AC边上一点，ADE与ABC相似，已知3AB=，1AD=，AC=AE=__________．时，ADE ABC，∥AB AC3223时，AED ABC，∥AE AD1AE21．如图，在平面直角坐标系中，O为坐标原点，正方形OABC的顶点A在y轴的负半轴上，点C在x轴的正半轴上，经过点A、B的抛物线y＝a（x﹣2）2+c（a＞0）的顶点为E．若∥ABE为等腰直角三角形，则a的值为__．22．如图，一次函数的图象y x b=-+与反比例函数的图象ayx=交于A(2,﹣4)，B(m, 2)两点.当x满足条件______________时，一次函数的值大于反比例函数值.23．已知函数y=x 2﹣4x+3，则函数值y 随x 的增大而减小的x 的取值范围是______．24．已知点P 是线段AB 的黄金分割点，且AP PB >，若1AB =．则AP =_____． 解：点25．已知二次函数y ＝2x 2－6x ＋1，当0≤x ≤5时，y 的取值范围是______________．26．如图，有一斜坡OA ，已知斜坡上一点A 的坐标为()2A ，过点A 作AB x⊥轴，垂足为点B ，将∥AOB 以坐标原点0为位似中心缩小为原图形的12，得到∥COD ，则OC 的长度是______________，此时斜坡OA 的坡度为________________．轴，将AOB 以坐标原点()227．已知1(1,)A y -、2(0,)B y 、3(3,)C y 是二次函数2(2)1y a x =-+（0a ＞）图像上的三点，则1y ，2y ，3y 之间的大小关系为 _____（用“＞”连接）． 【答案】123y y y ＞＞【分析】由二次函数2(2)1y a x =-+（0a ＞），得到对称轴为直线2x =，根据2(1)2032----＞＞，从而判定123y y y ＞＞．【详解】∥二次函数2(2)1y a x =-+（0a ＞）， ∥对称轴为直线2x =，∥2(1)2032----＞＞， ∥123y y y ＞＞．故答案为：123y y y ＞＞．【点睛】本题考查了抛物线的对称性和增减性，函数值的大小比较，熟练掌握抛物线的性质，特别是增减性是解题的关键．28．已知Rt∥ABC 中，AC =3，BC = 4，过直角顶点C 作CA 1∥AB ，垂足为A 1，再过A 1作A 1C 1∥BC ，垂足为C 1，过C 1作C 1A 2∥AB ，垂足为A 2，再过A 2作A 2C 2∥BC ，垂足为C 2，…，这样一直做下去，得到了一组线段CA 1，A 1C 1，C 1A 2，…，则CA 1=______，8999C A A C =_______【答案】29．在平面直角坐标系中两点P （x ，y ），Q （x ，y ′），其中y ′＝00yx y x >⎧⎨-≤⎩（）（），则称Q 点是P 点的可控点．若P （x ，y ）满足y ＝－x 2＋16，其中（－5≤x ≤a ）时，可控点Q（x，y′）满足－16≤y′≤16，则a的取值范围为____．【点睛】本题考查了二次函数图象应用问题，解决此类问题：首先根据题意，大致画出函数图象，依据图象确定数值的取值范围．二、解答题30．已知反比例函数y ＝2kx-的图象经过点A （3，﹣2）． （1）求k 的值．（2）点C （x 1，y 1），B （x 2，y 2）均在反比例函数y ＝2kx-的图象上，若0＜x 1＜x 2，直接写出y 1，y 2的大小关系． 8k ；（2））将点A 的坐标代入反比例函数的解析式即可得；）根据反比例函数的增减性即可得．2k y x得：2-8k ；）由（1）得：反比例函数的解析式为6x ，在每一象限内，11,),(C x y 12y y ∴<．【点睛】本题考查了反比例函数的图象与性质，熟练掌握待定系数法是解题关键．31．（1）已知一次函数的图象经过点（0，1）和（1，3），求这个函数的表达式． （2）已知y 是x 的反比例函数，且当=2x 时，=3y ，求当x ＝﹣3时y 的值． 【答案】（1）21y x =+；（2）=2y -.【分析】（1）根据待定系数法将（0，1）和（1，3）代入所设的一次函数解析式中，即可求得函数的表达式；（2）由待定系数法，先求出反比例函数的解析式，再将x ＝﹣3代入解析式，可求出y 的值.【详解】解：（1）设这个函数的表达式是y kx b =+ ∥因为函数的图象经过点（0，1）和（1，3）∥13b k b =⎧⎨+=⎩，解得：21k b =⎧⎨=⎩32．如图：已知∥ABC 为等腰直角三角形，∥ACB =90°，延长BA 至E ，延长AB 至F ，∥ECF =135° 求证：∥EAC ∥∥CBF【答案】见解析【分析】利用有两组角对应相等的两个三角形相似来证明∥EAC ∥∥CBF ． 【详解】解：∥∥ABC 为等腰直角三角形，∥ACB =90°， ∥∥CAB =∥CBA =45°，∥∥E +∥ECA =45°（三角形外角定理）． 又∥ECF =135°，∥∥ECA +∥BCF =∥ECF -∥ACB =45°， ∥∥E =∥BCF ； 同理，∥ECA =∥F ， ∥∥EAC ∥∥CBF ．33．已知关于x 的二次函数()220y ax ax c a =++≠，且3c a =-．(1)若1a =-，求该二次函数的解析式和顶点坐标；(2)在（1）的条件下，求出下表中k 、n 的值，并在以下平面直角坐标系中，用描点法画出该二次函数的图象；根据图象回答：当02x ≤≤时，直接写出y 的最小值． (3)当30x -≤≤时，y 有最小值-4，若将该二次函数的图象向右平移()1m m >个单位长度，平移后得到的图象所对应的函数'y 在30x -≤≤的范围内有最小值-3，求函数y ax m =+的解析式．【答案】(1)223y x x =--+，顶点坐标为()1,4- (2)3k =，0n =，图见解析，最小值为5- (3)2y x =+【分析】（1）利用待定系数法带入=1x -，4y =结合3c a =-即可求得函数解析数，把二次数解析式整理为顶点式即可求得顶点坐标．（2）由（1）函数解析式分别代入当0x =和1x =时即可求得k 、n 的值，根据描点法画函数图象步骤即可．（3）根据题意把函数整理为顶点式，即可知对称轴为直线=1x -，由=1x -在30x -≤≤范围内，即最值为顶点坐标的纵坐标，即可求出平移前的函数解析式，根据平移的性质即可求得答案．【详解】（1）解：3c a =-，22223y ax ax c ax ax a =++=+-，把=1x -，4y =代入上述函数得，423a a a =--， 解得1a =-，3c ∴=，∴二次函数的解析式为223y x x =--+，()222232131(1)4y x x x x x =--+=-++++=-++，所以顶点坐标为()1,4-．（2）（2）由（1）得223y x x =--+， 当0x =时3k =，当1x =时，1230n =--+=， 图象如图所示，由图，02x ≤≤时，y 随x 的增大而减小，∴当2x =时，y 最小，最小值为222235y =--⨯+=-．（3）∥3c a =-则2223(1)4y ax ax a a x a =-+=+-， ∥抛物线对称轴为直线=1x -，顶点坐标为()1,4a --， 由题意可得当30x -≤≤时，函数最小值为44a -=-， ∥1a =，()214y x =+-，二次函数的图象向右平移()1m m >个单位长度后得()2'14y x m =+--，抛物线对称轴为直线1x m =-， ∥1m >，10m ->， ∥对称轴在y 轴右侧，∥当0x =时，22'(1)4(1)4y x m m =+--=--为最小值，()2143m --=-，∥0m =（舍）或2m =， ∴1a =，2m =，∥这个函数表达式：2y x =+．【点睛】本题考查了待定系数法求函数解析式、用描点法画二次函数的图象、二次函数的性质、函数图象的平移，解题的关键在于熟练掌握待定系数法、描点法画函数图象及二次函数的图象及性质和函数图象的平移等知识．34．如图，某研究性学习小组在一次综合实践活动中发现如下问题：在楼底的B 处测得河对岸大厦上悬挂的条幅底端D 的仰角为33︒，在楼顶A 处测得条幅顶端C 的仰角为50︒．若楼AB 高度为21米，条幅CD 长度为43米，请你帮助他们求出大厦的高度CE ．（参考数据：sin330.54︒≈，cos330.84︒≈，tan330.65︒≈，sin500.77︒=，cos500.64︒=，tan50 1.20︒=）【答案】大厦的高度CE 为69m【分析】首先过点A 作AF∥CE 于点F ，易得四边形ABEF 是矩形，然后设BE=xm ，可得在Rt∥BDE 中，DE=0．65x （m ），在Rt∥ACF 中，CF=1．2x （m ），继而可得方程430.65 1.221x x +=+，解此方程即可求得答案． 【详解】过点A 作AF CE ⊥，垂足为F ．∥90AFE ∠=︒∥AB BE ⊥，CE BE ⊥， ∥90ABE CEB ∠=∠=︒ ∥四边形ABEF 是矩形35．某种植户计划将一片荒山改良后种植沃柑，经市场调查得知，当种植沃柑的面积x不超过15亩时，每亩可获得利润y=1900元；超过15亩时，每亩获得利润y（元）与种植面积x（亩）之间的函数关系:y=kx+b，并且当x=20时，y=1800；当x=25时，y=1700．（1）请求出y与x的函数关系式，并写出自变量的取值范围；（2）设种植户种植x亩沃柑所获得的总利润为w元，由于受条件限制，种植沃柑面积x不超过50亩，求该种植户种植多少亩获得的总利润最大，并求总利润w（元）的最大值．【答案】（1）y=﹣20x+2200（15＜x≤110）；（2）当种植50亩时获利最大，总利润的最大值为60000元【分析】（1）根据题意设y=kx+b，再运用待定系数法求解可得；（2）根据总利润=每亩利润×亩数，分0＜x≤15和15＜x≤110两种情况分别求解可得．【详解】解：（1）y=kx+b，将x=20、y=1800和x=25、y=1700代入得：201800251700k b k b +=⎧⎨+=⎩解得：202200k b =-⎧⎨=⎩∥y=﹣20x+2200 ∥-20x+2200≥0， 解得：x≤110，∥自变量的取值范围是：15＜x≤110； （2）当0＜x≤15时，W=1900x ， ∥当x=15时，W 最大=28500（元）； 当15＜x≤110时，W=（﹣20x+2200）x=﹣20x 2+2200x=﹣20（x ﹣55）2+60500 ∥x≤50∥当x=50时，W 最大=60000（元）；所以，当种植50亩时获利最大，总利润的最大值为60000元．【点睛】本题主要考查二次函数的应用，熟练掌握待定系数法和由题意依据相等关系列出函数解析式是解题的关键．36．二次函数2y ax bx c =++（a ，b ，c 为实数，且0a ≠）的图象经过点()1,1--，()3,3．(1)求ca的值； (2)若12a >，点()3,A m -在该二次函数图象上，求证：3m >； (3)设(),0t 是该函数图象与x 轴的一个交点，且满足34t <<，求a 的取值范围．37．如图，直线3y x =-交x 轴于点B ，交y 轴于点A ，抛物线24y ax x c =++经过点A ，B ，点C 为抛物线的顶点．(1)求抛物线的解析式及点C 的坐标；(2)将抛物线24y ax x c =++向下平移m 个单位长度． ∥当03x ≤≤时，用含m 的式子表示y 的取值范围；∥点C 的对应点为C '，连接AC '，BC '，若2ABC S '=△，求m 的值．令0x =，则=3y -，令0y =，则3x =()()0,3,3,0A B ∴-代入24y ax x c =++得09123a cc =++⎧⎨=-⎩ 解得13a c =-⎧⎨=-⎩∴2=+43y x x --()221x =--+点C 为抛物线的顶点 ∥()2,1C （2）解：将抛物线2=+43y x x --向下平移m 个单位长度，则平移后的解析式为243y x x m =-+--()221x m =--+-，顶点坐标为()2,1m -，对称轴为2x =∥当03x ≤≤时，最大值为1y m =-，2032->-，根据离对称轴越远的点，函数值越小，∴最小值为0x =时，3y m =-- 31m y m ∴--≤≤-，∥依题意，C '()2,1m -()()0,3,3,0A B -设直线AB 的解析式为y kx b =+303b k b =-⎧⎨=+⎩解得13k b =⎧⎨=-⎩ ∴直线AB 的解析式为3y x =-ABC S'=ABC S '=△2m ⨯-38．如图1，A 、B 、C 是表示某特产公司三个连锁门市，三个门市之间有AB 、BC 、AC 公路相连，点C 、B 分别位于点A 正东和北偏东60°的方向，六位同学分别利用不同途径获得A 、C 两点的距离如表：他们又调查了各门市该种特产的库存情况，绘制了下列尚不完整的统计图2，3．(1)求表中AC长度的平均数(2)求C处特产的吨数，并补充完整图2，图3．(3)用（1）中AC长度的平均数作为AC的长度，测得点C位于点B的东南方向，因市场原因，需将A、C两门市的库存全部都调往B处，若运送1吨特产1千米需0.5元，1.7 1.4）．求运送特产所需的总费用．BAD ∠=∥2AB x =∥3x x +解得x =20∥AB =40，39．如图，一次函数5y x =-+的图像与反比例函数()0ky k x=≠在第一象限内的图像交于()1,A n 和()4,B m 两点．()1求反比例函数的表达式；()2在第一象限内，当()50k x k x-+<≠的值时，写出自变量x 的取值范围；()3求AOB面积．40．【问题情境】如图1，在等腰直角三角形ABC 中，90ACB ∠=︒，F 是AC 边上一动点（点F 不与点A ，C 重合），以CF 为边在ABC 外作正方形CDEF ，连接AD ，BF ．(1)【探究展示】∥猜想：图1中，线段BF ，AD 的数量关系是__________，位置关系是__________．∥如图2，将图1中的正方形CDEF 绕点C 顺时针旋转α，BF 交AC 于点H ，交AD 于点O ，∥中的结论是否仍然成立？请说明理由．(2)【拓展延伸】如图3，将【问题情境】中的等腰直角三角形ABC 改为直角三角形ABC ，90ACB ∠=︒，正方形CDEF 改为矩形CDEF ，连接BF 并延长，交AC 于点H ，交AD 于点O ，连接BD ，AF ．若4AC =，3BC =，43CD =，1CF =，求22BD AF +的值．解：∥BF =AD ，BF ∥AD ； 延长BF 交AD 于点G ，∥等腰直角三角形ABC 中，90ACB ∠=︒， ∥AC =BC ，在正方形CDEF 中，CD =CF ，∥FCD =90°， ∥∥BCF =∥ACD ， ∥∥BCF ∥∥ACD ， ∥BF =AD ，∥CBF =∥CAD ， ∥∥CAD +∥ADC =90°， ∥∥CBF +∥ADC =90°， ∥∥BGD =90°，即BF ∥AD ， 故答案为BF =AD ，BF ∥AD ；∥∥中的结论仍然成立，理由如下： 等腰直角三角形ABC 中，90ACB ∠=︒， ∥AC =BC ，在正方形CDEF 中，CD =CF ，∥FCD =90°， ∥∥BCF =∥ACD ， ∥∥BCF ∥∥ACD ， ∥BF =AD ，∥CBF =∥CAD ，∥∥CBH +∥CHB =90°，∥CHB =∥AHO ， ∥∥CAD +∥AHO =90°， ∥∥AOH =90°，即BF ∥AD ， 故∥中的结论仍然成立； (2)如图，连接DF ，41．在平面直角坐标系xOy中，反比例函数myx=的图象经过点（1，-6）．（1）求m的值；（2）横、纵坐标都是整数的点叫做整点．记直线12y x b=+与反比例函数myx=的图象围成的区域为W（不含边界）．若区域W内恰有1个整点，结合函数图象，直接写出b 的取值范围．92b942b <<-22．42．如图在平面直角坐标系中，∥OAB 的顶点坐标分别是O(0，0)，A(2，4)，B(6，0).(1)以原点O 为位似中心，在点O 的异侧画出∥OAB 的位似图形∥OA 1B 1，使它与∥OAB 的相似比是1：2. (2)写出点A 1、B 1的坐标.(3)若∥OAB关于点O的位似图形∥OA2B2中，点A的对应点A2的坐标为(﹣3，﹣6)，则∥OA2B2与∥OAB的相似比为______.【答案】(1)见解析；(2)A1(﹣1，﹣2)，B1(﹣3，0)；(3)3：2.【分析】(1)由以原点O为位似中心，在点O的异侧画出∥OAB的位似图形∥OA1B1，使它与∥OAB的相似比是1：2，可求得各对应点的坐标，继而画出位似图形；(2)由(1)，可求得点A1、B1的坐标；(3)根据位似图形的性质，即可求得∥OA2B2与∥OAB的相似比.【详解】解：(1)如图：(2)A1(﹣1，﹣2)，B1(﹣3，0)；(3)∥A(2，4)，点A的对应点A2的坐标为(﹣3，﹣6)，∥∥OA2B2与∥OAB的相似比为：3：2.故答案为：3：2.【点睛】此题主要考查位似，解题的关键是熟知位似得性质及作图方法.43．如图1，正比例函数y＝kx的图象与反比例函数y＝mx（x＞0）的图象都经过点A（2，2）．（1）分别求这两个函数的表达式；（2）如图2，将直线OA向下平移n个单位长度后与y轴交于点B，与x轴交于点C，与反比例函数图象在第一象限内的交点为D，连接OD，tan∥COD＝14．∥求n的值．∥连接AB，AD，求∥ABD的面积．2244．如图，矩形ABCD中，AB=6，BC=8，E为AB上一点，且AE=2，M为AD上一动点（不与A、D重合），AM=x，连结EM并延长交CD的延长线于F，过M作MG⊥EF交直线BC于点G，连结EG、FG．（1）如图1，若M是AD的中点，求证：①⊥AEM⊥⊥DFM；②⊥EFG是等腰三角形；（2）如图2，当x为何值时，点G与点C重合？（3）当x=3时，求⊥EFG的面积．在∥AEM和∥DFM中，，∥，∥，∥∥AME+∥NMG=∥NMG+∥NGM=90°，∥∥AME=∥MGN，∥∥AEM∥∥NMG，∥====，∥MN=2AE=4，由勾股定理得：EM===，∥GM=2EM=2，∥AB∥CD，∥∥DMF∥∥NGM，∥=，解得：MF=，∥EF=EM+MF=，∥∥EFG的面积=EF•GM=．45．抛物线y＝ax2＋bx﹣2与x轴交于点A和B（﹣1，0），与y轴交于点C，直线y＝﹣12x＋m过A，C两点，点P是抛物线上的一个动点．（1）求抛物线的解析式；（2）如图，若点P在直线AC的上方，当S△P AC＝3时，求点P的坐标；（3）点M为抛物线上的一点，tan∥ACM＝25时，求点M的坐标．151PHA PHC S S ＋＝12∥2CEF ，＝2ECF ∠25CA ＝， EN ∥y 轴交46．某物流公司要把3000吨货物从M市运到W市．（每日的运输量为固定值）（1）从运输开始，每天运输的货物吨数y（单位：吨）与运输时间x（单位：天）之间有怎样的函数关系式？（2）因受到沿线道路改扩建工程影响，实际每天的运输量比原计划少20%，以致推迟1天完成运输任务，求原计划完成运输任务的天数．∥y＝（x＞0）（1﹣20%）＝，47．在平面直角坐标系中，点O为坐标原点，抛物线y=﹣x2+（k﹣1）x+k（k＞0）交x轴的负半轴于点A，交x轴的正半轴于点B，交y轴的正半轴于点C，且AB=4．（1）如图1，求k的值；（2）如图2，点D在第一象限的抛物线上，点E在线段BC上，DE//y轴，若DE=，求点D的坐标；（3）如图3，在（2）的条件下，F为抛物线顶点，点P在第四象限的抛物线上，FP 交直线DE于点Q，点G与点D关于y轴对称，若GQ=DP，求点P的坐标．48．【特例发现】如图1，在∥ABC中，AG∥BC于点G，以A为直角顶点，分别以AB，AC为直角边，向∥ABC外作等腰Rt∥ABE和等腰Rt∥ACF，过点E、F作射线GA 的垂线，垂足分别为P、Q．求证：EP=FQ．【延伸拓展】如图2，在∥ABC中，AG∥BC于点G，以A为直角顶点，分别以AB，AC为直角边，向∥ABC外作Rt∥ABE和Rt∥ACF，射线GA交EF于点H．若AB=kAE，AC=kAF，请思考HE与HF之间的数量关系，并直接写出你的结论．【深入探究】如图3，在∥ABC中，G是BC边上任意一点，以A为顶点，向∥ABC外作任意∥ABE和∥ACF，射线GA交EF于点H．若∥EAB=∥AGB，∥F AC=∥AGC，AB=kAE，AC=kAF，上一问的结论还成立吗？并证明你的结论．【应用推广】在上一问的条件下，设大小恒定的角∥IHJ分别与∥AEF的两边AE、AF 分别交于点M、N，若∥ABC为腰长等于4的等腰三角形，其中∥BAC=120°，且∥IHJ=∥AGB=θ=60°，k=2；求证：当∥IHJ在旋转过程中，∥EMH、∥HMN和∥FNH均相似，并直接写出线段MN 的最小值（请在答题卡的备用图中补全作图）．【答案】(1)证明参见解析；(2)HE=HF；(3)成立，证明参见解析；(4)证明参见解析，。

2021年九年级中考第二轮数学专题复习：圆的综合强化训练（一）1．如图，AB，CD是⊙O的两条直径，且AB⊥CD，点E，点F分别在半径OC，OD上（不与点O，点C，点D重合），连接AE，EB，BF，FA．（1）若CE＝DF，求证：四边形AEBF是菱形．（2）过点O作OG⊥EB，分别交EB，⊙O于点H，点G，连接BG．①若∠COG＝∠EBG，判断△OBG的形状，说明理由．②若点E是OC的中点，求的值．2．已知：在半径为2的扇形AOB中，∠AOB＝m°（0＜m≤180），点C 是上的一个动点，直线AC与直线OB相交于点D．（1）如图1，当0＜m＜90，△BCD是等腰三角形时，求∠D的大小（用含m的代数式表示）；（2）如图2，当m＝90点C是的中点时，联结AB，求的值；（3）将沿AC所在的直线折叠，当折叠后的圆弧与OB所在的直线相切于点E，且OE＝1时，求线段AD的长．3．如图，在矩形ABCD中，AB＝4，BC＝8，点P在边BC上（点P与端点B、C不重合），以P为圆心，PB为半径作圆，圆P与射线BD的另一个交点为点E，直线CE与射线AD交于点G．点M为线段BE的中点，联结PM．设BP＝x，BM＝y．（1）求y关于x的函数解析式，并写出该函数的定义域；（2）联结AP，当AP∥CE时，求x的值；（3）如果射线EC与圆P的另一个公共点为点F，当△CPF为直角三角形时，求△CPF的面积．4．如图所示，AB是⊙O的直径，点E为线段OB上一点（不与O，B重合），作CE⊥OB，交⊙O于点C，垂足为点E，作直径CD，过点C的切线交DB的延长线于点P，作AF⊥PC于点F，连接CB．（1）求证：AC平分∠FAB．（2）求证：BC2＝CE•CP．（3）当AB＝4时，求劣弧BC长度（结果保留π）．5．如图，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D在AB上，AD ＝2，以点A为圆心，AD长为半径的弧交AC于点E，与BC交于点F ，G，P是上一点．将AP绕点A逆时针旋转120°，得到AQ，连接CQ，AF．（1）若BP与所在圆相切，判断CQ与所在圆的位置关系．并加以证明；（2）求BF的长及扇形EAF的面积；（3）若∠PAB＝m°，当∠ACQ＝30°，直接写出m的值．6．如图，⊙O是△ABC的外接圆，AB＝AC，BO的延长线交AC于点D．（1）求证：∠BAC＝2∠ABD；（2）若＝，求tan∠ABD．7．已知：如图，在△ABC中，点I是△ABC的内心（三角形三条角平分线的交点），延长AI与△ABC的外接圆交于点D，连接BD，DC．求证：（1）DI＝DB；（2）若∠BAC＝60°，BC＝2，求DI的长．8．有一些代数问题，我们也可以通过几何方法进行求解，例如下面的问题：已知：a＞b＞0，求证：＞．经过思考，小明给出了几何方法的证明，如图：①在直线l上依次取AB＝a，BC＝b；②以AC为直径作半圆，圆心为O；③过B点作直线l的垂线，与半圆交于点D，连接OD．请回答：（1）连接AD，CD，由作图的过程判断，∠ADC＝90°，其依据是；（2）根据作图过程，试求线段BD、OD（用a，b的代数式表示），请写出过程；（3）由BD⊥AC，可知BD＜OD，其依据是，由此即证明了这个不等式．9．如图，⊙O是△ABC的外接圆，∠ACB＝90°．D是⊙O上一点，连接CD，与AB交于点F，过点A作⊙O的切线交DC延长线于点E，已知AC＝EC．（1）求证：AD＝AE；（2）若AE＝2，EF＝2，求⊙O的直径．10．如图，已知Q是∠BAC的边AC上一点，AQ＝15，cot∠BAC＝，点P 是射线AB上一点，联结PQ，⊙O经过点A且与QP相切于点P，与边AC 相交于另一点D．（1）当圆心O在射线AB上时，求⊙O的半径；（2）当圆心O到直线AB的距离为时，求线段AP的长；（3）试讨论以线段PQ长为半径的⊙P与⊙O的位置关系，并写出相应的线段AP取值范围．11．如图，已知扇形AOB的半径OA＝4，∠AOB＝90°，点C、D分别在半径OA、OB上（点C不与点A重合），联结CD．点P是弧AB上一点，PC＝PD．（1）当cot∠ODC＝，以CD为半径的圆D与圆O相切时，求CD的长；（2）当点D与点B重合，点P为弧AB的中点时，求∠OCD的度数；（3）如果OC＝2，且四边形ODPC是梯形，求的值．12．如图，已知半圆O的直径AB＝4，点P在线段OA上，半圆P与半圆O 相切于点A，点C在半圆P上，CO⊥AB，AC的延长线与半圆O相交于点D，OD与BC相交于点E．（1）求证：AD•AP＝OD•AC；（2）设半圆P的半径为x，线段CD的长为y，求y与x之间的函数解析式，并写出定义域；（3）当点E在半圆P上时，求半圆P的半径．13．如图所示，AC与⊙O相切于点C，线段AO交⊙O于点B．过点B作BD ∥AC交⊙O于点D，连接CD，OC，且OC交DB于点E．若．（1）求∠COB的大小和⊙O的半径长．（2）求由弦CD，BD与弧BC所围成的阴影部分的面积（结果保留π）．14．如图1，▱ABCF的顶点A，B，C在⊙O上，AB＝AC．（1）求证：AF为⊙O的切线；（2）如图2，CF与⊙O交于点E，连接BE．若AB＝BE，CE＝EF，求cos∠BEC的值．15．四边形ABCD内接于⊙O，AB是⊙O的直径，AD＝CD．（1）如图1，求证∠ABC＝2∠ACD；（2）过点D作⊙O的切线，交BC延长线于点P（如图2）．若tan∠CAB ＝，BC＝1，求PD的长．参考答案1．解：（1）在⊙中，OA＝OB＝OC＝OD，∵CE＝DF，∴OC﹣CE＝OD﹣DF，∴OE＝OF，∵AB⊥CD，即AB⊥EF，∴四边形AEBF是菱形．（2）①△OBG是等边三角形．理由如下：∵AB⊥CD，OG⊥EB，∴∠COB＝∠OHB＝90°，∴∠COG＝90°﹣∠BOH＝∠EBO，∵∠COG＝∠EBG，∴∠EBO＝∠EBG，∵BH＝BH，∠BHO＝∠BHG＝90°∴△BHO≌△BHG（ASA）∴OB＝GB，∵OB＝OG，∴OB＝OG＝GB，∴△OBG是等边三角形．②设⊙的半径长为2m，则OC＝OG＝OB＝2m，∵点E是OC的中点，∴OE＝m，∴BE＝＝m；∵∠EOH＝90°﹣∠BOH＝∠EBO，∴＝＝cos∠EBO，∴＝，∴HO＝m，∴GH＝2m﹣m，∴＝＝．2．解：（1）C在AB弧线上，∴∠OBC为锐角，∴∠CBD为钝角，则△BCD是等腰三角形时，仅有BC＝BD这一种情况，∴∠D＝∠BCD，连接OC则OA＝OC＝OB，∴∠OAC＝∠OCA，∠OCD＝∠OBC，∴∠OBC＝∠D+∠BCD＝2∠D，在△OCD中，∠COD+2∠D+2∠D＝180°，∴∠AOC＝m°﹣∠COD＝m°+4∠D﹣180°，∴∠AOC＝×（180°﹣∠AOC）＝180°﹣﹣2∠D，在△AOD中，m°+∠OAC+∠D＝180°，∴180°+﹣∠D＝180°，∴∠D＝；（2）过D作DM⊥AB延长线于M，连接OC，∵C为中点，∴AC＝BC，∴∠BAC＝∠ABC且AO＝CO＝BO，∴∠OAC＝∠OCA＝∠OCB＝∠OBC，∴∠ACO+∠BCO＝×（360°﹣90°）＝135°，∴∠BCD＝45°，∴45°+∠ODA＝∠ABC+∠ABD＝45°+∠ABC，∴∠ABC＝∠ADO＝∠BAC，∴BD＝AB＝2（勾股定理），∴BM＝DM＝2（∠MBD＝∠OBA＝45°，∴BM＝DM），∴AM＝AB+BM＝2+2，∴AN＝AB＝，又∵CN⊥AB，DM⊥AB，∴△ANC∽△AMD，∴，∴＝＝6+4；（3）图2如下：∵E为弧线AEC与OB切点，∴A、E、C在半径为2的另一个圆上，∵O′E＝2，OE＝1，∴OO′＝（勾股定理），又∵OA＝OC＝2，O′A＝O′C＝2，∴四边形AOCO′是菱形，∴AC⊥OO′且AC、OO′互相平分，且∠O′OE共角，∴△O′OE∽△DOP，∴＝且OP＝OO′＝，∴OP＝，∴AP＝＝（Rt△APO′的勾股定理）∴AD＝AP+PD＝．3．解：（1）在矩形ABCD中，CD＝AB＝4，BC＝8，∠BCD＝90°，∴BD＝＝4，∵M为弦BE的中点，P为圆心，∴PM⊥BE，∠BMP＝90°，∵AD∥BC，∴∠PBM＝∠DBC，∴＝＝cos∠DBC，∴＝，∴y＝x，当点G与点A重合时，则点E为BD中点，此时y＝BD＝，由x＝，得x＝，∴y关于x的函数解析式y＝x（≤x＜8）；（2）如图1，当AP∥CE时，则四边形APCG是平行四边形，AG＝PC，∴DG＝BP＝x．由BM＝x，得BE＝x，DE＝4﹣x∵DG∥BC∴△DGE∽△BCE，∴＝＝＝；∴＝，整理，得x2+8x﹣40＝0，解得x 1＝﹣4+2，x2＝﹣4﹣2（不符合题意，舍去）.∴x＝﹣4+2．（3）如图2，若∠PFC＝90°，则点F与点E重合，不符合题意；如图3，当∠PCF＝90°时，则点E与点D重合，此时y＝×4＝2，由x＝2，得x＝5，∴PC＝8﹣5＝3，CF＝CD＝4，∴S△CPF＝×3×4＝6；如图4，当∠CPF＝90°时，过点E作EQ⊥BC交BC的延长线于点Q，在BC边上取一点H，连接DH，使DH＝BH，由图3得，当点E与点D重合时，则点P与图4中的点H重合，此时，CH ＝3，DH＝5，∴CH：CD：DH＝3：4：5，∵∠EPQ＝∠DHC＝2∠DBC，∠Q＝∠DCH＝90°，∴△EPQ∽△DHC，∴PQ：EQ：PE＝3：4：5，∵PE＝BP＝PF＝x，∴EQ＝x，PQ＝x∵PF∥EQ，∴△CPF∽△CQE，∴＝＝＝，∴PC＝PQ＝×x＝x，∴8﹣x＝x，解得x＝6，∴PC＝8﹣6＝2，PF＝6，∴S△CPF＝×2×6＝6．综上所述，△CPF的面积为6．4．（1）证明：连接AC，BC，∵OC＝OA，∴∠OCA＝∠OAC，∵PF是⊙O的切线，CE⊥AB，∴∠OCP＝∠F＝90°，∴AF∥OC，∴∠FAC＝∠OCA，∴∠FAC＝∠OAC，∴CA平分∠FAB．（2）证明：∵CD是直径，∴∠CBD＝90°，∴∠CBP＝90°，∵CE⊥OB，∴∠CEB＝∠CBP＝90°，∵PC切⊙O于点C，∴∠PCB＝∠CAB，∵AB是直径，∴∠ACB＝90°，∴∠ABC+∠CAB＝90°，∠BCE+∠ABC＝90°，∵∠CAB＝∠BCE，∴∠PCB＝∠BCE，∴△BCE∽△PCB，∴，∴BC2＝CE•CP；（3）解：，设CF＝3a，CP＝4a，∵BC2＝CE•CP＝3a•4a＝12a2，∴BC＝2a，在Rt△BCE中，sin∠CBE＝，∴∠CBE＝60°，∴∠BCE＝30°，∴△COB是等边三角形，∵AB＝4，∴OB＝BC＝2，∴劣弧BC的长＝＝π．5．解：（1）CQ与所在圆相切；证明：由旋转知，AP＝AQ，∠PAQ＝120°，∵∠BAC＝120°，∴∠PAQ＝∠BAC，∴∠PAQ﹣∠PAC＝∠BAC﹣∠PAC，∴∠ACQ＝∠ABP，∵AC＝AB，∴△ACQ≌△ABP（SAS），∴∠AQC＝∠APB，∵BP与所在圆相切，∴∠APB＝90°，∴∠AQC＝90°，∵AQ＝AP，∴CQ与所在圆相切；（2）如图，过点A作AN⊥BC于N，∵AB＝AC＝2，∠BAC＝120°，∴∠ABC＝30°，∴AN＝AB＝，∴BN＝AN＝3，①当点F在点G的左边时，过点F作FM⊥AB于M，设FM＝m，在Rt△BMF中，BF＝2m，BM＝m，∴AM＝AB﹣BM＝（2﹣m），在Rt△AMF中，根据勾股定理得，FM2+AM2＝AF2，∴m2+[（2﹣m）]2＝22，∴m＝1或m＝2，∴BF＝2m＝2或4（舍），∴BF＝AF，∴∠BAF＝∠ABC＝30°，∴∠EAF＝90°，∴S扇形EAF＝＝π；②当点F在点G的右边时，同①的方法得，BF＝4，S扇形EAF＝﹣＝；即当BF＝2时，扇形EAF的面积为π，当BF＝4时，扇形EAF的面积为；（3）由（1）知，△ACQ≌△ABP，∴∠ABP＝∠ACQ＝30°，∵∠ABP＝30°，∴点P在BC上，即点P与点F或G重合，当点P与点F重合时，∠PAB＝∠BAF，由（2）知，∠BAF＝30°，∴m＝30，当点P与点G重合时，∠PAB＝∠BAG＝90°，∴m＝90，即m的值为30或90．6．解：（1）连接AO，并延长交BC于点H，∵AB＝AC，∴．∴AH⊥BC．∴AH平分∠BAC．∴∠BAC＝2∠BAH．∵OA＝OB，∴∠ABD＝∠BAH．∴∠BAC＝2∠ABD．（2）过A作AE∥BC，交BD延长线于点E，∵AE∥BC，∴．∵AB＝AC，AH⊥BC，∴BH＝BC．∴．∵AE∥BC，∴．设OB＝OA＝4a，则OH＝3a．∴BH＝．AH＝OA+OH＝7a．∵∠ABD＝∠BAH，∴tan∠ABD＝tan∠BAH＝．7．（1）证明：连接BI，如图1所示：∵点I是△ABC的内心，∴AD平分∠BAC，∴∠BAD＝∠CAD，∠ABI＝∠CBI，∵∠BID＝∠BAI+∠IBA，∠IBD＝∠CBI+∠CBD，∠CBD＝∠CAD，∴∠BID＝∠IBD，∴DI＝DB；（2）解：过点D作DE⊥BC于E，如图2所示：由（1）得：∠BAD＝∠CAD，∴，∴BD＝CD，∵DE⊥BC，∴BE＝CE＝BC＝，∵∠BAC＝60°，∴∠BAD＝∠CAD＝30°，∴∠DBC＝∠BCD＝30°，∴DE＝BE＝1，BD＝2DE＝2，∴DI＝BD＝2．8．解：（1）∵AC为直径，∴∠ADC＝90°（直径所对的圆周角是直角）．故答案为：直径所对的圆周角是直角；（2）∵BD⊥AC，∴∠ABD＝∠CBD＝90°．∴∠BAD+∠ADB＝90°．∵∠ADC＝90°，∴∠CDB+∠ADB＝90°．∴∠BAD＝∠CDB．∴△ABD∽△DBC．∴．∴BD2＝AB•BC＝ab．∴BD＝．∵AB＝a，BC＝b，∴AC＝a+b．∴OD＝．（3）∵BD⊥AC，∴BD＜OD（直线外一点到直线上各点的所有连线中，垂线段最短）．∴＞．故答案为：垂线段最短．9．（1）证明：∵∠ACB＝90°．∴AB是⊙O的直径，∵EA是⊙O的切线，∴BA⊥EA，∴∠EAC+∠CAB＝90°，∵∠B+∠CAB＝90°，∴∠EAC＝∠B，∵AC＝EC，∴∠EAC＝∠E，∴∠E＝∠B，∵∠B＝∠D，∴∠E＝∠D，∴AD＝AE；（2）解：∵∠EAF＝90°，AE＝2，EF＝2，∴AF＝＝2，由（1）知：AD＝AE＝2，∵∠B＝∠E，∠ACB＝∠EAF＝90°，∴△ACB∽△FAE，∴＝，∴AB＝AC，如图，过点A作AG⊥CD于点G，设AC＝EC＝t，则CF＝2﹣t，∵tan∠E＝＝，sin∠E＝＝＝，∴AG＝，∴FG＝＝，∴EG＝EC+CG，∴CG＝CF﹣FG＝2﹣t﹣＝﹣t，∵AC2＝AG2+CG2，∴t2＝（）2+（﹣t）2，解得t＝，∴AB＝AC＝t＝3．∴⊙O的直径是3．10．解：（1）如图1中，∵点O在PA上，PQ是⊙O的切线，∴PQ⊥AP，∵cot∠PAQ＝＝，∴可以假设PA＝3k，PQ＝4k，则AQ＝5k＝15，∴k＝3，∴PA＝9，PQ＝12，∴⊙O的半径为．（2）如图2﹣1中，当点O在射线AB的上方时，过点Q作QK⊥AB于K，过点O作OH⊥AB于H．∵PQ是⊙O的切线，∴∠PHO＝∠OPQ＝∠PKQ＝90°，∴∠OPH+∠QPK＝90°，∠QPK+∠PQK＝90°，∴△PHO∽△QKP，∴＝，设PA＝2m，则AH＝PH＝m，PK＝9﹣2m，∴＝，解得，m＝或﹣3，经检验，x＝是分式方程的解，且符合题意．∴AP＝3．如图2﹣2中，当点O在射线AB的下方时，同法可得AP＝．综上所述，满足条件的AP的值为3或．（3）如图3﹣1中，当⊙P与⊙O内切时，由△PHO∽△QKP，可得＝＝，∵OH⊥AP，∴AH＝PH，∴AP＝2PH，QK＝2PH，∴PA＝QK＝12，如图3﹣2中，当⊙O与AC相切于点A时，∵∠OAQ＝∠OPQ＝90°，OQ＝OQ，OA＝OP，∴Rt△OAQ≌Rt△OPQ（HL），∴AQ＝PQ，∵OA＝OP，∴OQ垂直平分线段AP，∴AP＝2AH＝18，观察图像可知：当⊙O与⊙P内含时，0＜AP＜12．当⊙O与⊙P内切时，AP＝12．当⊙O与⊙P相交时，12＜AP＜18．11．解：（1）如图1中，∵∠COD＝90°，cot∠ODC＝＝，∴可以假设OD＝3k，OC＝4k，则CD＝5k，∵以CD为半径的圆D与圆O相切，∴CD＝DB＝5k，∴OB＝OC＝8k，∴AC＝OC＝4k＝2，∴k＝，∴CD＝．（2）如图2中，连接OP，过点P作PE⊥OA于E，PF⊥OB于F．∵＝，∴∠AOP＝∠POB，∵PE⊥OA，PF⊥OB，∴PE＝PF，∵∠PEC＝∠PFB＝90°，PD＝PC，∴Rt△PEC≌Rt△PFB（HL），∴∠EPC＝∠FPB，∵∠PEO＝∠EOF＝∠OFP＝90°，∴∠EPF＝90°，∴∠EPF＝∠CPB＝90°，∴∠PCB＝∠PBC＝45°，∵OP＝OB，∠POB＝45°，∴∠OBP＝∠OPB＝67.5°，∴∠CBO＝67.5°﹣45°＝22.5°，∴∠OCD＝90°﹣22.5°＝67.5°．（3）如图3﹣1中，当OC∥PD时，∵OC∥PD，∴∠PDO＝∠AOD＝90°，∵CE⊥PD，∴∠CED＝90°，∴四边形OCED是矩形，∴OC＝DE＝2，CE＝OD，设PC＝PD＝x，EC＝OD＝y，则有，可得x＝2﹣2（不合题意的已经舍弃），∴PD＝2﹣2，∴＝＝﹣1．如图3﹣2中，当PC∥OD时，∵PC∥OD，∴∠COD＝∠OCE＝∠CED＝90°，∴四边形OCED是矩形，∴OC＝DE＝2，CE＝OD，∵OP＝4，OC＝2，∴PC＝＝＝2，∴PD＝PC＝2，∴PE＝＝＝2，∴EC＝OD＝2﹣2，∴＝＝＝3+，综上所述，的值为﹣1或3+．12．解：（1）连接CP，如图：∵AP＝CP，AO＝DO，∴∠A＝∠ACP＝∠ADO，∴△ACP∽△ADO，∴，∴AD•CP＝OD•AC，∴AD•AP＝OD•AC；（2）∵半圆O的直径AB＝4，∴AO＝2，∵半圆P的半径为x，∴OP＝2﹣x，∵CO⊥AB，∴∠COP＝90°，∴CO2＝CP2﹣OP2＝x2﹣（2﹣x）2＝4x﹣4，Rt△AOC中，AC＝＝2，∵∠A＝∠ACP＝∠ADO，∴CP∥DO，∴，又线段CD的长为y，∴，变形得：y＝，x范围是0＜x≤2；（3）设半圆P与AB交于G，连接EG，过E作EH⊥AB于H，如图：设半圆P的半径为x，由（2）知AC＝2，∵CO⊥AB，∴BC＝AC＝2，∵CP∥DO，∴，而OB＝2，PB＝4﹣x，∴，∴BE＝，∵点E在半圆P上，∴∠EGB＝∠ACB，且∠B＝∠B，∴△CAB∽△GEB，∴＝，∴，∴EG＝，∵AC＝BC，∴EG＝BG，而BG＝AB﹣AG＝4﹣2x，∴＝4﹣2x，解得x＝或（大于2，舍去），∴半圆P的半径为x＝．13．解：（1）∵AC与⊙O相切于点C，∴∠ACO＝90°∵BD∥AC，∴∠BEO＝∠ACO＝90°，∴DE＝EB＝BD＝（cm），∵∠D＝30°，∴∠O＝2∠D＝60°，在Rt△BEO中，sin60°＝，∴＝，∴OB＝5，故⊙O的半径长为5cm；（2）由（1）可知，∠O＝60°，∠BEO＝90°，∴∠EBO＝∠D＝30°∵∠CED＝∠BEO，BE＝ED，，∴△CDE≌△OBE（ASA），∴S阴影＝S扇形＝＝（cm2）．答：阴影部分的面积为cm2．14．（1）证明：连接OB，OC，OA，延长AO交BC于点D，∵AB＝AC，OB＝OC，∴AD⊥BC，∴∠ADB＝90°，∵四边形ABCF为平行四边形，∴AF∥BC，∴∠FAO＝∠ADB＝90°，∴AF为⊙O的切线；（2）解：连接AE，过点B作BH⊥FC，交FC的延长线于点H，∵四边形ABCF为平行四边形，∴AF＝BC，AF∥BC，∴∠FAC＝∠ACB，∵AB＝AC，∴∠ABC＝∠ACB，∵∠AEC+∠AEF＝180°，∠AEC+∠ABC＝180°，∴∠AEF＝∠ABC＝∠ACB＝∠FAC，∵∠F＝∠F，∴△FAE∽△FCA，∴，∴AF2＝FE•FC，设CE＝EF＝1，CH＝x，∴AF2＝2，∴AF＝，∴CF＝AB＝AC＝BE＝2，BC＝，∵BH2＝BC2﹣CH2＝BE2﹣EH2，∴，解得，x＝，∴EH＝，∴cos∠BEC＝＝．15．解：（1）证明：∵AD＝CD，∴∠DAC＝∠ACD，∴∠ADC+2∠ACD＝180°，∵四边形ABCD内接于⊙O，∴∠ABC+∠ADC＝180°，∴∠ABC＝2∠ACD，（2）连接OD交AC于E，如图：∵PD为⊙O切线，∴OD⊥DP，∵AD＝CD，∴弧AD＝弧CD，∴OD⊥AC，AE＝CE，∵∠DEC＝90°，∵AB为直径，∴∠ACB＝90°，∴∠ECP＝90°，∴四边形DECP是矩形，∴DP＝EC，∵tan∠CAB＝，BC＝1，∴＝＝，∴AC＝，∴EC＝AC＝．。

上海进才中学数学初中九年级平行四边形选择题易错题压轴难题综合训练一、易错压轴选择题精选：平行四边形选择题1．如图，在平行四边形ABCD 中，按以下步骤作图：①以A 为圆心，AB 长为半径画弧，交边AD 于点；②再分别以B ，F 为圆心画弧，两弧交于平行四边形ABCD 内部的点G 处；③连接AG 并延长交BC 于点E ，连接BF ，若BF ＝3，AB ＝2.5，则AE 的长为（ ）A ．2B ．4C ．8D ．52．如图，点O 为正方形ABCD 的中心，BE 平分∠DBC 交DC 于点E ，延长BC 到点F ，使FC=EC ，连结DF 交BE 的延长线于点H ，连结OH 交DC 于点G ，连结HC ．则以下四个结论中：①OH ∥BF ，②GH=14BC ，③BF=2OD ，④∠CHF=45°．正确结论的个数为( )A ．4个B ．3个C ．2个D ．1个3．如图，矩形ABCD 的面积为20cm 2，对角线相交于点O ．以AB 、AO 为邻边画平行四边形AOC 1B ，对角线相交于点O ；以AB 、AO 为邻边画平行四边形AO 1C 2B ，对角线相交于点O 2 ：……以此类推，则平行四边形AO 4C 5B 的面积为（ ）A ．58cm 2B ．54cm 2C ．516cm 2D ． 5 32cm 2 4．如图，矩形ABCD 中，O 为AC 的中点，过点O 的直线分别与AB 、CD 交于点E 、F ，连接BF 交AC 于点M ，连接DE 、BO ．若60COB ∠=︒，2FO FC ==，则下列结论：①FB OC ⊥；②EOB CMB △≌△；③四边形EBFD 是菱形；④23MB =( )A ．1个B ．2个C ．3个D ．4个5．如图，在ABC 中，AB=5，AC=12，BC=13，P 为边BC 上一动点，PE ⊥AB 于E ，PF ⊥AC 于F ，M 为EF 中点，则AM 的最小值为（ ）A ．6013B ．3013C ．2413D ．12136．如图，在菱形ABCD 中，AB=AC=1，点E 、F 分别为边AB 、BC 上的点，且AE=BF ，连接CE 、AF 交于点H ，连接DH 交AC 于点O ，则下列结论：①△ABF ≌△CAE ；②∠FHC=∠B ；③△ADO ≌△ACH ；④=3ABCD S 菱形；其中正确的结论个数是（ ）A ．1个B ．2个C ．3个D ．4个 7．如图，正方形ABCD 的边长为10，AG=CH=8，BG=DH=6，连接GH ，则线段GH 的长为（ ）A ．2.8B ．22C ．2.4D ．3.58．如图，ABCD 的对角线,AC BD 交于点,O DE 平分ADC ∠交BC 于点,60,E BCD ∠=︒2,AD AB =连接OE ．下列结论：ABCD SAB BD =⋅①；DB ②平分ADE ∠；AB DE =③；CDE BOC S S =④，其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个9．如图，正方形ABCD 中，延长CB 至E 使2CB EB =，以EB 为边作正方形EFGB ，延长FG 交DC 于M ，连接AM ，AF ，H 为AD 的中点，连接FH 分别与AB ，AM 交于点,N K ．则下列说法：①ANH GNF △≌△；②DAM NFG ∠=∠；③2FN NK =；④:2:7AFN DMKH S S =△四边形．其中正确的有（ ）A ．4个B ．3个C ．2个D ．1个10．已知，如图，在菱形ABCD 中．（1）分别以C ，D 为圆心，大于12CD 长为半径作弧，两弧分别交于点E ，F ；（2）作直线EF ，且直线EF 恰好经过点A ，且与边CD 交于点M ；（3）连接BM ．根据以上作图过程及所作图形，判断下列结论中错误．．的是（ ）A ．∠ABC =60°B ．如果AB =2，那么BM =4C ．BC =2CMD ．2ABM ADM S S =△△11．如图的△ABC 中，AB>AC>BC,且D 为BC 上一点．现打算在AB 上找一点P ,在AC 上找一点Q,使得△APQ 与以P 、D 、Q 为顶点的三角形全等，以下是甲、乙两人的作法： 甲：连接AD,作AD 的中垂线分别交AB 、AC 于P 点、Q 点，则P 、Q 两点即为所求； 乙：过D 作与AC 平行的直线交AB 于P 点，过D 作与AB 平行的直线交AC 于Q 点，则P 、Q 两点即为所求；对于甲、乙两人的作法，下列判断何者正确（ ）A ．两人皆正确B ．两人皆错误C ．甲正确，乙错误D ．甲错误乙正确12．如图，正方形ABCD 和正方形CEFG 中，点D 在CG 上，BC ＝1，CE ＝3，H 是AF 的中点，那么CH 的长是（ ）A ．2B ．52C ．332D ．5 13．如图，Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，D 是AB 上一动点，过点D 作DE ⊥AC 于点E ，DF ⊥BC 于点F ，连结EF ，则线段EF 的长的最小值是( )A ．2.5B ．2.4C ．2.2D ．2 14．如图，四边形ABCD 为平行四边形，D ∠为锐角，BAD ∠的平分线AE 交CD 于点F ，交BC 的延长线于点E ，且AF FE =．若25AB =，ABCD 面积为300，则AF 的长度为（ ）A ．30B ．15C ．40D ．2015．如图，在菱形ABCD 中，若E 为对角线AC 上一点，且CE CD =，连接DE ，若5,8AB AC ==，则DE AD=（ ）A ．104B 10C ．35D ．4516．如图，在△ABC 中，AB=3，AC=4，BC=5，P 为边 BC 上一动点，PE ⊥AB 于 E ，PF ⊥AC 于 F ，M 为 EF 中点，则 AM 的最小值为（ ）A ．1B ．1.3C ．1.2D ．1.517．如图，平行四边形ABCD 中，对角线AC 、BD 相交于点O ，AD ＝12AC ，M 、N 、P 分别是OA 、OB 、CD 的中点，下列结论：①CN ⊥BD ；②MN ＝NP ；③四边形MNCP 是菱形；④ND 平分∠PNM ．其中正确的有（ ）A ．1 个B ．2 个C ．3 个D ．4 个 18．如图，点O （0，0），A （0，1）是正方形1OAA B 的两个顶点，以1OA 对角线为边作正方形121OA A B ，再以正方形的对角线2OA 作正方形121OA A B ，…，依此规律，则点8A 的坐标是（ ）A ．（－8，0）B ．（0，8）C ．（0，2D ．（0，16）19．如图，在△ABC 中，∠ABC 和∠ACB 的角平分线相交于点O ．过点O 作EF ∥BC 交AB 于E ．交AC 于F ．过点O 作OD ⊥AC 于D ．下列五个结论：其中正确的有（ ）（1） EF=BE+CF ； （2）∠BOC=90°+12∠A ；（3）点O 到△ABC 各边的距离都相等；（4）设OD=m ．若AE 十AF =n ，则S △AEF = mn ；（5）S △AEF=S △FOC ．A ．2个B ．3个C ．4个D ．5个20．如图，矩形ABCD 中，O 为AC 中点，过点O 的直线分别与AB ，CD 交于点E ，F ，连接BF 交AC 于点M ，连接DE ，BO ．若60COB ∠=，FO FC =，则下列结论：①FB OC ⊥，OM CM =；②EOB CMB ≅；③四边形EBFD 是菱形；④:3:2MB OE =．其中正确结论的个数是（ ）A ．1B ．2C ．3D ．4【参考答案】***试卷处理标记，请不要删除一、易错压轴选择题精选：平行四边形选择题1．B【分析】连接EF ，先证AF =AB =BE ，得四边形ABEF 是菱形，据此知AE 与BF 互相垂直平分，继而得OB 的长，由勾股定理求得OA 的长，继而得出答案．【详解】由题意得：AF =AB ，AE 为∠BAD 的角平分线，则∠BAE =∠FAE ．又∵四边形ABCD 是平行四边形，则AD ∥BC ，∠BAE =∠FAE =∠BEA ，∴AF =AB =BE ． 连接EF ，则四边形ABEF 是菱形，∴AE 与BF 互相垂直平分，设AE 与BF 相交于点O ，OB 2BF ==1.5．在Rt △AOB 中，OA 22222515AB OB =-=-=．．2，则AE =2OA =4．故选B．【点睛】本题考查了作图﹣复杂作图，解题的关键是掌握菱形的性质与判定，平行四边形的性质，角平分线的尺规作图方法等．2．B【分析】①只要证明OH是△DBF的中位线即可得出结论；②根据OH是△BFD的中位线，得出GH=12CF，由GH＜14BC，可得出结论；③易证得△ODH是等腰三角形，继而证得OD=12 BF；④根据四边形ABCD是正方形，BE是∠DBC的平分线可求出Rt△BCE≌Rt△DCF，再由∠EBC=22.5°即可求出结论．【详解】解：∵EC=CF，∠BCE=∠DCF，BC=DC，∴△BCE≌△DCF，∴∠CBE=∠CDF，∵∠CBE+∠BEC=90°，∠BEC=∠DEH，∴∠DEH+∠CDF=90°，∴∠BHD=∠BHF=90°，∵BH=BH，∠HBD=∠HBF，∴△BHD≌△BHF，∴DH=HF，∵OD=OB∴OH是△DBF的中位线∴OH∥BF；故①正确；∴OH=12BF，∠DOH=∠CBD=45°，∵OH是△BFD的中位线，∴DG=CG=12BC，GH=12CF，∵CE=CF，∴GH=12CF=12CE∵CE＜CG=12 BC，∴GH＜14BC，故②错误．∵四边形ABCD是正方形，BE是∠DBC的平分线，∴BC=CD，∠BCD=∠DCF，∠EBC=22.5°，∵CE=CF，∴Rt△BCE≌Rt△DCF（SAS），∴∠EBC=∠CDF=22.5°，∴∠BFH=90°-∠CDF=90°-22.5°=67.5°，∵OH是△DBF的中位线，CD⊥AF，∴OH是CD的垂直平分线，∴DH=CH，∴∠CDF=∠DCH=22.5°，∴∠HCF=90°-∠DCH=90°-22.5°=67.5°，∴∠CHF=180°-∠HCF-∠BFH=180°-67.5°-67.5°=45°，故④正确；∴∠ODH=∠BDC+∠CDF=67.5°，∴∠OHD=180°-∠ODH-∠DOH=67.5°，∴∠ODH=∠OHD，∴OD=OH=12BF；故③正确．故选：B．【点睛】此题考查了全等三角形的判定和性质、等腰三角形的判定与性质以及正方形的性质．解答此题的关键是作出辅助线，构造等腰直角三角形，利用等腰直角三角形的性质结合角平分线的性质逐步解答．3．A【分析】设矩形ABCD的面积为S=20cm2，由O为矩形ABCD的对角线的交点，可得平行四边形AOC1B底边AB上的高等于BC的12，依此类推可得下一个图形的面积是上一个图形的面积的12，然后求解即可．【详解】设矩形ABCD的面积为S=20cm2，∵O为矩形ABCD的对角线的交点，∴平行四边形AOC 1B 底边AB 上的高等于BC 的12， ∴平行四边形AOC 1B 的面积=12S ， ∵平行四边形AOC 1B 的对角线交于点O 1，∴平行四边形AO 1C 2B 的边AB 上的高等于平行四边形AOC 1B 底边AB 上的高的12， ∴平行四边形AO 1C 2B 的面积=12×12S=22S ， ……依此类推，平行四边形AO 4C 5B 的面积=52S =5202=58（cm 2）， 故选：A ．【点睛】本题考查了矩形的对角线互相平分，平行四边形的对角线互相平分的性质，得到下一个图形的面积是上一个图形的面积的12是解题的关键． 4．B【分析】连接BD ，先证明△BOC 是等边三角形，得出BO=BC ，又FO=FC ，从而可得出FB ⊥OC ，故①正确；因为△EOB ≌△FOB ≌△FCB ，故△EOB 不会全等于△CBM ，故②错误；再证明四边形EBFD 是平行四边形，由OB ⊥EF 推出四边形EBFD 是菱形，故③正确；先在Rt △BCF 中，可求出BC 的长，再在Rt △BCM 中求出BM 的长，从而可知④错误，最后可得到答案．【详解】解：连接BD ，∵四边形ABCD 是矩形，∴AC=BD ，AC 、BD 互相平分，∵O 为AC 中点，∴BD 也过O 点，∴OB=OC ，∵∠COB=60°，∴△OBC 是等边三角形，∴OB=BC ，又FO=FC ，BF=BF ，∴△OBF ≌△CBF （SSS ），∴△OBF 与△CBF 关于直线BF 对称，∴FB ⊥OC ，∴①正确；∵∠OBC=60°，∴∠ABO=30°，∵△OBF≌△CBF，∴∠OBM=∠CBM=30°，∴∠ABO=∠OBF，∵AB∥CD，∴∠OCF=∠OAE，∵OA=OC，易证△AOE≌△COF，∴OE=OF，∵OB=OD，∴四边形EBFD是平行四边形．又∠EBO=∠OBF，OE=OF，∴OB⊥EF，∴四边形EBFD是菱形，∴③正确；∵由①②知△EOB≌△FOB≌△FCB，∴△EOB≌△CMB错误，∴②错误；∵FC=2，∠OBC=60°，∠OBF=∠CBF，∴∠CBF=30°，∴BF=2CF=4，∴3∴CM=123BM=3，故④错误．综上可知其中正确结论的个数是2个．故选：B．【点睛】本题考查矩形的性质、菱形的判定、等边三角形的判定和性质、全等三角形的判定和性质、含30°的直角三角形的性质以及勾股定理等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．5．B【分析】先求证四边形AFPE是矩形，再根据直线外一点到直线上任一点的距离，垂线段最短，利用面积法可求得AP最短时的长，然后即可求出AM最短时的长．【详解】解：连接AP，在ABC中，AB＝5，AC＝12，BC＝13，∴AB2+AC2＝BC2，∴∠BAC＝90°，∵PE⊥AB，PF⊥AC，∴四边形AFPE是矩形，∴EF＝AP．∵M是EF的中点，∴AM＝12 AP，根据直线外一点到直线上任一点的距离，垂线段最短，即AP⊥BC时，AP最短，同样AM也最短，∴S△ABC＝1122BC AP AB AC⋅=⋅，∴1113512 22AP⨯=⨯⨯，∴AP最短时，AP＝60 13，∴当AM最短时，AM＝12AP＝3013．故选：B．【点睛】此题主要考查学生对勾股定理逆定理的应用、矩形的判定和性质、垂线段最短和直角三角形斜边上的中线的理解和掌握，此题涉及到动点问题，有一定难度．6．B【分析】根据菱形的性质，利用SAS证明即可判断①；根据△ABF≌△CAE得到∠BAF=∠ACE，再利用外角的性质以及菱形内角度数即可判断②；通过说明∠CAH≠∠DAO，判断△ADO≌△ACH不成立，可判断③；再利用菱形边长即可求出菱形面积，可判断④.【详解】解：∵在菱形ABCD中，AB=AC=1，∴△ABC为等边三角形，∴∠B=∠CAE=60°，又∵AE=BF，∴△ABF≌△CAE（SAS），故①正确；∴∠BAF=∠ACE，∴∠FHC=∠ACE+∠HAC=∠BAF+∠HAC=60°，故②正确；∵∠B=∠CAE=60°，则在△ADO和△ACH中，∠OAD=60°=∠CAB，∴∠CAH≠60°，即∠CAH≠∠DAO，∴△ADO≌△ACH不成立，故③错误；∵AB=AC=1，过点A作AG⊥BC，垂足为G，∴∠BAG=30°，BG=12， ∴AG=22AB BG -=3, ∴菱形ABCD 的面积为：BC AG ⨯=312⨯=32，故④错误； 故正确的结论有2个，故选B.【点睛】本题考查了全等三角形判定和性质，菱形的性质和面积，等边三角形的判定和性质，外角的性质，解题的关键是利用菱形的性质证明全等.7．B【分析】延长BG 交CH 于点E ，根据正方形的性质证明△ABG ≌△CDH ≌△BCE ，可得GE=BE-BG=2，HE=CH-CE=2，∠HEG=90°，从而由勾股定理可得GH 的长．【详解】解：如图，延长BG 交CH 于点E ，∵四边形ABCD 是正方形，∴∠ABC=90°，AB=CD=10，∵AG=8，BG=6，∴AG 2+BG 2=AB 2，∴∠AGB=90°，∴∠1+∠2=90°，又∵∠2+∠3=90°，∴∠1=∠3，同理：∠4=∠6，在△ABG 和△CDH 中，AB＝CD＝10AG＝CH＝8BG＝DH＝6∴△ABG≌△CDH（SSS），∴∠1=∠5，∠2=∠6，∴∠2=∠4，在△ABG和△BCE中，∵∠1＝∠3，AB＝BC，∠2＝∠4，∴△ABG≌△BCE（ASA），∴BE=AG=8，CE=BG=6，∠BEC=∠AGB=90°，∴GE=BE－BG=8－6=2，同理可得HE=2，在Rt△GHE中，GH=故选：B．【点睛】本题主要考查正方形的性质、全等三角形的判定与性质、勾股定理及其逆定理的综合运用，通过证三角形全等得出△GHE为直角三角形且能够求出两条直角边的长是解题的关键．8．D【分析】求得∠ADB＝90°，即AD⊥BD，即可得到S▱ABCD＝AD•BD；依据∠CDE＝60°，∠BDE＝30°，可得∠CDB＝∠BDE，进而得出DB平分∠CDE；依据Rt△BCD中，斜边上的中线DE＝斜边BC的一半，即可得到AD＝BC＝2DE，进而得到AB＝DE；依据OE是中位线，即可得到OE∥CD，因为两平行线间的距离相等，进而得到S△CDE＝S△OCD，再根据OC是△BCD的中线，可得S△BOC＝S△COD，即可得到S△CDE＝S△BOC．【详解】∵∠BCD＝60°，四边形ABCD是平行四边形，∴∠ADC＝180°－∠BCD＝120°，BC//AD，BC＝AD，∵DE平分∠ADC，∴∠CDE＝∠CED＝60°＝∠BCD，∴△CDE是等边三角形，∴CE＝CD＝ AD＝ BC，∴E是BC的中点，∴DE＝BE，∴∠BDE＝∠CED＝30°，∴∠CDB＝90°，即CD⊥BD，∴S▱ABCD＝CD•BD＝AB•BD，故①正确；∵∠CDE＝60°，∠BDE＝30°，∴∠ADB ＝30°＝∠BDE ，∴DB 平分∠CDE ，故②正确；∵△CDE 是等边三角形，∴DE ＝CD ＝AB ，故③正确；∵O 是BD 的中点，E 是BC 的中点，∴OE 是△CBD 的中位线，∴OE ∥CD ，∴S △OCD ＝S △CDE ，∵OC 是△BCD 的中线，∴S △BOC ＝S △COD ，∴S △CDE ＝S △BOC ，故④正确，故选D ．【点睛】本题考查了平行四边形的性质、等边三角形的判定与性质、三角形中位线、平行线间的距离相等、直角三角形斜边上的中线等于斜边的一半等，综合性较强，熟练掌握和灵活运用相关性质与定理是解题的关键.9．A【分析】根据正方形的性质，以及中点的性质可得△FGN ≌△HAN ，即证①；利用角度之间的等量关系的转换可以判断②；根据△AKH ∽△MKF ，进而利用相似三角形的性质即可判断③；设AN=12AG=x ，则AH=2x ，FM=6x ，根据△AKH ∽△MKF 得出2163AH x MF x ==，再利用三角形的面积公式求出△AFN 的面积，再利用DHKM ADM AKH S SS =-即可求出四边形DHKM的面积，作比即可判断④．【详解】 ∵四边形EFGB 是正方形，CE=2EB ，四边形ABCD 是正方形∴G 为AB 中点，∠FGN=∠HAN=90°，AD=AB即FG=AG=GB=12AB 又H 是AD 的中点 AH=12AD ∴FG=HA又∠FNG=∠HNA∴△FGN ≌△HAN ，故①正确；∵∠DAM+∠GAM=90°又∠NFG+∠FNG=90°即∠FNG=∠GAM∵∠FNG+∠NFG+90°=180°∠AMD+∠DAM+90°=180°∠FNG=∠GAM=∠AMD∴DAM NFG ∠=∠，故②正确；由图可得：MF=FG+MG=3EB△AKH ∽△MKF ∴13KH AH KF MF == ∴KF=3KH又∵NH=NF且FH=KF+KH=4KH=NH+NF∴NH=NF=2KH∴KH=KN∴FN=2NK ，故③正确；∵AN=GN 且AN+GN=AG∴可设AN=12AG=x ，则AH=2x ，FM=6x 由题意可得：△AKH ∽△MKF 且相似比为：2163AH x MF x == ∴△AKH 以AH 为底边的高为：11242x x ⨯= ∴212AFN S AN FG x =⨯⨯= 112225DHKM ADM AKH S S S AD DM AH x =-=⨯⨯-⨯⨯ 211172422222x x x x x =⨯⨯-⨯⨯= ∴2:7AFN DHKM S S =，故④正确； 故答案选择A ．【点睛】本题考查了矩形、全等三角形的判定与性质以及相似三角形的判定与性质，难度较大，需要熟练掌握相关基础知识．10．B【分析】连接AC ，根据线段重直平分线的性质及菱形的性质即可判断A 选项正确；根据线段垂直平分线的性质及菱形的性质求出∠BAM=90°，利用三角函数求出AM ，即可利用勾股定理求出BM ，由此判断B 选项；根据线段垂直平分的性质和菱形的性质可得BC=2CM ，由此判断C 选项；利用同底等高的性质证明△ABM 的面积=△ABC 的面积=△ACD 的面积，再利用线段垂直平分线的性质即可判断D 选项．【详解】如图，连接AC ，由题意知：EF 垂直平分CD ，∴AC=CD ，∵四边形ABCD 是菱形，∴AD=AB=BC=CD ，∴AC=AD=CD=AB=BC ，∴△ABC 和△ACD 都是等边三角形，∴∠BAC=∠CAD=∠ABC=60°，故A 正确；∵AM 垂直平分CD ，∴∠CAM=∠DAM=30°，∴∠BAM=90°，∴S △ABM =S △ABC =S △ABD =2S △ADM ，故D 项正确；∵AB=2，∴AC=CD=2，∴AM=AC ·cos30°=233 ∴22AB AM +()222+37B 项错误；由AM 垂直平分CD 可得CM=12CD ， 又∵BC=CD ，∴CM=12BC ，即BC=2CM ，故C 项正确； 故选：B ．【点睛】本题考查线段垂直平分线的作图，线段垂直平分线的性质，等边三角形的判定及性质，菱形的性质，三角函数，勾股定理，是一道综合题，掌握知识点是解题关键．11．A【分析】如图1，根据线段垂直平分线的性质得到PA=PD ，QA=QD ，则根据"SSS"可判断APQ ≌DPQ ，则可对甲进行判断；如图2，根据平行四边形的判定方法先证明四边形APDQ 为平行四边形，则根据平行四边形的性质得到PA=DQ ，PD=AQ ， 则根据"SSS"可判断△APQ ≌△DQP ,则可对乙进行判断.【详解】解：如图1，∵PQ垂直平分AD，∴PA= PD,，QA= QD，∵PQ= PQ，∴△APQ≌△DPQ (SSS)，所以甲正确；如图2，∵PD ∥AQ，DQ ∥AP，∴四边形APDQ为平行四达形，∴PA=DQ,，PD=AQ，∵PQ=QP，∴△APQ≌△DQP (SSS)，所以乙正确；故选：A.【点睛】本题考查了作图-复杂作图，复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法，解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作，也考查了线段垂直平分线的性质、平行四边形的判定与性质和三角形全等的判定.12．D【分析】根据正方形的性质得到AB=BC=1，CE=EF=3，∠E=90°，延长AD交EF于M，连接AC、CF，求出∠ACF=90°，得到CH=12AF，根据勾股定理求出AF的长度即可得到答案.【详解】∵正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，∴AB=BC=1，CE=EF=3，∠E=90°，延长AD交EF于M，连接AC、CF，则AM=BC+CE=1+3=4，FM=EF-AB=3-1=2，∠AMF=90°，∵四边形ABCD和四边形GCEF是正方形，∴∠ACD=∠GCF=45°，∴∠ACF=90°，∵H为AF的中点，∴CH=12 AF，在Rt△AMF中，由勾股定理得：AF=22224225AM MF+=+=，∴CH=5，故选：D．【点睛】此题考查了正方形的性质，勾股定理，直角三角形斜边上的中线等于斜边一半的性质，正确引出辅助线得到∠ACF=90°是解题的关键.13．B【分析】连接CD，利用勾股定理列式求出AB，判断出四边形CFDE是矩形，根据矩形的对角线相等可得EF=CD，再根据垂线段最短可得CD⊥AB时，线段EF的值最小，然后根据三角形的面积公式列出方程求解即可.【详解】如图，连结CD.∵∠ACB＝90°，AC＝3，BC＝4，∴AB22AC BC+5.∵DE⊥AC，DF⊥BC，∠ACB＝90°，∴四边形CFDE是矩形，∴EF＝CD.由垂线段最短可得CD⊥AB时，线段EF的长最小，此时，S△ABC＝12BC·AC＝12AB·CD，即12×4×3＝12×5·CD，解得CD＝2.4，∴EF＝2.4.故选B.【点睛】本题考查了矩形的判定与性质，垂线段最短的性质，勾股定理，判断出CD⊥AB时，线段EF的值最小是解题的关键，难点在于利用三角形的面积列出方程．14．B【分析】由题意先根据ASA 证明△ADF ≌△ECF ，推出300ABE ABCD S S ==，再证明BE=AB=25，根据等腰三角形三线合一的性质得出BF ⊥AE ．设AF=x ，BF=y ，由∠ABF ＜∠BAF 可得x ＜y ，进而根据勾股定理以及△ABE 的面积为300列出方程组并解出即可．【详解】解：∵四边形ABCD 为平行四边形，∴AD//BC 即AD//BE ，AB//CD ，∴∠DAF=∠E ．在△ADF 与△ECF 中，DAF E AF EFAFD EFC ⎧⎪⎨⎪∠∠∠⎩∠＝＝＝， ∴△ADF ≌△ECF （ASA ），∴ADF ECF S S =△△，∴300ABE ABCD S S ==．∵AE 平分∠BAD ，∴∠BAE=∠DAF ，∵∠DAF=∠E ，∴∠BAE=∠E ，∴BE=AB=25，∵AF=FE ，∴BF ⊥AE ．设AF=x ，BF=y ，∵∠D 为锐角，∴∠DAB=180°-∠D 是钝角，∴∠D ＜∠DAB ， ∴12∠ABC ＜12∠DAB ， ∴∠ABF ＜∠BAF ，∴AF ＜BF ，x ＜y ． 则有22222520013x y x y ⎧+⎪⎨⎪⎩＝＝，解得：1520x y ⎧⎨⎩＝＝或2015x y ＝＝（舍去）， 即AF=15．故选：B ．【点睛】本题考查平行四边形的性质以及全等三角形的判定与性质和等腰三角形的性质和勾股定理等知识．由题意证明出300ABE ABCD SS ==以及BF ⊥AE 是解题的关键．15．B【分析】 连接BD ，与AC 相交于点O ，则AC ⊥BD ，142AO AC ==，由5AD AB ==，根据勾股定理求出DO ，求出EO ，由勾股定理求出DE ，即可得到答案.【详解】解：连接BD ，与AC 相交于点O ，则AC ⊥BD ，在菱形ABCD 中，142AO AC ==， ∵5AD AB CD ===， 在Rt △AOD 中，由勾股定理，得：22543DO =-=，∵=5CE CD =，8AC =，∴853AE =-=，∴431OE =-=，在Rt △ODE 中，由勾股定理，得223110DE +∴10DE AD =. 故选：B.【点睛】 本题考查了菱形的性质，勾股定理，以及线段的和差关系，解题的关键是正确作出辅助线，利用勾股定理求出DE 的长度.16．C【分析】首先证明四边形AEPF 为矩形，可得AM=12AP ，最后利用垂线段最短确定AP 的位置，利用面积相等求出AP 的长，即可得AM.【详解】在△ABC 中，因为AB 2+AC 2=BC 2，所以△ABC 为直角三角形，∠A=90°，又因为PE ⊥AB ，PF ⊥AC ，故四边形AEPF为矩形，因为M 为 EF 中点，所以M 也是 AP中点，即AM=12 AP，故当AP⊥BC时，AP有最小值，此时AM最小，由1122ABCS AB AC BC AP=⨯⨯=⨯⨯，可得AP=125，AM=12AP=61.25=故本题正确答案为C.【点睛】本题考查了矩形的判定和性质,确定出AP⊥BC时AM最小是解题关键.17．C【分析】证出OC＝BC，由等腰三角形的性质得CN⊥BD，①正确；证出MN是△AOB的中位线，得MN∥AB，MN＝12AB，由直角三角形的性质得NP＝12CD，则MN＝NP，②正确；周长四边形MNCP是平行四边形，无法证明四边形MNCP是菱形；③错误；由平行线的性质和等腰三角形的性质证出∠MND＝∠PND，则ND平分∠PNM，④正确；即可得出结论．【详解】解：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，BC＝AD，OA＝OC＝12 AC，∵AD＝12 AC，∴OC＝BC，∵N是OB的中点，∴CN⊥BD，①正确；∵M、N分别是OA、OB的中点，∴MN是△AOB的中位线，∴MN∥AB，MN＝12 AB，∵CN⊥BD，∴∠CND＝90°，∵P是CD的中点，∴NP＝12CD＝PD＝PC，∴MN＝NP，②正确；∵MN∥AB，AB∥CD，∴MN∥CD，又∵NP ＝PC ，MN ＝NP ，∴MN ＝PC ，∴四边形MNCP 是平行四边形，无法证明四边形MNCP 是菱形；③错误；∵MN ∥CD ，∴∠PDN ＝∠MND ，∵NP ＝PD ，∴∠PDN ＝∠PND ，∴∠MND ＝∠PND ，∴ND 平分∠PNM ，④正确；正确的个数有3个，故选：C ．【点睛】本题考查了平行四边形性质和判定，三角形中位线定理，直角三角形斜边上的中线性质，等腰三角形的性质等；熟练掌握三角形中位线定理、等腰三角形的性质、直角三角形斜边上的中线性质是解题的关键．18．D【分析】根据题意和图形可看出每经过一次变化，都顺时针旋转45°A 到A 3变化后的坐标，再求出A 1、A 2、A 3、A 4、A 5，继而得出A 8坐标即可.【详解】解：根据题意和图形可看出每经过一次变化，都顺时针旋转45° ∵从A 到3A 经过了3次变化，∵45°×3＝135°，1×3＝∴点3A 所在的正方形的边长为3A 位置在第四象限，∴点3A 的坐标是（2，－2），可得出：1A 点坐标为（1，1），2A 点坐标为（0，2），3A 点坐标为（2，－2），4A 点坐标为（0，－4），5A 点坐标为（－4，－4），6A （－8，0），A 7（－8，8），8A （0，16），故选D.【点睛】本题考查了规律题，点的坐标，观察出每一次的变化特征是解答本题的关键.19．B【分析】由在ABC ∆中，ABC ∠和ACB ∠的平分线相交于点O ，根据角平分线的定义与三角形内角和定理，即可求得②1902BOC A ∠=+∠︒正确；由平行线的性质和角平分线的定义得出BEO ∆和CFO ∆是等腰三角形得出EF BE CF =+故①正确；由角平分线定理与三角形面积的求解方法，即可求得③设OD m =，AE AF n +=，则12AEF S mn ∆=，故③错误；E 、F 不可能是三角形ABC 的中点，则EF 不能为中位线故④正确．【详解】解：在ABC ∆中，ABC ∠和ACB ∠的平分线相交于点O ， 12OBC ABC ∴∠=∠，12OCB ACB ∠=∠，180A ABC ACB ∠+∠+∠=︒， 1902OBC OCB A ∴∠+∠=︒-∠， 1180()902BOC OBC OCB A ∴∠=︒-∠+∠=︒+∠；故（2）正确； 在ABC ∆中，ABC ∠和ACB ∠的平分线相交于点O ，OBC OBE ∴∠=∠，OCB OCF ∠=∠，//EF BC ，OBC EOB ∴∠=∠，OCB FOC ∠=∠，EOB OBE ∴∠=∠，FOCOCF ∠=∠， BE OE ∴=，CF OF =，EF OE OF BE CF ∴=+=+，故（1）正确；过点O 作OM AB ⊥于M ，作ON BC ⊥于N ，连接OA ，在ABC ∆中，ABC ∠和ACB ∠的平分线相交于点O ，ON OD OM m ∴===，1111()2222AEF AOE AOF S S S AE OM AF OD OD AE AF mn ∆∆∆∴=+=+=+=；故（3）正确，（4）错误；12EOB S BE OM ∆=，12OCF S FC OD ∆=， OM OD =，BE 不一定等于CF ，EOB S ∆∴不一定等于FOC S ．故（5）错误，综上可知其中正确的结论是（1）（2）（3），故选：B ．【点睛】此题考查了三角形中位线定理的运用，以及平行线的性质、等腰三角形的判定与性质．此题难度适中，解题的关键是注意数形结合思想的应用．20．C【分析】①证明△OBC是等边三角形，即可得OB=BC，由FO=FC，即可得FB垂直平分OC，①正确；②由FB垂直平分OC，根据轴对称的性质可得△FCB≌△FOB，根据全等三角形的性质可得∠BCF=∠BOF=90°，再证明△FOC≌△EOA，所以FO=EO，即可得OB垂直平分EF，所以△OBF≌△OBE，即△EOB≌△FCB，②错误；③证明四边形DEBF是平行四边形，再由OB垂直平分EF，根据线段垂直平分线的性质可得BE=BF，即可得平行四边形DEBF为菱形，③正确；④由OBF≌△EOB≌△FCB得∠1=∠2=∠3=30°，在Rt△OBE中，可得OE=，在Rt△OBM中，可得，即可得BM ：OE =3：2，④正确.【详解】①∵矩形ABCD中，O为AC中点，∴OB=OC，∵∠COB=60°，∴△OBC是等边三角形，∴OB=BC，∵FO=FC，∴FB垂直平分OC，∴FB⊥OC，OM=CM；①正确；②∵FB垂直平分OC，根据轴对称的性质可得△FCB≌△FOB，∴∠BCF=∠BOF=90°，即OB⊥EF，∵OA=OC，∠FOC=∠EOA，∠DCO=∠BAO，∴△FOC≌△EOA，∴FO=EO，∴OB垂直平分EF，∴△OBF≌△OBE，∴△EOB≌△FCB，②错误；③∵△FOC≌△EOA，∴FC=AE，∵矩形ABCD，∴CD=AB，CD∥AB，∴DF∥EB，DF=EB，∴四边形DEBF是平行四边形，∵OB垂直平分EF，∴BE=BF，∴平行四边形DEBF为菱形；③正确；④由OBF≌△EOB≌△FCB得∠1=∠2=∠3=30°，在Rt△OBE中，3，在Rt△OBM中，BM=32OB,∴BM ：OE =32：=33OB=3：2.④正确；所以其中正确结论的个数为3个；故选C.【点睛】本题考查了矩形的性质、等腰三角形的性质、全等三角形的性质和判定、线段垂直平分线的性质、菱形的判定及锐角三角函数，是一道综合性较强的题目，解决问题的关键是会综合运用所学的知识分析解决问题．。