2019国家公务员考试行测钟表及相遇追击问题

2019年国家公务员考试数学运算备考难题(二) 在备考2019国家公务员考试中，行程题目是不能忽略的，但是有些行程问题，特别是火车相遇追及问题的计算，这是困扰很多考生的难题。

小编提醒大家在解决这类行程题目时，需要我们有缜密的思维，根据题目中相遇追及的基本公式，并结合火车自身的长度，来全面考虑。

这类问题的关键和难点就是火车等的长度，对题目的解答构成障碍，是我们必须要考虑清楚的。

下面介绍几种常见的自带长度等的火车或者队伍的行程问题的解题思路。

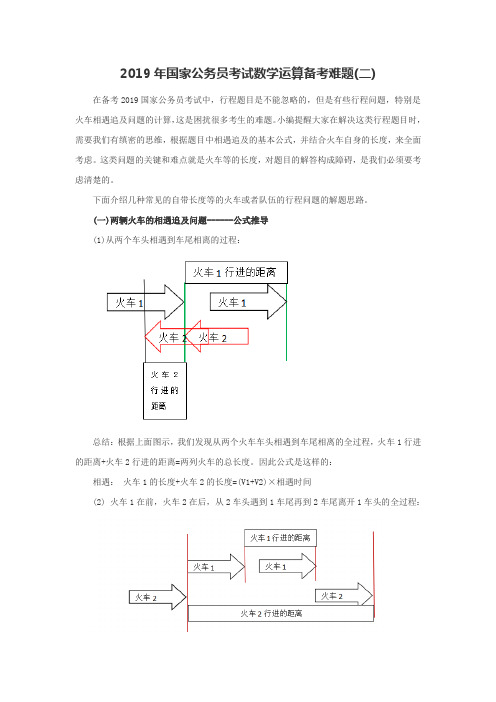
(一)两辆火车的相遇追及问题------公式推导(1)从两个车头相遇到车尾相离的过程：总结：根据上面图示，我们发现从两个火车车头相遇到车尾相离的全过程，火车1行进的距离+火车2行进的距离=两列火车的总长度。

因此公式是这样的：相遇：火车1的长度+火车2的长度=(V1+V2)×相遇时间(2) 火车1在前，火车2在后，从2车头遇到1车尾再到2车尾离开1车头的全过程：总结：根据上面图示，我们发现两列火车的前进的路程的差是：火车1的长度+火车2的长度。

因此公式是这样的：追及：火车1的长度+火车2的长度=(V2-V1)×追及时间(二)两辆火车的相遇追及问题-----公式应用【例】一列高铁列车A车长420米，另一列高铁列车B车长300米，在平行的轨道上相向而行，从两个车头相遇到车尾相离经过30秒。

如果两车同向而行，列车B在前，列车A 在后，从列车A车头遇到列车B车尾再到列车A车尾离开列车B车头经过120秒。

那么列车A的速度为( )。

A、每小时54公里B、每小时100公里C、每小时200公里D、每小时300公里思路剖析：1.题干比较复杂，出现了两列火车，而且明确给出两列火车的长度，需要细心考虑。

2.题目中给的米和秒，而问题问的是每小时多少公里，需要单位换算。

3.描述了两列火车的相遇和追及，需要寻找他们之间速度的关系，利用给定的长度和时间来求解。

【解析】当两车相向而行时，从两个车头相遇到车尾相离经过30秒，一共行驶了420+300=720米，设A的速度为a，B的速度为b，则有：30(a+b)=720;当两车同向而行时，从列车A车头遇到列车B车尾再到列车A车尾离开列车B车头经过120秒也是共行驶了420+300=720米，因此有120(a-b)=720。

行测专题（二）时针分针与路程问题一、基本知识点：1 、基本公式：s=v*t2 、相遇追及问题：相遇距离s =（vl + v2 ）*相遇时间t追及距离S = ( vl - v2 ) * 追及时间t3 、环形运动问题：环形周长s =（v1 + v2 ) * 相向运动的两人两次相遇的时间间隔t环形周长s = ( v1 - v2 ) * 同向运动的两人两次相遇的时间间隔t4 、流水行船问题：顺流路程＝顺流速度*顺流时间＝（船速＋水速）* 顺流时间逆流路程＝逆流速度*逆流时间＝（船速一水速）* 逆流时间5 、电梯运动问题：能看到的电梯级数＝（人速十电梯速度）* 沿电梯运动方向运动所需时间能看到的电梯级数＝（人速一电梯速度）* 逆电梯运动方向运动所需时间答案与解析1 ．求在8 点几分时，时针和分针重合在一起？A.8 点43 ( 7 / 11 ）分B.8 点43 分C.8点43(5/1l）分D.8点53(7/11）分解析：时针的问题和路程问题解题思路是一致的，考虑8 点时、分针落后时针40 个格（每分为一格），而时针速度为每分1 / 12 格，分针速度每分一格，有追及问题可得：40 /（1 一1 / 12 ) = 43 ( 7 / 11 )2 ．时钟的时针和分针在6 点钟恰好反向成一条直线，问下一次反向成一条直线是什么时间？（准确到秒）A7 点5 分27 秒 B7 点5 分28 秒 C7 点5 分29 秒 D7 点5 分30 秒解析：在7 点的时候、时针与分针之间的夹角是210 度，分针每分钟6 度，时针每分钟走0 . 5 度。

假设在经过N 分钟时针和分针成一条直线。

这样就把问题转换为追击问题。

210 + O.5N - 6N = 180 得N=5 ( 5 / 11 ）约等于5 分27 秒3 ．某解放军队伍长450 米，以每秒1 . 5 米的速度前进，一通讯员以每秒3 米的速度从排尾到排头并立即返回排尾，整个过程通讯员走了多少米？A . 950B . 1000C . 1100D . 1200解析：从排尾到排头用时为：450 /（3 -1.5 ）=300 （秒），从排头到排尾用的时间是400 / ( 3 + 1.5 ) = 100 秒，一共用了400 秒，3 * 400 = 1200 。

时钟问题1.知识点1.时针一昼夜转2圈，每分钟走0.5度，2.分针一昼夜转24圈，每分钟走6度3.时分针一昼夜重合22次，每隔65分重合一次4.追击时间=差度÷5.5，相遇时间=和度÷6.55.时间快慢问题用比去做：先写出快慢两表时间比，题中又会告诉一个表走的时间，再根据这个比求另一个表走的时间。

6.表盘分成12大格，每格30度7.镜面时间+实际时间=12小时1．行程问题中时钟的标准制定；2．时钟的时针与分针的追及与相遇问题的判断及计算；3．时钟的周期问题。

时钟问题可以看做是一个特殊的圆形轨道上2人追及或相遇问题，不过这里的两个“人”分别是时钟的分针和时针。

时钟问题有别于其他行程问题是因为它的速度和总路程的度量方式不再是常规的米每秒或者千米每小时，而是2个指针“每分钟走多少角度”或者“每分钟走多少小格”。

对于正常的时钟，具体为：整个钟面为360度，上面有12个大格，每个大格为30度；60个小格，每个小格为6度。

分针速度：每分钟走1小格，每分钟走6度时针速度：每分钟走十二分之一小格，每分钟走0.5度注意：但是在许多时钟问题中，往往我们会遇到各种“怪钟”，或者是“坏了的钟”，它们的时针和分针每分钟走的度数会与常规的时钟不同，这就需要我们要学会对不同的问题进行独立的分析。

要把时钟问题当做行程问题来看，分针快，时针慢，所以分针与时针的问题，就是他们之间的追及问题。

另外，在解时钟的快慢问题中，要学会十字交叉法。

例如：时钟问题需要记住标准的钟，时针与分针从一次重合到下一次重合，所需时间为65又11分之5 分。

总结基本思路：1、按照行程问题中的思维方法解题；2、不同的表当成速度不同的运动物体；3、路程的单位是分格（表一周为60分格）；4、时间是标准表所经过的时间；合理利用行程问题中的比例关系；解题技巧/思路：数量关系技巧包含了数学运算技巧和数字推理技巧两大部分，公务员考试数学运算是最为考生所头疼，其所占分值高并且难度也高。

16.时钟问题时钟问题是研究钟面上时针和分针关系的问题。

一般类型包括时针和分针重合、成一直线或直角问题，实际上相当于时针和分针的追及问题或相遇问题。

时钟问题可以细分为表针问题和快慢问题。

（1）表针问题常见的表针问题有：求某一时刻时针与分针的夹角角度，计算两针重合、两针垂直、两针成直线时的时刻等类型。

表针问题是在公考中经常出现的题目，也是考生需要熟练掌握的题型之一。

【例题1】每天钟表的分针追上时针每次间隔（）分钟？A.55.45B.60C.64D.65.45【例题解析】本题最简便的思路是这样的。

分针每12小时追上时针共11次，由于分钟与时针都是匀速的，这样次间隔时间为12小11时，即约等于65.45分钟。

答案为D【思路点拨】本题是考察表针问题中的基本关系，分针追及时针的所用时间。

考生若是仔细阅读我们总结出的注意要点，就可以直接得出答案。

【例题2】小明晚上八点多开始做作业，此时钟表的分针与时针正好在一条直线上，当分针与时针第一次重合的时候，小明刚好做完作业。

请问小明做作业一共用了（ ）分钟？A.32.73B.35.71C. 38D.41.54【例题解析】方法一：设8点x 分，分针与时针在一条直线上，则有x+30=5×8+12x （分针每走12分钟，时针走一格），解得：x=11120，设8点y 分时第一次重合，y=5×8+12y ，y=11480 y-x=11360≈32.73分 方法二：由上题我们可知，由于时针、分针都是匀速转动，所以每12小时重合11次，每次需用1112小时，因为匀速从两针成一条直线到相重合，就应该是1112÷2=116小时=32.73分钟。

故应选择A 选项。

【思路点拨】对待表针问题，考生不要急于直接做题。

充分理解题意后，可以像“方法二”一样，快速解答本题。

【例题3】（2006年国考一卷第45题）从12时到13时，钟的时针与分针可成直角的机会有（ ）。

公务员考试总题-相遇追及问题1、一次长跑比赛在周长为400米的环形跑道上进行。

比赛中，最后一名在距离第3圈终点150米处被第1名完成超圈（即比他多跑1圈），50秒后，他又在距离第3圈终点45米处被第2名完成超圈。

假定所有选手均是匀速，那么第2名速度约为（）。

[2021真题]A.2.83米/秒B.2.9米/秒C.2.82米/秒D.2.1米/秒2、如右图，正方形的迷你轨道边长为1米，1号电子机器人从点A 以1米/秒的速度顺时针绕轨道移动，2号电子机器人从点A以3米/秒的速度逆时针绕轨道移动，则它们的第2021次相遇在（）。

[2021真题]A.点AB.点CC.点BD.点D3、某机场一条自动人行道长42米，运行速度0.75米/秒。

小王在自动人行道的起始点将一件包裹通过自动人行道传递给位于终点位置的小明。

小明为了节省时间，在包裹传递时，沿着自动人行道逆行领取包裹并返回。

假定小明的步行速度是1米/秒，则小明拿到包裹并回到自动人行道终点共需要的时间是（）。

[2021真题]A.24秒B.42秒C.48秒D.56秒4、甲车从A地，乙车从B地同时出发匀速相向行驶，第一次相遇距离A地100千米。

两车继续前进到达对方起点后立即以原速度返回，在距离A地80千米的位置第二次相遇。

则AB两地相距多少千米?（）[2021真题]A.170B.180C.190D.2005、一辆动车组列车和一辆快速列车相向而行，动车组列车的车长是260米，快速列车的车长是455米。

坐在动车组列车上的人看快速列车驶过的时间是7秒，那么坐在快速列车上的人看动车组列车驶过的时间是（）。

[2021真题]A.3秒B.4秒C.5秒D.6秒6、小张家距离工厂15千米，乘坐班车20分钟可到工厂。

一天，他错过班车，改乘出租车上班。

出租车出发时间比班车晚4分钟，送小张到工厂后出租车马上原路返回，在距离工厂1.875千米处与班车相遇。

如果班车和出租车都是匀速运动且不计上下车时间，那么小张比班车早多少分钟到达工厂?（）[2021真题]A.3B.4C.5D.67、在猫鼠游戏中，跑道为无顶和底的圆柱形，底或顶的圆周长度为5米。

数量关系备考知识——相遇追击问题知识点介绍相遇追击问题总体上说是隶属于行程问题的范畴。

这是历年国家公务员考试行测数量关系中常考的一类题型。

试题的题型也是千变万化，但是所运用到的基础知识却是我们中学甚至小学都涉及到的内容。

基本公式下面老师来为考生朋友们总结此类问题的常用公式和基本解题要点。

相遇问题基本数量关系：路程和＝速度和×相遇时间；追击问题基本数量关系：路程差＝速度差×追击时间；背离问题基本数量关系：路程和＝速度和×背离时间。

对于多次相遇问题：首先要理清各自的行程路线，然后可以通过画相遇问题相关示意图来帮助打开解题思路。

真题链接下面通过真题，来具体把握相遇追击问题的解题方法及技巧。

（2011国考）甲、乙两人在长30米的泳池内游泳，甲每分钟游37.5米，乙每分钟游52.5米，两人同时分别从泳池的两端出发，触壁后原路返回，如是往返。

如果不计转向的时间，则从出发开始计算的1分50秒内两人共相遇了多少次？（）A. 2B. 3C. 4D. 5京佳解析：多次相遇问题。

由甲、乙两人速度和为90米/分钟，1分50秒内两人游的路程和为165米。

两人第一次相遇时，两人须共游的路程和为30米，而后每次相遇，两人须共游60米，（165-30）÷60≈2，即从第一次相遇后，两人相遇2次要游行的路程和是120米，所以在1分50秒时，两人已经相遇了3次。

故应选择B选项。

（2011河南）高速公路上行驶的汽车A的速度是100公里每小时，汽车B的速度是120公里每小时，此刻汽车B前方80公里处，汽车A中途加油停车10分钟后继续向前行驶，那么从两车相距80公里处开始，汽车B至少要多长时间可以追上汽车A？（）A. 2小时B. 3小时10分C. 3小时50分D. 4小时10分京佳解析：相遇追击问题。

开始追击时，两车相距80公里。

追击的前10分钟，B行驶20公里，A停车10分钟。

接下来，B车继续120公里每小时行驶，A车100公里每小时行驶，两车还相距60公里。

⾏测数量关系技巧：相遇追及问题解题技巧 相遇追及问题是⾏测考试中常⻅的考试题型，备考中重视此题型⾮常有利于考试，下⾯店铺⼩编为你准备了“⾏测数量关系技巧：相遇追及问题解题技巧”内容，仅供参考，祝⼤家在本站阅读愉快！⾏测数量关系技巧：相遇追及问题解题技巧 ⾏程问题作为⼀个重点题型，在⾏测考试中会多次出现，并且考查内容较多，相遇追及是⾏程中的⼀个相对来说较为重要的内容，此考点的出现已经较为常⻅，结合⽇常⽣活背景⽕⻋过桥和过隧道问题就显得略有创新。

在隧道上和桥上的相遇和追及问题会以何种内容出现，⼜会以何种形式进⾏考查，⼩编为⼲⼤考⽣进⾏如下解答： 基础题型 例1.⼀列⻓90⽶的⽕⻋以每秒30⽶的速度匀速通过⼀座⻓1200⽶的桥，所需时间为( )秒。

A.37B.40C.43D.46 【答案】C。

解析：传统的⾏程问题中⼀个⼈或者⼀辆轿⻋经过桥⻓的时间，都是将⼈或者轿⻋看作⼀个点进⾏操作，所以⾏驶的总路程可以直接看做桥⻓。

但是⽕⻋并⾮如此，从⽕⻋的⻋头上桥开始到⽕⻋的⻋尾下桥为⽌停⽌计时，可以得到⽕⻋通过⼤桥所⾛的距离不光是桥⾝⻓，还需要考虑⽕⻋本⾝的⻓度，即总路程为桥⻓加上⼀倍的⻋⾝⻓度，因此该⽕⻋通过⼤桥所需的时间为(1200+90)/30=43秒。

选择答案C。

进阶题型 例2.⼀列⽕⻋途经两个隧道和⼀座桥梁，第⼀个隧道⻓600⽶，⽕⻋通过⽤时18秒;第⼆个隧道⻓480⽶，⽕⻋通过⽤时15秒;桥梁⻓800⽶，⽕⻋通过时速度为原来的⼀半，则⽕⻋通过桥梁所需的时间为：A.29秒B.25秒C.40秒D.46秒【答案】D。

解析：⽕⻋过桥问题，需要考虑⽕⻋⾃⾝的⻓度。

设⽕⻋⾃⾝⻓度为x⽶，则，解得x=120，则⽕⻋速度为(120+600)÷18=40⽶/秒，则⽕⻋过桥时速度为20⽶/秒，路程为800+120=920⽶，所需时间为920÷20=46秒。

例3.有⼀⾏⼈和⼀骑⻋⼈都从A向B地前进，速度分别是⾏⼈3.6千⽶/⼩时，骑⻋⼈为10.8千⽶/⼩时，此时道路旁有列⽕⻋也由A地向B地疾驶，⽕⻋⽤22秒超越⾏⼈，⽤26秒超越骑⻋⼈，这列⽕⻋⻋⾝⻓度为( )⽶。

国考行测数量关系——直线型相遇追及问题【答题妙招】相遇问题：相遇距离=（大速度＋小速度）×相遇时间追及问题：追及距离=（大速度－小速度）×追及时间【例1】公路上有三辆同向行驶的汽车，其中甲车的时速为63公里，乙、丙两车的时速均为60公里，但由于水箱故障，丙车每连续行驶30分钟后必须停车2分钟。

早上10点，三车到达同一位置，问1小时后，甲、丙两车最多相距多少公里（）A.5B.7C.9D.11【答案】B。

在这1个小时中，丙车最多休息4分钟，也即丙在一个小时内最少行程为56公里。

而甲车持续行驶，可达63公里。

因此两车最多相距7公里。

【例2】甲、乙两人分别从A.B两地同时出发，相向而行，乙的速度是甲的2/3，两人相遇后继续前进，甲到达B地，乙到达A地立即返回，已知两人第二次相遇的地点距离第一次相遇的地点是3000米，求A.B两地的距离是（）米。

A.6000B.6500C.7000D.7500【答案】D 。

解法一：如图所示，设甲第一次走的路程为S 1，乙第一次走的路程为S 2。

可以看出，从第一次相遇到第二次相遇，甲走的路程为2S 2+3000，乙走的路程为2S 1-3000。

由路程与速度成正比可列方程：S 1:S 2=（2S 2+3000）:（2S 1-3000）=2:3，解得S 1=4500，S 2=3000。

因此A.B 两地相距4500+3000=7500米。

因此答案选择D 选项。

解法二：设总路程为S ，分析题意可知，甲速：乙速=3：2，所以第一次相遇时，甲乙总路程为1个全程，乙的路程应为总路程的S 52；第二次相遇时，甲乙总路程为3个全程，甲的路程为S 54S S 59+=。

所以第一次相遇点距离第二次相遇点为3000S 52S 52S 54==-，S=7500米。

因此答案选择D 选项。

【例3】往返A 市和B 市的长途汽车以同样的发车间隔从两个城市分别发车，以每小时40公里的速度前往目标城市。

行测考试中相遇问题的解题技巧行程问题中的相遇追击问题可以说是公务员行测考试问题中的一个母题，很多行程问题中的小题型如牛吃草问题、多次相遇问题、青蛙跳井问题、间隔发车问题、钟表问题等等都是由追击相遇的基本模型展开的，而展开的前提就是时间，就此为考生梳理一下追击相遇的基本公式：相遇模式：路程和=速度和×时间追击模式：路程差=速度差×时间广大考生朋友要注意的是，这里的追击相遇模式，并不代表真正的追击和相遇，只要是满足时间一定(几个量完成路程所花的时间一定)时，我们知道路程和就可以用相遇模式，知道路程差就是追击模式。

(一) 相遇追击模式之钟表问题另：相邻小时刻度间距为30度对于钟表问题而言，我们做题的入手点就是，我们通过判断可以得到路程和还是路程差。

知道路程和，就可以用相遇模式解决;知道路程差我们可以用追击模式来解决。

通过例题来看一下：现在为北京时间15:00，请问多少分钟后时针与分针第一次重合?这道题的入手点就是判断已知路程和路程差的问题，我们都知道北京时间15:00时分针与时针的间距为90度，题目要求分针与时针第一次重合，所以可以判断这90度就是分针和时针的路程差，所以由15：00变成分针与时针重合用的时间等于90/(6-0.5)。

(二)相遇追击模式之牛吃草问题牛吃草问题又称之为牛顿牧场问题或者是消长问题，它的母题也是相遇追击模式。

首先我们通过一道例题来认识一下牛吃草问题：一片牧草(牧草每天均匀生长或者均匀枯萎)，可以供7头牛吃8天，可以供12头牛吃5天。

请问：(1)如果牧草每天均匀生长可以供9头牛吃几天?(2)如果牧草每天均匀生长，要使牧草永远不被吃光，最多可以养多少头牛?(3)如果牧草每天均匀枯萎可以供9头牛吃几天?这时我们可以发现，如果牧场每天均匀生长，那么这道题目就是一个基本的追击模型，就是牛吃草量—草生长量=原牧草的量。

草永远不被吃光就是每天牛吃的量=每天草长的量。

如果牧草每天枯萎那么就是一道相遇的模型：牛吃草量+草枯萎量=原牧场的量。

公务员行测考试时钟角度题示例在行测数量关系部分中，我们有时会遇到一种特别的题型，时钟的指针转动角度和时间的换算和运算问题。

这种题常常环绕时针和分针之间的位置关系进行设问。

下面作者给大家带来关于公务员行测考试时钟角度题示例，期望会对大家的工作与学习有所帮助。

公务员行测考试时钟角度题示例由于时针和分针都是按顺时方向转动，所以这类问题可以类比行程问题的追及问题(环形路线)进行学习记忆。

分针总在“追赶”时针，则两者的“追及距离”其实即为顺时针方向的角度差。

我们一样把12点(0点)整作为运算起点。

时针每小时转动角度：360°/12=30°，则每分钟转动：30°/60=0.5°;同理得出，分钟每分钟走6°。

所以两针每分钟产生的角度差为6-0.5=5.5°，即角速度差为5.5°/min。

设角度差为Δα，耗费时间为t，则公式为：Δα=5.5t。

下面通过例题来体会如何运用上述思路和公式吧：【例1】钟表有一个时针和一个分针，24小时内时针和分针成直角共多少次?A.28B.36C.44D.48【解析】以12点整，两针重合开始运算。

第一需要知道题干中的“成直角”其实就是角度差Δα=90°的意思，接下来就很好推敲了。

直接代入公式得：90=5.5t，则t=180/11。

也就是说每经过180/11分钟，时针与分针的角度差就扩大90°，形成一个90°→180°→270°→360°(即0°)的周期循环，每个循环包括4次，其中有2次(90°和270°时成直角，另外两次成平角)符合题意。

24小时的时间总量换算成分钟是：24×60=1440min。

则总的周期循环数为：1440min除以(180/11)min再除以4次=22个周期。

22个周期循环里，每个循环有2次时针和分针成直角，则24小时内所有成直角次数为：22×2=44次。