第07章 图(C++)

习 题7-1 用积分法求图示各悬臂梁自由端的挠度和转角，梁的抗弯刚度EI 为常量。

7－1（a ） 0M()M x = ''0EJ M y ∴='0EJ M y x C =+ 201EJ M 2y x Cx D =++ 边界条件: 0x =时 0y = ；'0y = 代入上面方程可求得：C=D=0201M 2EJ y x ∴='01=M EJ y x θ= 01=M EJ B l θ 201=M 2EJ B y l（b ）222()1M()222q l x qx x ql qlx -==-+- 2''21EJ 22qx y ql qlx ∴=-+-3'2211EJ 226qx y ql x qlx C =-+-+422311EJ 4624qx y ql x qlx Cx D =-+-++边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=04223111()EJ 4624qx y ql x qlx ∴=-+-'2231111=(-)EJ 226y ql x qlx qx θ=+-3-1=6EJ B ql θ 4-1=8EJB y ql（c ）()()()()()0303''04'050()1()()286EJ 6EJ 24EJ 120l xq x q lq l x M x q x l x l x l q y l x l q y l x Cl q y l x Cx Dl-=-⎛⎫=--=-- ⎪⎝⎭∴=-=--+=-++边界条件：0x = 时 0y = ；'0y = 代入上面方程可求得：4024q l C l -= 50120q l D l=()455000232230120EJ 24EJ 120EJ(10105)120EJq q l q l y l x x l l l q x l l lx x l ∴=---+-=-+- 3024EJ B q l θ=- 4030EJB q l y =-(d)'''223()EJ 1EJ 211EJ 26M x Pa Pxy Pa Pxy Pax Px C y Pax Px Cx D=-=-=-+=-++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=023'232321112611253262B C C B y Pax Px EJy Pax Px EJ Pa Pa Pay y a a EJ EJ EJPa EJθθθ⎛⎫∴=- ⎪⎝⎭⎛⎫==-⎪⎝⎭=+=+==(e)()()()21222''1'211231113()02()2223EJ 231EJ ()2231EJ ()46a M x q qax x a q M x a x a x a a y q qaxa y qa x x C a y qa x x C x D =-+≤≤=--≤≤=-+=-++=--+++ 边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C=D=0()()()22118492024EJ 12EJ qax qax y a x a x x a ∴=--=--≤≤''2223'222242232221EJ ((2)4)21EJ (42)2312EJ (2)2312y q a ax x x y q a x ax C x y q a x ax C x D =--+=--++=---+++边界条件：x a = 时 12y y = ；12θθ=代入上面方程可求得：2296a C = 4224qa D =-()()43223421612838464162384q y x ax a x a a a x a EJ-=-+-+≤≤43412476B B qa y EJqa EJθ=-=-(f)()()221222''212'231122341115()20225()2225251EJ 22251EJ 26511EJ 4324qa qx M x qax x a qa qa a M x qax x a x a a y q ax x a y q x ax x C a y q x ax x C x D =-+-≤≤⎛⎫=-+--≤≤ ⎪⎝⎭⎛⎫=--+ ⎪⎝⎭⎛⎫=--++ ⎪⎝⎭⎛⎫=--+++ ⎪⎝⎭边界条件：0x = 时 0y = ；'0y =代入上面方程可求得：C 1=D 1=0''22'2222223222EJ (2)1EJ (2)21EJ ()6y q a ax y q a x ax C y q a x ax C x D =--=--+=---++ 边界条件：x a = 时 12y y = ； ''''12y y =3296a C =- 4224a D =-437124136B B qa y EJqa EJθ=-=-7-2 用积分法求图示各梁的挠曲线方程，端截面转角θA 和θB ，跨度中点的挠度和最大挠度，梁的抗弯刚度EI 为常量。

第七章人工蜂群算法习题与答案1. 填空题（1）人工蜂群算法的缩写是，它模拟了机制，可以解决问题。

（2）在人工蜂群算法中，有三种蜜蜂执行不同的任务，它们分别是、和。

解释：本题考查人工蜂群算法的基础知识。

具体内容请参考课堂视频“第7章人工蜂群算法”及其课件。

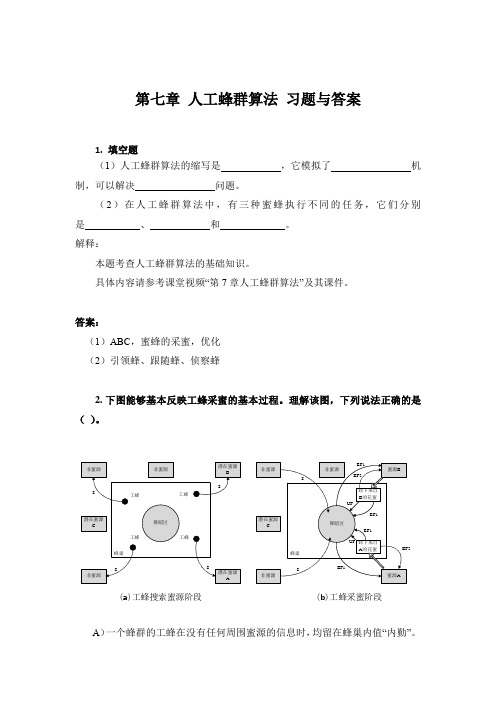
答案：（1）ABC，蜜蜂的采蜜，优化（2）引领蜂、跟随蜂、侦察蜂2.下图能够基本反映工蜂采蜜的基本过程。

理解该图，下列说法正确的是（）。

(a)工蜂搜索蜜源阶段 (b)工蜂采蜜阶段A）一个蜂群的工蜂在没有任何周围蜜源的信息时，均留在蜂巢内值“内勤”。

B）引领蜂从蜜源（A和B）处携带花蜜返回蜂巢，并将花蜜卸载到储存花蜜的位置，在卸下花蜜以后放弃蜜源。

C）引领蜂到舞蹈区跳上一只圆圈舞蹈或“8”字形舞蹈招募其他工蜂到该蜜源处采蜜，舞蹈的持续时间暗示蜜源与蜂巢之间的距离。

D）引领蜂在找到蜜源后选择继续在该蜜源采蜜而不招募任何蜜蜂，直到蜜源采集殆尽，再去开采新的蜜源。

解释：本题考查对工蜂采蜜过程的掌握及理解。

具体内容请参考课堂视频“第7章人工蜂群算法”及其课件。

答案：C一个蜂群在没有任何周围蜜源的信息时，大多数的工蜂都首先留在蜂巢内值“内勤”，仍有少数工蜂作为“侦察员”专门搜索新的蜜源，因此A错误。

侦察蜂将从蜜源A和B处分别携带花蜜返回蜂巢，并将花蜜卸载到储存花蜜的位置，在卸下花蜜以后，侦察蜂有以下三种可能：（1）到舞蹈区招募其他工蜂到该蜜源处采蜜，此时的侦察蜂称为引领蜂，被招募来的工蜂称为跟随蜂，具体过程如下：引领蜂在舞蹈区跳上一支圆圈舞蹈或“8”字形舞蹈招募蜜蜂到该蜜源处采蜜（如图中过程EF1），其中，舞蹈的持续时间暗示蜜源与蜂巢之间的距离，舞蹈的剧烈程度反映蜜源的质量，身上附着的花粉味道则反映蜜源的种类。

蜜源离蜂巢越近、花蜜越多，代表蜜源越好，所招募的跟随蜂也越多；（2）放弃蜜源成为未雇佣蜂进入舞蹈区（如图中过程UF），未雇佣蜂包括跟随蜂和侦察蜂；（3）继续在该蜜源采蜜而不招募任何蜜蜂（如图中过程EF2）。

GET《微观经济学：原理与模型》第7章一般均衡与福利理论学习要求⏹重点掌握◇一般均衡和帕累托最优标准问题⏹一般掌握◇社会福利最大化问题⏹一般了解◇交易和生产各自的帕累托最优条件严格地说，上述微观经济学各章讨论的内容均属局部均衡范畴，为使研究深入，应该引申到一般均衡分析。

在一般均衡的基础上，应该分析市场经济均衡状态是否具有经济效率，这就是福利理论问题。

本章主要讲述一般均衡理论和帕累托最优状态、交易的帕累托最优条件、生产的帕累托最优条件、交易和生产的帕累托最优条件和社会福利最大化问题。

第一节局部均衡与一般均衡一、局部均衡及其假定条件局部均衡(partial equilibrium),是指单个市场或部分市场的供求与价格之问的关系或均衡状态。

其特点是假定一个市场价格变动对其他市场价格没有显著影响条件下的供求与价格关系分析或均衡状态分析。

这种假定内容有三：（注：马歇尔（Alfred Marshall）是局部均衡的代表人物。

）(1)对商品市场而言，商品A的价格变化不影响其替代品B和互补品C的价格变化，商品B和商品C价格变化不影响其替代品1B，1C和补充品B，2C价格的变化，最终B，C，1B，1C，2B和2C商品价格变2化不影响A商品的价格变化。

(2)对要素市场而言，要素F的价格变化不影响其替代要素G和补充要素H价格的变化，要素G和H价格的变化不影响其替代要素G，1H1和补充要素G，2H的变化。

最终G，H，1G，1H，2G和2H要素价2格的变化不影响要素，价格的变化。

(3)商品市场和要素市场之间，没有联系互不影响，即商品市场价格不影响要素市场价格，要素市场价格也不影响商品市场。

现实经济生活中，这三种假定是不符合实际情况的，这里只是为分析问题方便而确定的假设。

二、一般均衡及其案例分析一般均衡(general equilibrium)是指在承认供求与市场上各种商品价格存在相互关系和相互影响条件下，所有市场上各种商品的价格与供求的关系或均衡状态。