多边形和圆的初步认识(习题)

北师大版数学七年级上册第四章5多边形和圆的初步认识同步练习一、选择题1.过多边形的一个顶点的所有对角线把多边形分成8个三角形，这个多边形的边数是（）A．8B．9C．10D．11答案：C解析：解答：设多边形有n条边，则n－2＝8，解得n＝10．故这个多边形的边数是10．故选：C．分析：经过n边形的一个顶点的所有对角线把多边形分成（n－2）个三角形，根据此关系式求边数．2.从一个多边形的任何一个顶点出发都只有5条对角线，则它的边数是（）A．6B．7C．8D．9答案：C解析：解答：设这个多边形是n边形．依题意，得n－3＝5，解得n＝8．故这个多边形的边数是8．故选C．分析：根据多边形的对角线的定义可知，从n边形的一个顶点出发，可以引（n－3）条对角线，由此可得到答案．3.过多边形某个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形是（）A．八边形B．九边形C．十边形D．十一边形答案：B解析：解答：设多边形有n条边，则n－2＝7，解得：n＝9．所以这个多边形的边数是9，故选：B．分析：经过n边形的一个顶点的所有对角线把多边形分成（n－2）个三角形，根据此关系式求边数．4.七边形的对角线共有（）A．10条B．15条C．21条D．14条答案：D解析：解答：七边形的对角线总共有：()773142⨯-=条．故选D．分析：可根据多边形的对角线与边的关系求解．5.连接多边形的一个顶点与其他顶点的线段把这个多边形分成了6个三角形，则原多边形是（）边形．A．五B．六C．七D．八答案：D解析：解答：设原多边形是n 边形， 则n －2＝6， 解得n ＝8． 故选：D ．分析：根据n 边形从一个顶点出发可把多边形分成（n －2）个三角形进行计算． 6.一个多边形有五条对角线，则这个多边形的边数为（ ） A ．8 B ．7 C ．6 D ．5 答案：D解析：解答：设多边形的边数为n ，则()352n n -=，整理得23100n n --=， 解得15n =，22n =-（舍去）． 所以这个多边形的边数是5． 故选：D ．分析：根据n 边形的对角线公式()32n n -进行计算即可得解．7.已知过一个多边形的某一个顶点共可作2014条对角线，则这个多边形的边数是（ ） A ．2011 B ．2014 C ．2016 D ．2017 答案：D解析：解答：∵多边形从一个顶点出发可引出2014条对角线， 设多边形为n 边形，则 n －3＝2014， 解得n ＝2017． 故选：D ．分析：根据从多边形的一个顶点可以作对角线的条数公式（n－3）求出边数即可得解．8.若从一多边形的一个顶点出发，最多可引10条对角线，则它是（）A．十三边形B．十二边形C．十一边形D．十边形答案：A解析：解答：设这个多边形是n边形．依题意，得n－3＝10，∴n＝13．故这个多边形是13边形．故选：A．分析：根据多边形的对角线的定义可知，从n边形的一个顶点出发，可以引（n－3）条对角线，由此可得到答案．9.高中要好的五个学生，相互约定在毕业后的一周，每两人通话一次．则在毕业后的一周，这五位同学一共通讯（）次．A．8B．10C．14D．12答案：B解析：解答：5×（5－1）÷2＝5×4÷2＝20÷2＝10（次）．故选：B．分析：5个人每两个人通话一次，则每个人都要和其他4个人分别通话，则每人通话的次数为：5－1＝4次，则所有的人通话的次数为：5×4＝20次，由于通话是在两个人之间进行的，所以共通话20÷2＝10次．10.图中的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A点到B点，甲虫沿1ADA 、1A E 2A 、2A F 3A 、3A GB 路线爬行，乙虫沿AC 1B 路线爬行，则下列结论正确的是（ ）A ．甲先到B 点 B ．乙先到B 点C ．甲、乙同时到BD ．无法确定 答案：C解析：解答：12π（A 1A ＋1A 2A ＋2A 3A ＋3A B ）12π×AB ，因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等， 因此两个同时到B 点． 故选C ．分析：甲虫走的路线应该是4段半圆的弧长，那么应该是12π（A 1A ＋1A 2A ＋2A 3A ＋3A B ）＝12π×AB ，因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等，因此两个同时到B 点．11.下列说法，正确的是（ ） A ．弦是直径 B ．弧是半圆 C ．半圆是弧D ．过圆心的线段是直径 答案：C解析：解答：A.弦是连接圆上任意两点的线段，只有经过圆心的弦才是直径，不是所有的弦都是直径．故本选项错误；B.弧是圆上任意两点间的部分，只有直径的两个端点把圆分成的两条弧是半圆，不是所有的弧都是半圆．故本选项错误；C.圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．所以半圆是弧是正确的．D.过圆心的弦才是直径，不是所有过圆心的线段都是直径，故本选项错误．故选：C．分析：根据弦，弧，半圆和直径的概念进行判断．弦是连接圆上任意两点的线段．弧是圆上任意两点间的部分．圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．直径是过圆心的弦．12.有下列四个说法：①半径确定了，圆就确定了；②直径是弦；③弦是直径；④半圆是弧，但弧不一定是半圆．其中错误说法的个数是（）A．1B．2C．3D．4答案：B解析：解答：①圆确定的条件是确定圆心与半径，是假命题，故此说法错误；②直径是弦，直径是圆内最长的弦，是真命题，故此说法正确；③弦是直径，只有过圆心的弦才是直径，是假命题，故此说法错误；④半圆是弧，但弧不一定是半圆，圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫半圆，所以半圆是弧．但比半圆大的弧是优弧，比半圆小的弧是劣弧，不是所有的弧都是半圆，是真命题，故此说法正确．其中错误说法的是①③两个．故选：B．分析：根据弦的定义、弧的定义、以及确定圆的条件即可解决．13.下列说法中，结论错误的是（）A．直径相等的两个圆是等圆B．长度相等的两条弧是等弧C．圆中最长的弦是直径D．一条弦把圆分成两条弧，这两条弧可能是等弧答案：B解析：解答：A.直径相等的两个圆是等圆，正确，不符合题意；B.长度相等的两条弧圆周角不一定相等，它们不一定是等弧，原题的说法是错误的，符合题意；C.圆中最长的弦是直径，正确，不符合题意；D.一条直径把圆分成两条弧，这两条弧是等弧，正确，不符合题意， 故选：B ．分析：利用圆的有关定义进行判断后利用排除法即可得到正确的答案；14.有两个圆，⊙1O 的半径等于地球的半径，⊙2O 的半径等于一个篮球的半径，现将两个圆都向外膨胀（相当于作同心圆），使周长都增加1米，则半径伸长的较多的圆是（ ） A ．⊙1O B ．⊙2OC ．两圆的半径伸长是相同的D ．无法确定 答案：C解析：解答：设⊙1O 的半径等于R ，膨胀后的半径等于R ′；⊙2O 的半径等于r ，膨胀后的半径等于r ′，其中R ＞r ．由题意得，2πR ＋1＝2πR ′，2πr ＋1＝2πr ′，解得R ′＝R ＋12π，R ′＝R ＋12π； 所以R ′－R ＝12π，R ′－R ＝12π，所以，两圆的半径伸长是相同的． 故选C ．分析：由L ＝2πR 计算出半径的伸长量，然后比较大小． 15.下列语句中，不正确的个数是（ ）①直径是弦；②弧是半圆；③长度相等的弧是等弧；④经过圆内一定点可以作无数条直径． A ．1个 B ．2个 C ．3个 D ．4个答案：C解析：解答：①根据直径的概念，知直径是特殊的弦，故正确；②根据弧的概念，知半圆是弧，但弧不一定是半圆，故错误；③根据等弧的概念：在同圆或等圆中，能够互相重合的弧是等弧．长度相等的两条弧不一定能够重合，故错误；④如果该定点和圆心不重合，根据两点确定一条直线，则只能作一条直径，故错误．故选C．分析：根据弦、弧、等弧的定义即可求解．二、填空题16.若点M取在多边形的一条边上（不是顶点），再将点M与n边形个顶点连结起来，将此多边形分割成9个三角形，则n边形是_____边形．答案：十解析：解答：多边形一条边上的一点M（不是顶点）出发，连接各个顶点得到9个三角形，则这个多边形的边数为9＋1＝10．故答案为：十．分析：可根据多边形的一点（不是顶点）出发，连接各个顶点得到的三角形个数与多边形的边数的关系求解．17.从多边形的一个顶点出发引对角线，可以把这个多边形分割成7个三角形，则该多边形为_____边形．答案：九解析：解答：由题意可知，n－2＝7，解得n＝9．则这个多边形的边数为9，多边形为九边形．故答案为：九．分析：从一个n边形的某个顶点出发，可以引（n－3）条对角线，把n边形分为（n－2）的三角形．18.从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是_____．答案：8解析：解答：设多边形有n条边，则n－2＝6，解得n＝8．故答案为：8．分析：根据从一个n边形的某个顶点出发，可以引（n－3）条对角线，把n边形分为（n－2）的三角形作答．19.如图，MN为⊙O的弦，∠M＝50°，则∠MON等于_____．答案：80°解析：解答：∵OM＝ON，∴∠N＝∠M＝50°，∴∠MON＝180°－∠M－∠N＝80°，故答案为80°．分析：利用等腰三角形的性质可得∠N的度数，根据三角形的内角和定理可得所求角的度数．20.如图，以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E，连结OD、OE，若∠A ＝65°，则∠DOE＝_____．答案：50°解析：解答：如图，连接BE．∵BC为⊙O的直径，∴∠CEB＝∠AEB＝90°，∵∠A＝65°，∴∠ABE＝25°，∴∠DOE＝2∠ABE＝50°，（圆周角定理）故答案为：50°．分析：如图，连接BE．由圆周角定理和三角形内角和定理求得∠ABE＝25°，再由“同弧所对的圆周角是所对的圆心角的一半”进行答题．三、解答题21.（1）六边形从一个顶点可引出几条对角线？共有几条对角线？答案：3|9解答：（1）六边形从一个顶点可引出对角线：6－3＝3（条），共有对角线：() 66392⨯-=（条）；（2）n边形从一个顶点可以引出几条对角线？共有几条对角线？答案：（n－3）|()32 n n-解答：n边形从一个顶点可以引出（n－3）条对角线，共有()32n n-条对角线．解析：分析：根据n边形从一个顶点可引出（n－3）条对角线，及n边形一共()32n n-条对角线可求解（1）与（2）．22.在凸多边形中，四边形的对角线有两条，五边形的对角线有5条，经过观察、探索、归纳，你认为凸九边形的对角线为多少？简单扼要地写出你的思考过程．答案：27条．解答：27条．通过四边形和五边形的对角线图形可知，过n边形的1个顶点可以作（n－3）条对角线，故过n个顶点可作n（n－3）条对角线，而这些对角线重复一遍，故n边形的对角线为()32n n-条，所以凸九边形的对角线为()993272⨯-=．解析：分析：作出四边形与五边形的对角线，然后观察从一个顶点作出的对角线的条数，从而确定规律并求出n边形的对角线的条数公式，再令n＝9进行计算即可得解．23.画出下面多边形的全部对角线．答案：解答：如图所示：解析：分析：此图为5边形，有()55352⨯-=条对角线，依次画出即可．24.实践探究：有一个周长62.8米的圆形草坪，准备为它安装自动旋转喷灌装置进行喷灌，现有射程为20米、15米、10米的三种装置，你认为应选哪种比较合适？安装在什么地方？答案：选射程为10米的喷灌装置，安装在圆形草坪的中心处．解答：设圆形草坪的半径为R，则由题意知，2πR＝62.8，解得：R≈10m．所以选射程为10米的喷灌装置，安装在圆形草坪的中心处．解析：分析：具体应选哪一种装置，取决于圆形草坪的半径，周长为62.8米的圆的半径约是10米．25.（1）经过凸n边形（n＞3）其中一个顶点的对角线有_______条；答案：（n－3）．解答：n边形过每一个顶点的对角线有（n－3）条；故答案为：（n－3）．（2）一个凸边形共有20条对角线，它是几边形；答案：八解答：根据()32n n-＝20，解得：n＝8或n＝－5（舍去），∴它是八边形．（3）是否存在有18条对角线的凸多边形？如果存在，它是几边形？如果不存在，说明得出结论的道理．答案：不存在，理由：()3n n-＝18，解得：n=，∵n不为正整数，∴不存在．解析：分析：（1）根据n边形从一个顶点出发可引出（n－3）条对角线即可求解；（2）根据任意凸n边形的对角线有()32n n-条，即可解答；（3）不存在，根据()32n n-＝18，解得：n，n不为正整数所以不存在．。

多边形和圆的初步人认识练习一、选择题1.下列图形中，多边形有()．A. 1个B. 2个C. 3个D. 4个2.当时刻为下午3：30时，钟表上的时针与分针间的夹角是()A. 60°B. 70°C. 75°D. 85°3.下列说法正确的是()A. 对角线相等且互相垂直的四边形是菱形B. 对角线互相平分的四边形是正方形C. 对角线互相垂直的四边形是平行四边形D. 对角线相等且互相平分的四边形是矩形4.若一个多边形截去一个角后，变成十四边形，则原来的多边形的边数可能为()A. 14或15B. 13或14C. 13或14或15D. 14或15或165.若n边形共有54条对角线，则n的值是()．A. 9B. 10C. 11D. 126.如图所示，用不同颜色的马赛克覆盖一个圆形的台面，估计15°的圆心角的扇形部分大约需要34片马赛克片．已知每箱装有125片马赛克片，那么应该购买多少箱马赛克片才能铺满整个台面()．A. 6箱B. 7箱C. 8箱D. 9箱7.将一个四边形截去一个角后，它不可能是()A. 六边形B. 五边形C. 四边形D. 三角形8.将一个正方形桌面砍下一个角后，桌子剩下的角的个数是()A. 3个B. 4个C. 5个D. 3个或4个或5个9.下列说法正确的是()A. 圆的一部分是扇形B. 一条弧和经过弧的两条半径围成的图形叫做扇形C. 三角形是最简单的多边形D. 由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形10.如图，将一块直角三角板的直角顶点O放在直尺的一边CD上，如果∠AOC=28°，那么∠BOD等于()A. 72°B. 62°C. 52°D. 28°11.从多边形一条边上的一点(不是顶点)出发，分别连接这个点和其余各个顶点得到2017个三角形，则这个多边形的边数为()A. 2015B. 2016C. 2017D. 201812.以线段a=7，b=8，c=9，d=11为边作四边形，可作()A. 一个B. 2个C. 3个D. 无数个13.某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分(如图)，发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是()A. 两点之间线段最短B. 两点确定一条直线C. 垂线段最短D. 经过直线外一点，有且只有一条直线与这条直线平行14.如图，点O在直线AB上，若∠BOC=60°，则∠AOC的大小是()A. 60°B. 90°C. 120°D. 150°二、填空题15.若一个多边形截去一个角后，变成八边形，则原来多边形的边数可能是________．16.如图，扇形AOB(阴影部分)的圆心角等于周角的1，8则∠AOB的度数是__________．17.如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是_________．18.多边形：在同一平面内，由不在同一条直线上的若干条线段(线段的条数不小于3)______形成的图形叫做多边形．19.如图，将五边形ABCDE沿虚线裁去一个角得到六边形ABCDGF，则该六边形的周长一定比原五边形的周长______(填：大或小)，理由为______．三、解答题20.如图，已知∠AOB=90°，∠COD=90°，OE为∠BOD的平分线，∠BOE=17°18′，求∠AOC的度数．。

北师大版（2024）七年级上册《4.3多边形和圆的初步认识》2024年同步练习卷一、选择题：本题共9小题，每小题3分，共27分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.如图所示的图形中，属于多边形的有()A.1个B.2个C.3个D.4个2.过某个多边形一个顶点的所有对角线，将这个多边形分成5个三角形，则这个多边形的边数为()A.6B.7C.8D.93.过多边形一个顶点的所有对角线，将这个多边形分成8个三角形，这个多边形的边数是()A.8B.9C.10D.114.下列说法正确的是()A.弧就是一条弯曲的线B.扇形就是一条弧和两条半径组成的图形C.若干个小扇形组成一个圆D.弧是圆周的一部分5.从六边形的一个顶点出发，可以画出m条对角线，它们将六边形分成n个三角形．则m、n的值分别为()A.4，3B.3，3C.3，4D.4，46.从多边形一条边上的一点不是顶点出发，连接各个顶点得到2023个三角形，则这个多边形的边数为()A.2021B.2025C.2024D.20267.已知从一个顶点出发有4条对角线的正多边形的周长为42cm，则这个正多边形的边长为()A.6cmB.7cmC.D.8.扇子最早称“翣”，在我国已有两千多年历史.“打开半个月亮，收起兜里可装，来时荷花初放，去时菊花正黄.”这则谜语说的就是扇子.如图，一竹扇完全打开后，外侧两竹条AB，AC夹角为，AB的长为30cm，扇面BD的长为20cm，则扇面面积为A. B. C. D.9.在学习完多边形后，小华同学将一个五边形沿如图所示的直线1剪掉一个角后，得到一个多边形，下列说法正确的是()A.这个多边形是一个五边形B.从这个多边形的顶点A出发，最多可以画4条对角线C.从顶点A出发的所有对角线将这个多边形分成4个三角形D.以上说法都不正确二、填空题：本题共4小题，每小题3分，共12分。

10.如图所示，将一个圆分成4个扇形，已知扇形AOB，AOD，BOD的圆心角的度数之比为2：3：4，OC为的平分线，圆心角的度数为______.11.如图，甲、乙、丙、丁四个扇形的面积之比是1：2：3：4，则扇形“丁”的圆心角度数是______.12.如图所示，若扇形甲、乙的圆心角的度数之比为2：1，则扇形甲圆心角的度数为______；扇形丙圆心角的度数为______.13.已知扇形的面积为圆心角为，则它的半径为______.三、解答题：本题共4小题，共32分。

4.5多边形和圆的初步认识1．在以下实际生活中的物体，其外表形状可近似地看作多边形的是( ) A．硬币B．六角螺丝C．菊花D．日光灯2．以下平面图形中，不是多边形的是( )A．三角形B．五边形C．扇形D．八边形3．过多边形一个顶点与其他顶点连线把图形分割成三角形，可以分成4个三角形的是( )A．四边形B．五边形C．六边形D．七边形4．扇形是由一条________和经过______________的两条半径所组成的图形．5．多边形是由一些_______组成的封闭图形．6．从三角形内部一点出发，分别连接这点与三个顶点，可将原三角形分成_______个三角形．7．如图，图中有多少个不同的四边形?此图看起来有些像什么?8．如图，图中有多少个三角形?思维能力拓展9．以下说法错误的选项是( )A．多边形是平面图形，平面图形不一定是多边形B．四边形由四条线段组成，但四条线段组成的图形不一定是四边形C．多边形是一个封闭图形，但封闭图形不一定是多边形D．封闭的平面图形一定是多边形10．在一个圆中任意画四条半径，可以把这个圆分成几个扇形?请你画图说明．11．(1)从n边形的一个顶点出发，分别连接这个顶点与其余各顶点(相邻顶点除外)，可把这个n边形分割成________个三角形．(2) 从n边形一边上任一点(除顶点)出发，分别连接这个点与其余各顶点(左、右相邻顶点除外)，可把这个n边形分割成________个三角形．(3)从n边形内部任意一点出发，分别连接这个点与各顶点，可把这个n边形分割成________个三角形．中考名题演练12.如图，边长为l2 m的正方形池塘的周围是草地，池塘边A、B、C、D处各有一棵树，且AB=BC=CD=3m．现用长4m的绳子将一头羊拴在其中一棵树上．为了使羊在草地上活动区域的面积最大，应将绳子拴在( )A．A处B．B处C．C处D．D处参考答案：1. B2. C3. C4.弧；这条弧的端点思维能力拓展9. D11. (1)n－2; (2) n－1; (3) n.中考名题演练12. D1.3 截一个几何体一、判断题1．用一个平面去截一个正方体，截出的面一定是正方形或长方形.〔〕2．用一个平面去截一个圆柱，截出的面一定是圆.〔〕3．用一个平面去截圆锥，截出的面一定是三角形.〔〕4．用一个平面去截一个球，无论如何截，截面都是一个圆.〔〕二、填空题5．用一个平面去截一个球体所得的截面图形是__________．6．如图1，长方体中截面BB1D1D是长方体的对角面，它是__________．7．在正方体中经过从一个顶点出发的三条棱的中点的截面是_________．三、选择题8．用一个平面去截圆锥，得到的平面不可能是〔〕9．用一个平面去截一个圆柱，得到的图形不可能是〔〕10．用一个平面去截一个正方体，截面图形不可能是〔〕A．长方形; B．梯形; C．三角形; D．圆11．用一个平面去截一个几何体，如果截面的形状是圆，那么这个几何体不可能是〔〕A．圆柱; B．圆锥; C．正方体; D．球12．截去四边形的一个角，剩余图形不可能是〔〕A．三角形; B．四边形; C．五边形; D．圆四、解答题13．用平面去截一个正方体，截面的形状可能是平行四边形吗？截一截，想一想．14．用一个平面去截圆锥，可以得到几种不同的图形？动手试一试．15．指出以下几何体的截面形状．______________________ 16．编写一道自己感兴趣并与本节内容相关的题，解答出来．参考答案一、1．×2．×3．×4．√二、5．圆6．矩形7．三角形三、8．C9．D 10．D11．C12．D四、13．可能14．略15．四、五边形圆形16．略。

4.5多边形和圆的初步认识1.(8 分) 如图三角形的对角线有 0 条, 四边形的对角线有 2 条, 五边形的对角线有 5 条, 六边形的对角线有 9 条.经过剖析上边的资料 , 请你谈谈十边形的对角线有多少条 ?你能总结出n 边形的对角线有多少条吗 ?2.(8 分) 一个圆和一个扇形的半径相等 , 已知圆的面积是 30cm2, 扇形的圆心角是 36°. 求扇形的面积 .【拓展延长】3.(10 分) 已知扇形的圆心角为120°, 面积为 300π. 求扇形的弧长 .答案分析1.【分析】十边形的对角线有错误！未找到引用源。

=5×7=35(条),n 边形的对角线有错误！未找到引用源。

条.2.【分析】设半径为 r, 则 30÷π =r 2,错误！未找到引用源。

=错误！未找到引用源。

=3(cm2).2答: 扇形的面积是 3cm.3.【分析】设扇形的半径为 R,依据题意 , 得 300π=错误！未找到引用源。

,因此 R2=900,由于 R>0,因此 R=30.因此扇形的弧长 =错误！未找到引用源。

=20π.【知识拓展】扇形的弧长公式我们知道圆心角为n°, 半径为 R的扇形面积为错误！未找到引用源。

,这个公式是借助扇形面积与圆面积的比而求出的. 借助推导这一公式的思想方法 , 我们能够推导出其所对弧的长度的公式, 即:l弧=错误！未找到引用源。

, 则 l 弧=错误！未找到引用源。

×2πR=错C误！未找到引用源。

.。

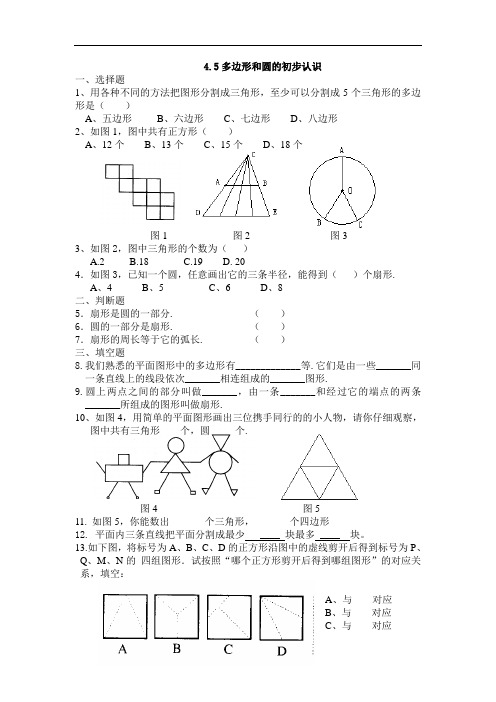
4.5多边形和圆的初步认识一、选择题1、用各种不同的方法把图形分割成三角形，至少可以分割成5个三角形的多边形是（）A、五边形B、六边形C、七边形D、八边形2、如图1，图中共有正方形（）A、12个B、13个C、15个D、18个图1 图2 图33、如图2，图中三角形的个数为（）A.2B.18C.19D. 204．如图3，已知一个圆，任意画出它的三条半径，能得到（）个扇形.A、4B、5C、6D、8二、判断题5．扇形是圆的一部分. （）6．圆的一部分是扇形. （）7．扇形的周长等于它的弧长. （）三、填空题8.我们熟悉的平面图形中的多边形有_____________等.它们是由一些_______同一条直线上的线段依次_______相连组成的_______图形.9.圆上两点之间的部分叫做_______，由一条_______和经过它的端点的两条_______所组成的图形叫做扇形.10、如图4，用简单的平面图形画出三位携手同行的的小人物，请你仔细观察，图中共有三角形____个，圆_____个.图4 图511. 如图5，你能数出_______个三角形，_______个四边形12. 平面内三条直线把平面分割成最少 ____ 块最多 ____ 块。

13.如下图，将标号为A、B、C、D的正方形沿图中的虚线剪开后得到标号为P、Q、M、N的四组图形．试按照“哪个正方形剪开后得到哪组图形”的对应关系，填空：A、与____对应B、与____对应C、与____对应D、与_____对应14.（1）从一个五边形的同一顶点出发，分别连接这个顶点与其余各顶点，可以把这个五边形分成_______个三角形.若是一个六边形，可以分割成_______个三角形.n边形可以分割成______个三角形.（2）若将n边形内部任意取一点P，将P与各顶点连接起来，则可将多边形分割成多少个三角形？（3）若点P取载多边形的一条边上（不是顶点）,在将P与n边形各顶点连接起来，则可将多边形分割成多少个三角形？15、如果从一个多边形的一个顶点出发，分别连接这个定点与其余各顶点，可将这个多边形分割成2003个三角形，那么此多边形的边数为多少？16、已知扇形AOB的圆心角为240o ,其面积为8cm2 .求扇形AOB所在的圆的面积。

4.5 多边形和圆的初步认识1.从一个七边形的某个顶点出发，分别连接这个点与其余各顶点，可以把一个七边形分割成( )个三角形．A ．6B ．5C ．8D ．72．如图，多边形的相邻两边均互相垂直，那么这个多边形的周长为( )A ．21B ．26C ．37D ．423．(1)十边形的一个顶点的对角线把十边形分成________个三角形． (2)正多边形是指________，________的多边形．4．如下图，∠BOC＝∠COD＝∠DOE＝12∠AOE，那么∠DOE＝________.5．如图，正方形ABCD 的边长为2，E ，F ，G ，H 分别为各边中点，EG ，FH 相交于点O ，以O 为圆心，OE 为半径画圆，那么图中阴影局部的面积为________．6．如下图，从一个多边形内任意取一点，分别连接这一点与各顶点．(1)数一数，每一个多边形各被分成了多少个三角形？ (2)总结一下，三角形的个数与多边形的边数有怎样的关系？7．一个圆被分成三个扇形，其中一个扇形的圆心角为72°，另外两个扇形的圆心角度数的比为3∶5，求这两个扇形的圆心角的度数．8．(1)如图(1)所示是四边形，小明作出它对角线为2条，算法为4×4－32＝2.(2)如图(2)是五边形，小明作出它的对角线有5条，算法为5×5－32＝5. (3)如图(3)是六边形，可以作出它的对角线有________条，算法为________．(4)猜测边数为n的多边形对角线条数的算法及条数．(2021·铜仁)如图，第1个图形中一共有1个平行四边形，第2个图形中一共有5个平行四边形，第3个图形中一共有11个平行四边形，……，那么第10个图形中平行四边形的个数是( )A．54 B．110C．19 D．109课后作业1．B 可以分成7－2＝5个三角形． 2．D 周长为(16＋5)×2＝42.3．(1)8 (2)各边相等 各角相等 4.36° 5.π2图中阴影局部可以拼成一个半圆，根据圆的面积公式计算即可．由题意可得：OE ＝1，阴影面积＝12π×12＝π2.6．解：(1)四边形被分成了4个三角形；五边形被分成了5个三角形；六边形被分成了6个三角形；(2)以这种方式分割，n 边形被分成了n 个三角形．7．解：另外两个扇形占整个圆的比例是：1－72360＝45，因为另外两个扇形的圆心角度数的比为3∶5，所以其中一个扇形占整个圆的45×38＝310，另一个扇形占整个圆的45×58＝12.所以360°×310＝108°，360°×12＝180°，所以另外两个圆心角分别为108°，180°.8．(3)9 6×6－32＝9 (4)n n －32中考链接D 第1个图形中有1个平行四边形；第2个图形中有1＋4＝5个平行四边形；第3个图形中有1＋4＋6＝11个平行四边形；第4个图形中有1＋4＋6＋8＝19个平行四边形；…；第n 个图形中有1＋2(2＋3＋4＋…＋n)个平行四边形；那么第10个图形中有1＋2(2＋3＋4＋5＋6＋7＋8＋9＋10)＝109个平行四边形．应选D .6.1 数据的收集1.某市期末考试中，甲校总分值人数占本校总人数的4%，乙校总分值人数占本校总人数的5%，那么两校总分值人数相比( )A ．甲校多于乙校B ．甲校与乙校一样多C ．甲校少于乙校D ．不能确定2．假设你想知道你们班级里的同学遇到烦恼时主要用哪几种方式排解，还想知道男、女同学排解烦恼的主要方式是否一样，你必须进行调查，然后对你调查出的结果加以总结，那么：(1)你的调查问题是______________________________； (2)你的调查对象是______________________________；(3)你感兴趣的是调查对象的______________________；(4)你的调查方法是______________________________．3．在数学、外语、语文3门学科中，某校七年级开展了同学们最喜欢学习哪门学科的调查(七年级共有200人)．(1)调查的问题是什么？(2)调查的对象是谁？(3)假设在被调查的200名学生中，有40人最喜欢学习语文，60人最喜欢学习数学，80人最喜欢学习外语，其余的人选择其他，求最喜欢学习数学的学生人数占被调查学生总数的比例．4．光明中学环保小组对某8个餐厅一天的快餐饭盒使用个数作了调查，结果如下：125,115,140,270,110,120,100,140.(1)这8个餐厅平均每个餐厅一天用多少个饭盒？(2)如果该区共有这种类似的餐厅62个，且所调查的8个餐厅是从这62个餐厅中随机抽取的，试问该地区一天共使用的快餐饭盒大约有多少个？5．为了帮助数学成绩差的学生，老师对180名数学成绩差的学生进行了问卷调查，设计的问题是“你的数学作业完成情况如何〞，并给出五个选项(独立完成、辅导完成、有时抄袭完成、经常抄袭完成、经常不完成)供学生选择．结果老师发现选择独立完成和辅导完成这两项的学生一共占了总调查人数的52%，明显高于他平时观察到的比例，你能解释这个统计数字失真的原因吗？(2021·荆门模拟)某住宅小区六月份中1日至6日每天用水量的变化情况如下折线图所示，那么这6天的平均用水量是( )A．30吨B．31吨C．32吨D．33吨课后作业1．D甲校总人数与乙校总人数不一定相等，应选D.2．解：(1)同学们主要用哪几种方式排解烦恼或男、女同学排解烦恼的主要方式是否一样(2)同班同学(3)排解烦恼的各种方式的数目(4)问卷调查或采访调查3．解：(1)在数学、外语、语文3门学科中，你最喜欢学习哪一门学科？(2)某校七年级的全体同学．(3)最喜欢学习数学的学生人数占被调查学生总数的比例为60200×100%＝30%.4．解：(1)(125＋115＋140＋270＋110＋120＋100＋140)÷8＝140(个)．(2)140×62＝8 680(个)．5．解：大家都知道抄袭和不完成作业是不好的行为，所以有些人不愿意成认抄袭和不完成作业也在情理之中，这个问题设计得不好，容易导致调查结果失真．中考链接C(30＋34＋32＋37＋28＋31)÷6＝32(吨)，应选C.。

多边形和圆的初步认识类型一、多边形及正多边形1．如图，（1）从正六边形的顶点A 出发,可以画出 条对角线，分别用字母表示出来为 ；（2）这些对角线把六边形分割成 个三角形.2、过多边形某个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形是（ ）A ．八边形B ．九边形C ．十边形D ．十一边形3、若一个多边形的内角和等于720°，则从这个多边形的一个顶点引出对角线 条．4、一个多边形除一个内角外其余内角的和为1510°，则这个多边形对角线的条数是（ ）A ．27B ． 35C ． 44D ． 545、同学们在平时的数学活动中会遇到这样一个问题：把正方形纸片截去一个角后，还剩多少角，余下的图形是几边形，亲爱的同学们，你知道吗?6、一个多边形共有20条对角线，则多边形的边数是（ ）.A.6B.7C.8D.97、下列说法中，结论错误的是（B ）A ．直径相等的两个圆是等圆B ．长度相等的两条弧是等弧C ．圆中最长的弦是直径D ．一条弦把圆分成两条弧，这两条弧可能是等弧8、有下列四个说法：①半径确定了，圆就确定了；②直径是弦；③弦是直径；④半圆是弧，但弧不一定是半圆．其中错误说法的个数是（ B ）A ．1B ． 2C ． 3D ． 49、下列说法正确的是（ ④ ）填序号．①半径不等的圆叫做同心圆； ②优弧一定大于劣弧；③不同的圆中不可能有相等的弦； ④直径是同一个圆中最长的弦10、如图是对称中心为点的正六边形．如果用一个含角的直角三角板的角，借助点（使角的顶点落在点处），把这个正六边形的面积等分，那么的所有可能的值是 ___________ __ .11、如图，MN 为⊙O 的弦，∠M=50°，则∠MON 等于 ． E A B CF D12、将一个半径为3的圆形草坪分割成三个扇形，分别种植三种花草，他们的圆心角的度数之比为2：3：4，求这三个圆心角的度数，并尝试求他们的面积，你还能求他们的面积之比吗，你发现了什么13、一个扇形圆心角120°，以扇形的半径为边长画一个正方形，这个正方形的面积是16平方厘米．这个扇形的面积为多少？。

4.5多边形和圆的初步认识课堂达标测试题1.多边形:由若干条_________________的线段首尾_________组成的封闭平面图形.（不在同一条直线上，顺次相连）2.多边形的对角线:多边形中连接_______两个顶点的线段.（不相邻）3.正多边形:各边_____,各角也_____的多边形.（相等、相等）4.圆:平面上,一条线段绕着它固定的一个端点_________,另一个端点形成的图形.（旋转一周）5.圆弧:圆上任意_____间的部分叫做圆弧，简称___.（两点、弧）6.扇形：一条弧和经过这条弧的端点的两条_____所组成的图形.（半径） 7.圆心角：顶点在_____的角.（ 圆心）8.扇形的面积公式:圆心角为n°,半径为R 的扇形的面积为______.（）9按下图中的两种分割方式分割多边形:A B CD E(1)数一数,每个多边形各被分成多少个三角形?(2)总结一下,三角形的个数与多边形的边数有怎样的关系?(三角形的个数与多边形的边数相等)（当从一个多边形的同一顶点出发,分别连接这个顶点与它不相邻的各顶点时,若多边形的边数为n,则能连出(n-3)条线段,将n边形分成(n-2)个三角形）.10、1.从一个七边形的某个顶点出发,分别连接这个点与其余各顶点,可以把一个七边形分割成几个三角形(n-2 )A.6B.5C.8D.7【解析】选B.画图可知,可以把一个七边形分割成7-2=5个三角形.11、.七边形的对角线总共有( n(n-3)/2 )A.12条B.13条C.14条D.15条【解析】选C.七边形的对角线总共有：7(73)2⨯-=14(条)．12、1.如图所示,阴影部分扇形的圆心角是( )A.15°B.23°C.30°D.36°【解析】选D.360°×(1-64%-26%)=36°.13、已知扇形的圆心角为60°，半径为6，则扇形的面积为( )A.24πB.12πC.6πD.2π【解析】选C.扇形的面积=26066 360π⨯=π．。

第四章 基本平面图形4.5 多边形和圆的初步认识精选练习一、单选题1．（2022·湖北·武汉二中广雅中学八年级阶段练习）六边形的对角线共有（ ）条．A ．5B ．9C ．12D ．142．（2022·河北· 沧州渤海新区京师学校八年级阶段练习）用三个不同的正多边形能够铺满地面的是（ ）A ．正三角形、正方形、正五边形B ．正三角形、正方形、正六边形C ．正三角形、正方形、正七边形D ．正三角形、正方形、正八边形3．（2020·山东淄博·期中）下列判断：（1）各边长相等的多边形是正多边形；（2）各角都相等的多边形是正多边形；（3）等边三角形是正多边形：（4）长方形是正多边形．其中正确的有（ ）A ．1个B ．2个C ．3个D ．4个4．（2022·全国·七年级专题练习）下面几何图形中，不属于平面图形的是( )A ．圆锥B ．正方形C ．扇形D ．五角星5．（2022·四川乐山·七年级期末）一个正多边形每个内角都等于150°，若用这种多边形拼接地板，需与下列选项中哪种正多边形组合（ ）A ．正三角形B ．正四边形C ．正五边形D ．正六边形6．（2022·吉林长春·七年级期末）下列正多边形中和正三角形组合，不能铺满地面的是（ ）A ．正方形B ．正八边形C ．正十二边形D ．正六边形二、填空题7．（2022·河北· 沧州渤海新区京师学校八年级阶段练习）从()5n +边形的一个顶点出发可引______条对角线，它们将n 边形分为______个三角形．8．（2021·山东·泰安市泰山区大津口中学七年级阶段练习）已知从九边形的一个顶点出发，可引出m 条对角线，这些对角线可以把这个九边形分成n 个三角形，则m n -=________；十三边形的共有________条对角线．9．（2022·广东湛江·八年级期中）从多边形的一个顶点出发，连接这个点和其他顶点，把多边形分割成16个三角形，则这个多边形的边数是 _____．10．（2022·安徽·定远县程桥学校七年级阶段练习）如图，图中阴影部分的面积可以用字母表示为 _____．三、解答题11．（2021·吉林·乾安县教师进修学校八年级期中）一个多边形的内角和是它的外角和的4倍，求这个多边形的边数和对角线条数．12．（2022·湖北·大悟县实验中学七年级阶段练习）求出下图阴影部分的周长和面积．单位：厘米（圆周率用π表示）一、填空题1．（2022·陕西汉中·七年级期末）用等边三角形和正方形作平面镶嵌，则在它的每个顶点周围有3个等边三角形和______ 个正方形．2．（2022·山东威海·七年级期中）已知：从n 边形的一个顶点出发共有4条对角线；从m 边形的一个顶点出发的所有对角线把m 边形分成6个三角形；正t 边形的边长为7，周长为63．则()t n m -的值为________．3．（2021·全国·八年级专题练习）正多边形的一个外角是40°，则这个正多边形从一个顶点出发有__条对角线．4．（2021·全国·九年级专题练习）一个n 边形共有n 条对角线，将这个n 边形截去一个角后它的边数为__．5．（2022·湖北武汉·九年级期末）如图，是编号为1、2、3、4的400m 跑道，每条跑道由两条直的跑道和两端是半圆形的跑道组成，每条跑道宽1m ，内侧的1号跑道长度为400m ，则2号跑道比1号跑道长_____m；若在一次200m比赛中（每个跑道都由一个半圆形跑道和部分直跑道组成），要使得每个运动员到达同一终点线，则4号跑道起跑点比2号跑道起跑点应前移_____m（π取3.14）．二、解答题6．（2022·陕西·子洲县张家港希望中学七年级阶段练习）将一根底面半径是5厘米的圆柱体木料锯成三段（每段都是圆柱体），其表面积增加了多少平方厘米？（p取3.14）7．（2021·全国·七年级）有一个著名的希波克拉蒂月牙问题．如图：以AB为直径作半圆，C是圆弧上一点，（不与A、B重合），以AC、BC为直径分别作半圆，围成两个月牙形1、2（阴影部分）．已知直径AC为4，直径BC为3，直径AB为5．（1）分别求出三个半圆的面积（结果保留π）；（2）请你猜测，这两个月牙形的面积与三角形ABC的面积之间有何等量关系，请写出你的猜想，并通过计算说明．8．（2022·全国·八年级）请仔细观察下面的图形和表格，并回答下列问题：多边形的顶点数/个45678……n从一个顶点出发的对角线的条数/条12345……①___________多边形对角线的总条数/条2591420……②___________（1）观察探究：请自己观察上面的图形和表格，并用含n的代数式将上面的表格填写完整，其中①______________________；②______________________；（2）实际应用：数学社团共分为6个小组，每组有3名同学．同学们约定，大年初一时不同组的两位同学之间要打一个电话拜年，请问，按照此约定，数学社团的同学们一共将拨打电话多少个？。