大学物理学之 机械能守恒
- 格式:ppt
- 大小:1.37 MB
- 文档页数:48


机械能守恒定律详解机械能守恒定律是物理学中的基本定律之一,它描述了一个封闭系统中机械能的守恒性质。
在本文中,我们将详细解释机械能守恒定律的概念、含义和适用条件,帮助读者更好地理解和应用这一定律。
一、机械能的概念机械能是指物体在力的作用下所具有的能力,它包括了物体的动能和势能两个方面。
具体而言,动能是物体由于运动而具有的能力,它与物体的质量和速度有关;势能是物体由于位置而具有的能力,它与物体的质量、重力加速度以及位置的高度有关。
二、机械能守恒定律的表述机械能守恒定律的表述可以用如下方式表示:在一个封闭系统中,当没有外力做功或外力做功等于零时,系统的总机械能保持不变。
三、机械能守恒定律的含义机械能守恒定律的核心意义在于系统总机械能的守恒性质。
当一个封闭系统中没有外力做功或外力做功等于零时,系统的总机械能保持恒定。
这意味着系统内部动能和势能之间可以相互转化,但总的机械能值始终保持不变。
四、机械能守恒定律的适用条件机械能守恒定律适用于满足以下条件的物理系统:1. 封闭系统:机械能守恒定律只适用于封闭系统,即系统与外界没有能量交换。
2. 无外力做功或外力做功为零:当外力对系统没有做功或做功等于零时,机械能守恒定律成立。
3. 弹性碰撞、无耗散:机械能守恒定律常用于弹性碰撞情况,因为在弹性碰撞中没有能量的损失和转化。
五、机械能守恒定律的应用举例1. 自由落体运动:当物体自由下落时,只受到重力作用,重力做负功,而势能的减少等于动能的增加,也即机械能守恒。
2. 弹簧振子:弹簧振子是一个典型的机械能守恒的例子,当弹簧振子在运动过程中,弹性势能和动能之间不断进行相互转化,但总的机械能保持不变。
六、机械能守恒定律的应用意义机械能守恒定律在物理学中有着重要的应用意义。
首先,它帮助我们深入理解和解释了物体的运动规律,以及能量在物理系统中的转化和守恒。
其次,机械能守恒定律在解决实际问题时具有指导性的作用,例如在动力学、机械工程和天体物理等领域都离不开对机械能守恒定律的应用。



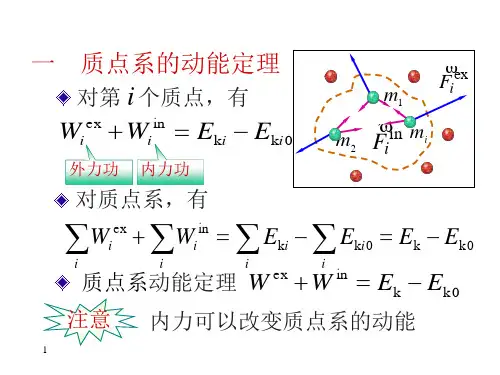
第四讲功能原理 机械能守恒定律 能量守恒定律k k k i i i i ii e E E E v m v m W W ∆=-=-=+∑122122)2121(系统的外力和内力作功的总和等于系统动能的增量。
回顾前面学过的知识点:1. 质点系动能定理P1p 2p )(E E E W ∆-=--=2. 保守力作功等于势能的减少3. 成对力的功只与作用力和相对位移有关:r d F dW '⋅= 22/16※ 质点系功能原理1、系统的机械能: 动能与势能的总和称为机械能3、由势能的定义,保守内力的功总等于系统势能的减少pin c E W ∆-= 2、内力的功可分为: 保守内力的功和非保守内力功pk E E E +=(保守内力的功由势能代替)第四讲 功能原理 机械能守恒定律 能量守恒定律 in ncin c in in W W W W i i+==∑非保守内力的功将导致机械能与其他形式的能量转换。
inncex p k W W E E E +=∆+∆=∆k in ncp ex in nc in c ex in ex E W E W W W W W W ∆=+∆-=++=+ 4、系统的功能原理 (由质点系动能定理)在选定的质点系内,在任一过程中,质点系总机械能的增量等于所有外力的功与非保守内力的功的代数和。
4/16※ 机械能守恒定律问题1:有非保守内力作功,系统的机械能不守恒 ?例如:摩擦力作功,机械能转变成热能。
0=+in nc ex W W 0=∆+∆=∆p k E E E 常量=+p k E E 由功能原理:则:或:如果: 如果系统内只有保守内力作功,其他内力和一切外力都不作功,或元功之和恒为零,则系统内各物体的动能和势能可以相互转换,但总机械能保持不变。
问题2:有摩擦力作功:机械能守恒?in nc ex p k W W E E E +=∆+∆=∆力 f 作正功,f ' 作负功,总和为零,机械能守恒。

机械能守恒定律解析机械能守恒定律是物理学中的重要定律之一,它可以用来描述机械能的转化和守恒。
在物体受到外力作用的过程中,机械能可以从一种形式转化为另一种形式,但总的机械能保持不变。
本文将对机械能守恒定律进行详细解析,探讨其原理及应用。
一、机械能的定义及分类机械能是指物体由于位置、形状或状态而具有的能力,它包括动能和势能两个方面。
动能是物体由于运动而具有的能力,它与物体的质量和速度有关;势能是物体由于位置、形状或状态而具有的能力,例如重力势能、弹性势能等。
机械能等于动能和势能的总和。
机械能可以根据物体的运动状态分为定值机械能和变值机械能。
定值机械能指的是在某一特定运动状态下,机械能保持不变。
例如,一个自由下落的物体只具有重力势能和动能,其机械能保持不变。
而变值机械能指的是在物体的运动过程中,机械能发生了变化。
例如,一个被弹力拉伸的弹簧具有势能和动能,在释放时,势能会转化为动能,机械能发生了变化。
二、机械能守恒定律的表述机械能守恒定律表述了一个封闭系统中总机械能的守恒。
在没有外力做功和机械能转化损耗的情况下,机械能守恒定律成立。
这意味着系统中的总机械能,在运动过程中会保持不变。
机械能守恒定律的数学表达式为:E = K + U = 常数其中,E表示总机械能,K表示动能,U表示势能。
根据机械能守恒定律,一个物体在运动过程中可以将动能转化为势能,或将势能转化为动能,但总的机械能保持不变。
三、机械能守恒定律的原理解析机械能守恒定律的原理可以从能量守恒定律和功的定义来解析。
根据能量守恒定律,一个封闭系统中的总能量在没有能量流入或流出时保持不变。
而根据功的定义,功可以用来描述力对物体所做的能量转化。
由于机械能包括了动能和势能,力对物体所做的功可以分别转化为动能和势能的变化。
当一个物体在受到外力作用的过程中,如果没有能量流入或流出系统,只有力对物体做功,机械能守恒定律就成立。
在这种情况下,在物体运动过程中动能和势能的变化互相抵消,总机械能保持不变。



机械能守恒大学物理中动能与势能的转化与守恒在大学物理中,机械能守恒是一个非常重要的概念。
它描述了一个系统中动能与势能之间的转化与守恒关系。
在本文中,我们将详细探讨机械能守恒的原理和应用。
1. 机械能的定义和表达式机械能是指一个物体的动能和势能之和。
动能是物体由于运动而具有的能量,通常用K表示。
势能是物体由于位置而具有的能量,通常用U表示。
因此,一个物体的机械能E可以表示为E = K + U。
2. 动能与势能的转化动能和势能之间存在一种转化关系。
当物体进行运动时,它的动能会增加,而势能会减少。
当物体停止运动时,动能消失,而势能达到最大值。
这个过程可以通过一个简单的例子来解释。
假设有一个小球从某个高度释放,下落到地面。
在初始时刻,小球具有势能,而没有动能。
随着小球下落,它的势能逐渐减少,而动能逐渐增加。
当小球触及地面时,它的势能被完全转化为动能,达到最大值。
可以通过公式来表示这个转化过程。
3. 机械能守恒定律根据机械能的定义和动能与势能的转化关系,我们可以得出一个重要的结论,即机械能守恒定律。
该定律表明,在一个封闭系统中,机械能的总量保持不变。
换句话说,机械能在系统内部的转化过程中是守恒的。
这个定律可以通过许多实际情况进行验证。
例如,当一个物体在重力场中自由下落时,它的机械能守恒。
在下落过程中,重力势能逐渐减少,而动能相应增加。
但总的机械能保持不变。
4. 机械能守恒定律的应用机械能守恒定律在物理学中有许多应用。
一个常见的应用是解决机械问题,例如弹簧振子的周期和振幅问题。
通过分析系统的机械能守恒,我们可以推导出一些与物体运动相关的量。
此外,机械能守恒定律还可以用于解释许多其他物理现象。
例如,当一个人骑自行车爬坡时,他需要将自行车的动能转化为势能来克服重力,以保持平衡。
同样地,当他下坡时,势能转化为动能,使他能够加速。
总结:在大学物理中,机械能守恒是一个重要的概念,它描述了动能和势能之间的转化与守恒关系。

机械能守恒机械能守恒定律和应用机械能守恒——机械能守恒定律和应用机械能守恒是动力学中的一个基本定律,表明在没有外力做功和无能量损失的情况下,机械能将保持不变。
本文将详细介绍机械能守恒定律的原理和应用。
一、机械能守恒的原理机械能守恒是基于动力学中的能量守恒定律。
在理想条件下,一个物体的机械能等于其动能和势能之和。
动能由物体的质量和速度决定,而势能则由物体的质量、重力加速度和高度决定。
根据机械能守恒定律,一个系统的机械能在任何时刻都保持不变。
二、机械能守恒定律的应用1. 自由落体运动自由落体是指只有重力作用的物体运动,根据机械能守恒定律,自由落体运动中物体的势能转化为动能,其总量保持不变。
例如,一个物体从高处自由落下,其势能逐渐减小,而动能逐渐增加,最终达到最大值。
2. 弹簧振子弹簧振子是一种涉及机械能转化的系统。
当弹簧振子偏离平衡位置时,它具有势能;当它通过振动重新回到平衡位置时,势能转化为动能。
根据机械能守恒定律,弹簧振子在振动过程中机械能保持不变。
3. 动能转化机械能守恒定律也适用于动能在不同形式之间的转化。
例如,当一个物体由静止开始沿斜面滑下时,其势能减少,而动能增加,保持总机械能不变。
同样地,当一个物体沿反方向上升时,动能减少,势能增加,机械能仍然保持不变。
4. 能量利用和设计机械能守恒定律在工程设计和能量利用中有着广泛的应用。
例如,水力发电利用水的下落产生的机械能,转化为电能。
再如,机械能守恒定律可以帮助工程师设计高效的机械系统,以最大限度地利用能量,减少能量浪费。
总结:机械能守恒定律是动力学中的重要定律,描述了一个系统中机械能保持不变的原理。
通过对机械能守恒定律的应用,可以解释自由落体运动、弹簧振子等物理现象,并在工程设计和能量利用中发挥重要作用。
理解和应用机械能守恒定律有助于我们深入理解能量转化和守恒的基本原理。
机械能的守恒定律机械能的守恒定律是物理学中的一个基本原理,对于许多力学问题都起着重要的作用。
在日常生活中,我们经常会遇到各种物体之间的相互作用,而机械能的守恒定律则可以帮助我们更好地理解这些现象。
首先,让我们来看一个简单的例子。
假设我们有一个小球从高处自由落下,只受到重力的作用。
当小球下落到最低点时,它的动能已经完全转化为势能。
这一过程中,机械能被守恒了下来。
这意味着机械能在过程中既没有增加也没有减少,它只是从一种形式转化为另一种形式。
同样地,在一个弹簧振子的例子中,弹簧受到外力推动而上升,然后再回到原来的位置。
在这个过程中,机械能也是守恒的。
当弹簧振子上升时,它的势能增加,而动能减少。
当弹簧振子下降时,势能减少,动能增加。
无论是上升还是下降,机械能总量都保持不变。
机械能的守恒定律可以用一个简单的公式来表示:机械能=势能+动能。
在上述两个例子中,我们可以观察到,势能和动能之间存在一种平衡,它们的总和保持不变。
这个定律在实际生活中有着广泛的应用。
例如,在电梯的运行过程中,人们常常会感受到不同的加速度。
当电梯上升时,人们会感觉到向上的加速度,身体会受到往上的力的作用。
而当电梯下降时,人们会感觉到向下的加速度,身体会受到往下的力的作用。
在这个过程中,机械能也是守恒的。
电梯的动能和势能之间相互转化,总的机械能保持不变。
同样地,在过山车的运行过程中,乘客可能会感受到各种不同的力的作用。
当过山车顶点时,乘客会感受到失重的感觉,这是因为过山车的速度变为零,动能减小到最小。
而在过山车下坡时,乘客会感受到加速度和向下的力,速度增加,动能增大。
在这个过程中,机械能同样是守恒的。
机械能的守恒定律不仅可以帮助我们更好地理解力学问题,还可以应用到工程建设和物理实验中。
在工程建设中,例如在建造高楼大厦或桥梁时,守恒定律可以帮助工程师计算出合适的材料强度,以确保结构的稳定和安全。
在物理实验中,守恒定律可以帮助研究人员设计合适的实验条件和方法,以保证实验结果的准确性。
机械能守恒的知识点
1. 机械能守恒就是能量不会凭空消失或出现呀!就像你骑自行车从坡上冲下来,速度越来越快,重力势能转化成了动能,但总的机械能是不变的哟!例子:你想想,是不是感觉很神奇呀?
2. 嘿,机械能守恒还有个特点呢,在只有重力或弹力做功的情况下就一直成立哦!比如弹弓把石子射出去,橡皮筋的弹性势能就变成了石子的动能呢!这不是很有意思吗?
3. 要注意哦,机械能要是不守恒那可就出问题啦!比如有摩擦之类的其他力做功。
就像汽车在路上跑,摩擦力会让一部分机械能损耗掉呢!你说是不是呀?
4. 机械能守恒在生活中可常见啦!像秋千荡来荡去,就是动能和重力势能在相互转化呀,但它们加起来始终不变呢,多神奇呀!你难道不觉得很有趣吗?
5. 哎呀,如果没有机械能守恒,那世界该多混乱呀!好比钟摆如果不守恒,那还怎么有规律地摆动呀?这多让人不可思议呀!
6. 大家可要记住机械能守恒这个厉害的知识点呀!它就像一个神奇的魔法,让各种能量有序变化呢!例如跳水运动员从跳台上跳下,就是重力势能转化为动能啦!是不是超级酷呀?
7. 机械能守恒真的是太重要啦!它让我们理解了许多物理现象呢。
就像游乐园里的过山车,忽上忽下的,全靠机械能守恒在维持呀!你不惊叹它的奇妙吗?
我的观点结论:机械能守恒真的是非常神奇又重要的物理知识点呀,它在我们的生活和各种运动中都有着广泛的体现呢!。
物理中的机械能守恒物理学中的机械能守恒是一个非常重要的概念。
它描述了在一个封闭系统中,机械能的总量保持不变。
机械能包括动能和势能两部分,它们在物体的运动和位置改变时相互转换,但总量保持不变。
本文将探讨机械能守恒的原理、应用以及一些相关实例。
一、机械能守恒的原理机械能守恒的原理可以通过动能和势能的转化来解释。
动能是物体运动所具有的能量,它与物体的质量和速度有关,可以用公式K=0.5mv²表示,其中K表示动能,m表示质量,v表示速度。
势能是物体位置所具有的能量,常见的势能有重力势能和弹性势能。
重力势能可以用公式PE=mgh表示,其中PE表示重力势能,m表示质量,g 表示重力加速度,h表示高度。
弹性势能可以用公式PE=0.5kx²表示,其中PE表示弹性势能,k表示弹簧的弹性系数,x表示弹簧的变形长度。
在一个封闭系统中,机械能守恒的原理可以概括为:当物体只受内力和重力等保守力作用时,机械能保持不变。
在这种情况下,机械能的转化可以用如下公式表示:K₁+PE₁=K₂+PE₂,其中K₁和K₂分别表示物体在不同状态下的动能,PE₁和PE₂分别表示物体在不同位置下的势能。
二、机械能守恒的应用机械能守恒的原理在物理学中有许多实际应用。
下面将介绍几个常见的例子。
1. 钟摆的运动钟摆是一个典型的机械能守恒的例子。
当钟摆处于最高点或最低点时,动能为零,势能最大;当钟摆通过最低点时,动能最大,势能为零。
在整个运动过程中,钟摆的总机械能保持不变。
2. 瀑布的落差瀑布是另一个机械能守恒的例子。
当水从瀑布上方自由落体下落时,其势能逐渐转化为动能。
当水落到底部时,势能为零,动能最大。
在这个过程中,水的总机械能保持不变。
3. 弹簧振子弹簧振子也是一个机械能守恒的典型例子。
当振子到达最大位移时,动能为零,弹性势能最大;当振子通过平衡位置时,动能最大,弹性势能为零。
在振动的整个过程中,振子的总机械能保持不变。
三、机械能守恒的实例分析机械能守恒的概念可以帮助我们分析一些实际情况。