当前位置：文档之家 › 大学物理第3章刚体的定轴转动精品文档36页

大学物理第3章刚体的定轴转动精品文档36页

  • 格式：ppt
  • 大小：829.00 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

力矩 刚体绕定轴转动定律-精品文档

力矩 刚体绕定轴转动定律-精品文档
力矩 刚体绕定轴转动定律
一、刚体绕定轴转动的力矩
z
F//
F
F对点O转动的力矩:
MO
O
Mz
y
x
r
P
F
F对定轴z转动的力矩:
M r F O r F r F //
M r F z
二、定轴转动定律
M β z J
M J Fr 2 M Fr 39 . 2 [ rad /s ]
mg T ma
Tr J
J
r
O
T
F
mg
(2)
ar
21 . 8 [ rad /s]
2
例: 均匀细直棒m 、l ，可绕轴 O 在竖直平面内转动 初始时它在水平位置 m l O 求: 它由此下摆 角时的
转动惯量与转轴有关
例: 求圆环绕中心轴旋转的转动惯量
2 解: dm 转动惯量 d JR d m
2 J R d m R d m mR 2 2 0 0 L L
dl R o
m
例: 求圆盘绕中心轴旋转的转动惯量 m 2 mr m d S 解: d 2 2πrdr 2 dr πR R dm 转动惯量 d J r2d m
M r d f df 的力矩 d
R
2 d M mgR 圆盘摩擦力矩 M 0 2 1 2d 3 mgR mR
d M

d 3 转动定律 MJ dt 3R0 t 0 3 R t d t d 0 4g g 04
2
d t
例: 一均质棒，长度为 l，现有一水平打 击力F 作用于距轴 l 处。 求: l =? 时, 轴对棒作用力的水平分量为 0。

大学物理 刚体的定轴转动-2

大学物理 刚体的定轴转动-2
第3章 刚体的定轴转动
Rotating of a Rigid Body About a Fixed Axis
第1节 刚体的平动和转动 第2节 刚体定轴转动定律 第3节 刚体转动的功和能 第4节 刚体的角动量定理
和角动量守恒定律 第5节 进动
思考. 1、一轻绳跨过一质量为 m、半径为 R
的定滑轮（视为圆盘），绳两端各悬两物， m1 < m2 ， 所受的摩擦阻力矩为 Mr ，绳与滑 轮间无相对滑动。试求：物体的加速度和绳 的张力。
质对点质角点动：量J =Lrm=r，2rr ×r仅mvr⊥rrvr部⊥ v分r L = mr2ω J
例1. 一轻绳跨过一质量为M 、半径为 R的定滑轮
（摩视擦为阻圆力盘矩）为，M绳r ，两绳端与各滑悬轮两间物无，相m对1 <滑m动T2 ，1。=所试T受求2的：??
物体的加速度和绳的张力。 arτ = βr × rr 解: 一、隔离法 研究对象 m1 m2 M
m1
.m R
m2
定轴O
m·
R 2、已知：绳轮无相对滑动，绳不可
伸长,下落时间t=3,R=0.2m,m=1kg,
绳 v0=0
h=1.5m, v0 =0.求：轮对轴的J
m
t h 3、刚体系统内力矩做功吗？
一、刚体的平动
质心运动定理 Fr合外 = Marc pr = Mvrc
rrc =
∑ mirri ∑ mi
Ek + Ep = C
Ek + Ep = C
∑ J = ∆miri2 (分立) Mz = 0 L = Jω
m r
J = 2 mR2 + mr2 5
发动机带动套
m 管上下移动时， ω变化

大学物理第3章刚体的定轴转动

大学物理第3章刚体的定轴转动

13
【例5】长为 l、质量为 m 的匀质细杆，绕与杆垂直的 质心轴转动，求转动惯量 J。
【解】建立坐标系，分割质量元
J x2dm

l2 l 2
x2Байду номын сангаас
ml dx
1 ml 2 12
x o x dx
【例6】长为 l、质量为 m 的匀质细杆，绕细杆一端轴 转动，求转动惯量 J。
【解】J x2dm
L
L
11
【例2】半径为 R 质量为 M 的圆环，绕垂直于圆环平 面的质心轴转动，求转动惯量J。
【解】分割质量元，环上各质元到轴的距离相等。
M
J
R2dm R2
M
dm
MR2
0
0
【例3】在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的质点，可绕 O轴转动，求质点系的转动惯量J。
刚体作定轴转动时, 刚体上各质点都作圆周运动。 各质点运动的线量一般不同，但角量完全相同。
1.角坐标
OP与极轴之间的夹角称 为角坐标（或角位置）
角坐标为标量，但可有正负。
o
P

x
在定轴转动过程中，角坐标是时间的函数： =(t)，称为转动方程。
3
2.角位移
角坐标的增量 称为刚体的角位移
i
i
i
得 LJ

v i m i ri
29
由刚体定轴转动定律
得到
MJ J
d dt
d( J ) dt

dL dt
M dL 定轴转动刚体角动量定理微分形式 dt
t
L
Mdt d
t0
L0
LLL0

第三章刚体的运动(大学物理)

第三章刚体的运动(大学物理)
第三章 刚体的定轴转动
3-1 刚体的基本运动 一、刚体 F
t
A B C
t + t 才 感受到力
在任何情况下物体的形状和大小都不会变化，因 而可以瞬时传递力。
即：质元间保持不变，称“不变质点系” 。刚体 是个理想化的模型。
二、刚体的运动形式 1.平动 *刚体上所有质元都 沿平行路径运动,各 个时刻的相对位置都 彼此固定。
1.角速度矢量 的规定： 大小
d dt
ω
v
r
刚体
P r
方向：沿瞬时轴，与转向成 右螺旋关系。 2.线速度与角速度的关系：
× 基点O 瞬时轴
v r
r
例题1 一刚体以每分钟60转绕z轴做匀速转动 沿z轴正方向）。设某时刻刚体上一点P的位 （ 置矢量为r 3i 4 j 5k ，则该时刻P点速度。
m1 g T1 m1a T2 m2 g m2a
T2 m2 g
M T1 T
m1
1
a
m1 g
对定滑轮
1 rT1 rT2 Mr 2 2 且有 a r
(m1 m2 ) g 可得 M (m1 m2 )r 2
(m1 m2 ) g a M m1 m2 2
①对O点：rom T 0
rom mg lsin （mg）
锥摆
O
T l
m
O
合力矩不为零，角动量变化。
v mg
（ mg） 0 ②对O点： rom T rom
rom mg rom T
合力矩为零，角动量大小、方向都不变。
2.刚体定轴转动的角动量定理
M r F m
Or
·

第3章刚体的定轴转动

第3章刚体的定轴转动
（第3版）
转动平面
(rad / s2)
2–6 刚体的定轴转动
2.角量与线量的关系
大学物理学 6
（第3版）
当刚体绕固定轴转动时，刚体上某质元i
vi ri ai ri ain 2ri
刚体上各质元的角量相同，而各质元的线量大小 与质元到转轴的距离成正比．
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动
1.刚体定轴转动的转动定律
在刚体上任取一质元Δmi 在转动平面内，设它所受的合外力
为 Fi，合内力为 fi，
Fi
fi
m iai
Fi sin i fi sini ) miai miri
将切向方程的两边各乘以ri，可得
Firi sin i firi sini miri2
第2章 运动定律与力学中的守恒定律
§3.2 刚体定轴转动的转动定理
一、刚体定轴转动的转动定律 方向平行于轴的力，在定轴问题 中，不影响物体绕轴转动状态。 方向垂直于轴的力，在平行于 轴的方向上产生一个力矩，此 力矩改变物体绕轴转动状态， 称为力对轴的矩。
第2章 运动定律与力学中的守恒定律
大学物理学 （第3版）
7
2–6 刚体的定轴转动
第2章 运动定律与力学中的守恒定律
2–6 刚体的定轴转动
三 刚体定轴转动的描述 1.角位移、角速度和角加速度
角位移：Δθ＝θ2－θ1
平均角速度：
t 角速度： lim d
t0 t dt
平均角加速度：
t
角加速度： lim d
t0 t dt
第2章 运动定律与力学中的守恒定律
大学物理学 5
J
dJ
RLeabharlann 2r3dr1

第3章 刚体的定轴转动(I)

第3章 刚体的定轴转动(I)

主讲: 刘玉波刚体：在力的作用下, 物体的大小和形状都保持不变，称为刚体.在讨论问题时可以忽略由于受力而引起的形状和体积的改变的理想模型。

第3章刚体的定轴转动研究方法：运动学：用角量研究整体运动。

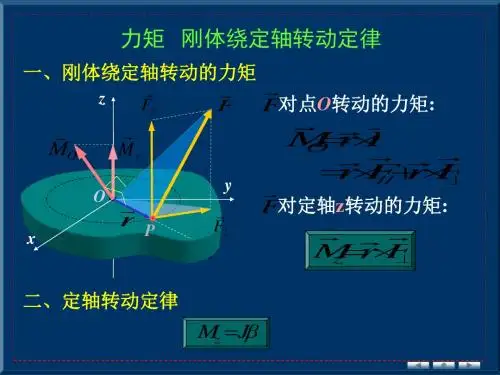
动力学：整体运动的原因及规律(力矩)。

力矩的时间、空间积累效应。

研究思路：把刚体质点化，把质点运动规律应用于质点系，从而导出刚体整体运动规律。

3.1 刚体定轴转动的运动学一刚体的平动与转动刚体运动：平动转动{定轴转动非定轴转动{刚体平动质点运动平动：若刚体中所有点的运动轨迹都保持完全相同，或者说刚体内任意两点间的连线总是平行于它们的初始位置间的连线.转动：刚体中所有的点都绕同一直线做圆周运动. 转动又分定轴转动和非定轴转动.刚体的非定轴转动.+刚体的一般运动质心的平动绕质心的转动二刚体绕定轴转动的角速度和角加速度1 角速度和角加速度刚体内各点都绕同一直线(转轴)作圆周运动，而刚体转动时，转轴固定不动—定轴转动.)θz xP 'P Oθd t d 参考平面上一点P ：可用位矢、角坐标确定位置。

r)(t θθ=用的正、负表示其方位(约定：逆时针为正，顺时针为负）。

θ角速度：描述转动快慢的物理量。

td d θω=矢量方向：右手螺旋法则。

单位：弧度/秒( rad/s )。

ω ω刚体定轴转动(一维转动)的转动方向可以用角速度的正负来表示。

角加速度：描述角速度变化快慢的物理量。

td d ωβ =瞬时角加速度，矢量。

方向：用正、负号表示(如图)。

单位：弧度/秒2 (rad/s 2)。

若已知求，或已知求，用积分。

ωθωβ⎰⎰=t d d βω⎰⎰=t d d ωθββ>∆ω0<∆ωz z1）每一质点均作圆周运动，圆面为转动平面；2）任一质点运动均相同，但不同；3）运动描述仅需一个坐标.βωθ,,∆a ,v 定轴转动的特点2 匀变速转动公式ω、β本来是矢量，由于在定轴转动中轴的方位不变，故只有沿轴的正负两个方向，可以用标量代替。

大学物理3_1 刚体的定轴转动


d 5 t dt 2
（1）t = 4 s 时， 则有
d 2 rad s dt
5 2 2 4 4 0 2 2
3–1
刚体的定轴转动
第三章 刚体的转动
5 3 4 rad s 2 2 d rad s 2 dt
刚体的一般运动 质心的平动
+
绕质心的转动

平动：若刚体中 所有点的运动轨迹都 保持完全相同，或者 说刚体内任意两点间 的连线总是平行于它 们的初始位置间的连 线.
刚体平动
质点运动
3–1
刚体的定轴转动
第三章 刚体的转动
转动：刚体中所有的点都绕同一直线做圆周运 动. 转动又分定轴转动和非定轴转动 .
第三章 刚体的转动
三
刚体定轴转动的运动学描述
物理量 位置坐标 运动方程 位移 速度 加速度
刚体的定轴转动
质点的直线运动
(t )

x x(t )
x
d
dx
v dx dt
a dv dt d x dt
2 2
d dt 2 2 d dt d dt
3–1
d lim0 t t dt

参考轴
方向:

右手螺旋方向
3–1
刚体的定轴转动
第三章 刚体的转动
刚体定轴转动（一 维转动）的转动方向可 以用角速度的正负来表 示.
角加速度

>0
z

z

<0
d dt


定轴转动的特点 1） 每一质点均作圆周运动，圆面为转动平面；

大学物理第3章第1节-刚体的定轴转动

1 2 1 2 1 2 1 2 A I2 I1 A mv2 mv1 2 2 2 2
角动量定理 (对轴)—动量定理

律
Mdt I 2 I1 Fdt mv2 mv1

角动量守恒定律 (对轴) —动量守恒定
( I ) 2 ( I )1
I R 2 dm R 2 dm mR2
0 0
R
dm

m

m
例 3.6 半径为 R 质量为 m 的匀质圆盘, 绕垂直于圆盘平面的质心轴转动, 求转动惯 m 量. 解 取半径为 dr 宽度 o r R dr 为 r 的圆环, 圆环对质心轴的转动惯量
2m 3 1 2 r d r mR I r d m 2 R 2 0 m
t
说明: 此处 T1 T1 T2 T2.
例 3.6 如图所示, 固定在一起的两个同 r 轴均匀圆柱体可 R O O 绕其光滑的水平 m 对称轴 OO 转动. M m1 m2 设大小圆柱体的 半径分别为 R 和 h r , 质量分别为 M 和 m . 绕在两柱体上的细绳分别与物体 m1 和 m2相连, m1 和 m2 挂在圆柱体的两侧. 设 R 0.2
z
m, L
解 细杆上不同位 置的线元的质量不同, 摩擦力也不同. 在距 o 端 r 处取 线元 d r , 对应质量
z
dr
dm
r
o
kr d m d r k r dr
(1)
1 2 m k r d r kL 0 2 2m k 2 L

L
(2)
线元受到的摩擦力
d f (d m) g
m1 g T1 m1a1

大学物理 第三章 刚体的定轴转动

由于绳子与滑轮间无相对滑动，所以
a1 = β r1 , a2 = β r2
联立以上 5 个方程可得，两物体的加速度和绳子中的张力分别为
a1 = a2 =
( m1r1 − m2 r2 ) r1 g
J1 + J 2 + m1r12 + m2r22
( m1r1 − m2 r2 ) r2 g
1
(J T =
1
解 设滑轮的半径为 R ,转动惯量为 J ，如图 3.5 所示。使用大小等于 mg ，方向向下的力拉
ww
对物体有： 对滑轮有：
绳子时，如图 3.5（a）,滑轮产生的角加速度为 β =
绳下段挂一质量为 m 的物体时，如图 3.5（b） ，若设绳子此时的拉力为 T，则
此时滑轮产生的角加速度为
mgR J + mR 2 比较可知，用大小等于 mg ，方向向下的拉力拉绳子时，滑轮产生的角加速度变大，本题 β=
习题精解
3-1 某刚体绕定轴做匀速转动， 对刚体上距转轴为 r 处的任意质元的法向加速度为和切线加 速度来正确的是（） A. an ， aτ 大小均随时间变化 C. an 的大小变化， aτ 的大小保持不变 B. an ， aτ 大小均保持不变 D. an 大小保持不变， aτ 的大小变化
解 刚体绕定轴做匀变速转动时，因为 an = rω 2 , aτ = r β ，而 β 为恒量，所以 ω = ω0 + β t ， 故 an = r ( ω0 + β t ) , aτ = r β 。可见： an 的大小变化， aτ 的大小保持恒定，本题答案为 C. 3-2 一飞轮以的角速度转动 300rad • min ，转动惯量为 5kg • m ，现施加一恒定的制动

大学物理第3章刚体的定轴转动


2. M、J、是对同一轴而言的。
3. 具有瞬时性，是力矩的瞬时效应。
4. 转动惯量J是刚体转动惯性大小的量度。
8 8
3、转动惯量的计算
转动惯量： J miri2
i
质量连续分布的刚体： J r2dm
质量为线分布： dm dl
面分布： dm ds
体分布： dm dV
R
T2
m2 g T2 m2a2 T1 T1
T 2
RT2

RT1

(
1 2
m3
R
2
)
无相对滑动： a1 a2 R
T2 ,T1
m2 mg
2
15
例 一均匀细棒，可绕通过其端点并与棒垂直的水
平轴转动。已知棒长l，质量m，开始时棒处于水平 位置。令棒由静止下摆，求：（1）棒在任意位置时
M z Fr sin Fh Ftr
2）力不在转动平面内
F// 对轴的力矩为零

F//

F

h
r

A
Ft F Fn
M z rF sin Fh Ftr
5
说明
在定轴转动问题中，力对转轴的矩等于转动平 面内的分力对转轴的力矩。
同一个力对不同转轴的矩不一样；
的角加速度；（2） 角为300，900时的角速度。
解: 选垂直纸面向里为转轴正向
棒在任意位置时质元dm对O轴 o
的重力矩
dM mg dr r cos

l


r
dr
d
dm g
M

dM

l
0
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

19
讨论 当不计滑轮质量和摩擦力矩时:
m = 0, Mf = 0 ，
【例6】长为 l、质量为 m 的匀质细杆，绕细杆一端轴 转动，求转动惯量 J。
【解】J x2dm
l x2 m dx 1 ml 2
0l
3
x o x dx
13
计算转动惯量J 的三条有用的定理
（1）叠加定理: 对同一转轴 J 有可叠加性
J Ji
（2）平行轴定理:
JAJc md2
所以 Jc 总是最小的。
这章学习方法: 对比法（对比质点力学） 刚体-----形状与大小都不变的物体（理想模型）
刚体是一个特殊的质点系 -----质点之间的距离与相对位置都保持不变
§3.1 刚体定轴转动的描述
3.1.1 刚体的运动
1. 平动 2. 转动
定轴转动 定点转动（有瞬时轴）
1
3.1.2 刚体的角量描述
刚体作定轴转动时, 刚体上各质点都作圆周运动。 各质点运动的线量一般不同，但角量完全相同。
mR
轴上的摩擦力矩为 Mf（设绳轻，且 不伸长,与滑轮无相对滑动）。
求:物体的加速度及绳中张力。
m1
m2 【解】分别对m1, m2, m分析
17
因绳不伸长，有 a1= a2= a
因绳轻，有 T1T1,T2T2
对m1有 T1- m1g - = m1 a ----（1） 对 m2有 m2g - T2= m2 a ----（2）
JC
JA
dm C
平行
14
（3）垂直轴定理:（对薄平板刚体） z
r2d m x 2 y 2d m
xi
Jz JxJy
x
O
ri
Δ
m
i
yi
y
【例7】求对薄圆盘的一条直径的转动惯量
Jz
1 2
mR2
Jx
Jy
Jz
1 2
m R2
Jx
Jy
1 4
m R2
z
x0r y y x
15
【例8】 计算钟摆的转动惯量（已知：摆锤质量为m， 半径为r，摆杆质量也为m，长度为2r）。
1.角坐标
OP与极轴之间的夹角称 为角坐标（或角位置）
角坐标为标量，但可有正负。
o
P
x
在定轴转动过程中，角坐标是时间的函数： =(t)，称为转动方程。
2
2.角位移
角坐标的增量 称为刚体的角位移
3.角速度 平均角速度 ω
t
角速度 lim d
t0 t d t
角速度方向：满足右手定则，沿 刚体转动方向右旋大拇量
J (miri2)
刚体的转动惯量与刚体的形状、大小、质 量的分布以及转轴的位置有关。
对于质量连续分布的刚体
J r2dm r2dV
V
V
J r2dm r2dS （面质量分布）
S
S
J r2dm r2dl （线质量分布）
L
L
10
【例2】半径为 R 质量为 M 的圆环，绕垂直于圆环平 面的质心轴转动，求转动惯量J。
对所有质元求和，得到
F ir i tf ir t iΔ i a ir i t m ( Δ ir i 2 ) m
左边第一项表示合外力矩，记作M。
左边第二项表示内力矩之和，等于零。
(miri2)只与刚体的质量和质量相对转轴的分布
有关，称为刚体对轴的转动惯量，记作J。 则上式可简写成
MJ 刚体定轴转动定律
at
dv dt
r d r
dt
an
v2 r
( r )2
r
r2
p
s
p
o
rx
5
§3.2 刚体定轴转动定律
3.2.1 刚体定轴转动定律 1.力对转轴的矩 力对固定点的矩 M rF
力对固定轴的矩
把力分解为平行于转轴的分 量和垂直于转轴的分量。
平行转轴的力不产生转动效 果，对轴的矩为零。
MrF
ω
3
4.角加速度
平均角加速度
t
角加速度
lim d
t0 t d t
d 2 dt2
角速度和角加速度都是矢量，但对于定轴转动的刚 体，角速度和角加速度的方向只有两个，我们用正 负表示角速度和角加速度的方向。
4
5.角量与线量的关系
路程与角位移的关系 sr
线速度与角速度的关系 vr
圆周运动时加速度与角量的关系
【解】 dm2πrdr
J r2dm 2πr3dr
J2π Rr3dr 0
πR4
1mR2
22
o r dr R
12
【例5】长为 l、质量为 m 的匀质细杆，绕与杆垂直的 质心轴转动，求转动惯量 J。
【解】建立坐标系，分割质量元
J x2dm
l2 l 2
x2
ml dx
1 ml 2 12
x o x dx
【解】 摆杆转动惯量：
J1
1m2r2
3
4m2r 3
摆锤转动惯量：
O r
J2J Cm2 d 2 1m 2 r m 3 r21 2m 92 r
JJ1J24 3m2 r1 2m 92 r6 6m 52r
16
3.2.3 刚体定轴转动定律的应用
【例8】已知：两物体 m1、m2（m2 m1 ) 滑轮 m、R, 可看成质量均匀的圆盘,
【解】分割质量元，环上各质元到轴的距离相等。
M
J
R2dm R2
M
dm
MR2
0
0
【例3】在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的质点，可绕 O轴转动，求质点系的转动惯量J。
2
【解】 J miri2 2m2bm(3b)2 11mb2 i 1
11
【例4】一质量为m，半径为R的均匀圆盘，求对通过 盘中心并与盘面垂直的轴的转动惯量。
M
O r
F
d
Pr
6
【例1】一匀质细杆，长为 l 质量为 m ，在摩擦系数
为 的水平桌面上转动，求摩擦力的力矩 M阻。
【解】杆上各质元均受摩擦力作用，各质元所受的 摩擦阻力矩不同。
细杆的质量密度 m
l
质元质量 dmdx
质元受阻力矩
o
xl dm m dx
x
dM阻dmgx
细杆受的阻力矩
M阻
dM阻
N
M
T1
f
R T 2
mg
对滑轮 m 由转动方程
T 2RT 1RM f J1 2m2 R---（3）
T a1
1
再从运动学关系上有
m1g
aat R ---- （4）
联立四式解得：
T2 a2
m2g
18
a
m2
m1
g
Mf R
m1
m2
1 2
m
T1 m1ga2m2m1m 2m m21gm 2m1R Mf
T2 m2ga2m1mm 12m m22gm 2m2R Mf
l 0
gxdx
1 2
gl 2
1 2
m gl
7
2. 刚体定轴转动定律 考虑刚体上某一质元 ，其受力如图所示。对质元应 用牛顿第二定律：
F ifi m iai 法向分力的力矩为零，对切向力有
FitfitΔm iait
F ir tifir ti m iair ti
8
F ir tifir ti m iair ti