【大学物理上册课后答案】第3章 刚体的定轴转动
- 格式:doc
- 大小:750.00 KB
- 文档页数:10


大学物理第三章 课后习题答案3-1 半径为R 、质量为M 的均匀薄圆盘上,挖去一个直径为R 的圆孔,孔的中心在12R 处,求所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量。
分析:用补偿法〔负质量法〕求解,由平行轴定理求其挖去部分的转动惯量,用原圆盘转动惯量减去挖去部分的转动惯量即得。
注意对同一轴而言。
解:没挖去前大圆对通过原圆盘中心且与板面垂直的轴的转动惯量为:2112J MR =① 由平行轴定理得被挖去部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:2222213()()2424232c M R M R J J md MR =+=⨯⨯+⨯= ②由①②式得所剩部分对通过原圆盘中心且与板面垂直的轴的转动惯量为:2121332J J J MR =-=3-2 如题图3-2所示,一根均匀细铁丝,质量为M ,长度为L ,在其中点O 处弯成120θ=︒角,放在xOy 平面内,求铁丝对Ox 轴、Oy 轴、Oz 轴的转动惯量。
分析:取微元,由转动惯量的定义求积分可得 解:〔1〕对x 轴的转动惯量为:2022201(sin 60)32Lx M J r dm l dl ML L ===⎰⎰ 〔2〕对y 轴的转动惯量为:20222015()(sin 30)32296Ly M L M J l dl ML L =⨯⨯+=⎰〔3〕对Z 轴的转动惯量为:22112()32212z M L J ML =⨯⨯⨯=3-3 电风扇开启电源后经过5s 到达额定转速,此时角速度为每秒5转,关闭电源后经过16s 风扇停止转动,已知风扇转动惯量为20.5kg m ⋅,且摩擦力矩f M 和电磁力矩M 均为常量,求电机的电磁力矩M 。
分析:f M ,M 为常量,开启电源5s 内是匀加速转动,关闭电源16s 内是匀减速转动,可得相应加速度,由转动定律求得电磁力矩M 。
解:由定轴转动定律得:1f M M J β-=,即11252520.50.5 4.12516f M J M J J N m ππβββ⨯⨯=+=+=⨯+⨯=⋅ 3-4 飞轮的质量为60kg ,直径为0.5m ,转速为1000/min r ,现要求在5s 内使其制动,求制动力F ,假定闸瓦与飞轮之间的摩擦系数0.4μ=,飞轮的质量全部分布在轮的外周上,尺寸如题图3-4所示。


习题33.1选择题(1) 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为 (A)2ωmR J J+ (B) 02)(ωR m J J + (C)02ωmR J(D) 0ω [答案: (A)](2) 如题3.1(2)图所示,一光滑的内表面半径为10cm 的半球形碗,以匀角速度ω绕其对称轴OC 旋转,已知放在碗内表面上的一个小球P 相对于碗静止,其位置高于碗底4cm ,则由此可推知碗旋转的角速度约为 (A)13rad/s (B)17rad/s (C)10rad/s (D)18rad/s(a) (b)题3.1(2)图[答案: (A)](3)如3.1(3)图所示,有一小块物体,置于光滑的水平桌面上,有一绳其一端连结此物体,;另一端穿过桌面的小孔,该物体原以角速度 在距孔为R的圆周上转动,今将绳从小孔缓慢往下拉,则物体(A)动能不变,动量改变。
(B)动量不变,动能改变。
(C)角动量不变,动量不变。
(D)角动量改变,动量改变。
(E)角动量不变,动能、动量都改变。
[答案:(E)]3.2填空题(1) 半径为30cm的飞轮,从静止开始以0.5rad·s-2的匀角加速转动,则飞轮边缘上一点在飞轮转过240˚时的切向加速度aτ= ,法向加速度a n= 。
[答案:0.15; 1.256](2) 如题3.2(2)图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴O转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则在此击中过程中,木球、子弹、细棒系统的守恒,原因是。
木球被击中后棒和球升高的过程中,对木球、子弹、细棒、地球系统的守恒。
题3.2(2)图[答案:对o轴的角动量守恒,因为在子弹击中木球过程中系统所受外力对o 轴的合外力矩为零,机械能守恒](3) 两个质量分布均匀的圆盘A和B的密度分别为ρA和ρB (ρA>ρB),且两圆盘的总质量和厚度均相同。

第一章质点运动学1、(习题1.1):一质点在xOy 平面内运动,运动函数为2x =2t,y =4t 8-。
(1)求质点的轨道方程;(2)求t =1 s t =2 s 和时质点的位置、速度和加速度。
解:(1)由x=2t 得,y=4t 2-8 可得: y=x 2-8 即轨道曲线 (2)质点的位置 : 22(48)r ti t j =+- 由d /d v r t =则速度: 28v i tj =+ 由d /d a v t =则加速度: 8a j =则当t=1s 时,有 24,28,8r i j v i j a j =-=+= 当t=2s 时,有 48,216,8ri j v i j a j =+=+=2、(习题1.2): 质点沿x 在轴正向运动,加速度kv a -=,k 为常数.设从原点出发时速度为0v ,求运动方程)(t x x =.解:kv dtdv-= ⎰⎰-=t vv kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt ev dx tk tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动,其加速度为a = 4t (SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式. 解:=a d v /d t 4=t d v 4=t d t⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出,求:(1)小球的运动方程;(2)小球在落地之前的轨迹方程; (3)落地前瞬时小球的d d r t ,d d v t ,tv d d . 解:(1) t v x 0= 式(1)2gt 21h y -= 式(2) 201()(h -)2r t v t i gt j =+(2)联立式(1)、式(2)得 22v 2gx h y -=(3)0d -gt d rv i j t = 而落地所用时间 gh2t = 所以0d -2g h d r v i j t =d d v g j t =- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、 已知质点位矢随时间变化的函数形式为22r t i tj =+,式中r 的单位为m ,t 的单位为s .求:(1)任一时刻的速度和加速度;(2)任一时刻的切向加速度和法向加速度。


大学物理第3章-刚体力学习题解答第3章 刚体力学习题解答3.13 某发动机飞轮在时间间隔t 内的角位移为):,:(43s t rad ct bt at θθ-+=。
求t 时刻的角速度和角加速度。
解:23212643ct bt ct bt a dt d dtd -==-+==ωθβω3.14桑塔纳汽车时速为166km/h ,车轮滚动半径为0.26m ,发动机转速与驱动轮转速比为0.909, 问发动机转速为每分多少转?解:设车轮半径为R=0.26m ,发动机转速为n 1, 驱动轮转速为n 2, 汽车速度为v=166km/h 。
显然,汽车前进的速度就是驱动轮边缘的线速度,909.0/2212Rn Rn v ππ==,所以:min/1054.1/1024.93426.014.3210166909.02909.013rev h rev n R v ⨯=⨯===⨯⨯⨯⨯π3.15 如题3-15图所示,质量为m 的空心圆柱体,质量均匀分布,其内外半径为r 1和r 2,求对通过其中心轴的转动惯量。
解:设圆柱体长为h ,则半径为r ,厚为dr 的薄圆筒的质量dm 为:2..dm h r dr ρπ=对其轴线的转动惯量dI z 为232..z dI r dm h r dr ρπ==212222112..()2r z r I h r r dr m r r ρπ==-⎰ 3.17 如题3-17图所示,一半圆形细杆,半径为,质量为,求对过细杆二端轴的转动惯量。
解:如图所示,圆形细杆对过O 轴且垂直于圆形细杆所在平面的轴的转动惯量为mR 2,根据垂直轴定理z x y I I I =+和问题的对称性知:圆形细杆对过轴的转动惯量为12mR 2,由转动惯量的可加性可求得:半圆形细杆对过细杆二端轴的转动惯量为:214AA I mR '=3.18 在质量为M ,半径为R 的匀质圆盘上挖出半径为r 的两个圆孔,圆孔中心在半径R 的中点,求剩余部分对过大圆盘中心且与盘面垂直的轴线的转动惯量。
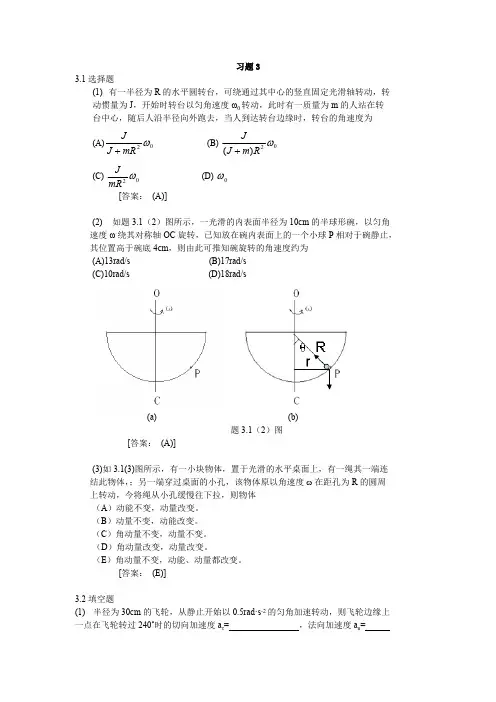
习题33.1选择题(1) 有一半径为R 的水平圆转台,可绕通过其中心的竖直固定光滑轴转动,转动惯量为J ,开始时转台以匀角速度ω0转动,此时有一质量为m 的人站在转台中心,随后人沿半径向外跑去,当人到达转台边缘时,转台的角速度为(A) (B) 02ωmRJ J +02)(ωR m J J +(C) (D) 02ωmRJ 0ω[答案: (A)](2) 如题3.1(2)图所示,一光滑的内表面半径为10cm 的半球形碗,以匀角速度ω绕其对称轴OC 旋转,已知放在碗内表面上的一个小球P 相对于碗静止,其位置高于碗底4cm ,则由此可推知碗旋转的角速度约为(A)13rad/s (B)17rad/s(C)10rad/s (D)18rad/s (a)(b)题3.1(2)图[答案: (A)](3)如3.1(3)图所示,有一小块物体,置于光滑的水平桌面上,有一绳其一端连结此物体,;另一端穿过桌面的小孔,该物体原以角速度ω在距孔为R 的圆周上转动,今将绳从小孔缓慢往下拉,则物体(A )动能不变,动量改变。
(B )动量不变,动能改变。
(C )角动量不变,动量不变。
(D )角动量改变,动量改变。
(E )角动量不变,动能、动量都改变。
[答案: (E)]3.2填空题(1) 半径为30cm 的飞轮,从静止开始以0.5rad·s -2的匀角加速转动,则飞轮边缘上一点在飞轮转过240˚时的切向加速度a τ= ,法向加速度a n = 。
0.15; 1.256[答案:](2) 如题3.2(2)图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴O转动,今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则在此击中过程中,木球、子弹、细棒系统的 守恒,原因是 。
木球被击中后棒和球升高的过程中,对木球、子弹、细棒、地球系统的 守恒。
题3.2(2)图[答案:对o轴的角动量守恒,因为在子弹击中木球过程中系统所受外力对o轴的合外力矩为零,机械能守恒](3) 两个质量分布均匀的圆盘A和B的密度分别为ρA和ρB (ρA>ρB),且两圆盘的总质量和厚度均相同。


第3章 刚体的定轴转动习题解答3-1 一汽车发动机曲轴的转速在12s 内由每分钟1200转匀加速地增加到每分钟2700转,求:(1)角加速度;(2)在此时间内,曲轴转了多少转?解:(1))/(401s rad πω= )/(902s rad πω=)/(1.13)/(6251240902212s rad s rad t≈=-=∆-=πππωωβ匀变速转动(2))(78022122rad πβωωθ=-=)(3902圈==πθn3-2 一飞轮的转动惯量为J ,在0=t 时角速度为0ω,此后飞轮经历制动过程。
阻力矩M 的大小与角速度ω的平方成正比,比例系数0>K 。
求:(1)当30ωω=时,飞轮的角加速度;(2)从开始制动到30ωω=所需要的时间。
解:(1)依题意 2ωβK J M -== )/(92202s rad JK JK ωωβ-=-=(2)由JK dtd 2ωωβ-==得⎰⎰-=3200ωωωωK Jd dt tωK J t 2=3-3 如图所示, 发电机的轮A 由蒸汽机的轮B 通过皮带带动。
两轮半径A R =30cm ,=B R 75cm 。
当蒸汽机开动后,其角加速度π8.0=B βrad/s 2,设轮与皮带之间没有滑动。
求(1)经过多少秒后发电机的转速达到A n =600rev/min ?(2)蒸汽机停止工作后一分钟内发电机转速降到300rev/min ,求其角加速度。
解:(1)t A A βω= t B B βω=因为轮和皮带之间没有滑动,所以A 、B 两轮边缘的线速度相同,即B B A A R R ωω=又)/(20606002s rad A ππω=⨯=联立得)(10s R R t BB A A ==βω(2))/(10603002s rad A ππω=⨯=)/(62s rad tAAA πωωβ=-'=3-4 一个半径为=R 1.0m 的圆盘,可以绕过其盘心且垂直于盘面的转轴转动。

第三章 刚体定轴转动一、思考讨论题1、刚体转动时,若它的角速度很大,那么作用它上面的力是否一定很大?作用在它上面的力矩是否一定很大?解:刚体转动时,它的角速度很大,作用在它上面的力不一定大,作用在它上面的力矩也不一定大。
ω增大,则增大增大,M , βωI dtd I ==, 又⨯= 更无直接关系。
与无直接关系,则有关,与与ωωβF M 2、质量为m =4kg 的小球,在任一时刻的矢径j t i t r 2)1(2+-=,则t s =3时,小球对原点的角动量=?从t =1s 到t s =3的过程中,小球角动量的增量=?。
解:角动量)22(]2)1[(2t m j t i t dtd m m +⨯+-=⨯=⨯= t s =3j i t m j t i t 80)26(4)68()22(]2)1[(23-=+⨯+=+⨯+-==j t m j t i t 16)22(42)22(]2)1[(21-=+⨯=+⨯+-==64)16(8013-=---==∆==3、如图5.1,一圆形台面可绕中心轴无摩擦地转动,有一辆玩具小汽车相对于台面由静止开始启动,绕作圆周运动,问平台面如何运动?若经过一段时间后小汽车突然刹车,则圆台和小汽车怎样运动?此过程中,对于不同的系统,下列表中的物理哪些是守恒量,受外力,合外力矩情况如何?解:平台绕中心轴转动,方向与小车转动方向相反。
小车突然刹车,圆台和小车同时减速、同时静止。
分别考虑小车和圆台在垂直和水平方向的受力。
图5.1tf n小车圆台4、绕固定轴作匀变速转动的刚体,其中各点都绕轴作圆周运动,试问刚体上任一点是否具有切向加速度?是否具有法向加速度?法向加速度和切向加速度大小是否变化? 解:刚体上的任何一点都有切向加速度。
也有法向加速度。
大小不发生变化。
5、在一物体系中,如果其角动量守恒,动量是否也一定守恒?反之,如果该系统的动量守恒,角动量是否也一定守恒?解:在一物体系中,角动量守恒,动量不一定守恒。
第三章 刚体的定轴转动3-1 (1)铁饼离手时的角速度为(rad/s)250125===.//R v ω(2)铁饼的角加速度为2222539.8(ra d /s )222 1.25ωβ===θ⨯π⨯(3)铁饼在手中加速的时间为t ,则t ω=β(s)628025251222..=⨯⨯==πωθt3-2 (1)初角速度为(rad/s)9206020020./=⨯=πω末角速度为(rad/s)3146030002=⨯=/πω角加速度为231420.941.9(ra d /s )t7.0ω-ω-β===(2)转过的角度为)186(rad 101717231492023圈=⨯=⨯+=+=..t ωωθ(3)切向加速度为2t a R 41.90.28.38(m /s )=β=⨯=法向加速度为)(m /s10971203142422n ⨯=⨯==..R a ω总加速度为)(m/s10971)10971(378242422n 2t ⨯=⨯+=+=...a a a总加速度与切向的夹角为9589378101.97arctanarctan4tn '︒=⨯==.a a θ3-3 (1)对轴I 的转动惯量222219)cos602(])cos60()cos60([2maa a m a a a m J =︒++︒++︒=对轴II 的转动惯量2223)sin60(4maa m J =︒=(2)对垂轴的转动惯量2222312)2()cos30(222maa m a m maJ =+︒+=3-4 (1)设垂直纸面向里的方向为正,反之为负,则该系统对O 点的力矩为mgl l mg l mg l mg l mgM438141418343430=⋅-⋅-⋅+=(2)系统对O 点的总转动惯量等于各部分对O 点的转动惯之和,即22222432104837)43()43)(43(31)4)(4(31)4(mll m l m l m l m J J J J J =+++=+++= (3)由转动定律 βJ M = 可得lg mlmglJ M37364837432===β3-5 (1)摩擦力矩恒定,则转轮作匀角加速度运动,故角加速度为0001201)-(0.8ωωωωβ.-==∆-=t第二秒末的角速度为0000260220ωωωβωω..=⨯-=+=t(2)设摩擦力矩r M 与角速度ω的比例系数为α,据题设可知αωωαω==tJMrd d 即,t Jt Jtαωωαωωωω==⎰⎰0lnd d 0据题设s 1=t 时,0180ωω.=,故可得比例系数80ln .J =α由此s 2=t 时,转轮的角速度2ω为ln0.82ln2=ωω002264080ωωω..==∴3-6 设飞轮与闸瓦间的压力为N ,如图示,则二者间摩擦力N f r μ=,此摩擦力形成阻力矩f r,由转动定律βJ R f r =其中飞轮的转动惯量2mRJ =,角加速度n t520πωωβ-=-=,故得14(N)30.25(1000/60)605252-mnRf r =⨯⨯⨯-=-=ππ见图所示,由制动杆的平衡条件可得0= )(121l N l l F '-+r f N N '==μ得制动力(N)3140.75)(0.54050314)(211=+⨯=+=..l l l f F r μ3-7 如图所示,由牛顿第二定律 对11111:a m g m T m =- 对22222:a m T g m m =- 对整个轮,由转动定律β⎪⎭⎫⎝⎛+=-22221111222121R MR M R T R T 又由运动学关系 1122a /R a /R β== 联立解以上诸式,即可得222221111122)2/()2/()(R m MR m M gR m R m +++-=β3-8 设米尺的总量为m ,则直尺对悬点的转动惯量为习题3-6图习题3-7图2211222211J m l m l 331212m 0.4m 0.635351.4m150.093m=+=⨯⨯+⨯⨯==mg 1.02152mg 522153mg 53=⨯⨯-⨯⨯=M又 1.4M J I m 15=β=2M 0.1m g 1510.5(ra d s)J 1.4m-⨯∴β===从水平位置摆到竖直位置的过程中机械能守恒(以水平位置为O 势能点)221ωJ mghc=即 25.14.1211.0ωm mg ⨯=⨯21=⇒ω3-9 m 视为质点,M 视为刚体(匀质圆盘)。
《大学物理》试题库管理系统内容第三章 刚体的定轴转动1 题号:03001 第03章 题型:选择题 难易程度:较难试题: 某刚体绕定轴作匀变速转动,对刚体上距转轴为r 处的任一质元的法向加速度n a 和切向加速度τa 来说正确的是( ).A.n a 的大小变化,τa 的大小保持恒定B.n a 的大小保持恒定,τa 的大小变化C.n a 、τa 的大小均随时间变化D.n a 、τa 的大小均保持不变 答案: A2 题号:03002 第03章 题型:选择题 难易程度:适中试题: 有A 、B 两个半径相同、质量也相同的细环,其中A 环的质量分布均匀,而B 环的质量分布不均匀.若两环对过环心且与环面垂直轴的转动惯量分别为B A J J 和,则( ).A. B A J J =B. B A J J >C. B A J J <D. 无法确定B A J J 和的相对大小 答案: A3 题号:03003 第03章 题型:选择题 难易程度:适中试题: 一轻绳绕在具有水平转轴的定滑轮上,绳下端挂一物体,物体的质量为m ,此时滑轮的角加速度为β,若将物体取下,而用大小等于mg 、方向向下的力拉绳子,则滑轮的角加速度将( ).A.变大B.不变C.变小D.无法确定 答案: A4 题号:03004 第03章 题型:选择题 难易程度:适中试题: 一人张开双臂手握哑铃坐在转椅上,让转椅转动起来,若此后无外力矩作用,则当此人收回双臂时,人和转椅这一系统的( ).A.系统的角动量保持不变B.角动量加大C.转速和转动动能变化不清楚D.转速加大,转动动能不变 答案: A5 题号:03005 第03章 题型:选择题 难易程度:较难试题: 某力学系统由两个质点组成,它们之间仅有引力作用.若两质点所受外力的矢量和为零,则此力学系统( ).A.动量守恒,但机械能和角动量是否守恒不能确定B.动量和角动量守恒,但机械能是否守恒不能确定C.动量、机械能守恒,但角动量是否守恒不能确定D.动量、机械能以及对某一转轴的角动量一定守恒 答案: A6 题号:03006 第03章 题型:选择题 难易程度:较难试题: 如图所示,两个质量均为m 、半径均为R 的匀质圆盘形滑轮的两端,用轻绳分别系着质量为m 和2m 的小物块.若系统从静止释放,则释放后两滑轮之间绳内的张力为( ). A.mg 811 B.mg 23C.mg 21D.mg答案: A7 题号:03007 第03章 题型:选择题 难易程度:较难试题: 某质点受的力为kx e F F -=0,若质点从静止开始运动(即,0=x 时0=v ),则该质点所能达到的最大动能为( ).A.k F 0 B. k eF0 C. k e kF 0 D. 0kF 答案: A8 题号:03008 第03章 题型:选择题 难易程度:适中试题: 如图所示,在水平光滑的圆盘上,有一质量为m 的质点,拴在一根穿过圆盘中心光滑小孔的轻绳上.开始时质点离中心的距离为r ,并以角速度? 转动.今以均匀速率向下拉绳,将质点拉至离中心2r 处时,拉力做的功为( ).A.2223ωmr B. 2225ωmr C. 2227ωmr D. 2221ωmr答案: A9 题号:03009 第03章 题型:选择题 难易程度:适中试题: 已知地球的质量为m ,太阳的质量为M ,地心与日心的距离为R ,引力常数为G ,则地球绕太阳作圆周运动的角动量为( ).A.GMR mB.R G MmC.R GMmD.RGMm 2 答案: A10 题号:03010 第03章 题型:选择题 难易程度:适中试题: 卫星绕地球做椭圆运动,地心为椭圆的一个焦点,在运动过程中,下列叙述中正确的是( ).A.角动量守恒B.动量守恒C.机械能不守恒D.动量和角动量都不守恒 答案: A11 题号:03011 第03章 题型:选择题 难易程度:适中试题: 三个完全相同的轮子可绕一公共轴转动,角速度的大小都相同,但其中一轮的转动方向与另外两轮的转动方向相反.若使三个轮子靠近啮合在一起,则系统的动能与原来三个轮子的总动能相比为( ).A.减小到1/9B.减小到1/3C.增大9倍D.增大3倍 答案: A12 题号:03012 第03章 题型:选择题 难易程度:较难 试题: 下列说法中,错误的是( ).A.对于给定的刚体而言,他的质量和形状是一定的,则其转动惯量也是唯一确定的B.刚体定轴转动的转动定律为βJ M =,其中M 、J 和β均是对同一转轴而言的C.刚体的转动动能等于刚体上各质元的动能之和D.刚体作定轴转动时,其上各点的角速度相同而线速度不同 答案: A13 题号:03013 第03章 题型:选择题 难易程度:适中 试题: 下列说法中,正确的是( ).A.作用在定轴转动刚体上的合力矩越大,刚体转动的角加速度越大B.作用在定轴转动刚体上的合力矩越大,刚体转动的角速度就越大C.作用在定轴转动刚体上的合力矩为零,刚体转动的角速度就为零D.作用在定轴转动刚体上的合力越大,刚体转动的角加速度就越大答案: A14 题号:03014 第03章 题型:选择题 难易程度:难试题: 轮圈半径为R 、其质量M 均匀分布在轮缘上,长为R 、质量为m 的匀质辐条固定在轮心和轮缘间,辐条共有2N 根.今若将辐条数减少N 根,但保持轮对通过轮心、垂直于轮平面轴的转动惯量不变,则轮圈的质量应为( ).A.M m N +3 B.M m N +6 C.M m N +12 D. M m N +32 答案: A15 题号:03015 第03章 题型:选择题 难易程度:适中试题: 如图一质量为m 的匀质杆长为l ,绕铅直轴O O '成θ角转动,其转动惯量为( ).A.θ22sin 31mlB.231mlC.θ22sin 41mlD.2121ml 答案: A16 题号:03016 第03章 题型:选择题 难易程度:适中试题: 如图一质量为m 的匀质杆长为l ,绕铅直轴O O '成θ角转动,则匀质杆所受的合外力矩为( ).A.θsin 21mgl B.θcos 21mgl C.θsin mgl D.θcos mgl 答案: A17 题号:03017 第03章 题型:选择题 难易程度:适中 试题: 如图一质量为m 的匀质杆长为l ,绕铅直轴O O '成θ角转动,则匀质杆的角动量为( ).A.θω22sin 31mlB.ω231mlC.ω2121mlD.θω22sin 41ml 答案: A18 题号:03018 第03章 题型:选择题 难易程度:难试题: 如图一质量为m 的匀质杆长为l ,绕铅直轴O O '成θ角转动,则匀质杆的角加速度为( ).A.θsin 23l g B.l g θsin 23C.l g θsin 32D.θsin 32l g答案: A19 题号:03019 第03章 题型:选择题 难易程度:难试题: 如图所示,两根长度和质量分别相等的细杆分别绕着光滑的水平轴1O 和2O 转动,设他们自水平位置从静止释放时,角加速度分别为1β和2β,则二者角加速度之间的关系为( ).A. 21ββ=B.21ββ>C. 21ββ<D.不能确定 答案: A20 题号:03020 第03章 题型:选择题 难易程度:难试题: 如图所示,光滑的水平桌面上有一长为2l 、质量为m 的匀质细杆,可绕通过中点O 、且与杆垂直的竖直轴自由转动,开始时细杆静止.现有一质量为m 的小球,沿桌面正对着杆的一端,以速度v ρ运动,并与杆的A 端碰撞后与杆粘在一起转动,则这一系统碰撞后的转动角速度为( ).A. l v43 B. l v 2C. l v 32D. lv54 答案: A21 题号:03021 第03章 题型:填空题 难易程度:容易试题: 刚体是一理想模型,他虽然有一定的形状和大小,但形状和大小永远保持 . 答案: 不变22 题号:03022 第03章 题型:填空题 难易程度:容易 试题: 刚体定轴转动的运动方程的表示式是 . 答案: )(t θθ=23 题号:03023 第03章 题型:填空题 难易程度:较难试题: 把不涉及转动的原因,只研究如何描述刚体的定轴转动的问题称为 .1Ol O32lOl 2 mv ρm A答案: 刚体定轴转动运动学24 题号:03024 第03章 题型:填空题 难易程度:较难 试题: 把研究刚体定轴转动原因的问题称为 . 答案: 刚体定轴转动的动力学25 题号:03025 第03章 题型:填空题 难易程度:适中试题: 刚体的转动惯量取决于刚体的总质量、质量分布和 等三个因素. 答案: 转轴的位置26 题号:03026 第03章 题型:填空题 难易程度:较难试题: 一飞轮以1min rad 300-⋅的转速转动,转动惯量为2m kg 5⋅,现施加一恒定的制动力矩,使飞轮在2s 内停止转动,则该恒定制动力矩的大小为 . 答案: m N ⋅=5.78M27 题号:03027 第03章 题型:填空题 难易程度:适中 试题: 如图所示,质量为1m 和2m 的均匀细棒长度均为2l ,在两棒对接处嵌有一质量为m 的小球,对过A 的轴而言,若2222141127121ml l m l m J A ++=,则B J 为 . 答案:2222141127121ml l m l m ++ 28 题号:03028 第03章 题型:填空题 难易程度:较难试题: 质量为m 的匀质细杆,长为l ,以角速度ω绕过杆的端点且垂直于杆的水平轴转动,则杆的动量大小为 . 答案:ωml 2129 题号:03029 第03章 题型:填空题 难易程度:适中试题: 质量为m 的匀质细杆,长为l ,以角速度ω绕过杆的端点且垂直于杆的水平轴转动,则杆绕转动轴的动能为 . 答案:2261ωml 30 题号:03030 第03章 题型:填空题 难易程度:适中试题: 质量为m 的匀质细杆,长为l ,以角速度ω绕过杆的端点且垂直于杆的水平轴转动,则杆绕转动轴的角动量大小为 .A B答案: ω231ml31 题号:03031 第03章 题型:填空题 难易程度:适中试题: 若飞轮从静止开始作匀加速转动,在最初2min 转了3600转,则飞轮的角加速度为 . 答案: 2s rad -⋅=14.3β32 题号:03032 第03章 题型:填空题 难易程度:较难试题: 若飞轮从静止开始作匀加速转动,在最初1min 转了3600转,则飞轮在第50秒末的角速度为 . 答案: 1s rad -⋅=314ω33 题号:03033 第03章 题型:填空题 难易程度:适中试题: 若某飞轮绕其中心轴转动的运动方程为t t t 4223+-=θ,其中θ的单位为rad ,t 的单位为s ,则飞轮在第2秒末的角加速度为 . 答案: 2s rad -⋅=12β34 题号:03034 第03章 题型:填空题 难易程度:较难试题: 若某飞轮绕其中心轴转动的运动方程为t t t 4223+-=θ,其中θ的单位为rad ,t 的单位为s ,则飞轮从s 2=t 到s 4=t 这段时间内的平均角加速度为 . 答案: 2s rad -⋅=12β35 题号:03035 第03章 题型:填空题 难易程度:较难试题: 若质量为m 、半径为R 的匀质薄圆盘绕过中心且与盘面垂直轴的转动惯量为221mR ,则质量为m 、半径为R 、高度为h 的匀质圆柱体绕过中心且与端面垂直轴的转动惯量为 . 答案:221mR 36 题号:03036 第03章 题型:填空题 难易程度:适中试题: 一转动惯量为J 的刚体绕某固定轴转动,当他在外力矩M ρ的作用下,角速度从1ω变为2ω,则该刚体在此过程)(21t t →中所受的冲量矩⎰21t t dt M ρ等于 .答案: 12ωωJ J -37 题号:03037 第03章 题型:填空题 难易程度:适中试题: 一转动惯量为J 的刚体绕某固定轴转动,当他在外力矩M ρ的作用下,角速度从1ω变为2ω,则该刚体在此过程)(21θθ→中力矩所做的功⎰21θθθMd 等于 .答案:21222121ωωJ J - 38 题号:03038 第03章 题型:填空题 难易程度:容易 试题: 刚体角动量守恒的条件为 .答案: 0=外M ρ39 题号:03039 第03章 题型:填空题 难易程度:较难试题: 一质量为m 的粒子,相对于坐标原点处于j y i x r ρρρ+=点,速度为j v i v v y x ρρρ+=,则该质点相对于坐标原点的角动量为 .答案: k yv xv m L x y ρρ)(-=40 题号:03040 第03章 题型:填空题 难易程度:适中试题: 一飞轮的转动惯量为J ,0=t 时角速度为0ω,此后飞轮经历一制动过程,受到的阻力矩的大小与角速度成正比,即ωk M -=,式中k 为正的常量.当3ωω=时,飞轮的角加速度为 . 答案: Jk 30ωβ-= 41 题号:03041 第03章 题型:计算题 难易程度:适中 试题: 一条缆索绕过一个定滑轮拉动升降机,如图所示.滑轮的半径为m 5.0=r ,如果升降机从静止开始以加速度2s m 4.0-⋅=a 匀加速上升,求:(1)滑轮的角加速度;(2)开始上升后t = 5s 末滑轮的角速度; (3)在这5秒内滑轮转过的圈数;(4)开始上升后s 1='t 末滑轮边缘上一点的加速度(假定缆索和滑轮之间不打滑).答案: 为了图示清晰,将滑轮放大为如图所示.(1)由于升降机的加速度和滑轮边缘上的一点的切向加速度相等,所以滑轮的角加速度为2s rad 8.0-⋅===rar a τβa ρv ρ(2)由于00=ω,所以5秒末滑轮的角速度为1s rad 0.4-⋅==t βω(3)在这5秒内滑轮转过的角度为rad 10212==t βθ 所以在这5秒内滑轮转过的圈数为圈6.1210==πN (4)结合题意,由图可以看出2s m 4.0-⋅==a a τ2222s m 32.0-⋅===t r r a n βω由此可得滑轮边缘上一点在升降机开始上升后s 1='t 时的加速度为222s m 51.0-⋅=+='τa a a n这个加速度的方向与滑轮边缘的切线方向的夹角为117.384.032.0tan tan =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫⎝⎛=--ταa a n 42 题号:03042 第03章 题型:计算题 难易程度:难试题: 一绳跨过定滑轮,两端分别系有质量分别为m 和M 的物体,且m M >.滑轮可看作是质量均匀分布的圆盘,其质量为m ',半径为R了摩擦阻力矩阻M 的作用.设绳不可伸长且与滑轮间无相对滑动.求物体的加速度及绳中的张力.答案: 力矩的作用,因此滑轮两侧绳子中的拉力一定不相等.设两侧绳子中的拉力分别为1T 和2T ,则滑轮及两侧物体的受力如图所示,其中11T T '=,22T T '=(作用力与反作用力大小相等). 因为m M >,所以左侧物体上升,右侧物体下降.设其加速度分别为1a 和2a ,据题意可知,绳子不可伸长,则21a a =,令它们为a .滑轮以顺时针转动,设其角加速度为β,则摩擦阻力矩阻M 的指向为逆时针方向,如图所示.对于上下作平动的两物体,可以视为质点,由牛顿第二运动定律得⎩⎨⎧=-=-Ma T Mg M mamg T m 21:对:对 (1) a ρ1a滑轮作定轴转动,受到的外力矩分别为R T 2'和R T 1'及阻M (轴对滑轮的支持力N 通过了转轴,其力矩为零).若以顺时针方向转的力矩为正,逆时针转的方向为负,则由刚体定轴转动的转动定律得ββ⎪⎭⎫⎝⎛'==--21221R m J M R T R T 阻 (2)据题意可知,绳与滑轮间无相对滑动,所以滑轮边缘上一点的切向加速度和物体的加速度相等,即βτR a a == (3)联立(1)、(2)、(3)三个方程,得2)(m m M R M g m M a '++--=阻2)22()(1m m M R mM mg m M a g m T '++-'+=+=阻2)22()(2m m M R MM Mg m m a g M T '+++'+=-=阻43 题号:03043 第03章 题型:计算题 难易程度:适中试题: 求长为L ,质量为m 的均匀细棒AB 的转动惯量.(1)对于通过棒的一端与棒垂直的轴;(2)对于通过棒的中点与棒垂直的轴.答案: (1)如图所示,以过A 端垂直于棒的o o '为轴,沿棒长方向为x 轴,原点在轴上,在棒上取一长度元dx ,则这一长度元的质量为dx L m dm =,所以 202231mL dx L m x dm x J L m =⎪⎭⎫ ⎝⎛==⎰⎰端点 (2)同理,如图所示,以过中点垂直于棒的o o '为轴,沿棒长方向为x 轴,原点在轴上,在棒上取一长度元dx ,因此22222121mL dx L m x dm x J L L m=⎪⎭⎫ ⎝⎛==⎰⎰-中点 由此可见,对于同一均匀细棒,转轴的位置不同,棒的转动惯量不同.o AA44 题号:03044 第03章 题型:计算题 难易程度:容易试题: 试求质量为m 、半径为R 的匀质圆盘对垂直于平面且过中心轴的转动惯量. 答案: 已知条件如图所示.由于质量连续分布,所以220222mR dl R m R dm R J Rm=⎪⎭⎫ ⎝⎛==⎰⎰ππ 45 题号:03045 第03章 题型:计算题 难易程度:适中试题: 试求质量为m 、半径为R 的匀质圆环对垂直于平面且过中心轴的转动惯量. 答案: 已知条件如图所示.由于质量连续分布,设圆盘的厚度为l ,则圆盘的质量密度为lR m2πρ=.因圆盘可以看成是许多有厚度的圆环组成,所以()ρππρl R ldr r r dm r J R m 4022212=⋅⋅==⎰⎰代入圆盘的质量密度,得221mR J =46 题号:03046 第03章 题型:计算题 难易程度:较难试题: 如图所示,一质量为M 、半径为R 的匀质圆盘形滑轮,可绕一无摩擦的水平轴转动.圆盘上绕有质量可不计的绳子,绳子一端固定在滑轮上,另一端悬挂一质量为m 的物体,问物体由静止落下h 高度时,物体的速率为多少? 答案: 法一 用牛顿第二运动定律及转动定律求解.受力分析如图所示,对物体m 用牛顿第二运动定律得ma T mg =- (1)对匀质圆盘形滑轮用转动定律有βJ R T =' (2)物体下降的加速度的大小就是转动时滑轮边缘上切向加速度,所以βR a = (3)又由牛顿第三运动定律得T T '=(4)物体m 落下h 高度时的速率为ah v 2= (5)dml因为221MR J =,所以联立以上(1)、(2)、(3)、(4)和(5)式,可得物体m 落下h 高度时的速率为mM mghv 22+=(小于物体自由下落的速率gh 2).解法二 利用动能定理求解.如图所示,对于物体m 利用质点的动能定理有222121mv mv Th mgh -=- (6) 其中0v 和v 是物体的初速度和末速度.对于滑轮利用刚体定轴转动的转动定理有222121ωωθJ J TR -=∆ (7) 其中θ∆是在拉力矩TR 的作用下滑轮转过的角度,0ω和ω是滑轮的初角速度和末角速度.由于滑轮和绳子间无相对滑动,所以物体落下的距离应等于滑轮边缘上任意一点所经过的弧长,即θ∆=R h .又因为00=v ,00=ω,R v ω=,221MR J =,所以联立(6)和(7)式,可得物体m 落下h 高度时的速率为mM mghv 22+=.解法三 利用机械能守恒定律求解.若把滑轮、物体和地球看成一个系统,则在物体落下、滑轮转动的过程中,绳子的拉力T 对物体做负功(Th -),T '对滑轮做正功(Th )即内力做功的代数和为零,所以系统的机械能守恒.若把系统开始运动而还没有运动时的状态作为初始状态,系统在物体落下高度h 时的状态作为末状态,则0212121222=-+⎪⎭⎫ ⎝⎛⋅⎪⎭⎫ ⎝⎛mgh mv R v MR 所以物体m 落下h 高度时的速率为mM mghv 22+=.47 题号:03047 第03章 题型:计算题 难易程度:容易试题: 哈雷慧星绕太阳运行的轨道是一个椭圆,如图所示,它离太阳最近的距离是m 1075.810⨯=近日r ,此时速率为-14s m 1046.5⋅⨯=近日v ;它离太阳最远时的速率为-12s m 1008.9⋅⨯=远日v ,这时它离太阳的距离?远日=r答案: 彗星受太阳引力的作用,而引力通过了太阳,所以对太阳的力矩为零,故彗星在运行的过程中角动量守恒.于是有远日远日近日近日v r v r ρρρρ⨯=⨯因为远日远日近日近日,v r v r ρρρρ⊥⊥,所以有远日近日近日远日v v r r =代入数据,得m 1026.512⨯=远日r48 题号:03048 第03章 题型:计算题 难易程度:较难试题: 如图所示,一个长为l 、质量为M 的匀质杆可绕支点o 自由转动.一质量为m 、速率为v 的子弹以与水平方向成060角的方向射入杆内距支点为a 处,使杆的偏转角为030.问子弹的初速率为多少?答案: 把子弹和匀质杆作为一个系统,由于该系统所受的外力有重力及轴对杆的约束力,在子弹射入杆的极短过程中,重力和约束力都通过了转轴o ,因此它们对转轴的力矩均为零,故该系统的角动量守恒.设子弹射入杆后与杆一同前进的角速度为ω,则碰撞前的角动量等于碰撞后的角动量,即 ()ω⎪⎭⎫ ⎝⎛+=2203160cos ma Ml a v m子弹在射入杆后与杆一起摆动的过程中只有重力做功,所以由子弹、杆和地球组成的系统机械能守恒,因此有()()0022230cos 1230cos 13121-⋅+-=⎪⎭⎫ ⎝⎛+l Mg mga ma Ml ω 联立上述这两个方程得子弹的初速率为()()22326322ma Ml ma Ml g mav ++-=49 题号:03049 第03章 题型:计算题 难易程度:较难试题: 如图所示,一根质量为M 、长为2 l 的均匀细棒,可以在竖直平面内绕通过其中心的光滑水平轴转动,开始时细棒静止于水平位置.今有一质量为m 的小球,以速度u ρ垂直向下落到了棒的端点,设小球与棒的碰撞为完全弹性碰撞.试求碰撞后小球的回跳速度v ρ及棒绕轴转动的角速度ω.答案: 以棒和小球组成的系统为研究对象,则该系统所受的外力有小球的重力、棒的重力和轴给予棒的支持力, 后两者的作用线都通过了转轴,对轴的力矩为零.由于碰撞时间极短,碰撞的冲力矩远大于小球所受的重力矩,所以小球对轴的力矩可忽略不计.分析v ρomu可知所取系统的角动量守恒.由于碰撞前棒处于静止状态,所以碰撞前系统的角动量就是小球的角动量lmu . 由于碰撞后小球以速度v 回跳,其角动量为lmv ;棒获得的角速度为ω,棒的角动量为()ωω22312121Ml l M =⎥⎦⎤⎢⎣⎡.所以碰撞后系统的角动量为ω231Ml lmv +.由角动量守恒定律得ω231Ml lmv lmu += (1) 注意:上式中u ,v 这两个速度是以其代数量来表示.以碰撞前小球运动的方向为正,即0>u ;碰撞后小球回跳,u 与v 的方向必然相反,应该有0<v .由题意知,碰撞是完全弹性碰撞,所以碰撞前后系统的动能守恒,即222231212121ω⎪⎭⎫⎝⎛+=Ml mv mu (2) 联立(1)和(2)式,可得小球的速度为u Mm M m v +-=33棒的角速度为luM m m ⋅+=36ω讨论:由于碰撞后小球回跳,所以v 与u 的方向不同,而0>u ,则0<v .从结果可以看出,要保证0<v ,则必须保证m M 3>.否则,若M m 31≥,无论如何,碰撞后小球也不能回跳,杂耍运动员特别注意这一点.50 题号:03050 第03章 题型:计算题 难易程度:较难试题: 如图所示,一长为l 、质量为m 的匀质细棒竖直放置,其下端与一固定铰链o 相连结,并可绕其转动.由于此竖直放置的细棒处于非稳定平衡状态,当其受到微小扰动时,细棒将在重力的作用下由静止开始绕铰链o 转动.试计算细棒转到与竖直位置成θ角时的角加速度和角速度.答案: 法一 利用定轴转动的转动定律求解.分析受力如图所示,其中G ρ为细棒所受的重力、N ρ为铰链给细棒的约束力.由于约束力N ρ始终通过转轴,所以其作用力矩为零;铰链与细棒之间的摩擦力矩题中没有给定可认为不存在.又由于细棒为匀质细棒,所以重力G ρ的作用点在细棒中心.故由定轴转动的转动定律可得βθ⎪⎭⎫ ⎝⎛=231sin 21ml mgl 因此细棒转过θ角时的角加速度为θβsin 23lg=由角加速度的定义可得θθθωsin 23lgdt d d d =⋅ 整理可得θθωωd l g d ⎪⎭⎫⎝⎛=sin 23 由于0=t 时,0=θ,0=ω;而t t =时,θθ=,ωω=.所以上式两边取积分有θθωωθω⎰⎰⎪⎭⎫⎝⎛=0sin 23d l g d 因此细棒转过θ角时的角速度为()θωcos 13-=lg解法二 利用机械能守恒定律求解.以细棒和地球组成的系统为研究对象,由于细棒所受的重力为保守内力,铰链给细棒的约束力不做功,铰链与细棒之间的摩擦力题中没有给定可认为不存在,因此系统的机械能守恒.于是有()223121cos 12ωθ⎪⎭⎫ ⎝⎛=-⋅ml l mg 因此细棒转过θ角时的角速度为()θωcos 13-=lg此时的角加速度为θωβsin 23lgdt d ==解法三 利用定轴转动的动能定理求解.铰链的约束力对细棒不做功,摩擦力矩没有给定可以认为不存在,只有重力矩做功,所以对于细棒而言,合外力所做的功就是重力矩所做的功,即()θθθθθθcos 121sin 200-=⎪⎭⎫⎝⎛==⎰⎰mgl d l mg Md W由定轴转动的动能定理得()223121cos 121ωθ⎪⎭⎫ ⎝⎛=-ml mgl 因此细棒转过θ角时的角速度为()θωcos 13-=lg此时的角加速度为θωβsin 23lgdt d ==51 题号:03051 第03章 题型:计算题 难易程度:适中试题: 如图所示,在光滑的水平面上有一长为l 、质量为m 的匀质细棒以与棒长方向相互垂直的速度v ρ向前平动,平动中与一固定在桌面上的钉子o 相碰撞,碰撞后,细棒将绕点o 转动,试求其转动的角速度.答案: 由于细棒在光滑的水平面上运动,所以细棒与钉子o 碰撞的过程中遵守角动量守恒定律,则碰撞后碰撞前L L =对于转轴o 而言:⎪⎭⎫⎝⎛=4l mv L 碰撞前方向垂直于纸面向外;ωω⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+==242l l m J J L o 中心轴碰撞后ωω2224874121ml l m ml =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛+=方向垂直于纸面向外.所以有ω24874ml l mv =⎪⎭⎫⎝⎛ 故细棒碰撞后绕轴o 转动的角速度为lv712=ω 52 题号:03052 第03章 题型:计算题 难易程度:适中试题: 如图所示,在光滑的水平面上有一劲度系数为k 的轻质弹簧,它的一端固定,另一端系一质量为M 的滑块.最初滑块静止时,弹簧处于自然长度0l .现有一质量为m 的子弹以速度0v 沿水平方向并垂直于弹簧轴线射向滑块且留在其中,滑块在水平面内滑动.当滑块被拉伸到长度为l 时,求滑块速度的大小和方向.答案: 此题的物理过程有两个,第一个过程为子弹与滑块的碰撞过程.在该过程中子弹与滑块组成的系统所受的合外力为零,所以系统的动量守恒.于是有()V m M mv +=0第二个过程为滑块与子弹一起,以共同的速度V 在弹簧的约束下运动的过程.在该过程中弹簧的弹力不断增大,但始终通过转轴o ,它的力矩为零,所以角动量守恒;与此同时若以子弹、滑块、弹簧和地球组成的系统为研究对象,则该过程也满足机械能守恒定律.因此有()()θsin 0v m M l V m M +=+()()()2022212121l l k v m M V m M -++=+ 其中θ为滑块运动方向与弹簧轴线方向之间的夹角.联立以上三个方程可得滑块速度的大小和方向分别为()m M l l k m M mv v +--⎪⎪⎭⎫⎝⎛+=2020 ()()⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡+--⎪⎪⎭⎫ ⎝⎛++=--212020001sin m M l l k m M mv m M l l mv θ 53 题号:03053 第03章 题型:计算题 难易程度:适中试题: 一飞轮半径r = 1m ,以转速1min r 1500-⋅=n 转动,受制动均匀减速,经s 50=t 后静止.试求:(1)角加速度β和从制动开始到静止这段时间飞轮转过的转数N ;(2)制动开始后s 25=t 时飞轮的角速度ω;(3)在s 25=t 时飞轮边缘上一点的速度和加速度.答案: (1)角加速度20s rad 14.35060150014.325020-⋅-=⨯⨯-=-=-=ntπωωβ从制动开始到静止这段时间飞轮转过的转数62514.325014.3215060150014.322212220=⨯⨯⨯-⨯⨯⨯=+=∆=πβωπθtt N 圈(2)制动开始后s 25=t 时飞轮的角速度10s rad 5.782514.360150014.322-⋅=⨯-⨯⨯=+=+=t n t βπβωω (3)在s 25=t 时飞轮边缘上一点的速度和加速度分别为11s m 5.78s m )15.78()(--⋅=⋅⨯==τττωρρρρr v()()τβωττρρρρρr n r a n a a n +=+=2()[]()232s m )14.31016.6(14.315.78-⋅-⨯=⨯-+⨯=ττρρρρn r n54 题号:03054 第03章 题型:计算题 难易程度:适中试题: 如图所示.细棒的长为l ,设转轴通过棒上离中心距离为d 的一点并与棒垂直.求棒对此轴的转动惯量o J '.试说明这一转动惯量o J '与棒对过棒中心并与此轴平行的转轴的转动惯量o J 之间的关系(此为平行轴定理). 答案: 如图所示,以过o '点垂直于棒的直线为轴,沿棒长方向为x '轴,原点在o '点处,在棒上取一长度元x d ',则 ()⎰'='m o dm x J 2()⎰⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛''=d l d l x d l m x 222 22121md ml +=所以o J '与o J 之间的关系为2md J J o o +='55 题号:03055 第03章 题型:计算题 难易程度:适中试题: 如图所示.两物体的质量分别为1m 和2m ,滑轮的转动惯量为J ,半径为r .若2m 与桌面的摩擦系数为μ,设绳子与滑轮间无相对滑动,试求系统的加速度a 的大小及绳子中张力1T 和2T 的大小.答案: 分析受力如题图所示.21m m 和设其加速度分别为1a 和2a ,则由牛顿运动定律得22221111⎩⎨⎧=-=-a m g m T a m T g m μ 滑轮作定轴转动,则由转动定律有βJ r T r T =-21由于绳子与滑轮间无相对滑动,所以r a a a β===21联立以上四个方程可得,系统的加速度a 的大小及绳子中张力1T 和2T 的大小分别为d ox 'x 1。
第三章刚体的定轴转动选择题3-1 如图所示,四个质量相同、线度相同而形状不同的物体,它们对各自的几何对称轴的转动惯量最大的是( A )(A) (B) (C) (D)3-2 在上题中,它们对各自的几何对称轴的转动惯量最小的是( C )3-3 如图所示,P、Q、R、S是附于刚体轻细杆上的四个质点,它们的质量分别为4m、3m、2m和m,PQ QR RS l===,该系统对O O'轴的转动惯量为( A )(A) 29m l.10m l; (D) 214m l; (C) 250m l; (B) 23-4 均匀细棒O A,可绕通过点O与棒垂直的光滑水平轴转动,如图所示.如果使棒从水平位置开始下落,在棒到竖直位置的过程中,下列陈述正确的是( A )(A) 角速度从小到大,角加速度从大到小;(B) 角速度从小到大,角加速度从小到大;(C) 角速度从大到小,角加速度从大到小;(D) 角速度从大到小,角加速度从小到大.3-5 几个力同时作用在一个具有固定转轴的刚体上.如果这几个力的矢量和为零,则下列陈述正确的是( D )(A) 刚体必然不会转动; (B) 刚体的转速必然不变;(C) 刚体的转速必然会变; (D) 刚体的转速可能变,也可能不变.3-6 在光滑的桌面上开一个小孔,把系在绳的一端质量为m的小球置于桌面上,绳的另一端穿过小孔而执于手中.设开始时使小球以恒定的速率v 在水平桌面上作半径为1r 的圆周运动,然后拉绳使小球的轨道半径缩小为2r ,新的角速度2ω和原来的角速度1ω的关系为( B ) (A) 1212r r ωω⎛⎫ ⎪⎝⎭=; (B) 21212r r ωω⎛⎫⎪⎝⎭=;(C) 2211r r ωω⎛⎫ ⎪⎝⎭=; (D) 22211r r ωω⎛⎫⎪⎝⎭=.3-7 在上题中,新的动能和原来的动能之比为 ( A )(A) 212r r ⎛⎫ ⎪⎝⎭; (B) 12r r ; (C) 21rr ; (D) 221r r ⎛⎫ ⎪⎝⎭.3-8 刚体绕定轴高速旋转时,下列陈述正确的是 ( D )(A) 它受的外力一定很大; (B) 它受的外力矩一定很大;(C) 它的角加速度一定很大; (D) 它的角动量和转动动能一定很大. 3-9 芭蕾舞演员绕通过脚尖的竖直轴旋转,当她伸长手臂时的转动惯量为J ,角速度为ω.她将手臂收回至前胸时,转动惯量减小为3J ,此时她的角速度为 ( A )(A) 3ω; (D) 13ω.3-10 三个完全相同的转轮绕一公共轴旋转.它们的角速度大小相同,但其中一轮的转动方向与另外两个轮相反.今沿轴的方向施力,将三者靠在一起,使它们获得相同的角速度.此时靠在一起后系统的动能与原来三转轮的总动能相比是 ( B )(A) 减少到13; (B) 减少到19;(C) 增大到3倍; (D) 增大到9倍.计算题3-11 一电动机的电枢转速为11800r min -⋅,当切断电源后,电枢经20s 停下.求:(1) 切断电源后电枢转了多少圈;(2) 切断电源后10s 时,电枢的角速度以及电枢边缘上一点的线速度、切向加速度和法向加速度(设电枢半径为10cm ).解 (1) 切断电源时,电枢的转速为11018002πrad s60πrad s60ω--⨯=⋅=⋅电枢的平均角加速度为22060πrad s3.0πrad s20tωα----==⋅=-⋅∆由2202ωωαθ-=∆,且0ω=,可得切断电源后电枢转过的角度为()()22060πrad 600πrad 223πωθα--∆===⨯-转过的圈数为600πr 300r 2π2πN θ∆===(2) 切断电源后10s 时,电枢的角速度为()11060π 3.0π10rad s30πrad s t ωωα--=+=-⨯⋅=⋅此时电枢边缘上一点的线速度、切向加速度和法向加速度分别为()111222t 222222n 0.1030πm s3.0πm s9.42m s0.10 3.0πm s0.30πm s0.942m s0.1030πm s90πm s888m sr a r a r ωαω---------==⨯⋅=⋅=⋅==-⨯⋅=-⋅=-⋅==⨯⋅=⋅=⋅v3-12 一飞轮由直径为0.30m 、厚度为22.010m -⨯的圆盘和两个直径为0.10m 、长为28.010m -⨯的圆柱体组成.设飞轮的密度为337.810kg m -⨯⋅,求飞轮对转轴的转动惯量.解 飞轮上的圆盘的半径为10.15m r =,圆柱体的半径为20.05m r =. 飞轮上的圆盘质量为2322111π7.810π0.15 2.010kg 11.0kg m r h ρ-==⨯⨯⨯⨯=圆柱体的质量为2322222π7.810π0.058.010kg 4.90kgm r h ρ-==⨯⨯⨯⨯⨯=飞轮的转动惯量是圆盘和两个圆柱体的转动惯量之和为22222211221111.00.15 4.900.05kg m 0.136kg m 22J m r m r ⎛⎫=+=⨯⨯+⨯⋅=⋅ ⎪⎝⎭3-13 如图所示,质量分别为2m 、3m 和4m 的三个小球,用长均为l 、质量均为m 的三根均匀细棒相连,如图所示(小球的半径r l <<,可视为质点).求该物件对通过点O 垂直于图面的转轴的转动惯量.解 该物件的转动惯量是三个小球和三根细棒的转动惯量之和为2222212343103J m l m l m l m l m l =+++⨯=3-14 细棒长为l ,质量为m ,设转轴通过棒上离中心为h 的一点并与棒垂直.求棒对此轴的转动惯量.解 由平行轴定理,细棒的转动惯量为22222c 111212J J m h m l m h m l h ⎛⎫=+=+=+ ⎪⎝⎭3-15 一个半径为R 质量为m 的均匀圆盘,挖去直径为R 的一个圆孔,如图所示.求剩余部分对通过圆心O 且与盘面垂直的轴的转动惯量.解 开孔圆盘的转动惯量等于完整圆盘的转动惯量减去位于圆孔部位的被挖去的小圆盘的转动惯量:2222111322424232m R m R J m R m R ⎡⎤⎛⎫⎛⎫=-+=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦ 3-16 如图所示,某飞轮的直径为0.50m 、转动惯量为22.4k g m ⋅、转速为311.010r min-⨯⋅.如果制动时闸瓦对轮的压力为490N ,闸瓦与轮之间的滑动摩擦因数为0.4,求制动后飞轮转多少圈才停止.解 制动前,飞轮的转速为31102π 1.010rad s105rad s60ω--⨯⨯=⋅=⋅飞轮所受的制动力矩为n 0.44900.25N m 49N m M F R μ=-=-⨯⨯⋅=-⋅根据转动定律,M J α=,可得制动后飞轮的角加速度为2249rad s20.4rad s2.4M J α---==⋅=-⋅由2202ωωαθ-=∆,且0ω=,可得制动后飞轮转过角度为220105rad 270rad 22(20.4)ωθα--∆===⨯-转过的圈数为270r 43.0r 2π2πN θ∆===3-17 如图所示,一物体质量为5kg ,从一倾角为o 37的斜面滑下,物体与斜面的摩擦因数为0.25.一滑轮装在固定轴O 处,轻绳的一端绕在滑轮上,另一端与物体相连.若滑轮可视为是实心圆盘,其质量为20kg 、半径为0.2m ,绳与轮间无相对滑动,且轮轴的摩擦阻力矩忽略不计.求:(1) 物体沿斜面下滑的加速度; (2) 绳中的张力.解 物体和滑轮的示力图以及坐标选取如图所示.图中P 为重力,N F 为正压力,r F 为摩擦力,T F 为张力,T T F F '=.O x 轴沿斜面向下,Oy 垂直于斜面.设物体的质量为1m ,滑轮的质量为2m ,滑轮的半径为r .对物体,根据牛顿第二定律,在O x 和Oy 方向分别有o1T r 1sin 37m g F F m a --=oN 1cos 370F m g -=重力2P 和轮轴对滑轮的压力N 2F 均通过转轴,对转轴的力矩为零.以垂直纸面向里为正方向,滑轮所受的力矩为T T M F r F r '=⋅=⋅.对滑轮,根据转动定律,有T F r J α⋅=而a r α=r N F F μ=2212J m r =联立解以上方程,可得物体沿斜面下滑的加速度和绳中的张力分别为()oo11222sin 37cos 3712345 0.259.8 m s 1.31 m s1555202m a gm m μ--=-+⎛⎫=-⨯⨯⨯⋅=⋅ ⎪⎝⎭+⨯T 21120 1.31 N 13.1 N 22F Jm a rα===⨯⨯=3-18 如图所示,长为l 、质量为m 的均匀细棒可绕点O 转动.此棒原先静止在竖直位置,受微小扰动而倒下.若不计摩擦和空气阻力,求细棒倒至与竖直位置成θ角时的角加速度和角速度.解 细棒的倒下,可看成定轴转动,其转轴通过地面上细棒端点,垂直于细棒的转动平面.在细棒倒下的过程中,细棒与地球组成的系统机械能守恒.以地面为势能零点,设细棒倒至与竖直方向成θ角时,角速度为ω,有21cos 222l l J m gm gωθ+=而213J m l =由此可得,角速度为ω=只有细棒所受的重力对转轴有力矩.以垂直纸面向里为正方向,细棒倒至与竖直方向成θ角时,重力对转轴的力矩为sin 2l M m g θ=.设此时的角加速度为α,则对细棒,根据转动定律,有sin 2l m gJ θα= 将213J m l =代入上式,可得角加速度为3sin 2g lαθ=3-19 如图所示,两个物体质量分别为1m 和2m .定滑轮的质量为m 、半径为R ,可视为圆盘.已知2m 与桌面间的摩擦因数为μ.设轻绳与轮间无相对滑动,且可不计滑轮轴的摩擦力矩,求1m 下落的加速度和滑轮两边绳中的张力.解 两个物体和滑轮的示力图以及坐标选取如图所示.图中P 为重力,N F 为正压力,r F 为摩擦力,T F 为张力,T1T1F F '=,T 2T 2F F '=.O x 轴水平向右,Oy 轴竖直向下.两个物体的加速度虽方向不同,但大小相同,12a a a ==.对物体1m ,根据牛顿第二定律,在Oy 方向有1T 11m g F m a -=对物体2m ,根据牛顿第二定律,在O x 方向有T 2r 2F F m a -=滑轮所受的重力和转轴对滑轮的压力都通过转轴,对转轴的力矩为零.以垂直纸面向里为正方向,滑轮所受的力矩为T 1T 2M F R F R =-.对滑轮,根据转动定律,有T 1T 2F R F R J α-=而212J m R =a R α=r 2F m gμ=联立解以上方程,可得物体的加速度与绳中的张力分别为()1212222m m a g m m mμ-=++()2T 11122122m m F m gm m m μ++=++()1T 22122122m m F m gm m mμ++=++3-20 一圆盘状的均匀飞轮,其质量为100kg 、半径为0.5m ,绕几何中心轴转动.在30s 内,由起始转速13000r m in-⋅均匀地减速至11000r m in -⋅.求阻力矩所做的功.解 飞轮初、末角速度分别为1102π3000rad s100πrad s60ω--⨯=⋅=⋅112π1000100rad sπrad s603ω--⨯=⋅=⋅飞轮的转动惯量为2222111000.5kg m 12.5kg m 22J m R ==⨯⨯⋅=⋅根据动能定理理,外力矩对飞轮所做的功等于飞轮转动动能的增量,可得在飞轮减速的过程中,阻力矩对飞轮所做的功为()222200225111()2221100π 12.5100πJ 5.4810J23A J J J ωωωω=-=-⎡⎤⎛⎫=⨯⨯-=-⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦3-21 质量为m '、半径为R 的转台,可绕过中心的竖直轴转动.质量为m 的人站在转台的边缘.最初人和转台都静止,后来人在转台的边缘开始跑动.设人的角速度(相对于地面)为ω,求转台转动的角速度(转台可看成质量均匀分布的圆盘,并忽略转轴处的摩擦力矩和空气的阻力).解 人和转台组成的系统对中心轴角动量守恒.以人的角速度的方向为正方向,设转台的角速度为1ω,有210J m R ωω+=而212J m R '=由此可得12m m ωω-='式中的负号表明,转台的转动方向与人的转动方向相反.3-22 如图所示,一个转动惯量为J 、半径为R 的圆木盘,可绕通过中心垂直于圆盘面的轴转动.今有一质量为m 的子弹,在距转轴2R 的水平方向以速度0v 射入,并嵌在木盘边缘.求子弹嵌入后木盘转动的角速度.解 子弹和木盘组成的系统,对转轴角动量守恒.以垂直于纸面向外为正方向,设子弹嵌入后,木盘转动的角速度为ω,有2()2R J m R m ω+=v由此可得022()m R J m R ω=+v3-23 如图所示,一均匀细棒长为l 、质量为m ,可绕经过端点O 的水平轴转动.棒被拉到水平位置由静止轻轻放开,下落至竖直位置时,下端与放在地面上的静止物体相撞.若物体的质量也为m ,物体与地面间的摩擦因数为μ,物体滑动s 距离后停止.求: (1) 棒与物体碰撞后,物体的速度;(2) 棒与物体碰撞后,棒的角速度.解 (1)根据动能定理,摩擦力对滑块所做的功等于滑块动能的增量.设物体因碰撞而获得的速度为v ,有2102m gs m μ-=-v由此可得=v (2) 细棒下落的过程中,细棒与地球组成的系统机械能守恒定律.以地面为势能零点,设细棒下落至竖直位置时的角速度为0ω,有20122l J m gω=而213J m l =由此可得0ω=.碰撞过程中角动量守恒.以垂直纸面向外为正方向,设碰撞后,细棒的角速度为ω,有0J m l J ωω+=v将213J m l =、=v 和0ω=代入上式,可得lω=若0ω>,碰撞后细棒继续向右转动, 若0ω<,碰撞后细棒向左转动.。
大学物理教程上册(范仰才著)课后答案大学物理教程上册(范仰才著)内容提要绪论第一篇力学第1章质点运动学1.1 参考系和坐标系质点1.2 质点运动的描述1.3 自然坐标系中的速度和加速度1.4 不同参考系中速度和加速度的变换关系思考题习题第2章质点动力学2.1 牛顿运动定律2.2 惯性系与非惯性系2.3 力的空间积累效应2.4 保守力的功势能机械能守恒定律2.5 力的时间积累效应动量守恒定律__2.6 质心质心运动定理阅读材料(1)混沌及其特征思考题习题第3章刚体的定轴转动3.1 刚体及刚体定轴转动的描述3.2 刚体定轴转动定律3.3 定轴转动的功和能3.4 角动量定理和角动量守恒定律__3.5 进动阅读材料(2)对称性与守恒律思考题习题第二篇热学第4章气体动理论4.1 平衡态态参量理想气体物态方程 4.2 理想气体的压强公式4.3 理想气体的`温度公式4.4 能量按自由度均分理想气体的内能 4.5 麦克斯韦速率分布律__4.6 玻耳兹曼分布律4.7 分子的平均碰撞频率和平均自由程__4.8 气体内的输运过程__4.9 范德瓦尔斯方程真实气体阅读材料(3)低温与超导思考题习题第5章热力学基础5.1 准静态过程功热量和内能5.2 热力学第一定律及其在理想气体等值过程的应用 5.3 绝热过程多方过程5.4 循环过程卡诺循环5.5 热力学第二定律5.6 热力学第二定律的统计意义熵阅读材料(4)热学熵与信息熵思考题习题第三篇振动和波动第6章振动学基础6.1 简谐振动的运动学旋转矢量表示法6.2 简谐振动的动力学特征6.3 简谐振动的能量6.4 简谐振动的合成6.5 阻尼振动受迫振动共振思考题习题第7章波动学基础7.1 机械波的形成和传播7.2 平简谐波的波函数7.3 波的能量声波大学物理教程上册(范仰才著)目录《21世纪高等学校规划教材:大学物理教程(上)》可作为本科院校理工科各专业的大学物理教材,也可作为各类普通高等学校非物理类专业、各类成人高校物理课程的教材或教学参考书。
第3章动量守恒定律和能量守恒定律习题一选择题3-1 以下说法正确的是[ ](A)大力的冲量一定比小力的冲量大(B)小力的冲量有可能比大力的冲量大(C)速度大的物体动量一定大(D)质量大的物体动量一定大解析:物体的质量与速度的乘积为动量,描述力的时间累积作用的物理量是冲量,因此答案A、C、D均不正确,选B。
3-2 质量为m的铁锤铅直向下打在桩上而静止,设打击时间为t∆,打击前锤的速率为v,则打击时铁捶受到的合力大小应为[ ](A)mvmgt+∆(B)mg(C)mvmgt-∆(D)mvt∆解析:由动量定理可知,F t p mv∆=∆=,所以mvFt=∆,选D。
3-3 作匀速圆周运动的物体运动一周后回到原处,这一周期内物体[ ] (A)动量守恒,合外力为零(B)动量守恒,合外力不为零(C)动量变化为零,合外力不为零, 合外力的冲量为零(D)动量变化为零,合外力为零解析:作匀速圆周运动的物体运动一周过程中,速度的方向始终在改变,因此动量并不守恒,只是在这一过程的始末动量变化为零,合外力的冲量为零。
由于作匀速圆周运动,因此合外力不为零。
答案选C。
3-4 如图3-4所示,14圆弧轨道(质量为M)与水平面光滑接触,一物体(质量为m)自轨道顶端滑下,M与m间有摩擦,则[ ](A )M 与m 组成系统的总动量及水平方向动量都守恒,M 、m 与地组成的系统机械能守恒(B )M 与m 组成的系统动量不守恒, 水平方向动量守恒,M 、m 与地组成的系统机械能不守恒(C )M 与m 组成的系统动量不守恒, 水平方向动量不守恒,M 、m 与地组成的系统机械能守恒(D )M 与m 组成系统的总动量及水平方向动量都守恒,M 、m 与地组成的系统机械能不守恒解析:M 与m 组成的系统在水平方向上不受外力,在竖直方向上有外力作用,因此系统水平方向动量守恒,总动量不守恒,。
由于M 与m 间有摩擦,m 自轨道顶端滑下过程中摩擦力做功,机械能转化成其它形式的能量,系统机械能不守恒。
第3章 刚体的定轴转动习题解答3-1 一汽车发动机曲轴的转速在12s 内由每分钟1200转匀加速地增加到每分钟2700转,求:(1)角加速度;(2)在此时间内,曲轴转了多少转?解:(1))/(401s rad πω= )/(902s rad πω=)/(1.13)/(6251240902212s rad s rad t≈=-=∆-=πππωωβ匀变速转动(2))(78022122rad πβωωθ=-=)(3902圈==πθn3-2 一飞轮的转动惯量为J ,在0=t 时角速度为0ω,此后飞轮经历制动过程。
阻力矩M 的大小与角速度ω的平方成正比,比例系数0>K 。
求:(1)当30ωω=时,飞轮的角加速度;(2)从开始制动到30ωω=所需要的时间。
解:(1)依题意 2ωβK J M -== )/(92202s rad JK JK ωωβ-=-=(2)由JK dtd 2ωωβ-==得⎰⎰-=3200ωωωωK Jd dt tωK J t 2=3-3 如图所示, 发电机的轮A 由蒸汽机的轮B 通过皮带带动。
两轮半径A R =30cm ,=B R 75cm 。
当蒸汽机开动后,其角加速度π8.0=B βrad/s 2,设轮与皮带之间没有滑动。
求(1)经过多少秒后发电机的转速达到A n =600rev/min ?(2)蒸汽机停止工作后一分钟内发电机转速降到300rev/min ,求其角加速度。
解:(1)t A A βω= t B B βω=因为轮和皮带之间没有滑动,所以A 、B 两轮边缘的线速度相同,即B B A A R R ωω=又)/(20606002s rad A ππω=⨯=联立得)(10s R R t BB A A ==βω(2))/(10603002s rad A ππω=⨯=)/(62s rad tAAA πωωβ=-'=3-4 一个半径为=R 1.0m 的圆盘,可以绕过其盘心且垂直于盘面的转轴转动。
一根轻绳绕在圆盘的边缘,其自由端悬挂一物体。
若该物体从静止开始匀加速下降,在t ∆=2.0s 内下降的距离h =0.4m 。
求物体开始下降后第3秒末,盘边缘上任一点的切向加速度与法向加速度。
解:物体下落的加速度())/(2.0222s m t ha =∆=又 βR a a t == ,得圆盘的角加速度 )/(2.02s rad =β 第3秒末,圆盘的角速度)/(6.0s rad t ==βω 所以 )/(2.02s m a t = )/(36.022s m R a n ==ω3-5 一个砂轮直径为0.4m ,质量为20kg ,以每分钟900转的转速转动。
撤去动力后,一个工件以100N 的正压力作用在砂轮边缘上,使砂轮在11.3s 内停止,求砂轮和工件的摩擦系数(忽略砂轮轴的摩擦)。
解:βJ M =其中NR M μ-= ,得JNRJM dt d μωβ-===⎰⎰-=ωμωNRJd dt t, 即NRtJ 0ωμ=又)/(306090020s rad ππω=⨯=,)(4.022122m kg d m J ⋅=⎪⎭⎫⎝⎛=得167.0=μ3-6 如图所示,质量为m 的匀质圆环,半径为R ,当它绕通过环心的直径轴转动时,求圆环对轴的转动惯量J 。
解:方法一:设过环心且垂直于圆环所在平面的轴线为z 轴,过环心的两条互相垂直的直径分别为x 轴和y 轴,习题3-6图习题3-3图习题3-8图习题3-7图根据垂直轴定理y x z J J J += 由对称性可知y x J J =,又2mR J z = 得221mR J J J y x ===方法二:θλλRd dl dm ==,其中Rm πλ2=()θθλθd R R dm dJ 232sin sin ==23202321sin mR R d R J ===⎰λπθθλπ3-7 如图所示,长为L 2的匀质细棒,质量为M ,未端固定一质量为m 的质点,当它绕过棒中点的水平轴转动时,求转动惯量J 。
解:22M 31mL ML J J J m +=+=3-8 如图所示,从质量为M ,半径为R 的匀质薄圆板上挖去一个半径为r 的圆孔,圆孔的中心位于半径的中点。
求此时圆板对于原板中心且与板面垂直的轴线的转动惯量。
解:可以把带孔的圆板看成均匀的完整圆板减去一个跟圆孔大小一致的圆板,即孔板圆板J J J -=221MR J =圆板,22)2(21R m mrJ +=孔板,其中M Rr m 22ππ=得2242412121Mr Rr MMR J --=3-9 如图所示,把两根质量均为m ,长为l 的匀质细棒一端焊接相连,其夹角︒=120θ,取连接处为坐标原点,两个细棒所在的平面为Oxy 平面,求此结构分别对Ox 轴、Oy 轴、Oz 轴的转动惯量。
解:(1)x x x J J J 右左+=, 其中0=x J 右︒=30cos y l ,︒===30cos 222l dy my dl lm ydmy dJ x 左,⎰︒=︒=30cos 0224130cos l x ml l dy my J 左,即241ml J J J x x x =+=右左(2)y y y J J J 右左+=, 其中231ml J y =右︒=30sin x l , ︒===30sin 222l dx mx dl lm xdmxdJ y 左,⎰︒=︒=30sin 02212130sin l ml l dx mx J 左,所以2125ml J J J y y y =+=右左(3) 222323131ml ml mlJ z =+=或 2223212541ml mlml J J J y x z =+=+=3-10 如图所示,在边长为a 的正六边形的六个顶点上各固定一个质量为m 的质点,设这正六边形放在Oxy 平面内,求:(1)对Ox 轴、Oy 轴、Oz 轴的转动惯量;(2)对过中心C 且平行于Oy 的y O '轴的转动惯量。
解:(1)223)23(402ma a m J x =⨯+⨯=22229)2(1)23(2)2(201ma a m a a m J y =⨯+⨯+⨯+⨯=222212)2(1)3(2201ma a m a maJ z =⨯+⨯+⨯+⨯=(2)2223)2(42ma am ma J y =⨯+⨯='习题3-9图习题3-10图或根据平行轴定理2236ma a m J J y y =⨯-='3-11 匀质圆盘质量为m 、半径为R ,放在粗糙的水平桌面上,绕通过盘心的竖直轴转动,初始角速度为0ω,已知圆盘与桌面的摩擦系数为μ,问经过多长时间后圆盘静止?解:可以把圆盘看成由许许多多的小圆环组成,其中半径为r 、宽度dr 的质量为rdr dS dm πσσ2== ,其中2Rmπσ=,受到的摩擦力矩为dr gr dmgr dM 22πμσμ-=-=所以整体圆盘受到的摩擦力矩为mgR gR dr gr M Rμπμσπμσ3232232-=-=-=⎰又βJ M =, 221mR J =Rg J M dtd 34μωβ-===常量gR t μωβω43000=-=3-12如图所示,斜面倾角为θ,位于斜面顶端的卷扬机鼓轮半径为r 、转动惯量为J 、受到的驱动力矩M ,通过绳索牵引斜面上质量为m 的物体,物体与斜面间摩擦系数为μ,求重物上滑的加速度。
绳与斜面平行,不计绳质量。
解:⎪⎩⎪⎨⎧==--=-βθθμβr a ma mg mg T J Tr M sin cos得 2)sin cos (mrJ rmg umg M a +--=θθ3-13 如图所示,两物体质量分别为1m 和2m ,定滑轮的质量为m 、半径为r ,可视作均习题3-12图习题3-13图习题3-14图习题3-15图匀圆盘。
已知2m 与桌面间的滑动摩擦系数为k μ,求1m 下落的加速度和两段绳子中的张力各是多少?设绳子和滑轮间无相对滑动,滑轮轴受的摩擦力忽略不计。
解: ⎪⎪⎪⎩⎪⎪⎪⎨⎧===-=-=-r a mr J J r T r T a m g m T a m T g m k ββμ22122211121得 mm m g m g m a k ++-=212122)(2μmm m gmm g m m a g m T k ++++=-=211211122)1(2)(μ •mm m gmm g m m a m g m T k k k ++++=+=2122122222)1(2μμμ3-14 如图所示的飞轮制动装置,飞轮质量m =600kg ,半径R =0.25m ,绕其水平中心轴O 转动,转速为900rev/min 。
闸杆尺寸如图示,闸瓦与飞轮间的摩擦系数40.0=μ,飞轮的转动惯量可按匀质圆盘计算,现在闸杆的一端加一竖直方向的制动力N 100=F ,问飞轮将在多长时间内停止转动?在这段时间内飞轮转了几转?解:设作用在飞轮上的压力为N ,则有)75.05.0(5.0+⨯=⨯F N ,得)N (250=N)/(340221s rad mRNRJM -=-==μβ又)/(306090020s rad ππω=⨯=, 所以)(07.700s t ≈-=βω又βωθ2020-=,得)(532转==πθn3-15 如图所示,长为l ,•质量为M 的匀质细棒可绕过其端点的水平轴在竖直面内自由转动,现将棒提到水平位置并由静止释放,当棒摆到竖直位置时与放在地面上质量为m 的物体相碰。
设碰后棒不动,物体与地面的摩擦系数为μ,求碰撞后物体经过多少时间停止运动?解:由机械能守恒2212ωJ L Mg =,得J MgL =ω又角动量守恒得mvL J =ω,有LMgJ mmLJ v 1==ω又g a μ-=,得LMgJ mg av t μ10=-=又231ML J =,即gL mgM t 33μ=3-16 质量为M 、半径为R 的水平转台,可绕过中心的竖直轴无摩擦地转动。
质量为m 的人站在转台的边缘,人和转台原来都静止。
当人沿转台边缘走一周时,求人和转台相对地面转过的角度。
解:以人和转台组成的系统为研究对象,设人相对于转盘的角速度为ω',转台相对地的角速度为ω,由角动量守恒得ωωω2221)(MR mr =-'移项得 ωω)21(222mr MR mr +='即 d td mr MR dtd mr θθ)21(222+='两边消去dt ,并积分的⎰⎰+='θπθθ022202)21(d mr MRd mr解得 221222MRmrmr +=πθ3-17 质量为M 、半径为R 的水平转台,可绕过中心的竖直轴无摩擦地转动。
初角速度为0ω,当质量为m 的人以相对转台的恒定速率v 沿半径从转台中心向边缘走去,求转台转过的角度随时间t 的变化函数。