五年级行程问题——相遇讲义及练习

第31讲行程问题（四）一、专题简析：通过前面对行程应用题的学习，同学们可以发现，行程问题大致分为以下三种情况：（1）相向而行：相遇时间=距离÷速度和（2）相背而行：相背距离=速度×时间（3）同向而行：追及时间=追及距离÷速度差如果上述的几种情况交织在一起，组成的应用题将会丰富多彩、千变万化。

解答这些问题时，我们还是要理清题中已知条件与所求问题之间的关系，同时采用“转化”、“假设”等方法，把复杂的数量关系转化为简单的数量关系，把一复杂的问题转化为几个简单的问题逐一进行解决。

二、精讲精练例1甲、乙两地相距420千米，一辆汽车从甲地开到乙地共用了8小时，途中，有一段路在整修路面，汽车行驶这段路时每小时只能行20千米，其余时间每小时行60千米。

整修路面的一段路长多少千米？1、一辆汽车从甲城到乙城共行驶395千米，用了5小时。

途中一部分公路是高速公路，另一部分是普通公路。

已知汽车在高速公路上每小时行105千米，在普通公路上每小时行55千米。

汽车在高速公路上行驶了多少千米？2、小明家离体育馆2300米，有一天，他以每分钟100米的速度去体育馆看球赛。

出发几分钟后发现，如果以这样的速度走下去一定迟到，他马上改用每分钟180米的速度跑步前进，途中共用15分钟，准时到达了体育馆。

问：小明是在离体育馆多远的地方开始跑步的？例2 客、货两车同时从甲、乙两站相对开出，客车每小时行54千米，货车每小时行48千米。

两车相遇后又以原速前进，到达对方站后立即返回，两车再次相遇时客车比货车多行21.6千米。

甲、乙两站间的路程是多少千米？1、乙、慢两车同时从甲、乙两地相对开出并往返行驶。

快车每小时行80千米，慢车每小时行45千米。

两车第二次相遇时，快车比慢车多行了210千米。

求甲、乙两地间的路程。

2、甲、乙两地相距216千米，客货两车同时从甲、乙两地相向而行。

已知客车每小时行58千米，货车每小时行50千米，到达对方出发点后立即返回。

相遇问题（一）例1 东西两地间有一条公路长217.5千米，甲车以每小时25千米的速度从东到西地，1.5小时后，乙车从西地出发，再经过3小时两车还相距15千米。

乙车每小时行多少千米？分析:从图中可以看出，要求乙车每小时行多少千米，关键要知道乙车已经行了多少路程和行这段路程所用的时间。

解：（1）甲车一共行多少小时？1.5+3=4.5（小时）（2）甲车一共行多少千米路程？25×4.5=112.5（千米）（3）乙车一共行多少千米路程？217.5-112.5=105（千米）（4）乙车每小时行多少千米？(105-15)÷3=30（千米）答：乙车每小时行30千米。

【边学边练】AB两地间有一条公路长2800米，甲车从A地出发5分钟后，乙车从B地出发，又经过10分钟两车相遇。

已知乙车每分钟行100米，甲车每分钟行多少米？例2 兄妹二人同时从家里出发到学校去，家与学校相距1400米。

哥哥骑自行车每分钟行200米，妹妹每分钟走80米。

哥哥刚到学校就立即返回来在途中与妹妹相遇。

从出发到相遇，妹妹走了几分钟？相遇处离学校有多少米？分析:从图中可以看出，哥与妹妹相遇时他们所走的路程的和相当于从家到学校距离的2倍。

因此本题可以转化为“哥哥妹妹相距2800米，两人同时出发，相向而行，哥哥每分钟行200米，妹妹每分钟行80米，经过几分钟相遇？”的问题，解答就容易了。

解：（1）从家到学校的距离的2倍：1400×2=2800（米）（2）从出发到相遇所需的时间：2800÷（200+80）=10（分）（3）相遇处到学校的距离：1400-80×10=600（米）答：从出发到相遇，妹妹走了10分钟，相遇处离学校有600米。

【边学边练】妹妹从家出发到学校去，每分钟走80米，家与学校相距1400米。

5分钟后，哥哥骑自行车从家出发去学校，每分钟行200米。

哥哥刚到学校就立即沿原路返回，在途中与妹妹相遇。

多次相遇与追及问题一、由简单行程问题拓展出的多次相遇问题所有行程问题都是围绕“=⨯路程速度时间”这一条基本关系式展开的，多人相遇与追及问题虽然较复杂，但只要抓住这个公式，逐步表征题目中所涉及的数量，问题即可迎刃而解．二、多次相遇与全程的关系1. 两地相向出发：第1次相遇，共走1个全程；第2次相遇，共走3个全程；第3次相遇，共走5个全程；…………，………………；第N次相遇，共走2N-1个全程；注意：除了第1次，剩下的次与次之间都是2个全程。

即甲第1次如果走了N米，以后每次都走2N 米。

2. 同地同向出发：第1次相遇，共走2个全程；第2次相遇，共走4个全程；第3次相遇，共走6个全程；…………，………………；第N次相遇，共走2N个全程；3、多人多次相遇追及的解题关键多次相遇追及的解题关键几个全程多人相遇追及的解题关键路程差三、解多次相遇问题的工具——柳卡柳卡图，不用基本公式解决，快速的解法是直接画时间-距离图，再画上密密麻麻的交叉线，按要求数交点个数即可完成。

折线示意图往往能够清晰的体现运动过程中“相遇的次数”，“相遇的地点”，以及“由相遇的地点求出全程”，使用折线示意图法一般需要我们知道每个物体走完一个全程时所用的时间是多少。

如果不画图，单凭想象似乎对于像我这样的一般人儿来说不容易。

【例 1】甲、乙两名同学在周长为300米圆形跑道上从同一地点同时背向练习跑步，甲每秒钟跑3.5米，乙每秒钟跑4米，问：他们第十次相遇时，甲还需跑多少米才能回到出发点？【巩固】甲乙两人在相距90米的直路上来回跑步，甲的速度是每秒3米，乙的速度是每秒2米．如果他们同时分别从直路两端出发，10分钟内共相遇几次？【例 2】甲、乙两车同时从A地出发，不停的往返行驶于A，B两地之间。

已知甲车的速度比乙车快，并且两车出发后第一次和第二次相遇都在途中C地。

问：甲车的速度是乙车的多少倍？【巩固】甲、乙二人从相距 60千米的两地同时相向而行，6时后相遇。

知识概述1.相遇问题是行程问题的一种类型，它的结构特征是：两个运动的物体，同时或不同时从两地相向而行，经过一段时间相遇。

2.解答这类问题的关键是理解速度，时间，路程这三者之间的关系。

3.速度和×相遇时间=总路程总路程÷速度和=相遇时间总路程÷相遇时间=速度和例题精学例1 小军和小丽同时从两地对面走来，小军每分钟走36米，小丽每分钟走43米，两人在距中点14米处相遇，两地相距多少米？同步精练1.甲、乙两人同时从相距39千米的两地相向而行，甲步行每小时行3千米，乙骑自行车每小时行10千米。

多少小时后他们会在途中相遇？2.甲、乙两车同时从A、B两地相对开出，甲车每小时行92千米，乙车每小时行108千米，两车在离终点48千米的地方相遇。

A、B两地之间相遇多少千米？3.货车和客车同时由甲、乙两地相向而行，经过六小时相遇，相遇后客车再行5小时到达乙地。

已知货车每小时行50千米，求甲、乙两地相距多少千米？练习巩固1.小强和小明家相距2400米,两人同时从家相向而行,小强每分钟走50米,小明每分钟70米,他们经过多长时间相遇?2.甲乙两人同时从两地骑车相向而行，甲每小时行驶20千米，乙每小时行驶18千米，两人相遇时距离全程中点3千米，求全程长多少千米？3.甲乙两列火车从相距470千米的两城相向而行，甲车每小时行38千米，乙每小时行40千米，乙车先出发2小时后，甲车才出发，甲车行几小时后与乙车相遇？例题精学例2 一辆卡车和一辆摩托车同时从A、B两地相对开出,两车再途中距A地60千米处第一次相遇,然后,两车继续前进,车到达B地,摩托车到达A地后都立刻返回,两车又在途中距B地30千米处第二次相遇,A、B两地相距多少千米？【分析】根据题意可知，两辆车两次相遇走的总路程就是A,B两地总路程的3倍，每走一个A,B两地之间的距离，卡车就走60千米，卡车走的总路程60×3=180千米，也是A,B两地之间路程加30千米。

行程问题—相遇问题学生姓名年级学科授课教师日期时段核心内容相遇问题课型一对一/一对N教学目标1.理解相遇问题的总路程、相遇时间和速度和等相关概念，会分析相遇问题的已知和未知之间的相等关系。

2.掌握运动中的物体，速度、时间、路程之间的数量关系，会利用路程、时间和速度三量关系解决实际生活中的相遇问题。

3. 经历解决问题的过程，体验数学与日常生活密切相关，体现数学是源于生活的思想。

重、难点重点：理解相遇问题的结构特点，学会抓相遇问题中速度、时间、路程的数量关系解决相遇问题。

难点：掌握相遇问题的解题规律，让学生学会如何抓相遇问题的数量关系解决相遇问题。

课首沟通1.与学生沟通和分享最近的生活趣事，学生情况。

2.回顾前几次课的内容，让学生复述知识点和解题方法。

知识导图课首小测1. 小明从家去学校上学花了8分钟，已知小明的速度是100米/分，那么小明家到学校一共有多少米？ 2. 从广州到南宁的路程约1000千米，一辆长途客车从广州出发用了3小时行了300千米，这辆长途客车平均每小时行多少千米？3. 聪聪和明明国庆节乘飞机去了北京，飞机每小时飞行800千米，一共飞行了1600千米，那么飞机飞行了几小时？ 知识梳理 本讲学习的相遇问题属于行程问题中的一种典型问题，是解决两个运动物体方向相反的行程问题。

基本的运动模式是：两个运动物体同时从两地相向而行，在途中相遇，称为相遇问题。

例如甲车从A地到B地，乙车从B地到A地，然后甲、乙两车在A地和B地之间的某处相遇，实质上甲、乙两车一起走完了A地到B地的全程，我们称之为“总路程”，从同时出发到相遇，两车所用的时间相同，这个时间我们称为“相遇时间”，两车各自的速度的和称为“速度和”。

如果两车同时出发，相向而行，基本的数量关系如下：①速度和×相遇时间＝总路程②总路程÷速度和＝相遇时间③总路程÷相遇时间＝速度和 解决问题时一定要认真分析题意，弄清两个物体的运动模式，具体问题具体解决，有时可借助线段图帮助理解题意。

相遇问题学生姓名年级学科授课教师日期时段核心内容路程=速度×时间课型一对一/一对N 教学目标掌握相遇问题，并运用到生活中。

重、难点解答行程问题时，要理清路程、速度和时间之间的关系，紧扣基本数关系“路程=速度×时间”来思考，对具体问题要作仔细分析，弄清出发地点、时间和运动结果。

课首沟通在走路中涉及的数学问题，主要就是速度、时间和路程这三量之间的关系问题。

这三量之间是什么关系呢？让学生对具体问题要作仔细分析，得出公式并写在下面的知识导图中知识导图课首小测1.一辆汽车每小时行60千米，4小时行多少千米？2.一辆汽车4小时行了240千米，每小时行多少千米？3.一辆汽车每小时行60千米，行驶240千米需要几小时？4.甲、乙两地间的路程是600千米，上午8点客车以平均每小时60千米的速度从甲地开往乙地。

货车以平均每小时50千米的速度从乙地开往甲地。

要使两车在全程的中点相遇，货车必须在上午几点出发？5.AB两地相距900千米，甲车由A地到B地需15小时，乙车由B地到A地需10小时。

两车同时从两地开出，相遇时甲车距B地还有多少千米？知识梳理出发地点（同地、异地）行走方向（同向、相向、背向）出发时间（同时、不同时）运动结果（追上还是相遇，或还相差多远）运动路径（线段型还是环形、单程还是往返等）导学一：直线上的相遇问题知识点讲解 1：单个全程的相遇例 1. （举一反三）两辆汽车同时从某地出发，运送一批货物到距离165千米的工地。

甲车比乙车早到48分钟，当甲车到达时，乙车还距工地24千米。

甲车行完全程用了多少小时？例 2. 东西两地间有一条公路长217.5千米，甲车以每小时25千米的速度从东地开往西地，1.5小时后，乙车从西地出发，再经过3小时两车还相距15千米。

乙车每小时行多少千米？例 3. 两城市相距328千米，甲、乙两人骑自行车同时从两城出发，相向而行。

甲每小时行28千米，乙每小时行22千米，乙在中途修车耽误1小时，然后继续行驶，与甲相遇，求出发到相遇经过多少时间？例 4. 快车和慢车同时从甲乙两地相对开出，已知快车每小时行40千米，经过3小时快车已过中点12千米与慢车相遇，慢车每小时行多少千米？例 5. 王欣和陆亮两人同时从相距2000米的两地相向而行，王欣每分钟行110米，陆亮每分钟行90米。

行程问题之相遇问题【含义】两个运动的物体同时由两地出发相向而行，在途中相遇。

这类应用题叫做相遇问题。

【数量关系】相遇时间＝总路程÷（甲速＋乙速）总路程＝（甲速＋乙速）×相遇时间【解题思路和方法】简单的题目可直接利用公式，复杂的题目变通后再利用公式。

例1：甲乙二人同时从两地骑自行车相向而行，甲每小时行15千米，乙每小时行13千米，两人在距中点3千米处相遇，求两地的距离。

解: “两人在距中点3千米处相遇”是正确理解本题题意的关键。

从题中可知甲骑得快，乙骑得慢，甲过了中点3千米，乙距中点3千米，就是说甲比乙多走的路程是（3×2）千米，因此，相遇时间＝（3×2）÷（15－13）＝3（小时）两地距离＝（15＋13）×3＝84（千米）答：两地距离是84千米。

例2：甲、乙两辆汽车分别以不同的速度同时从A、B两地相对而行，途中相遇，相遇点距A地60千米。

相遇后两车以原速前进，到底目的地后，两车立即返回，在途中又第二次相遇，这时距A地40千米。

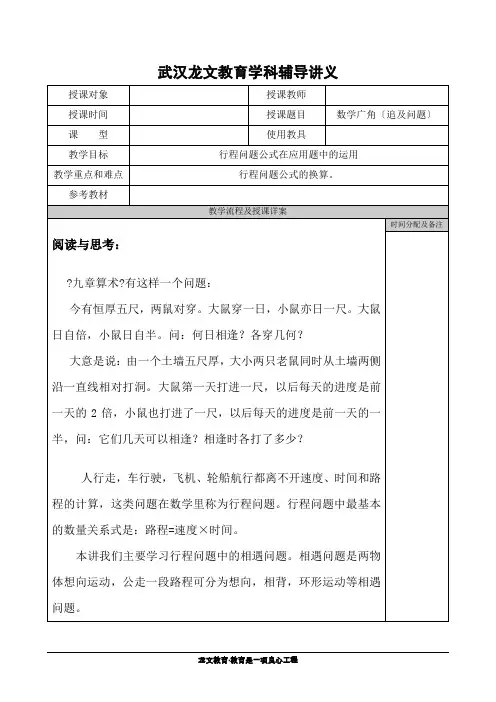
问第一次相遇点距B地多少千米？【解析】：甲、乙两辆汽车同时从A、B两地相对而行，行驶情况如下图：蓝色线条表示甲车行驶路线，红色线条表示乙车行驶路线；细线条是第一次相遇前两车行驶路程，粗线条表示两车从第一次相遇到第二次相遇之间行使的路程。

从图中可以看出，从出发到第一次相遇，两车合走了1个全程（细线条）；从第一次相遇到第二次相遇，两车合走了2个全程（粗线条）；两车总共合走了3个全程。

每辆汽车的速度是一定的，所以它们各自行驶的路程与时间成正比例。

解法一：如上图，第一次相遇时，即两车合走1个全程的时间里，甲走了60千米。

两车总共合走了3个全程，则甲车从A地出发，经过B地到达第二次相遇地点，总共行驶了3个60千米（蓝色线条全长），加上第二次相遇地点到A地40千米，共2个全程。

所以A、B两地的距离为：（60×3＋40）÷2＝110（千米）。

周二2022-2023学年小学五年级思维拓展专题 行程(多次相遇)问题知识精讲专题简析：通过前面对行程应用题的学习，同学们可以发现，行程问题大致分为以下三种情况：(1)相向而行：相遇时间=距离÷速度和(2)相背而行：相背距离=速度×时间(3)同向而行：追及时间=追及距离÷速度差如果上述的几种情况交织在一起，组成的应用题将会丰富多彩、千变万化。

解答这些问题时，我们还是要理清题中已知条件与所求问题之间的关系，同时采用“转化”、“假设”等方法，把复杂的数量关系转化为简单的数量关系，把一复杂的问题转化为几个简单的问题逐一进行解决。

典例分析1.(2019•岳麓区)甲、乙两人同时从A地出发，在直道A、B两地往返跑步，甲每分钟72米，乙每分钟48米，甲乙第二次迎面相遇与甲第二次从后面追上乙，两地相距80米，求A、B两地相距多少米？2.(2019•郑州)如图，ABCD是一个边长为6米的模拟跑道，甲玩具车从A出发顺时针行进，速度是每秒5厘米，乙玩具车从CD的中点出发逆时针行进(乙车速度小于甲车速度)，结果两车第二次相遇恰好是在B点，求乙车每秒走多少厘米？周二3.(2018春•江宁区期末)小欣和小鸣分别从一座桥的两端同时相向出发，往返于两端之间．小欣每分钟走65米，小鸣每分钟走70米，经过5分钟后两人第二次相遇．这座桥长多少米？4.(2018•广东)甲乙二人分别从A、B两地出发相向而行，到达目的地后马上掉头回到出发地，他们第一次相遇距A地800米，第二次距B地500米，A、B两地相距多少米？真题演练一、选择题(共5小题，满分5分，每小题1分)1.(1分)(2015秋•漳州期末)爸爸和儿子去2km外的公园，爸爸和儿子同时出发．儿子骑车到公园时，爸爸只走了一半路程．儿子立刻返回，遇到爸爸后又骑向公园，到公园又返回⋯直到爸爸到达公园．儿子从出发开始一共骑了()A.2kmB.4kmC.6km2.(1分)甲乙两人分别从桥的两端同时出发，往返于桥的两端之间。

第20讲行程问题讲义专题简析行程应用题是专门讲物体运动的速度、时间、路程三者关系的应用题。

行程问题的主要数量关系是:路程＝速度×时间。

知道三个量中的两个量，就能求出第三个量。

例1、甲、乙两辆汽车同时从东、西两地相向开出，甲车每小时行56千米，乙车每小时行48千米。

两车在距中点32千米处相遇。

东、西两地相距多少千米?练习1.甲、乙两汽车同时从两地出发，相向而行。

甲汽车每小时行50千米，乙汽车每小时行55千米，两车在距中点15千米处相遇。

求两地之间的路程是多少千米?2.一辆汽车和一辆摩托车同时从A、B两城相对开出，汽车每小时行60千米，摩托车每小时行70千米，当摩托车行到两城中点处时，与汽车还相距30千米。

求A、B两城之间的距离?3.下午放学时，小红从学校回家，每分钟走100米，同时，妈妈也从家里出发到学校去接小红，每分钟走120米，两人在距中点100米的地方相遇，小红家到学校有多少米?例2、快车和慢车同时从甲、乙两地相向开出，快车每小时行40千米，经过3小时快车已驶过中点25千米，这时快车与慢车还相距7千米。

慢车每小时行多少千米?练习1.兄弟二人同时从学校和家中出发，相向而行。

哥哥每分钟行120米，5分钟后哥哥已超过中点50米，这时兄弟二人还相距30米。

弟弟每分钟行多少米?2.汽车从甲地开往乙地，每小时行32千米，4小时后，剩下的路比全程的一半少8千米，如果改用每小时56千米的速度行驶，再行几小时到乙地?3.学校运来一批树苗，五(1)班的40个同学都去参加植树活动，如果每人植3棵，全班同学能植这批树苗的一半还多20棵。

如果这批树苗全部给五(1)班的同学去植，平均每人植多少棵树?例3、甲、乙二人上午8时同时从东村骑车到西村去，甲每小时比乙快6千米。

中午12时甲到西村后立即返回东村，在距西村15千米处遇到乙。

求东、西两村相距多少千米?练习1.甲、乙二人同时从A地到B地，甲每分钟走250米，乙每分钟走90米。

多次相遇与追及问题一、由简单行程问题拓展出的多次相遇问题所有行程问题都是围绕“=⨯路程速度时间”这一条基本关系式展开的，多人相遇与追及问题虽然较复杂，但只要抓住这个公式，逐步表征题目中所涉及的数量，问题即可迎刃而解．二、多次相遇与全程的关系1. 两地相向出发：第1次相遇，共走1个全程；第2次相遇，共走3个全程；第3次相遇，共走5个全程；…………，………………；第N次相遇，共走2N-1个全程；注意：除了第1次，剩下的次与次之间都是2个全程。

即甲第1次如果走了N米，以后每次都走2N 米。

2. 同地同向出发：第1次相遇，共走2个全程；第2次相遇，共走4个全程；第3次相遇，共走6个全程；…………，………………；第N次相遇，共走2N个全程；3、多人多次相遇追及的解题关键多次相遇追及的解题关键几个全程多人相遇追及的解题关键路程差三、解多次相遇问题的工具——柳卡柳卡图，不用基本公式解决，快速的解法是直接画时间-距离图，再画上密密麻麻的交叉线，按要求数交点个数即可完成。

折线示意图往往能够清晰的体现运动过程中“相遇的次数”，“相遇的地点”，以及“由相遇的地点求出全程”，使用折线示意图法一般需要我们知道每个物体走完一个全程时所用的时间是多少。

如果不画图，单凭想象似乎对于像我这样的一般人儿来说不容易。

【例 1】甲、乙两名同学在周长为300米圆形跑道上从同一地点同时背向练习跑步，甲每秒钟跑3.5米，乙每秒钟跑4米，问：他们第十次相遇时，甲还需跑多少米才能回到出发点？【巩固】甲乙两人在相距90米的直路上来回跑步，甲的速度是每秒3米，乙的速度是每秒2米．如果他们同时分别从直路两端出发，10分钟内共相遇几次？【例 2】甲、乙两车同时从A地出发，不停的往返行驶于A，B两地之间。

已知甲车的速度比乙车快，并且两车出发后第一次和第二次相遇都在途中C地。

问：甲车的速度是乙车的多少倍？【巩固】甲、乙二人从相距 60千米的两地同时相向而行，6时后相遇。

五年级上册数学思维奥数讲义火车行程问题知识梳理1、车头上桥到车尾下桥：路程=火车长+桥长2、车尾上桥到车头下桥：路程=桥长-火车长3、火车与人相遇：路程和=火车长4、火车与人追及：路程差=火车长5、火车与火车相遇（车头相遇到车尾相离）：路程和=甲车长+乙车长6、火车与火车追及（快车车头追上慢车车尾到快车车尾离开慢车车头）：路程差=快车长+慢车长知识精讲小热身（1）甲乙两人相距50米，相向而行，速度分别为3米/秒和2米/秒，多久后两人相遇？（2）甲乙两人相距50米，同向而行，速度分别为3米/秒和2米/秒，多久后甲追上乙？典例1 （1）一列高铁长180米，每秒钟行驶60米，这列高铁通过一座300米长的大桥时，从车头开始上桥到车尾完全过桥需要多少时间？（2）一列高铁以每秒钟70米的速度行驶，通过一条400米长的隧道时，从车头开始进入隧道到车尾完全通过隧道共用时8秒钟，请问这列高铁车长多少米？变式1 （1）一列动车以每秒钟60米的速度通过一条长1000米的隧道，从车头开始进入隧道到车尾完全通过隧道共用时20秒，请问这列动车的长度是多少米？（2）一列动车长150米，每秒钟行驶70米，这列动车通过一座200米长的大桥时，从车头开始上桥到车尾完全过桥需要多少时间？典例2 同一列动车完全通过（从车头进入到车尾离开）一条490米长的隧道需要10秒，完全通过一条370米长的大桥需要8秒，那么这列动车的速度是每秒钟多少米？车长多少米？变式2 同一列高铁完全通过（从车头进入到车尾离开）一条长800米的大桥需要14秒，完全通过一条长540米深的隧道时需要10秒钟，请问高铁的速度是多少米？车长多少米？典例3 某铁路桥长1000米，现有一列火车从桥上通过，测得火车从开始上桥到完全过桥共用1分，整列火车完全在桥上的时间为40秒。

求火车的长度和速度。

变式3某条隧道长900米，现有一列100米长的火车从隧道中通过，测得火车从开始进入隧道到完全通过隧道共用20秒，则整列火车完全在隧道里的时间是多长？典例4 （1）一名行人沿着与铁路平行的公路散步，每秒走1米，迎面过来一列长120米的动车，已知动车每秒钟行驶59米，请问：从动车头与行人相遇到动车尾离开他共用了多长时间？（2）一人以每分钟60米的速度沿着与铁路平行的公路散步，一列长180米的动车从他身后开来，动车的速度是每秒钟61米，动车从他身边经过用了多长时间？变式4 （1）一人以每分钟60米的速度沿着与铁路平行的公路散步，一列长180米的动车从对面开来，从他身边经过用了3秒钟，动车的速度是每秒钟多少米？（2）小明在铁路旁边沿着与铁路方向平行的公路散步，他散步的速度是2米/秒，这时背后开来一列火车，从车头追上他到车尾离开他一共用了3秒，已知火车速度是42米/秒，请问：火车的车长多少米？典例5 （1）一列火车车长180米，每秒行驶40米，另一列火车长200米，每秒行驶36米，两车相向而行，它们从车头相遇到车尾相离要经过多长时间？（2）甲火车长420米，每秒钟行驶30米，乙火车在甲火车后，长300米，每秒钟行驶42米，两车同向行驶，请问：乙车从追上甲车到完全超过共需要多长时间？变式5 （1）已知快车长240米，每秒钟行驶38米，慢车长360米，两车相向而行，它们从车头相遇到车尾相离共用时10秒，请问：慢车速度是多少？（2）已知快车长240米，每秒钟行驶66米，慢车长360米，两车同向而行，它们从快车追上到完全超越慢车共用时20秒，请问：慢车速度是多少？课后训练1、一列火车长200米，以每分钟500米的速度通过一座长1300米的大桥，从车头上桥到车尾离开桥需要多少分钟？2、一列高铁车长120米，通过一条长720米的大桥时，从车头开始上桥到车尾完全过桥需要14秒，这列高铁完全通过（从车头进入隧道到车尾离开隧道）一条长360米长的隧道时需要多少秒？3、一列高铁车长100米，通过一条长700米的大桥时，高铁完全在桥上（车尾上桥到车头离开桥）的时间是10秒钟，这列高铁的速度是多少？4、一人以每分钟60米的速度沿着与铁路平行的公路散步，一列动车从他身后开来，动车的速度是每秒钟61米，3秒钟后动车从他身边经过，请问这列动车长多少米？5、有两列火车，一列长360米，每秒行驶36米，另一列长240米，每秒行驶60米，两车同向而行，快车赶超慢车（从追上到完全超过）需要多少秒？6、甲火车每秒行驶50米，乙火车每秒行驶30米，两列火车相向而行时，它们从车头相遇到车尾相离要经过4秒，请问：如果两列火车同向行驶时，甲火车从追上乙火车到完全超过共需要多长时间？7、现在有两列火车同时同方向齐头行进，快车每秒行驶18米，慢车每秒行驶10米，行驶12秒后快车超过慢车。