离散信源的信息熵

实验报告实验名称关于信源熵的实验课程名称信息论与编码姓名xxx 成绩90班级电子信息1102学号**********日期2013.11.22地点综合实验楼实验一关于信源熵的实验一、实验目的1. 掌握离散信源熵的原理和计算方法。

2. 熟悉matlab 软件的基本操作，练习使用matlab 求解信源的信息熵。

3. 自学图像熵的相关概念，并应用所学知识，使用matlab 或其他开发工具求解图像熵。

4. 掌握Excel的绘图功能，使用Excel绘制散点图、直方图。

二、实验原理1. 离散信源相关的基本概念、原理和计算公式产生离散信息的信源称为离散信源。

离散信源只能产生有限种符号。

随机事件的自信息量I（xi）为其对应的随机变量xi 出现概率对数的负值。

即： I （xi ）= -log2p ( xi)随机事件X 的平均不确定度（信源熵）H（X）为离散随机变量 xi 出现概率的数学期望，即：2.二元信源的信息熵设信源符号集X={0，1} ，每个符号发生的概率分别为p(0)= p，p(1)= q，p+ q =1，即信源的概率空间为：则该二元信源的信源熵为：H( X) = - plogp–qlogq = - plogp –(1 - p)log(1- p)即：H (p) = - plogp –(1 - p)log(1- p) 其中 0 ≤ p ≤13. MATLAB二维绘图用matlab 中的命令plot( x , y) 就可以自动绘制出二维图来。

例1-2，在matlab 上绘制余弦曲线图，y = cos x ，其中 0 ≤ x ≤2。

>>x =0:0.1:2*pi； %生成横坐标向量，使其为 0，0.1，0.2，…，6.2>>y =cos(x )； %计算余弦向量>>plot(x ,y ) %绘制图形4. MATLAB求解离散信源熵求解信息熵过程：1) 输入一个离散信源，并检查该信源是否是完备集。

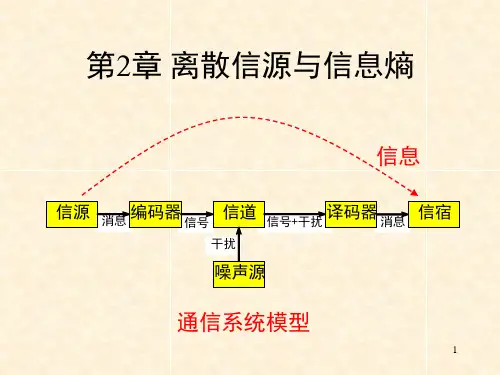
第2章离散信源与信息熵信号 信号+干扰 消息干扰消息 信源 编码器 信道 译码器 信宿 噪声源通信系统模型信息2.1 信源的分类和描述信源是信息的发源地，可以是人、生物、机器或其他事物。

信源的输出是包含信息的消息。

消息的形式可以是离散的或连续的。

信源输出为连续信号形式（如语音），可用连续随机变量描述。

连续信源←→模拟通信系统信源输出是离散的消息符号（如书信），可用离散随机变量描述。

离散信源←→数字通信系统离散信源…X i…X j…离散无记忆信源：输出符号Xi Xj之间相互无影响；离散有记忆信源：输出符号Xi Xj之间彼此依存。

3离散信源无记忆有记忆发出单个符号发出符号序列马尔可夫信源非马尔可夫信源y j将一粒棋子随意地放在棋盘中的某列；棋子放置的位置是一个随机事件；可看做一个发出单个符号的离散信源。

x i1212,,...,(),(),...,()m m x x x X P p x p x p x ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦就数学意义来讲，信源就是一个概率场，可用概率空间来描述信源。

由离散随机变量X 表示棋子位置：10()1,()1m i ii p x p x =≤≤=∑i x 其中，代表随机事件的某一结果。

2.2离散信源的信息熵信息的可度量性是信息论建立的基础；香农的信息论用事件发生概率的对数来描述事件的不确定性，得到消息的信息量，建立熵的概念。

2.2.1自信息量–定义2.1 任意随机事件x i 的自信息量定义为：i i i 1(x )log log (x )(x )I P P ==-小概率事件所包含的不确定性大，自信息量大。

大概率事件所包含的不确定性小，自信息量小。

概率为1的确定性事件，自信息量为零。

i i i 1(x )log log (x )(x )I P P ==-信息量的单位与公式中的对数取底有关。

以2为底，单位比特（bit ）；以e 为底，单位奈特（nat ）；()22log log ,log log ln log c a c b b x e x a==⋅–例：棋盘共8列，甲随手一放，将一枚棋子放在了第3列。

离散和连续信源熵正负离散和连续信源熵正负一、信源熵的定义及概念信源熵是信息论中的基本概念，它是用来度量一个随机变量的不确定性或者信息量大小的。

在信息论中，随机变量表示一种不确定性的度量，信源则是产生这种不确定性的物理系统。

二、离散信源熵离散信源熵是指在一个有限符号集合中，每个符号出现的概率已知，且各符号出现概率之和为1时，该离散信源所产生的平均信息量。

1. 离散信源熵的计算公式设离散信源S={s1,s2,…,sn}，其每个符号si出现的概率为pi，则该离散信源所产生的平均信息量H(S)为：H(S)=-Σ(pi*log2(pi))其中log2表示以2为底数的对数。

2. 离散信源熵值特点(1) H(S)>=0：由于log2(pi)<=0，因此pi*log2(pi)<=0，从而Σ(pi*log2(pi))<=0。

因此H(S)<=0。

又因为pi>=0且Σpi=1，则必有至少一个pi=1且其他pi=0时取到等号。

即当所有符号都相等时取到最小值0。

(2) H(S)越大，该离散信源的不确定性越大，产生的信息量也就越多。

(3) H(S)的单位是比特(bit)，它表示每个符号所需的平均信息量。

三、连续信源熵连续信源熵是指在一个连续随机变量中，各取值概率密度函数已知时，该连续信源所产生的平均信息量。

1. 连续信源熵的计算公式设连续信源X的概率密度函数为f(x)，则该连续信源所产生的平均信息量H(X)为：H(X)=-∫f(x)*log2(f(x))dx其中∫表示积分符号。

2. 连续信源熵值特点(1) 连续信源熵与离散信源熵不同，它可以是负数。

(2) 连续信源熵越大，该连续信源的不确定性越大，产生的信息量也就越多。

(3) 由于f(x)*log2(f(x))<=0，因此H(X)>=0。

当概率密度函数f(x)=常数时取到最小值0。

但由于积分范围无限大，在实际应用中很难出现这种情况。

离散信源熵信道容量实验报告实验目的：通过模拟离散信源熵和信道容量的实验，掌握熵和信道容量的概念及计算方法。

实验原理：离散信源：离散信源是指其输出符号集合为有限的离散符号集合，通常用概率分布来描述其输出符号的概率分布，称为离散概率分布。

离散信源的熵是度量这一离散概率分布的不确定度的量度，其单位是比特。

离散信源的熵公式为：H(S)=-Σpi×log2pi其中，H(S)为离散信源的熵，pi为消息符号i出现的概率，log2为以2为底的对数。

信道容量：信道容量是指在某一固定的信噪比下，能够传送的最大信息速率。

信道容量的大小决定了数字通信系统的最高可靠传输速率。

离散无记忆信道的信道容量公式为：C=max{I(X;Y)}其中，X为输入符号，Y为输出符号，I为信息熵。

实验步骤：1. 生成随机概率分布对于3种不同的符号数量，生成随机的符号及其概率分布。

在生成时，要求概率之和为1。

2. 计算离散信源的熵根据所生成的随机概率分布计算离散信源的熵。

3. 构建离散无记忆信道构建一个离散的2进制对称信道，并存储在一个概率矩阵中，利用生成的概率分布对该矩阵进行初始化。

4. 计算信道容量根据所构建的离散无记忆信道计算其信道容量。

实验结果分析：以下是实验结果分析，其中H(S)表示离散信源的熵，C表示离散无记忆信道的信道容量。

符号数量为3时：符号概率a 0.2b 0.3c 0.5H(S) = 1.485构建的离散无记忆信道的概率矩阵为：| 0 | 1 |--------------------------a | 0.20 | 0.80 |--------------------------b | 0.60 | 0.40 |--------------------------c | 0.80 | 0.20 |--------------------------C = 0.823从实验结果可以看出，当符号数量增加时，熵的值也会随之增加，这是由于符号集合增加，随机性增强所导致的。

信息熵与信息效用值在当今信息化时代，信息的重要性日益凸显。

为了有效地处理、传输和存储信息，我们需要对信息进行量化分析。

信息熵和信息效用值是信息论中的两个核心概念，它们在诸多领域，如通信、计算机科学、统计学、物理学等，都具有广泛的应用。

本文将详细阐述信息熵和信息效用值的定义、性质、计算方法以及它们在实际应用中的作用，并探讨它们之间的内在关系。

一、信息熵1.1 定义信息熵（Entropy）是度量信息不确定性或随机性的一个指标。

在信息论中，信息熵表示信源发出信息前的平均不确定性，也可以理解为某事件发生时所包含的信息量。

信息熵越大，表示信息的不确定性越高，所需的信息量也就越大。

1.2 性质信息熵具有以下几个基本性质：（1）非负性：信息熵的值始终大于等于0，当且仅当信源发出的信息完全确定时，信息熵等于0。

（2）对称性：信息熵与信源符号的排列顺序无关。

（3）可加性：对于独立信源，其联合熵等于各信源熵之和。

（4）极值性：在所有具有相同符号数的信源中，等概率信源的信息熵最大。

1.3 计算方法对于离散信源，信息熵的计算公式为：H(X) = - Σ P(xi) log2 P(xi)其中，X表示信源，xi表示信源发出的第i个符号，P(xi)表示符号xi出现的概率。

二、信息效用值2.1 定义信息效用值（Information Value，简称IV）是衡量某一特征或变量对目标变量的预测能力的一个指标。

在数据挖掘和机器学习领域，信息效用值通常用于特征选择，以评估特征与目标变量之间的相关性。

信息效用值越大，表示该特征对目标变量的预测能力越强。

2.2 性质信息效用值具有以下性质：（1）有界性：信息效用值的取值范围在0到1之间。

当特征与目标变量完全独立时，信息效用值为0；当特征能完全预测目标变量时，信息效用值为1。

（2）单调性：对于同一目标变量，当特征的信息量增加时，其信息效用值也会相应增加。

2.3 计算方法信息效用值的计算公式基于互信息和信息增益等概念。

信息熵的概念及其在信息论中的应用信息熵是信息论中一个重要的概念，它被用来衡量一段信息的不确定性或者说信息的平均编码长度。

熵的概念最早由克劳德·香农在1948年提出，对于信息的量化和信源编码具有重要的理论和实际应用。

本文将对信息熵的概念进行详细的介绍，并探讨其在信息论中的应用。

一、信息熵的定义信息熵可以看作是一个信源所产生的信息的不确定性度量。

当一个信源产生的符号具有均匀分布时，熵的值最大；而当信源的输出符号呈现高度集中的分布时，熵的值最小。

具体地，对于一个离散型信源，其熵的定义如下：H(X) = -Σp(x)log2p(x)，其中，H(X)表示信源X的熵，p(x)表示信源X输出符号x出现的概率。

二、信息熵的解释信息熵可以理解为对信息的平均编码长度的期望。

在信息论中，我们可以通过霍夫曼编码等方法对信息进行编码，使得熵最小化，从而达到最高的编码效率。

假设信源X有n个符号，出现的概率分别为p1, p2, ..., pn，则信源X的平均编码长度L为：L = ΣpiLi，其中，Li为信源X的符号i的编码长度。

根据不等式关系log2(p1/p2) <= p1/p2，我们可以得到：H(X) = -Σp(x)log2p(x) <= Σp(x) * (-log2p(x)) = Σp(x)log2(1/p(x)) = Σp(x)log2n = log2n，即熵的值小于等于log2n，其中n为符号的个数。

当n个符号均匀分布时，熵的值达到最大，即log2n。

三、信息熵的应用信息熵在信息论中具有广泛的应用，下面将介绍几个常见的应用场景。

1. 数据压缩信息熵在数据压缩中起到重要的作用。

根据信息论的原理，我们可以利用数据的统计特性进行有损压缩。

对于频率出现较高的符号，我们可以分配较短的编码，而对于出现频率较低的符号，则分配较长的编码。

通过这种方式，我们可以大大减少数据的存储空间，提高传输效率。

2. 通信系统信息熵在通信系统中也有重要应用。