实验四 面向系统结构图的仿真验证

实验二、面向结构图的仿真一、实验过程1.线性系统仿真（1）定义参数并为参数赋值，求解Kc、bc、Kd 、ad 、a1 、K1、a2 、K2等参数；（2）为uc(1)、ud(1)、u1(1)、u2(1)、xc(1)、xd(1)、x1(1)、x2(1)、yd(1)、yc(1)、y1(1)、y2(1)参数赋值为0；（3）迭代求解uc(k)、ud(k)、xc（k）、xd（k）等输入输出变量；（4）将液位高度转换为转换为百分比高度；（5）绘制响应曲线；（6）用MATLAB 求出从输入到输出的传递函数，并将其用c2d 函数，利用双线性变换法转换为离散模型，再用dstep()函数求离散模型的阶跃响应，阶跃幅值为3。

2.含有非线性环节的控制系统仿真非线性环节控制系统与线性控制系统实验方法相同，但离散化模型存在不同，同时需要增加饱和环节判断。

二、实验程序1、线性系统仿真clcclear all%%%%%%%%%%%%%%%%%%%%%定义参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%A=2; %水箱横截面积ku=0.1/0.5; %阀门流量系数H10=1.5; %水箱1的平衡高度H20=1.4; %水箱2的平衡高度alpha12 = 0.25/sqrt(H10); %水箱1流向水箱2流量系数alpha2 = 0.25/sqrt(H20); %水箱2流出水流量系数R12=2*sqrt(H10)/alpha12; %线性化数学模型中的参数R2=2*sqrt(H20)/alpha2; %线性化数学模型中的参数H1SpanLo=0; %水箱1量程下限H2SpanLo=0; %水箱2量程下限H1SpanHi=2.52; %水箱1量程上限H2SpanHi=2.52; %水箱2量程上限Kp=1.78; %PI控制器比例系数Ti=85; %PI控制器积分时间常数Kc=Kp/Ti; %式(4)中参数bc=Ti; %式(4)中参数Kd = 1/A; %式(5)中参数ad = 1/(A*R12); %式(5)中参数a1 = 1/(A*R12); %式(6)中参数K1 = ku/A; %式(6)中参数a2 = 1/(A*R2); %式(7)中参数K2 = 1/(A*R12); %式(7)中参数%%%%%%%%%%%%%%%%%%%%%%%%%%%赋初值%%%%%%%%%%%%%%%%%%%%%%%%%uc(1)=0;ud(1)=0;u1(1)=0;u2(1)=0;xc(1)=0;xd(1)=0;x1(1)=0;x2(1)=0;yd(1)=0;yc(1)=0;y1(1)=0;y2(1)=0;k=2;Qd=0; %干扰流量H20_percent=(H20-H2SpanLo)/(H2SpanHi-H2SpanLo)*100;H2=80;tend = 700; %总长T=10;%%%%%%%%%%%%%%%%%%%迭代求解输入输出变量%%%%%%%%%%%%%%%%%%%%%for t=T:T:tenduc(k)= (H2 - (y2(k-1)+H20-H2SpanLo)/(H2SpanHi-H2SpanLo)*100)/100; ud(k)=Qd;u1(k)=yc(k-1);u2(k)=y1(k-1); %扰动为零xc(k) = xc(k-1) + Kc*T*uc(k-1);yc(k)=xc(k)+bc*Kc*uc(k);xd(k) = exp(-ad*T)*xd(k-1) + Kd/ad*(1-exp(-ad*T))*ud(k);yd(k)=xd(k);x1(k) = exp(-a1*T)*x1(k-1) + K1/a1*(1-exp(-a1*T))*u1(k);y1(k)=x1(k);x2(k) = exp(-a2*T)*x2(k-1) + K2/a2*(1-exp(-a2*T))*u2(k);y2(k)=x2(k);k=k+1; %递增end%%%%%%%%%%%%%%%%%%%转换为百分比高度%%%%%%%%%%%%%%%%%%%%%%%Hlevel(:,1)=(y1+H10-H1SpanLo)/(H1SpanHi-H1SpanLo)*100;Hlevel(:,2)=(y2+H20-H2SpanLo)/(H2SpanHi-H2SpanLo)*100;yc=(yc+0.5)*100;H2setpoint=H2*ones(size(y1')); %%%%%%%%%%%%%%%%%%%%%%%%%%%%绘图%%%%%%%%%%%%%%%%%%%%%%%%%% textPositionH1=max(Hlevel(:,1));textPositionH2=max(Hlevel(:,2));H2Steady=Hlevel(size(Hlevel(:,1),1),1)*ones(size(y1'));scrsz = get(0,'ScreenSize');gca=figure('Position',[5 10 scrsz(3)-10 scrsz(4)-90]);set(gca,'Color','w');plot(0:T:tend,Hlevel(:,1),'r','LineWidth',2)hold onplot(0:T:tend,Hlevel(:,2),'b','LineWidth',2)hold onplot(0:T:tend,yc,'k','LineWidth',2)hold onplot(0:T:tend,H2setpoint,'g','LineWidth',2)hold onplot(0:T:tend,H2Steady,'y','LineWidth',2)line([500 525],[105 105],'Color','r','LineWidth',6)text(525,105,' 第1个水箱的液位H1','FontSize',16)line([500 525],[101 101],'Color','b','LineWidth',6)text(525,101,' 第2个水箱的液位H2','FontSize',16)line([500 525],[97 97],'Color','g','LineWidth',6)text(525,97,' 第2个水箱的液位给定值','FontSize',16)line([500 525],[93 93],'Color','k','LineWidth',6)text(525,93,' 阀位变化情况','FontSize',16)axis([0 700 50 110]);text(145,112,' 实验二不考虑阀位饱和特性时的控制效果','FontSize',22) grid2、线性系统仿真（采用c2d函数）clcclear all%%%%%%%%%%%%%%%%%%%%%定义参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%A=2; %水箱横截面积ku=0.1/0.5; %阀门流量系数H10=1.5; %水箱1的平衡高度H20=1.4; %水箱2的平衡高度alpha12 = 0.25/sqrt(H10); %水箱1流向水箱2流量系数alpha2 = 0.25/sqrt(H20); %水箱2流出水流量系数R2=2*sqrt(H20)/alpha2; %线性化数学模型中的参数H1SpanLo=0; %水箱1量程下限H2SpanLo=0; %水箱2量程下限H1SpanHi=2.52; %水箱1量程上限H2SpanHi=2.52; %水箱2量程上限Kp=1.78; %PI控制器比例系数Ti=85; %PI控制器积分时间常数Kc=Kp/Ti; %式(4)中参数bc=Ti; %式(4)中参数Kd = 1/A; %式(5)中参数ad = 1/(A*R12); %式(5)中参数a1 = 1/(A*R12); %式(6)中参数K1 = ku/A; %式(6)中参数a2 = 1/(A*R2); %式(7)中参数K2 = 1/(A*R12); %式(7)中参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% numc=[Kc*bc,Kc];denc=[1,0];numd=[Kd]dend=[1,ad]num1=[K1]den1=[1,a1]num2=[K2]den2=[1,a2]Gc=tf(numc,denc);G1=tf(num1,den1);G2=tf(num2,den2);Sysq=Gc*G1*G2;SysG=feedback(Sysq,1);GG=c2d(SysG,10,'tustin');dstep(3*GG.num{1},GG.den{1});3、含有非线性环节的控制系统仿真clcclear all%%%%%%%%%%%%%%%%%%%%%定义参数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% A=2; %水箱横截面积ku=0.1/0.5; %阀门流量系数H10=1.5; %水箱1的平衡高度H20=1.4; %水箱2的平衡高度alpha12 = 0.25/sqrt(H10); %水箱1流向水箱2流量系数alpha2 = 0.25/sqrt(H20); %水箱2流出水流量系数R12=2*sqrt(H10)/alpha12; %线性化数学模型中的参数H1SpanLo=0; %水箱1量程下限H2SpanLo=0; %水箱2量程下限H1SpanHi=2.52; %水箱1量程上限H2SpanHi=2.52; %水箱2量程上限Kp=1.78; %PI控制器比例系数Ti=85; %PI控制器积分时间常数Kc=Kp/Ti; %式(4)中参数bc=Ti; %式(4)中参数Kd = 1/A; %式(5)中参数ad = 1/(A*R12); %式(5)中参数a1 = 1/(A*R12); %式(6)中参数K1 = ku/A; %式(6)中参数a2 = 1/(A*R2); %式(7)中参数K2 = 1/(A*R12); %式(7)中参数%%%%%%%%%%%%%%%%%%%%%%%%%%%赋初值%%%%%%%%%%%%%%%%%%%%%%%%%A=2; uc(1)=0;uv(1)=0;ud(1)=0;u1(1)=0;u2(1)=0;xc(1)=0;xv(1)=0;xd(1)=0;x1(1)=0;x2(1)=0;yc(1)=0;yv(1)=0;yd(1)=0;y1(1)=0;y2(1)=0;nCounter = 70;T=10;k=1;deltaQd=0;c=0.5;H20_percent=(H20-H2SpanLo)/(H2SpanHi-H2SpanLo)*100;H2set_percent=80;tend = nCounter*T;%%%%%%%%%%%%%%%%%%%迭代求解输入输出变量%%%%%%%%%%%%%%%%%%%%%for t=T:T:tendk=k+1;uc(k)=(H2set_percent-(y2(k-1)+H20-H2SpanLo)/(H2SpanHi-H2SpanLo)*100)/100;uv(k)=yc(k-1);ud(k)=deltaQd;if uv(k)>cyv(k)=c;endif uv(k)<-cyv(k)=0;endif uv(k)<=c & uv(k)>=-cyv(k)=uv(k);endu1(k)=yv(k);u2(k)=y1(k-1);xc(k) = xc(k-1) + Kc*T*uc(k-1);yc(k)=xc(k)+bc*Kc*uc(k);xd(k) = exp(-ad*T)*xd(k-1) + Kd/ad*(1-exp(-ad*T))*ud(k);yd(k)=xd(k);x1(k) = exp(-a1*T)*x1(k-1) + K1/a1*(1-exp(-a1*T))*u1(k);y1(k)=x1(k);x2(k) = exp(-a2*T)*x2(k-1) + K2/a2*(1-exp(-a2*T))*u2(k);y2(k)=x2(k);end%%%%%%%%%%%%%%%%%%%转换为百分比高度%%%%%%%%%%%%%%%%%%%%%%%Hlevel(:,1)=(y1+H10-H1SpanLo)/(H1SpanHi-H1SpanLo)*100;Hlevel(:,2)=(y2+H20-H2SpanLo)/(H2SpanHi-H2SpanLo)*100;yc=(yc+0.5)*100;y2sp=H2set_percent*ones(size(y1')); %%%%%%%%%%%%%%%%%%%%%%%%%%%%绘图%%%%%%%%%%%%%%%%%%%%%%%%%% textPositionH1=max(Hlevel(:,1));textPositionH2=max(Hlevel(:,2));H2Steady=Hlevel(size(Hlevel(:,1),1),1)*ones(size(y1'));scrsz = get(0,'ScreenSize');gca=figure('Position',[5 10 scrsz(3)-10 scrsz(4)-90])set(gca,'Color','w');plot(0:T:tend,Hlevel(:,1),'r','LineWidth',2)hold onplot(0:T:tend,Hlevel(:,2),'b','LineWidth',2)hold onplot(0:T:tend,yv,'k','LineWidth',2)hold onplot(0:T:tend,y2sp,'g','LineWidth',2)hold onplot(0:T:tend,H2Steady,'y','LineWidth',2)line([500 525],[105 105],'Color','r','LineWidth',6)text(525,105,' 第1个水箱的液位H1','FontSize',16)line([500 525],[101 101],'Color','b','LineWidth',6)text(525,101,' 第2个水箱的液位H2','FontSize',16)line([500 525],[97 97],'Color','g','LineWidth',6)text(525,97,' 第2个水箱的液位给定值','FontSize',16)line([500 525],[93 93],'Color','k','LineWidth',6)text(525,93,' 阀位变化情况','FontSize',16)axis([0 700 50 110]);text(145,112,' 实验三考虑阀位饱和特性时的控制效果','FontSize',22) grid三、实验分析离散模型的阶跃响应四、实验思考1.在未考虑调节阀饱和特性时，讨论一下两个水箱液位的变化情况，工业上是否允许？讨论阀位的变化情况，工业上是否能实现？2.实验三与实验二相比，考虑调节阀饱和特性前后，响应有何不同？五、实验总结。

Ab A BkC
为系统闭环系数矩阵，而输入矩阵B和输出矩阵C不变。 根据求得的系统仿真模型，观察可知，该式其实是一个一 阶微分方程组的矩阵表达形式，采用四阶龙格-库塔法， 即可根据典型闭环系统的结构图进行仿真。
（二）仿真实现 由以上确定的仿真模型，采用四阶龙格-库塔法求解。 由式3 X A X Br b 知
yk 1 CX k 1
Байду номын сангаас
按以上算式，取K＝0，1…N不断递推，即求得所需时间 t0，t1….各点的状态变量x（tk）和输出量y（tk）。 采用四阶龙格-库塔法，即可根据典型闭环系统的结构图 进行仿真。
（三）仿真程序框图与实现 构成一个完整的仿真程序，必须至少建立： （1）输入数据块 （2）初始化块 （3）运行计算块 （4）输出结果块 作为系统仿真程序，使用时应尽可能方便，使用者只要 将开环传递函数G（s）的分母、分子各系数和反馈系数 输入计算机，计算机就掌握了关于该系统的基本信息， 然后形成开、闭环状态方程各阵等步骤均由仿真程序自 动完成，无需人工干预。因此，程序应用输入数据模块 和初始化程序模块。
1. 程序框图
Y (s) b0 s m bm1 s bm G( s) U (s) a0 s n an1 s an
2. 程序语句如下： （1）输入数据
2. 程序语句如下： （2）形成开、闭环系数阵
2. 程序语句如下： （3）运算求解
2. 程序语句如下： （4）输出结果
第二节
面向系统结构图的数字仿真
控制系统计算机仿真是建立在控制系统数学模型 基础上的一门技术，自动控制系统的种类繁多， 为通过仿真手段进行分析和设计，就要借助于 系统的数学模型。现行控制系统的数学模型的 表示形式有微分方程、传递函数、状态方程、 结构图形式等。实际工程中常常给出的是结构 图形式的数学模型，对此类形式的系统进行仿 真分析，自动求解各环节变量的动态变化情况， 从而得到关于系统输出各变量的有关数据、曲 线等，可方便的对系统进行分析和设计。 本节将对控制系统的典型结构形式二次模型化， 并采用数值积分算法得到系统相应的仿真结果。

1.实验目的：
熟悉面向结构图的线性系统仿真算法及其流程，编制相应的程序完成仿真。
2.实验内容：
(1)学习MATLAB语言实现面向结构图的线性系统仿真建模。
(2)学习使用仿真程序进行系统分析。
3.实验方案（程序设计说明）
（1）、打开Matlab界面,使用Simulink按照系统结构图搭好仿真模块图，去信号为阶跃信号，将输出信号和输出信号同时输入scope模块进行对比；在输出端添加display模块，用以显示仿真数值解。
（2）、单机[simulination]菜单下[configuration parameter]选项，在弹出仿真设置界面中进行仿真器参数设置。
（3）、运行仿真，观察仿真的结果。
4.实验步骤或程序（经调试后正确的源程序）
5．程序运行ห้องสมุดไป่ตู้果
6．出现的问题及解决方法
通过对于参数的修改，最终得到图线。

系统仿真实验报告范文四川大学课程实验报告课程名称：系统仿真综合实验学生姓名：学生学号：专业：实验目的系统仿真是运用仿真软件（如imio）创造模型来构建或模拟现实世界的虚拟实验室，它能过帮助你探寻你所关注的系统在给定的条件下的行为或状态，它还能帮助你在几乎没有风险的情况下观察各种改进和备选方案的效果。

尤其是对一些难以建立物理模型和数学模型的复杂的随机问题，可通过仿真模型来顺利地解决预测、分析和评价等系统问题。

实验地点及环境四川大学工商管理学院的学院大楼综合实验室，运用PC机及imio系统仿真软件，在老师的指导下完成此次系统仿真实验。

实验步骤㈠、建立模型1.ModelⅠ首先加入一个ource、三个erver、一个ink、一个ModeEntity，并用path连接。

将ource更名为arrive，ink更名为depart，ModelEntity更名为cutomer。

设置运行时间8小时。

在Animation中添加StatuLabel到arrive，E某preion为arrive.OutputBuffer.Content。

同样为erver和dapart添加StatuLabel，E某preion分别为Server1.InputBuffer.Content、Server2.InputBuffer.Content、Server3.InputBuffer.Content、depart.InputBuffer.NumberEntered，来记录每个位置的排队人数和通过人数。

为每个erver添加一个Te某tScale为1的Statupie，来显示和观察服务台的利用率变化。

保存命名为ModelⅠ。

2.ModelII首先加入一个ource、三个erver、一个ink、一个ModelEntity，并用path连接。

将ource更名为arrive，ink更名为depart，ModelEntity更名为cutomer。

在Animation中添加StatuLabel到arrive，E某preion为arrive.OutputBuffer.Content。

系统建模与仿真实验报告系统建模与仿真实验报告1. 引言系统建模与仿真是一种重要的工程方法，可以帮助工程师们更好地理解和预测系统的行为。

本实验旨在通过系统建模与仿真的方法，对某个实际系统进行分析和优化。

2. 实验背景本实验选择了一个电梯系统作为研究对象。

电梯系统是现代建筑中必不可少的设备，其运行效率和安全性对于整个建筑物的使用体验至关重要。

通过系统建模与仿真，我们可以探索电梯系统的运行规律，并提出优化方案。

3. 系统建模为了对电梯系统进行建模，我们首先需要确定系统的各个组成部分及其相互关系。

电梯系统通常由电梯、楼层按钮、控制器等组成。

我们可以将电梯系统抽象为一个状态机模型，其中电梯的状态包括运行、停止、开门、关门等，楼层按钮的状态则表示是否有人按下。

4. 仿真实验在建立了电梯系统的模型之后，我们可以通过仿真实验来模拟系统的运行过程。

通过设定不同的参数和初始条件，我们可以观察到系统在不同情况下的行为。

例如，我们可以模拟电梯在高峰期和低峰期的运行情况，并比较它们的效率差异。

5. 仿真结果分析通过对仿真实验结果的分析，我们可以得出一些有价值的结论。

例如，我们可以观察到电梯在高峰期的运行效率较低，这可能是由于大量乘客同时使用电梯导致的。

为了提高电梯系统的运行效率，我们可以考虑增加电梯的数量或者改变乘客的行为规则。

6. 优化方案基于对仿真结果的分析，我们可以提出一些优化方案来改进电梯系统的性能。

例如，我们可以建议在高峰期增加电梯的数量，以减少乘客等待时间。

另外，我们还可以建议在电梯内设置更多的信息显示，以便乘客更好地了解电梯的运行状态。

7. 结论通过本次实验，我们深入了解了系统建模与仿真的方法，并应用于电梯系统的分析和优化。

系统建模与仿真是一种非常有用的工程方法，可以帮助我们更好地理解和改进各种复杂系统。

在未来的工作中，我们可以进一步研究和优化电梯系统，并将系统建模与仿真应用于更多的实际问题中。

8. 致谢在本次实验中，我们受益于老师和同学们的帮助与支持，在此表示诚挚的感谢。

仿真验证的常见方法仿真验证是一种帮助设计、优化和评估运行中的系统的常见方法。

它通过模拟系统的行为和性能来获得关于系统行为的详细信息，从而传达设计决策的影响和改进方案的潜在效果。

随着计算能力的提升，仿真验证已成为工程领域不可或缺的工具。

本文将介绍几种常见的仿真验证方法。

1.离散事件仿真（DES）：离散事件仿真适用于模拟系统中离散事件的发生和处理过程。

它将系统建模为由一系列事件组成的网络，每个事件代表一个系统状态的改变。

通过模拟事件的发生和处理过程，离散事件仿真可以帮助评估不同的决策方案对系统性能的影响。

2.连续仿真（CS）：连续仿真适用于模拟连续系统的行为。

它将系统建模为一组连续的方程和约束条件，并使用数值方法来模拟系统的运行。

连续仿真在评估系统的动态性能和响应性方面非常有用。

3. 蒙特卡罗仿真（Monte Carlo Simulation）：蒙特卡罗仿真是一种基于随机抽样的方法，用于评估系统在不同参数组合下的行为和性能。

它通过从概率分布中抽取大量样本，利用这些样本的统计特性来估计系统的行为。

蒙特卡罗仿真可以帮助评估系统的风险和不确定性。

4. Agent-Based Modeling（ABM）：Agent-Based Modeling是一种建立于个体行为的仿真方法。

它将系统建模为一组独立的个体，每个个体都有自己的行为规则和互动方式。

通过模拟个体之间的互动，Agent-Based Modeling可以帮助评估不同决策对系统整体行为的影响。

5. 虚拟现实仿真（Virtual Reality Simulation）：虚拟现实仿真是一种基于计算机生成的环境和交互技术的仿真方法。

它通过模拟真实场景和用户交互，提供一种沉浸式的仿真体验。

虚拟现实仿真可以帮助评估设计决策在真实环境中的效果和用户体验。

6. 博弈论仿真（Game Theory Simulation）：博弈论仿真是一种用于评估决策者之间策略选择和博弈行为的仿真方法。

AX BU X Y CX
（式2）
由图一可知，控制量U=R-Ky,带入式2得
AX BU X AX B (r ky) AX B (r kCX ) ( A BkC) X Br Ab X Br
（式3）
式3即为系统的闭环状态方程，也就是系统的仿真模型。 其中
式中
A
A 0 C 0
1
A2
A n n
0
nBLeabharlann B 01B2
B n n
0
n
1
C
C2
C n n
0
n
D D 0
1
D2
D n n
0
n
A，B，C，D都是 n n 维的 y u
Ci Dis Ai Bis
(i 1,2,, n)
(2.9 - 1)
利用这个典型环节，只要改变系数便可组成其它常 用环节： 积分环节
K s
对应于 Ai 0, Bi 1, Ci K , Di 0
比例 积分环节 K 1s K 2 对应于 Ai 0, Bi 1, Ci K 2, Di K 1
第二节
面向系统结构图的数字仿真
控制系统计算机仿真是建立在控制系统数学模型 基础上的一门技术，自动控制系统的种类繁多， 为通过仿真手段进行分析和设计，就要借助于 系统的数学模型。现行控制系统的数学模型的 表示形式有微分方程、传递函数、状态方程、 结构图形式等。实际工程中常常给出的是结构 图形式的数学模型，对此类形式的系统进行仿 真分析，自动求解各环节变量的动态变化情况， 从而得到关于系统输出各变量的有关数据、曲 线等，可方便的对系统进行分析和设计。 本节将对控制系统的典型结构形式二次模型化， 并采用数值积分算法得到系统相应的仿真结果。

网络系统仿真设计的模型构建与验证一、引言网络系统仿真是指使用计算机程序模拟网络系统的行为和性能。

它是一种有效的工具，可以帮助研究人员和工程师在实际系统投入使用之前评估和改进系统的设计。

在进行网络系统仿真时，模型的构建和验证是非常重要的步骤。

本文将重点讨论网络系统仿真模型的构建与验证。

二、网络系统仿真模型的构建1. 确定仿真目标：在构建网络系统仿真模型之前，需要明确仿真的目标，例如评估系统的性能、研究系统的稳定性等。

这有助于选择合适的建模方法和技术。

2. 收集系统数据：为了构建可靠的仿真模型，需要收集系统的相关数据，例如网络拓扑结构、数据流量、网络设备特性等。

这些数据将用于确定系统的输入和输出。

3. 选择建模方法：根据仿真目标和数据的特点，选择合适的建模方法。

常用的建模方法包括离散事件仿真（Discrete Event Simulation, DES）、连续仿真（Continuous Simulation）和混合仿真（Hybrid Simulation）等。

4. 设计模型结构：根据所选择的建模方法，设计网络系统仿真模型的结构。

模型结构应能够准确地反映真实系统的特性，并且具有可扩展性和灵活性。

5. 简化模型：在构建网络系统仿真模型时，往往需要对模型进行简化。

简化模型可以减少计算复杂性，提高仿真的效率。

然而，简化模型也会带来一定的误差，因此需要在精度和计算效率之间进行权衡。

三、网络系统仿真模型的验证1. 确定验证指标：为了验证网络系统仿真模型的准确性，需要确定一些验证指标，例如网络时延、吞吐量、丢包率等。

这些指标应与实际系统的性能指标相对应。

2. 收集实际数据：为了验证仿真模型的准确性，需要收集实际系统的性能数据。

可以通过监测网络流量、记录设备运行状态等方式获取实际数据。

3. 对比实际数据与仿真结果：将实际数据与仿真结果进行对比分析，评估仿真模型的准确性。

如果仿真结果与实际数据相符，说明仿真模型是可靠的；如果存在较大误差，需要进一步改进模型。

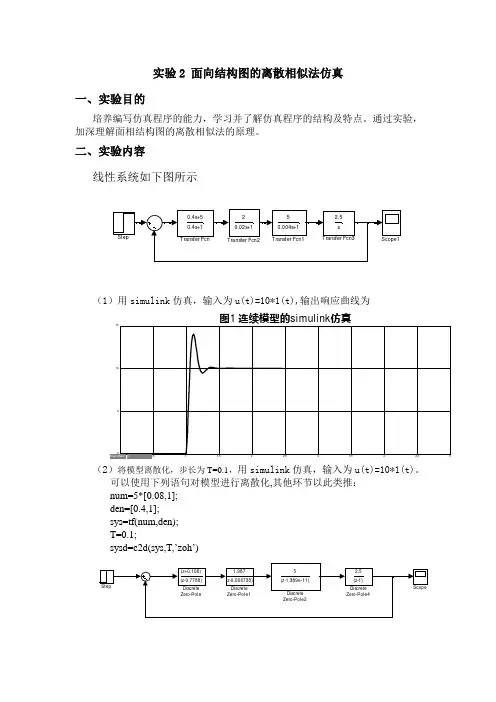
实验2 面向结构图的离散相似法仿真一、实验目的培养编写仿真程序的能力，学习并了解仿真程序的结构及特点。

通过实验，加深理解面相结构图的离散相似法的原理。

二、实验内容线性系统如下图所示2.5s Transfer Fcn320.02s+1Transfer Fcn250.004s+1Transfer Fcn10.4s+50.4s+1Transfer FcnStepScope1（1）用simulink 仿真，输入为u(t)=10*1(t),输出响应曲线为00.51 1.52 2.53 3.54 4.5551015图1 连续模型的simulink 仿真（2）将模型离散化，步长为T=0.1，用simulink 仿真，输入为u(t)=10*1(t)。

可以使用下列语句对模型进行离散化,其他环节以此类推： num=5*[0.08,1]; den=[0.4,1]; sys=tf(num,den); T=0.1;sysd=c2d(sys,T,’zoh ’)StepScope2.5(z-1)Discrete Zero-Pole45(z-1.389e-11)Discrete Zero-Pole21.987(z-0.006738)Discrete Zero-Pole1(z+0.106)(z-0.7788)Discrete Zero-Pole02468101214161820-0.50.511.522.533.5x 1010图2 离散模型的simulink仿真（T=0.1）由图2可知，当离散步长T=0.1时，系统是发散的，不稳定。

（3）采用离散化步长T=0.1，写出系统完整的按环节离 散化模型。

环节分为数4个环节，按从左至右依次编号为①②③④I 环节之间的连接方程II 环节内部离散模型①超前滞后环节②惯性环节)()(10)()()1(4.0)()1(11115.215.21k u k x k y k u e k x e k x T T +=-+=+--)()()()1(2)()1(222502502k x k y k u e k x e k x T T =-+=+--③惯性环节④积分环节)()()()1(5)()1(33325032503k x k y k u e k x e k x T T =-+=+--)()()(T 5.2)()1(44444k x k y k u k x k x =+=+)()()()()()()()()(34231241k y k u k y k u k y k u k y k r k u ===-=)(0001)(010*******011-000)()()(0k r k y k r W k y W k u ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫⎝⎛=⋅+⋅=得到环节内部动态方程环节输出方程系统输出方程（4）仿真程序为分别采用步长T=0.001，0.01,0.1,0.5，进行仿真，得出下列图形)(0001)(11110)()()(k u k x k u D k x C k y ⎪⎪⎪⎪⎪⎭⎫⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⋅+⋅=())(1000)()(k y k y Q k p =⋅=)(T 5.2)1(5)1(2)1(4.0)(1)()()1(250505.2250505.2k u e e e k x e e e k Hu k Gx k x T TT T T T ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=+=+------function[t,p]=w_DisNodesSimu(tstart,tstop,h,x0,y0,r0,W,W0,G,H,C,D,Q)t=[tstart:h:tstop];%t 数一个行序列 cntnodes=size(W,1);%得到环节的个数 cntt=size(t,2);%返回列数cnty=size(Q,1);%返回y 的维数 p=zeros(cnty,cntt);%构造一个空矩阵，用来存储结果 p(:,1)=Q*y0; % for i=1:1:cntt-1for j=1:1:cntnodes u(j)=W(j,:)*y0+W0(j,:)*r0; x0(j)=G(j,j)*x0(j)+H(j,j)*u(j); y0(j)=C(j,j)*x0(j)+D(j,j)*u(j); end ; p(:,i+1)=Q*y0 ;%将y0作为输出的第1列endfunction simutstart=0;tstop=20;x0=[0;0;0;0];u0=[10];h =0.1;%面向环节离散化仿真W=[0,0,0,-1;1,0,0,0;0,1,0,0;0,0,1,0]; W0=[1,0,0,0]';C=diag([10,1,1,1]); D=[1,0,0,0;0,0,0,0;0,0,0,0;0,0,0,0]; Q=[0,0,0,1];G=diag([exp(-2.5*h),exp(-50*h),exp(-250*h),1]);H=diag([(1-exp(-2.5*h))/2.5,2*(1-exp(-50*h)),5*(1-exp(-250*h)),2.5*h]); y0=x0;[t,y1]=w_DisNodesSimu(tstart,tstop,h,x0,y0,u0,W,W0,G,H,C,D,Q);stairs(t,y1,'-b*');xlabel('x');ylabel('y');title('图3 逐个环节刷新（T=0.1）');2468101214161820-2.5-2-1.5-1-0.50.51x 10103xy图3 逐个环节刷新（T=0.1）246810121416182002468101214xy图4 逐个环节刷新（h=0.01）246810121416182002468101214xy图5 逐个环节刷新（T=0.001）02468101214161820-8-7-6-5-4-3-2-11x 1067xy图6 逐个环节刷新（T=0.5）分析上面的曲线可知，当逐个环节刷新，离散步长为T=0.1时，与simulink仿真的结果一致，系统均不稳定；当离散步长为T=0.01，0.001时，曲线表现为收敛，及系统稳定；当离散步长为T=0.5时，曲线发散，系统不稳定。

ACD法的建模方法与建模过程

常用术语




实体。是指组成系统的各种要素，是ACD产生活动的主体。 活动。表示实体正处于某种动作状态。活动的持续时间也 称为周期。 队列。用来表示实体处于静止或等待状态。 实体的行为模式。实体的行为始终遵循“…→活动→队列 →活动→…”的交替变化规则。 直联活动和虚拟队列。如果在任何情况下，某一活动完成 后，其后续活动就立即开始，则称后续活动为直联活动。 直联活动与前面活动之间为一个等待时间为0的队列，即 虚拟队列。 合作活动。指一个活动要求有多于一个的实体参加才能开 始。



实体流程图方法：采用与计算机程序流程图类似的图示符 号和原理，建立表示临时实体产生、在系统中流动、接受 永久实体服务以及消失等过程的流程图。 建模思路： （1）辨识组成系统的实体和属性。将队列作为一种特殊的实 体考虑。 （2）分析各种实体的状态和活动，及其相互间的影响。队列 实体的状态是队列的长度。 （3）确定引起实体状态变化的事件。 （4）分析各种事件发生时，实体状态的变化规律。 （5）在一定的服务流程下，分析与队列实体有关的特殊操作 （如换队等）。 （6）通过以上分析，以临时实体为主线，画实体流程图。 （7）给出模型参数的取值、参变量的计算方法及属性描述变 量的取值方法。属性描述变量，例如顾客到达时间、服务 时间等，可以取一组固定值，可以由某一计算公式取值， 还可以是一个随机变量（此时应给出分布函数）。 （8）给出队列的排队规2到达。由于理发员 忙，顾客2只好排队等待，队列长度变为1。 下一个最早发生的事件为“顾客1离去”，离去 时刻d1=58（<a3=a2+A3=47+24=71） （4）在TIME＝58时刻，顾客1离去。按规则3， 由于队列长度为1，理发员开始为顾客2理发， 队列长度为0。顾客2离去时刻 d2=TIME+S2=58+36=94 下一个最早发生的事件为“顾客3到达”，顾客 3到达的时刻为 a3=a2+A3=47+24=71。 （5）在TIME＝71时刻，顾客3到达，……

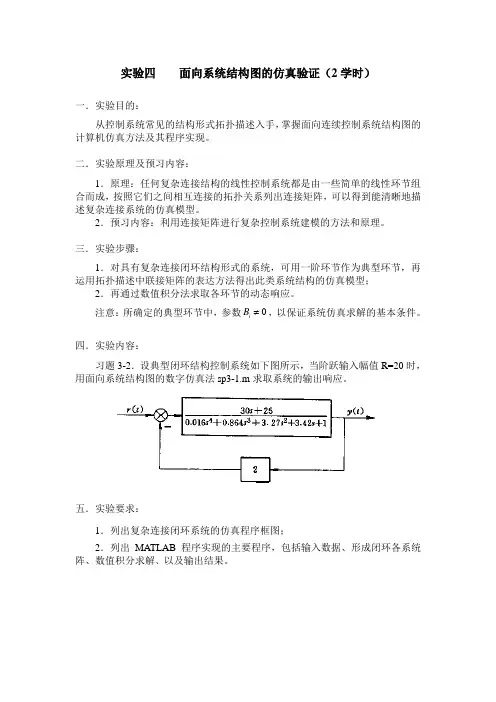
实验四面向系统结构图的仿真验证（2学时）
一．实验目的：
从控制系统常见的结构形式拓扑描述入手，掌握面向连续控制系统结构图的计算机仿真方法及其程序实现。

二．实验原理及预习内容：
1．原理：任何复杂连接结构的线性控制系统都是由一些简单的线性环节组合而成，按照它们之间相互连接的拓扑关系列出连接矩阵，可以得到能清晰地描述复杂连接系统的仿真模型。

2．预习内容：利用连接矩阵进行复杂控制系统建模的方法和原理。

三．实验步骤：
1．对具有复杂连接闭环结构形式的系统，可用一阶环节作为典型环节，再运用拓扑描述中联接矩阵的表达方法得出此类系统结构的仿真模型；
2．再通过数值积分法求取各环节的动态响应。

注意：所确定的典型环节中，参数0
B ，以保证系统仿真求解的基本条件。

i
四．实验内容：
习题3-2．设典型闭环结构控制系统如下图所示，当阶跃输入幅值R=20时，用面向系统结构图的数字仿真法sp3-1.m求取系统的输出响应。

五．实验要求：
1．列出复杂连接闭环系统的仿真程序框图；
2．列出MATLAB程序实现的主要程序，包括输入数据、形成闭环各系统阵、数值积分求解、以及输出结果。

学号：2010133330课程设计面向结构图的连续系统数题目字仿真学院计算机科学与信息工程学院专业自动化班级2010级2班学生姓名小指导教师吴诗贤2013 年12 月20 日面向结构图的连续系统数字仿真姓名：陶园班级：10自动化3班学号：2010133330摘要根据自动控制系统中面向结构图的数字仿真的基本思想，探讨了仿真过程中典型环节的规范性、系统的连接矩阵、仿真求解、程序框图问题，并应用到实际的范例当中，并分析了结果总结了相关特点和相关结论。

自动控制系统常常是由许多环节组成的，要应用数字仿真方法对系统进行分析和研究，首先需要求出总的传递函数，再转化为状态空间表达式的形式，然后对其求解。

当改变系统某一环节的参数时，尤其是要改变小闭环中某一环节的参数时，以上整个过程又需要重新计算，这对研究对象参数变化对整个控制系统的影响是十分不便的，为了克服这些缺点，同时大多数从事自动化工作的科技人员更习惯于用结构图的形式来分析和研究控制系统，为此产生了面向结构图的仿真方法。

该方法只需将各个环节的参数及各环节间的连接方式输入计算机，仿真程序就能自动求出闭环系统的状态空间表达式。

本课程设计主要介绍典型环节参数和连接关系构成闭环系统的状态方程的方法，而动态响应的计算，仍采用四阶龙格-库塔法。

这种方法具有便于研究各个环节参数对系统的影响，并可以得到每个环节的动态响应，以及对多输入输出系统的进行仿真的有点。

关键字：结构图；典型环节；连接矩阵；数字仿真；1、设计任务已知某一系统结构如下图所示，编写matlab程序求a分别为2,4,6,8,10,12时输出量y的动态响应。

图12、需求分析及概要设计2.1 需求分析根据上述设计任务我们可以基本明确在我们课程设计当中应该明确以下几个方面：✓熟悉在数字计算机仿真技术中常用的四阶龙格-库塔算法。

✓明确在面向结构图的连续系统数字仿真，典型环节及其系数矩阵确定。

✓明确各连接矩阵的确定。

✓能够熟练运用MATLAB仿真软件。

仿真模型的创建与验证技巧及常见问题解答仿真模型是指利用计算机模拟现实世界系统的行为和性能的一种方法。

创建和验证仿真模型是进行仿真研究的关键环节，它直接影响到得到准确、可靠的仿真结果。

本文将介绍一些创建与验证仿真模型的技巧，并解答一些常见的问题，帮助读者更好地理解和应用仿真模型。

一、创建仿真模型的技巧1.明确研究目的：在创建仿真模型之前，需要明确研究的目的和问题。

明确目的可以帮助确定所需数据、模型的复杂度以及所使用的仿真工具。

2.收集数据：创建仿真模型需要使用真实系统的数据作为输入。

根据研究目的，收集合适的数据，包括系统动力学、输入变量、参数值等。

数据采集的准确性和完整性对于模型的有效性至关重要。

3.选择合适的仿真工具：根据需要选择合适的仿真工具，常见的仿真工具有MATLAB、Simulink、Arena等。

选择工具时要考虑其功能、易用性、计算效率等因素。

4.建立系统结构：根据研究目的和数据，建立系统结构。

系统结构包括系统的组成部分、相互关系和交互方式。

可以采用流程图、状态转换图等方法表示系统结构。

5.确定模型假设：模型中的假设对于仿真的准确性和可靠性具有重要影响。

根据实际情况，确定模型的假设条件和限制，并进行合理的假设简化。

6.确定模型参数：根据实际数据和假设条件，确定模型的参数值。

参数值的确定要考虑系统的变化范围、不确定性和敏感性。

7.编写仿真代码：根据系统结构、模型假设和参数值，编写仿真代码。

仿真代码可以使用编程语言（如MATLAB、Python等）或者仿真工具自带的建模语言（如Simulink）来实现。

8.初始化与验证：在进行仿真之前，需要对模型进行初始化，并进行验证。

验证方法包括与实际数据对比、与已有模型对比等。

如果验证结果不符合预期，需要检查模型的假设、参数和代码是否存在问题。

二、常见问题解答1.如何确定模型的复杂度？模型的复杂度需要根据研究目的和数据的可获得性来确定。

过于简单的模型可能无法准确地反映系统行为，而过于复杂的模型可能会导致计算效率低下和信息量过大。

实验一 连续系统的数字仿真一、实验目的1． 熟悉Matlab 中m 文件的编写；2． 掌握龙格－库塔法的基本原理。

二、实验设备计算机、MATLAB 软件三、实验内容假设单变量系统如图所示。

试根据四阶龙格－库塔法，求系统输出y 的动态响应。

1．首先把原系统转化为状态空间表达式：⎪⎩⎪⎨⎧=+=•CXy bu AX X ，根据四阶龙格－库塔公式，可得到： ⎪⎩⎪⎨⎧=++++=+++1143211)22(6k k k k CX y K K K K h X X （1） 其中： ⎪⎪⎪⎩⎪⎪⎪⎨⎧+++=+++=+++=+=)()()2()2()2()2()(3423121h t bu hK X A K h t bu K h X A K h t bu K h X A K t bu AX K k k k k k k k k （2） 根据（1）、（2）式编写仿真程序。

2．在Simulink 环境下重新对上述系统进行仿真，并和1中结果进行比较。

四、实验结果及分析要求给出系统输出响应曲线，并分析计算步长对龙格－库塔法的影响。

计算步长对龙格－库塔法的影响：单从每一步看，步长越小，截断误差就越小，但随着步长的缩小，在一定求解范围内所要完成的步数就增加，不但引起计算量的增大，而且可能导致舍入误差严重积累，因此同积分的数值计算一样，微分方程的解法也有选择步长的问题。

源程序：r=5;numo=[1];deno=[1 4 8 5];numh=1;denh=1;[num,den]=feedback(numo,deno,numh,denh);[A,b,C,d]=tf2ss(num,den);Tf=input('仿真时间 Tf= ');h=input('计算步长 h=');x=[zeros(length(A),1)];y=0;t=0;for i=1:Tf/h;K2=A*(x+h*K1/2)+b*r;K3=A*(x+h*K2/2)+b*r;K4=A*(x+h*K3)+b*r;x=x+h*(K1+2*K2+2*K3+K4)/6;y=[y;C*x];t=[t;t(i)+h];endplot(t,y)Tf=5 h=0.02五、思考题1．试说明四阶龙格－库塔法与计算步长关系，它与欧拉法有何区别。

面向系统动态结构图的状态仿真
汪光阳
【期刊名称】《安徽工业大学学报（自然科学版）》
【年(卷),期】2000(017)004
【摘要】针对目前一般仿真软件根据系统动态结构图进行仿真时,只能仿真各环节的输出而不能仿真状态的问题,建立了面向状态的数学模型,以实现对系统各环节状态的仿真,并用MATLAB语言进行了实现,编制了通用的仿真软件,丰富了MATLAB 语言的仿真功能.
【总页数】4页(P331-334)
【作者】汪光阳
【作者单位】华东冶金学院计算机科学系,安徽马鞍山243002
【正文语种】中文
【中图分类】TP391.9
【相关文献】
1.面向电气原理结构图的串级调速系统的建模与仿真 [J], 宋永英;朱希荣;周渊深
2.面向结构图的输水系统仿真方法研究 [J], 钟登华;黄伟;熊开智;
3.面向动态结构图的离散相似法仿真 [J], 王燕平;张艳辉
4.面向结构图的电力系统动态仿真 [J], 陈礼义;李海
5.基于ActiveX技术的面向结构图的系统仿真环境开发 [J], 宗晓萍;刘欣;王霞因版权原因，仅展示原文概要，查看原文内容请购买。

(4.1.2)
根据(2.4.9)式可得
(T ) e At 1
u
a0
x
1y sx
m (T )
T e A(T t) Bd
0
T
0a0d a0T
ˆm (T )
T e A(T t) Bd
0
T
Bd
0

a0T 2
图4.1.1 积分环节结构图
三、仿真算例及分析
用该程序求某四阶系统（结构图见图4.2.3）在阶 跃函数作用下的过渡过程。
y0
u1 s b1 y1 u2 1 y2 u3 a3 y3 u4 a4
y4

s a1
s
s a3
s a4
图4.2.3 四阶系统结构图
首先，确定典型环节类型和环节编号，本例从左到 右顺序排号 ，第一块类型号 H (1) 3，第二块类型 号H(2) 0，第三块类型号 H(3) 2，第四块类型号H(4) 2 根据图4.2.3所示可写出连接矩阵为
递函数，则很容易将其离散化，各个环节的输入―输
出关系为
u1 1
u2


0
u3 0
u4

0
0 1 0 0
0 0 1 1
1 0 0 0
0
1
0
0

y0

y1

y2

y3

y4
(4.2.3)
U WY
(4.2.4)
4.2 结构图离散相似法仿真
由前述可知，对于H (I )
=0和H (I )=1两种典型环 节，计算状态变量的公

6、设某船舶柴油机转速控制系统转速指令为2.0y 0=的阶跃作用，如图4-38所示。

试采用面向系统的结构图方法，选用合理的步长，对该船舶柴油机转速控制系统的特性进行动态仿真。

其中：环节1表示柴油机的调速器，3-1101⨯=T ，是柴油机调速器阻尼系数；52106.1-⨯=T ,表示柴油机调速器飞快质量，环节1的输出是柴油机油门位移信号。

环节2表示液压伺服执行机构，其输出是柴油机油门齿条的位移。

环节3表示柴油机的输出速度。

7、解：将环节1化为两个惯性环节再加上一个负反馈形式，如下图：由公式：α++=S A S A A uy 12211，3-1101⨯=T ，52106.1-⨯=T ，可得：解得：写出系统的传递关系如下：1024213243u y y y u y u y u y =--⎧⎪=⎪⎨=⎪⎪=⎩系统的连接矩阵为：00y W WY U+=，其中：1u 2u 3u 3y 2y 1y 2.00=y +11122++S T S T S1.011+S211+123()384-1u 3u 4u 4y 3y 2.00=y +S1.011+S211+2u αSA 11112+S A 1y 2y 1324-⎪⎩⎪⎨⎧=⨯=⨯=1106.11012-23-1αA A ⎪⎩⎪⎨⎧===111221αT A T A A -⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=010001000011010W ，⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=00010W设环节1、2、3、4的系统矩阵分别为A 、B 、C 、D ：则可得：⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=1000010000100000A ，⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⨯⨯=--200001.00000106.1000010123B⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=1000100000100001C ，⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=000000000000000D 利用MA TLAB 软件编制四阶龙格一库塔法进行仿真计算，取仿真步长t=0.002计算可得如下仿真结果图：附具体的计算过程如下：请输入系统的阶数：N=4请输入阶跃函数的幅度：y0=0.2请输入仿真的步长：h=0.002请输入仿真的开始时间：t0=0请输入仿真的终止时间：tmax=2请输入打印的时间间隔：Nti=0.1打印变量数：NP=4输出变量的编号1：N1=1输出变量的编号2：N2=2输出变量的编号3：N3=3输出变量的编号4：N4=4请输入A(i,i),B(i,i),C(i,i),D(i,i),Y(i),i=1,...,n A(i,i)=0B(i,i)=0.001C(i,i)=1D(i,i)=0Y(i)=0A(i,i)=1B(i,i)=0.016C(i,i)=1D(i,i)=0Y(i)=0A(i,i)=1B(i,i)=0.1C(i,i)=10D(i,i)=0Y(i)=0A(i,i)=1B(i,i)=2C(i,i)=1D(i,i)=0Y(i)=0请输入反馈系数：v=1I1,J1,W1=?:i=1j=0w=1i=1j=2w=-1i=1j=4w=-1i=2j=1w=1i=3j=2w=1i=4j=3w=1i=0j=0w=0========================================t=y1=y2=y3=y4=0 0 0 0 00.1000 0.1372 0.1585 1.1659 0.03420.2000 0.0955 0.1058 1.2587 0.09450.3000 0.0498 0.0562 0.9405 0.14410.4000 0.0230 0.0263 0.5812 0.17390.5000 0.0120 0.0131 0.3246 0.18690.6000 0.0102 0.0101 0.1879 0.18980.7000 0.0121 0.0117 0.1378 0.18820.8000 0.0148 0.0144 0.1346 0.18560.9000 0.0168 0.0166 0.1489 0.18341.0000 0.0180 0.0179 0.1646 0.18211.1000 0.0185 0.0184 0.1758 0.18161.2000 0.0185 0.0185 0.1817 0.18151.3000 0.0184 0.0185 0.1838 0.18151.4000 0.0183 0.0183 0.1839 0.18171.5000 0.0182 0.0183 0.1832 0.18171.6000 0.0182 0.0182 0.1826 0.18181.7000 0.0182 0.0182 0.1821 0.1818 1.8000 0.0182 0.0182 0.1818 0.18181.9000 0.0182 0.0182 0.1817 0.18182.0000 0.0182 0.0182 0.1817 0.1818。