下载文档原格式
《固体物理学》部分习题解答补充：证明“晶体的对称性定律”。
证明：晶体中对称轴的轴次n并不是任意的,而是仅限于 n=1,2,3,4,6这一原理称为“晶体的对称性定律”。
现证明如下:设晶体中有一旋转轴n 通过某点O,根据前一条原理必有一平面点阵与你n 垂直,而在其中必可找出与 n垂直的属于平移群的素向量a,将a作用于O得到A 点将-a作用于O点得到A’点:若a= ,则L( )及L(- )必能使点阵复原,这样就可得点阵点B,B’,可得向量BB’,显然BB与a平行,因为空间点阵中任意互相平行的两个直线点阵的素向量一定相等,因而向量BB’的长度必为素向量a的整数倍即:BB’= ma由图形关系可得:=即m=0,±1,±2m n-2 -1 p 2-1 - 30 0 41 62 1 2p 1所以 n=1,2,3,4,6综上所述可得结论:在晶体结构中,任何对称轴或轴性对称元素的轴次只有一重,二种,三重,四重或六重等五种,而不可能存在五重和七重及更高的其它轴次,这就是晶体对称性定律。
晶体的对称性定律证明:1.3 证明：体心立方晶格的倒格子是面心立方；面心立方晶格的倒格子是体心立方 。
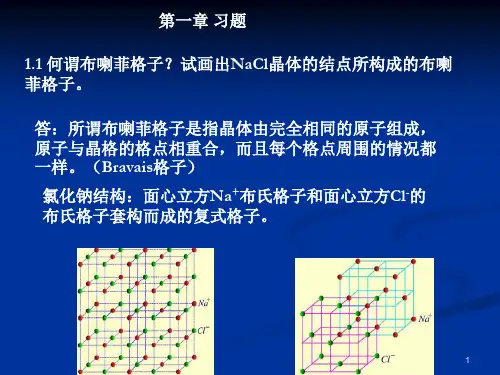
解 由倒格子定义2311232a a b a a a π⨯=⋅⨯ 3121232a a b a a a π⨯=⋅⨯ 1231232a a b a a a π⨯=⋅⨯体心立方格子原胞基矢123(),(),()222a a a a i j k a i j k a i j k =-++=-+=-+倒格子基矢231123022()()22a a a ab i j k i j k a a a v ππ⨯==⋅-+⨯+-⋅⨯202()()4a i j k i j k v π=⋅-+⨯+-2()j k a π=+ 同理31212322()a a b i k a a a aππ⨯==+⋅⨯32()b i j a π=+ 可见由123,,b b b为基矢构成的格子为面心立方格子 面心立方格子原胞基矢123()/2()/2()/2a a j k a a k i a a i j =+=+=+倒格子基矢2311232a a b a a a π⨯=⋅⨯ 12()b i j k a π=-++同理22()b i j k a π=-+ 32()b i j k a π=-+可见由123,,b b b为基矢构成的格子为体心立方格子1.4 证明倒格子原胞的体积为03(2)v π，其中0v 为正格子原胞体积证 倒格子基矢2311232a a b a a a π⨯=⋅⨯3121232a a b a a a π⨯=⋅⨯1231232a a b a a a π⨯=⋅⨯倒格子体积*0123()v b b b =⋅⨯3*23311230(2)()()()v a a a a a a v π=⨯⋅⨯⨯⨯ 3*00(2)v v π=1.5 证明：倒格子矢量112233G hb h b h b =++垂直于密勒指数为123()hh h 的晶面系。
固体物理习题与及解答固体物理习题与及解答⼀、填空题1. 晶格常数为a 的⽴⽅晶系 (hkl>晶⾯族的晶⾯间距为/a该(hkl>晶⾯族的倒格⼦⽮量hkl G ρ为 k al j a k i a h ρρρπππ222++ 。
2. 晶体结构可看成是将基元按相同的⽅式放置在具有三维平移周期性的晶格的每个格点构成。
3. 晶体结构按晶胞形状对称性可划分为 7 ⼤晶系，考虑平移对称性晶体结构可划分为 14 种布拉维晶格。
4. 体⼼⽴⽅[]{})(ex p 1l k h i f S hkl ++-+=π，其衍射消光条件是奇数=++l k h 。
5. 与正格⼦晶列[hkl]垂直的倒格⼦晶⾯的晶⾯指数为(hkl> ，与正格⼦晶⾯[hkl] 。
6. 由N 个晶胞常数为a 的晶胞所构成的⼀维晶格，其第⼀布⾥渊区边界宽度为a /2π，电⼦波⽮的允许值为 Na /2π的整数倍。
7. 对于体积为V,并具有N 个电⼦的⾦属, 其波⽮空间中每⼀个波⽮所占的体积为 ()V /23π，费M 波⽮为 3/123???? ??=V N k F π。
8. 按经典统计理论，N 个⾃由电⼦系统的⽐热应为 B Nk 23 ，⽽根据量⼦统计得到的⾦属三维电⼦⽓的⽐热为F B T T Nk /22π，⽐经典值⼩了约两个数量级。
9．在晶体的周期性势场中，电⼦能带在布⾥渊区边界将出现带隙，这是因为电⼦⾏波在该处受到布拉格反射变成驻波⽽导致的结果。
10. 对晶格常数为a的简单⽴⽅晶体,与正格⽮R=a i+2a j+2a k正交的倒格⼦晶⾯族的⾯指数为 (122> , 其⾯间距为.11. 铁磁相变属于典型的⼆级相变，在居⾥温度附近，⾃由能连续变化，但其⼀阶导数<⽐热）不连续。
12. 晶体结构按点对称操作可划分为 32 个点群，结合平移对称操作可进⼀步划分为 230 个空间群。
13．等径圆球的最密堆积⽅式有六⽅密堆74%。
14. ⾯⼼⽴⽅⾯⼼⽴⽅⼩；原⼦形状因⼦反映⼀个原⼦对于衍射能⼒⼤⼩。
固体物理习题解答《固体物理学》习题解答( 仅供参考)参加编辑学⽣柯宏伟（第⼀章），李琴（第⼆章），王雯（第三章），陈志⼼（第四章），朱燕（第五章），肖骁（第六章），秦丽丽（第七章）指导教师黄新堂华中师范⼤学物理科学与技术学院2003级2006年6⽉第⼀章晶体结构1. 氯化钠与⾦刚⽯型结构是复式格⼦还是布拉维格⼦，各⾃的基元为何？写出这两种结构的原胞与晶胞基⽮，设晶格常数为a 。
解：氯化钠与⾦刚⽯型结构都是复式格⼦。
氯化钠的基元为⼀个Na +和⼀个Cl －组成的正负离⼦对。
⾦刚⽯的基元是⼀个⾯⼼⽴⽅上的Ｃ原⼦和⼀个体对⾓线上的Ｃ原⼦组成的Ｃ原⼦对。
由于NaCl 和⾦刚⽯都由⾯⼼⽴⽅结构套构⽽成，所以，其元胞基⽮都为：123()2()2()2a a a ?=+??=+=+a j k a k i a i j 相应的晶胞基⽮都为：,,.a a a =??=??=?a ib jc k2. 六⾓密集结构可取四个原胞基⽮123,,a a a 与4a ,如图所⽰。
试写出13O A A '、1331A A B B 、2255A B B A 、123456A A A A A A 这四个晶⾯所属晶⾯族的晶⾯指数()h k l m 。
解：(1)．对于13O A A '⾯，其在四个原胞基⽮上的截矩分别为：１，１，12-，１。
所以，其晶⾯指数为()1121。
(2)．对于1331A A B B ⾯，其在四个原胞基⽮上的截矩分别为：１，１，12-，∞。
所以，其晶⾯指数为()1120。
(3)．对于2255A B B A ⾯，其在四个原胞基⽮上的截矩分别为：１，1-，∞，∞。
所以，其晶⾯指数为()1100。
(4)．对于123456A A A A A A ⾯，其在四个原胞基⽮上的截矩分别为：∞，∞，∞，１。
所以，其晶⾯指数为()0001。
3. 如将等体积的硬球堆成下列结构，求证球体可能占据的最⼤体积与总体积的⽐为：简⽴⽅：6π；六⾓密集：6；⾦刚⽯：。
![《固体物理学》答案[1]](https://img.taocdn.com/s1/m/f8d34b12866fb84ae45c8da9.png)
1.1 如果将等体积球分别排列成下列结构，设x 表示钢球所占体积与总体积之比，证明结构x简单立方π/ 6 ≈0.52 体心立方3π/ 8 ≈0.68 面心立方2π/ 6 ≈0.74六方密排2π/ 6 ≈0.74 金刚石3π/16 ≈0.34解：设钢球半径为r ，根据不同晶体结构原子球的排列，晶格常数a 与r 的关系不同，分别为：简单立方：a = 2r金刚石：根据金刚石结构的特点，因为体对角线四分之一处的原子与角上的原子紧贴，因此有1.3 证明：体心立方晶格的倒格子是面心立方；面心立方晶格的倒格子是体心立方。
证明：体心立方格子的基矢可以写为面心立方格子的基矢可以写为根据定义，体心立方晶格的倒格子基矢为同理与面心立方晶格基矢对比，正是晶格常数为4π/ a的面心立方的基矢，说明体心立方晶格的倒格子确实是面心立方。
注意，倒格子不是真实空间的几何分布，因此该面心立方只是形式上的，或者说是倒格子空间中的布拉菲格子。
根据定义，面心立方的倒格子基矢为同理而把以上结果与体心立方基矢比较，这正是晶格常数为4πa的体心立方晶格的基矢。
证明：根据定义，密勒指数为的晶面系中距离原点最近的平面ABC 交于基矢的截距分别为即为平面的法线根据定义，倒格子基矢为则倒格子原胞的体积为1.6 对于简单立方晶格，证明密勒指数为(h, k,l)的晶面系，面间距d 满足其中a 为立方边长。
解：根据倒格子的特点，倒格子与晶面族(h, k,l)的面间距有如下关系因此只要先求出倒格，求出其大小即可。
因为倒格子基矢互相正交，因此其大小为则带入前边的关系式，即得晶面族的面间距。
1.7 写出体心立方和面心立方晶格结构的金属中，最近邻和次近邻的原子数。
若立方边长为a ，写出最近邻和次近邻的原子间距。
答：体心立方晶格的最近邻原子数（配位数）为8，最近邻原子间距等于次近邻原子数为6，次近邻原子间距为a ；面心立方晶格的最近邻原子数（配位数）为12，最近邻原子间距等于次近邻原子数为6，次近邻原子间距为a 。
《固体物理学》部分习题解答1.3 证明：体心立方晶格的倒格子是面心立方；面心立方晶格的倒格子是体心立方 。
解 由倒格子定义2311232a a b a a a π⨯=⋅⨯ 3121232a a b a a a π⨯=⋅⨯ 1231232a a b a a a π⨯=⋅⨯体心立方格子原胞基矢123(),(),()222a a aa i j k a i j k a i j k =-++=-+=-+ 倒格子基矢231123022()()22a a a ab i j k i j k a a a v ππ⨯==⋅-+⨯+-⋅⨯202()()4a i j k i j k v π=⋅-+⨯+-2()j k a π=+ 同理31212322()a ab i k a a a a ππ⨯==+⋅⨯ 32()b i j aπ=+可见由123,,b b b 为基矢构成的格子为面心立方格子 面心立方格子原胞基矢123()/2()/2()/2a a j k a a k i a a i j =+=+=+ 倒格子基矢2311232a ab a a a π⨯=⋅⨯ 12()b i j k aπ=-++同理22()b i j k a π=-+ 32()b i j k aπ=-+ 可见由123,,b b b 为基矢构成的格子为体心立方格子1.4 证明倒格子原胞的体积为03(2)v π，其中0v 为正格子原胞体积证 倒格子基矢2311232a a b a a a π⨯=⋅⨯3121232a a b a a a π⨯=⋅⨯1231232a a b a a a π⨯=⋅⨯倒格子体积*0123()v b b b =⋅⨯3*23311230(2)()()()v a a a a a a v π=⨯⋅⨯⨯⨯ 3*00(2)v v π=1.5 证明：倒格子矢量112233G h b h b h b =++垂直于密勒指数为123()h h h 的晶面系。
证： 33121323,a a a a CA CB h h h h =-=- 容易证明12312300h h h h h h G CA G CB ⋅=⋅=112233G h b h b h b =++与晶面系123()h h h 正交。
1.6 如果基矢,,a b c 构成简单正交系证明晶面族()hkl 的面间距为2221()()()h k ld a b c=++ 说明面指数简单的晶面，其面密度较大，容易解理 证 简单正交系a b c ⊥⊥ 123,,a ai a bj a ck ===倒格子基矢2311232a a b a a a π⨯=⋅⨯ 3121232a a b a a a π⨯=⋅⨯ 1231232a a b a a a π⨯=⋅⨯123222,,b i b j b k a b cπππ=== 倒格子矢量123G hb kb lb =++222h i k j l k a b cπππ=++晶面族()hkl 的面间距2d Gπ=2221()()()h k l a b c=++ 面指数越简单的晶面，其晶面的间距越大晶面上格点的密度越大，这样的晶面越容易解理1.9 指出立方晶格(111)面与(100)面，(111)面与(110)面的交线的晶向 解 (111)面与(100)面的交线的AB －AB 平移， A 与O 重合。
B 点位矢B R aj ak =-+（111）与（100）面的交线的晶向AB aj ak =-+—— 晶向指数011⎡⎤⎣⎦(111)面与(110)面的交线的AB—— 将AB 平移，A 与原点O 重合，B 点位矢B R ai aj =-+(111)面与(110)面的交线的晶向AB ai aj =-+ ――晶向指数110⎡⎤⎣⎦2.1．证明两种一价离子组成的一维晶格的马德隆常数为2ln 2α=.证 设想一个由正负两种离子相间排列的无限长的离子键，取任一负离子作参考离子（这样马德隆常数中的正负号可以这样取，即遇正离子取正号，遇负离子取负号），用r 表示相邻离子间的距离，于是有(1)11112[ (234)ij rr r r r rα±'==-+-+∑ 前边的因子2是因为存在着两个相等距离i r 的离子，一个在参考离子左面，一个在其右面，故对一边求和后要乘2，马德隆常数为234(1) (34)n x x x x x x +=-+-+ 当X=1时，有1111 (2234)n-+-+= 2.3 若一晶体的相互作用能可以表示为()mnu r rrαβ=-+求 1）平衡间距0r 2）结合能W （单个原子的） 3）体弹性模量 4）若取02,10,0.3,4m n r nm W eV ==== ，计算,αβ值。
解 1）晶体内能()()2m n N U r r rαβ=-+ 平衡条件0r r dUdr== 11000m n m n r r αβ++-+= 10()n m n r m βα-= 2) 单个原子的结合能01()2W u r =-0()()m n r r u r r r αβ==-+ 1(1)()2mn m m n W n m βαα--=- 3) 体弹性模量0202()V UK V V∂=⋅∂ 晶体的体积3V NAr =—— A 为常数，N 为原胞数目 晶体内能()()2m n N U r r rαβ=-+ 1112[1...]234α=-+-+22n α∴=1121()23m n N m n r r NAr αβ++=-221121[()]23m n U N r m n V V r r r NAr αβ++∂∂∂=-∂∂∂ 体弹性模量0202()V UK V V∂=⋅∂22222000001[]29m n m n V V UN m n m n V V r r r r αβαβ=∂=-+-+∂ 由平衡条件1120001()023m n V V UN m n Vr r NAr αβ++=∂=-=∂00m n m n r r αβ=222220001[]29m n V V UN m n V V r r αβ=∂=-+∂ 体弹性模量0202()V U K V V∂=⋅∂ 000()2m n N U r r αβ=-+222220001[]29m n V V UN m n V V r r αβ=∂=-+∂2220001[]29m nV V UN m n m n V V r r αβ=∂=-+∂ （00m n m n r r αβ=） 2000[]29m nN nm V r r αβ=--+ 02022()9V V U mnU V V =∂=-∂ 009mn K U V = 4）00m n m n r r αβ= 10()n m n r m βα-= 1(1)()2mn m m n W n m βαα--=- 1002W r β=95101.1810eV m β-=⨯⋅ 20100[2]r W rβα=+ 1929.010eV m α-=⨯⋅2.6．用林纳德—琼斯(Lennard —Jones)势计算Ne 在bcc （球心立方）和fcc （面心立方）结构中的结合能之比值．解 1261261()4()(),()(4)()()2n l u r u r N A A r r r r σσσσεε⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦26661200612()1022r A A du r r u N r A A σε⎛⎫=⇒=⇒=- ⎪⎝⎭22066201212()12.25/9.11()/()0.957()14.45/12.13bcc bcc fcc fcc u r A A u r A A ωω'====' 2.7．对于2H ，从气体的测量得到Lennard —Jones 势参数为65010, 2.96.J A εσ-=⨯=计算2H 结合成面心立方固体分子氢时的结合能（以KJ/mol 单位），每个氢分子可当做球形来处理．结合能的实验值为0.751kJ ／mo1，试与计算值比较．解 以2H 为基团，组成fcc 结构的晶体，如略去动能，分子间按Lennard —Jones 势相互作用，则晶体的总相互作用能为：1261262.ij ij i j U N P P R R σσε--⎡⎤⎛⎫⎛⎫''=-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦∑∑61214.45392;12.13188,ijij jiP P --''==∑∑16235010, 2.96, 6.02210/.erg A N mol εσ-=⨯==⨯()()1262816 2.96 2.962602210/501012.1314.45 2.55/.3.16 3.16U U mol erg KJ mol -⎡⎤⎛⎫⎛⎫=⨯⨯⨯⨯⨯-≈-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦0将R 代入得到平衡时的晶体总能量为。
因此，计算得到的2H 晶体的结合能为2.55KJ ／mol ，远大于实验观察值0.75lKJ ／mo1．对于2H 的晶体，量子修正是很重要的，我们计算中没有考虑零点能的量子修正，这正是造成理论和实验值之间巨大差别的原因．3.1．已知一维单原子链，其中第j 个格波，在第n 个格点引起的位移为，sin(_)nj j j j j a t naq μωδ=+，j δ为任意个相位因子，并已知在较高温度下每个格波的平均能量为kT ，具体计算每个原子的平方平均位移。
解 任意一个原子的位移是所有格波引起的位移的叠加，即sin()n nj j j j j jja t naq μμωδ==++∑∑ （1）2*2*n nj nj nj nj nj j j j j j μμμμμμ''≠⎛⎫⎛⎫==+ ⎪⎪⎝⎭⎝⎭∑∑∑∑由于nj nj μμ⋅数目非常大为数量级，而且取正或取负几率相等，因此上式得第2项与第一项相比是一小量，可以忽略不计。
所以22n njjμμ=∑由于nj μ是时间t 的周期性函数，其长时间平均等于一个周期内的时间平均值为22211sin()2T jj j j j j a t naq dt a T μωδ=++=⎰（2） 已知较高温度下的每个格波的能量为kT ，nj μ的动能时间平均值为022222000111sin()224LT T nj j j nj j j j j j j d w a T dx dt L a t naq dt w La T dt T μρρωδρ⎡⎤⎛⎫==++=⎢⎥ ⎪⎢⎥⎝⎭⎣⎦⎰⎰⎰ 其中L 是原子链的长度，ρ使质量密度，0T 为周期。
所以221142nj j j T w La KT ρ== （3） 因此将此式代入（2）式有22nj jKTPL μω=所以每个原子的平均位移为 22221n nj jjjjjKT KTPL PL μμωω====∑∑∑3.2 讨论N 个原胞的一维双原子链(相邻原子间距为a)，其2N 个格波解，当M=m 时与一维单原子链结果一一对应解 质量为M 的原子位于 2n-1， 2n+1， 2n+3 ……。
