基本几何体六棱柱

8.1 基本几何图形第1课时棱柱、棱锥、棱台立体几何是研究三维空间中物体的形状、大小、位置关系的一门数学学科，而三维空间是人们生存发展的现实空间，学习立体几何对我们更好地认识客观世界，更好地生存与发展具有重要意义。

在立体几何初步部分,学生将先从对空间几何体观察入手、认识空间图形；再以长方体为载体，直观认识和理解空间点、线、面的位置关系。

本节内容既是义务教育阶段“空间与图形”课程的延续和提高，也是后续研究空间点、线、面位置关系的基础，既巩固了前面所学的内容，又为后面内容的学习做了知识上和方法上的准备，在教材中起着承前启后的作用。

课程目标1．通过对实物模型的观察，归纳认知简单多面体——棱柱、棱锥、棱台的结构特征．2．能运用棱柱、棱锥、棱台的结构特征来判断、描述现实生活中的实物模型．3．与平面几何体的有关概念、图形和性质进行适当类比,初步学会用类比的思想分析问题和解决问题．数学学科素养1。

数学抽象:多面体与旋转体等概念的理解；2.逻辑推理：棱柱、棱锥、棱台的结构特点；3.直观想象：判断空间几何体；4。

数学建模：通过平面展开图将空间问题转化为平面问题解决，体现了转化的思想方法.重点：掌握棱柱、棱锥、棱台的结构特征;难点：棱柱、棱锥和棱台的侧面展开图问题.教学方法:以学生为主体，小组为单位,采用诱思探究式教学，精讲多练。

教学工具：多媒体。

一、情景导入在平面几何中，我们认识了三角形，正方形，矩形，菱形，梯形，圆，扇形等平面图形。

但我们知道在我们周围存在着各种各样的物体,它们都占据着空间的一部分.如果我们只考虑这些物体的形状和大小，而不考虑其他因素，那么由这些抽象出来的空间图形就叫做空间几何体.那么对空间中各种各样的几何体，我们如何认识它们的结构特征？对空间中不同形状、大小的几何体我们如何理解它们的联系和区别？要求:让学生自由发言，教师不做判断.而是引导学生进一步观察.研探。

二、预习课本，引入新课阅读课本97-100页，思考并完成以下问题1、什么是空间几何体？什么是多面体与旋转体?2、多面体包含哪些图形?这些图形是怎样定义的？又有什么结构特点?要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题。

3.学生练习
4.老师改画并点评
学生作品
画面要求：
写生一张8开的石膏六棱柱体明暗素描，造型准确，表现其立体感和空间感
总结
加深对六棱柱体形态特征的理解，进一步熟悉明暗素描的画法，体现六棱柱体的立体感和空间感。
三造型准确，体现立体感空间感
教学准备：
画板,画架，素描纸，铅笔，橡皮擦，透明胶，美工刀，六棱柱体石膏，静物台，射灯教ຫໍສະໝຸດ ppt教学过
程
1．导入
通过上节课的六棱柱体结构素描回顾六棱柱体的形状特征
展示石膏六棱柱体，让学生观察其明暗变化的关系
对照实物指出六棱柱体的明暗三大面和五调子
二．新授
1.展示优秀的石膏六棱柱体的明暗素描作品
2.结合上节课的六棱柱体结构素描讲解并示范明暗素描的作画步骤
强调构图，形体，比例，结构，作画姿势，排线
先确定光源，把暗部调子与投影铺上大色调；
观察比较六棱柱各个面及背景的深浅变化；
从明暗交界线开始往暗部画，深入描绘，注意明暗调子的节奏变化；
由浅到深，循步深入，不能一下子画得过黑，最后画灰面和亮面；
加强背景和投影的刻画，增强黑白灰的明暗对比，体现立体感和空间感；
广电·新艺堂教案
课题
素描基础下第二课（六棱柱体明暗素描）
教学
重难点：
一明暗三大面、五调子
二六棱柱体明暗素描的明暗三大面、五调子的变化
三形体，结构，透视，比例
四明暗调子的铺设
教学目标：
一加深了解明暗与造型，明暗变化的基本规律
二熟悉明暗素描的观察方法、作画步骤、和明暗调子的铺设技巧。为上好其他绘画专业课奠定造型基础

1．空间几何体的定义
空间中的物体都占据着空间的一部分， 若只考虑这些物体的_形__状___和_大__小___，
而不考虑其他因素，那么由这些物体抽 象出来的空间图形就叫做空间几何体．
[问题1] 图片(1)(2)(3)中的物体的形状有何特点？ [提示] 由若干个平面多边形围成． [问题2] 图片(4)(5)(6)(7)的物体的形状与(1)(2)(3) 中有何不同？图片(4)(5)(6)(7)中的几何体可否看作 平面图形绕某定直线旋转而成？ [提示] 表面是由平面与曲面围成．可以。
DCFD′. 其中四边形ABEA′和四边形DCFD′是底面, A′D′，EF，BC，AD为侧棱.
8.如 图 ， 已 知 长 方 体 ABCD－ A1B1C1D1，过 BC 和 AD 分别作 一 个 平 面 交 底 面 A1B1C1D1 于 EF、PQ，则长方体被分成的三 个几何体中，棱柱的个数是________．
答案： D
下列的几何体是多面体吗？
答：这些不但是多面体，他们还是多面体 当中的一种，叫做棱锥。
你们思考一下这些棱锥有什么共同特点？
2.棱锥的结构特征
什么是棱锥？ 一般地，有一 个面是多边形，其余 各面都是有一个公共 点的三角形，由这些 面围成的多面体叫做 棱锥. 记为：棱锥S-ABCD
多边形 三角形
D'
E'
C'
D A'
B'
S A'B'C'D'E' S ABCDE
S' H '2 SH 2
E
O
C
AB
3. 棱台的结构特征
什么是棱台？ 一般地，用一个平行于棱锥底面的平面去截 棱锥，底面和截面中间的部分的多面体叫做棱台.

Z
X Y
正六棱柱的投影
7
③ 其余四个侧棱面均垂直于地面，在水平面积聚 为一条直线，正面投影和侧面均为类似形 （四边 形） 。
Z
X Y
正六棱柱的投影
8
9
4、棱柱三视图的画图步骤
①、画出个投影轴和中心线
②、画俯视图---特征视图，等分圆的六边形
③、根据“长对正”“高平齐”“宽相等”投影规
律及棱
柱的高度作上、下平面的主、左
答：12个点、六条棱、8个面 特点：上下表面全等且互相平行，侧 面为全等的六个矩形，且垂直于底面。
5
3、棱柱的投影特征
① 如图,为一正六棱柱。
六棱柱的上下表面平行于
Z
水平面， 在H面上投影
反映实形，为一个正六边
形，在正面及侧面投影积
聚为一直线
X Y
6
正六棱柱的投影
② 前后棱面为平行于v面，在正面投影反映实形且 与后面重影，水平及侧面投影积聚为一直线。
的有棱柱、棱锥。
➢曲面立体：表面为曲面或平面与曲面组
成。常见的有圆柱、圆锥、球体和圆环。
2

常见的基本几何体
平面立体
曲面立体
3
(二)讲授新课
第二章 基本几何体
4
第三节 棱柱的投影
1、棱柱的概念
上下表面平行且为多边形，侧面均为矩形的立体
2、棱柱的形体特征 问题：六棱柱有几个点？几条棱？几个 面？ 它们有什么特点？
视④图、投根影据“长对正”“高平齐”“宽相等”投影规
律作前、后平面的主、左视图投影
⑤、根据“长对正”“高平齐”“宽相等”投影规 律作其余四个平面的主、左视图投影
10
❖ 课堂练习：补画五棱柱的三视图

【教学过程】一、复习旧课结合作业复习直线和平面投影变换的作图方法和步骤。

二、引入新课题机器上的零件，不论形状多么复杂，都可以看作是由基本几何体按照不同的方式组合而成的。

基本几何体——表面规则而单一的几何体。

按其表面性质，可以分为平面立体和曲面立体两类。

1、平面立体——立体表面全部由平面所围成的立体，如棱柱和棱锥等。

（出示模型给学生看）。

2、曲面立体——立体表面全部由曲面或曲面和平面所围成的立体，如圆柱、圆锥、圆球等。

（出示模型给学生看）。

曲面立体也称为回转体。

三、教学内容（一）平面立体的投影及表面取点1．棱柱棱柱由两个底面和棱面组成，棱面与棱面的交线称为棱线，棱线互相平行。

棱线与底面垂直的棱柱称为正棱柱。

本节仅讨论正棱柱的投影。

（1）棱柱的投影以正六棱柱为例。

如图3－1（a）所示为一正六棱柱，由上、下两个底面（正六边形）和六个棱面（长方形）组成。

设将其放置成上、下底面与水平投影面平行，并有两个棱面平行于正投影面面。

上、下两底面均为水平面，它们的水平投影重合并反映实形，正面及侧面投影积聚为两条相互平行的直线。

六个棱面中的前、后两个为正平面，它们的正面投影反映实形，水平投影及侧面投影积聚为一直线。

其他四个棱面均为铅垂面，其水平投影均积聚为直线，正面投影和侧面投影均为类似形。

（a）立体图（b）投影图图3－1正六棱柱的投影及表面上的点边画图边讲解作图方法与步骤。

总结正棱柱的投影特征：当棱柱的底面平行某一个投影面时，则棱柱在该投影面上投影的外轮廓为与其底面全等的正多边形，而另外两个投影则由若干个相邻的矩形线框所组成。

（2）棱柱表面上点的投影方法：利用点所在的面的积聚性法。

（因为正棱柱的各个面均为特殊位置面，均具有积聚性。

）平面立体表面上取点实际就是在平面上取点。

首先应确定点位于立体的哪个平面上，并分析该平面的投影特性，然后再根据点的投影规律求得。

举例：如图3－1（b）所示，已知棱柱表面上点M的正面投影m′，求作它的其他两面投影m、m″。

2、画法步骤。
课
后
记
教学内容
教师活动
学生活动
2、棱柱的三视图画图步骤：
画出基准线，和俯视图
让学生观察模型总结三视图的形状。
画出轴线和基准线。
在俯视图中画出正六边形。
利用长对正画出主视图。
擦去
多余
线
利用
高平齐
画出
左视图
高
观察模
型分析
三视图
回答教
师问题
跟随教
师画出
轴线和
基准线
画出俯
视图中
画出正
六边形
跟随教
师画出
主视图
跟随教
师擦去
多余线
教 学 过 程 与 教 学 方 法
教学内容
教师活动
学生活动
利用
宽相等
画出
左视图
擦去
多余线
完成
三视图
画出左
视图。
擦去多
余线完
成三视
图。
小
结
基本结合形体的分类。
平面立体。
曲面立体。
正六棱柱的三视图画法
作
业
习题册35页4题。
板
书
设
计
基本几何体的分类：
平面立体
曲面立体
六棱柱的三视图：
1、分析三视图
课 时 教 案
备课
第一节基本几何体（六棱柱）
课型
新授课
教学
目标
知识目标
1.掌握基本结合形体的分类。
2.掌握平面立体。
1、掌握曲面立体。
4.掌握正六棱柱的三视图画法。
能力目标
提高作图技巧
德育目标
培养学生耐心细致的工作作风，严谨认真的工作态度。

（1）底面互相平行． 底面互相平行． （2）侧面都是 平行四边形． 平行四边形． 侧棱平行且相等． （3）侧棱平行且相等．
侧 面 侧棱
F A B E D C
底面
顶点
棱柱的表示
F′
E′ A′ B′
D′ C′
用底面各顶点的字母表示棱柱, 用底面各顶点的字母表示棱柱 如图所示的六棱柱表示为： 如图所示的六棱柱表示为： 棱柱ABCDEF—A'B'C'D'E'F'” “棱柱 ”
1. 侧棱不垂直于底的棱柱叫做斜棱柱． 侧棱不垂直于底的棱柱叫做斜棱柱 斜棱柱． 2.侧棱垂直于底的棱柱叫做直棱柱． 侧棱垂直于底的棱柱叫做直棱柱． 侧棱垂直于底的棱柱叫做直棱柱 3. 底面是正多边形的直棱柱叫做正棱柱． 底面是正多边形的直棱柱叫做正棱柱 正棱柱．
小结
通过本节课的学习,我们知道了棱柱的结构特 通过本节课的学习 我们知道了棱柱的结构特 征,从而了解了认识空间几何体结构特征的一般方 从而了解了认识空间几何体结构特征的一般方 法,即从构成几何体的几何元素间的基本关系出发 即从构成几何体的几何元素间的基本关系出发, 即从构成几何体的几何元素间的基本关系出发 去归纳它的结构特征. 去归纳它的结构特征
探究
长方体按如图截去一角后所得的两部分还是棱柱吗？ 长方体按如图截去一角后所得的两部分还是棱柱吗？
D’ C’ B’
A’
D C A B
探究
长方体按如图截去一角后所得的两部分还是棱柱吗？ 长方体按如图截去一角后所得的两部分还是棱柱吗？
D’ A’ F F’ B’ H D E A B C E’ H’ G G’ C’
三棱柱
四棱柱
五棱柱
探究
一个长方体，能作为棱柱底面的有几对？ 一个长方体，能作为棱柱底面的有几对？

高中数学立体几何知识点高中数学立体几何知识1柱、锥、台、球的结构特征(1)棱柱：定义：有两个面互相平行，其余各面都是四边形，且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体。

分类：以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。

表示：用各顶点字母，如五棱柱或用对角线的端点字母，如五棱柱几何特征：两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。

(2)棱锥定义：有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的几何体分类：以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示：用各顶点字母，如五棱锥几何特征：侧面、对角面都是三角形;平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方。

(3)棱台：定义：用一个平行于棱锥底面的平面去截棱锥，截面和底面之间的部分分类：以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示：用各顶点字母，如五棱台几何特征：①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点(4)圆柱：定义：以矩形的一边所在的直线为轴旋转，其余三边旋转所成的曲面所围成的几何体几何特征：①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。

(5)圆锥：定义：以直角三角形的一条直角边为旋转轴，旋转一周所成的曲面所围成的几何体几何特征：①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。

(6)圆台：定义：用一个平行于圆锥底面的平面去截圆锥，截面和底面之间的部分几何特征：①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。

(7)球体：定义：以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体几何特征：①球的截面是圆;②球面上任意一点到球心的距离等于半径。

2、空间几何体的三视图定义三视图：正视图(光线从几何体的前面向后面正投影);侧视图(从左向右)、俯视图(从上向下)注：正视图反映了物体上下、左右的位置关系，即反映了物体的高度和长度;俯视图反映了物体左右、前后的位置关系，即反映了物体的长度和宽度;侧视图反映了物体上下、前后的位置关系，即反映了物体的高度和宽度。

《机械制图》 第3章 基本体
资讯
3.1 基本体的投影
立体按构成不同可分为基本体和组合体。 通常将棱柱、棱锥、圆柱、圆锥、球体等简单几何体称为基本体。 按表面性质不同，又可将立体分为平面立体和曲面立体。 3.1.1 平面立体 由平面围成的立体称为平面立体，立体上相邻侧表面的交线称为 棱线。 1. 棱柱 (1) 棱柱的三视图 图3-1所示一放置在三投影面体 系中的正六棱柱。
图3-2 三棱锥的三视图
资讯
3.1.2 曲面立体 曲面立体的表面由曲面或曲面和平面组成。常见的曲面立体有圆 柱、圆锥和球体。 由于组成立体的曲面为回转面，故上述曲面立体也称为回转体。 有关回转面的几个概念如下。 回转面：一条线绕另一直线旋转所形成的运动轨迹。 回转面的轴线：不动的直线。 母线：即运动的线，回转面的母线可以是 直线也可以为任意曲线。 素线：母线位于回转面上任一位置时的线。
(a) 截切的圆锥
(b) 截切圆锥的视图
图3-17 圆锥的截交线
资讯
[例3-4] 完成被截切圆锥的视图。
(a) 求作截交线
(b) 整理图形 图3-18 圆锥的截交线
资讯
3. 球体的截交线 球体的截交线为圆，如图3-19所示。 由于截切的位置关系，球体截交线圆的投影可能为圆、直线或椭圆。 球体截交线的作图分析：当截交线的投影为圆或直线时，作图较为 简便。如是椭圆，则要利用找点的方法求得椭圆上若干点的投影后 再光滑连接各点。
资讯
若是沿圆柱轴线开一通孔，便称为圆筒。圆筒有内、外两个表面。 当截平面截切圆筒时，就会在内外表面上产生形状相同的截交线， 如图3-14所示。
(a)
(b)
图3-14 圆筒的截交线
资讯
圆筒被截切和开槽的情况如图3-15所示。

（2）棱锥：有一个面是多边形，其余各面都是有一个公共顶点的三角形. 底面是三角形、四边形、五边形……的棱锥分别叫做三棱锥、四棱锥、五棱锥 ……其中三棱锥又叫四面体。
棱锥也用顶点和底面各顶点字母表示，如棱锥S-ABCD。 （3）棱台：用一个平行于棱锥底面的平面区截棱锥，底面于截面之间的部分 叫做棱台。 原棱锥的底面和截面分别叫做棱台的下底面和上底面，棱台也有侧面、侧棱、 顶点。
题型二 简单结合体的判断
例2 如图所示，长方体ABCD－A1B1C1D1. (1)这个长方体是棱柱吗？如果是，是几棱柱？为什么？
(2)用平面BCFE把这个长方体分成两部分后，各部分形成的几何体还
是棱柱吗？如果是，是几棱柱？如果不是，说明理由．
【答案】(1)该长方体是棱柱，并且是四棱柱，祥见解析．
回顾
阅读课本97-100页，思考并完成以下问题 1、什么是空间几何体？什么是多面体与旋转体？ 2、多面体包含哪些图形？这些图形是怎样定义的？又有什么结构特点？
探索新知
1、空间几何体 定义：如果只考虑物体的形状和大小，而不考虑其它因素， 那么这些由物体抽象出来的空间图形就叫做空间几何体。 2、多面体与旋转体 多面体的定义：由若干平面多边形围成的几何体叫做多面体, 围成多面体的各个多边形叫做多面体的面；相邻两个面的公共 边叫做多面体的棱；棱与棱的公共点叫做多面体的顶点． 旋转体的定义：由一个平面图形绕它所在的平面内的一条定 直线旋转所形成的封闭几何体叫做旋转体．
(2)①正确．因为有六个面，属于六面体的范围．②错误．因为侧棱的延长线不能 交于一点，所以不正确．③正确．如果把几何体放倒就会发现是一个四棱柱． ④⑤都正确．如图所示． 解题技巧（判断结构特点的注意事项）
在解答关于空间几何体概念的判断题时，要注意紧扣定义判断，这就要求熟悉 各种空间几何体的概念的内涵和外延，切忌只凭图形主观臆断．

第三章　基本几何体的投影通常所说的基本几何体，包括棱柱体、棱锥体、圆柱体、圆锥体、球体和环等。

前两种立体的表面都是平面，称为平面立体；其余四种的表面是回转面或回转面与平面，称为回转体。

本章主要研究这些基本几何体的投影特性及其作图方法。

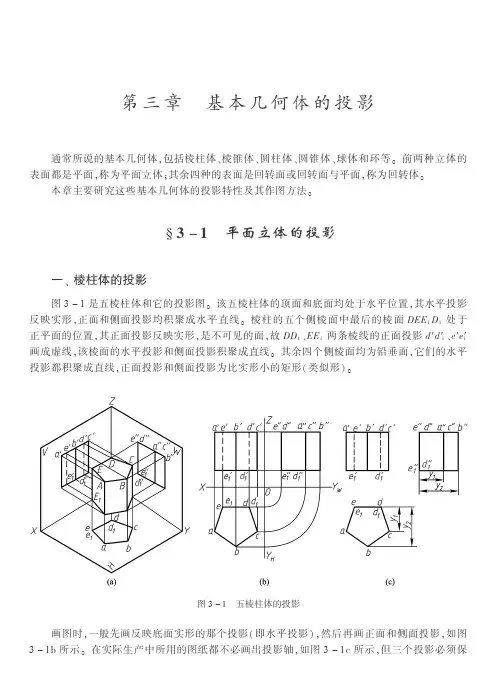
§3－1　平面立体的投影一、棱柱体的投影图３－１是五棱柱体和它的投影图。

该五棱柱体的顶面和底面均处于水平位置，其水平投影反映实形，正面和侧面投影均积聚成水平直线。

棱柱的五个侧棱面中最后的棱面DEE１D１处于正平面的位置，其正面投影反映实形，是不可见的面，故DD１、EE１两条棱线的正面投影d′d′１、e′e′１画成虚线，该棱面的水平投影和侧面投影积聚成直线。

其余四个侧棱面均为铅垂面，它们的水平投影都积聚成直线，正面投影和侧面投影为比实形小的矩形（类似形）。

图３－１　五棱柱体的投影画图时，一般先画反映底面实形的那个投影（即水平投影），然后再画正面和侧面投影，如图３－１ｂ所示。

在实际生产中所用的图纸都不必画出投影轴，如图３－１ｃ所示，但三个投影必须保持左右、上下、前后的对应关系，即V 、H 两面投影左右对正，V 、W 两面投影上下平齐，H 、W 两面投影前后相等。

二、棱锥体的投影图３－２是正三棱锥体和它的投影图。

该三棱锥体的底面处于水平位置，其水平面投影反映实形，正面和侧面投影积聚成水平直线。

三棱锥的右侧棱面SBC 为正垂面，其正面投影s ′b ′c ′积聚成直线，水平面投影sbc 和侧面投影s ″b ″c ″为类似形。

前棱面SAB 和后棱面SAC 均为一般位置平面，因而，它们的三面投影均为类似形（正面投影两个三角形重合）。

图３－２　正三棱锥体的投影画图时，先画出底面三角形ABC 和锥顶S 的投影，然后顺次连接各棱线SA 、SB 、SC 的同面投影，如图３－２ｂ所示。

通过棱柱和棱锥体的投影分析，可归纳如下几点：１）由于平面立体的棱线是直线，所以画平面立体的投影图就是先画出各棱线交点的投影，然后顺次连线，并注意区分可见性。

在工程设计和制造领域，三视图是表达物体形状的重要手段，正六棱柱三视图也不例外，对于理解和制作相关结构和产品具有重要意义。
正六棱柱三视图的重要性
正六棱柱三视图的绘制方法
02
根据正六棱柱的摆放位置，确定其正面方向。
确定正六棱柱的正面方向
在主视图中，绘制一个正六边形，表示正六棱柱的顶面。
绘制正六边形的轮廓
制图-正六棱柱三视图
正六棱柱三视图的基本概念 正六棱柱三视图的绘制方法 正六棱柱三视图的绘制实例 正六棱柱三视图的应用 总结与展望
正六棱柱三视图的基本概念
01
01
02
正六棱柱的定义
底面通常是一个正六边形，侧面是六个矩形。
正六棱柱是一种具有六个等边等长的侧棱和底面的几何体。
从正面观察物体得到的视图。
在室内设计中，正六棱柱三视图用于表示家具、隔断等物体的位置和尺寸，以便实现室内空间的合理布局和利用。
在建筑设计中的应用
室内设计
建筑模型
零件图
在机械制造中，正六棱柱三视图用于表示机械零件的形状、尺寸和加工要求，以确保零件的准确性和互换性。
装配图
正六棱柱三视图用于表示机械设备的装配关系，包括各个零件的位置、连接方式和配合要求，以确保设备的正常运行和维护。
实例一：简单正六棱柱的三视图
总结词：细节丰富
详细描述：这个实例展示了一个复杂的正六棱柱，其三视图在绘制时加入了更多的细节。例如，在主视图中，可以看到正六棱柱的顶面和底面；在左视图中，可以看到正六棱柱的侧面；在俯视图中，可以看到正六棱柱的顶面和底面的中心线。这些细节使得三视图更加真实地反映了正六棱柱的结构。
正六棱柱三视图的重要性和应用前景
未来发展的方向和趋势
标准化和规范化：随着工程制图技术的发展，正六棱柱三视图的标准化和规范化越来越受到重视。未来，将进一步完善正六棱柱三视图的制图标准和规范，提高制图的质量和效率。

六棱柱和三棱柱的知识点
一、六棱柱
1、六棱柱的定义
六棱柱是由六条直线相互垂直组成的几何体，也就是说，它是一种六侧面形的体积。

2、六棱柱的特点
六棱柱的六个侧面形状完全相同，可以由六条直线连接而成，形状类似于三角形，而整个体积的形状为正方形，其顶部是一个正方形，每个侧面的面积都相同。

3、六棱柱的应用
六棱柱的广泛应用在人们日常生活中，如水果篮、罐头、立方体、建筑物等。

二、三棱柱
1、三棱柱的定义
三棱柱是由三条直线相互垂直组成的几何体，也就是说，它是一种三侧面形的体积。

2、三棱柱的特点
三棱柱的三条侧面形状完全相同，可以由三条直线连接而成，形状类似于三角形，而整个体积的形状为正三角形，其顶部是一个正三角形，每个侧面的面积都相同。

3、三棱柱的应用
三棱柱也有广泛的应用，如冰棒、塑料盒子、木制品等。

六棱柱底面积公式
六棱柱是一种常见的几何体，它的底面是一个六边形，因此可以用六边形的面
积公式来计算六棱柱的底面积。

六边形的面积公式是：S=3a^2*√3/2，其中a是六边形的边长。

因此，六棱柱
的底面积公式可以表示为：S=3a^2*√3/2，其中a是六棱柱的边长。

六棱柱的底面积公式可以用来计算六棱柱的底面积，这对于计算几何体的体积
非常有用。

例如，如果我们想计算一个六棱柱的体积，我们可以先计算它的底面积，然后乘以它的高度，就可以得到它的体积。

此外，六棱柱的底面积公式还可以用来计算六棱柱的表面积。

表面积是指几何
体的外表面积，它是由几何体的底面积和侧面积之和组成的。

因此，如果我们想计算一个六棱柱的表面积，我们可以先计算它的底面积，然后再计算它的侧面积，最后将两者相加，就可以得到它的表面积。

总之，六棱柱的底面积公式是一个非常有用的公式，它可以用来计算六棱柱的
底面积、体积和表面积，这对于几何学的研究非常有用。

平面在三投影面体系中： 同时倾斜于三个投影面，称为 一般位置平面 ， 投影为 三类似形 ； 平行于一个投影面，同时垂直于另两个投影面，称为 投影面平行 面，投影为 一实形两直线 ；
垂直于一个投影面，同时倾斜于另两个投影面，称为 投影面垂直 面，投影为 一斜线两类似形 。
考考你
主视图（ B ） 左视图（ B ）
f2 e
a 先画H面投
影（反映六
棱柱特征）
1
d
P
集聚 b
c
P点是H与 W两面投 影的对应 基准点
45°
课堂练习：求正六棱柱表面上点的投影
【练习要求】： 想象出点在空 间的位置，找 准点在三视图 中的位置
n m
注意：给定面上点的可见性问题及其标注
课堂小课 堂结小：结
认识正六棱柱 正六棱柱中各组成表面的特征
图 正六棱柱的三视图
绘图步骤：作图
注意：严格遵循绘图的“三等”关系
得到六棱柱的三视图：
举一反三：
俯
左
六棱柱
六棱柱及表面取点
(f′) (e′) (e″)(d″)(c″)
点、线、面分析 a′b′ c′d′ f″ a″ b″投影特征：
1' (2')1" 2"
有两面投 影是矩形轮廓， 另一投影反映 棱柱特征。
分析正六棱柱的三视图并绘制 分析正六棱柱表面点的可见见性判断及其投影； 绘制注意点： （1）图纸布局要合理； （2）一般从最反映形体特征的视图画起； （3）严格遵循作图的“三等”关系。
作业
习题册:
P40 P41
P42
谢 谢 再 见
.
俯视图（ C ）
A
B
C
考考你