空间直线及其方程

第六节 空间直线及其方程教学目的：介绍空间曲线中最常用的直线，与平面同为本章的重点 教学重点：1.直线方程2.直线与平面的综合题教学难点：1.直线的几种表达式2.直线与平面的综合题教学内容：一、空间直线的一般方程空间直线可以看成是两个平面的交线。

故其一般方程为：⎩⎨⎧=+++=+++022221111D z C y B x A D z C y B x A 二、空间直线的对称式方程与参数方程平行于一条已知直线的非零向量叫做这条直线的方向向量。

已知直线上的一点),,(0000z y x M 和它的一方向向量},,{p n m =s ，设直线上任一点为),,(z y x M ，那么M M 0与s 平行，由平行的坐标表示式有：pz z n y y m x x 000-=-=- 此即空间直线的对称式方程（或称为点向式方程）。

（写时参照书上注释）如设t pz z n y y m x x =-=-=-000 就可将对称式方程变成参数方程（t 为参数）⎪⎩⎪⎨⎧+=+=+=ptz z nt y y mtx x 000 三种形式可以互换，按具体要求写相应的方程。

例1：用对称式方程及参数方程表示直线⎩⎨⎧=++-=+++043201z y x z y x ．解：在直线上任取一点),,(000z y x ，取10=x ⎩⎨⎧=--=++⇒063020000z y z y ，解得2,000-==z y ，即直线上点坐标)2,0,1(-．因所求直线与两平面的法向量都垂直，取}3,1,4{--=⨯=21n n s ，对称式方程为：321041-+=--=-z y x 参数方程： ⎪⎩⎪⎨⎧--=-=+=tz t y tx 3241．例2： 一直线过点)4,3,2(-A ，且和y 轴垂直相交，求其方程．解：因为直线和y 轴垂直相交，所以交点为)0,3,0(-B ，于是→==}4,0,2{BA s ，所求直线方程：440322-=+=-z y x 三、两直线的夹角： 两直线的方向向量的夹角（通常指锐角）叫做两直线的夹角。

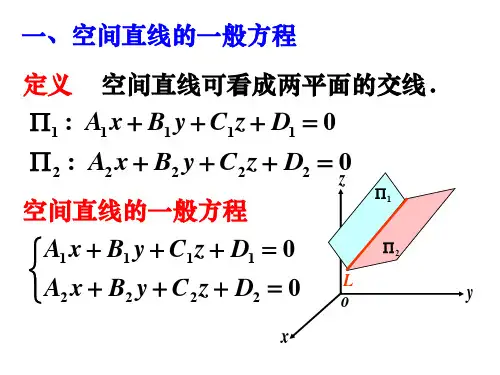
空间直线及其方程§8.4 空间直线及其方程ü直线的一般方程ü直线的参数方程和对称方程ü两直线的夹角ü直线与平面的夹角一、空间直线的一般方程定义空间直线可看成两平面的交线．Π1:A1x+B1y+C1z+D1Π2:A2x+B2y+C2z+D2A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0空间直线的一般方程y注：表示同一直线的一般方程不唯一。

确定空间直线的条件•由两个平面确定一条直线；•由空间的两点确定一条直线；•由空间的一点和一个方向来确定一条直线。

二、空间直线的参数方程与对称式方程r如果一非零向量sr一条已知直线L，向量s线L的方向向量．设定点M0(x0,y0,z0)∈L,方向向量的定义：yr∀M(x,y,z)∈L,0//srs={m,n,p},M0={x−x0,y−y0,z−z0}则{x−x0,y−y0,z−z0}=t{m,n,p} x=x0+mt y=y0+ntz=z+pt0消去参数t，有直线的参数方程x−xy−yz−z==直线的对称式方程mnp直线的一组方向数方向向量的余弦称为直线的方向余弦.注：1. 表示同一直线的对称方程不唯一；2. 对称式方程可转化为一般方程;x=x0,x−x0y−y0z−z0 3.==理解为:y−y=z−z.0np p n4. 任一条直线均可表示为对称式方程.设直线过两点M(x1,y1,z1),N(x2,y2,z2)r则s={x2−x1,y2−y1,z2−z1}x−x1y−y1z−z1直线的对称方程为：==x2−x1y2−y1z2−z1例1用对称式方程及参数方程表示直线x+y+z+1=0.2x−y+3z+4=0解在直线上任取一点(x0,y0,z0)y0+z0+2=0取x0=1⇒,y0−3z0−6=0解得y0=0,z0=−2点坐标(1,0,−2),因所求直线与两平面的法向量都垂直取rrrs=n1×n2={4,−1,−3}, x−1y−0z+2对称式方程==,4−1−3x=1+4t.参数方程y=−tz=−2−3t例2 一直线过点A(2,−3,4)，且和y轴垂直相交，求其方程.解因为直线和y轴垂直相交,所以交点为B(0,−3,0),r取s=={2,0,4},x−2y+3z−4==.所求直线方程204三、两直线的夹角定义两直线的方向向量的夹角称之.（锐角）x−x1y−y1z−z1直线L1:==,p1m1n1x−x2y−y2z−z2直线L2:==,m2n2p2 ^cos(L,L)=12|mm+nn+pp|m1+n1+p1⋅m2+n2+p2两直线的夹角公式222222两直线的位置关系：(1)L1⊥L2⇐⇒m1m2+n1n2+p1p2=0,m1n1p1==,(2)L1//L2⇐⇒m2n2p2r例如，直线L1:s1={1,−4,0},r直线L2:s2={0,0,1},rrrrQs1⋅s2=0,∴s1⊥s2,即L1⊥L2.x−4z=3例3 一直线L过点(-3,2,5)，且和直线2x−y−5z=1平行，求其方程.vi解rrrQs=n1×n2=1vj0vk−4=−{4,3,1}2−1−5∴所求直线方程v方法2:设s={m,n,p}x+3y−2z−5==.431m−4p=0mnpvvvvQs⊥n1,s⊥n2∴⇒==4312m−n−5p=0v取s={4,3,1}………x+1y−1z==例4 一直线过点M0(2,1,3)，且与直线L: 32−1垂直相交，求其方程.解设所求直线为l , 先求两直线的交点。

7.8 空间直线及其方程7.8.1空间直线方程的几种形式1．空间直线的一般式方程空间直线L 可看作是两个平面π与π的交线（图7.37）设有平面1π： 01111=+++D z C y B x A 和平面2π： 02222=+++D z C y B x A若},,{1111C B A n =与},,{2222C B A n =不平行，则平面1π与平面2π相交，那么空间直线L 上的点的坐标同时满足平面1π与平面2π的方程，即满足方程组⎩⎨⎧=+++=+++0022221111D z C y B x A D z C y B x A （1）反过来，若点M 不在直线上，则它的坐标不可能即满足平面1π的方程，又满足平面2π的方程，所以M 的坐标不满足方程组（1），因此直线L 可用方程组（1）来表示，称方程组为空间直线的一般方程或交面式方程.由于通过直线L 的平面有无数个，其中任何两个平面方程的联立都表示直线L 的方程,因此空间直线的方程不是唯一的，例如方程组⎩⎨⎧==00y x 与⎩⎨⎧=-=+0y x y x 都表示z 轴。

2，空间直线的点向式方程假如已知一点和一个不为零的向量},,{p n m s =那么通过已知点且平行于已知向量的直线在空间的位置就可以完全确定，已知非零向量s 叫做直线的方向向量.设空间直线通过点),,(0000z y x M ，且直线的方向向量为（图7.38）,下面求直线的方程.在直线L 上任取一点),,(z y x M ,由题意知,向量M 0与s 平行,而},,{0000z z y y x x M M ---= 所以pz z n y y m x x 000-=-=- (2) 即在直线上L 的点的坐标满足方程（2）.反过来若M 不在直线上，则M M 0与不平行，从而点M 的坐标不满足（2），所以（2）式就是我们所求的直线L 的方程，称（2）为直线的点向式方程或标准式方程或对称式方程.方程（2）中如果p n m ,,三数中有一个为零或两个为零,如0=m ,此时式子pz z n y y x x 0000-=-=- 应理解为⎪⎩⎪⎨⎧-=-=p z z n y y x x 000若0==n m ,此时式子 pz z y y x x 00000-=-=- 应理解为 ⎩⎨⎧==0y y x x若一直线通过两点),,(1111z y x M ,),,(2222z y x M ,则此直线的方向向量可取为 },,{12121221z z y y x x M M ---==于是通过21,M M 两点的直线方程为121121121z z z z y y y y x x x x --=--=-- (3)我们称（3）式为直线的两点式方程.若设t pz z n y y m x x =-=-=-000,则得到 ⎪⎩⎪⎨⎧+=+=+=ptz z nt y y mt x x 000 (4)方程组（4）称为空间直线的参数式方程，其中t 为参数.例1求过点)3,2,1(-,方向向量}2,1,2{-=的直线方程. 解 代入(2)式得直线的点向式方程; 231221-=-+=-z y x 它的参数方程是:⎪⎩⎪⎨⎧+=--=+=t z t y t x 23221也可以写成两面交线的形式:⎪⎪⎩⎪⎪⎨⎧-=-+-+=-23121221z y y x 或⎩⎨⎧+-=++=+-342421z y y x例2一直线通过点)2,0,1(-M ，且垂直于平面032=+-z y x ，求此直线的对称式方程和参数方程.解 所求直线与一平面垂直，则直线的方向向量与平面的法向量平行，故可取}3,1,2{-==,代入（2）式得直线的对称式方程为:321021+=--=-z y x 直线的参数方程为:⎪⎩⎪⎨⎧+-=-=+=t z t y t x 3221直线方程的几种形式之间可以互化，由标准方程可写出一般式方程和参数方程.下面的例子说明直线的一般方程可以化为标准方程.例3用对称式方程及参数方程表示直线⎩⎨⎧=++-=+++043201z y x z y x （5） 解 求直线的标准方程，需要求出直线上一个点和直线的方向向量.首先求直线上一点),,(000z y x ，方程（5）中两个方程三个未知数，可有无穷多组解，任意选定000,,z y x 中的一个为已知，例如可以取10=x ,代入方程（5）得 ⎩⎨⎧=--=+632z y z y解这个二元一次方程组得2,000-==z y ，于是求出)2,0,1(0-M 为直线上一点. 其次求出直线的方向向量,因为所求直线是平面1π:01=+++z y x 及平面2π:0432=++-z y x 的交线,所以直线同时垂直于1π与2π的法向量，故可取}3,1,4{1121--=-=⨯=n n代入（2）式得直线的对称式方程为：32141-+=-=-z y x 令 t z y x =-+=-=-32141即得所给直线的参数方程为：⎪⎩⎪⎨⎧--=-=+=t z t y tx 3241注意在本题中也可以用另一种方法得对称式方程，例如再设01=x 代入方程（5）得⎩⎨⎧=++-=++04301z y z y解之得45,4111-==z y ，因此又得直线上的另一点)45,41,0(1-M ，由于向量10M M 平行于直线，因此可取}43,41,1{10-==M M ，于是所求直线方程为4324111+==--z y x 即32141+==--z y x 7.8.2两直角的夹角空间两直线可相交也可不相交，两直线的夹角是指两直线的方向向量的夹角.设有两条直线:1L :111111p z z n y y m x x -=-=- 1L :222222p z z n y y m x x -=-=- 它们的方向向量分别为},,{1111p n m s =、},,{2222p n m s =，于是计算两直线之间夹角θ的公式为222222212121212121cos pn m pn m p p n n m m ++++++==θ （6）由此得到若直线1L 与直线2L 互相垂直，即1s 垂直于2s 的充分必要条件是 0212121=++p p n n m m若直线1L 与直线2L 平行，即1s 平行于2s 的充分必要条件是212121p p n n m m == 例4求两直线121123--=+=-z y x 和112713+=+=+z y x 间的夹角. 解 代入公式（6）得21121)1(121)1(2112cos 222222=++-++⨯-+⨯+⨯==θ 所以 3πθ=或π32.例5直线⎪⎩⎪⎨⎧+=-=+=tz t y t x 22332与⎪⎩⎪⎨⎧+=-==t z t y t x 25416平行还是垂直?解 两直线的方向向量分别为}1,2,3{1-=s 和}2,4,6{2-=,显然1s 与2s 平行,所以,两直线平行.必须注意,若两条直线的方向向量平行,则两直线平行.若两直线的方向向量不平行,则两直线或相交或为异面直线，须区别这两种情形.7.8.3直线和平面的夹角直线和它在平面上的投影直线所成的两邻角中的任何一个均可定义为直线与平面的夹角θ(图7.39).这两个角互为补角，它们的正弦相等，我们不妨规定20πθ≤≤.设直线L:pz z n y y m x x 000-=-=- 平面π: 0=+++D Cz By Ax求它们的夹角，直线L 的方向向量},,{p n m =，平面π的法向量},,{C B A =，s 与n 的夹角为θπ-2或θπ+2，又因为)2cos()2cos(sin θπθπθ+=-=，而)2cos()2cos(θπθπ+=-=所以 222222sin pn m CB A Cp Bn Am ++++++=θ （7）特别，若直线L 垂直于平面π，即平行于，其充分必要条件是pC n B m A == 若直线L 与平面π垂直，即垂直于，其充分必要条件是 0=++Cp Bn Am图7.39例6 当B A ,为何值时，平面086=+++z By Ax 与直线314321+=-+=+z y x 垂直. 解 平面的法向量为}6,,{B A n =,直线的方向向量为}3,4,2{-=s ,若直线与平面垂直必有3642=-=B A 解得 8,4-==B A例7 求过点)4,2,1(-且与平面0432=--+z y x 垂直的直线方程.解 由于所求直线与平面0432=--+z y x 垂直,所以直线的方向向量s 与向量}1,3,2{-=n 平行,故可取}1,3,2{-==n s ,所求直线的方程为143221--=+=-z y x 总结上两节对平面和直线的讨论可知，建立平面和直线方程的条件是，对于直线只须知道其通过的一个点和它的方向向量，对于平面，只须知道其通过的一个点和它的法向量，建立方程时，若给出的是其它条件，应设法找出一个点并得到直线的方向量，或平面的法向量，求两直线或两平面的夹角都归结为求方向向量或法向量的夹角，它们互相垂直或平行的条件也就是两向量垂直或平行的条件.习题7-81． 求过点)1,2,3(和)3,3,4(的直线方程.2．求过点)3,0,2(-且与直线⎩⎨⎧-=-+=+-1253742z y x z y x 垂直的平面方程.3．求过点)2,1,3(-且通过直线321121-=-+=-z y x 的平面方程. 4．求满足下列条件的直线方程 （1）过点)3,1,4(-且平行于直线5123-==-z y x ;（2）经过点)4,4,3(-，方向角为πππ32,4,3; （3）过)4,2,0(且与两平面23,12=-=+z y z x 平行（4）过点)2,0,1(-且与平面0643=+-+z y x 平行，又与直线才垂直？？？？？？？？？？. 5．试确定下列各组中直线与平面间的关系.（1）3224,37423=--=-+=-+z y x zy x ; （2）8723,723=+-=-=z y x z y x ;（3）3,431232=++--=+=-z y x z y x .6．求直线⎩⎨⎧=+-=+-1239335z y x z y x 与直线⎩⎨⎧=++=-+18832322z y x z y x 的夹角的余弦.7．求点)0,2,1(-在平面012=+-+z y x 上的投影.8．求点)2,1,3(-P 到直线⎩⎨⎧=-+-=+-+04201z y x z y x 的距离.。