四则运算知识点例题练习和巩固提高

小学数学四年级四则混合运算及运算法则知识点整理附练习题文章目录四则运算(一)加法运算定律：1、两个加数交换位置，和不变，这叫做加法交换律。

字母公式：a+b=b+a2、先把前两个数相加，或者先把后两个数相加，和不变，这叫做加法结合律。

字母公式：(a+b) +c=a+(b+c)(二)乘法运算定律：1、交换两个因数的位置，积不变，这叫做乘法交换律。

字母公式：a×b=b×a2、先乘前两个数，或者先乘后两个数，积不变，这叫做乘法结合律。

字母公式：(a×b)×c=a×(b×c)3、两个数的和与一个数相乘，可以先把它们与这个数分别相乘，再相加，这叫做乘法分配律。

用字母公式：(a+b)×c=a×c+b×c或a×(b+c) =a×b+a×c拓展：(a-b)×c=a×c-b×c或a×(b-c) =a×b-a×c(三)减法简便运算：1、一个数连续减去两个数，可以用这个数减去这两个数的和。

用字母表示：a-b-c=a-(b+c)2、一个数连续减去两个数，可以用这个数先减去后一个数再减去前一个数。

用字母表示：a-b-c=a—c-b(四)除法简便运算：1、一个数连续除以两个数，可以用这个数除以这两个数的积。

用字母表示：a÷b÷c=a÷(b×c)2、一个数连续除以两个数，可以用这个数先除以后一个数再除以前一个数。

用字母表示：a÷b÷c=a÷c÷b小学四年级数学“四则运算”知识点详解知识点一：四则运算的概念和运算顺序1、加法、减法、乘法和除法统称四则运算。

2、在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

3、在没有括号的算式里，既有乘、除法又有加、减法的，要先算乘除法，再算加减法。

初一数学上册综合算式专项练习题四则运算在初一数学上册中，四则运算是一个非常重要的基础知识点。

它包括了加法、减法、乘法和除法，是我们进行数学运算的基础。

在本文中，我将为大家提供一些综合算式专项练习题，帮助大家巩固四则运算的知识。

一、加法运算1. 计算下列算式的和：① 23 + 56② 78 + 94③ 102 + 309④ 456 + 789⑤ 248 + 5632. 用竖式计算下列算式的和：① 72 + 38② 275 + 194③ 536 + 427④ 682 + 157⑤ 876 + 394二、减法运算1. 计算下列算式的差：① 102 - 49② 328 - 121③ 497 - 205④ 675 - 312⑤ 828 - 5482. 用竖式计算下列算式的差：① 364 - 82② 527 - 234③ 726 - 317④ 845 - 532⑤ 931 - 654三、乘法运算1. 计算下列算式的积：① 5 × 8② 12 × 15③ 13 × 27④ 24 × 36⑤ 37 × 422. 用竖式计算下列算式的积：① 6 × 17② 23 × 14③ 45 × 28④ 72 × 39⑤ 86 × 53四、除法运算1. 计算下列算式的商，若有余数则写出余数：① 96 ÷ 7② 156 ÷ 9③ 309 ÷ 13④ 547 ÷ 8⑤ 754 ÷ 112. 用竖式计算下列算式的商，若有余数则写出余数：① 176 ÷ 6② 389 ÷ 7③ 528 ÷ 12④ 672 ÷ 8⑤ 941 ÷ 11通过以上的综合算式专项练习题，我们可以更好地巩固和提高自己在四则运算方面的能力。

希望大家认真对待，积极参与练习，相信在不断的努力下，数学成绩一定会有所提高！。

小学六年级数学重点知识归纳分数的四则运算技巧在小学六年级的数学学习中，分数的四则运算是一个重要的知识点。

掌握了分数的四则运算技巧，能够帮助我们更好地解决实际生活中的问题。

本文将对小学六年级数学中分数的四则运算技巧进行归纳总结，以帮助同学们更好地掌握这一知识。

一、分数的加法和减法1. 相同分母的分数相加减法当两个分数的分母相同时，我们只需要将分子相加（或相减），然后保持分母不变即可。

例如：1/3 + 2/3 = 3/3 = 1，1/4 - 1/4 = 0/4 = 0。

2. 不同分母的分数相加减法当两个分数的分母不同时，我们需要找到它们的最小公倍数，并将分数的分子和分母按照最小公倍数进行等比扩大或缩小，使得两个分数的分母相同，然后再进行相加（或相减）。

例如：1/2 + 1/3 = 3/6 + 2/6 = 5/6，1/3 - 1/4 = 4/12 - 3/12 = 1/12。

二、分数的乘法和除法1. 分数的乘法两个分数相乘时，我们将两个分数的分子相乘作为新分数的分子，分母相乘作为新分数的分母即可。

例如：1/2 * 2/3 = (1 * 2)/(2 * 3) = 2/6 = 1/3。

2. 分数的除法两个分数相除时，我们将第一个分数的分子乘以第二个分数的倒数，即将除法转化为乘法，然后按照乘法的规则进行计算。

例如：1/2 ÷ 3/4 = 1/2 * 4/3 = (1 * 4)/(2 * 3) = 4/6 = 2/3。

三、分数的混合运算在实际问题中，我们经常会遇到分数的混合运算。

处理混合运算时，我们需要先按照规定的优先级进行运算，可以使用括号来改变运算的次序。

例如：2/3 + 1/4 * 3 = 2/3 + 3/4 * 1 = 2/3 + 3/4 = (2 * 4 + 3 * 3)/(3 * 4)= 17/12。

四、练习与应用为了更好地掌握分数的四则运算技巧，同学们可以多进行练习和应用。

可以通过解题来巩固所学的知识，例如：例题1：计算 3/8 + 2/5。

小学数学四则运算实例解析数学是一门基础学科，对于小学生来说，掌握好四则运算是建立数学基础的关键。

四则运算包括加法、减法、乘法和除法，它们在日常生活中无处不在，不仅可以锻炼孩子的运算能力，还可以培养孩子的逻辑思维和解决问题的能力。

本文将通过一些实例解析小学数学四则运算。

一、加法加法是最简单的一种四则运算，它是指将两个或多个数相加，求出它们的和。

下面以实例进行解析。

例题1：小明有5个苹果，小红有3个苹果，他们一起有多少个苹果？解析：根据题目所给的信息，我们知道小明有5个苹果，小红有3个苹果。

那么他们一起有多少个苹果呢？我们可以用加法来计算，5+3=8。

答案是8个苹果。

例题2：小青在上午买了2本书，下午又买了3本书，她一共买了多少本书？解析：根据题目所给的信息，小青上午买了2本书，下午又买了3本书。

那么她一共买了多少本书呢？我们可以用加法来计算，2+3=5。

答案是5本书。

二、减法减法是指从一个数中减去另一个数，求出它们的差。

下面以实例进行解析。

例题1：小明有8个橙子，他吃掉了3个橙子，还剩下多少个橙子？解析：根据题目所给的信息，小明有8个橙子，他吃掉了3个橙子。

那么他还剩下多少个橙子呢？我们可以用减法来计算，8-3=5。

答案是5个橙子。

例题2：小红有10支铅笔，她送给了小明5支铅笔，她还剩下多少支铅笔？解析：根据题目所给的信息，小红有10支铅笔，她送给了小明5支铅笔。

那么她还剩下多少支铅笔呢？我们可以用减法来计算，10-5=5。

答案是5支铅笔。

三、乘法乘法是指将一个数按另一个数的倍数进行重复相加，求出它们的积。

下面以实例进行解析。

例题1：小明有3个苹果，他想把这些苹果平均分给他的2个朋友，每个人分得多少个苹果？解析：根据题目所给的信息，小明有3个苹果，他想把这些苹果平均分给他的2个朋友。

那么每个人分得多少个苹果呢？我们可以用乘法来计算，3÷2=1.5。

答案是每个人分得1.5个苹果。

例题2：小刚每天早上都会跑步练习，他每天跑3圈操场，每圈长200米。

四则混合运算练习题及答案四则混合运算练习题及答案数学是一门重要的学科，它不仅能培养我们的逻辑思维能力，还能提高我们的解决问题的能力。

而在数学中，四则混合运算是我们学习的重点之一。

通过练习四则混合运算，我们可以巩固基本的数学运算能力，提高我们的数学水平。

下面，我将给大家提供一些四则混合运算的练习题及答案，希望对大家的学习有所帮助。

1. 小明买了一本数学书，花费了35元，他还买了一本英语书，花费了45元。

请问他一共花费了多少钱？解答：小明花费了35元买数学书，45元买英语书，所以他一共花费了35 + 45 = 80元。

2. 某商店举办打折活动，原价100元的商品打8折，原价80元的商品打9折。

小明买了一件100元的商品和一件80元的商品，请问他一共花费了多少钱？解答：小明买了一件100元的商品打8折，折后价格为100 × 0.8 = 80元；他买了一件80元的商品打9折，折后价格为80 × 0.9 = 72元。

所以他一共花费了80 + 72 = 152元。

3. 小红去超市买水果，她买了3斤苹果，每斤5元，买了2斤橙子，每斤4元。

请问她一共花费了多少钱？解答：小红买了3斤苹果，每斤5元，所以苹果的总价格为3 × 5 = 15元；她买了2斤橙子，每斤4元，所以橙子的总价格为2 × 4 = 8元。

所以她一共花费了15 + 8 = 23元。

4. 一辆汽车以每小时60公里的速度行驶，行驶了4小时，那么它行驶的总距离是多少公里？解答：汽车以每小时60公里的速度行驶，行驶了4小时，所以它行驶的总距离为60 × 4 = 240公里。

通过以上的练习题，我们可以发现四则混合运算并不复杂，只需要将问题中的信息提取出来，然后根据运算规则进行计算即可。

在解答问题时，我们要注意单位的转换，确保计算结果的准确性。

除了以上的练习题，我们还可以通过编写自己的练习题来巩固四则混合运算的知识。

人教版小学六年级知识点巩固练习在小学六年级的学习过程中，各学科的知识点考察非常重要。

知识点的巩固练习可以帮助学生巩固所学的知识，提高学习效果。

本文将从数学、语文和英语三个学科的角度，介绍一些适用于小学六年级的知识点巩固练习方法。

一、数学知识点巩固练习1.基础四则运算训练四则运算是数学学习的基础，对于小学六年级学生来说尤为重要。

可以设计一些口算题和应用题，帮助学生熟练掌握加减乘除的运算技巧。

2.数列和函数关系练习数列和函数是六年级数学中的重要内容，学生应该能够识别和运用数列以及函数之间的关系。

可以设计一些数列填空和函数运算的题目，帮助学生进一步理解和巩固相关知识。

3.几何图形的认识和计算几何图形是小学六年级数学中的另一重要内容。

学生应该能够识别和计算各种几何图形的面积、周长和体积等属性。

可以设计一些应用题目，帮助学生巩固几何图形的相关知识。

二、语文知识点巩固练习1.词语的辨析和填空语文中有很多词语非常相近，学生需要通过训练熟练掌握它们的区别和正确使用。

可以设计一些词语辨析和填空题目，帮助学生提高词语的认识和运用能力。

2.语法知识的巩固训练语法是语文学习中的重要组成部分，学生应该熟悉和掌握各种句型和语法规则。

可以设计一些句子改写和语法填空的题目，帮助学生加深对语法知识的理解和记忆。

3.阅读理解和写作训练阅读理解和写作是语文学习中的关键能力，学生应该通过练习提高自己的阅读和写作水平。

可以设计一些阅读题目和写作任务，帮助学生培养自己的阅读理解和写作能力。

三、英语知识点巩固练习1.单词的记忆和拼写训练英语单词是英语学习的基础，学生应该能够熟记和正确拼写常用的单词。

可以设计一些单词的记忆和拼写题目，帮助学生巩固单词的认识和拼写能力。

2.语法知识的巩固训练英语语法是英语学习的重要组成部分，学生应该熟悉和掌握各种语法规则和句型。

可以设计一些语法填空和句子改写的题目，帮助学生加深对语法知识的理解和记忆。

3.阅读理解和口语训练英语阅读和口语表达是英语学习中的关键能力，学生应该通过练习提高自己的阅读和口语水平。

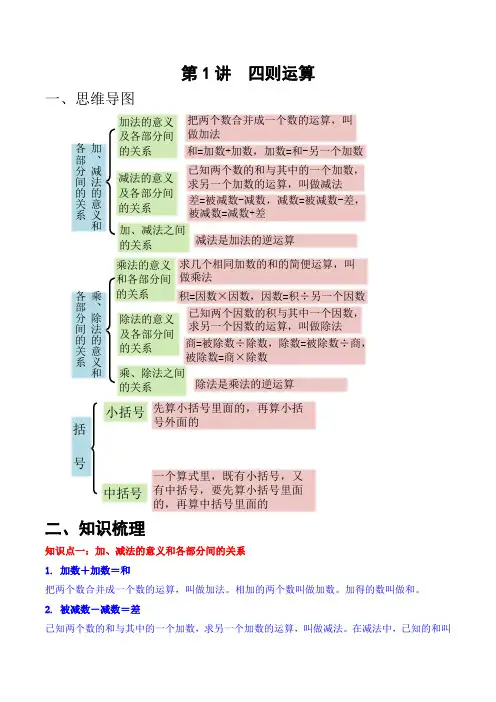
第1讲 四则运算一、思维导图加法的意义及各部分间的关系把两个数合并成一个数的运算，叫做加法减法的意义及各部分间的关系加、减法之间的关系减法是加法的逆运算已知两个数的和与其中的一个加数，求另一个加数的运算，叫做减法加、减法的意义和各部分间的关系和=加数+加数，加数=和-另一个加数差=被减数-减数，减数=被减数-差，被减数=减数+差乘法的意义和各部分间的关系求几个相同加数的和的简便运算，叫做乘法除法的意义及各部分间的关系乘、除法之间的关系除法是乘法的逆运算已知两个因数的积与其中一个因数，求另一个因数的运算，叫做除法乘、除法的意义和各部分间的关系积=因数×因数，因数=积÷另一个因数商=被除数÷除数，除数=被除数÷商，被除数=商×除数先算小括号里面的，再算小括号外面的 括号一个算式里，既有小括号，又有中括号，要先算小括号里面的，再算中括号里面的小括号中括号 二、知识梳理知识点一：加、减法的意义和各部分间的关系1. 加数＋加数＝和把两个数合并成一个数的运算，叫做加法。

相加的两个数叫做加数。

加得的数叫做和。

2. 被减数－减数＝差已知两个数的和与其中的一个加数，求另一个加数的运算，叫做减法。

在减法中，已知的和叫做被减数。

减法是加法的逆运算。

3. 各部分间的关系（1）加法各部分间的关系：和＝加数＋加数；加数＝和－另一个加数。

（2）减法各部分间的关系：差＝被减数－减数；减数＝被减数－差；被减数＝减数＋差。

知识点二：乘、除法的意义和各部分间的关系1.求几个相同加数的和的简便运算，叫做乘法。

积=因数×因数2.除法是已知两个因数的积和其中的一个因数求另一个因数的运算。

因数=积÷另一个因数3.除法是乘法的逆运算。

商=被除数÷除数，除数=被除数÷商，被除数=商×除数知识点三：括号算式中有小括号时，要先算小括号里面的。

知识点四：解决租船问题的策略先计算哪种船的租金便宜，就考虑先租这种船，如果船没坐满，就再进行调整，考虑租另一种船。

四则运算(一)一、知识点总结1.含义：加法、减法、乘法和除法统称四则运算。

2.同级运算顺序：在没有括号的算式里，如果只有加、减法或者只有乘、除法，都要从左往右按顺序计算。

3.混合运算顺序：在没有括号的算式里，有乘、除法和加、减法、要先算乘除法，再算加减法。

4.括号的运算顺序：要先算括号里面的，再算括号外面的；括号里面的算式计算顺序遵循以上的计算顺序。

5.关于“0”的运算（1）“0”不能做除数；字母表示：a÷0错误（2）一个数加上0还得原数；字母表示：a＋0=a（3）一个数减去0还得原数；字母表示：a－0=a（4）、被减数等于减数，差是0；字母表示：a－a=0（5）一个数和0相乘，仍得0；字母表示：a×0=0（6）0除以任何非0的数，还得0；字母表示：0÷a（a≠0）=0（7）0÷0得不到固定的商;5÷0得不到商.二、对应例题与练习1.四则运算的想法定义的法则。

例1.在一个算式里，如果只有加减法，要（）计算，如果只有乘除法，要（）计算。

考点分析：考察定义和法则。

要求：熟练掌握四则运算的相关定义和运算法则。

练习：1.在一个算式里，如果含有加、减、乘、除四种运算，要先算（），再算（）。

2.在一个算式里如果含有小括号，要先算（）。

2.同级运算法则和顺序例2.计算. 91+76-16＝ 95-38+12=28÷7×4= 11×5÷5=考点：同级运算的顺序要求：熟练掌握同级运算顺序：从左往右依次进行。

练习：脱式计算：49+56-38 132-56+18 1000÷20×5999÷9×113.混合运算顺序和法则：例3.计算：420+80÷2＝ 175－25÷5＝考点：混合运算的法要求：熟练掌握混合运算的法则：没有括号时，有乘除和加减运算时，先乘除后加减。

练习：脱式计算：91÷7+33 420－60÷4 530＋54×4÷24168－48×16÷32 420＋80×154.有括号的运算例4.计算。

第一部分：知识点总结（巩固与拓展）知识点一 0的运算（默写）1、“0”不能做除数；字母表示：a÷0错误2、一个数加上0还得原数；字母表示：a＋0= a3、一个数减去0还得原数；字母表示：a－0= a4、被减数等于减数，差是0；字母表示：a－a = 04、一个数和0相乘，仍得0；字母表示：a×0= 05、0除以任何非0的数，还得0；字母表示：0÷a（a≠0）= 0 知识点二运算定律（默写）1、加法交换律：a＋b＝b＋a2、加法结合律：(a＋b) ＋c＝a＋(b＋c)3、乘法交换律：a×b＝b×a4、乘法结合律：(a×b)×c＝a×(b×c)5、乘法分配律：(a＋b)×c＝a×c＋b×c 或 a×(b＋c)＝a×b＋a ×c拓展：(a－b)×c＝a×c－b×c 或 a×(b－c) ＝a×b－a×c6、连减：a—b—c＝a—(b＋c)7、连除： a÷b÷c＝a÷(b×c)一、常见乘法计算：25×4＝100 125×8＝1000二、加法交换律简算例子：三、加法结合律简算例子：50+98+50 488+40+60＝100+98 ＝488+100＝198 ＝588四、乘法交换律简算例子：五、乘法结合律简算例子：25×56×4 99×125×8＝25×4×56 ＝99×（125×8）＝100×56 ＝99×1000＝5600 ＝99000六、含有加法交换律与结合律的简便计算：65+28+35+72＝（65+35）+（28+72）＝100+100＝200七、含有乘法交换律与结合律的简便计算：25×125×4×8＝（25×4）×（125×8）＝100×1000＝100000知识点三简便计算二（默写或自己举例子）乘法分配律简算例子：一、分解式二、合并式25×（40+4） 135×12—135×2＝1000+100 ＝135×10＝1100 ＝1350三、特殊1 四、特殊299×256+256 45×102＝99×256+256×1 ＝45×（100+2）＝256×（99+1）＝45×100+45×2 ＝256×100 =4500+90＝25600 =4590五、特殊3 六、特殊499×26 35×8+35×6—4×35＝（100—1）×26 ＝35×（8+6—4）＝100×26—1×26 ＝35×10＝2600—26 ＝350＝2574知识点四简便计算三（默写或自己举例子）一、连续减法简便运算例子：528—65—35 528—89—128 528—（150+128）=528—（65+35） =528—128—89 =528—128—150 =528—100 =400—89 =400—150=428 =311 =250二、连续除法简便运算例子：3200÷25÷4=3200÷（25×4）=3200÷100=32三、其它简便运算例子：256—58+44 250÷8×4=256+44—58 =250×4÷8=300—58 =1000÷8=242 =125第二部分：混合运算1.用你喜欢的方法计算①4.7+7.69+5.3+2.31 ②53.78-13.6-37.4+6.22 ③57×101 - 57④ (520 + 480)÷50×4⑤400-（1300÷65+35）⑥ 60-（21.5-8.8）+7.32.计算下面各题，能简算的要简算。

数的运算知识要点1、四则运算的意义和法则12、四则运算的法则（1）加、减法整数、小数加减法：相同数位上的数对齐（小数点对齐），从低位算起，哪一位上的数相加满十（哪一位上的数不够减），向前一位进一（从前一位退一，当十再减）。

分数加减法：同分母分数相加减，用分子相加减，分母不变；异分母分数相加减，先通分，然后按照同分母分数加减法则进行计算。

（2）乘法整数乘法：先用一个因数每一位上的数分别去乘另一个因数。

用因数哪一位上的数去乘，乘得的数的末尾就要和哪一位对齐，再把几次乘得的数加起来。

小数乘法：先按照整数乘法的法则计算出积，再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

分数乘法：用分子相乘的积作分子，分母相乘的积作分母，计算过程中能约分的先要约分。

（3）除法整数除法：除数有几位，就看被除数的前几位，不够除就多看一位，除到被除数的哪一位，商就写在哪一位数上面，每次除后余下的数必须比除数小。

小数除法：先移动除数的小数点，使它变成整数；除数的小数点向右移动几位，被除数的小数点也要向右移动几位（位数不够时，在被除数的末尾用“0”补足），然后按照除数是整数的除法进行计算。

分数除法：甲数除以乙数（0除外），等于甲数乘乙数的倒数。

（4）各部分之间的关系①加、减法加数＋加数=和一个加数=和-另一个加数减数=被减数-差减数－减数=差被减数=差+减数②乘、除法因数×因数=积一个因数=积÷另一个因数被除数=商×除数被除数÷除数=商除数=被除数÷商23、四则混合运算1、四则混合运算的顺序在没有括号的算式里，如果只含有同一级运算，要按照从左到右的顺序计算；如果含有两级运算，要先算第二级运算，再算第一级运算。

在有括号的算式里，要先算小括号里面的，再算中括号里面的。

2、几种常用的简算方法（1）拆项法：这是对分配律的逆向运用，常用的方法是分数拆项，主要有以下几种形式：①分子、分母分别为两个相邻自然数的和与积时： n+(n+1)nx(n+1) =1n +1n+1②分母为两个相邻自然数的积时：1n(n+1) =1n -1n+1③分母是差为a(a ≠0)的两个自然数的积时：1n(n+a) =(1n -1n+a )×1a④分母为三个相邻自然数的积时：1n(n+1)(n+2) =12 【1n(n+1) -1(n+1)(n+2)】 （2）数字变形法：这是一种从数字特点出发，创新变形，巧妙地运用运算性质，规律达到简算目的的方法，如：19971998 较接近1，可将其转化为（1-11998），然后根据情况运用适当的方法。

小数四则运算综合知识点及例题一、运算定律 ⑴加法交换律：a b b a +=+的等比数列求和⑵加法结合律：()()a b c a b c ++=++⑶乘法交换律：a b b a ⨯=⨯⑷乘法结合律：()()a b c a b c ⨯⨯=⨯⨯⑸乘法分配律：()a b c a b a c ⨯+=⨯+⨯（反过来就是提取公因数） ⑹减法的性质：()a b c a b c --=-+⑺除法的性质：()a b c a b c ÷⨯=÷÷()a b c a c b c +÷=÷+÷()a b c a c b c -÷=÷-÷上面的这些运算律，既可以从左到右顺着用，又可以从右到左逆着用．二、要注意添括号或者去括号对运算符号的影响⑴在“+”号后面添括号或者去括号，括号内的“+”、“-”号 都不变；⑵在“-”号后面添括号或者去括号，括号内的“+”、“-”号都 改变，其中“+”号变成“-”号，“-”号变成“+”号；⑶在“⨯”号后面添括号或者去括号，括号内的“⨯”、“÷”号都 不变，但此时括号内不能有加减运算，只能有乘除运算；⑷在“÷”号后面添括号或者去括号，括号内的“⨯”、“÷”号 都改变，其中“⨯”号变成“÷”号，“÷”号变成“⨯”号， 但此时括号内不能有加减运算，只能有乘除运算．例一计算：1999 3.14199.931.419.99314⨯+⨯+⨯．解析：使用四则混合运算之提取公因数原式1999 3.143=⨯⨯200019.4218830.58=-⨯=（） 答案：18830.58例二计算：....⨯+⨯=103734171926 .解析：使用四则混合运算之提取公因数10.37 3.4 1.719.26⨯+⨯()10.37 3.4 3.49.6310.379.63 3.420 3.468=⨯+⨯=+⨯=⨯=答案：68例三计算：2.009×43+20.09×2.9+200.9×0.28= .原式20.09 4.320.09 2.920.09 2.8=⨯+⨯+⨯20.09(4.3 2.9 2.8)200.9=⨯++= 答案：200.9例四计算：200.920.08200.820.07⨯-⨯解析：使用四则混合运算之提取公因数原式200.920.0820.08200.7=⨯-⨯20.08(200.9200.7)=⨯-20.080.2=⨯4.016=答案：4.016例五计算：199.919.98199.819.97⨯-⨯解析1：使用原式199.919.9819.98199.7=⨯-⨯19.98(199.9199.7)=⨯-19.980.2=⨯3.996=解析2：使用凑整法来解决．原式(2000.1)19.98(2000.2)19.97=-⨯--⨯20019.980.119.9820019.970.219.97=⨯-⨯-⨯+⨯2 1.996=+3.996=答案：3.996例七计算：20.0931.5 2.009317200.9 3.68⨯+⨯+⨯= .解析：使用四则混合运算之提取公因数原式 2.009315 2.009317 2.009368=⨯+⨯+⨯()2.009315317368=⨯++2.00910002009=⨯=答案：2009例七计算：6.258.2716 3.750.8278⨯⨯+⨯⨯解析：使用四则混合运算之提取公因数原式 6.25168.27 3.750.88.27=⨯⨯+⨯⨯8.27(6.2516 3.750.8)=⨯⨯+⨯8.27(1003)=⨯+8.271008.273=⨯+⨯851.81=答案：851.81例八计算：20.0962200.9 3.97 2.87⨯+⨯-⨯= ．原式20.096220.093920.09=⨯+⨯-()20.0962391=⨯+-20.091002009=⨯=答案：2009例九计算：2.8947 1.53 1.4 1.1240.112880.530.1=⨯+-⨯+⨯+⨯- ．解析：使用四则混合运算之提取公因数原式=2.88×（0.47+0.53）+0.47+1.53+（24-14）×0.11-0.1=288+2+1=291答案：291例十计算：2237.522.312.523040.7 2.51⨯+⨯+÷-⨯+＝ ．解析：使用四则混合运算之提取公因数原式2237.5223 1.252300.2570.251=⨯+⨯+⨯-⨯+2238.752230.251223912008=⨯+⨯+=⨯+= 答案：2008例十一计算：19.9837199.8 2.39.9980⨯+⨯+⨯解析：使用四则混合运算之提取公因数原式19.983719.982319.9840=⨯+⨯+⨯19.983723401998=⨯++=（） 答案：1998例十二计算：3790.000381590.00621 3.790.121⨯+⨯+⨯解析：使用四则混合运算之提取公因数原式 3.790.0381590.00621 3.790.121=⨯+⨯+⨯3.790.0380.1210.159 6.21=⨯++⨯（）3.790.1590.159 6.210.159 3.79 6.210.15910 1.59=⨯+⨯=⨯+=⨯=（）答案：1.59例十三计算78.16 1.45 3.1421.841690.7816⨯+⨯+⨯解析：使用四则混合运算之提取公因数，不难看出式子中7816出现过两次：78.16和0.7816，由此可以联想到提取公因数原式78.16 1.45 3.1421.84 1.6978.16=⨯+⨯+⨯78.16=⨯(1.45 1.69+) 3.1421.84+⨯78.16 3.14 3.1421.84 3.14100314=⨯+⨯=⨯=答案：314例十四计算：7.816×1.45+3.14×2.184+1.69×7.816=_____。

四下运算律提高题
四则运算是我们学习数学时最基础、最重要的内容之一。

而掌握四则运算律是进行数学计算的基础。

在日常生活和学习中，我们经常需要进行各种四则运算，因此提高四则运算的能力非常重要。

下面我们来看一些提高四则运算能力的题目。

1. 计算：(25 - 9) × 3 ÷ 6 + 4。

解：首先计算括号内的运算，得到16；然后乘法和除法优先级高于加法，计算得到8；最后加法运算，答案为12。

2. 计算：72 ÷ (9 - 4) × 2 + 5。

解：首先计算括号内的运算，得到5；然后乘法和除法优先级高于加法，计算得到20；最后加法运算，答案为25。

3. 计算：8 × (6 - 3) ÷ 2 + 7。

解：首先计算括号内的运算，得到3；然后乘法和除法优先级高于加法，计算得到12；最后加法运算，答案为19。

4. 计算：(14 + 3) × 2 - 5 ÷ 5。

解：首先计算括号内的运算，得到17；然后乘法和除法优先级高于减法，计算得到34；最后减法运算，答案为33。

通过这些题目，我们可以锻炼自己的四则运算能力，掌握四则运算律，提高计算的准确性和速度。

四则运算是数学学习的基础，只有掌握了四则运算，才能更好地学习更高级的数学知识。

希望大家能够认真练习，提高自己的数学能力，更好地应对学习和生活中的各种挑战。

一、选择题1. 下面说法错误的是（）。

A．。

B．两个完成一样的梯形一定可以拼成一个平行四边形。

C．2台同样的抽水机，3小时可以浇地1.8公顷。

照这样计算，一台抽水机每小时可浇地0.3公顷。

2. 赵老师为五（1）班全班同学买笔记本，总共花了478.8元，每本笔记本3.8元，正好每人分3本。

五（1）班共有多少人？列式不正确的是（）。

A．B．C．3. 农场2台同样的抽水机3小时共浇地1.2公顷。

照这样计算，要求“一台抽水机每小时可以浇多少公顷”，下面算式错误的是（）。

A．1.2÷3÷2 B．1.2÷（3×2）C．1.2÷2÷3 D．1.2÷（3＋2）4. 一个修路队有5个人5天共修了252.5米的公路，平均每人每天修（）米的公路。

A．50 B．50.5 C．10.1 D．205. 小马虎在计算一个数除以4.05计算成乘4.05，得到的得数是360.855，这道题的正确答案是（）。

A．4.05 B．89.1 C．22二、口算和估算6. 直接写得数。

0.6×0.9＝6÷0.6＝7.8÷0.3＝50×0.02＝8.1÷10＝ 6.4÷0.08＝ 0.075×100÷10＝ 12÷2.5÷4＝三、填空题7. 乐乐在数学考试时，不小心把一个数除以4.75计算成乘4.75，结果是406.125。

这道题的正确答案应是( )。

8. 2.5千克大豆可榨0.6千克油，照这样计算，榨30千克油，需要大豆( )千克。

如果每个油桶可以装4.5千克油，装榨出的30千克油需准备( )个油桶。

9. 在括号里填“＞”“＜”或“＝”。

5.42＋2.28( )10－4.55 ( )1.3＋1.2÷0.254.8÷1.5( )4.8×1.5 0.72÷0.4÷0.2( )10. 小刚在计算一个数除以3.5时，结果将除号看成乘号，计算出的结果是14.7，那么正确的结果是( )。

六年级四则混合运算练习题六年级四则混合运算练习题数学是一门需要不断练习和巩固的学科，而四则混合运算是数学中的基础。

在六年级，学生们已经掌握了基本的加减乘除运算，接下来就是要通过练习题来巩固和提高他们的能力。

下面是一些六年级四则混合运算练习题，希望能够帮助学生们更好地理解和掌握这一知识点。

题目一：计算下列算式的结果1. 45 + 32 - 18 =2. 64 ÷ 8 × 2 =3. 15 × 4 ÷ 5 =4. 78 - 23 + 11 =解析：这些题目涵盖了加法、减法、乘法和除法四种运算。

学生们需要按照运算法则，先计算乘法和除法，再计算加法和减法。

例如，在第一题中，先计算45 + 32得到77，再减去18得到结果59。

题目二：填入适当的符号1. 8 __ 5 + 7 = 202. 12 ÷ 3 __ 4 = 13. 15 × 2 __ 8 = 224. 45 - 20 __ 10 = 15解析：这些题目考察了学生们对于不同运算符号的理解和运用。

学生们需要根据等式的意思，选择合适的运算符号填入空白处。

例如，在第一题中，由于8乘以5再加上7等于47，所以需要填入加号。

题目三：解决实际问题1. 小明有20块钱，他花掉了8块钱买了一本书，然后又花掉了3块钱买了一支笔。

请问他还剩下多少钱？2. 一辆汽车以每小时60公里的速度行驶，行驶了3小时后停下来休息，然后以每小时80公里的速度行驶2小时。

请问这辆汽车行驶的总路程是多少公里？解析：这些题目通过实际生活中的情境，让学生们将数学知识应用到实际问题中。

学生们需要将问题转化为数学表达式，并计算出结果。

例如，在第一题中，小明花掉了8块钱买书，再花掉了3块钱买笔，所以他还剩下20 - 8 - 3 = 9块钱。

通过这些练习题，学生们可以巩固和提高他们的四则混合运算能力。

同时，这些题目也帮助他们培养逻辑思维和解决实际问题的能力。

小升初数学四则运算：4大知识点7条定律
11道例题，收藏！
四则运算是数学最基本的运算，主要是加、减、乘、除四种运算。

在解决实际问题中我们还会用到一些运算规则，比如加法结合律、加法交换律、乘法分配率等多种运算定律。

四则运算是同学们学习数学的基础，小学阶段主要是学习简单的四则运算的概念和顺序。

很多小学生的数学不好主要就是四则运算学的不扎实，所以在考试的时候计算总会出问题，特别是稍微复杂一点的题型，孩子根本就无从下手了。

今天小编就大家带来了小学数学四则运算的详细知识点讲解，方便家长们辅导孩子！
小学的期末考试基本上已经结束了，家长们可以把这份资料收藏好，寒假的时候让孩子好好看看，巩固一下，特别是交换律与结合律都含有的题型！
中小学生记忆力不好，在学习中缺乏学习方法，单词记不住，学习效率不高。

家长可关注我。

微信：895375990（长按可复制），一起交流讨论学习方法！
本文为头条号作者发布，不代表今日头条立场。

百度搜索“就爱阅读”,专业资料,生活学习,尽在就爱阅读网,您的在线图书馆!。