当前位置：文档之家 › 第三讲 参数估计 (1)

第三讲 参数估计 (1)

  • 格式：pdf
  • 大小：4.05 MB
  • 文档页数：104

下载文档原格式

  / 104

合集下载

第三章参数估计

第三章参数估计

第三章 参数估计参数估计是推断统计研究的内容之一。

所谓参数估计就是根据样本统计量的数值对总体参数进行估计的过程。

在参数估计中，要涉及概率分布、样本统计值、总体参数以及抽样分布等有关概念，这些概念及理论构成了推断统计的基础。

第一节 参数估计的原理一、点估计与区间估计的概念在进行参数估计时，通常有两种方法：一种是点估计，一种是区间估计。

所谓点估计就是用样本统计量的某一具体数值直接推断未知的总体参数。

例如，在进行有关小学生身高的研究中，随机抽取1000名小学生并计算出他们的平均身高为1.45m 。

如果直接用这个1.45m 代表所有小学生的平均身高，那么这种估计方法就是点估计。

所谓区间估计，就是在推断总体参数时，还要根据统计量的抽样分布的特征，估计出总体参数的一个区间，而不是一个数值，并同时给出总体参数落在这一区间的可能性的大小——概率的保证。

在上例中，如果是按区间估计的方法推断小学生的平均身高，则会给出以下的表达：根据样本数据，估计小学生的平均身高在1.4～1.5m 之间，可靠程度为95%，这种估计就属于一个区间估计。

对总体参数进行点估计有一个不足之处，即这种估计方法不能提供参数的估计误差的大小。

对于一个总体来说，它的总体参数是一个常数值，而它的样本统计量却是一个随机变量。

当用一个随机变量去估计一个常数值时，误差是不可避免的，只用一个样本数值去估计总体参数是要冒很大风险的，因为这种误差风险的存在，并且风险的大小还未知，所以，点估计主要为许多定性研究提供一定的参考数据，或是对总体参数要求不精确时使用，而在需要精确总体参数的数据进行决策时则很少使用。

二、点估计—最小二乘法原理对总体参数进行点估计常用的方法有三种：矩估计法、最小二乘法和最大似然估计法。

这里主要介绍最小二乘法原理。

最小二乘法是参数估计常用的方法之一。

其基本思想是保证由新估参数得到的理论值与观测值间离差的平方和值为最小。

要想使离差平方和Q 为最小，可通过求Q 对待估参数的偏导数，并令其等于0，以求得参数估计值。

高考数学知识点解析参数估计的方法与性质

高考数学知识点解析参数估计的方法与性质

高考数学知识点解析参数估计的方法与性质高考数学知识点解析：参数估计的方法与性质在高考数学中，参数估计是一个重要的知识点，它在统计学和概率论中有着广泛的应用。

理解和掌握参数估计的方法与性质，对于解决相关的数学问题以及在实际生活中的数据分析都具有重要意义。

一、参数估计的基本概念参数估计是指从样本数据中估计总体参数的值。

总体参数是描述总体特征的数值，例如总体均值、总体方差等。

而样本则是从总体中抽取的一部分数据。

通过对样本数据的分析和处理，我们试图推测出总体参数的大致范围或准确值。

二、参数估计的方法1、点估计点估计是用一个具体的数值来估计总体参数。

常见的点估计方法有矩估计法和最大似然估计法。

（1）矩估计法矩估计法的基本思想是利用样本矩来估计总体矩，从而得到总体参数的估计值。

例如，对于总体均值的估计，可以用样本均值来代替；对于总体方差的估计，可以用样本方差来代替。

（2）最大似然估计法最大似然估计法是基于样本出现的概率最大的原则来估计参数。

假设总体服从某种分布，通过求解使得样本出现概率最大的参数值，即为最大似然估计值。

2、区间估计区间估计则是给出一个区间，认为总体参数落在这个区间内的可能性较大。

这个区间被称为置信区间，而与之对应的概率称为置信水平。

三、参数估计的性质1、无偏性如果一个估计量的期望值等于被估计的参数，那么这个估计量就是无偏估计量。

无偏性意味着在多次重复抽样和估计的过程中，估计量的平均值会趋近于真实参数值。

2、有效性在多个无偏估计量中，方差越小的估计量越有效。

有效性反映了估计量的精度，方差小表示估计值的波动较小，更接近真实值。

3、一致性当样本容量无限增大时，如果估计量的值越来越接近被估计的参数，那么这个估计量就是一致估计量。

一致性保证了在样本量足够大时，估计量能够准确地反映总体参数。

四、参数估计在实际问题中的应用1、质量控制在生产过程中，通过对样本产品的检测和参数估计，可以推断出整批产品的质量情况，从而决定是否需要调整生产流程。

3参数估计

3参数估计

65% 9.35%
55.65%,74.35%
故该城市下岗职工中女性比例的置信区间为55.65%～74.35%
24
3.3.5区间估计的SPSS应用
正态分布的区间估计
Analyze→Descriptive Statistics→Explore→Statistics
输出均数、中位数、众数、标准误、方差等
0
有，lim n
P(|
ˆn
| )
0
5
有效性
设 ˆ1 ˆ1(X1,..., X n )和 ˆ2 ˆ2 (X1,..., X n ) 都是参数的无偏估计
量，若对任意 ，D(ˆ1) D(ˆ2 ) ，且至少对于某个
上式中的不等号成立，则称 ˆ1 较 ˆ2 有效
注意：
无偏性、有效性、一致性之间并没有必然的联系。如无偏的未必 有效
某城市想要估计下岗职工中女性所占的比例，随机抽取了100个 下岗职工，其中65人为女性职工。试以95%的置信水平估计该城 市下岗职工中女性比例的置信区间。
解：已知n=100，p＝65%，1- =95%， 2 =1.96
p z 2
p(1 p) n
65% 1.96 65%(1 65%) 100
可靠度与精度是一对矛盾，一般是在保证可靠度的条件 下尽可能提高精度
15
3.3.2总体方差σ2已知时，总体均值μ的估计
X ~ N , 2 ，x1, x2,, xn为来自总体的样本
样本均值 x 服从数学期望为μ、方差为 2/n的正态分布，
x ~ N , 2 n
当 2已知时
U x ~ N 0,1
最大似然的思想
选择适当的 ˆ，使 L( ) 取得最大值，即
L(x1, x2, , xn,ˆ) max{f(x1,)f(x2,) f(xn,)}
参数估计的基本原理

参数估计的基本原理

参数估计的基本原理参数估计是统计学中的一个重要概念，它是指通过对已知的样本数据进行分析和计算，来估计总体参数的值。

在实际应用中，参数估计是非常常见的，比如在医学研究中，我们希望通过对一部分人群的数据进行分析，来估计整个人群的某种特征。

本文将介绍参数估计的基本原理，包括点估计和区间估计两种方法。

点估计是指通过样本数据来估计总体参数的值。

在点估计中，我们通常会选择一个统计量作为参数的估计值，比如样本均值、样本方差等。

以样本均值作为总体均值的估计值为例，我们可以通过对样本数据进行求和然后除以样本容量来得到样本均值，然后将样本均值作为总体均值的估计值。

值得注意的是，点估计得到的估计值通常是不准确的，因为样本数据只是总体数据的一部分，所以我们需要通过一定的方法来评估估计值的准确性。

区间估计是指通过样本数据来估计总体参数的范围。

在区间估计中，我们会计算出一个区间，这个区间包含了总体参数的真实值的概率。

以置信区间为例，我们可以通过对样本数据进行分析和计算，得到一个区间，这个区间有一定的概率包含了总体参数的真实值。

与点估计相比，区间估计能够提供更多的信息，因为它不仅给出了参数的估计值，还给出了估计值的准确程度。

参数估计的基本原理可以总结为，通过对样本数据进行分析和计算，来估计总体参数的值。

在实际应用中，我们通常会选择点估计或区间估计这两种方法来进行参数估计。

在进行参数估计时，我们需要注意样本数据的代表性和样本容量的大小，以及估计值的准确性和置信水平等因素。

通过合理的参数估计，我们可以更好地理解总体数据的特征，从而为实际问题的解决提供更有力的支持。

综上所述，参数估计是统计学中的重要概念，它通过对样本数据进行分析和计算，来估计总体参数的值。

点估计和区间估计是参数估计的两种基本方法，它们分别给出了参数的估计值和估计范围。

在进行参数估计时，我们需要考虑样本数据的代表性和样本容量的大小，以及估计值的准确性和置信水平等因素。

《统计学》第3章 参数估计

《统计学》第3章 参数估计


【例3.5】假定在一个箱子里放着黑、白两 种球共4只，且知道这两种球的数目之比为 1∶3，但不知道究竟哪一种颜色的球多。
设黑球所占的比例为P，由上述假定推知P仅 可能取1/4和3/4这两个值，现在采用有放 回抽样的方法，从箱子中随机地抽取三个 球，观察到球的颜色为黑、白、黑，你会 对箱子中的黑球数作出什么推断呢？即你 认为P的值是1/4，还是3/4？
或 为似然方程组。
ln L(1 , 2 ,, n ) 0 j
解得。上面方程组称
[注意] 上面的讨论中，我们没有提到似函 数 L( ) 取极大值的充分条件，对于具体的 函数可作验证。
【例3.6】设总体X服从参数为 的泊松分 布，求参数 的极大似然估计量。
解 设 X1，X2，X3，……，Xn 是来自 X 的样 本，
【例5.2】设X1，X2，……，Xn是取自总 体X的样本，已知X的概率密度为：
X 1 , 0 X 1 f ( X , ) 其他 0,
( 1)
试用矩估计法估计总体参数 。 解: 由于 E ( X ) xf ( X , )dx 1 样本均值为 X ，令E（X）= X ，得: X ,
又 ∵
1 1 n n ，即 ( 2 1 ) ( x( n) x(1) )
L(1,2 ) L( x(1) , x(n) )
∴ 1 , 2 的极大似然估计量分别为 x(1) , x(n) 。
三、估计量的优良标准
在对总体参数做出估计时并非所有的估计量 都是优良的，从而产生了评价估计量是否 优良的标准。对于点估计量来说，一个好 的估计量有如下三个标准：
(x
i 1 n
n
i
) 0 )
参数估计的基本理论

参数估计的基本理论

第3章 参数估计的基本理论信号检测：通过准则来判断信号有无；参数估计：由观测量来估计出信号的参数；解决1）用什么方法求取参数，2）如何评价估计质量或者效果严格来讲，这一章研究的是参数的统计估计方法，它是数理统计的一个分支。

推荐两本参考书高等教育出版社《数理统计导论》，《Nonlinear Parameter Estimation 》。

我们首先从一个估计问题入手，来了解参数估计的基本概念。

3.1 估计的基本概念3.1.1 估计问题对于观察值x 是信号s 和噪声n 叠加的情况：()x s n θ=+其中θ是信号s 的参数，或θ就是信号本身。

若能找到一个函数()f x ，利用()12,,N f x x x 可以得到参数θ的估计值 θ，相对估计值 θ，θ称为参数的真值。

则称()12,,N f x x x 为参数θ的一个估计量。

记作 ()12,,Nf x x x θ= 。

在上面的方程中，去掉n 实际上是一个多元方程求解问题。

这时，如果把n 看作是一种干扰或摄动，那么就可以用解确定性方程的方法来得出()f x 。

但是我们要研究的是参数的统计估计方法，所以上面的描述并不适合我们的讨论。

下面给出估计的统计问题描述。

（点估计）设随机变量x 具有某一已知函数形式的概率密度函数，但是该函数依赖于未知参数θ，Ω∈θ ，Ω称为参数空间。

因此可以把x 的概率密度函数表示为一个函数族);(θx p 。

N x x x ,,,21 表示随机样本，其分布取自函数族);(θx p 的某一成员，问题是求统计量 ()12,,Nf x x x θ= ，作为参数θ的一个估计量。

以上就是用统计的语言给出的参数估计问题的描述。

数。

统计量的两个特征：1，随机变量的函数，因此也是随机变量；2，不依赖于未知参数，因此当我们得到随机变量的一组抽样，就可以计算得到统计量的值。

例3-1：考虑由(1,2,,)i ix s n i N =+= ，给定的观测样本。

统计学：3-参数估计

统计学：3-参数估计

8. 置信水平只是告诉我们在多次估计得到的区间中大概 有多少个区间包含了参数的真值，而不是针对所抽取 的这个样本所构建的区间而言的
5 - 14
2008年8月
3.统1 计参学数估计的基本原理
三ST、(A第T三I区S版TI间C) S估计——置信区间的表述 (confidence interval)
点估计值
10. 实际应用中，过宽的区间往往没有实际意义
比如，天气预报说“在一年内会下一场雨”，虽然这很 有把握，但有什么意义呢？另一方面，要求过于准确(过 窄)的区间同样不一定有意义，因为过窄的区间虽然看上 去很准确，但把握性就会降低，除非无限制增加样本量， 而现实中样本量总是有限的
5 - 16
2008年8月
总体分布 样本量
2已知 2未知
正态分布 大样本 n≧30
正态分布 小样本
n˂30 非正态分布 大样本
n≧30
x Z
2
n
x Z
2
n
x Z
2
n
x Z
2
s n
x t (n 1)
2
s n
x Z
2
s n
5 - 19
2008年8月
3.统2 计一学个总体参数的区间估计
STATISTICS (第三版)
3.2 一个总体参数的区间估计
一、 总体均值的区间估计 二、 总体比例的区间估计 三、 总体方差的区间估计
3.统2 计一学个总体参数的区间估计
STATISTICS (第三版)
总体参数 均值 比例 方差
5 - 18
符号表示
2
样本统计量
x p s2
2008年8月
统计学 一个总体均值的区间估计
参 数 估 计

参 数 估 计

8
1.总体平均数的区间估计
用区间估计的方法来估计总体平均数 x ，必须具备三要
素：点估计量即样本平均数、平均数的抽样极限误差Δx 和置信度F(t)。公式如下：
P(x x X x x) F (t) 1
其中
x tx t x
9
1.总体平均数的区间估计
例6.7：从某校全部学生中，随机抽取 100名学生，x 平均体重 =58kg，x 抽样
（2）允许误差（极限误差）Δ，即Δ的数值。 （3）概率度t 。 （4）抽样方法。 （5）抽样的组织方式。
14
（二）必要抽样数目的计算
1．重复抽样条件下平均数的必要抽样数目的确定
因为
x tx
t x
t
n
所以
t 2 2
n x2
15
（二）必要抽样数目的计算
例6.10：某城市组织职工家庭生活抽样 调查，根据历史资料知，职工家庭平均每 户每月收入的标准差为11.50元 ,要求把 握程度为95.45% ,允许误差为1元,问需 抽选多少户?
20
（二）必要抽样数目的计算
例6.12，设某工地有土方工人2000名，拟用不重复抽 样推断，来测定其平均工作量，要求抽样误差不超过0.1 立方米，把握程度为99.73%，已知上次抽样调查所得 的方差为2.25，试求必要抽样数目。
3
一、点估计
(1) 无偏性。如果估计量 的ˆ数学期望值等于总体参数θ， 即E( )=θ，则是θ的ˆ 无偏估计量。
ˆ
(2) 即
有效,性。则如是果2 θ对 的比2*有任ˆ效何估一计个量估。计量
, 有最小方差，
ˆ (3)一致性。如果估计nl量im P[，ˆ 随着样 ]本 1容量n的增大而趋
近于θ，即ˆ 则 是θ的一致估计量。
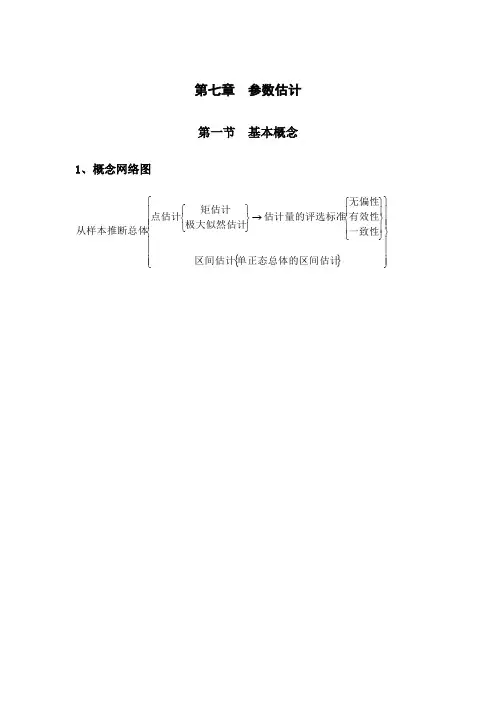
参数估计方法

参数估计方法

第七章 参数估计第一节 基本概念1、概念网络图{}⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧→⎭⎬⎫⎩⎨⎧单正态总体的区间估计区间估计一致性有效性无偏性估计量的评选标准极大似然估计矩估计点估计从样本推断总体2、重要公式和结论例7．1：设总体),(~b a U X ，求对a, b 的矩估计量。

例7．2：设n x x x ,,,,21 是总体的一个样本，试证（1）;2110351321x x x ++=∧μ （2）;12541313212x x x ++=∧μ（3）.12143313213x x x -+=∧μ都是总体均值u 的无偏估计，并比较有效性。

例7．3：设n x x x ,,,,21 是取自总体),(~2σμN X 的样本，试证∑=--=ni i x x n S 122)(11 是2σ的相合估计量。

第二节 重点考核点矩估计和极大似然估计；估计量的优劣；区间估计第三节 常见题型1、矩估计和极大似然估计例7．4：设0),,0(~>θθU X ，求θ的最大似然估计量及矩估计量。

例7．5：设总体X 的密度函数为⎪⎩⎪⎨⎧≥=--.,0,1)(/)(其他μθθμx e x f x其中θ>0, θ,μ为未知参数，n X X X ,,,21 为取自X 的样本。

试求θ,μ的极大似然估计量。

2、估计量的优劣例7．6：设n 个随机变量n x x x ,,,21 独立同分布，,)(11,1,)(122121∑∑==--===n i i n i i x x n S x n x x D σ 则（A ）S 是σ的无偏估计量；（B ）S 是σ的最大似然估计量； （C ）S 是σ的相合估计量；（D ）x S 与2相互独立。

例7．7：设总体X 的密度函数为⎪⎩⎪⎨⎧<<-=,,0,0),(6)(3其他θθθx x xx fn X X X ,,,21 是取自X 的简单随机样本。

（1） 求θ的矩估计量∧θ；（2） 求∧θ的方差D （∧θ）；（3） 讨论∧θ的无偏性和一致性（相合性）。

关于参数估计的几种方法

关于参数估计的几种方法

解上述优化问题可得： 解上述优化问题可得：
a1 是 ( X T X ) −1 ( X T Y )(Y T Y ) −1 (Y T X ) 的最大特征值对应的
特征向量； 特征向量；
b1 是 (Y T Y ) −1 (Y T X )( X T X ) −1 ( X T Y )的最大特征值对应
的特征向量； 的特征向量；
1.表内成分提取 1.表内成分提取——主成分分析 表内成分提取 主成分分析
数据表： 数据表：有P个变量 x1, x 2 , ..., x p ，对它们 个变量 进行n次观测 所构成矩阵即为一数据表。 次观测， 进行 次观测，所构成矩阵即为一数据表。 基本原理：对原数据表中的信息重新组合，提取 基本原理：对原数据表中的信息重新组合， 数据表中的信息重新组合 ），使这 使这m 出m个综合变量 F1 , F 2 , ... F m （m< p），使这 个综合变量 个综合变量能最多的概括原数据表的信息 原数据表的信息。 个综合变量能最多的概括原数据表的信息。 数据集合中的信息指的是集合中数据变异的情况。 数据集合中的信息指的是集合中数据变异的情况。 指的是集合中数据变异的情况 而在一张数据表中，数据集合的变异信息即为全部 而在一张数据表中，数据集合的变异信息即为全部 变量的方差和来表示 来表示。 变量的方差和来表示。
典型相关分析
不能较好的反映2组变 还不能较好的反映 组变
间的相关关系， 个典型成分。 量X与Y间的相关关系，还可以考虑第 、3…个典型成分。 与 间的相关关系 还可以考虑第2、 个典型成分
Fi
对应的典型主轴
ai 是矩阵( X T X )−1 ( X T Y )(Y T Y )−1 (Y T X )
T 1 1
F0 = t r + F1
参数估计的方法

参数估计的方法

参数估计的方法
1 参数估计的概念
参数估计（Parameter Estimation）是指基于样本观测数据，构
建统计模型，用来估计未观测总体参数得出最有效的模型解释参数结
果的过程。

参数估计是统计学里研究重要问题的一个根本步骤，它先
假设一个统计模型，然后求解模型的参数，从而最能满足观测数据的
条件。

2 参数估计的方法
1.参数最大似然估计（Maximum Likelihood Estimation）：最大
似然估计的基础是独立，同分布的随机变量的概率密度函数或概率分
布函数必须可知。

该方法下只需估计一个参数，则把样本数据的似然
函数定义为θ；如果需要估计多个参数，则把样本数据的似然函数定
义为$L(θ)=\prod\limits_i^nf(x_i;θ)$，其中f(x;θ)是关于未知
参数θ 的概率密度函数。

2.方差最小估计（Minimum Variance Estimation）：该方法的基
本思想是选择一种损失函数，把参数估计估计结果误差的.期望最小化，从而得出最优参数估计结果。

3.贝叶斯估计（Bayesian Estimation）：基于先验知识，建模到
后验知识的过程，利用样本信息改进模型参数和变量之间关系的方法。

3 参数估计的作用
参数估计是统计学里研究重要问题的一个根本步骤，它可以帮助我们识别变量之间的相互影响，从而更好的预测未来的发展趋势，决定合适的策略。

在企业战略决策，市场营销，生产服务运筹控制，经济营商模型分析决策管理，投资事前风险分析，社会环境分析等方面都有重要的作用。

概率论与数理统计课件：参数估计


n
n
p( X xi; ) p(xi; ).
i 1
i 1
事实上，它们仅是参数 的函数，称为似然函数，记
为L( ) ，即 L( ) L(x1, x2,
或
n
, xn; ) f (xi; ), i 1
n
L( ) L( X x1, X x2, , X xn; ) p(xi; ). i 1
一个随机变量，其服从 0的泊松分布，即X ~ P()，
其中， 为未知参数. 已知在某小时进入该商场的人数的
样本值见表7.1，试求参数 的点估计值.
表7.1 在某小时进入某商场人数的统计情况
每分钟平均一秒钟进 入该商场的人数 0
1
2
3
4
5
6
7 8
分钟数
6 18 17 9 5 2 2 1 0
参数估计
解：因为X E( 1) ，所以 E( X ) .
由于仅有一个未知参数 ，故仅列一个方程
即可.
1( ) A1
因为1( ) E(X ) 和 A1 X ，所以ˆ X .
参数估计
首页 返回 退出
例7.1.3 设随机变量X在区间[a, b]中均匀取值，即 X U (a,b) ，其中，a 与 b均为未知参数，试求 a与 b的
i 1
i 1
参数估计
首页 返回 退出
(3) 似然函数 L( ) 与经自然对数变换后的函数 ln L( ) 等价，即求L( )的最大值点等价于求 ln L( )的最大值 点. 函数ln L( ) 对未知参数 求导数，并令其为0，即
d ln L( ) 0.
d
(4) 求解上述方程，得到参数 的最大似然估计值 ˆ(x1, x2 , , xn ),

参 数 估 计


n i 1
Xi作为1( X )的估计量，有
2
1 n
n i 1
Xi
.
由此解得 的矩估计量
ˆ
2 n
n i 1
Xi
2X
.
而 的矩估计值就是
ˆ
2 n
n i 1
xi
2x.
3.1 参数的点估计
例3.2 设总体 X 的均值 和方差 2 都存在 , 且有
2 0, 但 和 2 均为未知, 又设 X1, X2 ,
1 n
n
(Xi
i 1
X )2.
3.1 参数的点估计
所得结果表明， 总体均值与方差的矩估计量的表达式 不因不同的总体分布而异.
例如，X ~ N (, 2 ), , 2 未知, 即得 , 2 的矩估计量
ˆ X ,
一般地,
ˆ 2
1 n
n
(Xi
i 1
X )2.
用样本均值
X
1 n
n i 1
Xi作为总体 X 的均值的矩估计,
应用数理统计与随机过程
第三章 参数估计
第一章 概率论基础
目录 Contentsຫໍສະໝຸດ 3.1参数的点估计
3.2
估计量的评价标准
3.3
区间估计
3.1 参数的点估计 点估计问题
设总体X 的分布函数形式已知, 但它的一个或多个 参数为未知, 借助于总体X的一个样本来估计总体 未知参数的值的问题称为点估计问题.
根据大数定律，当样本容量比较大时，样本的 k阶 原点矩依概率收敛到总体的 k 阶原点矩.
3.1 参数的点估计
矩估计的具体做法
设 X 为连续型随机变量 , 其概率密度为 f ( x;1,2 , ,k ),

第三讲参数估计


2019/12/7
商学院 李丽明
6
三、抽样分布的概念
总体(Population)：调查研究的事物或现象的 全体。
个体(Item unit)：组成总体的每个元素。 样本(Sample)：从总体中所抽取的部分个体。 样本容量(Sample size)：样本中所含个体的
数量。
2019/12/7
【例】某种零件长
度服从正态分布，
从该批产品中随
机抽取９件，测
得其平均长度为 21.4 mm。已知
总体标准差
=0.15mm，试建 立该种零件平均
长度的置信区间，
给定置信水平为 0.95。
解：已知Ｘ~N(，0.152)，x＝2.14, n=9, 1- = 0.95，Ｚ/2=1.96 总体均值的置信区间为
p
来推
断总体的比例p？
2019/12/7
商学院 李丽明
30
总体比例的置信区间
（1）假定条件 两类结果 总体服从二项分布 可以由正态分布来近似
（2）使用正态分布统计量Ｚ
Z pˆ p ~ N(0,1) p(1 p) n
（3）总体比例Ｐ 的置信区间为
pˆ Z 2
pˆ(1 pˆ) n
2019/12/7
商学院 李丽明
31
总体比例的置信区间
【例】某企业在一项
关于职工流动原
因的研究中，从
该企业前职工的
总体中随机选取 了200人组成一个 样本。在对其进 行访问时，有140 人说他们离开该
企业是由于同管
理人员不能融洽
相处。试对由于
这种原因而离开 该企业的人员的p 真正比例构造95% 的置信区间。
则称随机区间【L，U 】是 的置信水平为1- α 的 置信区间， L和 U分别称为 1- α 的置信下限和上
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

L( x1 , x2 , x3;q ) =ˆ Pq { X1 = x1 , X 2 = x2 , X 3 = x3 }
= Pq { X1 = x1 }Pq { X 2 = x2 }Pq { X 3 = x3 }
= p( x1;q ) p( x2;q ) p( x3;q ) = q x1 (1 − q )1− x1q x2 (1 − q )1− x2 q x3 (1 − q )1− x3
其它
其中 −1
是未知参数,
X1,X2,…,Xn是取自X的样本,求参数 的矩估计.
解:
数学期望
是一阶
1
=
= E(X
( + 1)
)
1
1
= x( 0
x +1dx
+ =
1)

x dx +1
原点矩由矩估计法,
X
=
0

+1
+2
总体矩
样本矩
+2
从中解得 ˆ = 2 X − 1 , 即为 的矩估计.
Gauss
Fisher
最大似然法的基本思想
先看一个简单例子： 某位同学与一位猎人一起外 出打猎 . 一只野兔从前方窜过 . 只听一声枪响，野兔应声倒下 . 如果要你推测，是谁打中的呢？ 你会如何想呢?
你就会想，只发一枪便打中, 猎人命中的概率 一般大于这位同学命中的概率 . 看来这一枪是猎人 射中的 .
最大似然估计法就是用使L(q )达到最大值的qˆ去估计q . 称qˆ为q 的最大似然估计（MLE）.
怎样求最大似然估计呢？ 因为lnx是x 的严格单增函数，lnL与L有相同的极大值点， 故一般只需求lnL的极大值点即可----令其一阶偏导为0，得到 似然方程（组），求解即可。
求最大似然估计的一般步骤：
1. 写出似然函数： n L( x1, x2 ,..., xn;q ) = p( xi ;q1,q 2 ,...,q m )
i =1
2. 对似然函数取对数： n ln L = ln p( xi ;q1,q 2 ,...,q m )
i =1
3. 对qj ( j=1,…,m )分别求偏导，并令其为 0 得似
0 xi，i = 1,, n 其它
当0 xi ，i = 1,, n时
2. 取对数：
ln
L
=
−n
ln q
−
1
q
n

i =1
xi
3. 求偏导：
令
d ln L
dq
=
−n
q
+
1
q2
n
xi
i =1
=
0
4. 求解得：
qˆ
=
1 n
n
Xi
i =1
=
X
代入具体数值可得q 的估计值为：
1
n
n i =1
最大似然估计法就是用使L(q )达到最大值的qˆ去估计q . 称qˆ为q 的最大似然估计（MLE）.
设X1,X2,…Xn是取自总体X的一个样本，样本的联合密度
(连续型)或联合分布律(离散型)为 f (X1,X2,…Xn;q ) .
当给定样本x1,x2,…xn时，定义似然函数为：
L(q ) = f ( x1, x2, xn;q )
然方程(组)： ln L = 0
( j = 1,2,..., m)
q j
4. 解似然函数方程组得 qˆ1 ,...,qˆm 即为所求。
例 指数分布的点估计
▪ 例 某电子管的使用寿命 X （单位：小时) (从
开始使用到首次失效为止）服从指数分布，
▪ ▪
X
~
f
(
x;q
)
=

1
q0
−
e
,
x
解: 总体的概率密度函数为
1
f ( x) = q
,0 x q
0 , else
从而可得似然函数
L( x1 ,..., xn;q ) =
1
q n
,0
xi
q
0 , else
注意： 该似然函数不能 用一般方法----通 过求导构造似然 方程。 尝试用其他方法 求解！
L=
q
,
x 0 (q 0)
其它
▪ 今取一组样本，数据如下，问如何估计θ？
16 29 50 68 100 130 140 270 280
340 410 450 520 620 190 210 800 1100
解： 可用两种方法估计： 矩法估计 和 最大似然估计
（一）矩法估计 E(X ) =
缺点是，当总体类型已知时，没有充分利用分布提供的 信息 . 一般场合下,矩估计量不具有唯一性 .
其主要原因在于建立矩法方程时，选取那些总体矩用相 应样本矩代替带有一定的随意性 .
二、 最大似然估计法
它首先是由德国数学家高斯在1821年提出的 ,
费歇尔在1922年重新发现了这一方法，并首先研究 了这种方法的一些性质 .
问题
(1)对于同一个参数究竟采用哪一个估计量好?
(2) 我们希望一个“好的”估计量具有什么特性？ (3) 怎样决定一个估计量是否比另一个估计量“好”？
评价估计量的标准是什么? 下面介绍几个常用标准.
第二节 估计量的评选标准
无偏性 有效性 相合性
一、无偏性
估计量是随机变量，对于不同的样本值会得到 不同的估计值 . 我们希望估计值在未知参数真值附 近摆动，而它的期望值等于未知参数的真值. 这就 导致无偏性这个标准 .
+
x

1
−
e
x
q
dx
=
q
0
q
令 X = q 则可得q 的矩法估计量为：
qˆ = X
代入具体数值可得q 的估计值为：
1
n
i
n =1
x
i
= 1 5723 18
318(小时)
▪ （二）最大似然估计
1. 构造似然函数：
L(
x1
,..., x
n ;q
)
=

q
−n

−1
eq
n

i =1
xi
0
作为对参数 qk ( k = 1,2,…,m )的估计,我们称之为参数 qk的估计
量。
思想：用统计量去估计真实值。
一. 矩估计法
它是基于一种简单的“替换” 思想建立起来的一种估计方法 .
是英国统计学家K.皮尔逊最早提出的 . 其基本思想是用样本矩估计总体矩 .
理论依据:大数定律
记总体k阶原点矩为 E( X k )
3
3
xi
3− xi
= q i=1 (1 − q ) i=1 , ( xi = 0,1 i = 1,2,3)
▪ 现将抽样的所有可能结果及其相应的概率列表如下：
(x1,x2,x3) (0,0,0) (0,0,1) (0,1,0) (1,0,0) (0,1,1) (1,0,1) (1,1,0) (1,1,1) Pq=0.25 .4219 .1406 .1406 .1406 .0469 .0469 .0469 .0156 Pq=0.75 .0156 .0469 .0469 .0469 .1406 .1406 .1406 .4219
第三讲 参数估计
总体 随机抽样
样本
描述
统计量
作出推断
参数估计问题是利用从总体抽样得到的信息来估计总 体的某些参数或者参数的函数.
在参数估计中，假定总体分布已知，未知的仅仅 是一个或几个参数.
参数估计是对已知分布类型的总体，利用样本对
其未知参数作出估计。
参数估计
点估计 区间估计
点估计的方法 矩估计法 最大似然法
xi
= 1 5723 18
318(小时)
#
例 设X1,X2,…Xn是取自总体 X~B(1, p) 的一个样本，求 参数p的最大似然估计量.
解：似然函数为:
L(p)= f (x1, x2,…, xn; p )
对数似然函数为：
对p求导并令其为0，
=0
得 即为 p 的最大似然估计值 .
从而 p 的最大似然估计量为
1
q n
,0
xi
q
=
1
q n
,
0

min{
1 i n
xi
},
max{Байду номын сангаас
1 i n
xi
}

q
0 , else
0 , else
如图所示，似然函数L在
q = m1iaxn {xi}处达到极大值 故q的最大似然估计量为：
qˆ
=
max{X
1i n
i}
#
从前例可以看到, 对于同一个参数, 用不同 的估计方法求出的估计量可能不相同, 而且, 很 明显, 原则上任何统计量都可以作为未知参数的 估计量.
这个例子所作的推断已经体现了最大似然法的 基本思想 .
例 最大似然法---简例
▪ 例 如果一个老兵和一个新兵同时打靶，但仅 有一人命中，问谁命中的可能性大？
▪
(1) 老兵 (2)新兵
大家首先想到的是老兵，因为它更符合情理！
例 若袋中有黑白两种球 ( 除颜色外别无差异 ) , 且 已知两种球数之比为 1:3 ，现任取一球，发现是白 色，问哪种颜色的球多一些？
1− X
例2 区间 [ 0 , q ]上均匀分布的矩估计
▪ 设样本X1，X2，… ，Xn是来自在区间[ 0 , q ] 上均匀分布的总体， q 未知，求q 的矩估计。