机械原理习题习题三：效率与自锁

第5章机械的效率和自锁5.1 复习笔记一、机械的效率1．功和效率（1）机械效率①驱动功机械上的驱动功（输入功）为W d，有效功（输出功）为W r，损失功为W f。

则有W d＝W r＋W f②机械效率a．定义机械的输出功与输入功之比称为机械效率，反映了输入功在机械中的有效利用程度，以η表示。

b．计算方法用功计算时η＝W r/W d＝1－W f/W d；用功率计算时η＝P r/P d＝1－P f/P d；式中，P d——输入功率；P r——输出功率；P f——损失功率。

（2）损失率①定义机械的损失功与输入功之比称为损失率，以ξ表示。

②计算方法由定义有ξ＝W f/W d＝P f/P d。

注：η＋ξ＝1，由于摩擦损失不可避免，故必有ξ＞0和η＜1。

（3）效率的简便计算方法为便于效率的计算，可应用下式进行计算η＝理想驱动力/实际驱动力＝理想驱动力矩/实际驱动力矩①斜面机构正反行程的机械效率分别为η＝tanα/tan（α＋φ）η′＝tan（α－φ）/tanα式中，α——斜面夹角；φ——总反力与法向反力的夹角。

②螺旋机构拧紧和放松螺母时的效率计算式分别为η＝tanα/tan（α＋φv）η′＝tan（α－φv）/tanα式中，α——中径升角；φv——螺旋副的摩擦角。

2．机器（或机组）的效率已知各机构的效率可计算确定整个机构的效率。

常用机构的效率见教材表5-1。

（1）串联①计算公式由k个机器串联组成的机组，设各机器的效率分别为η1、η2、…、ηk，机组的输入功率为P d，输出功率为P r。

则整个串联机组的机械效率为η＝P r/P d＝（P1/P d）（P2/P1）…（P k/P k－1）＝η1η2…ηk②特点a．前一机器的输出功率即为后一机器的输入功率；b．只要串联机组中任一机器的效率很低，就会使整个机组的效率极低；c．串联机器的数目越多，机械效率也越低。

③提高串联机组效率的措施a．减少串联机器的数目；b．优先提高效率最低机器的效率。

第五章 机械的效率和自锁
输入功—在一个机械系统中，驱动力（或驱动力矩）所作的功 称为输入功，用Wd 表示;
输出功—在一个机械系统中，克服工作阻力（或驱动力矩）所 作的功，称为输出功，用Wr 表示;
损失功—在一个机械系统中，克服有害阻力（如摩擦阻力、空） 气阻力等）所作的功，称为损失功，用Wf表示;
机械在稳定运转时期，输入功等于输出功与损耗功之和，即：
G0、M0 — 理想工作阻力、理想工作阻力矩；
G、M — 实际工作阻力、实际工作阻力矩；
当需计算整台机器或整个机组的机械效率时，常用以下三种 方法，其中在实际设计中，更常用到的是实验法和经验法， 即确定机械效率的三种方法分别为： 计算法 实验法 —对于已有的机器，可以用实验法直接测得机械效率。 经验法 —对于正在设计和制造的机器，不能直接用实验法测
定效率，但由于各种机器都是由一些基本机构组合而 成，而这些基本机构的效率通过实验积累的资料却是 可以预先估定的，在已知这些基本机构和运动副的机 械效率后，就可以通过计算确定出整个机器的效率。 同理，对于由多个机器组成的机组，只要知道各台机 器的效率，就可以根据各机组的组合情况用计算的办 法求出该机组的总效率。（见P76表5-1） 三种不同机器组合的效率计算
Pd
Pd
令式中: Pr
Pd
得到机械效率的表达式为：
1
Pf
令： Pf Wf
Pd
Pd Wd
效率恒小于1
— 机械损失系数 1
由于机械摩擦不可避免，故必有： 0, 1
由以上公式可知：为使其具有较高的机械效率，应尽量减小 机械中的损耗，主要是磨擦损耗。这就要求：一方面应尽量 简化机械传动系统，使功率传递通过的运动副数目越少越好。 另一方面，应设法减少运动副中的磨擦，如采用滚动磨擦代 替滑动磨擦，选用适当的润滑剂及润滑装置进行润滑，合理 选用运动副元素的材料等。

第3章平面机构的运动分析第4章平面机构的力分析第5章机械的效率和自锁第8章平面连杆机构及其设计一、填空题：α＝，则传动角γ＝___________度，传动角越大，1、铰链四杆机构的压力角040传动效率越___________。

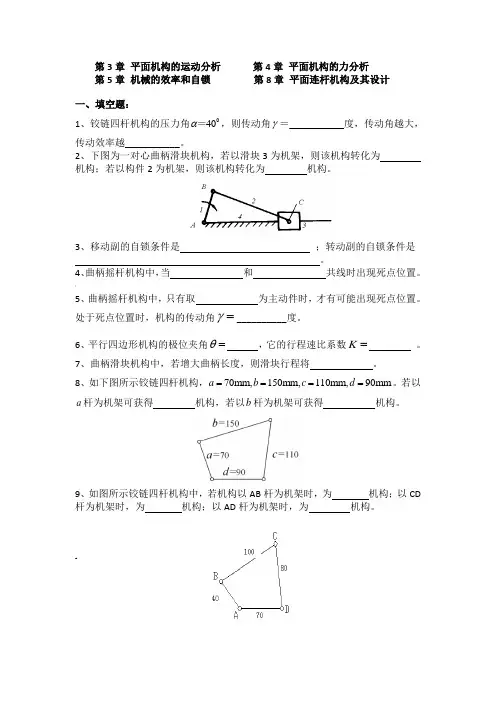
2、下图为一对心曲柄滑块机构，若以滑块3为机架，则该机构转化为机构；若以构件2为机架，则该机构转化为机构。

3、移动副的自锁条件是；转动副的自锁条件是。

4、曲柄摇杆机构中，当和共线时出现死点位置。

:5、曲柄摇杆机构中，只有取为主动件时，才有可能出现死点位置。

处于死点位置时，机构的传动角γ=__________度。

6、平行四边形机构的极位夹角θ=，它的行程速比系数K=。

7、曲柄滑块机构中，若增大曲柄长度，则滑块行程将。

8、如下图所示铰链四杆机构，70mm,150mm,110mm,90mm====。

若以a b c da杆为机架可获得机构，若以b杆为机架可获得机构。

9、如图所示铰链四杆机构中，若机构以AB杆为机架时，为机构；以CD 杆为机架时，为机构；以AD杆为机架时，为机构。

~10、在平面四杆机构中，和为反映机构传力性能的重要指标。

11、在曲柄摇杆机构中，如果将杆作为机架，则与机架相连的两杆都可以作运动，即得到双曲柄机构。

12、在摆动导杆机构中，若以曲柄为原动件，该机构的压力角为，其传动角为。

13、相对瞬心与绝对瞬心的相同点是，不同点是；在由N个构件组成的机构中，有个相对瞬心，有个绝对瞬心。

/二、判断题：1、对于铰链四杆机构，当机构运动时，传动角是不变的。

（）2、在四杆机构中，若有曲柄存在，则曲柄必为最短杆。

（）3、平面四杆机构的行程速度变化系数K 1，且K值越大，从动件急回越明显。

（）4、曲柄摇杆机构中，若以摇杆为原动件，则当摇杆与连杆共线时，机构处于死点位置。

（）5、曲柄的极位夹角θ越大，机构的急回特性也越显著。

（）6、在实际生产中，机构的“死点”位置对工作都是不利的，处处都要考虑克服。

§5 机械的效率和自锁填空题：1．设机器中的实际驱动力为rP ，在同样的工作阻力和不考虑摩擦时的理想驱动力为r P 0，则机器效率的计算式是η = r P 0/rP 。

2．设机器中的实际生产阻力为rQ ，在同样的驱动力作用下不考虑摩擦时能克服的理 想生产阻力为r Q 0,则机器效率的计算式是 η= r Q /rQ 0 。

3．假设某机器由两个机构串联而成，其传动效率分别为1η和2η，则该机器的传动效率为 1η*2η 。

4．假设某机器由两个机构并联而成，其传动效率分别为1η和2η，则该机器的传动效率为 （P 1*η1+ P 2*η2）/(P 1+P 2) 。

5. 从受力观点分析，移动副的自锁条件是 外力的作用线与运动方向法线的夹角小于等于摩擦角 ；转动副的自锁条件是 外力的作用线与摩擦圆相切或相割 ；从效率观点来分析，机械自锁的条件是 效率小于等于零 。

综合题1：某滑块受力如图所示，已知滑块与地面间摩擦系数f ，试求F 与Q 分别为驱动力时的机构运动效率。

F 为驱动力：f tg1-=ϕ于是由正弦定理：)90sin()90sin(00ϕθϕ--+=Q F 令0=ϕ，得)90sin(00θ-=QF 因此，其效率为)90sin()90sin()90sin(00θϕϕθη-+--==F F 当Q 为驱动力，F 变为阻力，取ϕ-代替上式中的ϕθ-)90sin()90sin(90sin(000ϕθϕθη+---==）F F 第四章习题中，综合题5，要求计算该机构效率。

（可直接利用前面的计算结果）0153077.8==-f tg ϕ由正弦定理：)90sin()2180sin(0210ϕβγϕ-=--+R P 和)90sin()2sin(012ϕϕβ+=-R Q 于是Q P *-+*---+=)2sin()90sin()90sin()2180sin(00ϕβϕϕβγϕ代入各值得：N P 7007.1430=取上式中的00=ϕ，可得N P 10000=于是6990.00==PP η综合题2：图 示 为 由 A 、B 、C 、D 四 台 机 器 组 成 的 机 械 系统，设 各 单 机 效 率 分 别 为ηA 、ηB 、ηC 、ηD ， 机 器B 、D 的 输 出 功 率 分 别 为N B 和N D 。

§5 机械的效率和自锁填空题：1．设机器中的实际驱动力为rP ，在同样的工作阻力和不考虑摩擦时的理想驱动力为r P 0，则机器效率的计算式是η = r P 0/rP 。

2．设机器中的实际生产阻力为rQ ，在同样的驱动力作用下不考虑摩擦时能克服的理 想生产阻力为r Q 0,则机器效率的计算式是 η= r Q /rQ 0 。

3．假设某机器由两个机构串联而成，其传动效率分别为1η和2η，则该机器的传动效率为 1η*2η 。

4．假设某机器由两个机构并联而成，其传动效率分别为1η和2η，则该机器的传动效率为 （P 1*η1+ P 2*η2）/(P 1+P 2) 。

5. 从受力观点分析，移动副的自锁条件是 外力的作用线与运动方向法线的夹角小于等于摩擦角 ；转动副的自锁条件是 外力的作用线与摩擦圆相切或相割 ；从效率观点来分析，机械自锁的条件是 效率小于等于零 。

综合题1：某滑块受力如图所示，已知滑块与地面间摩擦系数f ，试求F 与Q 分别为驱动力时的机构运动效率。

F 为驱动力：f tg1-=ϕ于是由正弦定理：)90sin()90sin(00ϕθϕ--+=Q F 令0=ϕ，得)90sin(00θ-=QF 因此，其效率为)90sin()90sin()90sin(00θϕϕθη-+--==F F 当Q 为驱动力，F 变为阻力，取ϕ-代替上式中的ϕ，并取倒数，得 QFθQF θQθϕ+090Fθϕ--090φ)90sin()90sin(90sin(0000ϕθϕθη+---==）F F 第四章习题中，综合题5，要求计算该机构效率。

（可直接利用前面的计算结果）0153077.8==-f tg ϕ由正弦定理：)90sin()2180sin(0210ϕβγϕ-=--+R P 和)90sin()2sin(012ϕϕβ+=-R Q 于是Q P *-+*---+=)2sin()90sin()90sin()2180sin(00ϕβϕϕβγϕ代入各值得：N P 7007.1430=取上式中的00=ϕ，可得N P 10000=于是6990.00==PP η综合题2：图示为由A、B、C、D四台机器组成的机械系统，设各单机效率分别为ηA、ηB、ηC、ηD，机器B、D的输出功率分别为N B和N D。

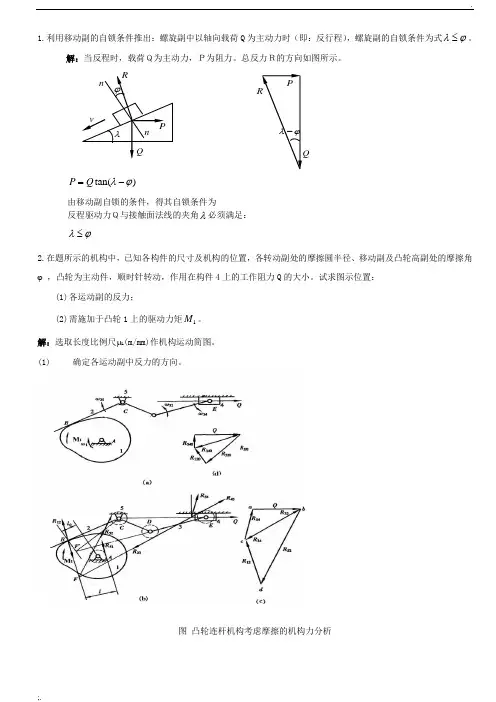
1.利用移动副的自锁条件推出：螺旋副中以轴向载荷Q 为主动力时（即：反行程），螺旋副的自锁条件为式ϕλ≤。

解：当反程时，载荷Ｑ为主动力，Ｐ为阻力。

总反力Ｒ的方向如图所示。

)tan(ϕλ-=Q P由移动副自锁的条件，得其自锁条件为反程驱动力Ｑ与接触面法线的夹角λ必须满足：ϕλ≤2.在题所示的机构中，已知各构件的尺寸及机构的位置，各转动副处的摩擦圆半径、移动副及凸轮高副处的摩擦角ϕ ，凸轮为主动件，顺时针转动，作用在构件4上的工作阻力Q 的大小。

试求图示位置：(1) 各运动副的反力；(2) 需施加于凸轮1上的驱动力矩1M 。

解：选取长度比例尺μL (m/mm)作机构运动简图。

(1)确定各运动副中反力的方向。

图 凸轮连杆机构考虑摩擦的机构力分析ϕλ-vλnQPPRRnϕ由主动件凸轮的转向，确定出机构中各个构件之间的相对运动方向，如图所示。

分析各个构件受到的运动副反力和外力。

构件1受到的力有R 51、R 21、1M ；构件2受到的力有R 52、R 12、R 32；构件3受到的力有R 23、R 43；构件4受到的力有R 34、R 54、Q 。

先确定凸轮高副处点B 的反力R 12的方向，与移动副反力方向确定方法相同，该力方向与接触点处的相对速度V B2B1的方向成900+ϕ角。

再由R 51应切于运动副A 处的摩擦圆，与R 21大小相等方向相反，且对A 之矩的方向与ω1方向相反，确定出R 51的方向。

R 51与R 21形成一个力偶与M 1平衡；由于连杆3为受拉二力构件，其在D 、E 两转动副处所受两力R 23及R 43应切于该两处摩擦圆，大小相等方向相反，在一条直线上。

同时，根据相对转速3432,ωω的方向，可确定出R 23及R 43的作用线和方向，亦即铰链点D 、E 的摩擦圆的内公切线。

；反力R 52应切于运动副C 处的摩擦圆，且对C 之矩的方向应与ω25的方向相反，同时构件2受有的三个力R 12、R 52、R 32应汇交于一点，由此可确定出R 52的方向线；滑块4所受反力R 54应与V 45的方向成900+ϕ角，它受到的三个力R 34、R 54及Q 也应汇交于一点，于是可定出R 54的方向线。

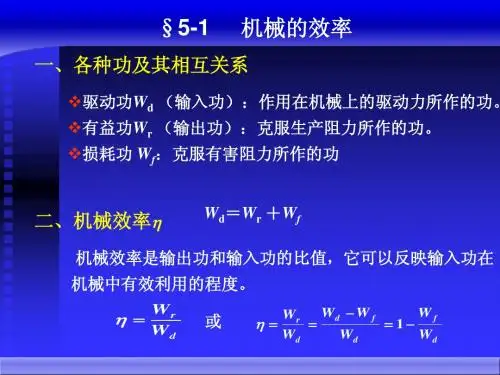
机械运转时：克服生产阻力所作的功为有效功(输出功)驱动力所作的功为驱动功(输入功)克服有害阻力(如运动副中摩擦力)所作的功为损失功W dW rW f 当机械稳定运转时：W d =W r + W f机械效率作用在机械上的力可分为驱动力、阻抗力两大类d r W W =ηdf d W W W -=d f W W 1-=η—输入功在机械中的有效利用程度阻抗力有效阻力（生产阻力）有害阻力d r W W =ηdf d W W W -=d f W W 1-=d r P P =ηdf d P P P -=d f P P 1-=由于损失功W f 或损失功率P f 不可能为零，所以η<1W f 或P f 越大，机械的效率就越低。

因此在设计机械时，为了使其具有较高的机械效率，应尽量减小机械中的损耗，主要是减小运动副中的摩擦损失。

用滚动代替滑动,考虑润滑,合理选材等上下分别除以做功时间则为功率η以功或功率的形式表达F —实际驱动力υF —驱动力作用点沿力作用线方向的速度Q —实际生产阻力υQ —阻力作用点沿力作用线方向的速度d r P P =η FQ F Q υυη=∴起重装置η以力或力矩的形式表达为进一步简化该式，现假设该机械为理想机械，即机械中不存在摩擦。

此时，F 0—为克服同样生产阻力Q 所需的理想驱动力 1F Q F 0Q 0＝因为理想机械υυη=由于W f 或P f 为零F0Q F Q υυ＝∴显然F 0 < F0d f d d r 1P P P P P ηη==-==∴F F 0F F υυη=F F 0=F Q F Q υυη=F 0起重装置η以力或力矩的形式表达F Q F Q υυη=同理，Q 0—为在同样驱动力F 下克服的理想生产阻力1F Q F Q00＝理想机械υυη= 由于W f 或P f 为零FQ 0F Q υυ＝∴显然Q 0 > Q 0df d d r 1P P P P P ηη==-==∴Q 0Q Q Q υυη=0Q Q =Q 0起重装置η以力或力矩的形式表达为进一步简化该式，现假设该机械为理想机械，即机械中不存在摩擦。

解: 此传动装置为一混联系统
圆柱齿轮1、2、3、4为串联 圆柱齿轮 、 、 、 为串联
η' = η12η34 = 0.952
圆锥齿轮5-6、7-8、9-10、 圆锥齿轮 、 、 、 11-12为并联。 为并联。 为并联 η'' = η56 = 0.92 此传动装置的总效率
η = η'⋅η'' = η12η34η56 = 0.952 ⋅ 0.92 = 0.83
四、机械效率的计算
1. 一般公式: 一般公式
QvQ Nr η= = Nd PvP
理想机械：不存在摩擦的机械。 理想机械：不存在摩擦的机械。 理想驱动力P 理想机械中，克服同样的生产阻力Q， 理想驱动力 0 ：理想机械中，克服同样的生产阻力 ， 所需的驱动力。 所需的驱动力。 等于1， 理想机械的效率 η0等于 ，即： η0 =
QvQ
QvQ P vP 0 =1
P0vP P0 M0 = = = ⇒ QvQ = P0vP ⇒η = M PvP PvP P
四、机械效率的计算（续） 机械效率的计算（
理想生产阻力Q 理想机械中，同样的驱动力P所能克 理想生产阻力 0 ：理想机械中，同样的驱动力 所能克 服生产阻力。 服生产阻力。
η0 =
Q0vQ Pv#39; ⇒η = = = = PvP Q0vQ Q0 M'0
QvQ
QvQ
机械效率的统一形式： 机械效率的统一形式：
理想驱动力 理想驱动力矩 η= = 实际驱动力 实际驱动力矩
实际生产阻力 实际阻力矩 = = 理想生产阻力 理想阻力矩
四、机械效率的计算（续） 机械效率的计算（
§5-1
机械的效率
一、各种功及其相互关系

G=
tan(α + )
F ≤0
F
令 G ≤ 0，得
tan(α + )
α + ≥ 90°
∴ 90° ≤ α < 90°
机械原理 第十一章 机械的效率和自锁
斜面机构正行程自锁条件 解法二 ：机械的效率≤ 0。
F0 tan α = η= F tan(α + )
令 η ≤ 0，得
tan α ≤0 tan(α + )
α + ≥ 90°
∴ 90° ≤ α < 90°
机械原理 第十一章 机械的效率和自锁
斜面机构反行程自锁条件 解法一：克服的阻抗力≤ 0。
F ' = G tan(α )
令 F’ ≤ 0，得
G tan(α ) ≤ 0
α ≤ 0°
∴ 0° < α ≤
机械原理 第十一章 机械的效率和自锁
斜面机构反行程自锁条件 解法二 ：机械的效率≤ 0。
G0 tan(α ) = η= G tan α
令 η ≤ 0，得
tan(α ) ≤0 tan α
α ≤ 0°
∴ 0° < α ≤
转动副的自锁条件：单驱动力作用在摩擦圆内( a ≤ ρ )。
机械原理 第十一章 机械的效率和自锁 3. 机械的自锁条件
1) 机械中所含的运动副自锁。 2) 机械所克服的阻抗力≤ 0。 3) 机械的效率≤ 0。 举例
机械原理 第十一章 机械的效率和自锁
斜面机构正行程自锁条件 解法一：克服的阻抗力≤ 0。
机械原理 第十一章 机械的效率和自锁 举例2：螺旋机构
螺旋机构由螺杆和螺母组成。由于 螺杆的螺纹可设想是一斜面卷绕在圆柱 体上形成，故螺杆和螺母之间的相互关 系，可简化为斜面和滑块的相互关系。 拧紧螺母，相当于斜面机构的正行 程。 F = G tan(α + v ) 拧紧力矩：

§5 -1 机械的效率 一、机械效率及其表达形式 1、机械效率
Wd =
Wr + Wf
损耗功 （摩擦等）
驱动功 有效功 （动力） （克服生产阻力）
机械效率： = Wr / Wd = 1 - Wf / Wd
损失不可避免， Wf＞ 0： < 1
2、机械效率的几种表达方式 1）用功表示的机械效率 ： = Wr / Wd = 1 - Wf / Wd 2）用功率表示的机械效率： = Pr /Pd = 1 - Pf / Pd 3）用力(或力矩)表示的机械效率： 右图中G为生产阻力， F为驱动力， G 和 F 分别为对应力的作用 点处沿力作用线方向 上的速度
作者：潘存云教授
P”r P’r
串联计算
Pd
P2 P’d2 P’d3 Pk 1作者：潘存云教授 2 “ “” 3 4 P P”d2 P”d3 r P”r P1 P2 Pr P’r P P1 3‘
‘’ 4P r
并联计算
Pd
1
2
k 作者：潘存云教授
P”r
串联计算
§5 -2 机械的自锁
一、自锁的概念
对于有些机构，由于摩擦的存在，致使无 论驱动力如何增大均不能使静止的机构产生运 动。这种现象称之为自锁。
η越小自锁越可靠。
2） 从生产阻抗力方面来判断
由于当自锁时，机械已不能运动，所以 这时它所能克服的生产阻抗力G将小于或等 于零，即： 自锁条件：G ≤０
例1、斜面压榨机：在回弹力G 作用下（F为阻抗力时）的 自锁条件(设：摩擦角均为 ）
1
G
90º (2)
FR13 FR23
90º
4 4 FR13 1 v FR2 31
G0 = F cot

2. 每一路的总效率分别为：
2
1
18 12 34 56 78
0.953 0.92 0.79
114 12 910 1112 1314
0.953 0.92 0.79
6
5
11 12
84
3 13
7
9 10
14
3.
整个机构的总效率为：
Pri
Pdi
Pri
Pdi
2
1
Pri P8 P14
小结： 用驱动力或驱动力矩表示的效率公式为：
F0 M 0
FM
用工作阻力或工作阻力矩表示的效率公式为：
G M
G0 M0
F0、M0 —理想驱动力、理想驱动力矩；
F、M —实际驱动力、实际驱动力矩；
G0、M0 — 理想工作阻力、理想工作阻力矩；
G、M — 实际工作阻力、实际工作阻力矩；
当需计算整台机器或整个机组的机械效率时，常用以下三种 方法，其中在实际设计中，更常用到的是实验法和经验法， 即确定机械效率的三种方法分别为： 计算法 实验法 —对于已有的机器，可以用实验法直接测得机械效率。
解：1. 分析机构 该机构为混联机构
串联部分：圆柱齿轮1、2
并联部分：锥齿轮3、4；5、6；
7、8 ； 9、10。
2. 分别计算效率
10
864
2
（1）串联部分： 12 0.95
（2）并联部分：
9
7 5 31
310
P4 P6 P8 P10 P4 P6 P8 P10
34 56 78 910
6
5
11 12
Pdi
P8
18
P14
114
Pri

第五章机械的效率和自锁效率是衡量机械性能优劣的重要指标，而一部机械效率的高低在很大程度上取决于机械中摩擦所引起的功率损耗。

研究机械中摩擦的主要目的在于寻找提高机械效率的途径。

机械的自锁问题及移动副自锁条件的求解是本章的难点之一。

本章知识点串讲【知识点1】机械效率及其计算定义：机械的输出功与输入功之比称为机械效率，η= W r / W d。

性质：η<1(η= 1——理想机器——永动机)表示方法：a. 功表示η= W r / W d = 1- W f/ W db. 功率表示η= p r / p d = 1- p f/ p dc. 力(矩)表示η= F0/ F= M0/ M1）串联机器(组)的总效率等于组成该机器(组)各机械部分效率的连乘积η=η1η2……ηK2）对于并联机构的总效率计算就相对麻烦一点。

N rη= (Nd1η1 + Nd2η2 + …+ NdK ηK) / (Nd1 + Nd 2 + …+ NdK) = (Nd1η1 + Nd2η2 + …+ NdK ηK) / Nd并联机组的效率，不仅与各个机构的效率有关，而且与效率的分配有关3）混联 兼有串联和并联的机构称为混联机构。

为了计算其总效率，可先将输入功至输出功的路线弄清，然后分别计算出总的输入功率和总的输出功率，最后计算其总的机械效率。

【知识点2】机械自锁条件的确定定义：由于摩擦的存在，沿某个方向的驱动力如何增大，也无法使受力对象产生运动的现象——称为机械的自锁。

同学们要注意的是，机械的自锁只是在一定的受力条件和受力方向下发生的，而在另外的情况下却是可动的，也就是说自锁具有方向性。

1）平面自锁条件：（1）当α>φ时，驱动力P 的作用线在摩擦角φ之外。

Px > F ，即滑块加速； （2）当α=φ时，P 与R 共线。

Px = F ： a. 滑块等速运动——原本运动； b.静止不动——原不动，具有运动趋势。

（3）当α＜φ时，驱动力P 的作用线在摩擦角φ之内。

谢谢！
ห้องสมุดไป่ตู้
机械原理5机械的效率和自 锁
31、别人笑我太疯癫，我笑他人看不 穿。(名 言网) 32、我不想听失意者的哭泣，抱怨者 的牢骚 ，这是 羊群中 的瘟疫 ，我不 能被它 传染。 我要尽 量避免 绝望， 辛勤耕 耘，忍 受苦楚 。我一 试再试 ，争取 每天的 成功， 避免以 失败收 常在别 人停滞 不前时 ，我继 续拼搏 。
33、如果惧怕前面跌宕的山岩，生命 就永远 只能是 死水一 潭。 34、当你眼泪忍不住要流出来的时候 ，睁大 眼睛， 千万别 眨眼!你会看到 世界由 清晰变 模糊的 全过程 ，心会 在你泪 水落下 的那一 刻变得 清澈明 晰。盐 。注定 要融化 的，也 许是用 眼泪的 方式。
35、不要以为自己成功一次就可以了 ，也不 要以为 过去的 光荣可 以被永 远肯定 。
61、奢侈是舒适的，否则就不是奢侈 。——CocoCha nel 62、少而好学，如日出之阳；壮而好学 ，如日 中之光 ；志而 好学， 如炳烛 之光。 ——刘 向 63、三军可夺帅也，匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里，与其说好 的教师 是幸福 ，不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战，就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿

Composition Principle and Structural Analysis of
王 Mechanisms 树 才
§5-1 机械的效率 §5-2 机械的自锁
§5-1 机械的效率
1.机械效率的概念及意义 （1）机械效率：机械的输出功(Wr)与输入功(Wd)的比值， 以η表示。 机械损失系数或损失率： 机械的损失功(Wf)与输入功(Wd) 的比值， 以ξ 表示。 η＝Wr/Wd ＝1－Wf/Wd ＝1－ ξ （2）机械效率的意义 机械效率反映了输入功在机械中的有效利用的程度。 它是 机械中的一个主要性能指标。 因摩擦损失是不可避免的，故必 有ξ >0和η <1。 降耗节能是国民经济可持续发展的重要任务之一。
G = FR23cos（α － 2φ）/cosφ （ ） 又因F 又因 R32 = FR23 ， F = G tg（α－2φ） （ － ） 令 F = G tg（α－2φ）≤0 （ － ） tg（α－2φ）≤0 即 （ － ） 于是机构的自锁条件为 α≤ 2φ
∑F ∑F
2
=0 =0
F + FR 12 + FR 32 = 0 G + FR 13 + FR 23 = 0
3
作力多边形，于是由正弦定律得： 作力多边形，于是由正弦定律得： F = FR32sin（α － 2φ）/cosφ （ ）
第四章 运动副中的摩擦和机械效率 偏心夹具，图示钻夹具在F力夹紧，去掉F 例5-11 ：偏心夹具，图示钻夹具在F力夹紧，去掉F后要求不能 松开，即反行程具有自锁性。分析其几何条件。 松开，即反行程具有自锁性。分析其几何条件。
例5-9 手摇螺旋千斤顶 其反行程驱动力与阻抗力矩的关系为 M′ /G = d2tan(α － φv)/2 当M′一定，G →∞时，则 tan(α －φv)＝0 即 α ＝φv 又因机械自锁时，其摩擦力一方应大于或等于驱动力一方， 故知其自锁的条件为α ≤φv。 举例： 例5-10 斜面压榨机 例5-11 偏心夹具 例5-12 凸轮机构的推杆

第三讲平面机构的力分析、效率和自锁平面机构的力分析知识点：一、作用在机械上的力1．驱动力：定义：驱使机械运动的力特征：该力与其作用点速度的方向相同或成锐角，其所作的功为正功，称为驱动功或输入功。

来源：原动机加在机械上的力2．阻抗力：定义：阻止机械产生运动的力称为阻抗力特征：该力与其作用点速度的方向相反或成钝角，其所作的功为负功，称为阻抗功。

分类：生产阻力（有效阻力）：有效功（输出功）有害阻力：非生产阻力：损失功二、构件惯性力的确定（考的较少）1、一般力学方法(1) 作平面复合运动的构件对于作平面复合运动且具有平行于运动平面的对称面的构件（如连杆2），其惯性力系可简化为一个加在质心S2 上的惯性力F I2和一个惯性力偶矩M I2, 即F I2 = －m2a S2 , M I2 = －J S2α2也可将其再简化为一个大小等于F I2，而作用线偏离质心S2一距离l h2的总惯性力F′I2,l h2 = M I2/ F I2F′I2对质心S2之矩的方向应与α2的方向相反。

(2) 作平面移动的构件如滑块3，当其作变速移动时，仅有一个加在质心S3上的惯性力F13＝－m3a S3。

(3) 绕定轴转动的构件如曲柄1，若其轴线不通过质心，当构件为变速转动时，其上作用有惯性力F I1＝－m1a S1及惯性力偶矩M I1＝－J S1α1，或简化为一个总惯性力F′I1；如果回转轴线通过构件质心，则只有惯性力偶矩M I1＝－JS1α1。

2、质量代换法（记住定义和条件）1．基本定义：（1）质量代换法：按一定条件将构件质量假想地用集中于若干个选定点上的集中质量来代替的方法叫质量代换法。

（2）代换点：选定的点称为代换点。

（3）代换质量：假想集中于代换点上的集中质量叫代换质量。

2．应满足条件（1）代换前后构件的质量不变。

（2）代换前后构件的质心位置不变。

（3）代换前后构件对质心的转动惯量不变。

三、运动副中的摩擦力的确定（受力分析为大题）1.移动副中摩擦力的确定、F f21＝f F N21＝f v G式中f v为当量摩擦系数。

的相对速度方向相反。 注意： 1 移动副中的总反力与法向反力偏斜的角度始终为摩擦角
或当量摩擦角吗？
2 槽面接触的摩擦力大于平面接触的摩擦力，是因 为槽面接触的摩擦系数大吗？
3 影响当量摩擦系数的因素有哪些？
你现在浏览的是第二十三页，共62页
5.2考虑摩擦时机构的受力分析
例5-1 如图所示的铰链四杆机构，曲柄1为主动件，在力矩
寿命，降低机械的运动精度。 3. 摩擦发热，造成机械卡死。 利用摩擦工作，如带传动、摩擦离合器、制动器等
。 研究摩擦的目的：尽量减少其不利影响，充分发挥
其有用的方面。
你现在浏览的是第三页，共62页
5.1.1 移动副中的摩擦
1）平面摩擦 滑块与平面构成的移动副，滑块
在驱动力F的作用下向左移动。
驱动力F的分解
dFN pds
摩擦力为 dF f fdNFfpds
dM f dfF fp ds
轴端所受的摩擦力矩
M f rRfp d s2frRp2d
你现在浏览的是第二十一页，共62页
M f rRfp d s2frRp2d
上式可分两种情况讨论。
A 新轴端
可认为整个轴端接触面上的压强处处相等
Mf 3 2fQR R2 3 rr3 2
你现在浏览的是第三十页，共62页
例5-4 图示机构，已知各构件的尺寸（包括转动副的 半径），各运动副中的摩擦系数，作用在滑块上的 生产阻力，试对该机构在图示位置时进行受力分析 （各构件的重量及惯性力均忽略不计），并确定加 于原动件1上的平衡力矩。
你现在浏览的是第三十一页，共62页
§5-3 机械的效率
B 跑合轴端 经过一段时间工作后的轴端。
轴端与轴承接触面的压强不再处处相等，而更符合

有效阻力即生产阻力——作功为有效功或输出功(Wr)。
有害阻力即非生产阻力——作功为损耗功(Wf)。如摩擦力、介 质阻力等。在某些情况下可转化为有效阻力或驱动力。
第四章 运动副中的摩擦和机械效率
机械效率
惯性力： 由运动构件质心的加速度引起的。在一个运动循环中，
惯性力作功为0。减速运动时，为驱动力；加速度运 动时，为阻力。
自锁条件

ρ
V12
1
F21 Q R21 F
ρ
P
2

F R21 F
ρ
1
R21 F V12
ρ
V12
V12
不自锁
2
自锁(边界动副中的摩擦和机械效率
2、斜面摩擦 1）滑块沿斜面等速上升（正行程）
运动副中的摩擦
Q——铅垂载荷(阻力)； P——水平驱动力； R21——滑块1所受的总反力。
水平力 铅垂载荷
arctan f
摩擦力，与 v12反向。
Q
1、总反力R21的方向恒与相对运动速度方向成一钝角 （90°+ ρ），与接触面公法线成ρ 。 2、当移动副的几何形状改变时，会改变N21的大小，产生 较平面摩擦大的摩擦力。
第四章 运动副中的摩擦和机械效率
R21 N21
ρ
运动副中的摩擦
-
Q
第四章 运动副中的摩擦和机械效率
分析前述摩擦中的自锁 下降： P '' Q tan( )
运动副中的摩擦
P S cos tan( ) 反 Q S sin tan
自锁时，0 则-0
->0——说明P’>0，保持匀速状态的力； -0——发生自锁，Q的分力不足以使滑动 产生，小于摩擦力，仅有运动趋势， 如想打破自锁状态，需外加驱动力P′。 表明只有工作阻力变为驱动力时,滑块才能运动。