机械制图的螺旋线和螺旋面
- 格式:ppt
- 大小:937.00 KB
- 文档页数:20



机械制中的螺纹表示方法螺纹是机械制造中常用的连接方式之一,它具有较高的可靠性和重复性,广泛应用于各种机械设备和零部件中。
为了确保螺纹的制造和装配的准确性,人们开发出了一系列螺纹表示方法。
本文将介绍机械制中的螺纹表示方法。
一、常用的螺纹表示方法1. 图形表示法在机械制图中,我们经常使用图形表示法来描述螺纹。
通过图中的线条和符号,可以清晰地表示螺纹的尺寸、形状和方向等信息。
根据国际标准,常用的图形表示法有三种:直线螺纹、斜面螺纹和锥面螺纹。
- 直线螺纹:使用直线段和斜线段组成的特定线型来表示,线型上标注线数和螺距等参数。
- 斜面螺纹:使用一组斜线段来表示,线型上标注线数和螺距等参数。
- 锥面螺纹:使用两组斜线段和一组圆弧线段来表示,线型上标注线数和螺距等参数。
2. 字母加数字表示法除了图形表示法,螺纹还可以通过字母和数字的组合来表示。
在这种表示方法中,字母表示螺纹类型,数字表示螺距和直径等参数。
例如,M8x1.25表示一种直径为8mm、螺距为1.25mm的度米制螺纹。
在字母加数字表示法中,常用的字母表示螺纹类型有以下几种:- M:度米制螺纹- G:管螺纹- RC:圆锥管螺纹- RP:圆柱管螺纹- NPT:美国标准圆锥管螺纹3. 螺纹牙规表示法螺纹牙规是一种专用的测量工具,常用于检验和表示螺纹的尺寸和质量。
通过使用螺纹牙规,我们可以直接测量螺纹的内、外直径、螺距等参数,并通过刻度盘上的刻度读数来表示。
螺纹牙规的使用需要一定的专业知识和技巧,但它是一种非常准确和直观的螺纹表示方法。
在机械制造中,螺纹牙规经常被用于螺纹加工和装配工序中。
二、如何选择适当的螺纹表示方法在实际应用中,选择适当的螺纹表示方法非常重要,它关系到螺纹加工和装配的准确性和效率。
在选择螺纹表示方法时,可以考虑以下几个因素:1. 设计要求根据机械设备和零部件的设计要求,选择合适的螺纹表示方法。
如果需要清晰地表达螺纹的尺寸和形状,图形表示法可能是一个不错的选择。


程制图圆柱螺旋线和螺旋面投影来源:定鼎园林绿化信息网作者:未知编辑:天地之心人气:0 日期:2006-11-24圆柱螺旋面应用于螺旋梯及转弯扶手.如图2-60所示。
圆柱螺旋面的导线是圆柱螺旋线。
一、圆柱螺旋线一动点沿圆柱的母线作等速直线运动,同时该母线又绕圆柱的轴线作等速回转运动.动点的这种复合运动的轨迹是圆柱螺旋线,如图2-61 (a)所示。
母线旋转一周,动点沿母线方向移动的距离S,称为导程。
圆柱螺旋线有左旋和右旋之分,若以母指表示动点沿母线移动的方向,其它四指表示母线旋转方向,符合左手情况的称为左螺旋线.符合右手情况的称为右螺旋线。
给出圆柱直径、导程和旋向三个基本要素,就可以画其投影图。
图2-61(l)中,先画圆柱的投影图并在其正面投影定出导程S的大小.将圆柱的H面投影圆周分为若干等分(例如十二等分),按旋向编号,在V面投影图上将导程作同样数目的等分。
由H面上各等分点作铅垂线,同时在V面上由等分点作水平线,交得了0′1′2′……,如图2-61(c)所示。
最后将各交点连成光滑曲线,即为螺旋线的正面投影。
螺旋线的水平投影积聚在圆周上。
当把导圆柱展开成矩形之后,螺旋线应该是这个矩形的对角线(图2-62)。
这条斜线与底边的倾角a同导程S和半径R有下面的关系:tgα=S/2πR这个a 角就叫做螺旋线的升角。
二、圆柱螺旋面一直母线以圆柱螺旋线为导线,并按一定规律运动,所形成的曲面称为圆柱螺旋面。
图2-63(a)所示一直母线沿圆柱螺旋线(曲导线)和螺旋线的轴线(直导线)移动,并始终与轴线垂直相交.这时所形成的圆柱螺旋面是正螺旋面。
因轴线垂于H面,故所有素线都是水平线。
图2-63(b)是正螺旋面的投影图,它的画法与螺旋线相同,为了清晰地表示出螺旋面,一般还画出一系列素线的投影。
图2-63(c)为中间有一同轴圆柱的正螺旋面投影图。
该圆柱与螺旋面的交线也是一条螺旋线,其导程与螺旋线导线的导程相同.画图时,只要画出两端点所形成的螺旋线,连接相应点即得一系列素线,并判断虚实。

机械制图剖视图、螺纹、弹簧、装配图等基础知识机械制图是机械设计中的基础,而剖视图、螺纹、弹簧、装配图则是机械制图中重要的几种图形表示方法。
剖视图所谓剖视图,就是将整个物体分成两部分,只展示一部分,而对另外一部分进行切割或挖去,以展示其内部结构的一种图形表示方法。
剖视图一般用于几何形状比较复杂的机械零件的设计,它能够充分显示零件内部的形状和结构。
在机械制图中,剖视图通常采用虚线来表示,剖面轮廓线上标明“剖面”的名称或编号。
此外,剖面需要指出切面方向和观察方向。
剖视图的类型有很多,根据切面方向的不同可分为:直线剖视图、圆柱剖视图、两点剖视图等。
其中最常用的是直线剖视图,它通常是沿着零件中心线或对称面进行切割,以切开的零件为主视图,剖面视图成为补充视图。
螺纹螺纹是机械加工中常见的一种连接元件,它在机械传动以及定位中起到重要作用。
对于螺纹的绘制,机械制图中通常采用螺旋线的方式来表示,以及主要参数的标注方式。
在机械制图中表示螺纹时,需要标注螺纹直径(d)、节距(P)、螺纹高度(h)、螺距(L)、螺纹轴向长度(L1)等参数。
螺旋线的绘制可以采用软件绘图工具或者手动绘制,需要注意要标注每一个螺纹的起始位置、朝向和两端位置。
此外,在机械制图中展示螺纹时一般采用三维立体图形表示,具有较好的立体感和视觉效果。
需要指出的是,在实际机械制图设计中,螺纹的参数标注是十分重要的。
正确的参数标注可以方便加工和制造,提高加工精度,避免出现安全隐患和使用问题。
弹簧弹簧是机械传动中重要的控制元件,主要起到承受压力或拉力的作用。
对于弹簧的绘制,机械制图中通常采用钢丝圈线的方式来表示,以及主要参数的标注方式。
在机械制图中表示弹簧时,需要标注弹簧直径(D)、线径(d)、圈数(n)、自由长度(L0)、收缩长度(L1)、拉伸长度(L2)等参数。
弹簧的绘制需要注意弹簧的起始位置和朝向,以及尽可能表现出弹簧的二维和三维立体感。
需要指出的是,在实际机械传动设计中,弹簧的设计和计算是十分重要的。
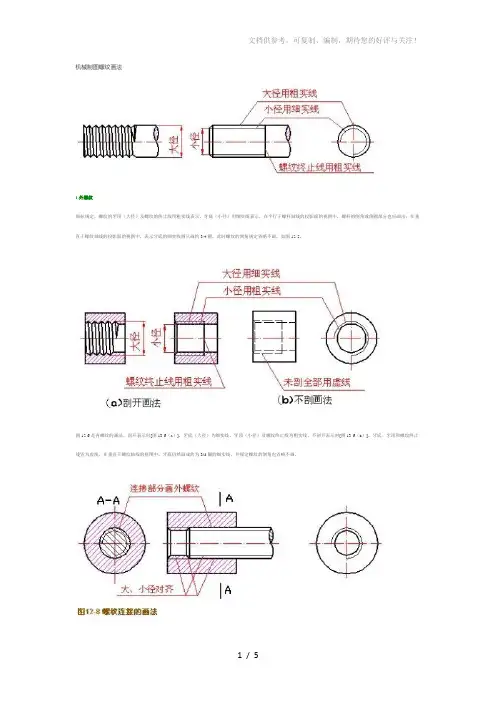
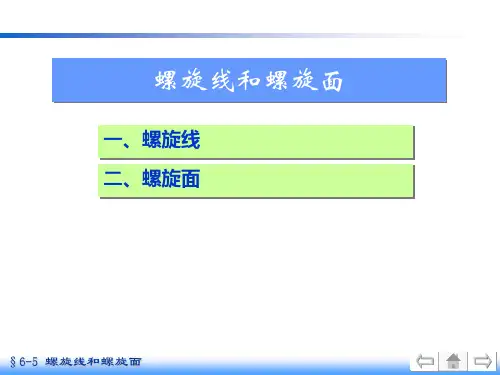
机械制图螺纹画法1.外螺纹国标规定,螺纹的牙顶(大径)及螺纹的终止线用粗实线表示,牙底(小径)用细实线表示,在平行于螺杆轴线的投影面的视图中,螺杆的倒角或倒圆部分也应画出;在垂直于螺纹轴线的投影面的视图中,表示牙底的细实线圆只画约3/4圆,此时螺纹的倒角规定省略不画,如图12-5。
图12-6是内螺纹的画法。
剖开表示时[图13-6(a)],牙底(大径)为细实线,牙顶(小径)及螺纹终止线为粗实线。
不剖开表示时[图13-6(b)],牙底、牙顶和螺纹终止线皆为虚线。
在垂直于螺纹轴线的视图中,牙底仍然画成约为3/4圈的细实线,并规定螺纹的倒角也省略不画。
绘制不穿通的螺孔时,一般应将钻孔的深度和螺纹部分的深度分别画出,如图12-7(a)。
当需要表示螺纹收尾时,螺纹尾部的牙底用与轴线成30o的细实线表示,如图12-7(b)。
图12-7(c)表示出螺纹孔中相贯线的画法。
3.内、外螺纹连接的画法如图12-8表示装配在一起的内、外螺纹连接的画法。
国标规定,在剖视图中表示螺纹连接时,其旋合部分应按外螺纹的画法表示,非旋合部分仍按各自的画法表示。
4.非标准螺纹的画法画非标准牙型的螺纹时,应画出螺纹牙型,并标注出所需的尺寸及有关要求,如图12-9。
图12-9螺纹的规定标注各种螺纹的画法相同,为了便于区别,还必须在图形上进行标注。
(1) 普通螺纹的标注标注内容为:特征代号公称直径×螺距旋向—中径、顶径公差代号—旋合长度代号其中:特征代号M单线粗牙螺纹只标公称直径,单线细牙螺纹标公称直径×螺距。
旋向:分为右旋、左旋,右旋不标注,左旋用LH表示。
螺纹中径、顶径公差带代号:由表示公差等级的数字和表示公差带位置的字母所组成,如:6H、6g(内螺纹用大写字母,外螺纹用小写字母)。
如果中径与顶径公差带代号相同,则只注一个代号,如:7h;如果螺纹的中径公差带与顶径公差带代号不同,则分别标注,如:5g6g。
旋合长度:螺纹旋合长度规定为短(S)、中(N)、长(L)三种,中旋合长度不标注,特殊需要时可注明旋合长度数值,如M10-6g-40。

机械学中的螺旋原理机械学是一门关于机械、运动和力的学科,是自然科学和工程学的重要分支,有着广泛的应用和深远的意义。
在机械学中,螺旋原理是一项非常重要的基础理论,被广泛应用于各种机械设计、制造和应用中。
螺旋的定义螺旋是一种平面内沿一定方向旋转并向这个方向线性移动的曲线。
它通常由一个中心点和一条直线(轴线)组成,其中轴线是螺旋线沿着的方向线。
螺旋线一般是升旋线或降旋线,即通常所说的右旋螺纹和左旋螺纹。
螺旋线的形状可以是圆柱形、圆锥形、双扭曲线形等。
螺旋原理的应用螺旋原理在机械学中有着广泛的应用。
螺纹的应用螺纹是指在一个圆柱形或圆锥形的表面上刻划或切割出的均匀分布的螺旋形凹槽或凸起。
在机械设计和制造中,螺纹的应用非常广泛,例如螺纹联轴器、螺纹连接件、螺纹传动、螺旋桨等。
螺纹的设计和制造需要根据螺纹原理进行计算和实现。
螺杆的应用螺杆是由一个螺纹和一个短柱体组成的机械元件,它的作用是将旋转运动转化为线性运动或者将线性运动转化为旋转运动。
螺杆的应用非常广泛,例如螺旋升降机、螺旋输送机、手摇螺丝刀等。
螺杆的设计需要根据螺旋原理进行计算和实现。
螺旋副的应用螺旋副是由两个相互嵌合的螺旋面组成的机械副,可以将旋转运动转化为旋转运动、以及旋转运动转化为线性运动。
螺旋副的应用非常广泛,例如齿轮传动、丝杆传动、平面摆线传动等。
螺旋副的设计需要根据螺旋原理进行计算和实现。
螺旋马达的应用螺旋马达是一种利用螺旋副原理工作的马达,具有高速和高功率的特点,可以广泛应用于机床、冶金、矿山、化工、建筑等领域。
螺旋马达的设计需要根据螺旋原理进行计算和实现。
螺旋泵的应用螺旋泵是一种利用螺杆原理工作的泵,具有体积小、噪音小、密封性好、适用于高粘度液体等优点,可以广泛应用于石油、化工、医药、食品、造纸等行业。
螺旋泵的设计需要根据螺旋原理进行计算和实现。
总结螺旋原理是机械学中的一项非常重要的基础理论,被广泛应用于各种机械设计、制造和应用中。
从螺纹、螺杆、螺旋副、螺旋马达到螺旋泵,螺旋原理的应用已经渗透到了各个领域。

大一下机械制图螺纹知识点大一下学期,机械制图是我们机械专业的一门基础课程。
在学习机械制图的过程中,我们接触到了很多的知识点,其中螺纹是一个非常重要且常见的内容。
本文将围绕螺纹知识点展开探讨,旨在帮助大家更好地理解和应用螺纹。
一、螺纹的定义及分类螺纹是一种具有螺旋形状的零件表面,其形状呈螺旋线状,并且通常是用来进行连接或者固定的。
根据其用途和形状特点,螺纹可以分为外螺纹和内螺纹。
外螺纹是指安装在零件外表面,内螺纹则是安装在零件内部。
二、螺纹的常用表示方法在机械制图中,为了清晰地表达螺纹的特征和尺寸,通常采用几种常用的表示方法,包括剖视表示法、斜线表示法和螺纹符号表示法。
剖视表示法是通过切割零件并展开表示,使得螺纹的各个特征面呈现在平面上,以便更清晰地观察和测量。
斜线表示法则是利用斜线来表示螺纹的高度和斜距,以及表示螺纹的方向和类型。
螺纹符号表示法是通过特定的符号和尺寸来表示螺纹的特征和尺寸,包括螺距、峰距、轮廓等信息。
三、螺纹的设计和应用螺纹的设计和应用是机械制图中的重要内容,它不仅涉及到零件的制造和加工,还关系到装配和使用的方便性。
在进行螺纹设计时,我们需要考虑到螺纹的型号和参数选择、螺纹的尺寸和公差、螺纹的加工工艺等因素。
不同类型和规格的螺纹适用于不同的工作环境和要求,因此在设计中,我们需要根据实际需要进行选择。
在螺纹的应用中,我们常常需要进行螺纹的配合和连接。
螺纹的配合是指内、外螺纹之间的连接,它可以分为干涉配合和间隙配合两种。
干涉配合是指内螺纹和外螺纹之间没有干涉,可以直接配合使用。
间隙配合则是在内、外螺纹之间留一定的间隙,形成一定的间隙配合。
对于不同的工作要求和零件设计,我们需要选择合适的螺纹配合方式。
四、螺纹的重要性和注意事项螺纹在机械制图和机械设计中具有非常重要的地位和作用。
它不仅可以连接和固定零件,还可以提高工作效率和质量。
在进行螺纹设计和使用时,我们也需要注意一些问题,以确保螺纹的质量和可靠性。
§9.3 螺旋线和螺旋面本课主要内容:(螺旋线、螺旋面)螺旋线螺旋线是应用比较广的一种空间曲线。
螺旋线可以在不同的曲面上形成,常见的螺旋线有圆柱螺旋线、圆锥螺旋线等。
1.圆柱螺旋线(1) 柱螺旋线的形成当一动点A沿着导圆柱的母线作等速直线运动,同时该母线又绕圆柱面轴线作等角速回转运动,点A的运动轨迹称为圆柱螺旋线(图9-19a)。
图 9-19;圆柱螺旋线形成、投影画法及螺旋线的展开(2) 圆柱螺旋线的基本要素(a)导圆柱面的直径D。
(b)导程Ph动点A绕圆柱面回转一周沿轴向移动的距离。
(c)旋向螺旋线的旋转方向有右旋及左旋之分。
(3) 圆柱螺旋线的画法根据圆柱螺旋线的三个基本要素,可画出圆柱螺旋线的投影图如图9-19b所示(右旋螺旋线)。
(a) 将导面的水平投影(圆周)等分为若干等分(图中为12等分),并按逆时针方向顺次标记为0、1、2…11、12各等分点;而在正面投影图上将导程Ph作同数等分(12等分)并自上而下标记为00、10、20、30…110、120、各等分点。
(b) 过等分点00 、10 、20 、30 …110 、120 作OX轴平行线与过水平投影各等分点0、1、2…11、12,作OX轴的垂线对应相交,可得0' 、1'、2'…11'、12',然后依次光滑连接即得螺旋线的正面投影(不可见部分画成虚线),螺旋线的水平投影在圆周上。
(c) 圆柱螺旋线的展开图6—19是圆柱螺旋线的展开图,螺旋线是周长πD和导程P h 为直角三角形的斜边。
每一导程螺旋线长度 L=。
图中的 a 为圆柱螺旋线的升角 tg a=,它的余角 b 称为螺旋角。
2.圆锥螺旋线一动点沿圆锥面上的直母线作匀速直线运动,而母线同时又绕圆锥轴线作等角速回转运动,则动点在锥面上的轨迹称为圆锥螺旋线。
母线回转一周时,动点沿轴线方向移动的距离 Ph 称为导程。
圆锥螺旋线的画法和圆柱螺旋线类似,也是将导面的底圆和图 9-20圆锥螺旋线画法导程分为同数等分(12等分);在圆锥面上作出各条素线的投影,各条素线的正面投影与过导程等分点所作的轴平行线相交,可得a'、 b'、c'…m',既为圆锥螺旋线上各点的正面投影,再求出相应的水平投影 a、b…m,然后依次光滑连接各点(不可见部分画为虚线),既得圆锥螺旋线的两面投影。