线性代数及其应用(李学银,盛集明主编)思维导图
- 格式：xmin
- 大小：5.50 KB
- 文档页数：1
下载文档原格式
合集下载
线性代数及应用PPT课件
上列各式出现的运算皆可行的前提是：矩阵的维数满 足运算要求。
证明矩阵乘法结合律：(AB)C=A(BC)=ABC 证：设
记
证明DC=AG。 因为 元为：
A的 i 行乘以B的 l 列
，
， 则DC的第i,j
得到DC的第i,j元等于AG的第i,j元。
证明 (AB)T =BTAT
证：
即
。
剩下的要证明它们的第i, j元都对应相等。设
通大学出版社
第一章 矩阵
§1.1 矩阵概念 1.1.1 矩阵概念 定义1 m × n元，排成m行n列的矩形阵列：
称作为：维是m × n的矩阵。 一般用黑体大写字母 A，B，C等表示。
简记为：
确定一个矩阵的两要素：
1．元：a ij 的值； 2．维：m，n的值。
矩阵的例： 问题：A的元和维是什么？
广矩阵进行一系列行初等变换，使得
R1R2 ••• R s [A |b]= [R1R2 ••• R s A | R1R2 ••• R s b ]=[ I n | Rb ]
(R= R1R2 ••• R s)。事实上R=A-1
可见只要将增广矩阵中A对应的那一块通过行初等变换化成 单位阵，对应b的那一块变成Rb= A-1 b，即
1.1.2 一些特殊矩阵 对于矩阵
本课程仅限于实矩阵。
n阶方阵：m=n时的矩阵，
a11 a12 a1n
A
a21 a22 a2n
或 An n
an1 an2 ann
列矩阵（列向量）：n=1，
行矩阵（行向量）：m=1，
数或标量：m=n=1。 向量的元称为分量，分量的个数称为向量的维。
例：
分别是3维列向量和4维行向量。
学习参考书目
线性代数的思维拓展核心概念总结与应用练习讲解
线性代数的思维拓展核心概念总结与应用练习讲解线性代数是一门数学领域的学科，探讨线性方程组、向量空间、线性变换等概念及其性质。
它是现代数学的重要组成部分，也是许多领域的基础，如物理学、计算机科学、经济学等。
本文将对线性代数的核心概念进行总结，并通过应用练习的方式进行讲解。
一、向量与线性方程组1. 向量的概念与基本性质向量是指具有大小和方向的量，常用箭头表示。
可以通过坐标表示，其中第i个坐标表示在第i个轴上的投影大小。
向量可以进行加法、标量乘法和内积等操作，具有交换律、结合律和分配律。
2. 线性方程组的表示与解法线性方程组是由一系列线性方程构成的方程组。
可以通过矩阵和向量的乘法表示，形如Ax=b，其中A为系数矩阵，x为未知向量，b为常数向量。
线性方程组的解可以通过高斯消元法、矩阵的逆等方式求解。
二、矩阵与线性变换1. 矩阵的概念与基本性质矩阵是由数个数构成的矩形阵列，常用大写字母表示。
矩阵的行数和列数称为矩阵的维度。
矩阵可以进行加法、标量乘法和矩阵乘法等操作，具有交换律、结合律和分配律。
2. 线性变换的定义与性质线性变换是指保持加法和数乘运算的运算法则的映射。
线性变换可以由矩阵表示，具有可逆性、保持直线与原点不变性等性质。
常见的线性变换包括旋转、缩放和切变等。
三、向量空间与特征值特征向量1. 向量空间的概念与性质向量空间是指由一组向量构成的集合，具有加法封闭性和标量乘法封闭性。
向量空间需要满足八个公理，包括零向量的存在性、加法逆元的存在性等。
2. 特征值与特征向量的定义与计算特征值是线性变换的一个重要概念，表示线性变换在某个方向上的缩放倍数。
特征向量是与特征值对应的非零向量。
计算特征值特征向量可以通过求解线性方程组(A-λI)x=0得到，其中A为变换矩阵，λ为特征值，x为特征向量。
四、矩阵的应用案例1. 线性方程组的应用线性方程组在实际问题中有广泛的应用，如平面定位、物质平衡等。
通过建立线性方程组模型，可以求解未知量的值，进而解决实际问题。
线性代数思维导图全6页及其总结
注意例5.4
若一个矩阵能与对角矩阵相似，则称此矩阵可对 角化
将给定的一组基转化成正交基
将给定的一个向量组变 为单位正交的向量组 先用施密特正交法将其 正交化，再将其单位化
n阶方阵A与对角矩阵相似的充要条件：A的每个 特征值对应的线性无关的特征向量的最大个数等
于该特征值的重数
求齐次方程组的解空间W的正交 基，并将其扩充
变为B的相似变换矩阵
施密特正交法
若矩阵A与其转置矩阵的乘 积为单位矩阵，则称A为正 交矩阵，即A的逆矩阵与其
转置矩阵相等
实对称矩阵一定能与对角矩阵相似 （可对角化），并且相似变换矩阵
可取为正交矩阵
相似矩阵秩相同
相似矩阵行列式相等
相似矩阵都可逆或不可逆，当它们都可逆时，它 们的逆矩阵也相似
相似矩阵有相同的特征多项式， 从而特征值也相同
设向量组A是子空间V中的线性无关组，且V中任 意向量是向量组A的线性组合，则称A为子空间
的一组基
注意例4.23
子空间
求已知向量在某组基下 的坐标
例4.29
行列式行与列的地位是对称的，即对 行成立的性质对列也成立，矩阵则不
然
线性代 数
对角矩阵相乘（必须同阶）， 等于各位置元素直接相乘'
(A*B)的转置等于B的转置乘以A的转置，注意B 在前，顺序换了，该性质可以推广到多元
有无穷多组解的充要条件是rank(A)=rank(B)<n 有惟一解的充要条件是rank(A)=rank(B)=n
求特征向量 和特征值
注意A必须为方阵
设A为n阶方阵，X为n维非零向量，k为常数 若 AX=kX
则称X为A的特征向量，k为特征向量X对应的特 征值，矩阵A-kE称为A的特征矩阵 det(A-kE)=0称为特征方程
人教版高中数学必修二章节思维导图全套
人教版高中数学必修二章节思维导图全套《6.1 平面向量的概念》思维导图
《6.3.1 平面向量的基本定理及加减数乘坐标运算》思维导图
《6.3.2 平面向量数量积的坐标表示》思维导图
《6.4.1平面向量在几何和物理中的运用》思维导图
《6.4.2 余弦定理、正弦定理》思维导图
《6.4.3 余弦定理、正弦定理的实际运用》思维导图
《7.1 复数的概念》思维导图
《7.2 复数的四则运算》思维导图
《7.3 复数的三角表示》思维导图
《8.1 基本立体图形》思维导图
《8.2 立体图形的直观图》思维导图
《8.3 简单几何体的表面积与体积》思维导图
《8.4 空间点、直线、平面之间的位置关系》思维导图
《8.5 空间直线、平面的平行》思维导图
《9.1 随机抽样》思维导图
《10.2 事件的相互独立性》思维导图
《10.3 频率与概率》思维导图。
线性代数知识点全面总结PPT课件
量 组 的
维 向 量 线性相关
判定 概念 判定
充要条件
线
概念
充分条件
性 相
线性无关
判定
充要条件 充分条件
关 性
概念
向
极大无关组 求法
量
概念
空
向量空间的基
间
线 Ax = b
解
有解判定R(A)≠R(B)无解 的
性 方 程 组
初行变换等阶梯形
R(A)=R(B)有解 结
构
R(A)=n仅有零解 基
Ax = 0
2、矩阵的乘法
(1)(AB)C = A ( BC ) ;
(2) A ( B + C ) =
(3) (kA)(lB) = (kl)AB;
(4) AO =OA = O.
3、矩阵的转置
(1)(AT)T = A; (3)(kA)T =kAT;
(2) (A+B)T = AT+BT; (4) (AB)T = BTAT.
A
A12
A22
An1
An2
A1n A2n
Ann
概 如果AB=BA=E,则A可逆， 念 B是A的逆矩阵.
用定义
逆 矩求
用伴随矩阵 A1 1 A
A
阵
法
分块对 A
角矩阵
0
0 1 A1
B
0
0 0
B1
B
A1 0
0
A1
B1
0
|A| ≠ 0 , A
证 法
可|A逆| =.0 , A不可 逆AB .= E , A与B互逆.
总 有 解R(A)<n有非零解
A+B = ( aij + biAj与) B同型
线性代数各章知识及脉络图
j1
j1
i, j1
2、设 A aij ， Aij 是 aij 在 det A 中的代数余子式，求证
-4-
cn c1 cn1cn L
c2c3
按第一行展开
a11 L a21 L M an1 L
a1,n1 a2,n1
1
a1n
1
a2n
M
a12 L a22 L M
xn x j
xn1 x j L
x3 x j
x2 x j
n1 j1
n2 j1
2 j1
1 j1
xn xn1 xn xn2 L xn x2 xn x1
xn1 xn2 xn1 xn3 L xn1 x2 xn1 x1
1
n i 1
1 ai
n i 1
ai
M
an n1
1 a1 b1 a1 b2 L
○2 a2 b1 1 a2 b2 O
M
OO
a1 bn a2 bn 。
M
an b1
an b2 L 1 an bn
1 b1
b2 L
0 1 a1 b1 a1 b2 L
1 n2
○3 爪型行列式专辑
爪型行列式形如：
方法：将 D 的第 i+1 列乘以 ci i 1, 2,L , n都加到第 1 列，得
ai
有些行列式经过适当的变化可以化为行列式，再采用上述方法计算。
a1 x x L x a2 x L 【例】： Dn x x a3 L M M MO
x x xL
1
L
1 an n1
1 1 1L
线性代数及应用
目录分析
第一节行列式概念的 引进
第二节排列
第三节 n阶行列式 第四节行列式的性质
01
第五节行列 式按行（列） 展开
02
第六节克莱 姆法则
03
第七节应用 实例
04
本章内容小 结
05
总习题一 （A）
06
总习题一 （B）
第一节矩阵的概念及 运算
第二节逆矩阵
第三节分块矩阵
第四节矩阵的初等变 换和初等矩阵
读书笔记
又一本教科书，摆定义，套公式。 有个说法，如果一本线性代数的树第一章是讲行列式的，那就不用看了。 书中知识点编写的浅显易懂，即使大学从没有学过线性代数的同学，也能看懂并学会，是一本很有用的书。 看了一下，这本书其实就是搬概念讲的，没有形象化的引入，对初学者一点不友好。 知识点和别的教材大同小异，甚至一些定理性质的证明说的还很笼统，但是部分例题的解题方法、大量难度 适中的习题和应用实例是本书的亮点。 为了以后看机器学习的书，重新简单过了一遍了线性代数。 当年大学的专业课程，现在读完，犹如醍醐灌顶，为当年学的很渣而惭愧，看完这本书，我决定把大学的数 学专业课程再学一遍……但愿能看完吧。 建议先在哔哩哔哩上先看一遍3blue1brown《线性代数的本质》系列课程，博主用图形化的方式解释了数字 背后的意义，非常棒。 大学时候我《线性代数》是满分，然而考完一次都没用过。
精彩摘录
这是《线性代数及应用》的读书笔记模板，可以替换为自己的精彩内容摘录。
感谢观看
第一节线性空间
第二节线性空间的基、 维数与坐标
第三节基变换与坐标 变换
第四节线性变换
第五节应用实 例
本章内容小结
第一节 MATLAB基本 操作
第二节矩阵算术运算
线性代数思维导图全6页及其总结
C(A+B)=CA+CB
k
(kA)B=A(kB)
0
AB AB Ak
*A l
E (E+A)(E+A)=E*exp(2)+2A+A*exp(2)
k
=0
|A|=0
AXA=0ĺ|A|X|A|=0|A|=0
En
E
k=
X
A Ak
n-1 A
A
ad-bc=0ĺa/b=c/d
=1 X
A
0
AB=BA=E
|A|
0
r(A)=m
变为B的相似变换矩阵
施密特正交法
若矩阵A与其转置矩阵的乘 积为单位矩阵，则称A为正 交矩阵，即A的逆矩阵与其
转置矩阵相等
实对称矩阵一定能与对角矩阵相似 （可对角化），并且相似变换矩阵
可取为正交矩阵
相似矩阵秩相同
相似矩阵行列式相等
相似矩阵都可逆或不可逆，当它们都可逆时，它 们的逆矩阵也相似
相似矩阵有相同的特征多项式， 从而特征值也相同
当系数矩阵为方阵时，要马上联系到行 列式
有一齐次方程组，AX＝0，其含n条方程，其必 定有解
有解的充要条件是rank(A)=rank(B)
无解的充要条件是rank(A)<rank(B) 若系数矩阵为方阵，方程组有唯一
解的充分条件为det(A)不等于0
当rank(A)=n,齐次方程组仅有零解 当rank(A)=r<n,齐次方程组有无穷多解
将nX2n矩阵(A | E)进行一系 列行初等变换，直到变成( E | A-1)，即得方阵A的逆矩阵
用初等变换逆 矩阵
若A是可逆矩阵则有det(A-1)=(detA)-1
大一线性代数知识点图文
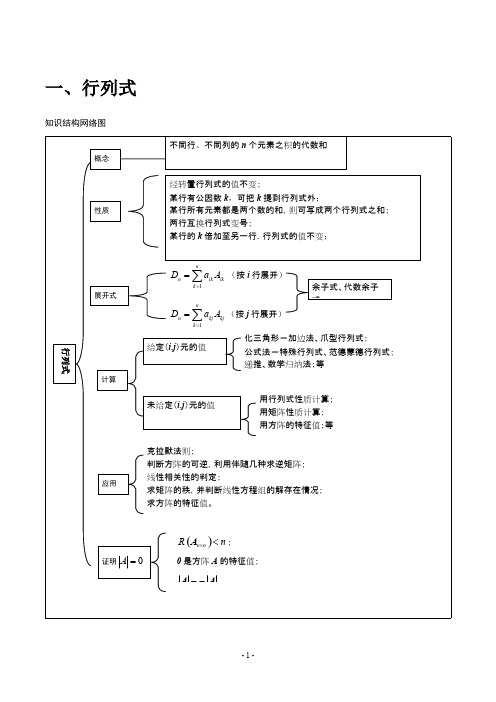
大一线性代数知识点图文线性代数是大一学生必修的一门数学课程，它主要研究向量空间、线性变换和矩阵等基本概念与性质。
本文将通过图文的方式介绍一些大一线性代数的基础知识点，帮助读者更好地理解这门课程。
1. 向量的基本概念向量是线性代数的基础，它可以表示空间中的一个点或一个方向。
向量通常用箭头表示，箭头的长度表示向量的大小，箭头的方向表示向量的方向。
【图片：向量示意图】在二维平面上，一个向量可以表示为 (x, y) 的形式，其中 x 和y 分别是向量在 x 轴和 y 轴上的分量。
在三维空间中，一个向量可以表示为 (x, y, z) 的形式，其中 x、y 和 z 分别是向量在 x 轴、y 轴和 z 轴上的分量。
2. 向量的加法与减法向量的加法与减法是线性代数中的基本运算。
两个向量相加，只需将它们的相应分量相加即可；两个向量相减，只需将它们的相应分量相减即可。
【图片：向量加法与减法示意图】3. 向量的数量积与向量积向量的数量积（也称为点积或内积）和向量积（也称为叉积或外积）是向量运算中的重要概念。
数量积的定义如下：设有两个向量 a 和 b，它们的数量积记为a·b，计算方法为a·b = |a| |b| cosθ，其中 |a| 和 |b| 分别表示向量 a 和b 的长度，θ 表示 a 和 b 之间的夹角。
【图片：数量积示意图】向量积的定义如下：设有两个向量 a 和 b，它们的向量积记为a×b，计算方法为a×b = |a| |b| sinθ n，其中 |a| 和 |b| 分别表示向量 a 和 b 的长度，θ 表示 a 和 b 之间的夹角，n 表示垂直于 a 和 b 所在平面的单位法向量。
【图片：向量积示意图】4. 矩阵的基本概念矩阵是线性代数中另一个重要的概念，它是一个以矩形为形状的数表。
矩阵的元素可以是实数或复数。
矩阵通常用大写字母表示，如 A、B。
【图片：矩阵示意图】矩阵有多种运算，包括矩阵的加法与减法、矩阵的乘法等。
线性代数及其应用PPT课件
金融数据的线性模型分析
线性回归模型
利用线性代数中的矩阵运算和线性方 程组求解方法，对金融数据进行回归 分析，预测未来趋势。
主成分分析
通过线性代数中的特征值和特征向量 计算，将金融数据降维，提取主要影 响因素，便于分析和决策。
图像处理中的矩阵运算
图像变换
利用矩阵运算对图像进行缩放、旋转 、平移等几何变换，实现图像的精确 控制。
征值和Байду номын сангаас征向量。
特征值计算 的算法
特征值计算是矩阵分析中的重要内容，可以用于解决 许多实际问题，如振动分析、控制论、经济学等。
数据降维与可视化
数据降维的必要性
数据降维的方法
可视化的意义
可视化的工具和技术
在处理高维数据时，数据的维 度可能非常高，导致数据难以 分析和处理。数据降维可以将 高维数据降为低维数据，便于 分析和可视化。
矩阵分解与特征值计算
矩阵分解是将一个复杂的矩阵分解为几个简单的、易 于处理的矩阵，以便进行计算和分析。
输入 矩阵标分题解的
方法
常见的矩阵分解方法包括LU分解、QR分解、SVD分 解等。这些方法可以将一个矩阵分解为一个下三角矩 阵、一个上三角矩阵和一个正交矩阵等。
矩阵分解的 定义
特征值计算 的应用
特征值计算的常用算法有QR算法、Jacobi方法、 Power方法等。这些算法可以用于计算给定矩阵的特
数值计算稳定性
数值计算稳定性
在进行数值计算时，由于计算机的舍入误差，可能会导致 计算结果的误差。线性代数中的一些算法和技巧可以帮助 提高数值计算的稳定性，减少误差。
数值稳定性的评估
评估数值稳定性的方法包括观察计算结果的收敛性和稳定 性，以及比较不同算法的误差和稳定性。