材料力学 平面图形的几何性质 安徽理工大学精品课程要点
- 格式：doc
- 大小：264.50 KB
- 文档页数：15
下载文档原格式
合集下载
平面图形的几何性质-材料力学
h
v
F
d
v=0
d
Fst
Fd
Ud
1 2
k
d
2
k12FdFdd
d
O
st
1 Ud 2 Fd d
mgT(h Vd )U12dFd d
F
d
mg
k Fd Fst
d st
Fst
Fd
mg(h
d
)
1 2
mg
d st
d
O
st
d 2 2 st d 2h st 0
实验证明，动载荷作用下，如构件的应力不超 过比例极限，胡克定律仍然适用。
动载荷：载荷导致构件各点均有加速度。
两类动载荷问题：
加速度恒定可知 构件匀加速过程
加速度未知 冲击问题
动静法
动力学普遍方程 或达朗贝尔原理
能量法
机械能守恒定理
§10-2 等加速直线运动或匀速转动时构件动 应力计算（动静法）
一、等加速度直线运动时构件动应力计算 吊笼质量m；钢索横截面积A，密度ρ。求吊 笼以匀加速度a上升时钢索任意截面上的应力。
ma mg
若吊笼无加速度
Fst gAx mg
动荷系数 Kd
Fd KKdd Fst d KKdd st
二、匀速转动时构件动应力计算 薄壁圆环，平均直径D，横截面积A，材料密度 ρ，求其以匀角速度ω转动时横截面动应力。
qd
qd
环 有内关q应，d 力 与与 截 面密A积度2 无和D2关线。速保度
材料力学
第十章 动载荷
基本要求
1. 理解动载荷、动应力的基本概念； 2. 掌握两类动载荷问题的求解方法； 3. 了解提高构件抗冲击能力的措施； 4. 了解冲击韧性的概念。
《材料力学》课程讲解课件附录I平面图形几何性质
解：
y
d
S x
yd A
A
2 yb( y) d y
0
b(y)
C
xc
yc
d
2 y2
R2 y2 d y d3
0
12
x
d
yc
Sx A
d3 12 πd 2 8
2d 3π
b( y) 2 R2 y2
29
yc
Sx A
d3 12 πd 2 8
2d 3π
y
2、求对形心轴 xc 的惯性矩
Ix
πd 4 64 2
3、惯性积是对轴而言。
y
z
dA
4、惯性积的取值为正值、负值、零。
y
5、规律：
o
z
20
5、规律：
Izy
zydA
A
0
y
dA z z dA
y
y
z
o
两坐标轴中，只要有一个轴为图形的对称轴，则 图形这一对坐标轴的惯性积为零。
21
对比记忆 静矩、形心；惯矩和惯性半径；它们都是反映截
面面积关于坐标轴分布情况的物理量。 静矩=（面积）（形心坐标） 惯矩=（面积）（惯性半径）2
z
o
dA y
z
全面积对z轴的惯性矩: I z y2dA,
2 z2 y2
全面积对y轴的惯性矩: I y A z2dA
A
15
Iz y2dA, I y z2dA
A
A
y
z
dA
y
o
z
2、量纲：［长度］4；单位：m4、cm4、mm4。 2 z2 y2
3、惯性矩是对轴而言（轴惯性矩）。
A
材料力学附录I 平面图形的几何性质2形心主轴和形心主惯性矩
i1
i1
i1
材料力学 附录I 平面图形的几何性质
例I-4-1：已知三角形对底边(x1轴)的惯性矩为bh3/12，
求其对过顶点的与底边平行的x2轴的惯性矩。
解：由于x1、x2轴均非形心轴，所以不
x2
能直接使用平行移轴公式，需先求出 三角形对形心轴xC的惯性矩，再求对
h xC
h/3
x1
x2轴的惯性矩，即进行两次平行移轴
3.求截面形心主惯性矩的方法
①建立坐标系
②计算面积和面积矩 ③求形心位置
x
Sy A
xi Ai A
y
Sx A
yi Ai A
④建立形心坐标系；求：IyC ， IxC ， IxCyC
⑤求形心主轴方向 — 0
tg2
0
2I xCyC I xC I yC
⑥求形心主惯性矩
I I
xC0 yC0
I
x
C
I 2
b
：
I xC
I x1
a12 A
bh3 12
h 2 3
bh 2
bh3 36
I x2
I xC
a22 A
bh3 36
2h 2 3
bh 2
bh3 4
材料力学 附录I 平面图形的几何性质
例I-4-2：求图示T型截面对形心轴的惯性矩。
30
5
30
5
材料力学 附录I 平面图形的几何性质
30
求T形截面对形心轴的惯性矩
C O
10 150yC x1
x
由于对称知： xC=0
材料力学 附录I 平面图形的几何性质
§I-2 惯性矩和惯性半径
一、惯性矩
第五章平面图形几何性质(讲稿)材料力学教案(顾志荣)
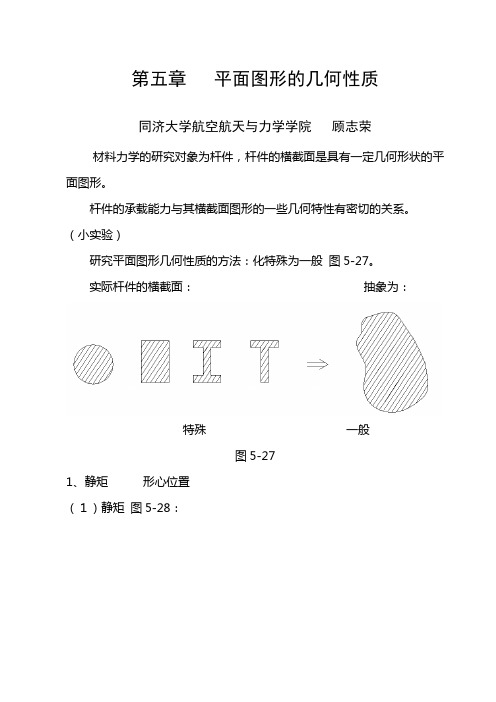
第五章平面图形的几何性质同济大学航空航天与力学学院顾志荣材料力学的研究对象为杆件，杆件的横截面是具有一定几何形状的平面图形。
杆件的承载能力与其横截面图形的一些几何特性有密切的关系。
（小实验）研究平面图形几何性质的方法：化特殊为一般图5-27。
实际杆件的横截面：抽象为：特殊一般图5-271、静矩形心位置（１）静矩图5-28：图5-28微面积dA 与Z 轴、Y 轴间距离的乘积ydA,zdA 分别称为微面积dA 对Z 轴、Y 轴的静矩。
整个截面对Z 轴、Y 轴的静矩可用下式来定义：（若把A 看作力）定义：截面A 对Z 轴：⎪⎭⎪⎬⎫==⎰⎰Ay A ZSZdA S ydA （４-1） 截面A 对Y 轴：计算：①对（４-1）式直接积分：②若已知截面的形心位置C ，则y Z S S ,可以写成：⎭⎬⎫==c Z c Y AY S AZ S （４-2）（２）形心的位置：⎪⎪⎭⎪⎪⎬⎫==A S Z A S Y y C Z C （４-3）性质：①截面对某一轴的静矩等于零，则该轴必通过形心。
②截面对通过形心的轴的静矩恒等于零，即： ;0=ZC S 0=YC S决定因素：静矩与截面尺寸、形状、轴的位置有关。
数值范围：可以为正、或负、或等于零。
单位：333,,m cm mm （３）组合截面的静矩：⎪⎪⎭⎪⎪⎬⎫==∑∑==n i i i y n i i i Z A S Y A z S 11（４-4） 即组合截面的整个图形对于某一轴的静矩，等于各组部分对于同一轴静矩代数和。
（４）组合截面的形心位置：⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫====∑∑∑∑====n i i ni i i y ni i ni i i z A Z A AS A Y A AS c c z y 1111（4-5） 例题5-7 求图5-29所示截面图形的形心。
图5-29解：把T 形看成为由矩形Ⅰ和Ⅱ组成 ∵y 轴是对称轴 ∴形心必在y 轴上① 求?'=Z S216002080mm A I =⨯= A Ⅱ=2240020120mm =⨯ mm y c 10=I （到Z ′轴） y c Ⅱ=60+20=80mm则：3120800802400101600'mm Y A ni ii z s =⨯+⨯==∑=②求c y＝？c y＝As z ＝∑∑==ni ini i i A Y A 11＝201202080208000⨯+⨯＝52mm 2、惯性矩（形心主惯性矩） 惯性半径 极惯性矩图5-30定义：（1）惯性矩⎪⎭⎪⎬⎫==⎰⎰A yA Z dA Z I dA y I 22（4-6） 定义为截面对z 轴,y 轴的惯性矩。
材料力学4平面图形的几何性质
分析：可用排除法分析 x "、y "为形心主惯性轴，图形为非对称图形 故有I x" ¹ I y" 依此可知正确答案为B 至于其它各项需要经过计算或分析得到
六 截面图形的几何性质部分习题及解答
【习题5-30】如图所示正方形截面，其中C点为形心，K为边界上任 一点，则过C点和K点主轴的对数为(B )。
(A)过C点有两对正交的形心主轴，过K点有一对正交主轴
五 转轴公式 截面的主惯性轴和主惯性矩
小结 设矩轴的原点为平面图形上任意点O，则其主惯性轴称 为过O点的主惯性轴 平面图形对过O点的主惯性轴有以下重要性质：
1、平面图形对主惯性轴的轴关性矩取极大（极小） 值；其中一个为极大值；另一个为极小值
2、平面图形对主惯性轴的惯性积必为零。 y
y’
x
dA
x1
y y1
α4 d D
)
=
D2 + d 2 4
Ix = iy =
πD4 64
(1 α=
α4 d D
)
IP
D2 + d 2 4
=
πD4 32
α=
(1- α4 )
d D
Ixy = 0
四 平行移轴定理
一、平行移轴定理：（与转动惯量的平行移轴定理类似）
y
y’
x y’ dA
a r
bC y
x’
以形心为原点，建立与原坐标轴平行
形心主惯性矩的大小为：
I y0 I z0
=
Iy
+ Iz 2
±
æ èç
Iy
2
Iz
ö ø÷
2
+
I
2 yz
58.2 = cm4
六 截面图形的几何性质部分习题及解答
【习题5-30】如图所示正方形截面，其中C点为形心，K为边界上任 一点，则过C点和K点主轴的对数为(B )。
(A)过C点有两对正交的形心主轴，过K点有一对正交主轴
五 转轴公式 截面的主惯性轴和主惯性矩
小结 设矩轴的原点为平面图形上任意点O，则其主惯性轴称 为过O点的主惯性轴 平面图形对过O点的主惯性轴有以下重要性质：
1、平面图形对主惯性轴的轴关性矩取极大（极小） 值；其中一个为极大值；另一个为极小值
2、平面图形对主惯性轴的惯性积必为零。 y
y’
x
dA
x1
y y1
α4 d D
)
=
D2 + d 2 4
Ix = iy =
πD4 64
(1 α=
α4 d D
)
IP
D2 + d 2 4
=
πD4 32
α=
(1- α4 )
d D
Ixy = 0
四 平行移轴定理
一、平行移轴定理：（与转动惯量的平行移轴定理类似）
y
y’
x y’ dA
a r
bC y
x’
以形心为原点，建立与原坐标轴平行
形心主惯性矩的大小为：
I y0 I z0
=
Iy
+ Iz 2
±
æ èç
Iy
2
Iz
ö ø÷
2
+
I
2 yz
58.2 = cm4
材料力学平面图形的几何性质
平面图形的剪切中心和弯曲中心
剪切中心：平面图形中，剪切中心是剪切面上各点剪切应变之和为零的点，与该点距离最近的各 点组成的剪切面称为剪切面。
弯曲中心：平面图形中，弯曲中心是弯曲面上各点弯曲应变之和为零的点，与该点距离最近的各 点组成的弯曲面称为弯曲面。
刚性特性：平面图形在剪切和弯曲变形下，其几何形状和尺寸保持不变的性质称为刚性特性。
剪切中心和弯曲中心在平面图形中的作用：在平面图形中，剪切中心和弯曲中心是确定平面图形 在剪切和弯曲变形下应力和应变分布的关键点，对于分析平面图形的受力特性和稳定性具有重要 意义。
平面图形的抗扭刚度和抗弯刚度
抗扭刚度：表示材料 抵抗扭转变形的能力， 与平面图形的几何形 状和尺寸有关。
抗弯刚度：表示材料 抵抗弯曲变形的能力， 与平面图形的几何形 状、尺寸和材料本身 的弹性模量有关。
计算方法：根据 几何学原理，可 以通过平面图形 的边长、角度等 参数计算面积和
周长
平面图形的形心、质心和重心
形心：平面图形 中所有点组成的 面积的平均位置， 表示图形的几何 中心。
质心：平面图形 中所有点组成的 物质质量的平均 位置，表示图形 的质量中心。
重心：平面图形 中所有点组成的 重力场强度的平 均位置，表示图 形的重力中心。
平面图形稳定性分析的方法：通过力学分析、数学建模、实验测试等方法，对平面图形的稳定性 进行分析。
平面图形稳定性在工程中的应用：广泛应用于桥梁、建筑、机械等领域，以确保结构的稳定性和 安全性。
平面图形失稳的临界力和临界应力
定义：临界力是 指使平面图形失 稳的最小外力， 而临界应力则是 指在该外力作用 下，平面图形达 到失稳状态时的 应力值。
平面图形的动力学特性
材料力学第5章 平面图形的几何性质
2 A
y
I y =∫ x 2 dA
二、极惯性矩： 极惯性矩： 矩。
A
x
dA y x
是面积对极点的二次
ρ
I ρ =∫ ρ 2 dA=I x +I y
A
材料力学
三、惯性积：面积与其到两轴距离之积。 惯性积：
I xy =∫ xydA
A
y 是对称轴， 如果 x 或 y 是对称轴，则Ixy =0 x dA y x
材料力学
x y
dA y1 x1 x
I x +I y Ix −I y I x1 = + 2 cos2α−I xysin2α 2
α
材料力学
I x +I y I x −I y I y1 = − 2 cos2α−Ixysin2α 2 I x −I y Ix1y1 = sin2α+Ixy cos2α 2
tg 2α 0 =−
2 I xCyC I xC − I yC
I x0 I x + I y I x −I y 2 2 主惯性矩： = ± ( ) + I xy 2 2 I y0
材料力学
2.形心主轴和形心主惯性矩： 主轴过形心时，称其为形心主轴。平面图形对形心主轴之 惯性矩，称为形心主惯性矩
i i
1
1
2
A2
A
A1 + A2
x
5×(−70×110) = =−20.3 120×80−70×110
图(b)
材料力学
§5 - 2
惯性矩、惯性积、 惯性矩、惯性积、极惯性矩
是面积与它到轴的距离的平方之积。
与转动惯量类似） 一、惯性矩：(与转动惯量类似） 惯性矩： 与转动惯量类似
y
I y =∫ x 2 dA
二、极惯性矩： 极惯性矩： 矩。
A
x
dA y x
是面积对极点的二次
ρ
I ρ =∫ ρ 2 dA=I x +I y
A
材料力学
三、惯性积：面积与其到两轴距离之积。 惯性积：
I xy =∫ xydA
A
y 是对称轴， 如果 x 或 y 是对称轴，则Ixy =0 x dA y x
材料力学
x y
dA y1 x1 x
I x +I y Ix −I y I x1 = + 2 cos2α−I xysin2α 2
α
材料力学
I x +I y I x −I y I y1 = − 2 cos2α−Ixysin2α 2 I x −I y Ix1y1 = sin2α+Ixy cos2α 2
tg 2α 0 =−
2 I xCyC I xC − I yC
I x0 I x + I y I x −I y 2 2 主惯性矩： = ± ( ) + I xy 2 2 I y0
材料力学
2.形心主轴和形心主惯性矩： 主轴过形心时，称其为形心主轴。平面图形对形心主轴之 惯性矩，称为形心主惯性矩
i i
1
1
2
A2
A
A1 + A2
x
5×(−70×110) = =−20.3 120×80−70×110
图(b)
材料力学
§5 - 2
惯性矩、惯性积、 惯性矩、惯性积、极惯性矩
是面积与它到轴的距离的平方之积。
与转动惯量类似） 一、惯性矩：(与转动惯量类似） 惯性矩： 与转动惯量类似
{材料力学}平面图形的几何性质
C(zc, yc)
面积A
z1
a
o
z
已知： I yc , I zc , I yczc 计算： I y , I z , I yz
y y1 a
z z1 b
z1 —y1为形心坐标系
19
Iz y2dA ( y1 a )2 dA y12dA 2a y1dA a2 dA
Izc 2a • zc • A a2 A Izc a2 A
dI z1 0
d
2(
I
z
2
I
y
sin
2
I
yz
cos
2
)
0
tg2 2I yz
Iz Iy
dI y1 0
d
说明取极大（或极小）惯性矩时
I y1z1 0
惯性积等于零
28
由方程 tg2 2I yz 求解出
Iz Iy
1, 2
1, 2 确定两个相互垂直的轴 —— 主惯性轴
也就是说：1、对于给定的截面
坐标转换的矩阵形式
y1 z1
cos sin
sin y
cos
z
23
操作式的推导 A( y, z) A( y1, z1) 用投影代替转动 《y 变 y1 的操作》
1、y（AF）向 y1 轴投影得 y1 + GF
y cos y1 GF
2、再减去GF 得y1
y1 y cos GF y cos z sin
y2 cos2 dA z2 sin 2dA 2 yz sin cosdA
1
cos 2
2
y2dA
1 cos 2
2
z2dA sin
2
yzdA
1 cos 2
材料力学 附录A+平面图形的几何性质
yC
S x A yC 0
S y A xC 0
yC 0
C
A O
xc
xC 0
x
性质1: 图形对形心轴的静矩为零。反之，图形对某轴的静矩为 零，则该轴必为形心轴。
例1 试确定下图的形心。
10
解：组合图形，用正负面积法求解。
y
120 C2 C1(0,0) C2(-35,60)
特别指出：
惯
惯
性
性
矩——对某一轴而言
积——对某一对正交轴而言
极 惯 性 矩——对某一点而言
四、惯性半径 在力学计算中，有时把惯性矩写成
I x A i x2
即：
I y A i y2
ix
iy
试问 即： 注意：
Ix A Iy
——图形对 x 轴的惯性半径 单位： m
A
A
——图形对 y 轴的惯性半径
⑥求形心主惯性矩
I xC I yC 2 2 I xC0 I xC I yC ( ) I xCyC 2 2 I yC0
例3 在矩形内挖去一与上边内切的圆，求图形的形心 主轴。(b=1.5d) y 2d d
yC
O
x1
解： ①建立坐标系如图。 ②求形心位置。
xi Ai 0 0 x A A 2 d d y A y i i 2 4 0.177d 2 A 2 d 3d 4
附录A A1 A2 A3 A4 静矩与形心
平面图形的几何性质
惯性矩、惯性积、极惯性矩 惯性矩和惯性积的平行移轴定理 转轴公式 主惯性矩
平面图形的几何性质 ——反映平面图形的形状与尺寸的几何量。 如： 在轴向拉（压）中：
S x A yC 0
S y A xC 0
yC 0
C
A O
xc
xC 0
x
性质1: 图形对形心轴的静矩为零。反之，图形对某轴的静矩为 零，则该轴必为形心轴。
例1 试确定下图的形心。
10
解：组合图形，用正负面积法求解。
y
120 C2 C1(0,0) C2(-35,60)
特别指出：
惯
惯
性
性
矩——对某一轴而言
积——对某一对正交轴而言
极 惯 性 矩——对某一点而言
四、惯性半径 在力学计算中，有时把惯性矩写成
I x A i x2
即：
I y A i y2
ix
iy
试问 即： 注意：
Ix A Iy
——图形对 x 轴的惯性半径 单位： m
A
A
——图形对 y 轴的惯性半径
⑥求形心主惯性矩
I xC I yC 2 2 I xC0 I xC I yC ( ) I xCyC 2 2 I yC0
例3 在矩形内挖去一与上边内切的圆，求图形的形心 主轴。(b=1.5d) y 2d d
yC
O
x1
解： ①建立坐标系如图。 ②求形心位置。
xi Ai 0 0 x A A 2 d d y A y i i 2 4 0.177d 2 A 2 d 3d 4
附录A A1 A2 A3 A4 静矩与形心
平面图形的几何性质
惯性矩、惯性积、极惯性矩 惯性矩和惯性积的平行移轴定理 转轴公式 主惯性矩
平面图形的几何性质 ——反映平面图形的形状与尺寸的几何量。 如： 在轴向拉（压）中：
材料力学课件—平面图形几何性质
Sy zd A zd A zd A zd A
A
A1
A2
An
S y1 S y2 S yn S yi Ai zCi
Sz Szi Ai yCi
例：平面图形如图所示，试确定该图形的 形心位置，并计算该图形对z 轴的面积矩。
50
z
10
60 y 10
50 10
C1
O
y
z
dA A
∫ z
Sy = zdA
A
S z =∫ ydA A
量纲：长度3， 单位：m3
y
1.面积矩不仅与平面图形的面积有关，
还与平面图形的形状、坐标轴的位置有关。
2.面积矩可正、可负，也可为零。
二、形心的位置
∫ zdA
zC =
A
A
= Sy／A
∫ ydA
yC =
A
A
= Sz／A
S y = zC ·A
2
z d cos
2
y、z 是对称轴
P332 表A-1
I yz 0
§3 惯性矩和惯性积的平行移轴公式
z
O
a C
y'
b z' dA
zC
I z = IzC ＋ a 2 A I y = IyC ＋ b 2 A
在一组相互平行的轴中，平
y
yC
面图形对形心轴的惯性矩最小。
I y z = IyC zC ＋ ab A
Ⅱ Ⅰ
h C
① 计算惯性矩Iy、Iz和惯性积Iyz
Iy
IⅠy
I
Ⅱ y
I
Ⅲ y
z
Ⅲ
d
hd
3
db3
[
bd (b d
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
本章重点
1、静矩与形心
2、惯性矩、极惯性矩和惯性积
3、平行移轴公式、转轴公式
关键概念
静矩、惯性矩、极惯性矩、惯性积、主惯性轴、形心主惯性轴目录
§I-1 静矩和形心
§I-2极惯性矩·惯性矩·惯性积§I-3 平行移轴公式
§I-4 惯性矩和惯性积的转轴公式.截面的
§I-1 静矩和形心
一、基本概念
1. 静矩（或一次矩）
x⋅dAy⋅dA——微面积对y轴的静矩——微面积对x轴的静矩Sy=⎰AxdA——整个平面图形对y轴的静矩
Sx=⎰AydA——整个平面图形对x轴的静矩
常用单位：m3或mm3。
数值：可为正、负或0 。
2.形心坐标公式
x=xdA =Sy
AAy=ydA
ASx=A
3.静矩与形心坐标的关系
Sy=A xSx=A y
推论：截面对形心轴的静矩恒为0，反之，亦然。
二、讨论：
1.组合截面的静矩
根据静矩的定义：整个平面图形对某轴的静矩应等于它的各组成部分对同一轴的静矩的代数和，即：
Sy=∑Ai xii=1nSx=∑Ai
yii=1n
2.组合截面的形心坐标公式
组合截面静矩
Sy=∑Ai xii=1nSx=∑Aiyii=1
nn组合截面面积
A=∑Aii=1
组合截面的形心坐标公式为：
例I—1：计算由抛物线、y轴和z轴所围成的平面图形对y轴和z轴的静矩，并确定图形的形心坐标。
2z=h⎛⎝1-y⎫b2
⎪⎭22
y⎫4bh2
2⎪dy
b⎭=15
Sz=⎰ydA=
A⎰yh22 ⎫bh0⎝1-b2⎪⎭dy=4
b2
A=⎰dA=
A⎰h⎛ 1-y20⎝b形心坐标为:
⎧2⎪bh⎪ySz⎪C=A=2bh=⎪⎨3⎪4bh2⎪⎪zC=Sy==2h⎪A2bh5⎩3 例I—2：确定图示图形形心C的位置。
解：
ySC=zA=10⨯120⨯5+70⨯10⨯45
1200+700=19.7mm
zC==目录
（即截面对一点的极惯性矩，等于截面对以该点为原点的任意两正交坐标轴的惯性矩之和。
）
3.惯性积
Ixy=⎰AxydA
（其值可为正、为负或为零)
结论：截面对于包含对称轴在内
的一对正交轴的惯性积为0。
4.惯性半径
iy
y=I
Aix=Ix
A（单位：长度的一次方）
例I—3：试计算矩形截面对于其对称轴（即形心轴）x和y的惯性矩。
解：取平行于x轴的狭长条
则dA=b dy
2h
2h-2
3Ix=⎰AydA=⎰
同理bhbydy=1223hbIy=
12思考题I—1：平行四边形对形心轴x 的惯性矩应怎样计算？
§I-3 平行移轴公式
1.平行移轴公式推导左图是一面积为A的任意形状的平面，c为其形心，xcyc为形心坐标轴。
与该形心坐标轴分别平行的任意坐标轴为xy,形心c在oxy坐标系下的坐标为(a , b)任意微面元dA在两坐标系下的
坐标关系为：
x=
xC+by=yC+a
=⎰ydA=⎰(yc+a)dAIx AA22
=⎰ycdA+2a⎰ycdA+aAA22⎰AdA=Ixc+Sxc+aA
=Ixc+aA22
同理，有：⎧⎪Iy=Iyc+bA⎨I=I+abA⎪xyxycc⎩2注：式中的a、b代表坐标值，有时可能取负值。
例I—4：求图示直径为d的半圆对其自身形心轴xc的惯性矩。
解：
（1）求形心坐标b(y)=2R2-y2dSx=⎰AydA=⎰20yb(y)dyd3=⎰20y⋅2R2-y2dy=d123y=Sxd2dcA=πd2=3π（2）求对形心轴xc的惯性矩
πd44
Iπd
x=2=128
思考题I—2：O为直角三角形ABD斜边上的中点，x、y轴为过点Ｏ且分别平行于两条直角边的两根轴，关于惯性积和惯性矩有四种答案(已知b>a)：
（A）Ixy＞０（B）Ixy<０
(C)Ixy=０（D）Ix=IyA（思考题I—2）x（思考题Ibx
思考题I—3：x、y轴是过斜边中点的任意一对坐标轴（即图中α:
(1)惯性积Ixy＝＿＿(2)惯性矩Ix＝＿＿、Iy＿＿＿。
目录
§I-4惯性矩和惯性积的转轴公式.截面的
主惯性轴和主惯性矩
1. 转轴公式
新坐标系ox1y1旧坐标系o x yx1=xcosα+ysinαy1=ycosα-xsinα将上述关系代入平面图形对x1轴的惯性矩：Ix1=
⎰y2A1dA
规定：上式中的α的符号为：逆时针为正，顺时针为负。
讨论：将上述转轴公式中的前两式相加可得：
Ix1+Iy1=Ix+Iy
即，截面对于通过同一点的任意一对相互垂直的坐标轴的两惯性矩之和为一常数，并等于截面对该坐标原点的极惯性矩。
2.截面的主惯性轴和主惯性矩
从惯性积的转轴公式可推知，随着坐标轴旋转，惯性积将随着α角作周期性变化，且有正有负。
因此，必有一特定的角度α0，使截面对与该角对应的新坐标轴x0、y0的惯性积为零。
依此进行如下定义：
(1) 主惯性轴:截面对其惯性积等于0的一对坐标轴。
(2) 主惯性矩:截面对于主惯性轴的惯性矩。
(3)形心主惯性轴：当一对主惯性轴的交点与截面的形心重合时。
(4) 形心主惯性矩:截面对于形心主惯性轴的惯性矩。
3.主惯性轴位置的确定
设坐标轴转动角度为α0，则由惯性积的转轴公式及主惯性轴的定义，得：
Ix-Iy
2
经整理，得sin2α0+Ixycos2α0=0
tan2α0=-2Ixy
Ix-Iy
4.主惯性矩的确定
由上面tan2α0的表达式求出cos2α0、sin2α0后，再代入惯性矩的转轴公式，化简后可得主惯性矩的计算公式如下：
例I—6：计算截面的形心主惯性矩。
解：作形心坐标轴xcyc
图所示。
（1）求形心坐标：
(a
Ⅰ,bⅠ) 、 (aⅡ,bⅡ)
、Iyc1 , Ixc2 、Iyc2
（3）由平行移轴公式求整个截面的Ixc 、Iyc 、Ixcyc 如4）由转轴公式得
tan2α0=
-2IxcycIxc-Iyc
=1.093
y2α0=227.6 α0=113.8
Ixc0=Imax=
Ixc+Iyc
2
1+2
=321⨯10
4
mm
4
4
Iyc0=Imin=
Ixc+Iyc
2
1-2
I
xc
-Iyc
2
+4I
2xcyc
=57.4⨯10
mm
4
目录。