当前位置：文档之家 › 数学八年级下册第十八章平行四边形章末复习三作业课件 新人教版

数学八年级下册第十八章平行四边形章末复习三作业课件 新人教版

  • 格式：dps
  • 大小：1.02 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

人教版八年级数学下册第十八章-平行四边形- 小结与复习-课件PPT

人教版八年级数学下册第十八章-平行四边形- 小结与复习-课件PPT
PMEN为正方形．(请直接写出结果)
解：(1)证明：∵M、N、E分别是PD、PC、CD的
中点，
∴ME∥PC，EN∥PD. ∴四边形PMEN是平行四边形．
(2)解：当点P运动到AB的中点时，四边形PMEN是菱形．
理由如下：
∵P是AB中点，∴PA＝PB.
∵四边形ABCD是矩形， ∴∠A＝∠B＝90°，AD＝BC. ∴△PAD≌△PBC(SAS).∴PD＝PC.
1.两条平行线之间的距离： 两条平行线中，一条直线上任意一点到另一条直线的距离 叫做两条平行线之间的距离.
2.三角形的中位线定理： 三角形的中位线平行于第三边，并且等于第三边的一半.
3.直角三角形斜边上的中线： 直角三角形斜边上的中线等于斜边的一半.
考点讲练
考点一 平行四边形的性质与判定
例1 如图，在直角梯形ABCD中，AD∥BC，∠B＝90°， AG∥CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG.
D．8cm
2.在四边形ABCD中，对角线AC，BD相交于点O，给出下列四个
条件：①AD∥BC；②AD＝BC；③OA＝OC；④OB＝OD.从中任选
两个条件，能使四边形ABCD为平行四边形的选法有( B )
A．3种
B．4种
C．5种
D．6种
3.如图是某公交汽车挡风玻璃的雨刮器，其工作原理如图
．雨刷EF⊥AD，垂足为A，AB=CD，且AD=BC，这样能使雨 刷EF在运动时，始终垂直于玻璃窗下沿BC，请证明这一结
∵CF= 12BC， 2
2
∴DE∥FC，DE=FC，
∴四边形DEFC是平行四边形，
∴DC=EF， ∴EF= 1 AB=6．
2
针对训练
4.如图，等边三角形ABC中，点D，E分别为AB，AC 的中点，则∠DEC的度数为（ B ）

2019年八年级数学下册第十八章平行四边形章末知识复习课件(新版)新人教版

2019年八年级数学下册第十八章平行四边形章末知识复习课件(新版)新人教版
A FCG , AEF G , EF GF ,
∴△AEF≌△CGF(AAS).∴AF=FC,AE=GC, 又∵BE=GC,∴AE=BE, 即 E,F 分别是 AB,AC 的中点.
考点二:矩形的性质与判定 【例2】 (2018遵义一模)如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线 AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
CE,CF,如图所示.
(1)求证:△ABE≌△ADF;
(1)证明:∵四边形 ABCD 是正方形,∴AB=AD,∴∠ABD=∠ADB, ∴∠ABE=∠ADF,
AB AD, 在△ABE 与△ADF 中 ABE ADF , BE DF ,
章末知识复习
1.平行四边形的性质 四边形 ABCD 是平行四边形
1 两组对边分别平行 2 两组对边分别相等 3 两组对角分别相等 互相平分 4 对角线 5 邻角互补
2.平行四边形的判定
1 两组对边分别平行 从边看 2 一组对边 平行 且相等 相等 3 两组对边分别 从角看— 4 两组对角分别相等 从对角线看— 5 对角线互相 平分
平行,另一组对边相等且有一角为直角的四边形是矩形.其中,正确的个数是(C (A)2个 (B)3个 (C)4个 (D)5个 )
2.如图,平行四边形ABCD的对角线AC,BD交于点O,过点B作BP∥AC,过点C作CP∥BD,BP与
CP相交于点P.
(1)判断四边形BPCO的形状,并说明理由; 解:(1)四边形BPCO为平行四边形. 理由如下: 因为BP∥AC,CP∥BD, 即BP∥OC,BO∥CP, 所以四边形BPCO为平行四边形.
(2)若将平行四边形ABCD改为菱形ABCD,其他条件不变,得到的四边形BPCO是什么四边形,

人教版八年级下册第十八章平行四边形18.2.3课件(共14张PPT)

人教版八年级下册第十八章平行四边形18.2.3课件(共14张PPT)

A、正方形 B、菱形
C、矩形 D平行四边形
4．在四边形ABCD中，O是对角线的交点，能判定这
个四边形是正方形的是：（ A ） A．AO＝BO＝CO＝DO，AC⊥BD
B．AD∥BC ∠A＝∠C
C．AO＝CO BO＝DO AB＝BC
D．AC＝BD
11
已知：如图，ABCD是正方形，CE、BF交于O.且 CE=BF. 求证：CE⊥BF.
（）
7
【探究】平行四边形、矩形、菱形、正方形之 间的关系
平行四边形
正
矩形 方 菱形
形
8
判断下列说法是否正确：
1)正方形的一条对角线把正方形分成两个全等的等腰直பைடு நூலகம்三角形（ √ ）
×
2)对角线互相垂直且相等的四边形是正方形
（）
3)如果一个菱形的对角线相等，那么它一定是正方形 4)如果一个矩形的对角线互相垂直，那么它一定是正方形 5)四条边相等，且有一个角是直角的四边形是正方形
12
已知：如图，M为正方形ABCD的BC边上中点.将正 方形折起，使点A于M重合.设折痕为EF，若正方形 的面积为64. 求：△AEM的面积.
13
性质
图形
对边平行且相等
四条边都相等
对角相等 四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
每条对角线平分 一组对角
平行四 边形
矩形
菱形 正方形
14
3
特殊的平行四边形——正 方 形
4
一 .正 方 形 性质：角：四个角直角.
边：四边相等. 对角线：相等，互相垂直平分，且平分一组对角. 对轴性：既是中心对称图形，又是轴对称图形.
5

2019-2020人教版八年级数学下册第十八章平行四边形章末复习课件(共89张)

2019-2020人教版八年级数学下册第十八章平行四边形章末复习课件(共89张)

第十八章 特殊的平行四边形
解：(1)证明：∵△ABC 是等腰三角形, BC 为底边, ∴∠ABC=∠C. ∵EG∥BC, DE∥AC, ∴∠AEG=∠ABC=∠C, 四边形 CDEG 是平行四边形, ∴∠DEG=∠C. ∵BE=BF, ∴∠BFE=∠BEF=∠AEG=∠ABC, ∴∠BFE=∠DEG, ∴BF∥DE, ∴四边形 BDEF 为平行四边形.
第十八章 特殊的平行四边形
证明：如图 18-Z-10 所示, 连接 EG, DG.
∵BD, CE 分别是△ABC 的边 AC, AB 上的高, G 是 BC 的中点,
1
1
∴DG=2BC, EG=2BC,
∴DG=EG.
又∵F 是 DE 的中点,
∴GF⊥DE.
第十八章 特殊的平行四边形
相关题 4 如图 18-Z-11, 在△ABC 中, ∠ACB=90°, D, E, F 分别
AB=AC，

在△ABF 和△ACD 中, ∠ABF=∠ACD, BF=CD，
∴△ABF≌△ACD, ∴AF=AD, 即 AD=AF.
第十八章 特殊的平行四边形
(2)证明：由(1)知, AF=AD, △ABF≌△ACD,∴∠FAB=∠DAC. ∵∠BAC=90°, ∴∠EAB=∠FAD=∠BAC=90°, ∴∠EAF=∠BAD. ∵AB=AC, AC=AE, ∴AB=AE.
第十八章 特殊的平行四边形
相关题 2 如图 18-Z-6, 已知△ABC, 直线 PQ 垂直平分线段 AC, 与 边 AB 交于点 E, 连接 CE, 过点 C 作 CF 平行于 BA 交 PQ 于点 F, 连 接 AF． (1)求证：△AED≌△CFD； (2)求证：四边形 AECF 是菱形； (3)若 AD=3, AE=5, 则菱形 AECF 的面积是多少？

人教版八年级数学下册第十八章《平行四边形》单元复习课件

人教版八年级数学下册第十八章《平行四边形》单元复习课件

第5题图
6.(人教8下P62改编)如图，在△ABC中，中线BD，CE相交
于O，F，G分别为BO，CO的中点，则四边形EFGD的形状
是 平行四边形
.
第6题图
7.【例1】(全国视野)(2022丹东模拟)如图，在▱ABCD中，点
O是AD的中点，连接CO并延长交BA的延长线于点E，连接
AC，DE.求证：四边形ACDE是平行四边形.
AF于点G.
(1)求证：四边形ABCF是矩形；
(2)若EA＝EG，求证：ED＝EC.
或对角线相等.
2.如图，在Rt△ABC中，∠ACB＝90°，DE，DF是△ABC
的中位线，连接EF，CD.求证：EF＝CD.
证明：∵DE，DF是△ABC的中位线，
∴DE∥BC，DF∥AC，
∴四边形DECF是平行四边形，
∵∠ACB＝90°，∴四边形DECF
是矩形，
∴EF＝CD.
知识点三：菱形
(1)菱形的特殊性质：菱形的四条边相等、对角线互相垂直
＝
在Rt△ABG和Rt△AFG中，
，
＝
∴△ABG≌△AFG(HL).
(2)解：∵△ABG≌△AFG，∴BG＝FG，
设BG＝FG＝x，则GC＝6－x，
∵E为CD的中点，∴CE＝EF＝DE＝3，
∴EG＝3＋x，∴在Rt△CEG中，32＋(6－x)2＝(3＋x)2，
解得x＝2，∴BG＝2.
的中点，将△ADE沿AE对折至△AFE，延长EF交边BC于点
G，连接AG.
(1)求证：△ABG≌△AFG；
(2)求BG的长.
(1)证明：在正方形ABCD中，AD＝AB＝BC＝CD，
∠D＝∠B＝∠BCD＝90°，
∵将△ADE沿AE对折至△AFE，

八年级数学下册第十八章平行四边形章末复习三作业课件新版新人教版

八年级数学下册第十八章平行四边形章末复习三作业课件新版新人教版

B．8 2 C．8 3 D．10
A．8
5．(长春中考)如图，有一张矩形纸片ABCD，AB＝8，AD＝6.先将矩形纸片ABCD 折叠，使边AD落在边AB上，点D落在点E处，折痕为AF；再将△AEF沿EF翻折，
AF与BC相交于点G，则△GCF的周长2为__4＋2
6．(云南中考)如图，在四边形ABCD中，对角线AC，BD相交于点O，AO＝OC， BO＝OD，且∠AOB＝2∠OAD. (1)求证：四边形ABCD是矩形；
运动以后，以点P，D，Q，B为顶点构成平行四边形的次数有__3__次．
3．(本溪中考)如图，在四边形ABCD中，AB∥CD，AD⊥CD，∠B＝45°，延长 CD到点E，使DE＝DA，连接AE. (1)求证：AE＝BC；
(2)若AB＝3，CD＝1，求四边形ABCE的面积．
解：(1)证明：∵AB∥CD，∠B＝45°，∴∠C＋∠B＝180°，∴∠C＝ 135°.∵DE＝DA，AD⊥CD，∴∠E＝45°.∵∠E＋∠C＝180°，∴AE∥BC.又
(1)求证：▱ABCD是菱形； (2)若AB＝5，AC＝6，求▱ABCD的面积． 解：(1)证明：∵四边形ABCD是平行四边形，∴∠B＝∠D，∵AE⊥BC，AF⊥CD， ∴∠AEB＝∠AFD＝90°，∵BE＝DF，∴△AEB≌△AFD，∴AB＝AD，
∴▱ABCD是菱形
(2)连接 BD 交 AC 于 O.∵四边形 ABCD 是菱形，AC＝6，∴AC⊥BD，AO＝OC＝1AC 2
4∶3， ∴∠AOB∶∠ABO＝4∶3，∴∠BAO∶∠AOB∶∠ABO＝3∶4∶3，∴∠ABO＝
54°. ∵∠BAD＝90°，∴∠ADO＝90°－54°＝36°
知识点三 菱形的性质和判定 7．如图，广场中心菱形花坛ABCD的周长是16米，∠A＝60°，则A，C两点之间

新人教版八年级初二数学下册第十八章平行四边形复习课课件


例 3 (内江中考)如图 18-F-6 所示,已知菱形 ABCD 的两条对角线分 别为 6 和 8,M、 N 分别是边 BC、 CD 的中点,P 是对角线 BD 上一点, 则 PM+PN 的最小值= .
图 18-F-6
分析:作 M 关于 BD 的对称点 Q,连接 NQ,交 BD 于 P,连接 MP,此时 MP+NP 的值最小,连接 AC,根据勾股定理求出 BC 长,证出 MP+NP=QN=BC,即可得出答案. 解:如图 18-F-7 所示, 作 M 关于 BD 的对称点 Q,连接 NQ,交 BD 于 P,连接 MP,
●跟踪训练 2.(新疆中考)如图 18-F-5 所示,在▱ABCD 中,点 O 是 AC 与 BD 的交 点,过点 O 的直线与 BA、DC 的延长线分别交于点 E、F.
图 18-F-5
(1)求证:△AOE≌△COF; (2)请连接 EC、AF,则 EF 与 AC 满足什么条件时,四边形 AECF 是 矩形,并说明理由.
10
.
图 18-F-8
例 4 (鞍山中考)如图 18-F-9 所示,在正方形 ABCD 中,E 是 AB 上一 点,F 是 AD 延长线上一点,且 DF=BE.
图 18-F-9
(1)求证:CE=CF; (2)若点 G 在 AD 上,且∠GCE=45° ,则 GE=BE+GD 成立吗?为什么?
分析:(1)由 DF=BE,四边形 ABCD 为正方形可证△CEB≌△CFD,从 而证出 CE=CF. (2)由(1)得,CE=CF,∠BCE+∠ECD=∠DCF+∠ECD 即∠ECF=∠ BCD=90° 又∠GCE=45° ,所以可得∠GCE=∠GCF,故可证得△ECG ≌△FCG,即 EG=FG=GD+DF.又因为 DF=BE,所以可证出 GE=BE+GD 成立.

人教版八年级数学下册第十八章平行四边形小结复习课件(共22张PPT)

E
A
)
M
C
N F
D
（3）如图，矩形ABCD沿AE折叠，使D点落在BC边上的F点处， 如果∠BAF=60°，那么∠DAE等于（ A ） A．15° B．30° C．45° D．60°
1、如图，在菱形ABCD中，AB=10，OA=8， 40 OB=6，则菱形的周长是_________ ，面积是 96 ___________
A
∠ACB＝90°
O
F
M B
E
３ １ ２
N
C
正方形ABCD的对角线相交于点O ，点 O是正方形 MNPO的一个顶点，如果两个正方形的边长相等，那么 正方形MNPO绕点O转动，试猜想两个正方形重叠 部分的面积四边形OEAF与正方形的面积有什么关系？ 并证明你的结论。 D C M E 0
有 谁 证 明 ？
B
A O C
D
3、在 ABCD中， ∠A:∠B= 4:5，那么 80° ，∠C=_________ 100° ∠B=__________
A
D O C
1、如图，在矩形ABCD中，AC、BD相交于点O， 12 ∠AOB= 60°，AB=6，则AC=_______ B
2、已知矩形的周长是24，相邻两边之比是1：2，那么这个矩 32 形的面积是__________
人教2013版 第十八章 平行四边形
平行四边形小结
一般平行四边形与特殊平行四边形的关系 （从定义观察）
菱 形 有一组邻边相等 平行四边形 有一个角是直角
正方形
有一个角是直角
矩 形
有一组邻边相等
几种平行四边形的特征比较
图形 元素 边
对边平行且相等
角
对角相等, 邻角互补

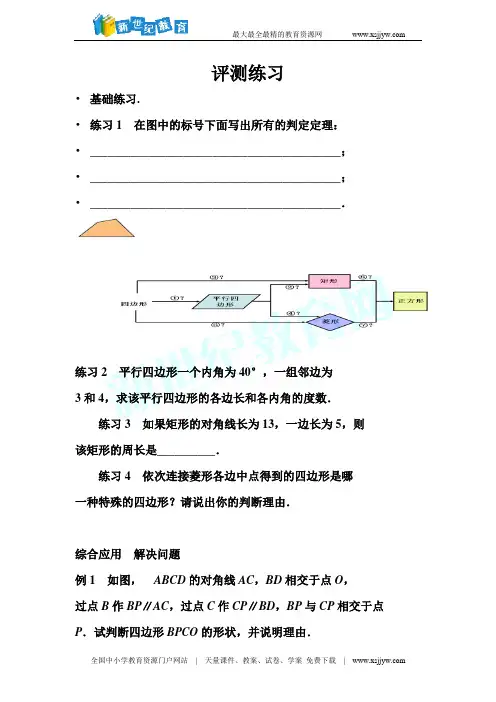
人教版数学八年级下册课件：第18章《平行四边形》单元复习(共15张PPT)

评测练习
•基础练习.
•练习1在图中的标号下面写出所有的判定定理：
•___________________________________________；
•___________________________________________；
•___________________________________________．
练习2平行四边形一个内角为40°，一组邻边为
3和4，求该平行四边形的各边长和各内角的度数．练习3如果矩形的对角线长为13，一边长为5，则
该矩形的周长是__________．
练习4依次连接菱形各边中点得到的四边形是哪
一种特殊的四边形？请说出你的判断理由．
综合应用解决问题
例1如图，ABCD的对角线AC，BD相交于点O，
过点B作BP∥AC，过点C作CP∥BD，BP与CP相交于点P．试判断四边形BPCO的形状，并说明理由．
变式1若连接OP得四边形ABPO，四边形ABPO是什么四边形？
变式2若将ABCD改为矩形ABCD，其他条件不变，得到的是什么四边形？
变式3得到矩形BPCO，应将条件中的ABCD 改为什么四边形？
变式4能否得到正方形BPCO？此时四边形ABCD 应该是什么形状？。

新人教版八年级数学下册第十八章平行四边形课件


2.已知 ABCD 的周长为28cm， AB∶BC=3∶4，求它的各边的长.
解：∵四边形ABCD为平行四边形， ∴AB=CD，AD=BC. 又∵C ABCD=AB+BC+CD+AD=28cm， 且AB∶BC=3∶4， ∴AB=CD=6cm，AD=BC=8cm.
综合应用
3.如图，在 ABCD 中，已知AD=8cm， AB=6cm，DE平分∠ADC交BC边于点E，则BE 的长为___2_cm____.
A
D
B
C
∠C=140°
知识点 3 两条平行线之间的距离
例1 如图， ABCD中，DE⊥AB，BF⊥CD， 垂足分别为E，F．求证：AE=CF．
证明： ∵四边形ABCD是平行四边形，
∴ ∠A= ∠C，AD=CB.
又∠AED= ∠CFB=90°，
∴ △ADE≌△CBF，
∴AE=CF.
变式：DE=BF 吗？
误区 诊断
误区 一 不理解平行四边形的对角、邻角等概念
1.在 ABCD中，∠A：∠B：∠C：∠D的 值可以是（ ）
A. 1:2:3:4
B. 1:2:2:1
C. 2:2:1:1
D. 2:1:2:1
错解：A、B或C
正解：D
错因分析：不理解平行四边形的对角、邻 角的概念，∠A与∠C，∠D与∠B是对角，平行 四边形的对角相等，∠A：∠C与∠D：∠B的比 值也应相等.
∴四边形ABCD是平行四边形（平行四边形的定义）．
知识点 2 平行四边形的边角关系
由平行四边形的定义， A
我们知道平行四边形的两组
对边分别平行.
B
D C
想 一 想 平行四边形还有什么性质？
探究
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

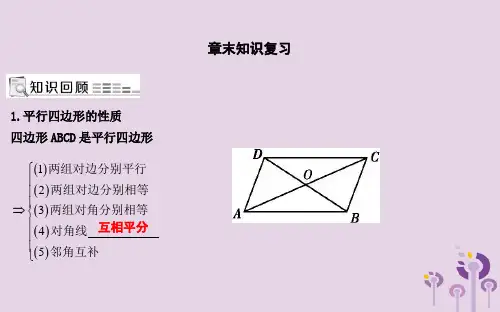
第十八章ꢀ平行四边形章末复习(三)ꢀ平行四边形
知识点一ꢀ平行四边形的性质和判定
1．如图所示，四边形ABCD中，AB＝CD，对角线AC，BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF，CE，若DE＝BF，则下列结论：①CF＝AE；②OE＝OF；③四边形ABCD是平行四边形；④图中共有四对
B
全等三角形．其中正确结论的个数是(
)
A．4B．3C．2D．1
2．如图，平行四边形ABCD中，AB＝8 cm，AD＝12 cm，点P在AD边上
以每秒1 cm的速度从点A向点D运动，点Q在BC边上以每秒4 cm的速度从点C出发，在C，B间往返运动，两个点同时出发，当点P到达点D时停止(同时点Q也停止)，在开始运动以后，以点P，D，Q，B为顶点构成平行四
3
边形的次数有____次．
3．(2019·湖州)如图，已知在△ABC中，D，E，F分别是AB，BC，AC的中点，连接DF，EF，BF.
(1)求证：四边形BEFD是平行四边形；
(2)若∠AFB＝90°，AB＝6，求四边形BEFD的周长．
知识点二ꢀ矩形的性质与判定
4．(杭州中考)如图，已知点P是矩形ABCD内一点(不含边界)，设∠PAD ＝θ，∠PBA＝θ，∠PCB＝θ，∠PDC＝θ，若∠APB＝80°，∠CPD＝50°，1234
A
则()
A.(θ＋θ)－(θ＋θ)＝30°
1423
B．(θ＋θ)－(θ＋θ)＝40°
2413
C．(θ＋θ)－(θ＋θ)＝70°
1234
D．(θ＋θ)＋(θ＋θ)＝180°
1234
6．(2019·连云港)如图，在△ABC中，AB＝AC.将△ABC沿着BC方向平移得到△DEF，其中点E在边BC上，DE与AC相交于点O.
(1)求证：△OEC为等腰三角形；
(2)连接AE，DC，AD，当点E在什么位置时，四边形AECD为矩形，并说明理由．
(1)证明：∵AB＝AC，∴∠B＝∠ACB，∵△ABC平移得到△DEF，
∴AB∥DE，∴∠B＝∠DEC，∴∠ACB＝∠DEC，∴OE＝OC，即△OEC为等腰三角形ꢀ
(2)解：当E为BC的中点时，四边形AECD是矩形，
理由是：如图，∵AB＝AC，E为BC的中点，∴AE⊥BC，BE＝EC，∵△ABC平移得到△DEF，∴BE∥AD，BE＝AD，∴AD∥EC，AD＝EC，∴四边形AECD是平行四边形，∵AE⊥BC，∴四边形AECD是矩形
知识点三ꢀ菱形的性质和判定
C 7．(2019·大庆)下列说法中不正确的是()
A．四边相等的四边形是菱形
B．对角线垂直的平行四边形是菱形
C．菱形的对角线互相垂直且相等
D．菱形的邻边相等
8．如图，四边形ABCD是菱形，∠DAB＝50°，对角线AC，BD相交于点O，
25
DH⊥AB于点H，连接OH，则∠DHO＝_____度．
10．(南宁中考)如图，在▱ABCD中，AE⊥BC，AF⊥CD，垂足分别为E，F，且BE＝DF.
(1)求证：▱ABCD是菱形；
(2)若AB＝5，AC＝6，求▱ABCD的面积．
知识点四ꢀ正方形的性质和判定
11．(梧州中考)如图，在正方形ABCD中，A，B，C三点的坐标分别是
(－1，2)，(－1，0)，(－3，0)，将正方形ABCD向右平移3个单位，则平
B
移后点D的坐标是()
A．(－6，2)ꢀB．(0，2)C．(2，0)D．(2，2)
13．(2019·天门)如图，E，F分别是正方形ABCD的边CB，DC延长线上的点，且BE＝CF，过点E作EG∥BF，交正方形外角的平分线CG于点G，连接GF.求证：
(1)AE⊥BF；
(2)四边形BEGF是平行四边形．。