Matlab实验第一次实验答案

第一次实验答案1． 设要求以0.01秒为间隔，求出y 的151个点，并求出其导数的值和曲线。

clcclearx=0:0.01:1.5;y=sqrt(3)/2*exp(-4*x).*sin(4*sqrt(3)*x+pi/3)y1=diff(y)subplot(2,1,1)plot(x,y)subplot(2,1,2)plot(x(1:150),y1)2绘制极坐标系下曲线（a,b,n 自定数据）clccleara=10;b=pi/2;n=5;theta=0:pi/100:2*pi;rho=a*cos(b+n*theta);polar(theta,rho)3. 列出求下列空间曲面交线的程序clcclearx=[-5:0.5:5];[X,Y]=meshgrid(x);z1=X.^2-2*Y.^2;z2=X.*2-Y.*3;xlabel('x')ylabel('y')zlabel('z')surf(X,Y,z1)hold onsurf(X,Y,z2)k=find(abs(z1-z2)<0.5);x1=X(k)y1=Y(k)z3=x1.^2-2*y1.^2hold onplot3(x1,y1,z3,'*')⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t ()θρn b a +=cos 2212y x z -=y x z 322-=4、设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y 把x=0~2π间分为101点，画出以x 为横坐标，y 为纵坐标的曲线，要求有图形标注。

clcclearx=-2*pi:0.1: 2*pi;y=cos(x).*(0.5+sin(x)*3./(1+x.^2));plot(x,y,'b*-');title('绘图');xlabel('x 坐标');ylabel('y 坐标');legend('原函数')gtext('y=cos(x)(0.5+3*sin(x)/(1+x^2))')5、求下列联立方程的解81025695832475412743-=+-+-=-+-=++-=--+w z y x w z x w z y x w z y x clccleara=[3,4,-7,-12;5,-7,4,2;1,0,8,-5;-6,5,-2,10];b=[4,-3,9,-8];c=b/a;x=c(1,1)y=c(1,2)z=c(1,3)w=c(1,4)6. 假设一曲线数据点为x = 0:2:4*pi;y = sin(x).*exp(-x/5);试将x 的间距调成 0.1，采用不同插值方法进行插值，并通过子图的形式将不同插值结果和原始数据点绘制在同一图形窗口。

MATLAB数学实验答案（全）第⼀次练习教学要求：熟练掌握Matlab 软件的基本命令和操作，会作⼆维、三维⼏何图形，能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。

补充命令vpa(x,n) 显⽰x 的n 位有效数字，教材102页fplot(‘f(x)’,[a,b]) 函数作图命令，画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位（1-9班）或4位（10班以上） 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx →∞-syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =，求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +??dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +? syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//⾼阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最⾼次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项（要求将结果⽤向量的形式给出）。

实验一 MATLAB 运算基础1、 先求下列表达式得值，然后显示MATLAB 工作空间得使用情况并保存全部变量。

(1) 0122sin 851z e =+(2) 21ln(2z x =+，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:0、5:2、5 解：4、 完成下列操作：(1) 求[100,999]之间能被21整除得数得个数。

(2) 建立一个字符串向量，删除其中得大写字母。

解：(1) 结果：(2)、 建立一个字符串向量 例如：ch='ABC123d4e56Fg9';则要求结果就是：实验二 MATLAB 矩阵分析与处理1、 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵与对角阵，试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。

解: M 文件如下；5、 下面就是一个线性方程组：1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程得解。

(2) 将方程右边向量元素b 3改为0、53再求解，并比较b 3得变化与解得相对变化。

(3) 计算系数矩阵A 得条件数并分析结论。

解： M 文件如下：实验三 选择结构程序设计1、 求分段函数得值。

2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现，分别输出x=-5、0,-3、0,1、0,2、0,2、5,3、0,5、0时得y 值。

（完整版）MATLAB）课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值，然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。

(1) 0122sin 851z e =+(2) 21ln(2z x =，其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--L (4) 2242011122123t t z t t t t t ?≤=-≤，其中t =0:0.5:2.5 解：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建⽴⼀个字符串向量，删除其中的⼤写字母。

解：(1) 结果：(2). 建⽴⼀个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?，其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵，试通过数值计算验证2 2E R RS A O S +??=。

解: M ⽂件如下；5. 下⾯是⼀个线性⽅程组：1231112340.951110.673450.52111456x x x ??=???(1) 求⽅程的解。

(2) 将⽅程右边向量元素b 3改为0.53再求解，并⽐较b 3的变化和解的相对变化。

(3) 计算系数矩阵A 的条件数并分析结论。

解： M ⽂件如下：123d4e56g9实验三选择结构程序设计1. 求分段函数的值。

2226035605231x x x x y x x x x x x x ?+-<≠-?=-+≤<≠≠??--?且且及其他⽤if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。

解：M ⽂件如下：2. 输⼊⼀个百分制成绩，要求输出成绩等级A、B、C、D、E。

MATLAB 实验一答案1.3 先自定义一个变量，然后分别用8种不同的数字显示格式显示查看。

>> a=pia =3.1416>> format long>> aa =3.14159265358979>> format short>> aa =3.1416>> format short e>> aa =3.1416e+000>> format long e>> aa =3.141592653589793e+000>> format hex>> aa =400921fb54442d18>> format bank>> aa =3.14>> format +>> aa =+>> format rat>> aa =355/1131.4 下面的语句用于画出函数()0.22x y x e -=在[0,10]区间的值x = 0:0.1:10;y = 2*exp(-0.2*x);plot(x,y)1.5 用Matlab 编辑器创建一个m 文件，把上述语句写入这个m 文件并命名为“test1.m ”，保存在当前路径中，然后在命令窗中键入test1，观察结果和运行程序后工作空间的变化.工作空间和结果均与1.4一样1.6 如何清空工作区间数据？键入 clear ；如何关闭图像窗口？键入close ；除了在命令窗输入文件名，还可以怎样运行一个m 文件程序？点击file ，打开m 文件，点击Run 按钮，运行m 文件程序。

1.7 通过以下两种方式得到关于exp 函数的帮助：(1) 在命令窗中输入help exp 命令；(2) 运用帮助空间窗口。

思考，用什么指令可以直接打开帮助空间中关于exp 函数的说明？键入doc exp1.8 假设x =3，y = 4，用Matlab 计算下列表达式：(1) ()232x y x y - (2) 43x y (3) 24x x π- (4) 33x x x y- >> x=3,y=4;>> x^2*(y^3)/(x-y)^2ans =576>> 4*x/(3*y)ans =1>> 4/x*(pi*x^(-2))ans =0.4654>> x^3/(x^3-y^x)ans =-0.72971.9 在当前目录下创建一个m文件，键入以下程序并保存，先把文件保存为“2.m”，运行后观察结果，总结m文件的文件名（包括Matlab标识符）命名规则。

Matlab 曲线绘图练习1. 绘出立方曲线3=。

y xx=-2::2;y=x.^3;plot(x,y)grid on2. 立方抛物线y=y=-2::2;x=y.^3;plot(x,y)grid on3. 高斯曲线2x y e -=。

clear; x=-2::2;y=exp(-x.^2); plot(x,y)以参数方程表示的曲线： 4. 奈尔抛物线2323,()x t y t y x ===clear; t=-2::2;x=t.^3;y=t.^2 plot(x,y)y =Columns 1 through 14Columns 15 through 28Columns 29 through 420 Columns 43 through 56Columns 57 through 70Columns 71 through 815. 半立方抛物线2323,()x t y t y x ===clear; t=-2::2;x=t.^2;y=t.^3 plot(x,y)y =Columns 1 through 14Columns 15 through 28Columns 29 through 420 Columns 43 through 56Columns 57 through 70 Columns 71 through 816. 迪卡尔曲线2332233,(30) 11at atx y x y axyt t==+-= ++clear;a=3;t=-2::2;x=3*a.*t./(1+t.^2);y=3*a.*t.^2./(1+t.^2); plot(x,y);grid on7. 蔓叶线233222,() 11at at xx y yt t a x ===++-clear;a=2;t=-10::10;x=a.*t.^2./(1+t.^2);y=a.*t.^3./(1+t.^2); plot(x,y);grid on8. 摆线(sin),(1cos)x a t t y b t=-=-。

MATLAB)课后实验答案[1]实验一 MATLAB 运算基础1. 先求下列表达式的值，然后显示MATLAB 工作空间的使用情况并保存全部变量。

(1) 0122sin851z e=+(2) 21ln(2z x =+，其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩，其中t =0:0.5:2.5 解：4. 完成下列操作：(1) 求[100,999]之间能被21整除的数的个数。

(2) 建立一个字符串向量，删除其中的大写字母。

解：(1) 结果：(2). 建立一个字符串向量例如：ch='ABC123d4e56Fg9';则要求结果是：实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦，其中E 、R 、O 、S分别为单位矩阵、随机矩阵、零矩阵和对角阵，试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。

解: M 文件如下；5. 下面是一个线性方程组：123d4e56g91231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程的解。

(2) 将方程右边向量元素b 3改为0.53再求解，并比较b 3的变化和解的相对变化。

(3) 计算系数矩阵A 的条件数并分析结论。

解： M 文件如下：实验三 选择结构程序设计1. 求分段函数的值。

2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现，分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。

实验一熟悉MATLAB环境本人自己做的，并不是标准答案，仅供参考。

［实验目的］1.熟悉MATLAB主界面，并学会简单的菜单操作。

2.学会简单的矩阵输入与信号输入。

3.掌握部分绘图函数。

［实验原理］MATLAB是以复杂矩阵作为基本编程单元的一种程序设计语言。

它提供了各种矩阵的运算与操作，并有较强的绘图功能。

用户第一次使用MATLAB时，建议首先在屏幕上键入demo命令，它将启动MATLAB的演试程序，用户可在此演示程序中领略MATLAB所提供的强大的运算与绘图功能。

也可以键入help进行进一步了解。

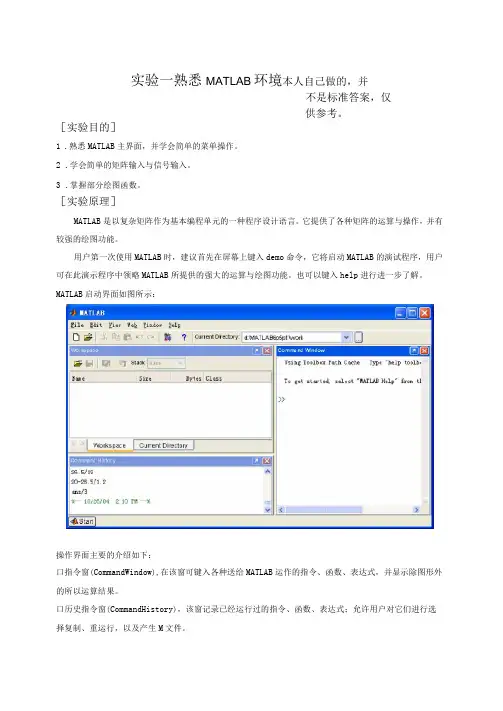
MATLAB启动界面如图所示：操作界面主要的介绍如下：口指令窗(CommandWindow),在该窗可键入各种送给MATLAB运作的指令、函数、表达式，并显示除图形外的所以运算结果。

口历史指令窗(CommandHistory)，该窗记录已经运行过的指令、函数、表达式；允许用户对它们进行选择复制、重运行，以及产生M文件。

口工作空间浏览器(WorkspaceBrowser)，该窗口罗列出MATLAB工作空间中所有的变量名、大小、字节数；并且在该窗中，可对变量进行观察、编辑、提取和保存其它还有当前目录浏览器（CurrentDirectoryBrowser）、M文件编辑/调试器（Editor/Debugger）以及帮助导航/浏览器（HelpNavigator/Browser）等，但通常不随操作界面的出现而启动。

利用File菜单可方便对文件或窗口进行管理。

其中File|New的各子菜单，M-file（M文件）、Figure（图形窗口）、或Model（SIMULINK编辑界面）分别可创建对应文件或模块。

Edit菜单允许用户和Windows的剪切板交互信息。

MATLAB语言最基本的赋值语句结构为：变量名列表=表达式。

表达式由操作符或其它字符，函数和变量名组成，表达式的结果为一个矩阵，显示在屏幕上，同时输送到一个变量中并存放于工作空间中以备调用。

MATLAB上机实验1答案实验1 Matlab 初步一、问题已知矩阵A 、B 、b 如下：-------------=031948118763812654286174116470561091143A------=503642237253619129113281510551201187851697236421B []1187531=b应用Matlab 软件进行矩阵输入及各种基本运算。

二、实验目的学会使用Matlab 软件构作已知矩阵对应的行（列）向量组、子矩阵及扩展矩阵，实施矩阵的初等变换及线性无关向量组的正交规范化，确定线性相关相关向量组的一个极大线性无关向量组，且将其余向量用极大线性无关向量组线性表示，并能编辑M 文件来完成所有的实验目的。

三、预备知识1、线性代数中的矩阵及其初等变换、向量组的线性相关性等知识。

2、 Matlab 软件的相关命令提示如下；（1）选择A 的第i 行做一个行向量：ai=A(i,:)；（2）选择A 的第j 行做一个列向量：ai=A(j,:)；（3）选择A 的某几行、某几列上的交叉元素做A 的子矩阵：A([行号],[列号])；（4） n 阶单位阵：eye(n)；n 阶零矩阵：zeros(n)；（5）做一个n 维以0或1为元素的索引向量L ，然后取A(:,L)，L 中值为1的对应的列将被取到。

（6）将非奇异矩阵A 正交规范化，orth(A) ；验证矩阵A 是否为正交阵，只需做A*A'看是否得到单位阵E 。

（7）两个行向量a1和a2的内积：a1*a2'。

（8）让A 的第i 行与第j 列互换可用赋值语句：A([i,j],:)=A([j,i],:)；（9）让K乘以A的第i行可用赋值语句：A(i,:)=K*A(i,:)；（10）让A的第i行加上第j行的K倍可用赋值语句：A(i,:)=A(i,:)+K*A(j,:)；（11）求列向量组的A的一个极大线性无关向量组可用命令：rref(A)将A化成阶梯形行的最简形式，其中单位向量对应的列向量即为极大线性无关向量组所含的向量，其它列向量的坐标即为其对应向量用极大线性无关组线性表示的系数。

实验一MATLAB 工作环境熟悉及简单命令的执行一、实验目的：熟悉MATLAB 的工作环境，学会使用MATLAB 进行一些简单的运算。

二、实验内容：MATLAB 的启动和退出，熟悉MATLAB 的桌面（Desktop ），包括菜单（Menu ）、工具条（Toolbar ）、命令窗口(Command Window)、历史命令窗口、工作空间(Workspace)等；完成一些基本的矩阵操作；学习使用在线帮助系统。

三、实验步骤：1、启动MATLAB ，熟悉MATLAB 的桌面。

2、在命令窗口执行命令完成以下运算，观察workspace 的变化，记录运算结果。

（1）（365-52⨯2-70）÷3 >>(365-52*2-70)/3 ans = 63.6667（2）>>area=pi*2.5^2 area = 19.6350（3）已知x=3，y=4，在MATLAB 中求z ：()232y x y x z -= >>x=3 >>y=4>>z = x ^2 * y ^3 / (x - y) ^2 z = 576（4）将下面的矩阵赋值给变量m1,在workspace 中察看m1在内存中占用的字节数。

m1=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡11514412679810115133216 执行以下命令>>m1 =[16 2 3 13 ; 5 11 10 8 ; 9 7 6 12 ; 4 14 15 1 ] >>m1( 2 , 3 ) ans = 10 >>m1( 11 ) ans = 6>>m1( : , 3 ) ans =3 10 6 15>>m1( 2 : 3 , 1 : 3 ) ans =5 11 10 9 7 6>>m1( 1 ,4 ) + m1( 2 ,3 ) + m1( 3 ,2 ) + m1( 4 ,1) ans = 34（5）执行命令>>help abs查看函数abs 的用法及用途，计算abs( 3 + 4i ) （6）执行命令>>x=0:0.1:6*pi; >>y=5*sin(x); >>plot(x,y)（6）运行MATLAB 的演示程序，>>demo ，以便对MATLAB 有一个总体了解。

（温馨提示：实验课结束后，请将所有作业（题目、代码、结果）利用word 整理成一个完整的实验报告，加上封面，打印，纸质档于18周周一交）第一次上机作业目的：1. 掌握MATLAB 各种表达式的书写规则2. 运行课堂上讲过的例子，熟悉矩阵、表达式的基本操作和运算。

作业：1. 熟悉matlab 集成环境界面。

回答以下问题，并操作相关的指令：（1） 分别写出清除命令窗口和清除变量的指令。

答： clc 和clear（2）在命令行输入命令后，matlab 的搜索过程是怎样的？答： （1）检查该命令对象是不是一个变量。

（2）检查该命令对象是不是一个内部函数。

（3）检查该命令对象是否为当前目录下的程序文件。

（4）检查该命令对象是否为MATLAB 搜索路径中其他目录下的M 文件。

（3）什么是matlab 的当前工作目录？写出两种设置当前工作目录的方法？ 答： 就是matlab 当前文件读取和存储的默认路径（1）在当前目录窗口中更改（2）在MATLAB 桌面工具栏中更改（3）使用cd 命令:cd c:\mydir---将c ：\mydir 设置为当前目录（4）什么是matlab 的搜索路径？写出两种设置搜索路径的方法？答： 指Matlab 运行文件时进行搜索的目录。

（1）用path 命令设置：（2）用Set Path 对话框设置（5）help 命令和doc 命令有什么作用，它们有什么区别？答： help 命令：最基本的帮助命令，查询信息直接显示在命令窗口。

doc 命令：在帮助窗口中显示HTML 帮助文档，显示函数的详细用法及 例子，比help 命令更详细。

2. 在matlab 中输入下列表达式，并求各表达式的值，显示MATLAB 工作空间的使用情况并用两种方式保存全部变量，变量保存的文件名必须包含自己的学号后四位数：（1）)1034245.01(26-⨯+⨯=w w=sqrt(2)*(1+0.34245*10^-6)w =1.4142（2）,)tan(22ac b e abc c b a x ++-+++=ππ 其中a=3.5,b=5,c=9.8。