【精品】广东省初中数学竞赛初赛试题及答案

初中数学竞赛初赛(市级选拔)试题一、选择题（共8小题，每小题5分，共40分）1．要使方程组⎩⎨⎧=+=+23223y x a y x 的解是一对异号的数，则a 的取值范围是（ ）（A ）334<<a （B ）34<a （C ）3>a （D ）343<>a a 或 2．一块含有︒30角的直角三角形（如图），它的斜边AB ＝8cm, 里面空 心DEF ∆的各边与ABC ∆的对应边平行，且各对应边的距离都是1cm,那么DEF ∆的周长是（ ）(A)5cm (B)6cm (C) cm )(36- (D) cm )(33+3．将长为15cm 的木棒截成长度为整数的三段，使它们构成一个三角形的三边，则不同的截法有( )(A)5种 (B) 6种 (C)7种 (D)8种4．作抛物线A 关于x 轴对称的抛物线B ，再将抛物线B 向左平移2个单位，向上平移1个单位，得到的抛物线C 的函数解析式是1122-+=)x (y ，则抛物线A 所对应的函数表达式是 ( )(A)2322-+-=)x (y (B) 2322++-=)x (y(C) 2122---=)x (y (D) 2322++-=)x (y5．书架上有两套同样的教材，每套分上、下两册，在这四册教材中随机抽取两册，恰好组成一套教材的概率是( )(A)32 (B) 31 (C) 21 (D) 61 6．如图，一枚棋子放在七边形ABCDEFG 的顶点处，现顺时针方向移动这枚棋子10次，移动规则是：第k 次依次移动k 个顶点。

如第一次移动1个顶点，棋子停在顶点B 处，第二次移动2个顶点，棋子停在顶点D 。

依这样的规则，在这10次移动的过程中，棋子不可能分为两停到的顶点是( )(A)C,E,F (B)C,E,G (C)C,E (D)E,F.7．一元二次方程)a (c bx ax 002≠=++中，若b ,a 都是偶数，C 是奇数，则这个方程( )(A)有整数根 (B)没有整数根 (C)没有有理数根 (D)没有实数根8．如图所示的阴影部分由方格纸上3个小方格组成，我们称这样的图案为L 形，那么在由54⨯ 个小方格组成的方格纸上可以画出不同位置的L 形图案个数是( )(A)16 (B) 32 (C) 48 (D) 64二、填空题：(共有6个小题，每小题5分，满分30分)9．已知直角三角形的两直角边长分别为3cm,4cm ，那么以两直角边为直径的两圆公共弦的长为 cm.10．将一组数据按由小到大(或由大到小)的顺序排列，处于最中间位置的数(当数据的个数是奇数时)，或最中间两个数据的平均数(当数据的个数是偶数时)叫做这组数据的中位数，现有一组数据共100个数，其中有15个数在中位数和平均数之间，如果这组数据的中位数和平均数都不在这100个数中，那么这组数据中小于平均数的数据占这100个数据的百分比是11.ABC ∆中，c ,b ,a 分别是C ,B ,A ∠∠∠的对边，已知232310-=+==C ,b ,a ，则C sin c B sin b +的值是等于 。

七年级数学竞赛试题一．选择题（每小题4分，共32分） 1．x 是随意有理数，则2 的值( ).A ．大于零B ． 不大于零C ．小于零D ．不小于零 2．在－0.1428中用数字3交换其中的一个非0数码后，使所得的数最大，则被交换的数字是（ ） A ．1 B ．4 C ．2 D ．83．如图，在数轴上1的对应点A 、B ， A 是线段的中点，则点C 所表示的数是( )A．2 B2 C1 D．14.桌上放着4张扑克牌，全部正面朝下，其中恰有1张是老K 。

两人做嬉戏，嬉戏规则是：随机取2张牌并把它们翻开，若2张牌中没有老K ，则红方胜，否则蓝方胜。

则赢的时机大的一方是（ ）A ．红方B ．蓝方C ．两方时机一样D ．不知道 5．假如在正八边形硬纸板上剪下一个三角形（如图①中的阴影局部），那么图②，图③，图④中的阴影局部，均可由这个三角形通过一次平移、对称或旋转而得到．要得到图②，图③，图④中的阴影局部，依次进展的变换不行行．．．的是（ ）Ａ．平移、对称、旋转 Ｂ．平移、旋转、对称 Ｃ．平移、旋转、旋转 Ｄ．旋转、对称、旋转6．计算：22221111(1)(1)(1)(1)2342007---⋅⋅⋅-等于（ ） A ．10042007 B ．10032007 C ．20082007D ．200620077．如图，三个天平的托盘中一样的物体质量相等。

图⑴、⑵所示的两个天平处于平衡状态要使第三个天平也保持平衡，则需在它的右盘中放置（ ）(3)(2)(1)A. 3个球B. 4个球C. 5个球D. 6个球8．用火柴棒搭三角形时，大家都知道，3根火柴棒只能搭成1种三角形，不妨记作它的边长分别为1，1，1；4根火柴棒不能搭成三角形；5根火柴棒只能搭成一种三角形，其边长分别为2，2，1；6根火柴棒只能搭成一种三角形，其边长分别为2，2，2；7根火柴棒只能搭成2种三角形，其边长分别为3，3，1和3，2，2；…；那么30根火柴棒能搭成三角形个数是（ ） A ．15 B ．16 C ．18 D ．19 二．填空题（每题4分，共28分）x图①图②图③ 图④9．定义a*,若3*31，则x 的值是。

2020年广东省初中数学竞赛初赛试卷初中数学讲明：考试时刻：60分钟。

总分120分。

每题4分。

在每题给出的四个选项中，只有 一项为哪一项符合题目要求的，并将答案填在下面的答题卡上。

1.直角坐标平面上将二次函数y=－2〔x －1〕2－2的图象向左平移1个单位，再向上平移1个单位，那么其顶点为〔 〕。

A. 〔0，0〕B. (1,－2)C. (0,－1)D.(－2,1) 2.以下的运算正确的选项是( ).A ．(ab 4)4=ab 8； B.(－3pq)2=－6p 2q 2C. x 2－21x ＋41=( x －21)2；D.3(a 2)3－6a 6=－3a 6 3.如图1.以直角三角形ABC 三边为直径的半圆面积分不是S 1、S 2、S 3，直角三角形ABC 面积是S ，那么它们之间的关系为〔 〕. A. S= S 1＋S 2＋S 3 B. S 1= S 2＋S 3 C. S= S 1＋S 2C. S= S 14. 一辆公共汽车从车站开出，加出速行驶一段时刻后匀速行驶，过了一段时刻，汽车到达下一个车站.乘客上下车后汽车开始加速，一段时刻后又开始匀速行驶，下面能够近似地刻画出汽车在这段时刻内的速度变化情形的是〔 〕.(A)时间速度(B)时间速度(C)时间速度(D)时间速度5.如下图，在边长为a 的正方形中挖去一个边长为b 的小正方形〔a ＞b 〕，再把剩余的部分剪拼成一个矩形，通过运算图形〔阴影部分 的面积，验证了一个等式是〔 〕.A. a 2－b 2=〔a+b 〕〔a-b 〕 B. 〔a+b 〕2= a 2+2ab+ b 2C. 〔a-b 〕2= a 2-2ab+ b 2D.〔a+2b 〕〔a-b 〕= a 2+ab-2b 26.在一个仓库里堆积着正方体的货箱假设干，要搬运这些箱子专门困难,但是仓库治理员要落实A 0xyB 0xyCxyxy一下箱子的数量,因此就想出一个方法:将这堆物资的三种视图画了出来,如图.你能依照三视图,帮他清点一下箱子的数量吗?这些正方体箱的个数是( ). A. 6 B. 7 C. 8 D. 9主视图 左视图 俯视图7.在Rt △ABC 中,∠C=90°,那么以下式子中不一定成立的是( ).A.sinA=sinBB. cosA=cosBC.sinA=cosBD. sin(A+B)=sinC8.体育课上全班女生进行了百米测验,达标成绩为18秒,下面是第一小组8名女生的成绩记录,其中正号表示成绩大于18秒,负号成表示绩小于18秒,那么这组女生的达标率是( ).A.41 B.2 C.4D.89.函数y=kx 和y=xk〔k ﹤0〕在同一坐标系中的图象是〔 〕.10.将一张正方形纸按图所示的方式二次折叠,折叠后再按图所示沿MN 裁剪,那么可得( ). A.多个等腰直角三角形； B.一个等腰直角三角形和一个正方形；C.四个相同的正方形；D.两个相同的正方形。

2019年全国初中数学竞赛（广东省赛区）选拔赛初赛试卷一、选择题（每小题6分，满分30分）1．已知＝0，a2+b2+c2＝1，则a+b+c的值等于（）A．1B．﹣1C．1或﹣1D．O2．若使函数的自变量x的取值范围是一切实数，则下面的关系中一定满足要求的是A．b＞c＞0B．b＞0＞c C．c＞0＞b D．c＞b＞03．如图，E、F、G、H、I、J、K、N分别是正方形各边的三等分点，要使中间阴影部分的面积是5，那么大正方形的边长应该是（）A．B．C．D．4．如图，△ABC是等边三角形，P是BC上任意一点，PD⊥AB，PE⊥AC，连接DE．记△ADE的周长为L1，四边形BDEC的周长为L2，则L1与L2的大小关系是（）A．L l＝L2B．L1＞L2C．L2＞L1D．无法确定5．一个盒子里有200只球，从101到300连续编号，甲、乙两人分别从盒子里拿球，直到他们各有100只球为止，其中甲拿到102号，乙拿到280号，则甲拿到的球的编号总和与乙拿到的球的编号总和之差最大是（）A．10000B．9822C．377D．9644二、填空题（每小题6分，满分30分）6．已知a2+4a+1＝0，且，则m＝．7．如图，由12根铅丝焊接成一个正方体框架．现要将每个正方形的4根铅丝分别涂上红、黄、蓝、白4种颜色．如果已将AD涂成红色，BF涂成黄色，GH涂成蓝色，那么该涂成白色的铅丝有．8．某旅游团一行50人到某旅社住宿，该旅社有三人间、双人间和单人间三种客房，其中三人间每人每晚20元，双人间每人每晚30元，单人间每晚50元．已知该旅行团住满了20间客房，且使总的住宿费用最省．那么这笔最省的住宿费用是元，所住的三人间、双人间、单人间的间数依次是．9．△ABC中，BC＝a，AC＝b，AB＝c．若AC、BC上的中线BE、AD垂直相交于点O，则c可用a、b 的代数式表示为．10．如图，AB为半圆O的直径，C为半圆上一点，∠AOC＝60°，点P在AB的延长线上，且PB＝BO ＝3cm．连接PC交半圆于点D，过P作PE⊥P A交AD的延长线于点E，求PE长．三、解答题（每小题15分，共60分）11．设等腰三角形的一腰与底边的长分别是方程x2﹣6x+a＝0的两根，当这样的三角形只有一个时，求a的取值范围．12．若干个工人装卸一批货物，每个工人的装卸速度相同．如果这些工人同时工作，则需10小时装卸完毕．现改变装卸方式，开始一个人干，以后每隔t（整数）小时增加一个人干，每个参加装卸的人都一直干到装卸结束，且最后增加的一个人装卸的时间是第一个人装卸时间的．问：（1）按改变后的装卸方式，自始至终需要多长时间？（2）参加装卸的有多少名工人？13．（15分）如图，在△ABC中，AB＝AC，D是底边BC上一点，E是线段AD上一点且∠BED＝2∠CED ＝∠A．求证：BD＝2CD．14．如图，已知抛物线y＝a（x﹣1）2+3（a≠0）经过点A（﹣2，0），抛物线的顶点为D，过O作射线OM∥AD．过顶点平行于x轴的直线交射线OM于点C，B在x轴正半轴上，连接BC．（1）求该抛物线的解析式；（2）若动点P从点O出发，以每秒1个长度单位的速度沿射线OM运动，设点P运动的时间为t（s）．问当t为何值时，四边形DAOP分别为平行四边形，直角梯形，等腰梯形？（3）若OC ＝OB，动点P和动点Q分别从点O和点B同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t（s），连接PQ，当t为何值时，四边形BCPQ的面积最小？并求出最小值及此时PQ的长．参考答案一、选择题（每小题6分，满分30分）1．【解答】解：∵＝＝0，∴bc+ac+ab＝0，又∵（a+b+c）2，＝a2+b2+c2+2（bc+ac+ab），＝1+0，＝1；∴a+b+c＝±1．故选：C．2．【解答】解：∵函数的自变量x取值范围是一切实数，∴分母一定不等于0，∴x2﹣2bx+c2＝0无解，即△＝4b2﹣4c2＝4（b+c）（b﹣c）＜0，解得：c＜b＜﹣c或﹣c＜b＜c．当c＞b＞0时，一定满足要求上面要求．故选：D．3．【解答】解：∵△BMI∽△ABI，∴MI＝BM，∴AI＝3MB+MB＝MB，又∵在直角△ABI中，AB：AI＝3：，∴AB＝×MB，∵MB与小正方形的边长相等，∴AB＝×＝＝5．故选：C．4．【解答】解：∵等边三角形各内角为60°，∴∠B＝∠C＝60°，∵∠BPD＝∠CPE＝30°，∴在Rt△BDP和Rt△CEP中，∴BP＝2BD，CP＝2CE，∴BD+CE＝BC，∴AD+AE＝AB+AC﹣BC＝BC，∴BD+CE+BC＝BC，L1＝BC+DE，L2＝BC+DE，即得L1＝L2，故选：A．5．【解答】解：甲拿201至300，然后用280换102 则标号之和是：（201+300）×﹣（280﹣102）＝24872；乙的编号之和是：（101+200）×+（280﹣102）＝15228 24872﹣15228＝9644．故选：D．二、填空题（每小题6分，满分30分）6．【解答】解：∵a2+4a+1＝0，∴a2＝﹣4a﹣1，＝＝＝＝＝5，∴（16+m）（﹣4a﹣1）+8a+2＝5（m﹣12）（﹣4a﹣1），原式可化为（16+m）（﹣4a﹣1）﹣5（m﹣12）（﹣4a﹣1）＝﹣8a﹣2，即[（16+m）﹣5（m﹣12）]（﹣4a﹣1）＝﹣8a﹣2，∵a≠0，∴（16+m）﹣5（m﹣12）＝2，解得m＝．故答案为．7．【解答】解：∵每个正方形的4根铅丝分别涂上红、黄、蓝、白4种颜色．AD涂成红色，BF涂成黄色，GH涂成蓝色．∴涂成红色的铅丝只能有EF、FG、CG，而FG不合题意，则涂成红色的铅丝有EF、CG；同理涂成黄色的铅丝有EH、CD；涂成蓝色的铅丝有AE、BC．则涂成白色的铅丝有：AB、DH、FG．故答案为：AB、DH、FG．8．【解答】解：设该旅行团住三人间x间，双人间y间，单人间z间，总住宿费为a元．则由题意得由②﹣①得2x+y＝30，即y＝30﹣2x④由②﹣①×2得x﹣z＝10，即z＝x﹣10 ⑤∵0≤y≤20，即0≤30﹣2x≤20，解得5≤x≤15 ⑥同理0≤z≤20，即0≤x﹣10≤20，解得10≤x≤30 ⑦由⑥⑦知10≤x≤15将④⑤代入③得a＝60x+60（30﹣2x）+50（x﹣10）＝1300﹣10x⇒x＝130﹣∴10≤≤15⇒1200≤a≤1150∴这笔最省的住宿费用是1150元，此时x＝15再将x的值代入④⑤得y＝0、z＝5故答案为1150，15、0、5．9．【解答】解：∵AC、BC上的中线BE、AD垂直相交于点O，于是，中线BE、AD，E和D是AC，BC上的中点由题可知，∴∠BOA＝90°，BD＝CD＝，AE＝EC＝，∵E，D为中点，故DE为中线＝AB＝，∴①BO2+DO2＝（）2，②AO2+EO2＝（）2，③DO2+EO2＝（）2，④BO2+AO2＝c2，∴①+②＝③+④，∴5c2＝a2+b2．故c＝．故答案为：c＝．10．【解答】解：如图，连接BD，BE，∵∠AOC＝60°，∴∠ADC＝∠PDE＝∠AOC＝30°，∵AB是⊙O的直径，∴∠ADB＝∠BDE＝90°，∵PE⊥P A，∴∠BPE＝90°，∴∠BDE＝∠BPE＝90°，∴∠BDE+∠BPE＝180°，∴点B，P，E，D四点共圆，∴∠PBE＝∠PDE＝30°，在Rt△BPE中，tan∠PBE＝，∴tan30°＝＝，∴PE＝．三、解答题（每小题15分，共60分）11．【解答】解：∵方程x2﹣6x+a＝0有实数根，∴△＝36﹣4a≥0，（1）当△＝0时，即△＝36﹣4a＝0，解得a＝9，此时三角形为等边三角形；（2）当△＞0，即△＝36﹣4a＞0时，解得a＜9，设两根为x1，x2（x1＜x2）此时存在一个等腰三角形底边为x1，腰为x2，此时不存在一个等腰三角形底边为x2，腰为x1即最短两边（即两腰）之和不大于最大边（即底边）即2x1≤x2，由根与系数的关系可得，3x1≤x1+x2＝6，∴x1≤2，∵x1+x2＝6，x1•x2＝a，∴a＝x1•（6﹣x1），＝6x1﹣（x1）2＝﹣（3﹣x1）2+9∴＝﹣（3﹣x1）2+9≤8，∴当0＜a≤8，a＝9时，三角形只有一个．12．【解答】解：（1）设装卸工作需x小时完成，则第一人干了x小时，最后一个人干了小时，两人共干活小时，平均每人干活小时，由题意知，第二人与倒数第二人，第三人与倒数第三人，平均每人干活的时间也是小时．根据题得，解得x＝16（小时）；（2）共有y人参加装卸工作，由于每隔t小时增加一人，因此最后一人比第一人少干（y﹣1）t小时，按题意，得，即（y﹣1）t＝12．解此不定方程得，，，，，即参加的人数y＝2或3或4或5或7或13．13．【解答】证明：作DO∥AB交AC于O．则由AB＝AC易知OD＝OC，且∠DOC＝∠BAC＝2∠CED，所以O为△EDC的外心，取F为△EDC的外接圆与AC的交点，连接DF，则OF＝OC＝OD，∠ACE＝∠ADF．所以△ACE∽△ADF，即有＝．再由DO∥AB，∠ADO＝∠BAE，∠AOD＝180﹣∠DOC＝180°﹣∠A＝180°﹣∠BED＝∠AEB，所以△ADO∽△BAE，即得＝＝＝．故AF＝OD＝OC＝CF，从而AO＝2OC．由DO∥AB，得：BD＝2CD．14．【解答】解：（1）∵抛物线y＝a（x﹣1）2+3（a≠0）经过点A（﹣2，0），∴0＝9a+3，∴a＝﹣（1分）∴二次函数的解析式为：y＝﹣x2+x+；（3分）（2）①∵D为抛物线的顶点，∴D（1，3），过D作DN⊥OB于N，则DN＝3，AN＝3，∴AD＝＝6，∴∠DAO＝60°．（4分）∵OM∥AD，①当AD＝OP时，四边形DAOP是平行四边形，∴OP＝6，∴t＝6（s）．（5分）②当DP⊥OM时，四边形DAOP是直角梯形，过O作OH⊥AD于H，AO＝2，则AH＝1（如果没求出∠DAO＝60°可由Rt△OHA∽Rt△DNA（求AH＝1）∴OP＝DH＝5，t＝5（s）（6分）③当PD＝OA时，四边形DAOP是等腰梯形，易证：△AOH≌△DPP′，∴AH＝CP，∴OP＝AD﹣2AH＝6﹣2＝4，∴t＝4（s）综上所述：当t＝6、5、4时，对应四边形分别是平行四边形、直角梯形、等腰梯形；（7分）（3）由（2）及已知，∠COB＝60°，OC＝OB，△OCB是等边三角形则OB＝OC＝AD＝6，OP＝t，BQ＝2t，∴OQ＝6﹣2t（0＜t＜3）过P作PE⊥OQ于E，则PE＝t（8分）∴S BCPQ＝×6×3×（6﹣2t）×t＝（t﹣）2+（9分）当t＝时，四边形BCPQ的面积最小值为．（10分）∴此时OQ＝3，OP＝，OE＝；∴QE＝3﹣＝，PE＝，∴PQ＝．（11分）。

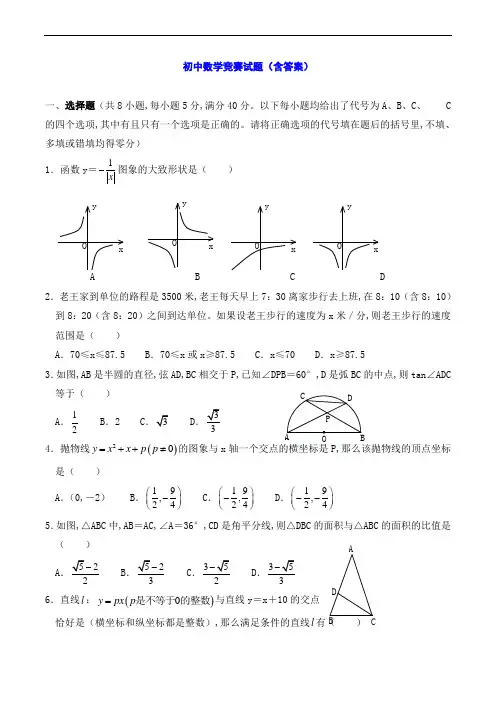
DC B A初中数学竞赛试题（含答案）一、选择题（共8小题,每小题5分,满分40分。

以下每小题均给出了代号为A 、B 、C 、 C 的四个选项,其中有且只有一个选项是正确的。

请将正确选项的代号填在题后的括号里,不填、多填或错填均得零分） 1．函数y ＝1x-图象的大致形状是（ ）A B C D2．老王家到单位的路程是3500米,老王每天早上7：30离家步行去上班,在8：10（含8：10）到8：20（含8：20）之间到达单位。

如果设老王步行的速度为x 米／分,则老王步行的速度范围是（ ）A ．70≤x ≤87.5B ．70≤x 或x ≥87.5C ．x ≤70D ．x ≥87.53．如图,AB 是半圆的直径,弦AD,BC 相交于P,已知∠DPB ＝60°,D 是弧BC 的中点,则tan ∠ADC 等于（ ） A ．12B．2 CD4．抛物线()20y x x p p =++≠的图象与x 轴一个交点的横坐标是P,那么该抛物线的顶点坐标是（ ）A ．（0,－2）B ．19,24⎛⎫- ⎪⎝⎭C ．19,24⎛⎫- ⎪⎝⎭D ．19,24⎛⎫-- ⎪⎝⎭5．如图,△ABC 中,AB ＝AC,∠A ＝36°,CD 是角平分线,则△DBC 的面积与△ABC 的面积的比值是（ ）ABCD 6．直线l ：()0y px p =是不等于的整数与直线y ＝x ＋10的交点恰好是（横坐标和纵坐标都是整数）,那么满足条件的直线l 有（） yxOyxOyxOyxOA ．6条B ．7条C ．8条D ．无数条7．把三个连续的正整数a,b,c 按任意次序（次序不同视为不同组）填入20x x ++= 的三个方框中,作为一元二次方程的二次项系数、一次项系数和常数项,使所得方程至少有一个整数根的a,b,c （ ）A ．不存在B ．有一组C ．有两组D ．多于两组 8．六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数主该点的纵坐标。

2020年广东省初中数学竞赛初赛试卷学校： 班级： 姓名：题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 答案题号 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 答案1．某校为了解学生的体能情况，随机抽查30名初三学生，测试1分钟内仰卧起坐的次数，并绘制成如图1所示的频数分布直方图，则仰卧起坐次数在25～30次的频率是（ ） A 、0.1 B 、0.2 C 、0.3 D 、0.4 2．若26321n n a a =-，则的值为（ ） A 、17 B 、35 C 、53 D 、14573．从一副扑克牌中抽出如下四张牌，其中是中心对称图形的有（ ）A 、1张B 、2张C 、3张D 、4张4．小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况，他发现这四个时刻向日葵影子的长度各不相同，那么影子最长的时刻为（ ）A 、上午12时B 、上午10时C 、上午9时30分D 、上午8时5．如图2所示的两个圆盘中，指针落在每一个数上的机会均等，则两 个指针同时落在偶数上的概率是（ ） A 、525 B 、625 C 、1025 D 、19256．若有一条公共边的两个三角形称为一对“共边三角形”，则图中以BC 为公共边的“共边三角形”有（ ） A 、2对 B 、3对 C 、4对 D 、6对7．点M （sin 60cos60-o o ，）关于x 轴对称的点的坐标是（ ） A 、31(2，） B 、31(2-，-） C 、31(2-，） D 、132--（，） 8．从鱼塘打捞草鱼300尾，从中任选10尾，称得每尾的质量分别是1.5，1.6，1.4，1.6，1.2，1.7，1.5，1.8，1.3，1.4（单位：kg ），依此估计这300尾草鱼的总质量大约是（ ）A 、450kgB 、150kgC 、45kgD 、15kg9．下列实数2221 sin 60 16 3.141597π-o （），，，，，属于无理数有（ ） A 、1个 B 、2个 C 、3个 D 、4个 10．在函数 0)ky k x=>（的图像上有三点111222333(,) (,) (,)A x y A x y A x y ，，，已知1230x x x <<<，则下列各式中正确的是（ ）6123454321E 图3D CBAA 、120y y <<B 、310y y <<C 、213y y y <<D 、312y y y << 11．如果关于1)11x a x a x a +>+<的不等式（的解集为，那么的取值范围是（ ） A 、0a > B 、0a < C 、1a >- D 、1a <- 12．如图4，E ，F 分别是正方形ABCD 的边CD ，AD 上的点，且CE=DF ，AE ，BF 相交于点O ，下列结论①AE=BF ；②AE ⊥BF ；③AO=OE ；④DEOF ABC S S =V 四边形中错误的有（ ） A 、1个 B 、2个 C 、3个 D 、4个 13．某市在“旧城改造”中计划在市内一块如图5所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米售价为a 元，则购买这种草皮至少需要（ ）A 、450a 元B 、300a 元C 、225a 元D 、150a 元14．观察下列算式：12345672=22=42=82=162=322=642=128=2568，，，，，，，2……通过观察，用你所发现的规律写出118的末位数字是（ ）A 、2B 、4C 、6D 、8 15．已知22125a b a b a b -=+=+，，的值为（ ） A 、7 B 、－7 C 、±7 D 、±916．某单位购买甲、乙两种纯净水若干桶，共用250元，其中甲种水每桶8元，乙种水每桶6元；乙种水桶数是甲种水桶数的75%。

全国初中数学联赛试题第一试一、选择题1．已知a＝355,b＝444,c＝533,则有［ ]A．a＜b＜c B．c＜b＜a C．c＜a＜b D．a＜c＜bA．1 B．2 C．3 D．43．如果方程(x－1)(x2－2x－m)＝0的三根可以作为一个三角形的三边之长，那么实数m的取值范围是4．如果边长顺次为25、39、52与60的四边形内接于一圆，那么此圆的周长为［ ]A．62πB．63π C．64πD．65π5．设AB是⊙O的一条弦，CD是⊙O的直径，且与弦AB相交，记M＝｜S △CAB－S△DAB｜，N＝2S△OAB，则[ ]A．M＞N B．M＝N C．M＜N D．M、N的大小关系不确定6．设实数a、b满足不等式｜｜a｜－(a＋b)｜＜｜a－|a＋b｜｜，则[ ]A．a＞0且b＞0 B．a＜0且b＞0C．a＞0且b＜0 D．a＜0且b＜0二、填空题1．在12，22，32…，952这95个数中，十位数字为奇数的数共有____个。

4．以线段AB为直径作一个半圆，圆心为O，C是半圆周上的点，且OC2＝AC·BC，则∠CAB＝______．第二试一、已知∠ACE＝∠CDE＝90°，点B在CE上，CA＝CB＝CD，经A、C、D三点的圆交AB于F（如图）求证F为△CDE的内心。

二、在坐标平面上，纵坐标与横坐标都是整数理由。

三、试证：每个大于6的自然数n，都可以表示为两个大于1且互质的自然数之和。

初中数学联赛参考答案第一试一、选择题1．讲解：这类指数幂的比较大小问题，通常是化为同底然后比较指数，或化为同指数然后比较底数，本题是化为同指数，有c＝(53)11＝12511＜24311＝(35)11＝a＜25611＝(44)11＝b。

选C。

利用lg2＝0.3010，lg3＝0.4771计算lga、lgb、lgc也可以，但没有优越性。

2．讲解：这类方程是熟知的。

先由第二个方程确定z＝1,进而可求出两个解：(2，21，1)、(20，3，1)．也可以不解方程组直接判断：因为x≠y(否则不是正整数)，故方程组①或无解或有两个解，对照选择支，选B。

2003年广东省初中数学竞赛初赛试卷（考试时间60分钟，满分100分）A 卷一、选择题（每小题2分，满分20分）1、如果0)(=-+a a ，则a 是（ ）A 、正数B 、负数C 、非正数D 、非负数2、如果2-=a ，那么2-a 的算术平方根（ ）A 、是a 的相反数B 、是a 的倒数C 、是a 的倒数的相反数D 、没有算术平方根3、某工厂原来平均每天用煤n 吨，注意节约能源后每天少用煤2吨，那么现存的m 吨煤比以前多用的天数是（ ）A 、)2(-n n mB 、)2(+n n mC 、)2(2-n n mD 、)2(2+n n m 4、不等式11254<-x 的正整数解有（ ） A 、2个 B 、3个 C 、4个 D 、5个5、已知点)8,(a 在抛物线2ax y =上，则a 的值是（ ）A 、2B 、2-C 、2±D 、22±6、如图，已知线段AB=5cm ，C 、D 、E 、F 、把AB 五等分，则小于3cm 的线段有（ ）A 、4条B 、5条C 、9条D 、12条7、下列命题中错误的是（ ）A 、一组对边平行且相等的四边形是平行四边形B 、一组对边平行，另一组对边相等的四边形是平行四边形C 、两组对边分别相等的四边形是平行四边形D 、两条对角线互相平分的四边形是平行四边形8、在RT △ABC 中，∠C ＝90°，a 、b 、c 分别是∠A 、∠B 、∠C 的对边，下列关系中错误的是（ ）A 、b=c.cosB B 、b=a.tanBC 、a=c.sinAD 、Bb a tan = 9、若∠A 是锐角，则sinA+cosA 的值（ ）A 、大于1B 、等于1C 、小于1D 、可能大于1，也可能小于110、两圆圆心距为3，其半径分别是方程0232=+-x x 的两根，那么两圆的位置关系是（ ）A 、相离B 、相交C 、内切D 、外切二、填空题（每小题2分，满分20分）11、81＝ ；12、已知22=+b a ，则)44(4122b ab a ++的值是 ； 13、如果a:b:c=2:3:4，则c b a c b a -++-= ； 14、已知1，2，2三个数，请你再添上一个数，写成比例式 ；15、设甲、乙两人在一次赛跑中，路程S 与时间t 的关系如图，那么从图象可以看到：（1）这是一次 米赛跑；（2）甲、乙两人先到达终点的是 ；16、夏季高山上的温度从山脚起每升高100米降低C 07.0，已知山脚的温度是C 020，山顶的温度是C 04.14，那么山的高度是 米；17、如图，A D ∥BC ，∠D ＝100°，CA 平分∠BCD ，则∠DAC ＝ 度；18、某同学带50元去购书中心买某种数学辅导书，已知该书每册定价9元4角，该同学买书后余下的钱数y 元和买的册数x 之间的函数关系式是 ；19、点),2(a -在第二象限的角平分线上，则a = ;20、如图，矩形ABCD 中，O 点是两对角线交点，A E ⊥BD 于点E ，OE ：OD ＝1：2，AE ＝cm 3，则DE ＝ 。

广东省九年级上学期基础学科竞赛数学试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）(2021·梁山模拟) 围棋起源于中国，古代称之为“弈”，至今已有多年的历史．年月，世界围棋冠军柯洁与人工智能机器人进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（）A .B .C .D .2. （2分）如图，如果可以在三个完全相同的正方形拼成的图案中随意取点，那么这个点取在阴影部分的概率是（）A .B .C .D .3. （2分）用一个5倍的放大镜去观察一个三角形，对此，四位同学有如下说法：甲说：三角形的每个内角都扩大到原来的5倍；乙说：三角形的每条边都扩大到原来的5倍；丙说：三角形的面积扩大到原来的5倍；丁说：三角形的周长都扩大到原来的5倍．上述说法中正确的是（）A . 甲和乙B . 乙和丙C . 丙和丁D . 乙和丁4. （2分）(2020·菏泽) 如果顺次连接四边形的各边中点得到的四边形是矩形，那么原来四边形的对角线一定满足的条件是（）A . 互相平分B . 相等C . 互相垂直D . 互相垂直平分5. （2分） (2019九上·大冶月考) 已知点A ，B ，C 在二次函数y=-3x2+k的图象上，则y1 ， y2 ， y3的大小关系是（）A .B .C .D .6. （2分）(2017·东光模拟) 若关于x的一元二次方程 x2+ x+tana=0有两个相等的实数根，则锐角a等于（）A . 15°B . 30°C . 45°D . 60°7. （2分） (2018九上·新乡期末) 如图，⊙O是△ABC的外接圆，∠OCB=40°，则∠A的大小为（）C . 80°D . 100°8. （2分） (2021九上·淮北月考) 下列各点中，不在双曲线上的点是（）A .B .C .D .9. （2分）如图所示，数学小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在圆的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得小桥拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，则小桥所在圆的半径为（）米．A .B . 5C .D . 610. （2分）(2013·义乌) 已知圆锥的底面半径为6cm，高为8cm，则这个圆锥的母线长为（）A . 12cmB . 10cmC . 8cmD . 6cm11. （2分） (2017九上·青龙期末) 已知两个相似三角形的周长之比为1：3，则它们相应的面积之比是（）A . 3：1D . 1：912. （2分）(2020·龙泉驿模拟) 二次函数的图象如图所示，下列结论正确的是（）A .B .C .D . 有两个不相等的实数根二、填空题 (共8题；共8分)13. （1分） (2018八上·开封期中) 等腰三角形的周长为13cm ，其中一边长为3cm ，则底边长等于cm.14. （1分）当m= 时，y=（m﹣2）是二次函数．15. （1分） (2020九上·临武月考) 如图，点M是反比例函数y＝（a≠0）的图象上一点，过M点作x 轴、y轴的平行线，若S阴影=8，则此反比例函数解析式为16. （1分） (2018九上·花都期末) 将一个底面半径为6cm，母线长为15cm的圆锥形纸筒沿一条母线剪开并展平，所得的侧面展开图的圆心角是度。

初中数学竞赛创新试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. -2B. 0C. 1D. 22. 如果一个圆的半径是5厘米，那么它的周长是多少厘米？A. 10πB. 15πC. 20πD. 25π3. 一个数的平方是16，这个数可能是：A. 2B. 4C. -2D. C和-24. 一个直角三角形的两条直角边分别为3和4，那么它的斜边长度是：A. 5B. 6C. 7D. 85. 如果一个数的绝对值是5，那么这个数可能是：A. 5C. A和BD. 06. 一个数的立方是-27，这个数是：A. -3B. 3C. -27D. 277. 一个数的倒数是1/4，那么这个数是：A. 4B. 1/4C. 1/2D. 18. 一个数的平方根是4，那么这个数是：A. 16B. -16C. 4D. -49. 如果一个数的平方是25，那么这个数的立方是：A. 125B. 250C. 375D. 62510. 一个数的立方根是-2，那么这个数是：A. -8B. 8D. 2二、填空题（每题3分，共15分）11. 一个数的平方是9，这个数是_________。

12. 如果一个数的平方根是2，那么这个数是_________。

13. 一个数的立方是64，这个数是_________。

14. 一个数的倒数是2/3，那么这个数是_________。

15. 如果一个数的立方根是3，那么这个数是_________。

三、解答题（每题5分，共55分）16. 一个直角三角形的斜边长度是13厘米，其中一个直角边是5厘米，求另一个直角边的长度。

17. 一个数列的前三项是1, 1, 2，每一项都是前两项的和，求这个数列的第10项。

18. 一个圆的直径是14厘米，求这个圆的面积。

19. 一个数的平方是25，求这个数的平方根。

20. 一个数的立方是-125，求这个数。

四、证明题（每题10分，共20分）21. 证明：对于任意一个正整数n，n的平方总是大于或等于n。

广东省初中数学竞赛试卷姓名:________ 班级:________ 成绩:________一、单选题 (共40题；共80分)1. （2分） (2016七下·蒙阴期中) 下列选项中能由左图平移得到的是（）A .B .C .D .2. （2分）已知抛物线y=ax2﹣2x+1与x轴没有交点，那么该抛物线的顶点所在的象限是（）A . 第四象限B . 第三象限C . 第二象限D . 第一象限3. （2分）(2020·嘉兴·舟山) 如图，在直角坐标系中，△OAB的顶点为O(0，0)，A(4，3)，B(3，0)。

以点O为位似中心，在第三象限内作与△OAB的位似比为的位似图形△OCD，则点C坐标为（）A . (-1，-1).B . (， -1)C . (-1， )D . (-2，-1).4. （2分）如图，将三角形向右平移3个单位长度，再向上平移2个单位长度，则平移后三个顶点的坐标为（）A . （-1，-1），（2，3），（5，1）B . （-1，1），（3，2），（5，1）C . （-1，1），（2，3），（5，1）D . （1，-1），（2，2），（5，1）5. （2分）(2018·泰安) 如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为1，经过平移后得到，若上一点平移后对应点为，点绕原点顺时针旋转，对应点为，则点的坐标为（）A .B .C .D .6. （2分）下列语句错误的是（）A . 连接两点的线段的长度叫做两点间的距离B . 两条直线平行，同旁内角互补C . 若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补角D . 平移变换中，各组对应点连成两线段平行且相等7. （2分） (2019八下·北京房山期末) 如图，是由绕着某点旋转得到的，则这点的坐标是（）A . （1，1）B . （2，0）C . （0，1）D . （3，1）8. （2分）(2017·曹县模拟) 如图，将正方形OABC放在平面直角坐标系中，O是原点，A的坐标为（1，），则点C的坐标为（）A . （﹣，1）B . （﹣1，）C . （，1）D . （﹣，﹣1）9. （2分）△DEF（三角形）是由△ABC平移得到的，点A（﹣1，﹣4）的对应点为D（1，﹣1），则点B（1，1）的对应点E，点C（﹣1，4）的对应点F的坐标分别为（）A . （2，2），（3，4）B . （3，4），（1，7）C . （﹣2，2），（1，7）D . （3，4），（2，﹣2）10. （2分）(2016·福州) 如图，以圆O为圆心，半径为1的弧交坐标轴于A，B两点，P是上一点（不与A，B重合），连接OP，设∠POB=α，则点P的坐标是（）A . （sinα，sinα）B . （cosα，cosα）C . （cosα，sinα）D . （sinα，cosα）11. （2分） (2017八下·东台期中) 如图，点A（a，1）、B（﹣1，b）都在双曲线y=﹣上，点P、Q 分别是x轴、y轴上的动点，当四边形PABQ的周长取最小值时，PQ所在直线的解析式是（）A . y=xB . y=x+1C . y=x+2D . y=x+312. （2分） (2020八下·汉阳期中) 如图，菱形的对角线交于点，，，将沿点到点的方向平移，得到，当点与点重合时，点与点之间的距离为（）A . 3B . 4C . 5D . 613. （2分） (2020九下·哈尔滨月考) 是⊙O的直径，切⊙O于点A，交⊙ 于点C;连接 ,若 ,则等于（）A . 20°B . 25°C . 30°D . 40°14. （2分） (2020七上·龙凤期末) 一列火车由甲市驶往相距600km的乙市，火车的速度是200km/时，火车离乙市的距离s(单位:km)随行驶时间t(单位:小时)变化的关系用图象表示正确的是（）A .B .C .D .15. （2分） (2020七下·孟村期末) 若不等式组的解为x<8，则m的取值范围是（）A . m≥8B . m<8C . m≤8D . m>816. （2分）如果⊙A的半径是4cm，⊙B的半径是10cm，圆心距AB＝8cm，那么这两个圆的位置关系是（）A . 外离B . 外切C . 相交D . 内切17. （2分） (2020九下·黄石月考) 已知：二次函数，下列说法错误的是（）A . 当时，随的增大而减小B . 若图象与轴有交点，则C . 当时，不等式的解集是 x＜1或x＞3D . 若将图象向上平移1个单位，再向左平移3个单位后过点，则18. （2分）一个袋子中有4个球，其中2个红球，2个蓝球，除颜色外其余特征均相同，若从这个袋子中任取1个球，是蓝色的概率是（）A .B .C .D .19. （2分）如图，半径为10的⊙O中，弦AB的长为16，则这条弦的弦心距为（）A . 6B . 8C . 10D . 1220. （2分） (2019八上·重庆月考) 如图，等腰△ABC中，AB＝AC，AB的垂直平分线MN交AC于点D，∠DBC ＝15°，则∠A的度数是（）A . 35°B . 40°C . 50°D . 55°21. （2分）(2020·定兴模拟) 如图，函数（k≠0，x＜0）的图像L经过点A（－4，2），直线AB与x轴交于点B（－5，0），经过点C（0，4）作y轴的垂线，分别交L和直线AB于点M，N，则MN=（）A . 1B . －5C . －1D . 522. （2分） (2018七下·东莞开学考) 已知a× =b÷62.5%=c× =1（a.b.c均不为0），a.b.c这三个数中最小的是（）。