《信号与线性系统》试题与答案

第一、二章自测题1、判断题（1）若x (t )是一连续时间周期信号，则y (t )=x (2t )也是周期信号。

（2）两个周期信号之和一定是周期信号。

（3）所有非周期信号都是能量信号。

（4）两个连续线性时不变系统相互串联的结果仍然是线性时不变系统。

（5）若)()()(t h t x t y *=，则)1()2()1(+*-=-t h t x t y 。

（6）一个系统的自由响应就等于它的零输入响应。

（7）一个系统的零状态响应就等于它的自由响应。

（8）零状态响应是指系统没有激励时的响应。

（9）系统的单位冲激响应是指系统在冲激信号作用下的全响应。

（10）两个功率信号之和必为功率信号。

2、判断下列信号是能量信号还是功率信号？ （1）3cos(15)0()0t t f t t π≥⎧=⎨<⎩ （2）50()0te tf t t -⎧≥=⎨<⎩（3）()6sin 23cos3f t t t =+ （4）|2|()20sin 2t f t e t -=3、填空题（1）已知)()4()(2t t t f ε+=，则)(''t f =__________________。

（2）=+-⋅+⎰∞∞-dt t t t )1()2(2δ__________________________。

（3）=-⎰∞∞-dt t ）（92δ_________________________ 。

（4）=-⎰∞∞-dt t t e t j ）（0δω_________________________ 。

（5）信号cos(15)cos(30)t t -的周期为 。

4、试画出下列各函数的波形图 （1）0 ),()(001>-=t t t t f ε （2）)]4()([3cos )(2--=t t t t f εεπ （3）][sin )(3t t f πε=5、已知f (t )的波形如图1.1所示，求f (2-t )与f (6-2t )的表达式，并画出波形图。

专升本《信号与线性系统》一、（共60题,共156分）1. 能量有限信号是指总能量为有限值而平均功率为____的信号。

（2分）.标准答案：1. 零;2. 系统响应中随时间增长而趋于稳定的部分称为________________分量。

（2分）.标准答案：1. 稳态响应;3. 单位函数响应h(k)是指离散时间系统对____________________________________________的零状态响应。

（2分）.标准答案：1. 单位函数（或δ(k)）;4. 若周期函数f (t)满足，则称其为________函数。

（2分）.标准答案：1. 奇谐;5. h(t)是连续因果LTI系统的冲激响应，则系统稳定的充要条件是________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ____________________。

（2分）.标准答案：1. ;6. ____。

（2分）.标准答案：1. 0;7. 时间函数中变化较____的信号必定具有较宽的频带。

（2分）.标准答案：1. 快;8. 信号的最小抽样频率为________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ____________________ Hz。

第1章基本概念K第1章习题k1.1解：（1）x(t)为周期信号，周期为T=10。

（2）x(t)为非周期信号。

（3）x[n]为非周期信号。

（4）x[n]为周期信号，周期为N=2。

（5）x(t)为非周期信号。

（6）x[n]为周期信号，周期为N=2。

1.2解：（1）x(t)为功率信号。

（2）x(t)既不是能量信号也不是功率信号。

（3）x[n]为能量信号。

（4）x(t)为能量信号。

（5）x(t)为能量信号。

（6）x[n]为能量信号。

1.3略。

1.4略。

1.5（原题有误）一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。

用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统，即x[n−k]=S−k(x[n])。

写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。

解：提示：可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。

1.6解：（1）因果、无记忆、非线性、时不变、BIBO稳定系统。

（2）因果、无记忆、线性、时变和BIBO稳定系统。

（3）因果、无记忆、线性、时变和非稳定系统。

（4）因果、记忆、线性、时不变和BIBO稳定系统。

（5）因果、无记忆、线性、时变和BIBO稳定系统。

（6）因果、记忆、时不变、非稳定系统。

–2/48–第1章基本概念（7）因果、无记忆、线性、时不变和BIBO稳定系统。

（8）非因果系统、无记忆、线性、时不变、BIBO稳定系统。

1.7证明略。

1.8解：（1）x[n]的响应为{1,1,−1,2,n=0,1,2,3}。

（2）x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。

（3）x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。

1.9证明提示：根据微积分的极限定义证明。

1.10解：（1）x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。

（2）x(t)的响应为[2(t+e−t)−2]u(t)。

信号与线性系统-8(总分：100.00，做题时间：90分钟)一、计算题(总题数：22，分数：100.00)绘出下列离散信号的图形。

（分数：8.00）2.00）__________________________________________________________________________________________ 正确答案：()解析：解是一个公比为的等比序列，且该序列起始于k=0。

其图形如图(a)所示。

(2).2δ(k)-ε(k)（分数：2.00）__________________________________________________________________________________________ 正确答案：()解析：解此序列也是起始于k=0的，其图形如图(b)所示。

2.00）__________________________________________________________________________________________ 正确答案：()解析：解此序列可看做是对连续时间信号(1+sin(2πt))ε(t)以每周期取16个样本点而得到的，故其图形如图(c)所示。

(4).k(2) -kε(k)（分数：2.00）__________________________________________________________________________________________ 正确答案：()解析：解此序列起始于k=1，其图形如图(d)所示。

绘出下列离散信号的图形。

（分数：8.00）(1).k[ε(k+4)-ε(k-4)]（分数：2.00）__________________________________________________________________________________________ 正确答案：()解析：解因故此信号的图形如图(a)所示。

1.下列信号的分类方法不正确的是（ A ）：A、数字信号和离散信号B、确定信号和随机信号C、周期信号和非周期信号D、因果信号与反因果信号2.下列说法正确的是（ D ）：A、两个周期信号x(t)，y(t)的和x(t)+y(t)一定是周期信号。

B、两个周期信号x(t)，y(t)的周期分别为2和，则其和信号x(t)+y(t) 是周期信号。

C、两个周期信号x(t)，y(t)的周期分别为2和，其和信号x(t)+y(t)是周期信号。

D、两个周期信号x(t)，y(t)的周期分别为2和3，其和信号x(t)+y(t)是周期信号。

3.下列说法不正确的是（ D ）。

A、一般周期信号为功率信号。

B、时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。

C、ε(t)是功率信号；D、e t为能量信号;4.将信号f(t)变换为（ A ）称为对信号f(t)的平移或移位。

A、f(t–t0)B、f(ｋ–k0)C、f(at)D、f(-t)5.将信号f(t)变换为（ A ）称为对信号f(t)的尺度变换。

A、f(at)B、f(t–k0)C、f(t–t0)D、f(-t)6.下列关于冲激函数性质的表达式不正确的是（ B ）。

A、 B、C、 D、7.下列关于冲激函数性质的表达式不正确的是（ D ）。

A、 B、C、 D、8.下列关于冲激函数性质的表达式不正确的是（ B ）。

A、 B、C、 D、9.下列基本单元属于数乘器的是（ A ）。

A、 B、C、 D、10.下列基本单元属于加法器的是（ C ）。

A、 B、C、 D、11.，属于其零点的是（ B ）。

A、-1B、-2C、-jD、j12.，属于其极点的是（ B ）。

A、1B、2C、0D、-213.下列说法不正确的是（ D ）。

A、H(s)在左半平面的极点所对应的响应函数为衰减的。

即当t→∞时，响应均趋于0。

B、H(s)在虚轴上的一阶极点所对应的响应函数为稳态分量。

C、H(s)在虚轴上的高阶极点或右半平面上的极点，其所对应的响应函数都是递增的。

信号与线性系统_华中科技大学中国大学mooc课后章节答案期末考试题库2023年1.设【图片】，若【图片】，则【图片】。

参考答案:错误2.已知某信号【图片】的傅里叶变换为【图片】，则该信号的导数【图片】的拉普拉斯变换及其收敛域为（）。

参考答案:2，全S平面3.单位脉冲响应为【图片】的LTI系统是非因果、不稳定的系统。

参考答案:错误4.已知某系统的系统函数H(s)，唯一决定该系统单位冲激响应h(t)函数形式的是（）。

参考答案:H(s)的极点5.双边序列【图片】的傅里叶变换为【图片】。

参考答案:错误6.已知某系统的频域系统函数为【图片】其中K和【图片】均为正常数，则该系统是一个（）。

参考答案:理想带通滤波器7.设离散信号【图片】的傅里叶变换为【图片】，则【图片】=（）。

参考答案:48.已知某因果信号的拉普拉斯变换【图片】，则其初值【图片】等于（）。

参考答案:-19.某连续LTI系统的阶跃响应为【图片】，则系统（）。

参考答案:一定是稳定的10.已知【图片】，【图片】，且【图片】，则y[1] = ( )。

参考答案:11.为减少欠采样的影响，工程实际中可先对信号进行低通滤波处理，低通滤波器的截止频率应该低于采样频率。

参考答案:错误12.信号f (t) 如下图所示，则其表达式为（）。

（注：r(t)表示单位斜坡信号）【图片】参考答案:(t − 1)u(t)13.若某因果序列【图片】的Z变换【图片】，则【图片】的值为（）。

参考答案:214.若离散时间信号x[n]如图1所示，则x[2n − 4]如图2所示。

【图片】参考答案:正确15.单位冲激响应为【图片】的LTI系统是（）。

参考答案:有记忆的、稳定的16.具有单位脉冲响应【图片】的LTI系统是（）。

参考答案:因果的、稳定的17.离散周期信号x[n]的傅里叶级数表示为【图片】，则x[n]是（）。

参考答案:纯虚的奇信号18.某连续时间LTI系统的频域系统函数为【图片】，若激励信号【图片】，则响应中基波和二次谐波分量的幅度之比为（）。

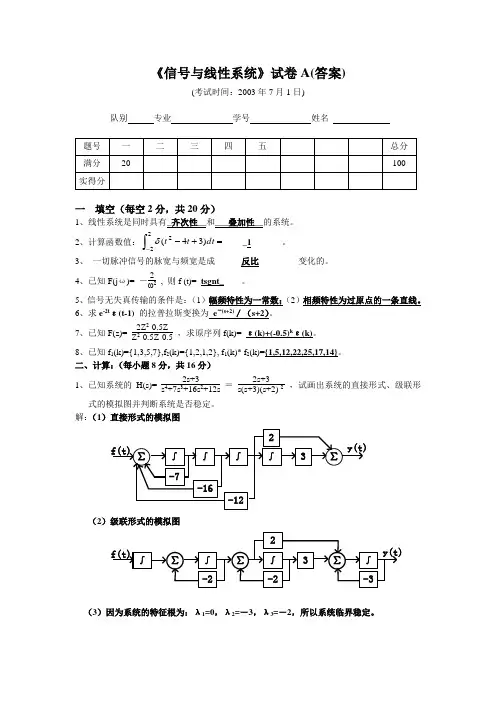
《信号与线性系统》试卷A(答案)(考试时间：2003年7月1日)队别 专业 学号 姓名一 填空（每空2分，共20分）1、线性系统是同时具有_齐次性__和___叠加性__的系统。

2、计算函数值：⎰-=+-222)34(dt t t δ_____1_______。

3、 一切脉冲信号的脉宽与频宽是成______反比_________变化的。

4、已知F(j ω)= －2ω2 , 则f (t)=_tsgnt_____。

5、信号无失真传输的条件是：（1）幅频特性为一常数；（2）相频特性为过原点的一条直线。

6、求e -2t ε(t-1) 的拉普拉斯变换为_e －(s+2)／（s+2）。

7、已知F(z)= 2Z 2-0.5Z Z 2-0.5Z-0.5 ，求原序列f(k)= ε(k)+(-0.5)k ε(k)。

8、已知f 1(k)={1,3,5,7},f 2(k)={1,2,1,2}, f 1(k)* f 2(k)={1,5,12,22,25,17,14}。

二、计算：（每小题8分，共16分） 1、已知系统的H(s)=2s+3s 4+7s 3+16s 2+12s＝2s+3s(s+3)(s+2) 2，试画出系统的直接形式、级联形式的模拟图并判断系统是否稳定。

解：（1）直接形式的模拟图（2）级联形式的模拟图（3）因为系统的特征根为：λ1=0，λ2=－3，λ3=－2，所以系统临界稳定。

2、一离散时间系统用以下差分方程描写：y(k+2)-5y(k+1)+6y(k)=e(k+2)-3e(k),是求此系统的 单位函数响应h(k)。

解：由差分方程得到移序算子方程（S 2-5S+6）y(k)=(S 2-3) e(k)则转移算子为H(S)＝S 2-3S 2-5S+6 =1 ＋ 5S-9S 2-5S+6 =1 ＋ 6S-3 － 1S-2则 h(k)=δ(k)＋(2×3k －2k-1) ε(k-1)三、（10分）已知系统函数65)(2++-=ωωωωj j j H ，系统的初始状态y(0)=2，y ’(0)=1，激励f(t)= e -t ε(t)。

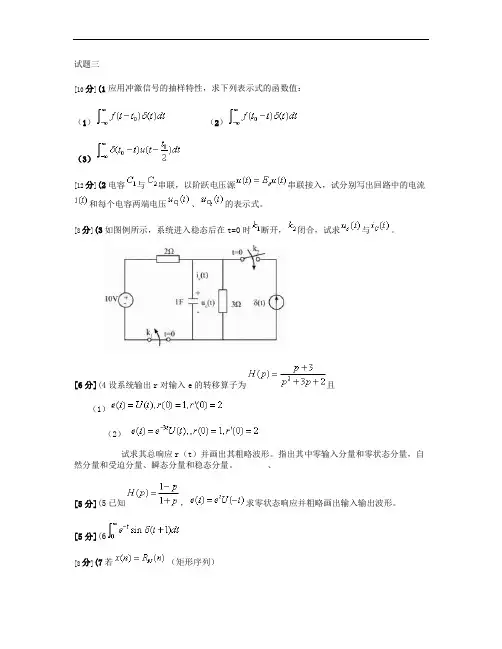
试题三[10分](1应用冲激信号的抽样特性，求下列表示式的函数值：（1）（2）（3）[12分](2电容与串联，以阶跃电压源串联接入，试分别写出回路中的电流和每个电容两端电压、的表示式。

[8分](3如图例所示，系统进入稳态后在t=0时断开，闭合，试求与。

[6分](4设系统输出r对输入e的转移算子为且（1）（2）试求其总响应r（t）并画出其粗略波形。

指出其中零输入分量和零状态分量，自然分量和受迫分量、瞬态分量和稳态分量。

、[5分](5已知，求零状态响应并粗略画出输入输出波形。

[5分](6[8分](7若（矩形序列）(1求； (2求；(3求频响特性，作幅度特性曲线图。

[6分](8已知网络函数的极点位于处，零点位于处，还知道。

此网络的阶路响应中，包含一项为。

讨论：若a从0变到5，相应的K1如何随之改变。

[8分](9求图习a、b、c、d所示电路的系统函数，并说明它们各为何种具体的网络函数。

电路中和表示激励源，表示电路的响应，M表示的理想变压器。

[6分](10在信号处理技术中应用的“短时傅里叶变换”有两种定义方式，假定信号源为x(t，时域窗函数为g(t，第一种定义方式;第二种定义方式为试从物理概念说明参变量的含义，并比较两种结果有何联系与区别[8分](11写出图习所示电路的状态方程。

[9分](12求下列函数的拉普拉斯变换。

（1）（2）（3）[9分](13（1）已知，用初值定理求在t=0时的值，且与直接求得之值核对；（2）已知系统转移函数，且有，求A和h(t；（3）已知系统转移函数与输入信号为①②求系统零状态响应的初值r(0和终值。

============================================================================= ===============================答案========================================== 一、04(13小题,共100分[10分](1解（1）（2）（3）[12分](2解由题意画出如下所示的电路图据KVL，有（1）又（2）式（1）两边微分，有（3）由（2）式得（4）（4）式代入（3）式得（5）对（5）式两边积分得（6）（6）式代入（1）式得（5）式代入（2）式得即[8分](3解：当t=0时断开，闭合时，系统的微分方程为算子方程为所以得在时，，代入方程得C=6因此系统的单位冲激响应，所以因此[6分](4[5分](5[5分](6[8分](7解(1(2(3[6分](8[8分](9 (a(b(c[6分](10解信号x(t在时间的短时傅里叶变换就是信号x (t乘上一个以为中心的分析窗g(t-所作的傅里叶变换,x(t称作基信号，由于乘上一个相当短的窗g(t-，等价于取出信号在分析点t=附近的一个小切片，所以短时傅里叶变换直接是信号在“分析时间”附近的局部谱。

综合测试(三)一、选择题（本题共6小题，每小题3分，共18分）1、若想使连续时间信号在通过线性非时变系统传输时，波形不会产生失真，而仅仅是延时一段时间输出，则要求系统的单位冲激响应必须满足（）A. B.C. D.2、序列和等于（）A. 1B.C. D.3、连续时间信号的单边拉普拉斯变换为（）A. B.C. D.4、下列各式中正确的是（）A． B.C.D．5、单边Z变换对应的原时间序列为（）A．B．C．D．6．请指出是下面哪一种运算的结果？（）A．左移6 B. 右移6C．左移2 D. 右移2三、描述某系统的微分方程为y”(t) + 4y’(t) + 3y(t) = f(t)求当f(t) = 2e-2t，t≥0；y(0)=2，y’(0)= -1时的解；（15分）解: (1) 特征方程为λ2 + 4λ+ 3 = 0 其特征根λ1= –1，λ2= –2。

齐次解为y h(t) = C1e -t + C2e -3t当f(t) = 2e–2 t时，其特解可设为y p(t) = Pe -2t将其代入微分方程得P*4*e -2t + 4(–2 Pe-2t) + 3Pe-t = 2e-2t解得P=2于是特解为y p(t) =2e-t全解为：y(t) = y h(t) + y p(t) = C1e-t + C2e-3t + 2e-2t其中待定常数C1,C2由初始条件确定。

y(0) = C1+C2+ 2 = 2，y’(0) = –2C1–3C2–1= –1解得C1 = 1.5 ，C2 = –1.5最后得全解y(t) = 1.5e–t –1.5e –3t +2 e –2 t, t≥0三、描述某系统的微分方程为 y ”(t) + 5y ’(t) + 6y(t) = f(t) 求当f(t) = 2e -t ，t ≥0；y(0)=2，y ’(0)= -1时的解；（ 15分）解: (1) 特征方程为λ2 + 5λ+ 6 = 0 其特征根λ1= –2，λ2= –3。

标准答案(一)一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。

它的调制方式有调幅、调频、调相。

2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。

3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。

4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。

5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。

6、调频电路有直接调频、间接调频两种方式。

7、检波有同步、和非同步检波两种形式。

8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。

9、变频器可由混频器、和带通滤波器两部分组成。

10、列出三个常见的频谱搬移电路调幅、检波、变频。

11、用模拟乘法器非线性器件实现调幅最为理想。

二、选择题（每小题2分、共20分）将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息（C ）A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含（B ）A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于（ A ）分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中，石英谐振器相当于（C ）元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为（ B ）A、|AF|=1，φA+φF= 2nπB、|AF| >1，φA+φF = 2nπC、|AF|>1，φA+φF ≠2nπD、|AF| =1，φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在（B ）状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为（ B ）A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为（ B ）A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是（D ）A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中，由于检波电容放电时间过长而引起的失真是（B）A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题，对的打“√”,错的打“×”（每空1分，共10分）1、谐振放大器是采用谐振回路作负载的放大器。

一、选择题（3分/每题，共21 分,单选题） 1、下列哪个系统不属于因果系统（ A ）A ]1[][][+-=n x n x n yB 累加器 ∑-∞==nk k x n y ][][C 一LTI 系统，其)()(2t u e t h t-= D LTI 系统的)(s H 为有理表达式，ROC ：1->σ 2、信号45[]cos()2jn x n n eππ=+，其基波周期为（A ）A 20B 10C 30D 5 3、设]3[]1[2][][---+=n n n n x δδδ和]1[2]1[2][-++=n n n h δδ，][*][][n h n x n y =，求=]0[y （ B ）A 0B 4C ][n δD ∞4、已知一离散LTI 系统的脉冲响应h[n]= δ[n]+2δ[n-1]-3δ[n-2]，则该系统的单位阶跃响应S[n]等于（B ）A δ[n ]+δ[n-1]-5δ[n-2]+ 3δ[n-3]B δ[n]+3δ[n-1]C δ[n]D δ[n]+ δ[n-1]-2δ[n-2]5、信号)}2()2({-+--t u t u dt d的傅立叶变换是（ C ）A ω2sin 2jB )(2ωπδC -2j ω2sinD 6、己知)(t x 的频谱函数⎩⎨⎧>=<==2rad/s ||0,2rad/s,||1,)X(j ωωω 设t t x t f 2cos )()(=，对信号)(t f 进行均匀采样的奈奎斯特率为（ C ）A 4 rad/sB 2 rad/sC 8 rad/sD 3 rad/s7、下列说法不正确的是（D ）A 当系统的频率响应具有增益为1和线性相位时，系统所产生的输出就是输入信号的时移；B 取样示波器和频闪效应是欠采样的应用；C 对离散时间信号最大可能的减采样就是使其频谱在一个周期内的非零部分扩 展到将π-到π的整个频带填满；D 听觉系统对声音信号的相位失真敏感。

信号与系统期末考试试题6课程名称： 信号与系统一、选择题（共10题，每题3分 ，共30分，每题给出四个答案，其中只有一个正确的）1、 卷积f 1(k+5)*f 2(k-3) 等于 。

（A ）f 1(k)*f 2(k) （B ）f 1(k)*f 2(k-8)（C ）f 1(k)*f 2(k+8)（D ）f 1(k+3)*f 2(k-3)2、 积分dt t t ⎰∞∞--+)21()2(δ等于 。

（A ）1.25（B ）2.5（C ）3（D ）5 3、 序列f(k)=-u(-k)的z 变换等于 。

（A ）1-z z （B ）-1-z z（C ）11-z （D ）11--z4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。

（A ）)2(41t y （B ）)2(21t y （C ）)4(41t y （D ）)4(21t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时，系统的零状态响应y f (t)等于（A ）(-9e -t +12e -2t )u(t) （B ）(3-9e -t +12e -2t )u(t)（C ）)(t δ+(-6e -t +8e -2t )u(t) （D ）3)(t δ +(-9e -t +12e -2t )u(t)6、 连续周期信号的频谱具有（A ） 连续性、周期性 （B ）连续性、收敛性 （C ）离散性、周期性 （D ）离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于（A ） 1（B ）2（C ）3（D ）4 8、序列和()∑∞-∞=-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u tet f t的单边拉氏变换()s F 等于()A ()()()232372+++-s e s s ()()223+-s e B s()()()2323++-s se C s ()()332++-s s e D s二、填空题（共9小题，每空3分，共30分）1、卷积和[（0.5）k+1u(k+1)]*)1(k -δ=________________________2、单边z 变换F(z)=12-z z的原序列f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换F(s)=1+s s，则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、单边拉普拉斯变换ss s s s F +++=2213)(的原函数f(t)=__________________________ 6、已知某离散系统的差分方程为)1(2)()2()1()(2-+=----k f k f k y k y k y ，则系统的单位序列响应h(k)=_______________________7、已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dx x f t y 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为()()()()()t f t f t y t y t y +=++''''52该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ，=kt 22三、（8分）已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换。