2019年复旦大学数学科学学院考研招生专业、招生人数、考试科目

2019中国人民大学金融专硕考研参考书目选择及复习经验解读2019考研的小伙伴已经开始准备考研了，金融专硕作为热门专业之一成为很多考研儿的目标专业，但是刚开始都不知道去哪里查询院校的相关信息，感到很迷茫，接下来跨考考研老师将重点讲解2019中国人民大学金融专硕考研相关的信息。

考研儿可以作为备考的参考。

复旦大学一共有三个学院招收金融专硕：经济学院、管理学院和数学科学学院。

学制均为2年，初试科目一致。

均为：101政治；204英语二（经院可以日语或俄语）；303数学三；431金融学综合。

1.关于中国人民大学金融专硕考研辅导班目前市面上经济学考研辅导班的有很多机构，但从近三年的通过成绩来看，跨考教育以郑炳带头辅导效果最好。

一方面在全国唯一按照院校进行定校辅导的教学体系，其教材教义也是行业独家——《金融硕士真题解析与习题详解》，尤其最后考前最后三套卷更是受学生追捧。

目前清华北大人民东财央财等经济学名校50%都是郑炳弟子。

2.中国人民大学金融专硕考研专业课参考书目人大金融专硕不指定参考书，结合考试大纲以及历年真题，推荐考生参照以下重点教材复习备考：（1）黄达《金融学》，中国人民大学出版社（2）罗斯《公司理财》，机械工业出版社说明几点：第一，基础阶段，不推荐大家看黄达《金融学》，可以看其他金融学教材，如蒋先玲《货币金融学》，等明白重难点之后，再看黄达《金融学》。

为什么不是特别推荐黄达《金融学》，因为这本书写得不是特别好，基础阶段看了和没看差不多。

第二，黄达《金融学》已出第四版，相对于第三版，第四版有不少变动，推荐大家用最新版。

跨考9月份会推出黄达《金融学》教材划重点，到时把重难点全部讲解。

第三，金融学部分，除了黄达《金融学》，还需要看：米什金《货币金融学》、、姜波克《国际金融新编》和庄毓敏《商业银行经营管理》。

米什金《货币金融学》特别棒，特别是如货币政策传导机制等，建议大家一定要认真看；不需要把姜波克《国际金融新编》这本书从头看到尾，只需要重点看“外汇与汇率”、“国际收支与国际资本流动”这两部分内容；人大金融专硕特别喜欢考商业银行经营管理，2017年就考过相关考题，所以特意推荐看庄毓敏《商业银行经营管理》。

总成绩
备注
421 91.6 87.9
425 90
87.5
413 88.4 85.5
407 86
83.7
398 87.6 83.6
409 85.4 83.6
392 88
83.2
402 85.2 82.8
376 90.2 82.7
377 88.8 82.1
391 86
82.1
397 84.4 81.9
372 88.4 81.4
10122
孙佳璇 中国语言文学系
10165
何思琴 中国语言文学系
10113
张溢露 中国语言文学系
10153
田一熙 中国语言文学系
10116
王晓云 中国语言文学系
10142
刘佳琪 中国语言文学系
10111
江玉娇 中国语言文学系
10169
周奕君 中国语言文学系
08328
端木佳睿 中国语言文学系
19756
365 86
79.5
359 83.4 77.6
325 88
76.5
338 83
75.3
338 80.4 74
331 79.2 72.7
339 76
71.9
342 75.2 71.8
332 76.4 71.4
319 78.6 71.2
315 73.6 68.3
315 73.2 68.1
320 69.4 66.7
复旦大学2019年拟录取硕士研究生公示名单（不含推荐免试硕士生）
考生编号 （后五位）
考生姓名
复试院系
复试专业
初试总成 绩
复试成绩
总成绩

项目管ห้องสมุดไป่ตู้ 085239 2004
物流工程 085240 2004
工程博士（Ｄ.E.）*
电子与信息 085271 2011
生物与医药 085273 2011 15 临床医学博士（M.D.）* 临床医学硕士（M.M.） 1051 内科学
105101 1998
儿科学 105102 1998
老年医学 105103 1998
神经病学 105104 1998
精神病与精神卫生学 105105 1998
皮肤病与性病学 105106 1998
影像医学与核医学 105107
1998
临床检验诊断学 105108 1998
外科学 105109 1998
妇产科学 105110 1998
眼科学 105111 1998
耳鼻咽喉科学 105112 1998
0551 英语笔译 055101 2007 11 新闻与传播硕士(MJC) 0552 新闻与传播 055200 2010 12 出版硕士(MP) 0553 出版 055300 2010 13 文物与博物馆硕士(M.C.H.M) 0651 文物与博物馆 065100 2010 14 工程硕士（M.E.） 0852 光学工程 085202 2004
材料工程 085204 2002
电子与通信工程 085208 2001
集成电路工程 085209 2006
计算机技术 085211 2001
软件工程 085212 2002
化学工程 085216 2004
环境工程 085229 2003
生物医学工程
085230 2005
生物工程 085238 2008
复旦大学培养研究生学科、专业目录（专业学位） （2012年10月）

102489121910912 102489121901696 102489121901714 102489121920228 102489121914225 102489121920478 102489121910109 102489121919064 102489121920317 102489121910111 102489121910608 102489121920992 102489121916619 102489121910340 102489121916622 102489121919953 102489121901692 102489121901716 102489121918231 102489121902007 102489121911727 102489121911932 102489121912774 102489121916659
2019年数学科学学院硕士研究生复试拟录取名单
考生编号 102489121911892 102489121914223 102489121901700 102489121912419 102489121911950 102489121916197 102489121911064 102489121910341 102489121917349 102489121912970 102489121912423 102489121914224 102489121901681 102489121920678 102489121912763 102489121918300 102489121916478 102489121916620 102489121918939 102489121901695 姓名 王顺章 谈晨 倪木子 王乐 陈安栋 黎芮琦 王科臻 孙雪 鲁堰鸾 陈思韵 周科杰 汤琳 张诗韵 张雯婷 徐紫愔 袁于良 周扬 原翼 周宇哲 章天爱 考试方式 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 全国统考 拟录取类别 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 非定向就业 拟录取院系 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 数学科学学院 拟录取专业 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 025200 应用统计 综合成绩 613 607 597 595 584 583 581 580 578 577 576 576 573 572 569 565 564 564 562 560

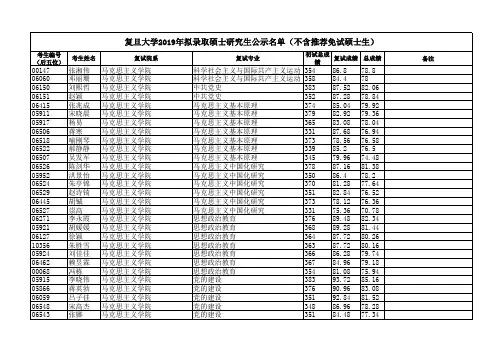
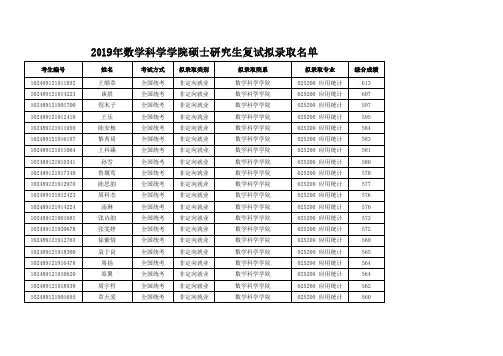
复旦大学2019研究生招生简章一、培养目标培养德、智、体全面发展，掌握本学科坚实的基础理论和系统的专业知识，具有创新精神和从事科学研究、教学、管理等工作能力的高层次学术型专门人才以及具有较强解决实际问题的能力、能够承担专业技术或管理工作、具有良好职业素养的高层次应用型专门人才。

二、招生名额和类型本年度拟招收硕士生约3500名（含推荐免试生），包括学术型硕士生和全日制专业学位硕士生两种类型，录取时将视生源状况和学校发展需要适当调整招生名额。

三、报考条件（一）学术型硕士生全国统一招生考试的报考条件如下：1.中华人民共和国公民。

2.拥护中国共产党的领导，愿为社会主义现代化建设服务，品德良好，遵纪守法。

3.学历必须符合下列条件之一：（1）国家承认学历的应届本科毕业生；（2）具有国家承认的大学本科毕业学历的人员；（3）已获硕士学位或博士学位人员（报考类别只能为委托培养或自筹经费）；（4）获得国家承认的高职高专毕业学历后2年（含2年）以上（计算年限截止日期为2019年9月1日，下同）、通过八门相关专业本科课程的考试（需提供成绩单）、经审核已达到与本科毕业生同等学力者（含国家承认学历的本科结业生和成人高校应届本科毕业生）。

4.年龄一般不超过40周岁（1979年8月31日以后出生），报考委托培养和自筹经费者年龄不限。

5.身体健康状况符合国家规定的体检标准（同高考体检标准）。

（二）专业学位硕士生全国统一招生考试的报考条件如下：1.报考法律（非法学）专业学位硕士生者，除符合上述（一）中的各项条件外，毕业专业应为非法学专业（普通高等学校本科专业目录中法学类专业[代码为0301]毕业生不得报考）。

2.报考法律（法学）专业学位硕士生者，除符合上述（一）中的各项条件外，毕业专业应为法学专业（仅普通高等学校本科专业目录中法学类专业[代码为0301]毕业生方可报考）。

3.报考工商管理、公共管理、旅游管理、工程硕士中的项目管理专业学位硕士生者，除符合上述（一）中第1、2、4、5项条件外，还应满足：大学本科毕业后有3年（含3年）以上工作经验（2016年9月1日前获得毕业证书）；获得国家承认的高职高专毕业学历后，有5年（含5年）以上工作经验（2014年9月1前获得毕业证书）；已获硕士学位或博士学位并有2年（含2年）以上工作经验（2017年9月1日前获得学位证书）。

复旦大学数学学院学生选课指南选课是大学和中学最大的不同之一，学生在大学学习阶段需要在一定的范围内自己决定学什么课程，这对习惯中小学按学校安排课程学习的学生来说经常会面临选择困境。

从2015年开始，数学学院对教学方案作了较大的调整，主要是增加了学生选课的自由度和灵活度，这自然增加了学生选课的难度，因此学院组织撰写选课指南帮助学生选课，请每个学生在选课之前仔细阅读。

大学数学课程的内容和难度都是中学数学不能比拟的，而且这个内容和难度随着年级的增加以很大的加速度增加，所以除了上课时间外，学生平均需要付出两三倍于上课的时间进一步学习巩固，留有足够多的思考时间对学好数学是非常重要的，不投入相当的时间精力是不可能学好任何一门数学课程的，肤浅地学一门数学是没有什么意义的。

所以我们建议学生一个学期选的数学专业的课程应该在每周15个课时左右（注意是课时，不是学分，课时通常是大于等于学分的），不可超过18个课时。

A．数学学院毕业学分要求：共144学分1. 通识课程：41学分。

2. 大类必修课：18 学分数学分析I，数学分析I，大学物理B（上), 大学物理B (下)。

3. 专业必修课: 24学分数学分析III，高等代数（上), 高等代数(下），解析几何，抽象代数I，拓扑I(内容包括欧氏空间拓扑). 高等数学A(上下)再加数学分析原理可以代替数学分析I,II,III.毕业论文: 4 学分, 按A,B,C,D方式给成绩, 申请A类成绩的学生需教师推荐, 递交论文并答辩.4. 限定必修课：27学分从下面12门课程中选9门(27个学分), 超过9门可以算成专业选修课: 常微分方程，泛函分析, 概率论, 拓扑II, 微分几何，基础力学, 数理方程, 抽象代数II, 复变函数, 实变函数, 数学建模，微分方程数值解.5. 专业选修课: 15 学分, 从培养方案所列选修课程中选(信息与计算专业有课程要求), 通常是5门课程. 包括限定必修课中的课程.6. 任意选修课: 15学分, 可选全校任意课程(包括数学学院专业选修课程). 包括专业选修课中的课程.B．学生选课指导：数学学院的学生需要修的数学课总数大约是：2门大类课程+6门专业必修9门专业限定必修+4门专业选修+4门任意选修+毕业论文，共25门课程加一个毕业论文，平均每个学期3门。

B 7 ! AB BA
, 2. 定义 Mn.C / 上的变
(1)求变换 T 的特征值. (2)若 A 可对角化，证明 T 也可对角化.
四.(20 分) A 为 n 阶实对称矩阵，令
S D fX jX T AX D 0, X 2 Rng
(1)求 S 为 Rn 中的一个子空间的充要条件并证明. (2)若 S 为 Rn 中的一个子空间，求 di mS .
C pn n
二.(15 分) 设 f .x/ 2 C Œa, b，f .a/ D f .b/，证明 9xn, yn 2 Œa, b, s.t . lim .xn yn/ D n!1 0，且 f .xn/ D f .yn/.
三.(15 分) 证明
Xn .
kD0
1/k
Cnk
k
C
1 m
C
1
D
X m .
kD0
1/k
Cmk
k
C
1 n
C
1
其中m, n是正整数
Y 1
X 1
四.(15 分) 无穷乘积 .1 C an/ 收敛，是否无穷级数 an 收敛？若是，证明这个
nD1
nD1
结论；若不是，请给出反例.
X 1
ż1
五.(15 分) 设 f .x/ D xn ln x，计算 f .x/dx.
0
nD1
六.(15 分) 设定义 .0, C1/ 上的函数 f .x/ 二阶可导，且 lim f .x/ 存在，f 00.x/ 有 x!C1 界，证明 lim f 0.x/ D 0. x!C1
(1)证明存在正交矩阵 P 使得
0
P T AP
D
BB@
a 0
0
1

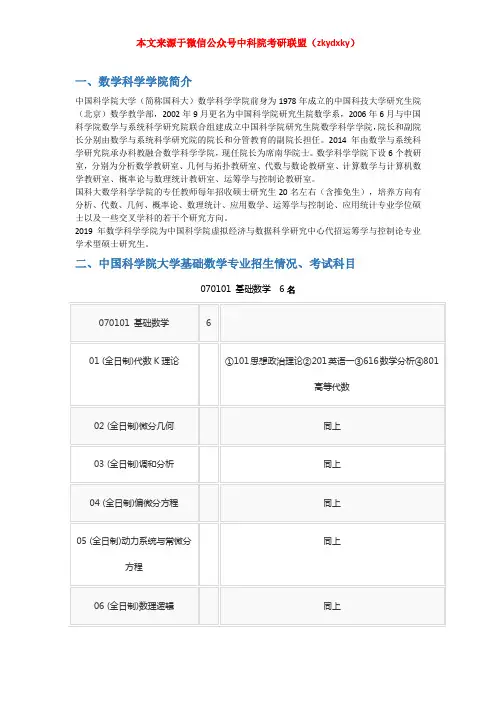
一、数学科学学院简介中国科学院大学（简称国科大）数学科学学院前身为1978年成立的中国科技大学研究生院（北京）数学教学部，2002年9月更名为中国科学院研究生院数学系，2006年6月与中国科学院数学与系统科学研究院联合组建成立中国科学院研究生院数学科学学院，院长和副院长分别由数学与系统科学研究院的院长和分管教育的副院长担任。

2014年由数学与系统科学研究院承办科教融合数学科学学院，现任院长为席南华院士。

数学科学学院下设6个教研室，分别为分析数学教研室、几何与拓扑教研室、代数与数论教研室、计算数学与计算机数学教研室、概率论与数理统计教研室、运筹学与控制论教研室。

国科大数学科学学院的专任教师每年招收硕士研究生20名左右（含推免生），培养方向有分析、代数、几何、概率论、数理统计、应用数学、运筹学与控制论、应用统计专业学位硕士以及一些交叉学科的若干个研究方向。

2019年数学科学学院为中国科学院虚拟经济与数据科学研究中心代招运筹学与控制论专业学术型硕士研究生。

二、中国科学院大学基础数学专业招生情况、考试科目三、中国科学院大学基础数学专业分数线2018年硕士研究生招生复试分数线2017年硕士研究生招生复试分数线四、中国科学院大学基础数学专业考研参考书目616数学分析现行（公开发行）综合性大学（师范大学）数学系用数学分析教程。

801高等代数[1] 北京大学编《高等代数》，高等教育出版社，1978年3月第1版，2003年7月第3版，2003年9月第2次印刷.[2] 复旦大学蒋尔雄等编《线性代数》，人民教育出版社，1988.[3] 张禾瑞，郝鈵新，《高等代数》，高等教育出版社，1997.五、中国科学院大学基础数学专业复试原则最后的复试成绩综合考虑以上“业务能力、英语听力和口语、综合素质和思想品德”四个方面的成绩，复试成绩满分100分，其中业务能力占50％，英语听力和口语占30％，综合素质和思想品德占20％。

（一）业务能力面试1. 考核形式：问答2. 考核目的：主要考核考生掌握专业知识的广度、深度与扎实程度，运用专业知识的能力，思维能力，应变能力，表达能力，研究兴趣，科研能力与发展潜力。

2011年金融学专业学位研究生入学考试专业课大纲第一部分国际金融一、国际收支和国际收支平衡表二、汇率基础理论三、内部均衡和外部平衡的短期调节四、内部均衡和外部平衡的中长期调节五、外汇管理制度和政策调节六、金融全球化对内外均衡的冲击七、金融全球化下的国际协调与合作第二部分货币银行学一、货币与货币制度二、信用三、金融市场四、商业银行五、中央银行六、金融抑制、深化和创新七、货币理论第三部分投资学一、投资环境二、投资目标三、投资策略四、资产价值分析五、投资组合构建六、投资组合业绩评价第四部分公司金融一、现值和价值评估二、风险和收益三、资本预算四、实物期权和资本预算五、长期融资六、衍生工具和风险管理七、资本结构理论八、股利政策九、公司财务规划十、短期财务计划和短期融资十一、流动资产管理十二、公司治理十三、并购十四、财务危机和财务预警十五、会计报表分析431 金融学综合一、考试性质《金融学综合》是2011年金融硕士（MF）专业学位研究生入学统一考试的科目之一。

《金融学综合》考试要力求反映金融硕士专业学位的特点，科学、公平、准确、规范地测评考生的基本素质和综合能力，选拔具有发展潜力的优秀人才入学，为国家的经济建设培养具有良好职业道德、具有较强分析与解决实际问题能力的高层次、应用型、复合型的金融专业人才。

二、考试要求测试考生对于与金融学和公司财务相关的基本概念、基础理论的掌握和运用能力。

三、考试方式与分值本科目满分150分，其中，金融学部分为90分，公司财务部分为60分，由各培养单位自行命题，全国统一考试。

四、考试内容（一）金融学1、货币与货币制度● 货币的职能与货币制度● 国际货币体系2、利息和利率● 利息● 利率决定理论● 利率的期限结构3、外汇与汇率● 外汇● 汇率与汇率制度● 币值、利率与汇率● 汇率决定理论4、金融市场与机构● 金融市场及其要素●货币市场● 资本市场● 衍生工具市场● 金融机构（种类、功能）5、商业银行● 商业银行的负债业务● 商业银行的资产业务● 商业银行的中间业务和表外业务● 商业银行的风险特征6、现代货币创造机制● 存款货币的创造机制● 中央银行职能● 中央银行体制下的货币创造过程7、货币供求与均衡● 货币需求理论● 货币供给● 货币均衡● 通货膨胀与通货紧缩8、货币政策● 货币政策及其目标● 货币政策工具● 货币政策的传导机制和中介指标9、国际收支与国际资本流动● 国际收支● 国际储备● 国际资本流动10、金融监管● 金融监管理论● 巴塞尔协议● 金融机构监管● 金融市场监管（二）公司财务1、公司财务概述● 什么是公司财务● 财务管理目标2、财务报表分析● 会计报表● 财务报表比率分析3、长期财务规划● 销售百分比法● 外部融资与增长4、折现与价值● 现金流与折现● 债券的估值● 股票的估值5、资本预算● 投资决策方法● 增量现金流● 净现值运用● 资本预算中的风险分析6、风险与收益● 风险与收益的度量● 均值方差模型● 资本资产定价模型● 无套利定价模型7、加权平均资本成本● 贝塔（β）的估计● 加权平均资本成本（WACC）8、有效市场假说● 有效资本市场的概念● 有效资本市场的形式● 有效市场与公司财务9、资本结构与公司价值● 债务融资与股权融资● 资本结构● MM定理10、公司价值评估● 公司价值评估的主要方法● 三种方法的应用与比较2011 431金融专硕基本完整名词解释 5*51.有效汇率2.利率期限结构3.流动性陷阱4.大宗交易机制5.正反馈投资策略(这概念还出了道简答)选择题5*41 套汇是什么样的行为 A保值 B投机 C盈利 D保值和投机2 哪个不属于商业银行资产管理理论的3 简单的戈登模型计算股价4 蒙代尔弗莱明模型的固定汇率情况货币政策无效计算题20*2互换的设计这题应该要分情况讨论并购题公司金融437页朱叶的那本书简答题10*21. 降低货币乘数央行的措施2. 用正反馈投资策略原理谈谈股市泡沫的形成论述题: 20+251. 现金股利的信号传递效应,并联合我国的股市谈谈现金股利的信号传递效应的有效性2.外汇储备需求决定因素与我国的外汇储备是否过度问题回复chancechance的帖子按照今年的专硕题看，吃透指定书目就够了吧，考试内容涉及比较广泛，不要想当然地去划一些重点非重点，往往很多重点反而考得比较少。

高 等 教 育 出 2004 年 版社
高 等 教 育 出 2004 年
治
版社
谷超豪、李大 数 学 物 理 方 高 等 教 育 出 2012 年
潜、陈恕行、 程
版社
郑宋穆、谭永
基
版次
第二版
第二版
第三版
备注
第 1-3，5-7 章 第 1-3 章
陈 文 斌 、 程 微 分 方 程 数 复 旦 大 学 出 2014 年
晋、吴新明、 值解
版社
李立康
盛 骤 、 谢 式 概 率 论 与 数 高 等 教 育 出 2008 年
千、潘承毅 理统计
版社
同 济 大 学 数 工程数学：线 高 等 教 育 出 2014 年
学系
性代数
版社
第一版 第四版 第六版
第 1-5 章 第 1-12 章
复旦大学 2020 年硕士研究生招生考试自命题科目考试大纲
科目代码 898
科目名称 数学综合知识
一、考试内容范围
大气与海洋科学是交叉学科特色很强的科学。需要气象学、海洋学、数学、物理、力
学、计算机和大数据等多门学科知识。特别，涉及的数学知识内容广泛。以下是数学综合
知识所考察的大纲内容。
一、高等数学：极限与连续，微分/导数及其应用，不定积分，定积分，反常积分，数
项级数以及函数项级数，Taylor 展式和插值多项式，无穷乘积Байду номын сангаасn 维欧氏空间，多元函数
的极限与连续，多元函数微分学，多元函数积分学(重积分，曲线曲面积分，场论) ，含参
变量积分，Fourier 级数，Fourier 变换。
二、微分方程及数值解：一阶常微分方程的初等解法、解的存在唯一性、解对初值的

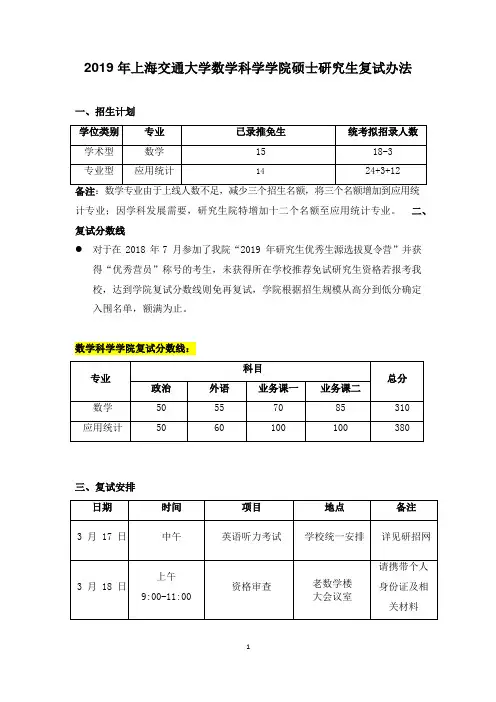
2019 年上海交通大学数学科学学院硕士研究生复试办法一、招生计划计专业；因学科发展需要，研究生院特增加十二个名额至应用统计专业。

二、复试分数线对于在 2018 年 7 月参加了我院“2019年研究生优秀生源选拔夏令营”并获得“优秀营员”称号的考生，未获得所在学校推荐免试研究生资格若报考我校，达到学院复试分数线则免再复试，学院根据招生规模从高分到低分确定入围名单，额满为止。

数学科学学院复试分数线：三、复试安排1、英语听力测试考生需要参加学校统一组织的研究生复试英语听力考试，时间为 3 月17 日中午。

详情请见研招办网站（）通知。

2、资格审查3 月 18 日上午 9:00-11:00，老数学楼大会议室。

应提供的材料：（1）本人第二代居民身份证件（原件和复印件）；（2）历届生的学历、学位证书（原件和复印件），《教育部学历证书电子注册备案表》（或“学历认证报告”）（打印件）；（3）应届生的学生证（原件和复印件）、《教育部学籍在线验证报告》（打印件）。

（4）持在境外获得学历、学位证书报考者，须提交教育部留学服务中心出具的《国外学历学位认证书》（原件和复印件）。

（5）大学期间的成绩单，四、六级成绩证明，学术成果证明，及各类获奖证书。

（原件和复印件）3、笔试专业课综合笔试：3 月19 日上午 8：30-11：30，陈瑞球楼 214。

专业课综合笔试主要考察主干课程的基本内容，其中：●数学专业包括：近世代数、复变函数、实变函数、常微分方程、偏微分方程、微分几何、泛函分析、概率论、科学计算。

●应用统计专业包括:高等数学、线性代数、概率论、数理统计、时间序列分析。

4、体检3 月 20 日上午，闵行校区校医院，详情请见研招办网站（）通知。

5、面试3 月 21 日 9：00-18：00，8:50 在陈瑞球楼 214 候场。

主要考核综合素质和能力（含外语能力），包括：思想道德品质，外语实际应用能力，科学素养、创新能力、培养潜力、协作性、人文素质、心理健康以及举止、表达和礼仪情况等。

一、中国科学院数学与系统科学研究院简介中国科学院数学与系统科学研究院由中科院数学研究所、应用数学研究所、系统科学研究所及计算数学与科学工程计算研究所四个研究所整合而成，此外还拥有科学与工程计算国家重点实验室、中科院管理决策与信息系统重点实验室、中科院系统控制重点实验室、中科院数学机械化重点实验室、华罗庚数学重点实验室、随机复杂结构与数据科学重点实验室，以及中科院晨兴数学中心和中科院预测科学研究中心等。

2010年11月成立国家数学与交叉科学中心，旨在从国家层面搭建一个数学与其它学科交叉合作的高水平研究平台。

数学与系统科学研究院拥有完整的学科布局，研究领域涵盖了数学与系统科学的主要研究方向。

共有16个硕士点和13个博士点（二级学科），分布在经济学、数学、系统科学、统计学、计算机科学与技术、管理科学与工程六个一级学科中，可以在此范围内招收和培养硕士与博士研究生。

在2006年全国学科评估中，我院数学学科的整体评估得分为本学科的最高分数。

数学与系统科学研究院硕士招生类别为硕士研究生、硕博连读生和专业学位硕士研究生。

2019年共计划招收122名。

二、中国科学院大学基础数学专业招生情况、考试科目三、中国科学院大学基础数学专业分数线2018年硕士研究生招生复试分数线2017年硕士研究生招生复试分数线四、中国科学院大学基础数学专业考研参考书目616数学分析现行（公开发行）综合性大学（师范大学）数学系用数学分析教程。

801高等代数[1] 北京大学编《高等代数》，高等教育出版社，1978年3月第1版，2003年7月第3版，2003年9月第2次印刷.[2] 复旦大学蒋尔雄等编《线性代数》，人民教育出版社，1988.[3] 张禾瑞，郝鈵新，《高等代数》，高等教育出版社， 1997.五、中国科学院大学基础数学专业复试原则在中国科学院数学与系统科学研究院招生工作小组领导下，按研究所成立招收硕士研究生复试小组，设组长1人、秘书1人。

晶体缺陷：a)点缺陷；b)位错的基本概念；c)位错的能量及交互作用；d)晶体中的界面。 . .
材料的相结构及相图：a)材料的相结构；b)二元相图及其类型；c)复杂相图分析；d)相 图的热力学基础；e)三元系相图及其类型。 . .
材料的凝固与气相沉积：a)材料凝固时晶核的形成；b)材料凝固时晶体的生长；c)固溶 体合金的凝固；d)共晶合金的凝固；e)制造工艺与凝固组织；f)用凝固法材料的制备技 术；g)材料非晶态；h)材料的气-固转变；i)气相沉积法的材料制备技术。 . .
冯端,师昌绪 材料科学导论 化学工业出版社 2002.5
版次 备注
复旦大学 2019 年硕士研究生招生考试自命题科目考试大纲
科目代码
850
科目名称
材料科学基础（物理卷）
一、考试内容范围
.
材料结构的基本知识：a)原子结构；b)原子结合键；c)原子排列方式；d)晶体材料的组 织。 . .
材料中的晶体结构：a)晶体学基础；b)纯金属的晶体结构；c)离子晶体的结构；d)共价 晶体的结构。 . .
备 出版时间 版次
注
石德珂
材 料 科 学 基 机械工业出版 2015 年 1 第 2
础
社
月
版
第1
冯端、师昌绪、刘治 材 料 科 学 基 化学工业出版 2002 年 5 版
国
础
社
月
扩散与固态相变：a)扩散定律及其应用；b)扩散机制；c)影响扩散的因素与扩散驱动力； d)几个特殊的有关扩散的实际问题；e)固态相变中的形核；f)固态相变的晶体生长；g) 扩散型相变；h)无扩散相变。 . .
材料的变形与断裂：a)金属变形概述；b)金属的弹性变形；c)滑移与孪晶变形；d)单晶 体的塑性变形；e)多晶体的塑性变形；f)纯金属的变形强化；g)合金的变形与强化；h) 冷变形金属的组织与性能；i)金属的断裂；j)冷变形金属的回复阶段；k)冷变形金属的 再结晶；l)金属的热变形、蠕变与超塑性；m)陶瓷晶体的变形。 . .

复旦⼤学数学学院⾼等代数历届期中考试⼤题精选之三（18级--20级）本⽂收集了复旦⼤学数学学院 18 级到 20 级⾼等代数期中考试的精选⼤题, 其中⼀部分⼤题由习题课⽼师或任课⽼师⾃编⽽来, ⼀部分⼤题从兄弟院校的⾼等代数教材或学习指导书中的习题或考研试题改编⽽来, 也有⼀部分⼤题已经融⼊到复旦⼤学⾼等代数学习指导书 (第三版) 中了. 由于篇幅所限, 这⾥我们不公布这些精选⼤题的解答, 但会根据情况附加⼀些注解, 以供读者参考.本科 18 级⾼代 I 期中考试⼆、(12分) 计算下列 n 阶⾏列式的值:|A |=1−a n 1b n11−a 1b 11−a n 1b n21−a 1b 2⋯1−a n 1b nn1−a 1b n1−a n 2b n11−a 2b 11−a n 2b n21−a 2b 2⋯1−a n 2b nn1−a 2b n⋮⋮⋮1−a n n b n11−a n b 11−a n n b n21−a n b 2⋯1−a n n b nn1−a n b n.五、(12分) 设函数 f (x )=m∑i =−k a ix i , 其中 k ,m 都是正整数. 设 n 阶⾮异阵 A 的每⾏元素之和都等于 c , 证明: f (A )=m∑i =−k a iA i 的每⾏元素之和都等于 f (c ).六、(10分) 设多项式 f (x )=a 0+a 1x +⋯+a n −1x n −1, ωk =cos 2k πn +i sin 2k πn (0≤k ≤n −1) 为全体 n 次单位根, 循环矩阵A =a 0a 1⋯a n −2a n −1a n −1a 0⋯a n −3a n −2⋮⋮⋮⋮a 2a 3⋯a 0a 1a 1a 2⋯a n −1a 0.证明: 恰有 n −r (A ) 个 n 次单位根是 f (x ) 的根 (不计重根数).七、(10分) 设 A ,B 为 n (n ≥3) 阶⽅阵, 满⾜ AB =0. 证明: |AB ∗+BA ∗|=0.注 第⼆⼤题⽤ Vander Monde ⾏列式. 第五⼤题是⽩⽪书例 2.22 的推⼴. 第六⼤题参考博⽂《》. 第七⼤题转化成矩阵秩的问题, 并⽤秩的不等式进⾏证明.本科 18 级⾼代 II 期中考试四、(10分) 设 n 阶⽅阵 A 的所有元素都是整数, p ,q 是互素的整数且 q >1, 证明: 线性⽅程组 Ax =pq x 只有零解.五、(10分) 设 A 1,⋯,A n 为两两乘法可交换的 2019 阶实⽅阵, f (x 1,⋯,x n ) 是 n 元实系数多项式. 令 B =f (A 1,⋯,A n ), 证明: 存在 B 的某个特征值 λ0, 使得⽅程 f (x 1,⋯,x n )−λ0=0 有⼀组实数解.六、(10分) 设 A 为 n 阶复⽅阵, 证明: A 不可对⾓化当且仅当存在⼀元多项式 f (x ), 使得 f (A ) ⾮零, I n +f (A ) 可逆, 并且 (I n +f (A ))−1 与 I n −f (A )相似.七、(10分) 设 A 是 n 阶复⽅阵, 证明: 存在复数 c 1,⋯,c n −1, 使得A −c 1e A −c 2e 2A −⋯−c n −1e (n −1)A是可对⾓化矩阵.||()注 第四⼤题是⽩⽪书例 6.4 的推⼴. 第五⼤题需要⽤到如下结论"两个乘法可交换的奇数阶实矩阵必有公共的实特征向量", 其证明可参考教学论⽂ 12 的例 3. 第六⼤题利⽤ Jordan-Chevalley 分解定理来做. 第七⼤题利⽤ Jordan 标准型的应⽤或 Jordan-Chevalley 分解定理来做.本科 19 级⾼代 I 期中考试五、(10分) 设 n 阶⾮零复⽅阵 A 满⾜ A ∗=¯A ′, 求证: A 是⾮异阵.六、(10分) 设 A 为数域 K 上的 n 阶幂零阵, B 为 n 阶⽅阵, 满⾜ AB =BA 且 r (AB )=r (B ). 求证: B =0.七、(10分) 设 A 为 m 阶实反对称阵, C 为 n 阶实反对称阵, B 为 m ×n 阶实矩阵. 证明: A +I m 和 C −I n −B ′(A +I m )−1B 都是⾮异阵.注 第五⼤题是⽩⽪书例 2.21 的复版本. 第六⼤题利⽤⽩⽪书的例 3.75 来证明. 第七⼤题的第 1 ⼩问是⽩⽪书的例 3.78 (利⽤线性⽅程组的求解理论), 第 2 ⼩问可通过降阶公式 (构造⼀个⼤矩阵) 转化为第 1 ⼩问.本科 19 级⾼代 II 期中考试四、(14分) 设 n (n >2) 阶复⽅阵 A 的秩等于 2, 试求 A 的 Jordan 标准型.五、(10分) 设 n 阶⽅阵 A 的所有元素都是整数, 其中阶数 n 为偶数, 并且对任意的 1≤r ≤n , A 的所有 r 主⼦式之和都是奇数. 证明: 不存在整数 k , 使得线性⽅程组 Ax =kx 有⾮零解.六、(10分) 设 A =(a ij ) 是 n 阶实⽅阵, 若对任意的 1≤i ≤n , 都有 |a ii |>∑j ≠i |aij |, 则称 A 是严格对⾓占优阵. 设 A ,B 均为主对⾓元都⼤于零的n 阶严格对⾓占优阵, 且满⾜ A 2(A +B )=(A +B )B 2, 证明: A =B .七、(10分) 设 a ,b 都是实数, 其中 b ≠0, 证明: 对任意的正整数 m , 存在 4 阶实⽅阵 A , 使得A m =a b 20−b a 2000a b 0−ba.注 第四⼤题先将 A 的 Jordan 标准型 J 写出, 通过计算 J 的秩可得到 5 个分类结果. 第五⼤题利⽤⽩⽪书的例 6.15, 再由反证法即得结论. 第六⼤题先利⽤⼽⽒圆盘定理得到 A ,B 特征值的实部都⼤于零, 再利⽤两次⽩⽪书的例 6.63 即得结论. 第七⼤题利⽤⼴义 Jordan 块 (⽩⽪书第366 页第 2 ⾏和第 3 ⾏的矩阵) 作为测试矩阵进⾏讨论.本科 20 级⾼代 I 期中考试四、记数域 K 上所有 n 阶⽅阵全体构成的线性空间为 M n (K). 对 A ∈M n (K), 考虑 C (A )={B ∈M n (K)∣AB =BA }.(1) 若 n =3, A =01000111, 求 C (A ) 的⼀组基.(2) 若 n =2, 试确定 dim C (A ) 的所有可能值.五、设 n 阶复⽅阵 A 不可逆, 证明: ⾄多只有两个复数 λ, 使得 λI n +A ∗ 不可逆.六、设 A ,B 为 n 阶⽅阵, 证明: |r (AB )−r (BA )|≤n2.七、设 A ,B 为 n 阶实⽅阵, 其中 A 是主对⾓元全⼤于零的上三⾓阵, 并且满⾜ AB +BA ′=2AA ′. 证明:(1) B 必为对称阵;(2) A 为对⾓阵当且仅当 B 2=AA ′;(3) |B |>0.本科 20 级⾼代 II 期中考试四、设 n 阶⽅阵 A 的极⼩多项式为 λ3−λ2, 试求 A 可能的互不相似的 Jordan 标准型的总个数.五、设 V 为线性空间, φ1,⋯,φk 是 V 上的线性变换, 满⾜: φ2i =φi (1≤i ≤k ), φi φj =0(1≤i ≠j ≤k ), 证明:()()V =k⨁i =1Im φi ⨁k⋂j =1Ker φj .六、设 n 阶复矩阵 A 的全体特征值都是属于开区间 (−1,1) 的实数, 证明: 矩阵⽅程 sin X =A 必有解.七、设 A ,B 为 n (n ≥2) 阶⽅阵, 满⾜: r (A )=n −1, AB =BA =0. 证明: A +B 为⾮异阵的充要条件是 A 的特征值 0 的代数重数等于 1 且 B 的秩等于 1.()Processing math: 100%。

本科华科电信，12年考上交电子系失败收场，之后找工作到某运营商，在工作期间跨考复旦大学计算机专业硕士成功录取，初试359，复旦计算机专硕考数学一专业课408 英语二政治，各科分数分别是111 111 75 62，初试成绩至少是专硕前五，初试和学硕的区别就是英语。

自觉得我的考研路有点特别，但是两次考研的经历有些感悟，希望和大家分享，希望对大家有启发。

一、是否考研是否决定考研需要根据自己的具体情况，想好自己要走的路。

如果是单纯想多学点东西，想进入IT行业，能入行就可以考虑直接工作了，工作中学到实用的东西绝对比读研多。

如果要搞学术，优先考虑出国，其次是国内读研读博。

如果是要进入体制内或其他对学历有硬性要求的地方，一些学历可以转化为职称的地方，那就刷学历吧。

如果想去大型IT公司又绝对没实力想在学校继续深造的可以考虑考研。

还有学历情结、名校情结等等原因。

我的情况是大四的考研失利导致错失找工作的最佳时期，进入运营商做后台，对工作不满想通过考研换专业换行业，提升自己专业能力的，其实最佳选择或许是本科找份合适的工作。

好了，先思考一下是否要考研，如果你决定考研了再往下看。

二、考研专业本科电子信息工程跨考计算机。

本身对电信的核心专业课就没有感觉。

第一次的考研失利及在运营商的工作经历让我对通信失去兴趣，当前互联网行业发展迅速，自身对计算机也比较兴趣，决定考研计算机。

总之，是要根据自己的兴趣和能力等具体情况选择。

PS.个人觉得当前最好的行业是金融，工科跨考金融的同学都令我佩服不已。

三、学硕专硕国家政策上是希望学硕做科研，专硕搞工程项目，实际中现在学硕和专硕的区别越来越小，实际最大的区别就是“钱”和“时间”！就是专硕学制短、奖学金少。

一些学校的某些专业已经一视同仁了，具体情况看学校的专业。

大趋势是学硕和专硕的待遇趋于一致，近些年但是一直在变化。

复旦计算机学硕3年，专硕2.5年，专硕奖学金少。

考学硕过专硕线科研调剂到专硕。

高 等 数 学（下）
总学时：90+18
Ⅱ 线性代数与空间解析几何（二）
五、线性空间和线性变换（2） （学时数：6+2）
教学内容 1．二次型及其标准形式 二次型与对称矩阵；化二次型为标准形的几种方法。 2．正定二次型 惯性定理；正定二次型和对称正定矩阵；二次曲线的分类；用 Cholesky 分解 解线性方程组。 教学要求 1．掌握二次型及其矩阵表示，了解二次型的标准形、规范形的概念，了解惯 性定理。 2．掌握化二次型为标准形的几种方法。 3．掌握二次型和对应矩阵的正定性及其判别法。
9
算。 7．Green 公式和 Stokes 公式 Green 公式；Stokes 公式。 8．旋度和无旋场 环量和旋度；无旋场、保守场和势量场；原函数。 9．Gauss 公式和散度 流场的流出量；Gauss 公式；散度；Hamilton 算符和 Laplace 算符。 教学要求 1．理解二重积分和三重积分的概念及性质。 2．掌握直角坐标系下二重积分和三重积分的计算，掌握二重积分和三重积分 计算中的变量代换法。 3．掌握用积分计算重心、转动惯量和引力的方法。 4．理解曲线弧长的概念，理解第一类曲线积分的概念性质，掌握第一类曲线 积分的计算。 5．理解第二类曲线积分的概念，性质，并掌握其计算。 6．了解两类曲线积分的关系。 7．理解曲面面积的概念，理解第一类曲面积分的概念，性质并掌握其计算。 8．了解有向曲面的概念，理解第二类曲面积分的概念，性质，并掌握其计算。 9．掌握 Green 公式、Stokes 公式和 Gauss 公式，并会利用它们计算积分。 10．了解环量与通量的概念，理解旋度与散度的概念。 11．理解无旋场，保守场和势量场的概念与关系，会求全微分的原函数，会 运用曲线积分与路径无关的条件。 12．了解 Hamilton 算符和 Laplace 算符，了解 Green 恒等式。