初中数学经典几何题及答案解析
- 格式:doc
- 大小:455.00 KB
- 文档页数:14

完整版)初中数学几何模型大全+经典题型(含答案)通过将倍长中点相关线段进行旋转变换,可以构造出旋转全等模型。
这种模型的特点是,将相邻等线段所成角的一半旋转后拼接在一起,形成对称全等。
同时,也可以通过将两个等腰三角形或正多边形的夹角进行变化,来构造出模型变形。
如果遇到复杂图形找不到旋转全等,可以先找到两个正多边形或等腰三角形的公共极点,然后围绕公共极点找到两组相邻等线段,分组组成三角形证全等。
幂定理可以用等线段、等比值、等乘积进行代换,从而将两个数之间的比值转换成乘积。
在相似证明中,常用的辅助线是平行线,根据题目条件来确定比值并做出相应的平行线。
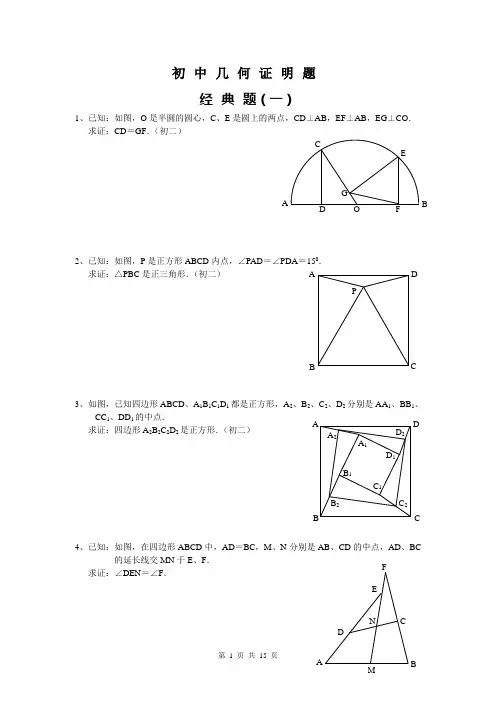
题目一:在半圆中,圆心为O,圆上有点C、E,CD垂直于AB,EF垂直于AB,EG垂直于CO。
证明CD等于GF。
题目二:在正方形ABCD内部,点P满足∠PAD=∠PDA=15度。
证明△PBC是正三角形。
题目三:在图中,ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点。
证明A2B2C2D2是正方形。
题目四:在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F。
证明∠DEN=∠F。
题目五:在△ABC中,H为垂心,O为外心,且OM垂直于BC于M。
1)证明AH等于2OM;2)如果∠BAC等于60度,证明AH等于AO。
1.设P为正三角形ABC内任意一点,连接PA,PB,PC,由三角形不等式可得PA+PB>AB。
PB+PC>BC。
PC+PA>CA。
将三式相加得到2PA+2PB+2PC>AB+BC+CA=3,即PA+PB+PC>3/2.又由于P到三角形三边的距离不超过1,所以PA+PB+PC<3,综上可得1.5≤PA+PB+PC<3,即所求不等式成立。
2.设P为正方形ABCD内任意一点,连接PA,PB,PC,PD。
由于正方形四边相等,所以PA+PC=2,PB+PD=2.又由于P到四边的距离不超过1,所以PA+PB+PC+PD<4.将前两式相加得到PA+PB+PC+PD=2(PA+PB)/2+2(PC+PD)/2≥2√(PA·PB)+2√(PC·P D)。
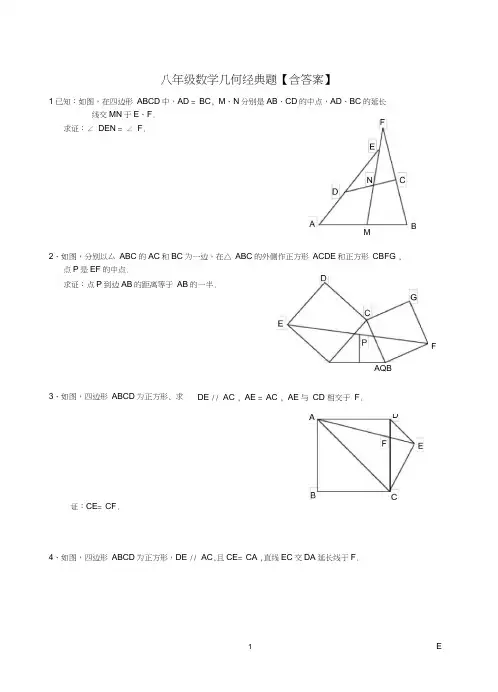
八年级数学几何经典题【含答案】1已知:如图,在四边形 ABCD 中,AD = BC , M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠ DEN = ∠ F .2、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于 AB 的一半.3、如图,四边形 ABCD 为正方形, 求证:CE = CF .4、如图,四边形 ABCD 为正方形,DE // AC ,且CE = CA ,直线EC 交DA 延长线于F .DE // AC , AE = AC , AE 与 CD 相交于 F .MAQBF求证:AE = AF .FB C7如图,△ ABC 中,∠ C 为直角,∠ A=30 ° ,分别以AB 、AC 为边在△ ABC 的外侧作正△ ABE 与正△ ACD , DE 与AB 交于F O求证:EF=FD o8如图,正方形 ABCD 中,E 、F 分别为AB 、BC 的中点,EC 和DF 相交于G ,连接AG ,求证:AG=AD o9、已知在三角形 ABC 中,AD 是BC 边上的中线,E 是AD 上的一点,且BE=AC 延长BE 交AC 与F,求证 AF=EF5、设P 是正方形 ABCD 一边BC 上的任一点,PF 丄AP , CF 平分∠ 求证:PA = PF .6、平行四边形ABCD AE = CF .求证:∠ 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且DPA =∠ DPC .BEC九年级数学【答案】1.如下图连接AC并取其中点Q,连接QN和QM所以可得∠ QMF= ∠ F, ∠ QNM= ∠ DEN和∠QMN= ∠ QNM ,从而得出∠ DEN = ∠ F O2.过E,C,F点分别作AB所在直线的高EG CI , FH可得PQ=E G +FH由厶EGA◎△ AIC ,可得EG=AI ,由△ BFHCBI ,可得FH=Bl。

初中数学经典几何题及答案1.题目:已知直角三角形的两条直角边分别为3cm和4cm,求斜边的长度。
解答:根据勾股定理,直角三角形中斜边的平方等于两直角边的平方和。
所以斜边的长度为√(3^2 + 4^2) = √(9 + 16) = √25 = 5cm。
2.题目:已知一个正方形的边长为6cm,求其对角线的长度。
解答:正方形的对角线可以看作是两个相等的直角三角形的斜边,所以可以使用勾股定理来计算对角线的长度。
正方形的边长为6cm,所以直角三角形的直角边为6cm,斜边即为对角线的长度。
所以对角线的长度为√(6^2+ 6^2) = √(36 + 36) = √72 ≈ 8.49cm。
3.题目:已知一个梯形的上底长为8cm,下底长为12cm,高为5cm,求梯形的面积。
解答:梯形的面积可以通过上底和下底的平均值乘以高来计算。
所以梯形的面积为(8 + 12) × 5 ÷ 2 = 20cm²。
4.题目:已知一个等边三角形的边长为10cm,求其面积。
解答:等边三角形的面积可以通过边长的平方乘以根号3再除以4来计算。
所以等边三角形的面积为(10^2 × √3) ÷ 4 = (100 × √3) ÷ 4 ≈ 43.30cm²。
5.题目:已知一个长方形的长为8cm,宽为5cm,求其周长。
解答:长方形的周长可以通过将长和宽分别乘以2再相加来计算。
所以长方形的周长为(8 × 2) + (5 × 2) = 16 + 10 = 26cm。
6.题目:已知一个圆的半径为6cm,求其面积。
解答:圆的面积可以通过半径的平方乘以π(约等于3.14)来计算。
所以圆的面积为6^2 × 3.14 ≈ 113.04cm²。
7.题目:已知一个正五边形的边长为4cm,求其周长。
解答:正五边形的周长可以通过边长乘以5来计算。
所以正五边形的周长为4 × 5 = 20cm。
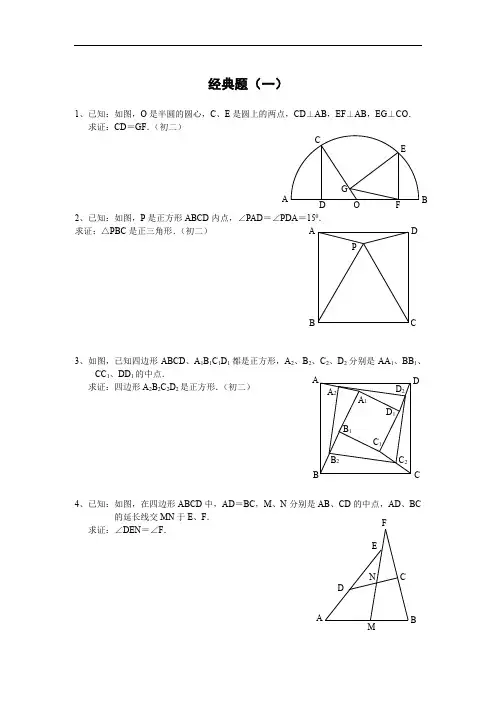
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A N FE CDMBP CG FB QA D E1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 分别交于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· A D HE M C B O · GAO D B EC Q P NM · O Q PB DEC N M · A1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)D AF D E C B E DA CB F F EP C B A O D BFAECP1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)AP C B P A D CB CB DAFPDE CBA1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.AP CB ACBPDEDCB A A CBPD1.如下图做GH⊥AB,连接EO。
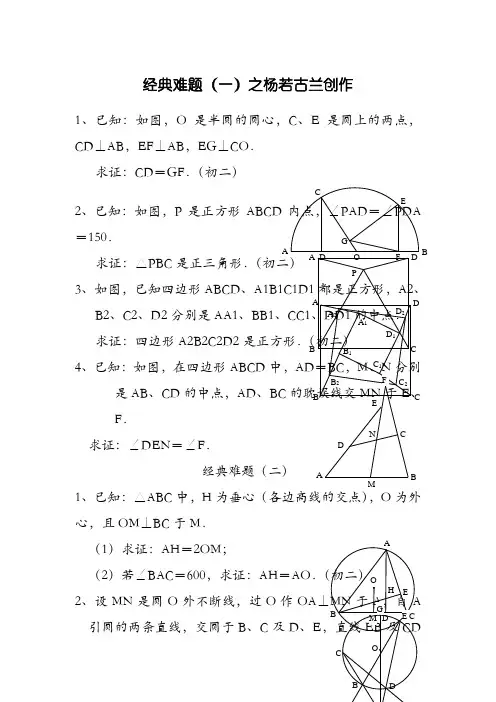
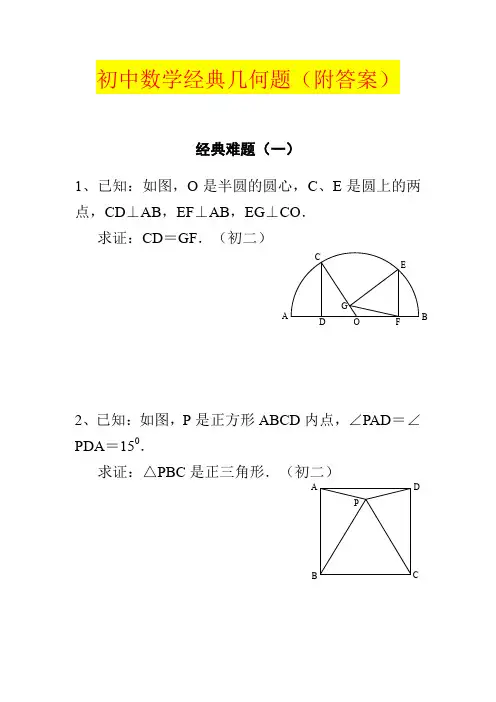
经典难题(一)之杨若古兰创作1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD=∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、B2、C2、D2分别是AA1、BB1、CC1求证:四边形A2B2C2D2是正方形.4、已知:如图,在四边形ABCD 中,AD 是AB 、CD 的中点,AD 、BCF .求证:∠DEN=∠F.经典难题(二)1、已知:△ABC 中,H 心,且OM⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC=600,求证:AH =AO .2、设MN 是圆O 外不断线,过O 作引圆的两条直线,交圆于B 、C 及D 、E AG CEB分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN DE ,设CD 、EB 分别交MN 于P 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC和BC 侧作正方形ACDE 和正方形求证:点P 到边AB 的距离等于1、如图,四边形ABCD 与CD 订交于F .求证:CE =CF .2、如图,四边形直线EC 交DA 求证:AE =AF .3、设P 是正方形平分∠DCE.求证:PA =PF .4、如图,PC 切圆O 线,AE 、AFBC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)3、设ABCD 为圆内接凸四边形,求证:AB·CD+AD·BC =AC·BD.(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 订交于P ,且AE =CF .求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L<2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.APC B PADCBCBDA FPDE CBAAP C BACBPD3、P为正方形ABCD内的一点,而且PA=a=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800 AB、AC上的点,∠DCA=300,∠EBA=200度数.经典难题(一)答案1.如下图做GH⊥AB,连接EO.因为GOFE ∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF =GOGH=COCD,又CO=EO,所以CD=GF得证.2. 如下图做△DGC使与△ADP全等,可得△PDG为等边△,从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG=150所以∠DCP=300 ,从而得出△PBC是正三角形3.如下图连接BC1和AB1分别找其中点F,E.连接C2F与A2E 并耽误订交于Q点,连接EB2并耽误交C2Q于H点,连接FB2并耽误交A2Q 于G点,由A2E=12A1B1=12B1C1= FB2 ,EB2=12AB=12BC=FC1 ,又∠GFQ+∠Q=900和∠GEB2+∠Q=900,所以∠GEB2=∠GFQ又∠B2FC2=∠A2EB2 ,可得△B2FC2≌△A2EB2 ,所以A2B2=B2C2 ,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形.4.如下图连接AC并取其中点Q,连接QN和QM,所以可得∠QMF=∠F,∠QNM=∠DEN和∠QMN=∠QNM,从而得出∠DEN=∠F.经典难题(二)1.(1)耽误AD到F连BF,做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM(2)连接OB,OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证.3.作OF⊥CD,OG⊥BE,连接OP,OA,OF,AF,OG,AG,OQ.因为22ADAC CD FD FD AB AE BE BG BG,由此可得△ADF≌△ABG,从而可得∠AFC=∠AGE. 又因为PFOA 与QGOA 四点共圆,可得∠AFC=∠AOP 和∠AGE=∠AOQ,∠AOP=∠AOQ,从而可得AP=AQ.4.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH.可得PQ=2EGFH .由△EGA≌△AIC,可得EG=AI ,由△BFH≌△CBI,可得FH=BI.从而可得PQ=2AIBI =2AB ,从而得证.经典难题(三)1.顺时针扭转△ADE,到△ABG,连接CG. 因为∠ABG=∠ADE=900+450=1350从而可得B ,G ,D 在一条直线上,可得△AGB≌△CGB. 推出AE=AG=AC=GC ,可得△AGC 为等边三角形. ∠AGB=300,既得∠EAC=300,从而可得∠A EC=750. 又∠EFC=∠D FA=450+300=750. 可证:CE=CF.2.连接BD 作CH⊥DE,可得四边形CGDH 是正方形.由AC=CE=2GC=2CH ,可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150,又∠FAE=900+450+150=1500,从而可晓得∠F=150,从而得出AE=AF.3.作FG⊥CD,FE⊥BE,可以得出GFEC为正方形.令AB=Y ,BP=X ,CE=Z ,可得PC=Y-X .tan∠BAP=tan∠EPF=XY =ZY X Z,可得YZ=XY-X2+XZ,即Z(Y-X)=X(Y-X) ,既得X=Z ,得出△ABP≌△PEF ,得到PA=PF ,得证.经典难题(四)1.顺时针扭转△ABP 600 ,连接PQ ,则△PBQ是正三角形.可得△PQC是直角三角形.所以∠APB=1500 .2.作过P点平行于AD的直线,并选一点E,使AE∥DC,BE∥PC.可以得出∠ABP=∠ADP=∠AEP,可得:AEBP共圆(一边所对两角相等).可得∠BAP=∠BEP=∠BCP,得证.3.在BD取一点E,使∠BCE=∠ACD,既得△BEC∽△ADC,可得:BE BC =ADAC,即AD•BC=BE•AC,①又∠ACB=∠DCE,可得△ABC∽△DEC,既得AB AC =DEDC,即AB•CD=DE•AC,②由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证.4.过D 作AQ⊥AE ,AG⊥CF ,由ADES=2ABCDS =DFC S ,可得:2AE PQ =2AEPQ,由AE=FC.可得DQ=DG ,可得∠DPA=∠DPC(角平分线逆定理).经典难题(五)1.(1)顺时针扭转△BPC 600 ,可得△P BE 为等边三角形.既得PA+PB+PC=AP++PE+EF 要使最小只需AP ,PE ,EF 在一条直线上,即如下图:可得最小L=;(2)过P 点作BC 的平行线交AB,AC 与点D ,F. 因为∠APD>∠ATP=∠ADP,推出AD>AP①又BP+DP >BP ② 和PF+FC>PC ③ 又DF=AF ④由①②③④可得:最大L< 2 ; 由(1)和(2)既得:≤L<2 .2.顺时针扭转△BPC 600 ,可得△PBE 为等边三角形.既得PA+PB+PC=AP+PE+EF 要使最小只需AP ,PE ,EF 在一条直线上,即如下图:可得最小PA+PB+PC=AF. 既得213(1)42= 23=4232= 231)2=1)2=622 .3.顺时针扭转△ABP 900 ,可得如下图: 既得正方形边长L =2222(2)()22a = 522a .4.在AB 上找一点F ,使∠BCF=600 ,连接EF ,DG ,既得△BGC 为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF , 得到BE=CF , FG=GE .推出 : △FGE 为等边三角形 ,可得∠AFE=800 , 既得:∠DFG=400① 又BD=BC=BG ,既得∠BGD=800 ,既得∠DGF=400② 推得:DF=DG ,得到:△DFE≌△DGE , 从而推得:∠FED=∠BED=300 .。
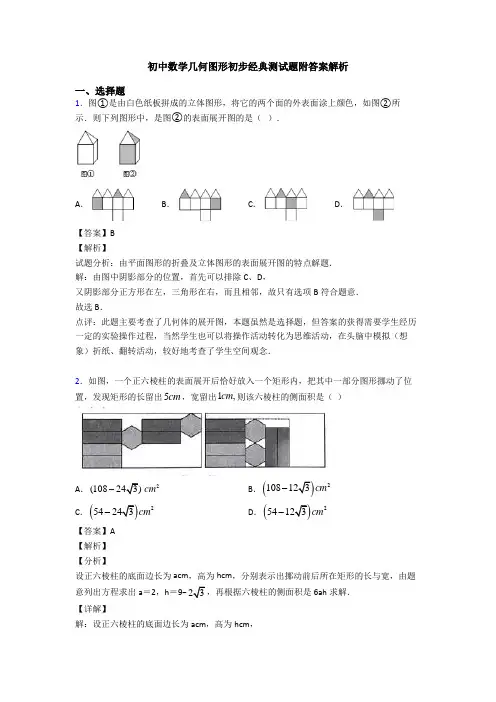
初中数学几何图形初步经典测试题附答案解析一、选择题1.图①是由白色纸板拼成的立体图形,将它的两个面的外表面涂上颜色,如图②所示.则下列图形中,是图②的表面展开图的是( ).A .B .C .D .【答案】B【解析】 试题分析:由平面图形的折叠及立体图形的表面展开图的特点解题.解:由图中阴影部分的位置,首先可以排除C 、D ,又阴影部分正方形在左,三角形在右,而且相邻,故只有选项B 符合题意.故选B .点评:此题主要考查了几何体的展开图,本题虽然是选择题,但答案的获得需要学生经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生空间观念.2.如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm ,宽留出1,cm 则该六棱柱的侧面积是( )A .210824(3) cm -B .(2108123cm -C .(254243cm -D .(254123cm -【答案】A【解析】【分析】 设正六棱柱的底面边长为acm ,高为hcm ,分别表示出挪动前后所在矩形的长与宽,由题意列出方程求出a =2,h =9−36ah 求解.【详解】解:设正六棱柱的底面边长为acm ,高为hcm ,如图,正六边形边长AB =acm 时,由正六边形的性质可知∠BAD =30°,∴BD =12a cm ,AD =32a cm , ∴AC =2AD =3a cm ,∴挪动前所在矩形的长为(2h +23a )cm ,宽为(4a +12a )cm , 挪动后所在矩形的长为(h +2a +3a )cm ,宽为4acm , 由题意得:(2h +23a )−(h +2a +3a )=5,(4a +12a )−4a =1, ∴a =2,h =9−23,∴该六棱柱的侧面积是6ah =6×2×(9−23)=210824(3) cm ;故选:A .【点睛】本题考查了几何体的展开图,正六棱柱的性质,含30度角的直角三角形的性质;能够求出正六棱柱的高与底面边长是解题的关键.3.将如图所示的Rt △ACB 绕直角边AC 旋转一周,所得几何体的主视图(正视图)是( )A .B .C .D .【答案】D【解析】解:Rt △ACB 绕直角边AC 旋转一周,所得几何体是圆锥,主视图是等腰三角形. 故选D .首先判断直角三角形ACB 绕直角边AC 旋转一周所得到的几何体是圆锥,再找出圆锥的主视图即可.4.一副直角三角板如图放置,其中∠C =∠DFE =90°,∠A =45°,∠E =60°,点F 在CB 的延长线上.若DE ∥CF ,则∠BDF 等于( )A .30°B .25°C .18°D .15° 【答案】D【解析】【分析】根据三角形内角和定理可得45ABC ∠=︒和30EDF ∠=︒,再根据平行线的性质可得45EDB ABC ==︒∠∠,再根据BDF EDB EDF =-∠∠∠,即可求出BDF ∠的度数.【详解】∵∠C =90°,∠A =45°∴18045ABC A C =︒--=︒∠∠∠∵//DE CF∴45EDB ABC ==︒∠∠∵∠DFE =90°,∠E =60°∴18030EDF E DFE =︒--=︒∠∠∠∴15BDF EDB EDF =-=︒∠∠∠故答案为:D .【点睛】本题考查了三角板的角度问题,掌握三角形内角和定理、平行线的性质是解题的关键.5.下列立体图形中,侧面展开图是扇形的是()A .B .C.D.【答案】B【解析】根据圆锥的特征可知,侧面展开图是扇形的是圆锥.故选B.6.如图,如果用剪刀沿直线将一个正方形图片剪掉一部分,发现剩下部分的周长比原正方形图片的周长要小,能正确解释这一现象的数学知识是()A.线段比曲线短B.经过一点有无数条直线C.经过两点,有且仅有一条直线D.两点之间,线段最短【答案】D【解析】【分析】如下图,只需要分析AB+BC<AC即可【详解】∵线段AC 是点A 和点C 之间的连线,AB+BC 是点A 和点C 经过弯折后的路径又∵两点之间线段最短∴AC <AB+BC故选:D【点睛】本题考查两点之间线段最短,在应用的过程中,要弄清楚线段长度表示的是哪两个点之间的距离7.一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )A .中B .考C .顺D .利【答案】C【解析】 试题解析:正方体的表面展开图,相对的面之间一定相隔一个正方形,“祝”与“考”是相对面,“你”与“顺”是相对面,“中”与“立”是相对面.故选C .考点:正方体展开图.8.如图,在平行四边形ABCD 中,4AB =,7AD =,ABC ∠的平分线BE 交AD 于点E ,则DE 的长是( )A .4B .3C .3.5D .2【答案】B【解析】【分析】 根据平行四边形的性质可得AEB EBC ∠=∠,再根据角平分线的性质可推出AEB ABE ∠=∠,根据等角对等边可得4AB AE ==,即可求出DE 的长.【详解】∵四边形ABCD 是平行四边形∴//AD BC∴AEB EBC ∠=∠∵BE 是ABC ∠的平分线∴ABE EBC ∠=∠∴AEB ABE ∠=∠∴4AB AE ==∴743DE AD AE =-=-=故答案为:B .【点睛】本题考查了平行四边形的线段长问题,掌握平行四边形的性质、平行线的性质、角平分线的性质、等角对等边是解题的关键.9.如图是由四个正方体组合而成,当从正面看时,则得到的平面视图是( )A .B .C .D .【答案】D【解析】【分析】 根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.根据图中正方体摆放的位置判定则可.【详解】解:从正面看,下面一行是横放3个正方体,上面一行最左边是一个正方体. 故选:D .【点睛】本题主要考查三视图的识别,解决本题的关键是要熟练掌握三视图的识别方法.10.已知:在Rt △ABC 中,∠C =90°,BC =1,AC 3D 是斜边AB 的中点,点E 是边AC 上一点,则DE +BE 的最小值为( )A.2B.31C.3D.23【答案】C【解析】【分析】作B关于AC的对称点B',连接B′D,易求∠ABB'=60°,则AB=AB',且△ABB'为等边三角形,BE+DE=DE+EB'为B'与直线AB之间的连接线段,其最小值为B'到AB的距离=AC=3,所以最小值为3.【详解】解:作B关于AC的对称点B',连接B′D,∵∠ACB=90°,∠BAC=30°,∴∠ABC=60°,∵AB=AB',∴△ABB'为等边三角形,∴BE+DE=DE+EB'为B'与直线AB之间的连接线段,∴最小值为B'到AB的距离3故选C.【点睛】本题考查的是最短线路问题及等边三角形的性质,熟知两点之间线段最短的知识是解答此题的关键.11.如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是()A.左转 80°B.右转80°C.右转 100°D.左转 100°【答案】C【解析】【分析】过C点作CE∥AB,延长CB与点D,根据平行线的性质得出∠A+∠ABH=180°,∠ECB=∠ABC,求出∠ABH=110°,∠ABC=80°,即可求出∠ECB=80°,得出答案即可.【详解】过C点作CE∥AB,延长CB与点D,如图∵根据题意可知:AF∥BH,AB∥CE,∴∠A+∠ABH=180°,∠ECB=∠ABC,∵根据题意可知:∠FAB=70°,∠HBC=30°,∴∠ABH=180°−70°=110°,∠ABC=110°−30°=80°,∴∠ECB=80°,∴∠DCE=180°−80°=100°,即方向的调整应是右转100°.故答案选C.【点睛】本题考查了平行线的判定与性质,解题的关键是熟练的掌握平行线的判定与性质.12.一把直尺和一块三角板ABC(含30°,60°角)的摆放位置如图,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CED =50°,那么∠BAF=()A .10°B .50°C .45°D .40°【答案】A【解析】【分析】 先根据∠CED =50°,DE ∥AF ,即可得到∠CAF =50°,最后根据∠BAC =60°,即可得出∠BAF 的大小.【详解】∵DE ∥AF ,∠CED =50°,∴∠CAF =∠CED =50°,∵∠BAC =60°,∴∠BAF =60°﹣50°=10°,故选:A .【点睛】此题考查平行线的性质,几何图形中角的和差关系,掌握平行线的性质是解题的关键.13.如图,在Rt ABC 中,90C ∠=︒,以顶点A 为圆心,适当长为半径画弧,分别交AC 、AB 于点M 、N ,再分别以点M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP 交边BC 于点D ,若4CD =,15AB =,则ABD △的面积是( )A .15B .30C .45D .60【答案】B【解析】【分析】作DE AB ⊥于E ,根据角平分线的性质得4DE DC ==,再根据三角形的面积公式求解即可.【详解】作DE AB ⊥于E由尺规作图可知,AD 是△ABC 的角平分线∵90C ∠=︒,DE AB ⊥∴4DE DC ==∴△ABD 的面积1302AB DE =⨯⨯= 故答案为:B .【点睛】本题考查了三角形的面积问题,掌握角平分线的性质、三角形面积公式是解题的关键.14.如图,ABC ∆为等边三角形,点P 从A 出发,沿A B C A →→→作匀速运动,则线段AP 的长度y 与运动时间x 之间的函数关系大致是( )A .B .C .D .【答案】B【解析】【分析】根据题意可知点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段,故可排除选项C 与D ;点P 从点B 运动到点C 时,y 是x 的二次函数,并且有最小值,故选项B 符合题意,选项A 不合题意.【详解】根据题意得,点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段,故选项C 与选项D 不合题意;点P 从点B 运动到点C 时,y 是x 的二次函数,并且有最小值,∴选项B 符合题意,选项A 不合题意.故选B .【点睛】本题考查了动点问题的函数图象:通过分类讨论,利用三角形面积公式得到y 与x 的函数关系,然后根据二次函数和一次函数图象与性质解决问题.15.下列图形中,是圆锥的侧面展开图的为( )A .B .C .D .【答案】B【解析】【分析】 根据圆锥的侧面展开图的特点作答.【详解】圆锥的侧面展开图是光滑的曲面,没有棱,只是扇形.故选B .【点睛】考查了几何体的展开图,圆锥的侧面展开图是扇形.16.如图,在ABC 中,90C ∠=︒,30B ∠=︒,如图:(1)以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ;(2)分别以M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ;(3)连结AP 并延长交BC 于点D .根据以上作图过程,下列结论中错误的是( )A .AD 是BAC ∠的平分线B .60ADC ∠=︒ C .点D 在AB 的中垂线上D .:1:3DAC ABD S S =△△【答案】D【解析】【分析】 根据作图的过程可以判定AD 是∠BAC 的角平分线;利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC 的度数;利用等角对等边可以证得△ADB 的等腰三角形,由等腰三角形的“三线合一”的性质可以证明点D 在AB 的中垂线上;利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.【详解】解:A 、根据作图方法可得AD 是∠BAC 的平分线,正确;B、∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD是∠BAC的平分线,∴∠DAC=∠DAB=30°,∴∠ADC=60°,正确;C、∵∠B=30°,∠DAB=30°,∴AD=DB,∴点D在AB的中垂线上,正确;D、∵∠CAD=30°,∴CD=12 AD,∵AD=DB,∴CD=12 DB,∴CD=13 CB,S△ACD=12CD•AC,S△ACB=12CB•AC,∴S△ACD:S△ACB=1:3,∴S△DAC:S△ABD≠1:3,错误,故选:D.【点睛】本题考查了角平分线的性质、线段垂直平分线的性质以及作图—基本作图.解题时,需要熟悉等腰三角形的判定与性质.17.用一副三角板(两块)画角,能画出的角的度数是()A.145C B.95C C.115C D.105C【答案】D【解析】【分析】一副三角板由两个三角板组成,其中一个三角板的度数有45°、45°、90°,另一个三角板的度数有30°、60°、90°,将两个三角板各取一个角度相加,和等于选项中的角度即可拼成.【详解】选项的角度数中个位是5°,故用45°角与另一个三角板的三个角分别相加,结果分别为:45°+30°=75°,45°+60°=105°,45°+90°=135°,故选:D.【点睛】此题主要考查学生对角的计算这一知识点的理解和掌握,解答此题的关键是分清两块三角板的锐角的度数分别是多少,比较简单,属于基础题.18.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为()A.圆锥,正方体,三棱锥,圆柱B.圆锥,正方体,四棱锥,圆柱C.圆锥,正方体,四棱柱,圆柱D.正方体,圆锥,圆柱,三棱柱【答案】D【解析】【分析】根据常见的几何体的展开图进行判断,即可得出结果.【详解】根据几何体的平面展开图,则从左到右,其对应的几何体名称分别为:正方体,圆锥,圆柱,三棱柱.故选D.【点睛】本题考查了常见几何体的展开图;熟记常见几何体的平面展开图的特征,是解题的关键.19.下列说法中正确的有()(1)如果互余的两个角的度数之比为1:3,那么这两个角分别是45°和135°(2)如果两个角是同一个角的补角,那么这两个角不一定相等(3)一个锐角的余角比这个锐角的补角小90°(4)如果两个角的度数分别是73°42′与16°18′,那么这两个角互余.A.1个 B.2个 C.3个 D.4个【答案】B【解析】【分析】根据余角和补角的定义依次判断即可求解.【详解】(1)由互余的两个角的和为90°可知(1)错误;(2)由同角的补角相等可知(2)错误;(3)设这个角为x,则其余角为(90°﹣x),补角为(18 0°﹣x),则(180°﹣x)﹣(90°﹣x)=90°,由此可知(3)正确;(4)由73°42+16°18′=90°可知(4)正确.综上,正确的结论为(3)(4),共2个.故选B.【点睛】本题考查了余角和补角的定义,熟练运用余角和补角的定义是解决问题的关键.∠,20.如图,已知直线AB和CD相交于G点,CG EG⊥,GF平分AGE∠=︒,则BGDCGF34∠大小为()A.22︒B.34︒C.56︒D.90︒【答案】A【解析】【分析】先根据垂直的定义求出∠EGF的度数,然后根据GF平分∠ABE可得出∠AGF的度数,再由∠AGC=∠AGF-∠CGF求出∠AGC的度数,最后根据对顶角相等可得出∠BGD的度数.【详解】解:∵CG⊥EG,∴∠EGF=90°-∠CGF=90°-34°=56°,又GF平分∠AGE,∴∠AGF=∠EGF=56°,∴∠AGC=∠AGF-∠CGF=56°-34°=22°,∴∠BGD=∠AGC=22°.故选:A.【点睛】本题考查了对顶角的性质,垂直的定义以及角平分线的定义,掌握基本概念和性质是解题的关键.。
初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC=AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC , 求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.APCBACBPDEDCB AA CBPD经典题(一)1.如下图做GH⊥AB,连接EO。

1.如图,直线l1∥l2,∠1=55°,∠2=65°,则∠3为()A.50° B.55° C.60° D.65°解析:如图所示:∵l1∥l2,∠2=65°,∴∠6=65°,∵∠1=55°,∴∠1=∠4=55°,在△ABC中,∠6=65°,∠4=55°,∴∠3=180°﹣65°﹣55°=60°.参考答案:C2.如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为()A.4 B.4 C.6 D.4解析:∵BC=8,∴CD=4,在△CBA和△CAD中,∵∠B=∠DAC,∠C=∠C,∴△CBA∽△CAD,∴=,∴AC2=CD•BC=4×8=32,∴AC=4;参考答案:B.3.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形的是②③④.(把所有正确答案的序号都填写在横线上)①∠BAD=∠ACD;②∠BAD=∠CAD;③AB+BD=AC+CD;④AB﹣BD=AC﹣CD.解析:证明:②当∠BAD=∠CAD时,AD是∠BAC的平分线,且AD是BC边上的高;∴△BAC是等腰三角形;(等腰三角形三线合一)③延长DB至E,使BE=AB;延长DC至F,使CF=AC;连接AE、AF;∵AB+BD=CD+AC,∴DE=DF,又AD⊥BC;∴△AEF是等腰三角形;∴∠E=∠F;∵AB=BE,∴∠ABC=2∠E;同理,得∠ACB=2∠F;∴∠ABC=∠ACB,即AB=AC,△ABC是等腰三角形;④△ABC中,AD⊥BC,根据勾股定理,得:AB2﹣BD2=AC2﹣CD2,即(AB+BD)(AB﹣BD)=(AC+CD)(AC﹣CD);∵AB﹣BD=AC﹣CD,∴AB+BD=AC+CD;∴两式相加得,2AB=2AC;∴AB=AC,∴△ABC是等腰三角形故填②③④.4.在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片ABCD沿过点A的直线折叠,使得点B落在CD上的点Q处.折痕为AP;再将△PCQ,△ADQ分别沿PQ,AQ折叠,此时点C,D落在AP上的同一点R处.请完成下列探究:(1)∠PAQ的大小为°;(2)当四边形APCD是平行四边形时,的值为.解析:(1)由折叠的性质可得:∠B=∠AQP,∠DAQ=∠QAP=∠PAB,∠DQA=∠AQR,∠CQP=∠PQR,∠D=∠ARQ,∠C=∠QRP,∵∠QRA+∠QRP=180°,∴∠D+∠C=180°,∴AD∥BC,∴∠B+∠DAB=180°,∵∠DQR+∠CQR=180°,∴∠DQA+∠CQP=90°,∴∠AQP=90°,∴∠B=∠AQP=90°,∴∠DAB=90°,∴∠DAQ=∠QAP=∠PAB=30°,故答案为:30;(2)由折叠的性质可得:AD=AR,CP=PR,∵四边形APCD是平行四边形,∴AD=PC,∴AR=PR,又∵∠AQP=90°,∴QR=AP,∵∠PAB=30°,∠B=90°,∴AP=2PB,AB=PB,∴PB=QR,∴=,参考答案为:.5.如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(=1.7).参考答案:解:如图,过点B作BE⊥CD于点E,根据题意,∠DBE=45°,∠CBE=30°.∵AB⊥AC,CD⊥AC,∴四边形ABEC为矩形.∴CE=AB=12m.在Rt△CBE中,cot∠CBE=,∴BE=CE•cot30°=12×=12.在Rt△BDE中,由∠DBE=45°,得DE=BE=12.∴CD=CE+DE=12(+1)≈32.4.答:楼房CD的高度约为32.4m.6.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为()A.B.2 C.D.解析:∵∠ABC=90°,∴∠ABP+∠PBC=90°,∵∠PAB=∠PBC,∴∠BAP+∠ABP=90°,∴∠APB=90°,∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,∴OC==5,∴PC=OC=OP=5﹣3=2.∴PC最小值为2.参考答案:B.7.如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.参考答案:解:过点D作l1的垂线,垂足为F,∵∠DEB=60°,∠DAB=30°,∴∠ADE=∠DEB﹣∠DAB=30°,∴△ADE为等腰三角形,∴DE=AE=20,在Rt△DEF中,EF=DE•cos60°=20×=10,∵DF⊥AF,∴∠DFB=90°,∴AC∥DF,由已知l1∥l2,∴CD∥AF,∴四边形ACDF为矩形,CD=AF=AE+EF=30,答:C、D两点间的距离为30m.8.在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有()A.∠ADE=20°B.∠ADE=30°C.∠ADE=∠ADC D.∠ADE=∠ADC解析:如图,在△AED中,∠AED=60°,∴∠A=180°﹣∠AED﹣∠ADE=120°﹣∠ADE,在四边形DEBC中,∠DEB=180°﹣∠AED=180°﹣60°=120°,∴∠B=∠C=(360°﹣∠DEB﹣∠EDC)÷2=120°﹣∠EDC,∵∠A=∠B=∠C,∴120°﹣∠ADE=120°﹣∠EDC,∴∠ADE=∠EDC,∵∠ADC=∠ADE+∠EDC=∠EDC+∠EDC=∠EDC,∴∠ADE=∠ADC,参考答案:D.9.如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是()A. 2B.3C.5 D.6解析:连接EF交AC于O,∵四边形EGFH是菱形,∴EF⊥AC,OE=OF,∵四边形ABCD是矩形,∴∠B=∠D=90°,AB∥CD,∴∠ACD=∠CAB,在△CFO与△AOE中,,∴△CFO≌△AOE,∴AO=CO,∵AC==4,∴AO=AC=2,∵∠CAB=∠CAB,∠AOE=∠B=90°,∴△AOE∽△ABC,∴,∴,∴AE=5.故选C.10.如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②△DEF∽△ABG;③S△ABG=S△FGH;④AG+DF=FG.其中正确的是.(把所有正确结论的序号都选上)解析:∵△BCE沿BE折叠,点C恰落在边AD上的点F处,∴∠1=∠2,CE=FE,BF=BC=10,在Rt△ABF中,∵AB=6,BF=10,∴AF==8,∴DF=AD﹣AF=10﹣8=2,设EF=x,则CE=x,DE=CD﹣CE=6﹣x,在Rt△DEF中,∵DE2+DF2=EF2,∴(6﹣x)2+22=x2,解得x=,∴ED=,∵△ABG沿BG折叠,点A恰落在线段BF上的点H处,∴∠3=∠4,BH=BA=6,AG=HG,∴∠2+∠3=∠ABC=45°,所以①正确;HF=BF﹣BH=10﹣6=4,设AG=y,则GH=y,GF=8﹣y,在Rt△HGF中,∵GH2+HF2=GF2,∴y2+42=(8﹣y)2,解得y=3,∴AG=GH=3,GF=5,∵∠A=∠D, ==, =,∴≠,∴△ABG与△DEF不相似,所以②错误;∵S△ABG=•6•3=9,S△FGH=•GH•HF=×3×4=6,∴S △ABG =S △FGH ,所以③正确;∵AG+DF=3+2=5,而GF=5,∴AG+DF=GF ,所以④正确.参考答案:①③④.12.如图,AD ∥FE ,点B 、C 在AD 上,∠1=∠2,BF=BC .(1)求证:四边形BCEF 是菱形;(2)若AB=BC=CD ,求证:△ACF ≌△BDE .参考答案:证明:(1)∵AD ∥FE ,∴∠FEB=∠2.∵∠1=∠2,∴∠FEB=∠1.∴BF=EF .∵BF=BC ,∴BC=EF .∴四边形BCEF 是平行四边形.∵BF=BC ,∴四边形BCEF 是菱形.(2)∵EF=BC ,AB=BC=CD ,AD ∥EF ,∴四边形ABEF 、CDEF 均为平行四边形.∴AF=BE ,FC=ED .又∵AC=2BC=BD ,∴△ACF ≌△BDE .13.在△ABC 中,∠ACB =90°,∠ABC =30°,将△ABC 绕顶点C 顺时针旋转,旋转角为,得到△.)1800(︒<<︒θθC B A '''A A ′ A C C C A ′ A ′ A D B ′ B B B B ′ B ′E P 第22题图(1) 第22题图(2) 第22题图(3)(1)如图(1),当∥时,设与CD 相交于点D ,证明:△是等边三角形;(2)如图(2),连接,设和的面积分别为和. 求证::=1:3.(3)如图(3),设AC 中点为E ,中点为P ,,连接,当 °时,EP 长度最大,最大值为 .参考答案:(1)证:由∥知∠=∠ABC =30°,∴∠=60°=∠,即△是等边三角形.(2)证:由题知:∠=∠=,,,所以△和△均为等腰三角形,且△∽△,:= (3)解:边CP ,则EP ≤CE+CP ,当EXP 共线时,EP 最大,由直角三角形斜边上中线性质可知,CP=0.5AB=0.5a ,故EP 的最大值为1.5a ,,没有旋转时,∠ACP=60°,从而当ECP 共线是时,旋转了120°。

几何经典难题1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初三)E2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15.求证:△PBC是正三角形.(初二)C3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1求证:四边形A2B2C2D2是正方形.(初二) A的中点.DDOF DBA1B2 2C4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.B5、已知:△ABC中,H为垂心(各边高线的交点)(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初三)第1 页共15 页6、设MN是圆O外一直线,过O作OA⊥MN于A,自A,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初三)7、如果上题把直线MN由圆外平移至圆)N设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.8、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE 和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.F第2 页共15 页9、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二)10、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.11、设P是正方形ABCD一边BC求证:PA=PF.(初二)EE12、如图,PC切圆O于C,AC为圆的直径,PEF为圆的割线,AE、AF与直线PO相交于B、D.求证:AB=DC,BC=AD.(初三)第3 页共15 页P13、已知:△ABC是正三角形,P是三角形内一点,PA=3,PB=4,PC=5.求:∠APB的度数.(初二)14、设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.(初二)C15、设ABCD为圆内接凸四边形,求证:AB·CD16、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.D17、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:第4 页共15 页≤L<2.18、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.DCC19、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.20、如图,△ABC中,∠ABC=∠ACB=80,D、E分别是AB、AC上的点,∠DCA=30,∠EBA=200,求∠BED的度数.第5 页解答1.如下图做GH⊥AB,连接EO。
初中数学经典几何题(附答案)经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F .D 2C 2B 2A 2D 1C 1B 1CBDAA 1ANFE C DMB经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)· ADHE M CBO ·GAO DBECQ PNMPC GFBQADE3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)· O QPBD EC N M · A经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)AF DECBEDACBF3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE . 求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)DFEPCBAOD BFAEC PAPCB2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)P ADCBCBDA经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.FPDE CBA APCB ACBPDACBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E 分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
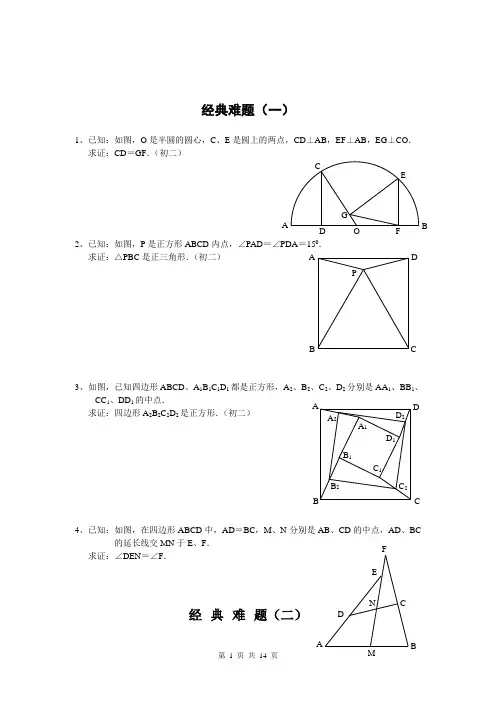
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC 是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。
(专题精选)初中数学几何图形初步经典测试题附答案解析一、选择题1.如图,将三个同样的正方形的一个顶点重合放置,如果145∠=°,330∠=°时,那么2∠的度数是( )A .15°B .25°C .30°D .45°【答案】A【解析】【分析】 根据∠2=∠BOD+EOC-∠BOE ,利用正方形的角都是直角,即可求得∠BOD 和∠EOC 的度数从而求解.【详解】∵∠BOD=90°-∠3=90°-30°=60°,∠EOC=90°-∠1=90°-45°=45°,∵∠2=∠BOD+∠EOC-∠BOE ,∴∠2=60°+45°-90°=15°.故选:A .【点睛】此题考查余角和补角,正确理解∠2=∠BOD+EOC-∠BOE 这一关系是解题的关键.2.下列图形经过折叠不能围成棱柱的是( ).A .B .C .D .【答案】B【解析】试题分析:三棱柱的展开图为3个矩形和2个三角形,故B 不能围成.考点:棱柱的侧面展开图.3.将一副三角板如下图放置,使点A 落在DE 上,若BC DE P ,则AFC ∠的度数为( )A .90°B .75°C .105°D .120°【答案】B【解析】【分析】 根据平行线的性质可得30E BCE ==︒∠∠,再根据三角形外角的性质即可求解AFC ∠的度数.【详解】∵//BC DE∴30E BCE ==︒∠∠∴453075AFC B BCE =+=︒+︒=︒∠∠∠故答案为:B .【点睛】本题考查了三角板的角度问题,掌握平行线的性质、三角形外角的性质是解题的关键.4.下列立体图形中,侧面展开图是扇形的是()A .B .C .D.【答案】B【解析】根据圆锥的特征可知,侧面展开图是扇形的是圆锥.故选B.5.如图所示是一个正方体展开图,图中六个正方形内分别标有“新”、“时”、“代”、“去”、“奋”、“斗”、六个字,将其围成一个正方体后,则与“奋”相对的字是( )A.斗B.新C.时D.代【答案】C【解析】分析:正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.详解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“时”相对的字是“奋”;“代”相对的字是“新”;“去”相对的字是“斗”.故选C.点睛:本题主要考查了正方体的平面展开图,解题的关键是掌握立方体的11种展开图的特征.6.如图,O是直线AB上一点,OC平分∠DOB,∠COD=55°45′,则∠AOD=()A.68°30′B.69°30′C.68°38′D.69°38′【答案】A【解析】【分析】先根据平分,求出∠COB,再利用互补求∠AOD【详解】∵OC平分∠DOB,∠COD=55°45′∴∠COB=55°45′,∠DOB=55°45′+55°45′=111°30′∴∠AOD=180-111°30′=68°30′故选:A【点睛】本题考查角度的简单推理,计算过程中,设计到了分这个单位,需要注意,分与度的进率是607.把正方体的表面沿某些棱剪开展成一个平面图形(如图),请根据各面上的图案判断这个正方体是( )A .B .C .D .【答案】C【解析】【分析】 通过立体图形与平面图形的相互转化,去理解和掌握几何体的展开图,要注意多从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形.【详解】结合立体图形与平面图形的相互转化,即可得出两圆应该在几何体的上下,符合要求的只有C ,D ,再根据三角形的位置,即可排除D 选项.故选C .【点睛】考查了展开图与折叠成几何体的性质,从实物出发,然后再从给定的图形中辨认它们能否折叠成给定的立体图形是解题关键.8.下列图形中1∠与2∠不相等的是( )A .B .C .D .【答案】B【解析】【分析】根据对顶角,平行线,等角的余角相等等知识一一判断即可.【详解】解:A、根据对顶角相等可知,∠1=∠2,本选项不符合题意.B、∵∠1+∠2=90°,∠1与∠2不一定相等,本选项符合题意.C.根据平行线的性质可知:∠1=∠2,本选项不符合题意.D、根据等角的余角相等,可知∠1=∠2,本选项不符合题意.故选:B.【点睛】本题考查平行线的性质对顶角的性质,等角的余角相等等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.9.如图,AB∥CD,EF平分∠GED,∠1=50°,则∠2=()A.50°B.60°C.65°D.70°【答案】C【解析】【分析】由平行线性质和角平分线定理即可求.【详解】∵AB∥CD∴∠GEC=∠1=50°∵EF平分∠GED∴∠2=∠GEF= 12∠GED=12(180°-∠GEC)=65°故答案为C.【点睛】本题考查的知识点是平行线性质和角平分线定理,解题关键是熟记角平分线定理.10.一把直尺和一块三角板ABC(含30°,60°角)的摆放位置如图,直尺一边与三角板的两直角边分别交于点D、点E,另一边与三角板的两直角边分别交于点F、点A,且∠CED =50°,那么∠BAF=()A.10°B.50°C.45°D.40°【答案】A【解析】【分析】先根据∠CED=50°,DE∥AF,即可得到∠CAF=50°,最后根据∠BAC=60°,即可得出∠BAF的大小.【详解】∵DE∥AF,∠CED=50°,∴∠CAF=∠CED=50°,∵∠BAC=60°,∴∠BAF=60°﹣50°=10°,故选:A.【点睛】此题考查平行线的性质,几何图形中角的和差关系,掌握平行线的性质是解题的关键.11.小张同学的座右铭是“态度决定一切”,他将这几个字写在一个正方体纸盒的每个面上,其平面展开图如图所示,那么在该正方体中,和“一”相对的字是()A.态B.度C.决D.切【答案】A【解析】【分析】正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,据此可得和“一”相对的字.【详解】正方体的平面展开图中,相对面的特点是之间一定相隔一个正方形,所以和“一”相对的字是:态.故选A.【点睛】注意正方体的空间图形,从相对面入手,分析及解答问题.12.如图,在Rt ABC V 中,90C ∠=︒,以顶点A 为圆心,适当长为半径画弧,分别交AC 、AB 于点M 、N ,再分别以点M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线AP 交边BC 于点D ,若4CD =,15AB =,则ABD △的面积是( )A .15B .30C .45D .60 【答案】B【解析】【分析】作DE AB ⊥于E ,根据角平分线的性质得4DE DC ==,再根据三角形的面积公式求解即可.【详解】作DE AB ⊥于E由尺规作图可知,AD 是△ABC 的角平分线∵90C ∠=︒,DE AB ⊥∴4DE DC ==∴△ABD 的面积1302AB DE =⨯⨯= 故答案为:B .【点睛】本题考查了三角形的面积问题,掌握角平分线的性质、三角形面积公式是解题的关键.13.如图,点C 是射线OA 上一点,过C 作CD ⊥OB ,垂足为D ,作CE ⊥OA ,垂足为C ,交OB 于点E ,给出下列结论:①∠1是∠DCE 的余角;②∠AOB =∠DCE ;③图中互余的角共有3对;④∠ACD =∠BEC ,其中正确结论有( )A .①②③B .①②④C .①③④D .②③④【答案】B【解析】【分析】 根据垂直定义可得BCA 90∠=o ,ADC BDC ACF 90∠∠∠===o ,然后再根据余角定义和补角定义进行分析即可.【详解】解:CE OA ⊥Q ,OCE 90o ∠∴=,ECD 190∠∠∴+=o ,1∠∴是ECD ∠的余角,故①正确;CD OB ⊥Q ,AOB COCE 90∠∠∴==o ,AOB OEC 90∠∠∴+=o ,DCE OEC 90∠∠+=o ,B BAC 90∠∠∴+=o ,1ACD 90∠∠+=o ,AOB DCE ∠∠∴=,故②正确;1AOB 1DCE DCE CED AOB CED 90∠∠∠∠∠∠∠∠+=+=+=+=o Q , ∴图中互余的角共有4对,故③错误;ACD 90DCE ∠∠=+o Q ,BEC 90AOB ∠∠=+o ,AOB DCE ∠∠=Q ,ACD BEC ∠∠∴=,故④正确.正确的是①②④;故选B .【点睛】考查了余角和补角,关键是掌握两角之和为90o 时,这两个角互余,两角之和为180o 时,这两个角互补.14.如图,将一副三角板如图放置,∠COD=28°,则∠AOB 的度数为( )A .152°B .148°C .136°D .144°【答案】A【解析】【分析】 根据三角板的性质得90AOD BOC ∠=∠=︒,再根据同角的余角相等可得62AOC BOD ==︒∠∠,即可求出∠AOB 的度数.【详解】∵这是一副三角板∴90AOD BOC ∠=∠=︒∵28COD =︒∠∴62AOC BOD ==︒∠∠∴62+28+62=152AOB AOC COD BOD =++=︒︒︒︒∠∠∠∠故答案为:A .【点睛】本题考查了三角板的度数问题,掌握三角板的性质、同角的余角相等是解题的关键.15.如图,在ABC V 中,90C ∠=︒,30B ∠=︒,如图:(1)以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ;(2)分别以M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ;(3)连结AP 并延长交BC 于点D .根据以上作图过程,下列结论中错误的是( )A .AD 是BAC ∠的平分线B .60ADC ∠=︒ C .点D 在AB 的中垂线上D .:1:3DAC ABD S S =△△【答案】D【解析】【分析】 根据作图的过程可以判定AD 是∠BAC 的角平分线;利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC 的度数;利用等角对等边可以证得△ADB 的等腰三角形,由等腰三角形的“三线合一”的性质可以证明点D 在AB 的中垂线上;利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.【详解】解:A、根据作图方法可得AD是∠BAC的平分线,正确;B、∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD是∠BAC的平分线,∴∠DAC=∠DAB=30°,∴∠ADC=60°,正确;C、∵∠B=30°,∠DAB=30°,∴AD=DB,∴点D在AB的中垂线上,正确;D、∵∠CAD=30°,∴CD=12 AD,∵AD=DB,∴CD=12 DB,∴CD=13 CB,S△ACD=12CD•AC,S△ACB=12CB•AC,∴S△ACD:S△ACB=1:3,∴S△DAC:S△ABD≠1:3,错误,故选:D.【点睛】本题考查了角平分线的性质、线段垂直平分线的性质以及作图—基本作图.解题时,需要熟悉等腰三角形的判定与性质.16.下列说法中,正确的个数为( )①过同一平面内5点,最多可以确定9条直线;②连接两点的线段叫做两点的距离;③若AB BC,则点B是线段AC的中点;④三条直线两两相交,一定有3个交点.A.3个B.2个C.1个D.0个【答案】D【解析】【分析】根据直线交点、两点间距离、线段中点定义分别判断即可得到答案.【详解】①过同一平面内5点,最多可以确定10条直线,故错误;②连接两点的线段的长度叫做两点的距离,故错误;,则点B不一定是线段AC的中点,故错误;③若AB BC④三条直线两两相交,可以都交于同一点,故错误;故选:D.【点睛】此题考查直线交点、两点间距离定义、线段中点定义,正确理解定义是解题的关键.17.用一副三角板(两块)画角,能画出的角的度数是()A.145C o B.95C o C.115C o D.105C o【答案】D【解析】【分析】一副三角板由两个三角板组成,其中一个三角板的度数有45°、45°、90°,另一个三角板的度数有30°、60°、90°,将两个三角板各取一个角度相加,和等于选项中的角度即可拼成.【详解】选项的角度数中个位是5°,故用45°角与另一个三角板的三个角分别相加,结果分别为:45°+30°=75°,45°+60°=105°,45°+90°=135°,故选:D.【点睛】此题主要考查学生对角的计算这一知识点的理解和掌握,解答此题的关键是分清两块三角板的锐角的度数分别是多少,比较简单,属于基础题.18.下列说法中不正确的是()①过两点有且只有一条直线②连接两点的线段叫两点的距离③两点之间线段最短④点B在线段AC上,如果AB=BC,则点B是线段AC的中点A.①B.②C.③D.④【答案】B【解析】【分析】依据直线的性质、两点间的距离、线段的性质以及中点的定义进行判断即可.【详解】①过两点有且只有一条直线,正确;②连接两点的线段的长度叫两点间的距离,错误③两点之间线段最短,正确;④点B 在线段AC 上,如果AB=BC ,则点B 是线段AC 的中点,正确;故选B .19.下列说法中正确的有( )(1)如果互余的两个角的度数之比为1:3,那么这两个角分别是45°和135°(2)如果两个角是同一个角的补角,那么这两个角不一定相等(3)一个锐角的余角比这个锐角的补角小90°(4)如果两个角的度数分别是73°42′与16°18′,那么这两个角互余.A .1个B .2个C .3个D .4个【答案】B【解析】【分析】根据余角和补角的定义依次判断即可求解.【详解】(1)由互余的两个角的和为90°可知(1)错误;(2)由同角的补角相等可知(2)错误;(3)设这个角为x ,则其余角为(90°﹣x ),补角为(18 0°﹣x ),则(180°﹣x )﹣(90°﹣x )=90°,由此可知(3)正确;(4)由73°42+16°18′=90°可知(4)正确.综上,正确的结论为(3)(4),共2个.故选B .【点睛】本题考查了余角和补角的定义,熟练运用余角和补角的定义是解决问题的关键.20.如图将两块三角板的直角顶点重叠在一起,DOB ∠与DOA ∠的比是2:11,则BOC ∠的度数为( )A .45︒B .60︒C .70︒D .40︒【答案】C【解析】【分析】 设∠DOB=2x ,则∠DOA=11x ,可推导得到∠AOB=9x=90°,从而得到角度大小【详解】∵∠DOB与∠DOA的比是2:11∴设∠DOB=2x,则∠DOA=11x∴∠AOB=9x∵∠AOB=90°∴x=10°∴∠BOD=20°∴∠COB=70°故选:C【点睛】本题考查角度的推导,解题关键是引入方程思想,将角度推导转化为计算的过程,以便简化推导。
中考数学经典几何证明题60例一、解答题(共60小题)1.(遵义)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;(2)证明四边形ADCF是菱形;(3)若AC=4,AB=5,求菱形ADCF的面积.2.(珠海)已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.(1)如图1,连接BD,AF,则BD AF(填“>”、“<”或“=”);(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.3.(镇江)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.(1)求证:△BAE≌△BCF;(2)若∠ABC=50°,则当∠EBA=°时,四边形BFDE是正方形.4.(漳州)如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.(1)求证:四边形DEFG为菱形;(2)若CD=8,CF=4,求的值.5.(玉林)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O 的切线CD交AB的延长线于点C,E为的中点,连接DE,EB.(1)求证:四边形BCDE是平行四边形;(2)已知图中阴影部分面积为6π,求⊙O的半径r.6.(永州)如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.(1)求证:∠ABC=∠EDC;(2)求证:△ABC≌△EDC.7.(营口)如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.(1)求证:PC是⊙O的切线;(2)若PD=,AC=8,求图中阴影部分的面积;(3)在(2)的条件下,若点E是的中点,连接CE,求CE的长.8.(徐州)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.(1)求证:四边形BFCE是平行四边形;(2)若AD=10,DC=3,∠EBD=60°,则BE=时,四边形BFCE是菱形.9.(宿迁)如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.(1)求证:四边形BDFC是平行四边形;(2)若△BCD是等腰三角形,求四边形BDFC的面积.10.(湘西州)如图,在▱ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.(1)求证:△ADE≌△CBF;(2)求证:四边形BFDE为矩形.11.(咸宁)已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)证明:不论m为何值时,方程总有实数根;(2)m为何整数时,方程有两个不相等的正整数根.12.(咸宁)如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.13.(梧州)如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.(1)求证:HF=AP;(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.14.(威海)如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若BD=2,BE=3,求AC的长.15.(铜仁市)已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.16.(通辽)如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE,求证:△ABC与△DEC全等.17.(铁岭)如图,矩形ABCD中,AB=8,AD=6,点E、F分别在边CD、AB上.(1)若DE=BF,求证:四边形AFCE是平行四边形;(2)若四边形AFCE是菱形,求菱形AFCE的周长.18.(天水)如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证:(1)AC•PD=AP•BC;(2)PE=PD.19.(泰安)如图,△ABC是直角三角形,且∠ABC=90°,四边形BCDE是平行四边形,E 为AC中点,BD平分∠ABC,点F在AB上,且BF=BC.求证:(1)DF=AE;(2)DF⊥AC.20.(随州)如图,射线PA切⊙O于点A,连接PO.(1)在PO的上方作射线PC,使∠OPC=∠OPA(用尺规在原图中作,保留痕迹,不写作法),并证明:PC是⊙O的切线;(2)在(1)的条件下,若PC切⊙O于点B,AB=AP=4,求的长.21.(绥化)如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.(1)求证:BD+2DE=BM.(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG=.22.(苏州)如图,在△ABC中,AB=AC,分别以B、C为圆心,BC长为半径在BC下方画弧.设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD(1)求证:AD平分∠BAC;(2)若BC=6,∠BAC=50°,求DE、DF的长度之和(结果保留π).23.(上海)已知,如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.(1)求证:DE⊥BE;(2)如果OE⊥CD,求证:BD•CE=CD•DE.24.(厦门)如图,在平面直角坐标系中,点A(2,n),B(m,n)(m>2),D(p,q)(q<n),点B,D在直线y=x+1上.四边形ABCD的对角线AC,BD相交于点E,且AB∥CD,CD=4,BE=DE,△AEB的面积是2.求证:四边形ABCD是矩形.25.(庆阳)如图,在正方形ABCD中,点E是边BC的中点,直线EF交正方形外角的平分线于点F,交DC于点G,且AE⊥EF.(1)当AB=2时,求△GEC的面积;(2)求证:AE=EF.26.(青海)如图,梯形ABCD中,AB∥DC,AC平分∠BAD,CE∥DA交AB于点E.求证:四边形ADCE是菱形.27.(钦州)如图,AB为⊙O的直径,AD为弦,∠DBC=∠A.(1)求证:BC是⊙O的切线;(2)连接OC,如果OC恰好经过弦BD的中点E,且tanC=,AD=3,求直径AB的长.28.(黔东南州)如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.(1)求证:PN与⊙O相切;(2)如果∠MPC=30°,PE=2,求劣弧的长.29.(潜江)如图,AC是⊙O的直径,OB是⊙O的半径,PA切⊙O于点A,PB与AC的延长线交于点M,∠COB=∠APB.(1)求证:PB是⊙O的切线;(2)当OB=3,PA=6时,求MB,MC的长.30.(盘锦)如图1,AB为⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为P,过点B的直线与线段AD的延长线交于点F,且∠F=∠ABC.(1)若CD=2,BP=4,求⊙O的半径;(2)求证:直线BF是⊙O的切线;(3)当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?请在图2中补全图象并证明你的结论.31.(内江)如图,将▱ABCD的边AB延长至点E,使AB=BE,连接DE,EC,DE交BC 于点O.(1)求证:△ABD≌△BEC;(2)连接BD,若∠BOD=2∠A,求证:四边形BECD是矩形.32.(南通)如图,在▱ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.(1)求证:△AED≌△CFB;(2)若∠A=30°,∠DEB=45°,求证:DA=DF.33.(南平)如图,AB是半圆O的直径,C是AB延长线上的一点,CD与半圆O相切于点D,连接AD,BD.(1)求证:∠BAD=∠BDC;(2)若∠BDC=28°,BD=2,求⊙O的半径.(精确到0.01)34.(南京)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.(1)求证:∠A=∠AEB;(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.35.(南充)如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB;(2)AF=2CD.36.(南昌)(1)如图1,纸片▱ABCD中,AD=5,S▱ABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE′的位置,拼成四边形AEE′D,则四边形AEE′D 的形状为A.平行四边形B.菱形C.矩形D.正方形(2)如图2,在(1)中的四边形纸片AEE′D中,在EE′上取一点F,使EF=4,剪下△AEF,将它平移至△DE′F′的位置,拼成四边形AFF′D.①求证:四边形AFF′D是菱形.②求四边形AFF′D的两条对角线的长.37.(梅州)如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连接BD,与AC交于点E,连接AD,CD.(1)求证:△ABC≌△ADC;(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.38.(龙岩)如图,E,F分别是矩形ABCD的边AD,AB上的点,若EF=EC,且EF⊥EC.(1)求证:AE=DC;(2)已知DC=,求BE的长.39.(柳州)如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.(1)求证:AB=AC;(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.40.(辽阳)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.(1)求证:直线FG是⊙O的切线;(2)若AC=10,cosA=,求CG的长.41.(连云港)如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F 处,DF交AB于点E.(1)求证;∠EDB=∠EBD;(2)判断AF与DB是否平行,并说明理由.42.(莱芜)如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD 交于点F.(1)判断四边形ACGD的形状,并说明理由.(2)求证:BE=CD,BE⊥CD.43.(酒泉)如图,平行四边形ABCD中,AB=3cm,BC=5cm,∠B=60°,G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF.(1)求证:四边形CEDF是平行四边形;(2)①当AE=cm时,四边形CEDF是矩形;②当AE=cm时,四边形CEDF是菱形.(直接写出答案,不需要说明理由)44.(荆门)已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O 于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.(1)求证:BD是⊙O的切线;(2)求证:CE2=EH•EA;(3)若⊙O的半径为5,sinA=,求BH的长.45.(吉林)如图①,半径为R,圆心角为n°的扇形面积是S扇形=,由弧长l=,得S扇形==••R=lR.通过观察,我们发现S扇形=lR类似于S三角形=×底×高.类比扇形,我们探索扇环(如图②,两个同心圆围成的圆环被扇形截得的一部分交作扇环)的面积公式及其应用.(1)设扇环的面积为S扇环,的长为l1,的长为l2,线段AD的长为h(即两个同心圆半径R与r的差).类比S梯形=×(上底+下底)×高,用含l1,l2,h的代数式表示S扇环,并证明;(2)用一段长为40m的篱笆围成一个如图②所示的扇环形花园,线段AD的长h为多少时,花园的面积最大,最大面积是多少?46.(黄石)在△AOB中,C,D分别是OA,OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.(1)如图1,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点,证明:①AC′=BD′;②AC′⊥BD′;(2)如图2,若△AOB为任意三角形且∠AOB=θ,CD∥AB,AC′与BD′交于点E,猜想∠AEB=θ是否成立?请说明理由.47.(黄冈)已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点M,交BC于点N,连接AN,过点C的切线交AB的延长线于点P.(1)求证:∠BCP=∠BAN(2)求证:=.48.(湖北)如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.(1)求证:BE=CF;(2)当四边形ACDE为菱形时,求BD的长.49.(葫芦岛)如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G、F两点.(1)求证:AB与⊙O相切;(2)若等边三角形ABC的边长是4,求线段BF的长?50.(呼伦贝尔)如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线.(1)求证:△ADE≌△CBF;(2)若∠ADB是直角,则四边形BEDF是什么四边形?证明你的结论.51.(呼伦贝尔)如图,已知直线l与⊙O相离.OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.(1)求证:AB=AC;(2)若PC=2,求⊙O的半径.52.(贺州)如图,AB是⊙O的直径,C为⊙O上一点,AC平分∠BAD,AD⊥DC,垂足为D,OE⊥AC,垂足为E.(1)求证:DC是⊙O的切线;(2)若OE=cm,AC=2cm,求DC的长(结果保留根号).53.(贺州)如图,将矩形ABCD沿对角线BD对折,点C落在E处,BE与AD相交于点F.若DE=4,BD=8.(1)求证:AF=EF;(2)求证:BF平分∠ABD.54.(河南)如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.(1)求证:△CDP≌△POB;(2)填空:①若AB=4,则四边形AOPD的最大面积为;②连接OD,当∠PBA的度数为时,四边形BPDO是菱形.55.(桂林)如图,在▱ABCD中,E、F分别是AB、CD的中点.(1)求证:四边形EBFD为平行四边形;(2)对角线AC分别与DE、BF交于点M、N,求证:△ABN≌△CDM.56.(贵港)如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E 是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.(1)若AB=4,求的长;(结果保留π)(2)求证:四边形ABMC是菱形.57.(甘南州)如图1,在△ABC和△EDC中,AC=CE=CB=CD;∠ACB=∠DCE=90°,AB与CE交于F,ED与AB,BC,分别交于M,H.(1)求证:CF=CH;(2)如图2,△ABC不动,将△EDC绕点C旋转到∠BCE=45°时,试判断四边形ACDM 是什么四边形?并证明你的结论.58.(东莞)如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG.(1)求证:△ABG≌△AFG;(2)求BG的长.59.(大庆)如图,四边形ABCD内接于⊙O,AD∥BC,P为BD上一点,∠APB=∠BAD.(1)证明:AB=CD;(2)证明:DP•BD=AD•BC;(2)证明:BD2=AB2+AD•BC.60.(赤峰)如图,AB为⊙O的直径,PD切⊙O于点C,与BA的延长线交于点D,DE⊥PO 交PO延长线于点E,连接PB,∠EDB=∠EPB.(1)求证:PB是的切线.(2)若PB=6,DB=8,求⊙O的半径.中考数学经典几何证明题60例参考答案与试题解析一、解答题(共60小题)1.(遵义)在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.(1)求证:△AEF≌△DEB;(2)证明四边形ADCF是菱形;(3)若AC=4,AB=5,求菱形ADCF的面积.考点:菱形的判定与性质;全等三角形的判定与性质;直角三角形斜边上的中线;三角形中位线定理.专题:证明题.分析:(1)根据AAS证△AFE≌△DBE;(2)利用①中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论;(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.解答:(1)证明:①∵AF∥BC,∴∠AFE=∠DBE,∵E是AD的中点,AD是BC边上的中线,∴AE=DE,BD=CD,在△AFE和△DBE中,,∴△AFE≌△DBE(AAS);(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.∵DB=DC,∴AF=CD.∵AF∥BC,∴四边形ADCF是平行四边形,∵,∠BAC=90°,D是BC的中点,E是AD的中点,∴AD=DC=BC,∴四边形ADCF是菱形;(3)解:设菱形DC边上的高为h,∴RT△ABC斜边BC边上的高也为h,∵BC==,∴DC=BC=,∴h==,菱形ADCF的面积为:DC•h=×=10.点评:本题考查了全等三角形的性质和判定,平行四边形的判定,菱形的判定的应用,菱形的面积计算,主要考查学生的推理能力.2.(珠海)已知△ABC,AB=AC,将△ABC沿BC方向平移得到△DEF.(1)如图1,连接BD,AF,则BD=AF(填“>”、“<”或“=”);(2)如图2,M为AB边上一点,过M作BC的平行线MN分别交边AC,DE,DF于点G,H,N,连接BH,GF,求证:BH=GF.考点:全等三角形的判定与性质;等腰三角形的性质;平移的性质.专题:证明题.分析:(1)根据等腰三角形的性质,可得∠ABC与∠ACB的关系,根据平移的性质,可得AC与DF的关系,根据全等三角形的判定与性质,可得答案;(2)根据相似三角形的判定与性质,可得GM与HN的关系,BM与FN的关系,根据全等三角形的判定与性质,可得答案.解答:(1)解:由AB=AC,得∠ABC=ACB.由△ABC沿BC方向平移得到△DEF,得DF=AC,∠DFE=∠ACB.在△ABF和△DFB中,,△ABF≌△DFB(SAS),BD=AF,故答案为:BD=AF;(2)证明:如图:MN∥BF,△AMG∽△ABC,△DHN∽△DEF,=,=,∴MG=HN,MB=NF.在△BMH和△FNG中,,△BMH≌△FNG(SAS),∴BH=FG.点评:本题考查了全等三角形的判定与性质,利用了平移的性质,相似三角形的判定与性质,全等三角形的判定与性质.3.(镇江)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.(1)求证:△BAE≌△BCF;(2)若∠ABC=50°,则当∠EBA=20°时,四边形BFDE是正方形.考点:菱形的性质;全等三角形的判定与性质;正方形的判定.专题:证明题.分析:(1)由题意易证∠BAE=∠BCF,又因为BA=BC,AE=CF,于是可证△BAE≌△BCF;(2)由已知可得四边形BFDE对角线互相垂直平分,只要∠EBF=90°即得四边形BFDE 是正方形,由△BAE≌△BCF可知∠EBA=∠FBC,又由∠ABC=50°,可得∠EBA+∠FBC=40°,于是∠EBA=×40°=20°.解答:(1)证明:∵菱形ABCD的对角线AC,BD相交于点O,∴AB=BC,∠BAC=∠BCA,∴∠BAE=∠BCF,在△BAE与△BCF中,∴△BAE≌△BCF(SAS);(2)∵四边形BFDE对角线互相垂直平分,∴只要∠EBF=90°即得四边形BFDE是正方形,∵△BAE≌△BCF,∴∠EBA=∠FBC,又∵∠ABC=50°,∴∠EBA+∠FBC=40°,∴∠EBA=×40°=20°.故答案为:20.点评:本题考查了菱形的性质,全等三角形的判定与性质以及正方形的判定.本题关键是根据SAS证明△BAE≌△BCF.4.(漳州)如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作分、FG∥CD,交AE于点G连接DG.(1)求证:四边形DEFG为菱形;(2)若CD=8,CF=4,求的值.考点:翻折变换(折叠问题);勾股定理;菱形的判定与性质;矩形的性质.专题:证明题.分析:(1)根据折叠的性质,易知DG=FG,ED=EF,∠1=∠2,由FG∥CD,可得∠1=∠3,易证FG=FE,故由四边相等证明四边形DEFG为菱形;(2)在Rt△EFC中,用勾股定理列方程即可CD、CE,从而求出的值.解答:(1)证明:由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,∵FG∥CD,∴∠2=∠3,∴FG=FE,∴DG=GF=EF=DE,∴四边形DEFG为菱形;(2)解:设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,在Rt△EFC中,FC2+EC2=EF2,即42+(8﹣x)2=x2,解得:x=5,CE=8﹣x=3,∴=.点评:本题主要考查了折叠的性质、菱形的判定以及勾股定理,熟知折叠的性质和菱形的判定方法是解答此题的关键.5.(玉林)如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O 的切线CD交AB的延长线于点C,E为的中点,连接DE,EB.(1)求证:四边形BCDE是平行四边形;(2)已知图中阴影部分面积为6π,求⊙O的半径r.考点:切线的性质;平行四边形的判定;扇形面积的计算.专题:证明题.分析:(1)由∠BOD=60°E为的中点,得到,于是得到DE∥BC,根据CD 是⊙O的切线,得到OD⊥CD,于是得到BE∥CD,即可证得四边形BCDE是平行四边形;(2)连接OE,由(1)知,,得到∠BOE=120°,根据扇形的面积公式列方程即可得到结论.解答:解:(1)∵∠BOD=60°,∴∠AOD=120°,∴=,∵E为的中点,∴,∴DE∥AB,OD⊥BE,即DE∥BC,∵CD是⊙O的切线,∴OD⊥CD,∴BE∥CD,∴四边形BCDE是平行四边形;(2)连接OE,由(1)知,,∴∠BOE=120°,∵阴影部分面积为6π,∴=6π,∴r=6.点评:本题考查了切线的性质,平行四边形的判定,扇形的面积公式,垂径定理,证明是解题的关键.6.(永州)如图,在四边形ABCD中,∠A=∠BCD=90°,BC=DC.延长AD到E点,使DE=AB.(1)求证:∠ABC=∠EDC;(2)求证:△ABC≌△EDC.考点:全等三角形的判定与性质.专题:证明题.分析:(1)根据四边形的内角和等于360°求出∠B+∠ADC=180°,再根据邻补角的和等于180°可得∠CDE+∠ADE=180°,从而求出∠B=∠CDE;(2)根据“边角边”证明即可.解答:(1)证明:在四边形ABCD中,∵∠BAD=∠BCD=90°,∴90°+∠B+90°+∠ADC=360°,∴∠B+∠ADC=180°,又∵∠CDE+∠ADC=180°,∴∠ABC=∠CDE,(2)连接AC,由(1)证得∠ABC=∠CDE,在△ABC和△EDC中,,∴△ABC≌△EDC(SAS).点评:本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,根据四边形的内角和定理以及邻补角的定义,利用同角的补角相等求出夹角相等是证明三角形全等的关键,也是本题的难点.7.(营口)如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.(1)求证:PC是⊙O的切线;(2)若PD=,AC=8,求图中阴影部分的面积;(3)在(2)的条件下,若点E是的中点,连接CE,求CE的长.考点:切线的判定;扇形面积的计算.专题:证明题.分析:(1)连接OC,证明△PAO≌△PCO,得到∠PCO=∠PAO=90°,证明结论;(2)证明△ADP∽△PDA,得到成比例线段求出BC的长,根据S阴=S⊙O﹣S△ABC 求出答案;(3)连接AE、BE,作BM⊥CE于M,分别求出CM和EM的长,求和得到答案.解答:(1)证明:如图1,连接OC,∵PA切⊙O于点A,∴∠PAO=90°,∵BC∥OP,∴∠AOP=∠OBC,∠COP=∠OCB,∵OC=OB,∴∠OBC=∠OCB,∴∠AOP=∠COP,在△PAO和△PCO中,,∴△PAO≌△PCO,∴∠PCO=∠PAO=90°,∴PC是⊙O的切线;(2)解:由(1)得PA,PC都为圆的切线,∴PA=PC,OP平分∠APC,∠ADO=∠PAO=90°,∴∠PAD+∠DAO=∠DAO+∠AOD,∴∠PAD=∠AOD,∴△ADP∽△ODA,∴,∴AD2=PD•DO,∵AC=8,PD=,∴AD=AC=4,OD=3,AO=5,由题意知OD为△的中位线,∴BC=6,OD=6,AB=10.∴S阴=S⊙O﹣S△ABC=﹣24;(3)解:如图2,连接AE、BE,作BM⊥CE于M,∴∠CMB=∠EMB=∠AEB=90°,∵点E是的中点,∴∠ECB=∠CBM=∠ABE=45°,CM=MB=3,BE=AB•cos45°=5,∴EM==4,则CE=CM+EM=7.点评:本题考查的是切线的判定和性质、扇形面积的计算和相似三角形的判定和性质,灵活运用切线的性质:圆的切线垂直于过切点的半径和切线的判定是解题的关键.8.(徐州)如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.(1)求证:四边形BFCE是平行四边形;(2)若AD=10,DC=3,∠EBD=60°,则BE=4时,四边形BFCE是菱形.考点:平行四边形的判定;菱形的判定.专题:证明题.分析:(1)由AE=DF,∠A=∠D,AB=DC,易证得△AEC≌△DFB,即可得BF=EC,∠ACE=∠DBF,且EC∥BF,即可判定四边形BFCE是平行四边形;(2)当四边形BFCE是菱形时,BE=CE,根据菱形的性质即可得到结果.解答:(1)证明:∵AB=DC,∴AC=DF,在△AEC和△DFB中,∴△AEC≌△DFB(SAS),∴BF=EC,∠ACE=∠DBF∴EC∥BF,∴四边形BFCE是平行四边形;(2)当四边形BFCE是菱形时,BE=CE,∵AD=10,DC=3,AB=CD=3,∴BC=10﹣3﹣3=4,∵∠EBD=60°,∴BE=BC=4,∴当BE=4 时,四边形BFCE是菱形,故答案为:4.点评:此题考查了相似三角形的判定与性质、全等三角形的判定与性质、平行四边形的判定与性质、菱形的判定与性质以及勾股定理等知识.此题综合性较强,难度适中,注意数形结合思想的应用,注意掌握辅助线的作法.9.(宿迁)如图,四边形ABCD中,∠A=∠ABC=90°,AD=1,BC=3,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.(1)求证:四边形BDFC是平行四边形;(2)若△BCD是等腰三角形,求四边形BDFC的面积.考点:平行四边形的判定与性质;等腰三角形的性质.专题:证明题.分析:(1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;(2)分①BC=BD时,利用勾股定理列式求出AB,然后利用平行四边形的面积公式列式计算即可得解;②BC=CD时,过点C作CG⊥AF于G,判断出四边形AGCB 是矩形,再根据矩形的对边相等可得AG=BC=3,然后求出DG=2,利用勾股定理列式求出CG,然后利用平行四边形的面积列式计算即可得解;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾.解答:(1)证明:∵∠A=∠ABC=90°,∴BC∥AD,∴∠CBE=∠DFE,在△BEC与△FED中,,∴△BEC≌△FED,∴BE=FE,又∵E是边CD的中点,∴CE=DE,∴四边形BDFC是平行四边形;(2)①BC=BD=3时,由勾股定理得,AB===2,所以,四边形BDFC的面积=3×2=6;②BC=CD=3时,过点C作CG⊥AF于G,则四边形AGCB是矩形,所以,AG=BC=3,所以,DG=AG﹣AD=3﹣1=2,由勾股定理得,CG===,所以,四边形BDFC的面积=3×=3;③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾,此时不成立;综上所述,四边形BDFC的面积是6或3.点评:本题考查了平行四边形的判定与性质,等腰三角形的性质,全等三角形的判定与性质,(1)确定出全等三角形是解题的关键,(2)难点在于分情况讨论.10.(湘西州)如图,在▱ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.(1)求证:△ADE≌△CBF;(2)求证:四边形BFDE为矩形.考点:矩形的判定;全等三角形的判定与性质;平行四边形的性质.专题:证明题.分析:(1)由DE与AB垂直,BF与CD垂直,得到一对直角相等,再由ABCD为平行四边形得到AD=BC,对角相等,利用AAS即可的值;(2)由平行四边形的对边平行得到DC与AB平行,得到∠CDE为直角,利用三个角为直角的四边形为矩形即可的值.解答:证明:(1)∵DE⊥AB,BF⊥CD,∴∠AED=∠CFB=90°,∵四边形ABCD为平行四边形,∴AD=BC,∠A=∠C,在△ADE和△CBF中,,∴△ADE≌△CBF(AAS);(2)∵四边形ABCD为平行四边形,∴CD∥AB,∴∠CDE+∠DEB=180°,∵∠DEB=90°,∴∠CDE=90°,∴∠CDE=∠DEB=∠BFD=90°,则四边形BFDE为矩形.点评:此题考查了矩形的判定,全等三角形的判定与性质,以及平行四边形的性质,熟练掌握矩形的判定方法是解本题的关键.11.(咸宁)已知关于x的一元二次方程mx2﹣(m+2)x+2=0.(1)证明:不论m为何值时,方程总有实数根;(2)m为何整数时,方程有两个不相等的正整数根.考点:根的判别式;解一元二次方程-公式法.专题:证明题.分析:(1)求出方程根的判别式,利用配方法进行变形,根据平方的非负性证明即可;(2)利用一元二次方程求根公式求出方程的两个根,根据题意求出m的值.解答:(1)证明:△=(m+2)2﹣8m=m2﹣4m+4=(m﹣2)2,∵不论m为何值时,(m﹣2)2≥0,∴△≥0,∴方程总有实数根;(2)解:解方程得,x=,x1=,x2=1,∵方程有两个不相等的正整数根,∴m=1或2,m=2不合题意,∴m=1.点评:本题考查的是一元二次方程根的判别式和求根公式的应用,掌握一元二次方程根的情况与判别式△的关系:△>0⇔方程有两个不相等的实数根;△=0⇔方程有两个相等的实数根;△<0⇔方程没有实数根是解题的关键.12.(咸宁)如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.(1)若∠B=30°,求证:以A、O、D、E为顶点的四边形是菱形.(2)若AC=6,AB=10,连结AD,求⊙O的半径和AD的长.考点:切线的性质;菱形的判定与性质;相似三角形的判定与性质.专题:证明题.分析:(1)连接OD、OE、ED.先证明△AOE是等边三角形,得到AE=AO=0D,则四边形AODE是平行四边形,然后由OA=OD证明四边形AODE是菱形;(2)连接OD、DF.先由△OBD∽△ABC,求出⊙O的半径,然后证明△ADC∽△AFD,得出AD2=AC•AF,进而求出AD.解答:(1)证明:如图1,连接OD、OE、ED.∵BC与⊙O相切于一点D,∴OD⊥BC,∴∠ODB=90°=∠C,∴OD∥AC,∵∠B=30°,∴∠A=60°,∵OA=OE,∴△AOE是等边三角形,∴AE=AO=0D,∴四边形AODE是平行四边形,∵OA=OD,∴四边形AODE是菱形.(2)解:设⊙O的半径为r.∵OD∥AC,∴△OBD∽△ABC.∴,即10r=6(10﹣r).解得r=,∴⊙O的半径为.如图2,连接OD、DF.∵OD∥AC,∴∠DAC=∠ADO,∵OA=OD,∴∠ADO=∠DAO,∴∠DAC=∠DAO,∵AF是⊙O的直径,∴∠ADF=90°=∠C,∴△ADC∽△AFD,∴,∴AD2=AC•AF,∵AC=6,AF=,∴AD2=×6=45,∴AD==3.点评:本题考查了切线的性质、圆周角定理、等边三角形的判定与性质、菱形的判定和性质以及相似三角形的判定和性质,是一个综合题,难度中等.熟练掌握相关图形的性质及判定是解本题的关键.13.(梧州)如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.(1)求证:HF=AP;(2)若正方形ABCD的边长为12,AP=4,求线段EQ的长.考点:正方形的性质;全等三角形的判定与性质;勾股定理.专题:证明题.分析:(1)先根据EQ⊥BO,EH⊥AB得出∠EQN=∠BHM=90°.根据∠EMQ=∠BMH得出△EMQ∽△BMH,故∠QEM=∠HBM.由ASA定理得出△APB≌△HFE,故可得出结论;(2)由勾股定理求出BP的长,根据EF是BP的垂直平分线可知BQ=BP,再根据锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故EF=BP=4,再根据EQ=EF﹣QF即可得出结论.解答:(1)证明:∵EQ⊥BO,EH⊥AB,∴∠EQN=∠BHM=90°.∵∠EMQ=∠BMH,∴△EMQ∽△BMH,∴∠QEM=∠HBM.在Rt△APB与Rt△HFE中,,∴△APB≌△HFE,∴HF=AP;(2)解:由勾股定理得,BP===4.∵EF是BP的垂直平分线,∴BQ=BP=2,∴QF=BQ•tan∠FBQ=BQ•tan∠ABP=2×=.由(1)知,△APB≌△HFE,∴EF=BP=4,∴EQ=EF﹣QF=4﹣=.点评:本题考查的是正方形的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.14.(威海)如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E.(1)求证:BE=CE;(2)若BD=2,BE=3,求AC的长.考点:相似三角形的判定与性质;等腰三角形的性质;圆周角定理.专题:证明题.分析:(1)连结AE,如图,根据圆周角定理,由AC为⊙O的直径得到∠AEC=90°,然后利用等腰三角形的性质即可得到BE=CE;(2)连结DE,如图,证明△BED∽△BAC,然后利用相似比可计算出AB的长,从而得到AC的长.解答:(1)证明:连结AE,如图,∵AC为⊙O的直径,∴∠AEC=90°,∴AE⊥BC,而AB=AC,∴BE=CE;(2)连结DE,如图,∵BE=CE=3,∴BC=6,∵∠BED=∠BAC,而∠DBE=∠CBA,∴△BED∽△BAC,∴=,即=,∴BA=9,∴AC=BA=9.点评:本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了角平分线的性质和圆周角定理.15.(铜仁市)已知,如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD.求证:AD=CE.考点:全等三角形的判定与性质;等边三角形的判定与性质.专题:证明题.分析:作DG∥BC交AC于G,先证明△DFG≌△EFC,得出GD=CE,再证明△ADG是等边三角形,得出AD=GD,即可得出结论.解答:证明:作DG∥BC交AC于G,如图所示:则∠DGF=∠ECF,在△DFG和△EFC中,,∴△DFG≌△EFC(AAS),∴GD=CE,。
(专题精选)初中数学几何图形初步经典测试题含答案解析一、选择题∠=∠的图形的个数是()1.如图,一副三角尺按不同的位置摆放,摆放位置中αβA.1B.2C.3D.4【答案】C【解析】【分析】根据直角三角板可得第一个图形∠β=45°,进而可得∠α=45°;根据余角和补角的性质可得第二个图形、第四个图形中∠α=∠β,第三个图形∠α和∠β互补.【详解】根据角的和差关系可得第一个图形∠α=∠β=45°,根据等角的补角相等可得第二个图形∠α=∠β,第三个图形∠α+∠β=180°,不相等,根据同角的余角相等可得第四个图形∠α=∠β,因此∠α=∠β的图形个数共有3个,故选:C.【点睛】此题主要考查了余角和补角,关键是掌握余角和补角的性质:等角的补角相等.等角的余角相等.2.∠1与∠2互余,∠1与∠3互补,若∠3=125°,则∠2=()A.35°B.45°C.55°D.65°【答案】A【解析】【分析】【详解】解:根据题意得:∠1+∠3=180°,∠3=125°,则∠1=55°,∵∠1+∠2=90°,则∠2=35°故选:A.【点睛】本题考查余角、补角的计算.3.一副直角三角板如图放置,其中∠C=∠DFE=90°,∠A=45°,∠E=60°,点F在CB的延长线上.若DE∥CF,则∠BDF等于()A .30°B .25°C .18°D .15° 【答案】D【解析】【分析】根据三角形内角和定理可得45ABC ∠=︒和30EDF ∠=︒,再根据平行线的性质可得45EDB ABC ==︒∠∠,再根据BDF EDB EDF =-∠∠∠,即可求出BDF ∠的度数.【详解】∵∠C =90°,∠A =45°∴18045ABC A C =︒--=︒∠∠∠∵//DE CF∴45EDB ABC ==︒∠∠∵∠DFE =90°,∠E =60°∴18030EDF E DFE =︒--=︒∠∠∠∴15BDF EDB EDF =-=︒∠∠∠故答案为:D .【点睛】本题考查了三角板的角度问题,掌握三角形内角和定理、平行线的性质是解题的关键.4.如图,直线a ∥b ,点B 在直线b 上,且AB ⊥BC ,∠1=55°,那么∠2的度数是( )A .20°B .30°C .35°D .50°【答案】C【解析】【分析】由垂线的性质可得∠ABC=90°,所以∠3=180°﹣90°﹣∠1=35°,再由平行线的性质可得到∠2的度数.【详解】解:由垂线的性质可得∠ABC=90°,所以∠3=180°﹣90°﹣∠1=35°,又∵a∥b,所以∠2=∠3=35°.故选C.【点睛】本题主要考查了平行线的性质.5.下列立体图形中,侧面展开图是扇形的是()A.B.C.D.【答案】B【解析】根据圆锥的特征可知,侧面展开图是扇形的是圆锥.故选B.6.如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是A.(0,0)B.(0,1)C.(0,2)D.(0,3)【答案】D【解析】【详解】解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,此时△ABC的周长最小,∵点A、B的坐标分别为(1,4)和(3,0),∴B′点坐标为:(-3,0),则OB′=3过点A作AE垂直x轴,则AE=4,OE=1则B′E=4,即B′E=AE,∴∠EB′A=∠B′AE,∵C′O∥AE,∴∠B′C′O=∠B′AE,∴∠B′C′O=∠EB′A∴B′O=C′O=3,∴点C′的坐标是(0,3),此时△ABC的周长最小.故选D.7.如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?()A.B.C.D.【答案】D【解析】分析:三棱柱的侧面展开图是长方形,底面是三角形,据此进行判断即可.详解:A选项中,展开图下方的直角三角形的斜边长为12,不合题意;B选项中,展开图上下两个直角三角形中的直角边不能与其它棱完全重合,不合题意;C选项中,展开图下方的直角三角形中的直角边不能与其它棱完全重合,不合题意;D选项中,展开图能折叠成一个三棱柱,符合题意;故选:D.点睛:本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.8.下列图形中,是正方体表面展开图的是()A.B.C.D.【答案】C【解析】【分析】利用正方体及其表面展开图的特点解题.【详解】解:A、B、D经过折叠后,下边没有面,所以不可以围成正方体,C能折成正方体.故选C.【点睛】本题考查了正方体的展开图,解题时牢记正方体无盖展开图的各种情形.9.如图是由四个正方体组合而成,当从正面看时,则得到的平面视图是()A.B.C.D.【答案】D【解析】【分析】根据从正面看到的图叫做主视图,从左面看到的图叫做左视图,从上面看到的图叫做俯视图.根据图中正方体摆放的位置判定则可.【详解】解:从正面看,下面一行是横放3个正方体,上面一行最左边是一个正方体.故选:D.【点睛】本题主要考查三视图的识别,解决本题的关键是要熟练掌握三视图的识别方法.10.下列各图经过折叠后不能围成一个正方体的是()A.B.C.D.【答案】D【解析】【分析】由平面图形的折叠及正方体的表面展开图的特点解题.只要有“田”“凹”“一线超过四个正方形”字格的展开图都不是正方体的表面展开图.【详解】解:A、是正方体的展开图,不符合题意;B、是正方体的展开图,不符合题意;C、是正方体的展开图,不符合题意;D、不是正方体的展开图,缺少一个底面,符合题意.故选:D.【点睛】本题考查了正方体的展开图,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.11.如图,DE∥BC,BE平分∠ABC,若∠1=70°,则∠CBE的度数为()A.20°B.35°C.55°D.70°【答案】B【解析】【分析】根据平行线的性质可得∠1=∠ABC=70°,再根据角平分线的定义可得答案.【详解】∵DE∥BC,∴∠1=∠ABC=70°,∵BE平分∠ABC,∴1352CBE ABC∠=∠=︒,故选:B.【点睛】此题主要考查了平行线的性质,以及角平分线的定义,解题的关键是掌握两直线平行,内错角相等.12.木杆AB斜靠在墙壁上,当木杆的上端A沿墙壁NO竖直下滑时,木杆的底端B也随之沿着射线OM方向滑动.下列图中用虚线画出木杆中点P随之下落的路线,其中正确的是()A.B.C.D.【答案】D【解析】解:如右图,连接OP,由于OP是Rt△AOB斜边上的中线,所以OP=12AB,不管木杆如何滑动,它的长度不变,也就是OP是一个定值,点P就在以O 为圆心的圆弧上,那么中点P 下落的路线是一段弧线.故选D .13.如图,点C 是射线OA 上一点,过C 作CD ⊥OB ,垂足为D ,作CE ⊥OA ,垂足为C ,交OB 于点E ,给出下列结论:①∠1是∠DCE 的余角;②∠AOB =∠DCE ;③图中互余的角共有3对;④∠ACD =∠BEC ,其中正确结论有( )A .①②③B .①②④C .①③④D .②③④【答案】B【解析】【分析】 根据垂直定义可得BCA 90∠=o ,ADC BDC ACF 90∠∠∠===o ,然后再根据余角定义和补角定义进行分析即可.【详解】解:CE OA ⊥Q ,OCE 90o ∠∴=,ECD 190∠∠∴+=o ,1∠∴是ECD ∠的余角,故①正确;CD OB ⊥Q ,AOB COCE 90∠∠∴==o ,AOB OEC 90∠∠∴+=o ,DCE OEC 90∠∠+=o ,B BAC 90∠∠∴+=o ,1ACD 90∠∠+=o ,AOB DCE ∠∠∴=,故②正确;1AOB 1DCE DCE CED AOB CED 90∠∠∠∠∠∠∠∠+=+=+=+=o Q , ∴图中互余的角共有4对,故③错误;ACD 90DCE ∠∠=+o Q ,BEC 90AOB ∠∠=+o ,AOB DCE ∠∠=Q ,ACD BEC ∠∠∴=,故④正确.正确的是①②④;故选B .【点睛】考查了余角和补角,关键是掌握两角之和为90o 时,这两个角互余,两角之和为180o 时,这两个角互补.14.如图是正方体的表面展开图,请问展开前与“我”字相对的面上的字是( )A .是B .好C .朋D .友【答案】A【解析】【分析】 正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.【详解】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,“我”与“是”是相对面,“们”与“朋”是相对面,“好”与“友”是相对面.故选:A .【点睛】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.15.如图,将一副三角板如图放置,∠COD=28°,则∠AOB 的度数为( )A .152°B .148°C .136°D .144°【答案】A【解析】【分析】 根据三角板的性质得90AOD BOC ∠=∠=︒,再根据同角的余角相等可得62AOC BOD ==︒∠∠,即可求出∠AOB 的度数.【详解】∵这是一副三角板∴90AOD BOC ∠=∠=︒∵28COD =︒∠∴62AOC BOD ==︒∠∠∴62+28+62=152AOB AOC COD BOD =++=︒︒︒︒∠∠∠∠故答案为:A .【点睛】本题考查了三角板的度数问题,掌握三角板的性质、同角的余角相等是解题的关键.16.如图,在ABC V 中,90C ∠=︒,30B ∠=︒,如图:(1)以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ;(2)分别以M 、N 为圆心,大于MN 的长为半径画弧,两弧交于点P ;(3)连结AP 并延长交BC 于点D .根据以上作图过程,下列结论中错误的是( )A .AD 是BAC ∠的平分线B .60ADC ∠=︒ C .点D 在AB 的中垂线上D .:1:3DAC ABD S S =△△【答案】D【解析】【分析】 根据作图的过程可以判定AD 是∠BAC 的角平分线;利用角平分线的定义可以推知∠CAD=30°,则由直角三角形的性质来求∠ADC 的度数;利用等角对等边可以证得△ADB 的等腰三角形,由等腰三角形的“三线合一”的性质可以证明点D 在AB 的中垂线上;利用30度角所对的直角边是斜边的一半、三角形的面积计算公式来求两个三角形的面积之比.【详解】解:A 、根据作图方法可得AD 是∠BAC 的平分线,正确;B 、∵∠C=90°,∠B=30°,∴∠CAB=60°,∵AD 是∠BAC 的平分线,∴∠DAC=∠DAB=30°,∴∠ADC=60°,正确;C 、∵∠B=30°,∠DAB=30°,∴AD=DB ,∴点D 在AB 的中垂线上,正确;D 、∵∠CAD=30°,∴CD=12AD , ∵AD=DB ,∴CD=12DB ,∴CD=13 CB,S△ACD=12CD•AC,S△ACB=12CB•AC,∴S△ACD:S△ACB=1:3,∴S△DAC:S△ABD≠1:3,错误,故选:D.【点睛】本题考查了角平分线的性质、线段垂直平分线的性质以及作图—基本作图.解题时,需要熟悉等腰三角形的判定与性质.17.一个角的补角比这个角的余角3倍还多10°,则这个角的度数为()A.140° B.130° C.50° D.40°【答案】C【解析】【分析】根据互为余角的两个角的和等于90°,互为补角的两个角的和等于180°,列出方程,然后解方程即可.【详解】设这个角为α,则它的余角为90°-α,补角为180°-α,根据题意得,180°-α=3(90°-α)+10°,180°-α=270°-3α+10°,解得α=50°.故选C.【点睛】本题考查了互为余角与补角的性质,表示出这个角的余角与补角然后列出方程是解题的关键.18.若∠AOB =60°,∠AOC =40°,则∠BOC等于()A.100°B.20°C.20°或100°D.40°【答案】C【解析】【分析】画出符合题意的两个图形,根据图形即可得出答案.解: 如图1,当∠AOC在∠AOB的外部时,∵∠AOB=60°,∠AOC=40°∴∠BOC=∠AOB+∠AOC=60°+40°=100°如图2,当∠AOC在∠AOB的内部时,∵∠AOB=60°,∠AOC=40°∴∠BOC=∠AOB-∠AOC=60°-40°=20°即∠BOC的度数是100°或20°故选:C【点睛】本题考查了角的有关计算的应用,主要考查学生根据图形进行计算的能力,分类讨论思想和数形结合思想的运用.19.如图,已知点P(0,3) ,等腰直角△ABC中,∠BAC=90°,AB=AC,BC=2,BC边在x轴上滑动时,PA+PB的最小值是()A102B26C.5 D.6【解析】【分析】过点P 作PD ∥x 轴,做点A 关于直线PD 的对称点A´,延长A´ A 交x 轴于点E ,则当A´、P 、B 三点共线时,PA +PB 的值最小,根据勾股定理求出A B '的长即可.【详解】如图,过点P 作PD ∥x 轴,做点A 关于直线PD 的对称点A´,延长A´A 交x 轴于点E ,则当A´、P 、B 三点共线时,PA +PB 的值最小,∵等腰直角△ABC 中,∠BAC=90°,AB=AC ,BC =2,∴AE=BE=1,∵P (0,3) ,∴A A´=4, ∴A´E=5, ∴22221526A B BE A E ''=+=+=,故选B.【点睛】本题考查了勾股定理,轴对称-最短路线问题的应用,解此题的关键是作出点A 关于直线PD 的对称点,找出PA +PB 的值最小时三角形ABC 的位置.20.某包装盒如下图所示,则在下列四种款式的纸片中,可以是该包装盒的展开图的是( )A .B .C.D.【答案】A【解析】【分析】将展开图折叠还原成包装盒,即可判断正确选项.【详解】解:A、展开图折叠后如下图,与本题中包装盒相同,故本选项正确;B、展开图折叠后如下图,与本题中包装盒不同,故本选项错误;C、展开图折叠后如下图,与本题中包装盒不同,故本选项错误;D、展开图折叠后如下图,与本题中包装盒不同,故本选项错误;故选:A.【点睛】本题主要考查了含图案的正方体的展开图,学生要经历一定的实验操作过程,当然学生也可以将操作活动转化为思维活动,在头脑中模拟(想象)折纸、翻转活动,较好地考查了学生空间观念.。
4e d c 经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.FPDE CBAAPCBACBPDEDCA A CBPD经典难题(一)1.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2. 如下图做△DGC使与△ADP全等,可得△PDG为等边△,从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG=150 所以∠DCP=300 ,从而得出△PBC是正三角形3.如下图连接BC1和AB1分别找其中点F,E.连接C2F与A2E并延长相交于Q点,连接EB2并延长交C2Q于H点,连接FB2并延长交A2Q于G点,由A2E=12A1B1=12B1C1= FB2,EB2=12AB=12BC=F C1 ,又∠GFQ+∠Q=900和∠GE B2+∠Q=900,所以∠GE B2=∠GFQ又∠B2FC2=∠A2EB2,可得△B2FC2≌△A2EB2,所以A2B2=B2C2,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形。
4.如下图连接AC并取其中点Q,连接QN和QM,所以可得∠QMF=∠F,∠QNM=∠DEN和∠QMN=∠QNM,从而得出∠DEN=∠F。
经典难题(二)1.(1)延长AD到F连BF,做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM(2)连接OB,OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证。
3.作OF ⊥CD ,OG ⊥BE ,连接OP ,OA ,OF ,AF ,OG ,AG ,OQ 。
由于22AD AC CD FD FD AB AE BE BG BG,由此可得△ADF ≌△ABG ,从而可得∠AFC=∠AGE 。
又因为PFOA 与QGOA 四点共圆,可得∠AFC=∠AOP 和∠AGE=∠AOQ , ∠AOP=∠AOQ ,从而可得AP=AQ 。
4.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
从而可得PQ=2AI BI=2AB,从而得证。
经典难题(三)1.顺时针旋转△ADE,到△ABG,连接CG.由于∠ABG=∠ADE=900+450=1350从而可得B,G,D在一条直线上,可得△AGB≌△CGB。
推出AE=AG=AC=GC,可得△AGC为等边三角形。
∠AGB=300,既得∠EAC=300,从而可得∠A EC=750。
又∠EFC=∠DFA=450+300=750.可证:CE=CF。
2.连接BD作CH⊥DE,可得四边形CGDH是正方形。
由AC=CE=2GC=2CH,可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150,又∠FAE=900+450+150=1500,从而可知道∠F=150,从而得出AE=AF。
3.作FG⊥CD,FE⊥BE,可以得出GFEC为正方形。
令AB=Y ,BP=X ,CE=Z ,可得PC=Y-X 。
tan∠BAP=tan∠EPF=XY=ZY X Z,可得YZ=XY-X2+XZ,即Z(Y-X)=X(Y-X) ,既得X=Z ,得出△ABP≌△PEF ,得到PA=PF ,得证。
经典难题(四)1.顺时针旋转△ABP 600,连接PQ ,则△PBQ是正三角形。
可得△PQC是直角三角形。
所以∠APB=1500。
2.作过P点平行于AD的直线,并选一点E,使AE∥DC,BE∥PC.可以得出∠ABP=∠ADP=∠AEP,可得:AEBP共圆(一边所对两角相等)。
可得∠BAP=∠BEP=∠BCP,得证。
3.在BD取一点E,使∠BCE=∠ACD,既得△BEC∽△ADC,可得:BE BC =ADAC,即AD•BC=BE•AC,①又∠ACB=∠DCE,可得△ABC∽△DEC,既得AB AC =DEDC,即AB•CD=DE•AC,②由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证。
4.过D 作AQ ⊥AE ,AG ⊥CF ,由ADE S=2ABCDS=DFCS,可得:2AE PQ =2AE PQ,由AE=FC 。
可得DQ=DG ,可得∠DPA =∠DPC (角平分线逆定理)。
经典难题(五)1.(1)顺时针旋转△BPC 600 ,可得△PBE 为等边三角形。
既得PA+PB+PC=AP++PE+EF 要使最小只要AP ,PE ,EF 在一条直线上, 即如下图:可得最小L=;(2)过P点作BC的平行线交AB,AC与点D,F。
由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得:最大L< 2 ;由(1)和(2)既得:≤L<2 。
2.顺时针旋转△BPC 600,可得△PBE为等边三角形。
既得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,即如下图:可得最小PA+PB+PC=AF。
既得AF=213(1)42= 23=4232=2(31)2 = 2(31)2 =622 。
3.顺时针旋转△ABP 900 ,可得如下图:既得正方形边长L = 2222(2)()22a = 522a 。
4.在AB上找一点F,使∠BCF=600,连接EF,DG,既得△BGC为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF ,得到BE=CF ,FG=GE 。
推出:△FGE为等边三角形,可得∠AFE=800,既得:∠DFG=400①又BD=BC=BG ,既得∠BGD=800,既得∠DGF=400②推得:DF=DG ,得到:△DFE≌△DGE ,从而推得:∠FED=∠BED=300。