浙教版7年级下册《因式分解》复习

因式分解专题复习一1.因式分解的概念把一个多项式化成几个整式的积的形式，叫做因式分解，把这一过程叫分解因式。

注意：（1）因式分解是恒等变形；（2）因式分解的结果是积的形式，每个因式都是整式；（3）必须分解到每个多项式的因式不能再分解为止。

2.因式分解与整式乘法的关系如果把整式乘法看做一个变形的过程，那么多项式的因式分解就是整式乘法的逆过程。

注意：分解因式时，变形的对象是多项式，即把一个多项式化成单项式多项式或多项式多项式的形式，所得的结果必须乘积的形式。

整式乘法和分解因式的互逆的恒等变形。

基础训练一、选择题：1．下列等式从左到右的变形是因式分解的是( )A ．6a 2b 2＝3ab·2abB ．21a －21ay ＝21a(1－y)C ．2x 2＋8x －1＝2x(x ＋4)－1D ．(x ＋1)(x －1)＝－1 2.下列因式分解正确的是（ ）A. B.C. ；D.3．若x 2+mx +16是完全平方式，则m 的值等于（ ）A ．－8B ．8C ．4D ．8或－84.下列运算正确的是…（ ）A ．（－2ab ）·（－3ab ）3＝－54a 4b 4B ．5x 2·（3x 3）2＝15x 12C ．（－0.16）·（－10b 2）3＝－b 7D ．（2×10n ）（×10n ）＝102n5.因式分解4＋a 2－4a 正确的是( ) A ． (2－a)2 B ．4(1－a)＋a 2 C ． (a －2)(2－a) D ． (2＋a)2。

6.下列各式中，不能继续分解因式的是（ ）A ．8xy －6x 2=2（4xy －3x 2）B ．3x －xy=x （6－y ）C ．4x 3+8x 2+4x=4x （x 2+2x+1）D ．16x 2－4=4（4x 2－1）7.把多项式提取公因式后，另一个因式是（ ）(A) ；（B）；（C）；（D）－1.8. 是一个完全平方式，则k值为（）（A）（B）（C）±（D）±9.已知a，b，c是三角形的三边，那么代数式a2－2ab+b2－c2的值（）A．大于零B．等于零C．小于零D．不能确定10.如图，在边长为a的正方形上剪去一个边长为b的小正方形（a>b），把剩下的部分剪拼成一个梯形，分别计算这两个图形阴影部分的面积，由此可以验证的等式是（ ）A．a2－b2=（a+b）（a－b）B．（a+b）2=a2+2ab+b2C．（a－b）2=a2－2ab+b2D．a2－ab=a（a－b）二、填空题11．多项式2ax2－12axy中，应提取的公因式是_______．12.（4a2－b2）÷（b－2a）=________．13. 因式分解：x2-2xy________.14. 把多项式提取公因式后，另一个因式是________.15. __ _____.16. 若a－b=2，则（a2+b2）－ab=_________．三、简答题17．分解因式：（1）－8a3b2+12ab3c－6a2b （2）3a（x－y）+9（y－x）（3）（4）18.（1）先化简，再求值：，其中.（2）.已知，求的值。

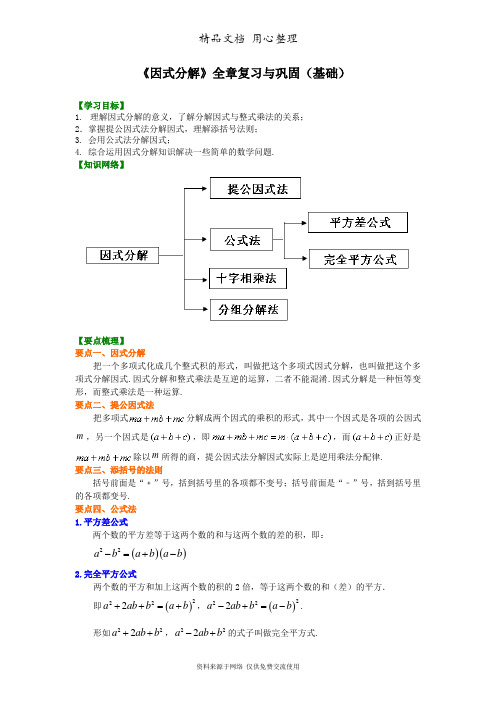
《因式分解》全章复习与巩固（基础）【学习目标】1. 理解因式分解的意义，了解分解因式与整式乘法的关系；2．掌握提公因式法分解因式，理解添括号法则；3. 会用公式法分解因式；4. 综合运用因式分解知识解决一些简单的数学问题.【知识网络】【要点梳理】要点一、因式分解把一个多项式化成几个整式积的形式，叫做把这个多项式因式分解，也叫做把这个多项式分解因式.因式分解和整式乘法是互逆的运算，二者不能混淆.因式分解是一种恒等变形，而整式乘法是一种运算.要点二、提公因式法 把多项式分解成两个因式的乘积的形式，其中一个因式是各项的公因式m，另一个因式是，即，而正好是除以m 所得的商，提公因式法分解因式实际上是逆用乘法分配律.要点三、添括号的法则括号前面是“﹢”号，括到括号里的各项都不变号；括号前面是“﹣”号，括到括号里的各项都变号.要点四、公式法1.平方差公式两个数的平方差等于这两个数的和与这两个数的差的积，即：()()22a b a b a b -=+-2.完全平方公式两个数的平方和加上这两个数的积的2倍，等于这两个数的和（差）的平方． 即()2222a ab b a b ++=+，()2222a ab b a b -+=-. 形如222a ab b ++，222a ab b -+的式子叫做完全平方式.要点诠释：（1）平方差公式的特点：左边是两个数（整式）的平方，且符号相反，右边是两个数（整式）的和与这两个数（整式）的差的积.（2）完全平方公式的特点：左边是二次三项式，是这两数的平方和加（或减）这两数之积的2倍. 右边是两数的和（或差）的平方.（3）套用公式时要注意字母a 和b 的广泛意义，a 、b 可以是字母，也可以是单项式或多项式.要点五、十字相乘法和分组分解法十字相乘法利用十字交叉线来分解系数，把二次三项式分解因式的方法叫做十字相乘法. 对于二次三项式2x bx c ++，若存在pq c p q b =⎧⎨+=⎩ ，则()()2x bx c x p x q ++=++ 分组分解法对于一个多项式的整体，若不能直接运用提公因式法和公式法进行因式分解时，可考虑分步处理的方法，即把这个多项式分成几组，先对各组分别分解因式，然后再对整体作因式分解——分组分解法.即先对题目进行分组，然后再分解因式.要点六、因式分解的一般步骤因式分解的方法主要有: 提公因式法, 公式法, 分组分解法, 十字相乘法, 添、拆项法等.因式分解步骤（1）如果多项式的各项有公因式，先提取公因式；（2）如果各项没有公因式那就尝试用公式法；（3）如用上述方法也不能分解，那么就得选择分组或其它方法来分解．（4）结果要彻底，即分解到不能再分解为止．【典型例题】类型一、提公因式法分解因式1、已知21x x +-＝0，求3223x x ++的值．【思路点拨】观察题意可知21x x +=，将原式化简可得出答案．【答案与解析】解：依题意得：21x x +=，∴3223x x ++，＝3223x x x +++，＝22()3x x x x +++，＝23x x ++，＝4；【总结升华】此题考查的是代数式的转化，通过观察可知已知与所求的式子的关系，然后将变形的式子代入即可求出答案．类型二、公式法分解因式2、已知2x －3＝0，求代数式()()2259x x x x x -+--的值．【思路点拨】对所求的代数式先进行整理，再利用整体代入法代入求解．【答案与解析】解：()()2259x x x x x -+--，＝322359x x x x -+--，＝249x -．当2x －3＝0时，原式＝()()2492323x x x -=+-＝0． 【总结升华】本题考查了提公因式法分解因式，观察题目，先进行整理再利用整体代入法求解，不要盲目的求出求知数的值再利用代入法求解．举一反三：【变式】()()33a y a y -+是下列哪一个多项式因式分解的结果（ ）A ．229a y+ B ．229a y -+ C ．229a y - D ．229a y -- 【答案】C ；3、在日常生活中，如取款、上网需要密码，有一种因式分解法产生密码，例如()()()4422x y x y x y x y -=-++，当x ＝9，y ＝9时，x y -＝0，x y +＝18，22x y +＝162，则密码018162．对于多项式324x xy -，取x ＝10，y ＝10，用上述方法产生密码是什么？【思路点拨】首先将多项式324x xy -进行因式分解，得到()()32422x xy x x y x y -=+-，然后把x ＝10，y ＝10代入，分别计算出()2x y +及()2x y -的值，从而得出密码．【答案与解析】解：()()()32224422x xy x x y x x y x y -=-=+-，当x ＝10，y ＝10时，x ＝10，2x ＋y ＝30，2x －y ＝10，故密码为103010或101030或301010．【总结升华】本题是中考中的新题型．考查了学生的阅读能力及分析解决问题的能力，读懂密码产生的方法是关键．举一反三：【变式】利用因式分解计算（1）16.9×18＋15.1×18（2） 22683317- 【答案】解：（1）16.9×18＋15.1×18＝()116.915.18⨯+ ＝13248⨯= （2）22683317-＝()()683317683317+⨯-＝1000×366＝366000．4、因式分解：（1）()()269a b a b ++++；（2）222xy x y--- （3）()()22224222x xy y x xy y -+-+．【思路点拨】都是完全平方式，所以都可以运用完全平方公式分解．完全平方公式法：()2222a b a ab b ±=±+．【答案与解析】解：（1）()()()22693a b a b a b ++++=++（2）()()2222222xy x y xy x yx y ---=-++=-+ （3）()()22224222x xy y x xy y -+-+＝()()24222x xy y x y -+=-【总结升华】本题考查了完全平方公式法因式分解，（3）要两次分解，注意要分解完全． 举一反三：【变式】下列各式能用完全平方公式进行分解因式的是（ ）A ．21x +B ．221x x +-C ．21x x ++D ．244x x ++【答案】D ；5、先阅读，再分解因式：()24422224444(2)2x x x x x x +=++-=+-()()222222x x x x =-+++，按照这种方法把多项式464x +分解因式．【思路点拨】根据材料，找出规律，再解答．【答案与解析】解：442264166416x x x x +=++-＝()222816x x +-＝()()228484x x x x +++-．【总结升华】此题要综合运用配方法，完全平方公式，平方差公式，熟练掌握公式并读懂题目信息是解题的关键．类型三、十字相乘法或分组分解法分解因式6、将下图一个正方形和三个长方形拼成一个大长方形，请观察这四个图形的面积与拼成的大长方形的面积之间的关系．（1）根据你发现的规律填空：2x px qx pq +++=()2x p q x pq +++=＿＿＿＿＿＿； （2）利用（1）的结论将下列多项式分解因式：①2710x x ++；②2712y y -+． 【思路点拨】（1）根据一个正方形和三个长方形的面积和等于由它们拼成的这个大长方形的面积作答；（2）根据（1）的结论直接作答．【答案与解析】解：（1）()()x p x q +⨯+（2）①()()271025x x x x ++=++ ②()()271234y y x x -+=-- 【总结升华】本题实际上考查了利用十字相乘法分解因式．运用这种方法的关键是把二次项系数a 分解成两个因数12,a a 的积12a a ，把常数项c 分解成两个因数12c c 的积12,c c ，并使1221a c a c +正好是一次项b ，那么可以直接写成结果：在运用这种方法分解因式时，要注意观察，尝试，并体会它实质是二项式乘法的逆过程．当首项系数不是1时，往往需要多次试验，务必注意各项系数的符号．举一反三：【变式】已知A ＝2a +，B ＝25a a -+，C ＝2519a a +-，其中a ＞2．（1）求证：B －A ＞0，并指出A 与B 的大小关系；（2）指出A 与C 哪个大？说明理由．解：（1）B －A ＝()21a -＋2＞0，所以B ＞A ；（2）C －A ＝25192a a a +---，＝2421a a +-，＝()()73a a +-．因为a ＞2，所以a ＋7＞0，从而当2＜a ＜3时，A ＞C ；当a ＝3时，A ＝C ；当a ＞3时，A ＜C ．。

浙教版七年级下册期末复习（第四章：因式分解） 学习目标知道因式分解的意义。

明白因式分解与整式乘法的关系。

会用提取公因式法分解因式。

清楚添括号法则。

会用平方差公式分解因式。

会用完全平方公式分解因式。

初步会综合运用因式分解知识解决一些简单的数学问题。

知识点1 因式分解的概念把一个多项式化成 的形式，这种变形叫做把这个多项式因式分解，也叫做把这个多项式分解因式 。

如：知识点2 提公因式法多项式ma+mb+mc 中的各项都有一个公共的因式 ,我们把这个因式 叫做这个多项式的公因式.ma+mb+mc = 就是把ma+mb+mc 分解成两个因式乘积的形式，其中一个因式是各项的公因式 ，另一个因式 是ma+mb+mc 除以m 所得的商，像这种分解因式的方法叫做提公因式法.例如：x 2 – x = x （ )，8a 2b-4ab+2a = 2a( )知识点3 公式法(1)平方差公式：a 2-b 2=( )( ).例如：4x 2-9=( )2-（ ）2=( )( ).(2)完全平方公式：a 2±2ab+b 2=( )2其中， 叫做完全平方式.例如：4x 2-12xy+9y 2=（ ）2一：选择题1．下列由左到右的变形中，是因式分解的是（ ）．A 、ax ＋bx ＋c ＝()c b a x ++B 、()()1112-=-+a a aC 、()ay ax y x a +=+D 、()22112-=+-m m m 2、下列分解因式中,正确的是（ ）．A 、()()y x y x y x -+=+22B 、()()y x y x y x -+=-22C 、()()y x y x y x --+-=+-22D 、()()y x y x y x -+-=--223．下列多项式中, 有（ ）个是完全平方式. ①412+-x x ②16922+-ab b a ③2293n mn m ++ ④25102--x x A 、1个 B 、2个 C 、3个 D 、4个X 2-1 (X+1)(X-1)（ ） （ ）4．某多项式分解因式结果为()()y x y x 22-+，那么这个多项式是（ ）．A 、224y x -B 、224y x -C 、224y x +D 、224y x +5．下列各式中,能运用平方差公式分解因式的是（ ）.A 、21x +-B 、22y x +C 、42--xD 、()22b a --- 6．若m x x +-82是一个完全平方式, 则m 的值为（ ）．A 、4B 、8C 、16D 、32二、解答题：把下列各式因式分解：（1）()()y x y x a ---3 （2）71472+-x x（3）962+-x x （4）3222y xy y x +-（5）()()()b a a b a b a +--+23322 （6）xy y x 43-（7）4233ay ax - （8）22363ay axy ax ++ （9）3123x x -（10）xy y x 4422+-- （11）25)(10)(2+---b a b a三. 已知：a +b =3，ab =2，求下列各式的值：（1）a 2b +ab 2 （2）a 2+b 2四. 若。

第四章 因式分解一、提公因式法.知识点1：分解因式的定义1．分解因式：把一个多项式化成几个_整式的乘的积，这种变形叫做分解因式，它与整式的 乘法互为逆运算。

分解因式需知；（1）只有多项式才能够分解因式，单项式不能分解因式（2）结果必须是整式，不能有分式出现（3）结果必须是积的形式【经典例题】判断下列从左边到右边的变形是否为分解因式：①8)3)(3(892+-+=+-x x x x （ ） ②)49)(49(4922y x y x y x -+=- （ ）③ 9)3)(3(2-=-+x x x （ ） ④)2(222y x xy xy xy y x -=+- （ ）知识点2：公因式公因式： 定义：我们把多项式各项都含有的相同因式，叫做这个多项式各项的公因式。

公因式的确定：（1）符号: 若第一项是负号则先把负号提出来（提出负号后括号里每一项都要变号）（2）系数：取系数的最大公约数；（3）字母：取字母（或多项式）的指数最低的；（4）所有这些因式的乘积即为公因式；【经典例题】：1错误！未指定书签。

．的公因式是多项式 963ab - aby abx -+_________2错误！未指定书签。

．多项式3223281624a b c a b ab c -+-分解因式时，应提取的公因式是（ ）A ．24ab c -B ．38ab -C ．32abD ．3324a b c3. 342)()()(n m m n y n m x +++-+的公因式是__________知识点3：用提公因式法分解因式提公因式法分解因式：如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成几个因式的乘积，这种分解因式的方法叫做提公因式法。

1可以直接提公因式的类型：（1）3442231269b a b a b a +-=________________； （2）11n n n a a a +--+=___________（3）（3）542)()()(b a b a y b a x -+---=_____________（4）不解方程组23532x y x y +=-=-⎧⎨⎩，求代数式()()()22332x y x y x x y +-++的值2.式子的第一项为负号的类型：（1）①33222864y x y x y x -+- =_______________②243)(12)(8)(4n m n m n m +++-+-=_______（2）若被分解的因式只有两项且第一项为负，则直接交换他们的位置再分解（特别是用到平方差公式时）如： 22188y x +- 【变式练习】1．多项式:aby abx ab 24186++-的一个因式是ab 6-,那么另一个因式是( )y x A 431..+-- y x B 431..-+ C y x 431--- D..y x 431--2.分解因式－5(y －x)3－10y(y －x)33. 公因式只相差符号的类型：公因式相差符号的，要先确定取哪个因式为公因式，然后把另外的只相差符号的因式的负号提出来，使其统一于之前确定的那个公因式。

期末专题复习--因式分解一．巩固基础： 典例精析：例1.(1)下列各式分解因式正确的是( )A. 22269(3)x xy y x y ++=+B. 222249(23)x xy y x y -+=- C. 22282(4)(4)x y x y x y -=+- D. ()()()()x x y y y x x y x y -+-=-+ (2)多项式34a a -分解因式的结果是( )A. 2(4)a a -B. 2(2)(2)a a -+C. (2)(2)a a a -+D. 2(2)a a - （3）若关于x 的二次三项式x 2+kx +b 因式分解为（x ﹣1）（x ﹣3），则k +b 的值为（ ） A ．﹣1B ．1C ．﹣3D ．3（4）分解因式：3x 2﹣6x 2y +3xy 2＝_______________ （5）将下列多项式因式分解，结果中不含有因式a+1的是（ ） A ．a 2﹣1B ．a 2+aC ．a 2+a ﹣2D ．（a+2）2﹣2（a+2）+1（6）对于非零的两个实数a ，b ，规定ab a b a -=⊗3，那么将16⊗a 结果再进行分解因式，则为（ ） A ．()()22-+a a aB ．()()44-+a a aC ．()()44-+a aD ．()42+a a(7)若多项式b ax x ++2分解因式的结果为()()21-+x x ，则b a +的值为 (8)y ﹣2x+1是4xy ﹣4x 2﹣y 2﹣k 的一个因式，则k 的值是（ ） A ．0B ．﹣1C ．1D ．4题组训练：1.下列变形属于因式分解的是（ ） A ．（x+2）（x ﹣2）=x 2﹣4 B ．x 2﹣2x+3=（x ﹣1）2+2 C ．x 2﹣6xy+9y 2=（x ﹣3y ）2D ．3（5﹣x ）=﹣3（x ﹣5）2．多项式4x ﹣x 3分解因式的结果是（ ）A ．x （4﹣x 2） B ．x （2﹣x ）（2+x ） C ．x （x ﹣2）（x +2） D ．x （2﹣x ）23．下列式子直接能用完全平方公式进行因式分解的是（ ） A ．21681a a ++B ．239a a -+C ．2441a a +-D ．2816a a --4．下列分解因式正确的是（ ） A ． )(222y x x xy x -=- B ．)2(22x xy y y xy xy --=-+- C ． 22)2(2882-=+-x x xD ．3)1(32--=--x x x x5．若代数式x 2+4x+m 通过变形可以写成（x+n ）2的形式，那么m 的值是（ ） A ．4B ．8C ．±4D ．166.多项式（x+2）（2x-1）-（x+2）可以因式分解成（x+m ）（2x+n ），则m-n 的值是（ ） A ．2 B ．-2 C ．4 D ．-47.多项式2x 2﹣8因式分解的结果是_______________8. 若多项式2x mx n -+（m 、n 是常数）分解因式后，有一个因式是x-3，则3m-n 的值 为____________________典例精析：例2.因式分解下列各式：（1）239ac abc - （2）()()x y b y x a -+-84（3）2249b a - （4）2243681y xy x +-（5）a ab ab ++22 （6）228ax a -（7）912422-+-b b a （8）()()1321222+++++x x x x题组训练：因式分解下列各式：（1）a a a 1812223-+- （2）49142+-x x（3）223363x y xy y -+ （4）()()x y b y x a -+-2249（5）()222164a a -+ （6）22882b ab a +-（7）5mx 2﹣10mxy +5my 2（8）3212422-+--b b a a二．应用提升：典例精析：例3.先阅读下列材料，然后解后面的问题．材料：一个三位自然数abc （百位数字为a ，十位数字为b ，个位数字为c ），若满足b c a =+，则称这个三位数为“欢喜数”，并规定F （abc ）=ac ．如374，因为它的百位上数字3与个位数字4之和等于十位上的数字7，所以374是“欢喜数”，∴F （374）=3×4=12．（1）对于“欢喜数abc ”，若满足b 能被9整除，求证：“欢喜数abc ”能被99整除；（2）已知有两个十位数字相同的“欢喜数”m ，n （m ＞n ），若F （m ）﹣F （n ）=3，求m ﹣n 的值．题组训练：1．给出三个多项式：12212-+x x ，14212++x x ，x x 2212-．请选择你最喜欢的两个多项式进行加法运算，并把结果因式分解．2.仔细阅读下面例题，解答问题：例题：已知二次三项式x 2﹣4x+m 有一个因式是（x+3），求另一个因式以及m 的值． 解：设另一个因式为（x+n ），得 x 2﹣4x+m=（x+3）（x+n ） 则x 2﹣4x+m=x 2+（n+3）x+3n ∴⎩⎨⎧=-=+nm n 343解得：n=﹣7，m=﹣21∴另一个因式为（x ﹣7），m 的值为﹣21 问题：仿照以上方法解答下面问题：已知二次三项式2x 2+3x ﹣k 有一个因式是52-x ，求另一个因式以及k 的值．典例精析：例4.发现与探索．（1）根据小明的解答将下列各式因式分解小明的解答：()()()1543599656222--=--=+-+-=+-a a a a a a a①20122+-a a , ②()()71812+---a a , ③2256b ab a +-（2）根据小丽的思考解决下列问题：小丽的思考：代数式()432+-a 无论a 取何值()23-a 都大于等于0，再加上4，则代数式()432+-a 大于等于4，则()432+-a 有最小值为4．①说明：代数式20122+-a a 的最小值为16-．②请仿照小丽的思考解释代数式()812++-a 的最大值为8，并求代数式8122-+-a a 的最大值．题组训练：教科书中这样写道：“我们把多项式222a ab b ++及222a ab b -+叫做完全平方式．”如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值、最小值等．例如：分解因式322-+x x =22(21)4(1)4(12)(12)x x x x x ++-=+-=+++-=(3)(1)x x +-；例如求代数式2246x x +-的最小值，222462(23)x x x x +-=+-=22(1)8x +-，可知当1x =-时，2246x x +-有最小值，最小值是8-．根据阅读材料用配方法解决下列问题：（1）分解因式：245m m --=_____________________ （2）当b a ,为何值时，多项式224618a b a b +-++有最小值，并求出这个最小值． （3）当b a ,为何值时，多项式22222427a ab b a b -+--+有最小值，并求出这个最小值．。

专题07 因式分解【考点剖析】1、因式分解的概念分解因式的定义：把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因式．注意：因式分解与整式乘法是相反方向的变形，二者是一个式子的不同表现形式．因式分解是两个或几个因式积的表现形式，整式乘法是多项式的表现形式．2、因式分解的常用方法：①提公因式法：pa+pb+pc=p(a+b+c)；②公式法：a2-b2=(a+b)(a-b)；a2+2ab+b2=(a+b)2；a2-2ab+b2=(a-b)2；③分组分解法：ac+ad+bc+cd=a(c+d)+b(c+d)=(a+b)(c+d)；④十字相乘法：a2+(p+q)a+pq=(a+p)(a+q) ．3、因式分解的一般步骤：（1）如果多项式的各项有公因式，那么先提取公因式；（2）在各项提出公因式以后或各项没有公因式的情况下，观察多项式的项数：2项式可以尝试运用公式法分解因式；3项式可以尝试运用公式法、十字相乘法分解因式；4项式及4项式以上的可以尝试分组分解法分解因式；（3）分解因式必须分解到每一个因式都不能再分解为止．4、因式分解的应用（1）利用因式分解解决求值问题；（2）利用因式分解解决证明问题；（3）利用因式分解简化计算问题．【规律方法】因式分解在求代数式值中的应用1．因式分解是研究代数式的基础，通过因式分解将多项式合理变形，是求代数式值的常用解题方法，具体做法是：根据题目的特点，先通过因式分解将式子变形，然后再进行整体代入．2．用因式分解的方法将式子变形时，根据已知条件，变形的可以是整个代数式，也可以是其中的一部分．因式分解的定义【典例】例1．下列各式从左边到右边的变形中，是因式分解的是（）A．ax﹣ay＝a（x﹣y）B．x2﹣4x+4＝x（x﹣4）+4C．x2﹣9+8x＝（x+3）（x﹣3）+8xD．（3a﹣2）（﹣3a﹣2）＝4﹣9a2【答案】A【解析】解：A、是因式分解，正确；B、结果不是整式的积的形式，故不是因式分解，选项错误；C、结果不是整式的积的形式，故不是因式分解，选项错误；D、结果不是整式的积的形式，故不是因式分解，选项错误．故选：A．【点睛】因式分解就是把多项式分解成整式的积的形式，依据定义即可判断．本题主要考查了因式分解的定义，因式分解与整式的乘法互为逆运算．是中考中的常见题型．【巩固练习】1．下列从左到右的变形中，属于因式分解的是（）A．（x+2）（x﹣2）＝x2﹣4B．a2﹣2ab+b2＝（a﹣b）2C．am+bm﹣1＝m（a+b）﹣1D．（x﹣1）2﹣1＝（x﹣1）（x﹣1）【答案】B【解析】解：A．属于整式的乘法运算，不合题意；B．符合因式分解的定义，符合题意；C．右边不是乘积的形式，不合题意；D．右边不是几个整式的积的形式，不合题意；故选：B．因式分解计算【典例】例1．因式分解：（1）x2y﹣2xy2+y3（2）4ax2﹣48ax+128a；（3）（x2+16y2）2﹣64x2y2【答案】见解析【解析】解：（1）x2y﹣2xy2+y3＝y（x2﹣2xy+y2）＝y（x﹣y）2；（2）4ax2﹣48ax+128a＝4a（x2﹣12x+32）＝4a（x﹣4）（x﹣8）；（3）（x2+16y2）2﹣64x2y2＝（x2+16y2+8xy）（x2+16y2﹣8xy）＝（x+4y）2（x﹣4y）2．【点睛】（1）此多项式有公因式，应先提取公因式，再对余下的多项式进行观察，有3项，可采用完全平方公式继续分解．（2）此多项式有公因式，应先提取公因式，再对余下的多项式根据十字相乘法分解因式；（3）先根据平方差公式分解因式，再采用完全平方公式继续分解．本题考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．【巩固练习】1．分解因式：（1）ax+ay（2）x4﹣b4（3）3ax2﹣6axy+3ay2【答案】见解析【解析】解：（1）ax+ay＝a（x+y）；（2）x4﹣b4＝（x2+b2）（x2﹣b2）＝（x2+b2）（x+b）（x﹣b）；（3）3ax2﹣6axy+3ay2＝3a（x2﹣2xy+y2）＝3a（x﹣y）2．2．因式分解（1）﹣4a3b3+6a2b﹣2ab（2）（x+1）（x+2）．【答案】见解析【解析】解：（1）﹣4a3b3+6a2b﹣2ab＝﹣2ab（2a2b2﹣3a+1）（2）（x+1）（x+2）＝x2+3x+2＝x2+3x＝（x）2．因式分解综合【典例】例1．阅读下列材料：在因式分解中，把多项式中某些部分看作一个整体，用一个新的字母代替（即换元），不仅可以简化要分解的多项式的结构，而且能使式子的特点更加明显，便于观察如何进行因式分解，我们把这种因式分解的方法称为“换元法”．下面是小涵同学用换元法对多项式（x2﹣4x+1）（x2﹣4x+7）+9进行因式分解的过程．解：设x2﹣4x＝y原式＝（y+1）（y+7）+9（第一步）＝y2+8y+16（第二步）＝（y+4）2（第三步）＝（x2﹣4x+4）2（第四步）请根据上述材料回答下列问题：（1）小涵同学的解法中，第二步到第三步运用了因式分解的______；A．提取公因式法B．平方差公式法C．完全平方公式法（2）老师说，小涵同学因式分解的结果不彻底，请你写出该因式分解的最后结果：______________；（3）请你用换元法对多项式（x2+2x）（x2+2x+2）+1进行因式分解．【答案】见解析【解析】解：（1）故选：C；（2）（x2﹣4x+1）（x2﹣4x+7）+9，设x2﹣4x＝y，原式＝（y+1）（y+7）+9，＝y2+8y+16，＝（y+4）2，＝（x2﹣4x+4）2，＝（x﹣2）4；故答案为：（x﹣2）4；（3）设x2+2x＝y，原式＝y（y+2）+1，＝y2+2y+1，＝（y+1）2，＝（x2+2x+1）2，＝（x+1）4．【点睛】（1）根据完全平方公式进行分解因式；（2）最后再利用完全平方公式将结果分解到不能分解为止；（3）根据材料，用换元法进行分解因式．本题考查了因式分解﹣换元法，公式法，也是阅读材料问题，熟练掌握利用公式法分解因式是解题的关键．例2．阅读与思考：整式乘法与因式分解是方向相反的变形，由（x+p）（x+q）＝x2+（p+q）x+pq，可得x2+（p+q）x+pq＝（x+p）（x+q）．利用这个式子可以将某些二次项系数是1的二次三项式分解因式．例如：将式子x2+3x+2分解因式．这个式子的常数项2＝1×2，一次项系3＝1+2，所以x2+3x+2＝x2+（1+2）x+1×2．解：x2+3x+2＝（x+1）（x+2）．上述分解因式x2+3x+2的过程，也可以用十字相乘的形式形象地表示：先分解二次项系数，分别写在十字交叉线的左上角和左下角；再分解常数项，分别写在十字交叉线的右上角和右下角；然后交叉相乘，求代数和，使其等于一次项系数（如图）．请仿照上面的方法，解答下列问题：（1）分解因式：x2﹣5x+6＝________________________；（2）若x2+px+8可分解为两个一次因式的积，则整数P的所有可能值是______________．【答案】见解析【解析】解：（1）x2﹣5x+6＝（x﹣2）（x﹣3）．故答案是：（x﹣2）（x﹣3）．（2）∵8＝1×8；8＝﹣8×（﹣1）；8＝﹣2×（﹣4）；8＝﹣4×（﹣2），则p的可能值为﹣1+（﹣8）＝﹣9；8+1＝9；﹣2+（﹣4）＝﹣6；4+2＝6．∴整数p的所有可能值是±9，±6，故答案为：±9或±6．【点睛】（1）、（2）发现规律：二次项系数为1的二次三项式x2+px+q的因式解，就是把常数项q分解成两个数的积且使这两数的和等于p，则x2+px+q＝（x+a）（x+b）．此题考查了因式分解﹣十字相乘法，弄清题中的分解因式方法是解本题的关键．【巩固练习】1．阅读下面的问题，然后回答，分解因式：x2+2x﹣3，解：原式＝x2+2x+1﹣1﹣3＝（x2+2x+1）﹣4＝（x+1）2﹣4＝（x+1+2）（x+1﹣2）＝（x+3）（x﹣1）上述因式分解的方法称为配方法．请体会配方法的特点，用配方法分解因式：（1）x2﹣4x+3（2）4x2+12x﹣7．【答案】见解析【解析】解：（1）x2﹣4x+3＝x2﹣4x+4﹣4+3＝（x﹣2）2﹣1＝（x﹣2+1）（x﹣2﹣1）＝（x﹣1）（x﹣3）（2）4x2+12x﹣7＝4x2+12x+9﹣9﹣7＝（2x+3）2﹣16＝（2x+3+4）（2x+3﹣4）＝（2x+7）（2x﹣1）．2．下面是某同学对多项式（x2﹣4x+2）（x2﹣4x+6）+4进行因式分解的过程．解：设x2﹣4x＝y，则原式＝（y+2）（y+6）+4＝y2+8y+16＝（y+4）2＝（x2﹣4x+4）2（1）该同学因式分解的结果是否彻底？__________（填“彻底”或“不彻底”）．若不彻底，请直接写出因式分解的最后结果______________．（2）请你模仿以上方法尝试对多项式（x2﹣2x）（x2﹣2x﹣2）﹣3进行因式分解．【答案】见解析【解析】解：（1）该同学因式分解的结果不彻底，原式＝（x2﹣4x+4）2＝[（x﹣2）2]2＝（x﹣2）4，故答案为：不彻底、（x﹣2）4．（2）设：x2﹣2x＝y．原式＝y（y﹣2）﹣3，＝（y﹣3）（y+1），＝（x2﹣2x﹣3）（x2﹣2x+1），＝（x﹣3）（x+1）（x﹣1）2．3．下面是某同学对多项式（x2﹣4x+2）（x2﹣4x+6）+4进行因式分解的过程解：设x2﹣4x＝y，原式＝（y+2）（y+6）+4（第一步）＝y2+8y+16（第二步）＝（y+4）2（第三步）＝（x2﹣4x+4）2（第四步）（1）该同学第二步到第三步运用了因式分解的______（填序号）．A．提取公因式B．平方差公式C．两数和的完全平方公式D．两数差的完全平方公式（2）该同学在第四步将y用所设中的x的代数式代换，得到因式分解的最后结果．这个结果是否分解到最后？______．（填“是”或“否”）如果否，直接写出最后的结果_____________．（3）请你模仿以上方法尝试对多项式（x2﹣2x）（x2﹣2x+2）+1进行因式分解．【答案】见解析【解析】解：（1）该同学第二步到第三步运用了因式分解的两数和的完全平方公式；故选：C；（2）这个结果没有分解到最后，原式＝（x2﹣4x+4）2＝（x﹣2）4；故答案为：否，（x﹣2）4；（3）（x2﹣2x）（x2﹣2x+2）+1＝（x2﹣2x）2+2（x2﹣2x）+1＝（x2﹣2x+1）2＝（x﹣1）4．因式分解的应用【典例】例1．已知a、b、c为△ABC的三边，且满足a2c2﹣b2c2＝a4﹣b4，则△ABC是（）A．直角三角形B．等腰三角形C．等腰三角形或直角三角形D．等腰直角三角形【答案】C【解析】解：移项得，a2c2﹣b2c2﹣a4+b4＝0，c2（a2﹣b2）﹣（a2+b2）（a2﹣b2）＝0，（a2﹣b2）（c2﹣a2﹣b2）＝0，所以，a2﹣b2＝0或c2﹣a2﹣b2＝0，即a＝b或a2+b2＝c2，因此，△ABC等腰三角形或直角三角形．故选：C．【点睛】移项并分解因式，然后解方程求出a、b、c的关系，再确定出△ABC的形状即可得解．本题考查了因式分解的应用，提取公因式并利用平方差公式分解因式得到a、b、c的关系式是解题的关键．【巩固练习】1．已知a、b、c是△ABC的三条边，且满足a2+bc＝b2+ac，则△ABC是（）A．锐角三角形B．钝角三角形C．等腰三角形D．等边三角形【答案】C【解析】解：已知等式变形得：（a+b）（a﹣b）﹣c（a﹣b）＝0，即（a﹣b）（a+b﹣c）＝0，∵a+b﹣c≠0，∴a﹣b＝0，即a＝b，则△ABC为等腰三角形．故选：C．2．如图，在一块边长为a米的正方形空地的四角均留出一块边长为米的正方形修建花坛，其余的地方种植草坪．利用因式分解计算当a＝13.6，b＝1.8时，草坪的面积．【答案】见解析【解析】解：由图可得，草坪的面积是：a2﹣4b2，当a＝13.6，b＝1.8时，a2﹣4b2＝（a+2b）（a﹣2b）＝（13.6+2×1.8）×﹣2×1.8）×10＝172，即草坪的面积是172．3．如图，一长方形模具长为2a，宽为a，中间开出两个边长为b的正方形孔．（1）求图中阴影部分面积（用含a、b的式子表示）（2）用分解因式计算当a＝15.7，b＝4.3时，阴影部分的面积．【答案】见解析【解析】解：（1）2a•a﹣2b2＝2（a2﹣b2）；（2）当a＝15.7，b＝4.3时，阴影部分的面积2（a2﹣b2）＝2（a+b）（a﹣b﹣4.3）＝456．。

第六章因式分解知识点回顾1、 因式分解的概念：把一个多项式分解成几个整式的积的形式，叫做因式分解。

因式分解和整式乘法互为逆运算2、常用的因式分解方法：（1）提取公因式法：)(c b a m mc mb ma ++=++（2）运用公式法： 平方差公式：))((22b a b a b a -+=-；完全平方公式：222)(2b a b ab a ±=+±（3）十字相乘法：))(()(2b x a x ab x b a x ++=+++（4）分组分解法：将多项式的项适当分组后能提公因式或运用公式分解。

（5）运用求根公式法：若)0(02≠=++a c bx ax 的两个根是1x 、2x ，则有：))((212x x x x a c bx ax --=++因式分解的一般步骤：（1）如果多项式的各项有公因式，那么先提公因式；（2）提出公因式或无公因式可提，再考虑可否运用公式或十字相乘法；（3）对二次三项式，应先尝试用十字相乘法分解，不行的再用求根公式法。

（4）最后考虑用分组分解法考点一、因式分解的概念因式分解的概念：把一个多项式分解成几个整式的积的形式，叫做因式分解。

因式分解和整式乘法互为逆运算1、下列从左到右是因式分解的是（ ）A. x(a-b)=ax-bxB. x 2-1+y 2=(x-1)(x+1)+y2 C. x 2-1=(x+1)(x-1) D. ax+bx+c=x(a+b)+c2、若2249a kab b ++可以因式分解为2(23)a b -，则k 的值为______3、已知a 为正整数，试判断2a a +是奇数还是偶数？4、已知关于x 的二次三项式2x mx n ++有一个因式(5)x +，且m+n=17，试求m ，n 的值考点二 提取公因式法提取公因式法：)(c b a m mc mb ma ++=++公因式：一个多项式每一项都含有的相同的因式，叫做这个多项式各项的公因式找公因式的方法：1、系数为各系数的最大公约数 2、字母是相同字母3、字母的次数-相同字母的最低次数习题1、将多项式3222012a b a bc -分解因式，应提取的公因式是（ ）A 、abB 、24a bC 、4abD 、24a bc2、已知(1931)(1317)(1317)(1123)x x x x -----可因式分解为()(8)ax b x c ++，其中a ，b ，c 均为整数，则a+b+c 等于（ ）A 、-12B 、-32C 、38D 、723、分解因式（1）6()4()a a b b a b +-+ （2）3()6()a x y b y x ---（3）12n n n x x x ---+ （4）20112010(3)(3)-+-4、先分解因式，在计算求值（1）22(21)(32)(21)(32)(12)(32)x x x x x x x -+--+--+ 其中x=1.5（2）22(2)(1)(1)(2)a a a a a -++--- 其中a=185、已知多项式42201220112012x x x +++有一个因式为21x ax ++，另一个因式为22012x bx ++，求a+b 的值6、若210ab +=，用因式分解法求253()ab a b ab b ---的值7、已知a ，b ，c 满足3ab a b bc b c ca c a ++=++=++=，求(1)(1)(1)a b c +++的值。