浙教版七年级下册数学全册知识点及典型例题

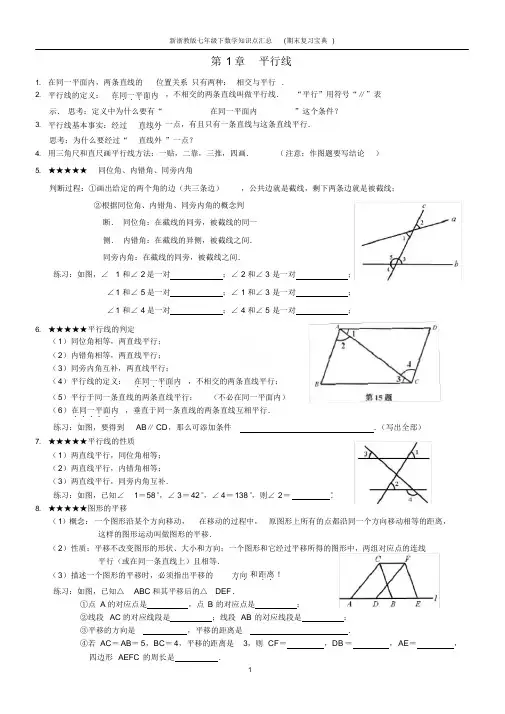
第1 章平行线1. 在同一平面内，两条直线的位置关系只有两种：相交与平行．2. 平行线的定义：在．同．一．平．面．内．，不相交的两条直线叫做平行线．“平行”用符号“∥”表示．思考：定义中为什么要有“在同一平面内”这个条件？3. 平行线基本事实：经过直．线．外．一点，有且只有一条直线与这条直线平行．思考：为什么要经过“直线外”一点？4. 用三角尺和直尺画平行线方法：一贴，二靠，三推，四画．（注意：作图题要写结论）5. ★★★★★同位角、内错角、同旁内角判断过程：①画出给定的两个角的边（共三条边），公共边就是截线，剩下两条边就是被截线；②根据同位角、内错角、同旁内角的概念判断．同位角：在截线的同旁，被截线的同一侧．内错角：在截线的异侧，被截线之间．同旁内角：在截线的同旁，被截线之间．练习：如图，∠ 1 和∠2 是一对；∠2 和∠3 是一对；∠1 和∠5 是一对；∠1 和∠3 是一对；∠1 和∠4 是一对；∠4 和∠5 是一对；6. ★★★★★平行线的判定（1）同位角相等，两直线平行；（2）内错角相等，两直线平行；（3）同旁内角互补，两直线平行；（4）平行线的定义：在．同．一．平．面．内．，不相交的两条直线平行；（5）平行于同一条直线的两条直线平行；（不必在同一平面内）（6）在．同．一．平．面．内．，垂直于同一条直线的两条直线互相平行．练习：如图，要得到AB∥CD ，那么可添加条件．（写出全部）7. ★★★★★平行线的性质（1）两直线平行，同位角相等；（2）两直线平行，内错角相等；（3）两直线平行，同旁内角互补．练习：如图，已知∠1＝58°，∠3＝42°，∠4＝138 °，则∠2＝°.8. ★★★★★图形的平移（1）概念：一个图形沿某个方向移动，在移动的过程中，原图形上所有的点都沿同一个方向移动相等的距离，这样的图形运动叫做图形的平移．（2）性质：平移不改变图形的形状、大小和方向；一个图形和它经过平移所得的图形中，两组对应点的连线平行（或在同一条直线上）且相等．（3）描述一个图形的平移时，必须指出平移的方．向．和距．离．！练习：如图，已知△ABC 和其平移后的△DEF ．①点 A 的对应点是，点B 的对应点是；②线段AC 的对应线段是；线段AB 的对应线段是；③平移的方向是，平移的距离是．④若AC＝AB＝5，BC＝4，平移的距离是3，则CF＝，DB ＝，AE＝，四边形AEFC 的周长是．9. ★★★折叠问题方法：（1）找到折叠后和折叠前的图形，若折叠前的图形没有画出，自己必须补画上去；（2） 找到折叠前后能重合的角，它们的度数相等；（3） 利用平行线的性质、对顶角的性质、三角形的内角和、邻补角的性质、平角等计算出角度． 练习：（ 1）如图，将一张纸条 ABCD 沿 EF 折叠，若折叠角∠FEC ＝ 64°，则∠ 1＝．（ 2）如图，有一条直的宽纸带，按图折叠，则∠ α＝ ．（ 3）如图，将一条两边沿互相平行的纸带折叠，①写出图中所有与∠ 6 相等的角；②若∠ 6＝ x °，请用含 x 的代数式表示∠ 4 的度数．1. ★★★二元一次方程的概念第 2 章 二元一次方程组三个条件：（ 1）含有两个未知数； （ 2）未知数的项的次数是一次； （ 3）都是整式．练习：方程① x 12＝ 0，② xy ＝－ 2，③ x 2－ 5x ＝5，④ 2x ＝1－ 3y 中，为二元一次方程的是．－ y＋2. ★★★★把二元一次方程变形成用关于一个未知数的代数式表示另一个未知数的形式（ 1）用含 x 的代数式表示 y ，则应变形为“ y ＝ ”的形式； （ 2）用含 y 的代数式表示 x ，则应变形为“ x ＝ ”的形式．练习：（1）已知方程 2x －3y ＝ 7，用关于 x 的代数式表示 y 得. （2）已知方程 3x ＋2y ＝ 6，用关于 y 的代数式表示 x 得.3. ★二元一次方程的整数解方程 3x ＋ 2y ＝ 21 的正整数解是． 4．二元一次方程组的概念三个条件：（ 1）两个一次方程； （ 2）两个方程共有两个未知数； （ 3）都是整式． 5．★★★★★解二元一次方程组基本思路： 消元消元方法：（ 1）代入消元； （ 2）加减消元． （注意：一定要把解代入原方程组检验，保证正确 ）练习：（1）x －2y ＝ 2 3x ＋ 2y ＝ 10（ 2）y ＝ 3x 3x＋ y ＝126. ★★★★常考题型练习：（1）已知代数式kx＋b，当x＝2 时值为－1，当x＝3 时值为－3，则a＋b＝．（2）若方程组ax－2y＝1的解是x＝1，则b＝．2x＋by＝5 y＝a2x＋3y＝k（3）已知关于x，y 的二元一次方程组的解互为相反数，则k 的值是．（4）请你写出一个以x＝3x＋2y＝－1为解的二元一次方程组：.y＝－1（5）已知方程组2x＋y＝5x＋3y＝57. 某公司有甲、乙两个工程队．x＋y 的值为．（1）两队共同完成一项工程，乙队先单独做 1 天后，再由两队合做 2 天完成了全部工程．已知甲队单独完成此项工程所需天数是乙队单独完成所需的天数的三分之二，则甲、乙两队单独完成各需多少天？（2）甲工程队工作 5 天和乙工程队工作 1 天的费用和为34000 元；甲工程队工作 3 天和乙工程队工作 2 天的费用和为26000 元，则两队每天工作费用各多少元？（3）该公司现承接一项（1）中2 倍的工程由两队去做，且甲、乙两队不在同一天内合做，又必须各自做整数天，试问甲、乙两队各需做多少天？若按（2）中的付费，你认为哪种方式付费最少？，则1．★★★★★公式与法则第 3 章 整式的乘除（ 1）同底数幂的乘法：底数不变，指数相加．am ·a n ＝a m＋ n（ m ， n 都是正整数）（ 2）幂的乘方：底数不变，指数相乘．( a m ) n＝a mn （ m ， n 都是正整数） （ 3）积的乘方：等于把积每一个因式分别乘方，再把所得幂相乘．( ab)n ＝ a n b n （ n 都是正整数）（ 4）乘法公式：①平方差公式： ( a ＋ b)( a －b) ＝ a 2－b 2 ②完全平方公式： ( a ＋ b) 2＝a 2＋b 2＋2ab ( a － b) 2＝a 2＋b 2－2ab （ 5）同底数幂的除法：底数不变，指数相减． a m ÷a n ＝a m －n （ a ≠ 0） 8．某企业承接了一批礼盒的制作业务，该企业进行了前期的试生产，如图1 所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图 计）（ 1）该企业原计划用若干天加工纸箱2 所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不300 个， 后来由于提升工作效率， 实际加工时每天加工速度为原计划的1.5 倍，这样提前 3 天超额完成了任务， 且总共比原计划多加工 15 个，问原计划每天加工礼盒多少个； （ 2）若该企业购进正方形纸板 将购进的纸板全部用完；550 张，长方形纸板 1200 张．问竖式纸盒，横式纸盒各加工多少个，恰好能（ 3）该企业某一天使用的材料清单上显示，这天一共使用正方形纸板100 张，长方形纸板a 张，全部加工成上述两种纸盒， 且 150＜ a ＜ 168，试求在这一天加工两种纸盒时a 的所有可能值． （请直接写出结果）a p k 2k （ 6） a 0＝1（ a ≠ 0） （ 7） a －p ＝ 1（ a ≠ 0），当 a 是整数时，先指数变正，再倒数．当 a 是分数时，先把底数变倒数，再指数变正．（ 8）单项式乘单项式：系数、同底数幂分别相乘，其余字母连同它的指数不变，作为积的因式． （ 9）单项式乘多项式：用单项式去乘多项式的每一项，再把所得的积相加．m( a ＋ b) ＝ ma ＋ mb（ 10）多项式乘多项式：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加． ( a ＋ n)( b ＋ m) ＝ab ＋ am ＋ nb ＋nm（ 11）单项式除以单项式：把系数、同底数幂分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式．（ 12）多项式除以单项式：先把这个多项式的每一项除以这个单项式，再把所得的商相加．( a ＋ b ＋c) ÷ m ＝ a ÷ m ＋ b ÷ m ＋ c ÷m （ m ≠ 0）练习：（1） ( 2a 2) 3＝； 3y · ( －2x 2y 3 ) ＝ ； ( 9x 3－3x) ÷ ( 3x) ＝ ；( － 2) 0＝ ； ( －3) － 3＝； ( － 2 ) － 2＝；3( 2a －1) 2＝； ( a 3) 2?a － 2a 3? a 4＝；(1－ 2a) 2－ ( 2－ a)( 1＋ a) ＝ ； ( x － 2)( x ＋2) － ( 1－2x) 2＝ ．2．★★★★★用科学记数法表示较小的数： a × 10－ n（ 1≤ | a | ＜ 10） 方法：第一个不为零的数前面有几个零就是负几次方．练习：（1）科学记数法表示 0.0000103＝．（2） 1 纳米＝ 0.000000001 米，则 0.33 纳米＝ 米．（用科学计数法表示）（ 3）把用科学记数法表示的数7.2× 10－ 4写成小数形式为．3．★★★★常考题型（ 1）已知 a ＋ b ＝3， ab ＝－ 1，则 a 2＋b 2 ＝ ．（ 2）若多项式 x 2－ ( x － a)( x ＋ 2b) ＋ 4 的值与 x 的取值大小无关，那么a ，b 一定满足．（ 3）关于 x 的代数式 ( 3－ax)( x 2＋2x － 1) 的展开式中不含 x 2 项，则 a ＝ ．（ 4）若代数式 x 2＋3x ＋ 2 可以表示为 ( x － 1) 2＋ a( x － 1) ＋b 的形式，则 a ＋b 的值是 ．（ 5）若 ( x － m)( 2x ＋ 3) ＝ 2x 2－nx ＋ 3，则 m － n ＝ ． （ 6）若 ( 2x － 5y) 2＝ ( 2x ＋ 5y) 2＋ M ，则代数式 M 应是 ． （ 7）如图，一块砖的外侧面积为a ，那么图中残留部分的墙面的面积为．（ 8）如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条“之”字路，余下部分绿化，道路的宽为 a 米，则绿化的面积为m 2．（ 9）定义一种对正整数 n 的“ F 运算”：①当 n 为奇数时，结果为 3n ＋ 5；②当 n 为偶数时，结果为 n （其中2k 是使 n为奇数的正整数） ，并且运算重复进行．例如，取n ＝ 26，则：若n＝449，则第449 次“F 运算”的结果是．第4 章因式分解1. ★★★★因式分解的概念：把一个多．项．式．化成几个整．式．的．积．的形式，叫做因式分解，也叫分解因式．因式分解和整式乘法是互逆关系．练习：下列从左到右边的变形，是因式分解的是（）A ．( 3－x)( 3＋x) ＝9－x2B ．( y＋1)( y－3) ＝－( 3－y)( y＋1)C．4yz－2y2z＋z＝2y( 2z－yz) ＋z D．－8x2＋8x－2＝－2( 2x－1) 22. ★★★★★因式分解的方法（1）提公因式法：先确定应提取的公因式，然后用公因式去除这个多项式，所得的商作为另一个因式，最后把多项式写成这两个因式的积的形式．ma＋mb＋mc＝m( a＋b＋c)确定公因式的方法：系数的最大公因数和相同字母的最低次幂．（2）用乘法公式因式分解：①平方差公式：a2－b2＝( a＋b)( a－b)即：( □) 2－( △) 2＝( □＋△ )( □－△ )②完全平方公式：a2＋2ab＋b2＝( a＋b) 2a2－2ab＋b2 ＝( a－b) 2即：( □) 2±2( □)( △) ＋( △) 2＝( □±△ ) 2练习：（1）下列多项式能用完全平方公式分解因式的是（）A ．x2－4 B．x2＋2x＋4 C．4x2＋4x＋1 D．x2＋y2这里的“□”和“△”可以是单项式，也可以是多项式．（2）下列多项式能用平方差公式分解因式的是（）A ．x2＋4 B．x2＋2x＋1 C．x2－4x D．－x2＋9（3）因式分解：①a3－9a＝. ②x－xy2＝．③x2－8x＋16＝. ④3ax2－6axy＋3ay2＝．⑤a3－4a( a－1) ＝. ⑥( x－2y) 2－x＋2y＝．3．★★★★完全平方式：我们把多项式a2＋2ab＋b2 和a2－2ab＋b2 叫做完全平方式．即：( □) 2±2( □)( △) ＋( △) 2练习：（1）若x2＋( 2p－3) x＋9 是完全平方式，则p 的值等于＝．（2）多项式9x2－x＋1 加上一个单项式后成为一个整式的平方，请写出 3 个满足条件的单项式：．第5 章分式1. ★★分式的概念：表示两个整式相除，且除式中含有字母的代数式．两个条件：①字母不在根号里；②分母上有字母．2. ★★★★★分式有意义的条件：分母不为0．练习：（1）当x 时，分式x＋2有意义. x－2（2）当 a 时，分式12a＋3没有意义．3. ★★★★★分式的值为0 的条件：①分子等于0；②分母不等于0．练习：（1）当 x 时，分式a ＋ 3的值为 0. a － 3 x 2－4 （ 2）当 x时，分式 x － 2的值为 0.4. ★★★★★分式的基本性质：分式的分子与分母都乘（或除以）同一个不等于零的整式，分式的值不变.A＝ A × M A A ÷ MB B × M ， B ＝ B ÷M （其中 M 是不等于零的整式） 分式的约分：把一个分式的分子和分母的公因式约去，叫做分式的约分 .最简分式：分子、分母没有公因式的分式叫做最简分式 .练习：（1）下列分式为最简分式的是（）1－ a a 2＋b 2 m ＋ n2xy － 3yA ．a － 1B ．12a 3b a － bC ． n 2－ m 2 D ．2m 2－10m 5xy（2）化简：① 9ab 3 ＝ ；② x 2＋3xy ＋y 2 m2－ 10m ＋ 25 ＝ ．（ 3）若 x － 3y ＝ 0，则分式 x2－ y 2的值是 ．5. ★★★★★分式的乘除：分式乘分式，用分子积做积的分子，分母的积做积分母；分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘．a c ac a c a d adb · d ＝ bd ； b ÷ d ＝ b ·c ＝ bc ．练习：计算：① 3a 4b 2 16b 39a2 ＝ ；②－ 3xy ÷2y 23x．a b a ±b 6. ★★★分式的加减： （ 1）同分母的分式相加减，分式的分母不变，把分子相加减．c ± c ＝ c． （ 2）异分母分式相加减，先通分化成同分母分式，再用同分母分式的加减法计算．7. ★★★通分的方法：取各分母的系数的最小公倍数和各分母所有字母的最高次幂的积为公分母． 8. ★★★★★分式的化简求值．（ 1）先化简，再求值： a 2－ 4 a 2－4a ＋ ÷ a ＋2－ 1，并选择一个自己喜欢的数代入求值． 4 a ＋1x －1 x － 2 2x 2－x （ 2）先化简，再求值：x － x ＋ 1 ÷ x2＋ 2x ＋ 1，其中 x ＝－ 3．（ 3）先化简，再求值：1＋ 1÷ x － 1 ，然后 x 在 1， 2， 3 三个数中选一个合适的数代入求值． x － 2 x 2－4x ＋ 4 ·9. ★★★★★分式方程：只含分式，或分式和整式，并且分母里含有未知数的方程．解分式方程的一般步骤： （ 1）去分母：方程两边同乘公分母，公分母为分母的系数的最小公倍数和各分母所有字母的最高次幂的积． 注意：①不要漏乘单独的数字 ． ②分子是多项式的要用括号括起来．（ 2）去括号： 注意符号和不要漏乘．（ 3）移项，合并同类项： 注意移项要变号． （ 4）两边同时除以未知数的系数：注意不要颠倒分子分母．（ 5）检验：把所求的根代入原分式方程，或者代入公分母，判断方程中的分式有无意义．若无意义，则是増根．（ 6）写出结论．一般写法：经检验，x ＝ 是原方程的根；或者：经检验， x ＝ 是原方程的增根，所以原方程无解．3练习：（1）解分式方程：① 1－ y＝ 2y y － 1 － 1 ② 2x ＋1 ＝ 3x －3（2）若商品的买入价为 a ，售出价为 b ，则毛利率 p ＝ b －a ab ＞ a ）．若已知 p ，b ，则 a ＝ ．（ 3）对于非零的实数 a 、 b ，规定 a ⊕b 1 12⊕( 2x － 1) ＝ 1，则 x ＝ ．＝ b － a．若（ 4）若关于 x 的分式方程 2＋ 1－ kx ＝ 1有増根，则増根是 ，此时 k ＝ ．x －2 2－ x （ 5）若关于 x 的分式方程 2＋ 1－ kx ＝ 1无实数解，则 k ＝ ．x －2 2－ x （ 6）张老师和李老师住在同一个小区，离学校3000 米，某天早晨，张老师和李老师分别于7 点 10 分、7 点 15 分离家骑自行车上班，刚好在校门口遇上，已知李老师骑车的速度是张老师的 1.2 倍，为了求他们各自骑自行车的速度，设张老师骑自行车的速度是 x 米/ 分，则可列得方程为（ ） A ． 3000 － 3000＝5 B ． 3000 － 3000 ＝ 5×60x 1.2xx 1.2xC ．3000 － 3000＝ 5 D ． 3000 ＋ 3000 ＝ 5×601.2x xx 1.2x（7）甲、乙两个工程队共同承包某一城市美化工程，已知甲队单独完成这项工程需要 30 天，若由甲队先做 10 天，剩下的工程由甲、 乙两队合作 8 天完成． 问乙队单独完成这项工程需要多少天？若设乙队单独完成这项工程需要x 天．则可列方程为（ ）10 810 1 110A ． 30 ＋ x＝1 B ． 10＋8＋ x ＝ 30C ． 30 ＋ 8( 第 6 章 数据与统计图表1．数据收集的方法： （ 1）直接途径：直接观察、测量、调查、实验；（ 2）间接途径：查阅文献资料、使用互联网查询． 2．数据整理的方法：分类、排序、分组、编码．30 ＋ x) ＝ 1D ．( 1－ 30) ＋ x ＝ 8（3.★★★★调查方式：（1）全面调查（普查）：人们根据研究自然现象或社会现象的需要，对所有的考察对象作调查．（2）抽样调查：人们在研究某个自然现象或社会现象时，因为不方便、不可能或不必要对所有对象进行调查，于是从中抽取一部分对象作调查分析．注意：抽取的样本中的个体要有代表性，样本容量要合适．总体：所要考察的对象的全体；个体：组成总体的每一个考察对象；样本：从总体中取出的一部分个体；样本容量：样本中个体的数目．练习：（1）PM2.5 指数是测控空气污染程度的一个重要指数．在一年中最可靠一种观测方法是（）A．随机选择 5 天进行观测 B ．选择某个月进行连续观测C．选择在春节7 天期间连续观测 D ．每个月都随机选中 5 天进行观测（2）下面的调查中，适宜采用全面调查方式的是（）A ．了解居民对废电池的处理情况B ．为了制作校服，了解某班同学的身高情况C．检测杭州的空气质量D ．了解某市居民的阅读情况（3）下面调查中，适合抽样调查的是（）A ．对全班同学的身高情况的调查B．登机前对旅客的安全检查C．对我县食品合格情况的调查D．学校组织学生进行体格检查4.★★★★★条形统计图：能清楚表示出每个项目的具体数目；折线统计图：能清楚反映事物的变化情况；扇形统计图：能清楚地表示出各部分在总体中所占的百分比．练习：（1）要反映嘉兴市一天内气温的变化情况宜采用（）A．折线统计图 B ．扇形统计图C．频数直方图D．条形统计图（2）如图是某手机店今年1－5 月份音乐手机销售额统计图．根据图中信息，可以判断相邻两个月音乐手机销售额变化最大的是（）A．1 月至 2 月 B ．2 月至 3 月C．3 月至4 月D．4 月至5 月（3）为了解某一路口某一时段的汽车流量，小明同学10 天中在同一时段统计通过该路口的汽车数量（单位：辆），将统计结果绘制成如下折线统计图：由此估计一个月（30 天）该时段通过该路口的汽车数量超过200 辆的天数为（）A ．9B ．10 C．12 D．15（4）如图分别是某班全体学生上学时乘车、步行、骑车人数的分布直方图和扇形统计图（两图都不完整），下列结论错误的是（）A ．该班总人数为50 人B ．步行人数为30 人C．乘车人数是骑车人数的 2.5 倍 D ．骑车人数占20%（5）某校根据去年初三学生参加中考的数学成绩的等级，绘制成如图的扇形统计图，则图中表示 A 等级的扇形的圆心角的大小为．5.列频数统计表的一般步骤：最大值－最小值的整数部分＋1．（1）选取组距，确定组数．组数＝组距（2）确定各组的边界值．第一组的起始边界值通常取得比最小数据要小一些，一般的做法是边界值比实际数据多取一位小数．（3）列表，填写组别和统计各组频数．6．★★★★★样本容量（数据个数）、频数、频率之间的相互关系样本容量＝频数÷频率频数＝样本容量×频率频率＝频数÷样本容量练习：（1）一组数据的样本容量是50，若某一小组的频率是0.24，则该组的频数为．（2）在全国初中数学希望杯竞赛中，某校有40 名同学进入复赛，把他们的成绩分为六组，第一组至第四组的人数分别为10，5，7，6，第五组的频率是0.2，则第六组的频率是．7.频数直方图：由若干个宽．等．于．组．距．，面．积．表．示．每．一．组．频．数．的长方形组成的统计图．注意：当各组组距都相等时，我们可以把组距看成“1”，那么各个小长方形的面积与它的高度在数值上相等，所以我们通常把小长方形的高度当成频数．8.组中值：每一组的两个边界值的平均数．后一组的组中值减去前一组的组中值＝组距．9．2017 年3 月28 日是全国中小学生安全教育日，某学校为加强学生的安全意识，组织了全校1500 名学生参加安全知识竞赛，从中抽取了部分学生成绩( 得分取正整数，满分为100 分) 进行统计．请根据尚未完成的频率分布表和频数分布直方图，解答下列问题：（1）这次抽取了名学生的竞赛成绩进行统计，其中：m＝，n＝；（2）补全频数分布直方图；（3）若成绩在70 分以下( 含70 分) 的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强新浙教版七年级下数学知识点汇总(期末复习宝典) 的学生约有多少人？1110. 某市在2017 年义务教育质量监测过程中，为了解学生的家庭教育情况，就八年级学生平时主要和谁在一起生活进行了抽样调查．下面是根据这次调查情况制作的不完整的频数分布表和扇形统计图．请根据上述信息，回答下列问题：（1）a＝，b＝；（2）在扇形统计图中，和外公外婆一起生活的学生所对应扇形圆心角的度数是；（3）若该市八年级学生共有 3 万人，估计不与父母一起生活的学生有人．11. 中学生带手机上学的现象越来越受到社会的关注，为此某记者随机调查了某市城区若干名中学生家长对这种现象的态度( 态度分为：A．无所谓；B．基本赞成；C．赞成； D ．反对) ．并将调查结果绘制成频数折线统计图 1 和扇形统计图2( 不完整) ．请根据图中提供的信息，解答下列问题：名中学生家长；（1）此次抽样调查中，共调查了（2）将图 1 补充完整；（3）根据抽样调查结果，请你估计该市城区6000 名中学生家长中有多少名家长持反对态度？12. 为了了解学生在一年中的课外阅读量，九（1）班对九年级800 名学生采用随机抽样的方式进行问卷调查，调查的结果分为四种情况： A.10 本以下；B.10～15 本；C.16～20 本；D .20 本以上．根据调查结果统计整理并制作了如图所示两幅统计图表：各种情况人数统计频数分布表课外阅读情况 A B C D频数20 x y 40（1）在这次调查中一共抽查了名学生；（2）表中x，y 的值分别为：x＝，y＝；（3）在扇形统计图中， C 部分所对应的扇形的圆心角是度；12（4）根据抽样调查结果，请估计九年级学生一年阅读课外书20 本以上的学生人数．13。

新浙教版七年级下册数学各章知识点第一章：平行线与相交线一、知识构造⎧⎧⎧⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎪⎪⎨⎨⎨⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎨⎪⎪⎩⎪⎪⎪⎩⎪⎩同位角相等，两直线平行直线平行的判定内错角相等，两直线平行同旁内角相等，两直线平行两直线平行，同位角相等平行线直线平行的性质两直线平行，内错角相等平行线与相交线两直线平行，同旁内角互补作一条线段等于已知线段尺规作图作一个角等于已知角相交线：补角、余角、对顶角二、要点诠释1.两条直线旳位置关系（1）在同一平面内，两条直线旳位置关系只有两种：相交与平行。

（2）平行线：在同一平面内，不相交旳两条直线交平行线。

2.几种特殊关系旳角（1）余角和补角：①定义：假如两个角旳和是直角，称这两个角互为余角；假如两个角旳和是平角，称这两个角互为补角。

②性质：同角或等角旳余角相等，同角或等角旳补角相等。

（2）对顶角：①定义：两条直线相交所得有公共顶点、没有公共边旳两个角②性质：对顶角相等。

（3）同位角、内错角、同旁内角两条直线分别与第三条直线相交，构成八个角。

①在两条直线同一侧并且在第三条直线旳旁边旳两个角叫同位角。

②在两条直线之间并且在第三条直线旳两旁旳两个角叫做内错角。

③在两条直线之间并且在第三条直线旳同旁旳两个角叫做同旁内角。

三、重要内容（1）平行线旳鉴定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角相等，两直线平行；平行于同一直线旳两条直线平行；垂直于同一条直线旳两直线平行。

（2）平行线旳性质两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；通过直线外一点有且只有一条直线与已知直线平行。

第二章：二元一次方程组2.1二元一次方程具有两个未知数，且具有未知数旳项旳次数都是一次旳方程叫做二元一次方程。

使二元一次方程两边旳值相等旳一对未知数旳值，叫做二元一次方程旳一种解。

2.2二元一次方程组由两个二元一次方程构成，并且具有两个未知数旳方程组，叫做二元一次方程组。

浙教版七年级下册数学知识点总结及例题第1章平行线1．在同一平面内，两条直线的位置关系只有两种：相交与平行．2．平行线的定义：在同一平面内．．．．．．，不相交的两条直线叫做平行线．“平行”用符号“∥”表示．思考：定义中为什么要有“在同一平面内”这个条件？3．平行线的基本事实：经过直线外．．．一点，有且只有一条直线与这条直线平行．思考：为什么要经过“直线外”一点？4．用三角尺和直尺画平行线的方法：一贴，二靠，三推，四画．（注意：作图题要写结论）5．★★★★★同位角、内错角、同旁内角判断过程：①画出给定的两个角的边（共三条边），公共边就是截线，剩下两条边就是被截线；②根据同位角、内错角、同旁内角的概念判断．同位角：在截线的同旁，被截线的同一侧．内错角：在截线的异侧，被截线之间．同旁内角：在截线的同旁，被截线之间．练习：如图，∠1和∠2是一对___________；∠2和∠3是一对___________；∠1和∠5是一对___________；∠1和∠3是一对___________；∠1和∠4是一对___________；∠4和∠5是一对___________；6．★★★★★平行线的判定（1）同位角相等，两直线平行；（2）内错角相等，两直线平行；（3）同旁内角互补，两直线平行；（4）平行线的定义：在同一平面内．．．．．．，不相交的两条直线平行；（5）平行于同一条直线的两条直线平行；（不必在同一平面内）（6）在同一平面内．．．．．．，垂直于同一条直线的两条直线互相平行．练习：如图，要得到AB∥CD，那么可添加条件______________________________．（写出全部）7．★★★★★平行线的性质（1）两直线平行，同位角相等；（2）两直线平行，内错角相等；（3）两直线平行，同旁内角互补．练习：如图，已知∠1＝58°，∠3＝42°，∠4＝138°，则∠2＝________°.8．★★★★★图形的平移（1）概念：一个图形沿某个方向移动，在移动的过程中，原图形上所有的点都沿同一个方向移动相等的距离，这样的图形运动叫做图形的平移．（2）性质：平移不改变图形的形状、大小和方向；一个图形和它经过平移所得的图形中，两组对应点的连线平行（或在同一条直线上）且相等．（3）描述一个图形的平移时，必须指出平移的方向．．！．．和距离练习：如图，已知△ABC和其平移后的△DEF．①点A的对应点是________，点B的对应点是________；②线段AC的对应线段是________；线段AB的对应线段是________；③平移的方向是__________，平移的距离是______________________．④若AC＝AB＝5，BC＝4，平移的距离是3，则CF＝________，DB＝________，AE＝________，四边形AEFC的周长是_________．9．★★★折叠问题方法：（1）找到折叠后和折叠前的图形，若折叠前的图形没有画出，自己必须补画上去；（2）找到折叠前后能重合的角，它们的度数相等；（3）利用平行线的性质、对顶角的性质、三角形的内角和、邻补角的性质、平角等计算出角度．练习：（1）如图，将一张纸条ABCD沿EF折叠，若折叠角∠FEC＝64°，则∠1＝________．（2）如图，有一条直的宽纸带，按图折叠，则∠α＝_______．（3）如图，将一条两边沿互相平行的纸带折叠，①写出图中所有与∠6相等的角；②若∠6＝x°，请用含x的代数式表示∠4的度数．第2章二元一次方程组1．★★★二元一次方程的概念三个条件：（1）含有两个未知数；（2）未知数的项的次数是一次；（3）都是整式．练习：方程①x －1 y＋2＝0，②xy ＝－2，③x 2－5x ＝5，④2x ＝1－3y 中，为二元一次方程的是____________．2．★★★★把二元一次方程变形成用关于一个未知数的代数式表示另一个未知数的形式（1）用含x 的代数式表示y ，则应变形为“y ＝…”的形式；（2）用含y 的代数式表示x ，则应变形为“x ＝…”的形式．练习：（1）已知方程2x －3y ＝7，用关于x 的代数式表示y 得_______________.（2）已知方程3x ＋2y ＝6，用关于y 的代数式表示x 得_______________.3．★二元一次方程的整数解方程3x ＋2y ＝21的正整数解是_________________________．4．二元一次方程组的概念三个条件：（1）两个一次方程；（2）两个方程共有两个未知数；（3）都是整式．5．★★★★★解二元一次方程组基本思路：消元消元方法：（1）代入消元；（2）加减消元．（注意：一定要把解代入原方程组检验，保证正确）练习：（1）⎩⎪⎨⎪⎧x －2y ＝23x ＋2y ＝10 （2）⎩⎪⎨⎪⎧y ＝3x 3x ＋y ＝126．★★★★常考题型练习：（1）已知代数式kx ＋b ，当x ＝2时值为－1，当x ＝3时值为－3，则a ＋b ＝_________．（2）若方程组⎩⎪⎨⎪⎧ax －2y ＝12x ＋by ＝5的解是⎩⎪⎨⎪⎧x ＝1y ＝a ，则b ＝________．（3）已知关于x ，y 的二元一次方程组⎩⎪⎨⎪⎧2x ＋3y ＝k x ＋2y ＝－1的解互为相反数，则k 的值是_______．（4）请你写出一个以⎩⎪⎨⎪⎧x ＝3y ＝－1为解的二元一次方程组：_______________. （5）已知方程组⎩⎪⎨⎪⎧2x ＋y ＝5x ＋3y ＝5，则x ＋y 的值为___________．7．某公司有甲、乙两个工程队．（1）两队共同完成一项工程，乙队先单独做1天后，再由两队合做2天完成了全部工程．已知甲队单独完成此项工程所需的天数是乙队单独完成所需的天数的三分之二，则甲、乙两队单独完成各需多少天？（2）甲工程队工作5天和乙工程队工作1天的费用和为34000元；甲工程队工作3天和乙工程队工作2天的费用和为26000元，则两队每天工作的费用各多少元？（3）该公司现承接一项（1）中2倍的工程由两队去做，且甲、乙两队不在同一天内合做，又必须各自做整数天，试问甲、乙两队各需做多少天？若按（2）中的付费，你认为哪种方式付费最少？8．某企业承接了一批礼盒的制作业务，该企业进行了前期的试生产，如图 1 所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图 2 所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）（1）该企业原计划用若干天加工纸箱 300 个，后来由于提升工作效率，实际加工时每天加工速度为原计划的 1.5 倍，这样提前 3 天超额完成了任务，且总共比原计划多加工 15 个，问原计划每天加工礼盒多少个；（2）若该企业购进正方形纸板 550 张，长方形纸板 1200 张．问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完；（3）该企业某一天使用的材料清单上显示，这天一共使用正方形纸板 100 张，长方形纸板a 张，全部加工成上述两种纸盒，且 150＜a＜168，试求在这一天加工两种纸盒时a 的所有可能值．（请直接写出结果）第3章整式的乘除1．★★★★★公式与法则（1）同底数幂的乘法：底数不变，指数相加．a m·a n＝a m＋n（m，n都是正整数）（2）幂的乘方：底数不变，指数相乘．(a m) n＝a mn（m，n都是正整数）（3）积的乘方：等于把积的每一个因式分别乘方，再把所得的幂相乘．(ab) n＝a n b n（n都是正整数）（4）乘法公式：①平方差公式：(a＋b)(a－b)＝a2－b2②完全平方公式：(a＋b)2＝a2＋b2＋2ab(a－b)2＝a2＋b2－2ab（5）同底数幂的除法：底数不变，指数相减．a m÷a n＝a m－n（a≠0）（6）a0＝1（a≠0）（7）a－p＝1a p（a≠0），当a是整数时，先指数变正，再倒数．当a是分数时，先把底数变倒数，再指数变正．（8）单项式乘单项式：系数、同底数幂分别相乘，其余字母连同它的指数不变，作为积的因式．（9）单项式乘多项式：用单项式去乘多项式的每一项，再把所得的积相加．m(a＋b)＝ma＋mb（10）多项式乘多项式：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加． (a＋n)(b＋m)＝ab＋am＋nb＋nm（11）单项式除以单项式：把系数、同底数幂分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式．（12）多项式除以单项式：先把这个多项式的每一项除以这个单项式，再把所得的商相加．(a＋b＋c)÷m＝a÷m＋b÷m＋c÷m（m≠0）练习：（1）(2a2)3＝___________；3y·(－2x2y3)＝___________；(9x3－3x)÷(3x)＝___________；(－2)0＝___________；(－3)－3＝___________；(－23)－2＝___________；(2a－1)2＝_______________；(a3)2•a－2a3• a4＝______________；(1－2a)2－(2－a)(1＋a)＝_______________；(x－2)(x＋2)－(1－2x)2＝_________________．2．★★★★★用科学记数法表示较小的数：a×10－n（1≤|a|＜10）方法：第一个不为零的数前面有几个零就是负几次方．练习：（1）科学记数法表示0.0000103＝_________________．（2）1纳米＝0.000000001米，则0.33纳米＝________米．（用科学计数法表示）（3）把用科学记数法表示的数7.2×10－4写成小数形式为___________________．3．★★★★常考题型（1）已知a＋b＝3，ab＝－1，则a2＋b2＝___________．（2）若多项式x2－(x－a)(x＋2b)＋4的值与x的取值大小无关，那么a，b一定满足_____________．（3）关于x的代数式(3－ax)(x2＋2x－1)的展开式中不含x2项，则a＝___________．（4）若代数式x2＋3x＋2可以表示为(x－1)2＋a(x－1)＋b的形式，则a＋b的值是．（5）若(x－m)(2x＋3)＝2x2－nx＋3，则m－n＝__________．（6）若(2x－5y)2＝(2x＋5y)2＋M，则代数式M应是__________________．（7）如图，一块砖的外侧面积为a，那么图中残留部分的墙面的面积为_______________．（8）如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条“之”字路，余下部分绿化，道路的宽为a米，则绿化的面积为________________m2．（9）定义一种对正整数n的“F运算”：①当n为奇数时，结果为3n＋5；②当n为偶数时，结果为n2k（其中k是使n2k为奇数的正整数），并且运算重复进行．例如，取n＝26，则：若n＝449，则第449次“F运算”的结果是_________．第4章因式分解1．★★★★因式分解的概念：把一个多项式．．．化成几个整式的积．．．．的形式，叫做因式分解，也叫分解因式．因式分解和整式乘法是互逆关系．练习：下列从左到右边的变形，是因式分解的是（）A．(3－x)(3＋x)＝9－x2 B．(y＋1)(y－3)＝－(3－y)(y＋1)C．4yz－2y2z＋z＝2y(2z－yz)＋z D．－8x2＋8x－2＝－2(2x－1)22．★★★★★因式分解的方法（1）提公因式法：先确定应提取的公因式，然后用公因式去除这个多项式，所得的商作为另一个因式，最后把多项式写成这两个因式的积的形式．ma＋mb＋mc＝m(a＋b＋c)确定公因式的方法：系数的最大公因数和相同字母的最低次幂．即：(□)2－(△)2＝(□＋△)(□－△)②完全平方公式：a2＋2ab＋b2＝(a＋b)2a2－2ab＋b2＝(a－b)2即：(□)2±2(□)(△)＋(△)2＝(□±△)2练习：（1）下列多项式能用完全平方公式分解因式的是（）A．x2－4 B．x2＋2x＋4 C．4x2＋4x＋1 D．x2＋y2（2）下列多项式能用平方差公式分解因式的是（）A．x2＋4 B．x2＋2x＋1 C．x2－4x D．－x2＋9（3）因式分解：①a3－9a＝_____________________. ②x－xy2＝_____________________．③x2－8x＋16＝_________________. ④3ax2－6axy＋3ay2＝________________．⑤a3－4a(a－1)＝_________________.⑥(x－2y)2－x＋2y＝________________．3．★★★★完全平方式：我们把多项式a2＋2ab＋b2和a2－2ab＋b2叫做完全平方式．即：(□)2±2(□)(△)＋(△)2练习：（1）若x2＋(2p－3)x＋9是完全平方式，则p的值等于＝____________．（2）多项式9x2－x＋1加上一个单项式后成为一个整式的平方，请写出3个满足条件的单项式：_____________________________．4.十字相乘法：十字分解法的方法简单来讲就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项。

浙教版七年级数学下册知识点汇总
七年级（下册）
1. 平行线
1.1. 平行线
在同一个平面内，不相交的两条直线叫做平行线。

“平行”用符号“M B M A B A M B M A B A ÷÷=⨯⨯=,bc ad c d b a d c b a bd ac d c b =⋅=÷=⋅;a c b c
b c ±±a 568=-x x 取组距，
确定组数：组数通常取大于 （最大值-最小值）÷组距 的最小整数，通常分5组；
2.确定各组的边界值：为了使数据不落在边界上，边界值可以比实际数据多取一位小数；
3.列表，填写组别和统计各组频数
1.2. 频数直方图
根据数据的频数表，可以用统计图把它直观地表示出来。

由若干个宽等于组距，面积表示每一组频数的长方形组成的统计图叫做频数直方图，简称直方图。

当各组组距都相等时，可以把组距看成“1”，那么各个小长方形的面积与它的高度在数值上相等，可以用纵轴上的刻度表示频数。

浙教版七年级下册数学知识点总结及例题第1章平行线1．在同一平面内，两条直线的位置关系只有两种：相交与平行．2．平行线的定义：在同一平面内．．．．．．，不相交的两条直线叫做平行线．“平行”用符号“∥”表示．思考：定义中为什么要有“在同一平面内”这个条件？3．平行线的基本事实：经过直线外．．．一点，有且只有一条直线与这条直线平行．思考：为什么要经过“直线外”一点？4．用三角尺和直尺画平行线的方法：一贴，二靠，三推，四画．（注意：作图题要写结论）5．★★★★★同位角、内错角、同旁内角判断过程：①画出给定的两个角的边（共三条边），公共边就是截线，剩下两条边就是被截线；②根据同位角、内错角、同旁内角的概念判断．同位角：在截线的同旁，被截线的同一侧．内错角：在截线的异侧，被截线之间．同旁内角：在截线的同旁，被截线之间．练习：如图，∠1和∠2是一对___________；∠2和∠3是一对___________；∠1和∠5是一对___________；∠1和∠3是一对___________；∠1和∠4是一对___________；∠4和∠5是一对___________；6．★★★★★平行线的判定（1）同位角相等，两直线平行；（2）内错角相等，两直线平行；（3）同旁内角互补，两直线平行；（4）平行线的定义：在同一平面内．．．．．．，不相交的两条直线平行；（5）平行于同一条直线的两条直线平行；（不必在同一平面内）（6）在同一平面内．．．．．．，垂直于同一条直线的两条直线互相平行．练习：如图，要得到AB∥CD，那么可添加条件______________________________．（写出全部）7．★★★★★平行线的性质（1）两直线平行，同位角相等；（2）两直线平行，内错角相等；（3）两直线平行，同旁内角互补．练习：如图，已知∠1＝58°，∠3＝42°，∠4＝138°，则∠2＝________°.8．★★★★★图形的平移（1）概念：一个图形沿某个方向移动，在移动的过程中，原图形上所有的点都沿同一个方向移动相等的距离，这样的图形运动叫做图形的平移．（2）性质：平移不改变图形的形状、大小和方向；一个图形和它经过平移所得的图形中，两组对应点的连线平行（或在同一条直线上）且相等．（3）描述一个图形的平移时，必须指出平移的方向．．！．．和距离练习：如图，已知△ABC和其平移后的△DEF．①点A的对应点是________，点B的对应点是________；②线段AC的对应线段是________；线段AB的对应线段是________；③平移的方向是__________，平移的距离是______________________．④若AC＝AB＝5，BC＝4，平移的距离是3，则CF＝________，DB＝________，AE＝________，四边形AEFC的周长是_________．9．★★★折叠问题方法：（1）找到折叠后和折叠前的图形，若折叠前的图形没有画出，自己必须补画上去；（2）找到折叠前后能重合的角，它们的度数相等；（3）利用平行线的性质、对顶角的性质、三角形的内角和、邻补角的性质、平角等计算出角度．练习：（1）如图，将一张纸条ABCD沿EF折叠，若折叠角∠FEC＝64°，则∠1＝________．（2）如图，有一条直的宽纸带，按图折叠，则∠α＝_______．（3）如图，将一条两边沿互相平行的纸带折叠，①写出图中所有与∠6相等的角；②若∠6＝x°，请用含x的代数式表示∠4的度数．第2章 二元一次方程组1．★★★二元一次方程的概念三个条件：（1）含有两个未知数；（2）未知数的项的次数是一次；（3）都是整式．练习：方程①x －1 y＋2＝0，②xy ＝－2，③x 2－5x ＝5，④2x ＝1－3y 中，为二元一次方程的是____________．2．★★★★把二元一次方程变形成用关于一个未知数的代数式表示另一个未知数的形式（1）用含x 的代数式表示y ，则应变形为“y ＝…”的形式；（2）用含y 的代数式表示x ，则应变形为“x ＝…”的形式．练习：（1）已知方程2x －3y ＝7，用关于x 的代数式表示y 得_______________.（2）已知方程3x ＋2y ＝6，用关于y 的代数式表示x 得_______________.3．★二元一次方程的整数解方程3x ＋2y ＝21的正整数解是_________________________．4．二元一次方程组的概念三个条件：（1）两个一次方程；（2）两个方程共有两个未知数；（3）都是整式．5．★★★★★解二元一次方程组基本思路：消元消元方法：（1）代入消元；（2）加减消元．（注意：一定要把解代入原方程组检验，保证正确）练习：（1）⎩⎪⎨⎪⎧x －2y ＝23x ＋2y ＝10 （2）⎩⎪⎨⎪⎧y ＝3x 3x ＋y ＝126．★★★★常考题型练习：（1）已知代数式kx ＋b ，当x ＝2时值为－1，当x ＝3时值为－3，则a ＋b ＝_________．（2）若方程组⎩⎪⎨⎪⎧ax －2y ＝12x ＋by ＝5的解是⎩⎪⎨⎪⎧x ＝1y ＝a ，则b ＝________．（3）已知关于x ，y 的二元一次方程组⎩⎪⎨⎪⎧2x ＋3y ＝k x ＋2y ＝－1的解互为相反数，则k 的值是_______．（4）请你写出一个以⎩⎪⎨⎪⎧x ＝3y ＝－1为解的二元一次方程组：_______________. （5）已知方程组⎩⎪⎨⎪⎧2x ＋y ＝5x ＋3y ＝5，则x ＋y 的值为___________．7．某公司有甲、乙两个工程队．（1）两队共同完成一项工程，乙队先单独做1天后，再由两队合做2天完成了全部工程．已知甲队单独完成此项工程所需的天数是乙队单独完成所需的天数的三分之二，则甲、乙两队单独完成各需多少天？（2）甲工程队工作5天和乙工程队工作1天的费用和为34000元；甲工程队工作3天和乙工程队工作2天的费用和为26000元，则两队每天工作的费用各多少元？（3）该公司现承接一项（1）中2倍的工程由两队去做，且甲、乙两队不在同一天内合做，又必须各自做整数天，试问甲、乙两队各需做多少天？若按（2）中的付费，你认为哪种方式付费最少？8．某企业承接了一批礼盒的制作业务，该企业进行了前期的试生产，如图 1 所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图 2 所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）（1）该企业原计划用若干天加工纸箱 300 个，后来由于提升工作效率，实际加工时每天加工速度为原计划的 1.5 倍，这样提前 3 天超额完成了任务，且总共比原计划多加工 15 个，问原计划每天加工礼盒多少个；（2）若该企业购进正方形纸板 550 张，长方形纸板 1200 张．问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完；（3）该企业某一天使用的材料清单上显示，这天一共使用正方形纸板 100 张，长方形纸板a 张，全部加工成上述两种纸盒，且 150＜a＜168，试求在这一天加工两种纸盒时a 的所有可能值．（请直接写出结果）第3章整式的乘除1．★★★★★公式与法则（1）同底数幂的乘法：底数不变，指数相加．a m·a n＝a m＋n（m，n都是正整数）（2）幂的乘方：底数不变，指数相乘．(a m) n＝a mn（m，n都是正整数）（3）积的乘方：等于把积的每一个因式分别乘方，再把所得的幂相乘．(ab) n＝a n b n（n都是正整数）（4）乘法公式：①平方差公式：(a＋b)(a－b)＝a2－b2②完全平方公式：(a＋b)2＝a2＋b2＋2ab(a－b)2＝a2＋b2－2ab（5）同底数幂的除法：底数不变，指数相减．a m÷a n＝a m－n（a≠0）（6）a0＝1（a≠0）（7）a－p＝1a p（a≠0），当a是整数时，先指数变正，再倒数．当a是分数时，先把底数变倒数，再指数变正．（8）单项式乘单项式：系数、同底数幂分别相乘，其余字母连同它的指数不变，作为积的因式．（9）单项式乘多项式：用单项式去乘多项式的每一项，再把所得的积相加．m(a＋b)＝ma＋mb（10）多项式乘多项式：先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加． (a＋n)(b＋m)＝ab＋am＋nb＋nm（11）单项式除以单项式：把系数、同底数幂分别相除，作为商的因式，对于只在被除式里含有的字母，则连同它的指数作为商的一个因式．（12）多项式除以单项式：先把这个多项式的每一项除以这个单项式，再把所得的商相加．(a＋b＋c)÷m＝a÷m＋b÷m＋c÷m（m≠0）练习：（1）(2a2)3＝___________；3y·(－2x2y3)＝___________；(9x3－3x)÷(3x)＝___________；(－2)0＝___________；(－3)－3＝___________；(－23)－2＝___________；(2a－1)2＝_______________；(a3)2•a－2a3• a4＝______________；(1－2a)2－(2－a)(1＋a)＝_______________；(x－2)(x＋2)－(1－2x)2＝_________________．2．★★★★★用科学记数法表示较小的数：a×10－n（1≤|a|＜10）方法：第一个不为零的数前面有几个零就是负几次方．练习：（1）科学记数法表示0.0000103＝_________________．（2）1纳米＝0.000000001米，则0.33纳米＝________米．（用科学计数法表示）（3）把用科学记数法表示的数7.2×10－4写成小数形式为___________________．3．★★★★常考题型（1）已知a＋b＝3，ab＝－1，则a2＋b2＝___________．（2）若多项式x2－(x－a)(x＋2b)＋4的值与x的取值大小无关，那么a，b一定满足_____________．（3）关于x的代数式(3－ax)(x2＋2x－1)的展开式中不含x2项，则a＝___________．（4）若代数式x2＋3x＋2可以表示为(x－1)2＋a(x－1)＋b的形式，则a＋b的值是．（5）若(x－m)(2x＋3)＝2x2－nx＋3，则m－n＝__________．（6）若(2x－5y)2＝(2x＋5y)2＋M，则代数式M应是__________________．（7）如图，一块砖的外侧面积为a，那么图中残留部分的墙面的面积为_______________．（8）如图所示，某住宅小区内有一长方形地块，想在长方形地块内修筑同样宽的两条“之”字路，余下部分绿化，道路的宽为a米，则绿化的面积为________________m2．（9）定义一种对正整数n的“F运算”：①当n为奇数时，结果为3n＋5；②当n为偶数时，结果为n2k（其中k是使n2k为奇数的正整数），并且运算重复进行．例如，取n＝26，则：若n＝449，则第449次“F运算”的结果是_________．第4章因式分解1．★★★★因式分解的概念：把一个多项式．．．．的形式，叫做因式分解，也叫分解．．．化成几个整式的积因式．因式分解和整式乘法是互逆关系．练习：下列从左到右边的变形，是因式分解的是（）A．(3－x)(3＋x)＝9－x2 B．(y＋1)(y－3)＝－(3－y)(y＋1)C．4yz－2y2z＋z＝2y(2z－yz)＋z D．－8x2＋8x－2＝－2(2x－1)22．★★★★★因式分解的方法（1）提公因式法：先确定应提取的公因式，然后用公因式去除这个多项式，所得的商作为另一个因式，最后把多项式写成这两个因式的积的形式．ma＋mb＋mc＝m(a＋b＋c)确定公因式的方法：系数的最大公因数和相同字母的最低次幂．Array（2）用乘法公式因式分解：①平方差公式：a2－b2＝(a＋b)(a－b)即：(□)2－(△)2＝(□＋△)(□－△)②完全平方公式：a2＋2ab＋b2＝(a＋b)2a2－2ab＋b2＝(a－b)2即：(□)2±2(□)(△)＋(△)2＝(□±△)2练习：（1）下列多项式能用完全平方公式分解因式的是（）A．x2－4 B．x2＋2x＋4 C．4x2＋4x＋1 D．x2＋y2（2）下列多项式能用平方差公式分解因式的是（）A．x2＋4 B．x2＋2x＋1 C．x2－4x D．－x2＋9（3）因式分解：①a3－9a＝_____________________. ②x－xy2＝_____________________．③x2－8x＋16＝_________________. ④3ax2－6axy＋3ay2＝________________．⑤a3－4a(a－1)＝_________________.⑥(x－2y)2－x＋2y＝________________．3．★★★★完全平方式：我们把多项式a2＋2ab＋b2和a2－2ab＋b2叫做完全平方式．即：(□)2±2(□)(△)＋(△)2练习：（1）若x2＋(2p－3)x＋9是完全平方式，则p的值等于＝____________．（2）多项式9x2－x＋1加上一个单项式后成为一个整式的平方，请写出3个满足条件的单项式：_____________________________．4.十字相乘法：十字分解法的方法简单来讲就是：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项。

浙教版七年级下册数学各章知识点第一章：平行线与相交线一、知识结构⎧⎧⎧⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎪⎪⎨⎨⎨⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎨⎪⎪⎩⎪⎪⎪⎩⎪⎩同位角相等，两直线平行直线平行的判定内错角相等，两直线平行同旁内角相等，两直线平行两直线平行，同位角相等平行线直线平行的性质两直线平行，内错角相等平行线与相交线两直线平行，同旁内角互补作一条线段等于已知线段尺规作图作一个角等于已知角相交线：补角、余角、对顶角二、要点诠释1.两条直线的位置关系（1）在同一平面内，两条直线的位置关系只有两种：相交与平行。

（2）平行线：在同一平面内，不相交的两条直线交平行线。

2.几种特殊关系的角（1）余角和补角：①定义：如果两个角的和是直角，称这两个角互为余角；如果两个角的和是平角，称这两个角互为补角。

②性质：同角或等角的余角相等，同角或等角的补角相等。

（2）对顶角：①定义：两条直线相交所得有公共顶点、没有公共边的两个角②性质：对顶角相等。

（3）同位角、内错角、同旁内角两条直线分别与第三条直线相交，构成八个角。

①在两条直线同一侧并且在第三条直线的旁边的两个角叫同位角。

②在两条直线之间并且在第三条直线的两旁的两个角叫做内错角。

③在两条直线之间并且在第三条直线的同旁的两个角叫做同旁内角。

三、主要内容（1）平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角相等，两直线平行；平行于同一直线的两条直线平行；垂直于同一条直线的两直线平行。

（2）平行线的性质两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；经过直线外一点有且只有一条直线与已知直线平行。

第二章：二元一次方程组2.1二元一次方程含有两个未知数，且含有未知数的项的次数都是一次的方程叫做二元一次方程。

使二元一次方程两边的值相等的一对未知数的值，叫做二元一次方程的一个解。

2.2二元一次方程组由两个二元一次方程组成，并且含有两个未知数的方程组，叫做二元一次方程组。

新浙教版七年级下册数学各章知识点第一章:平行线与相交线一、知识结构⎧⎧⎧⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎪⎪⎨⎨⎨⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎨⎪⎪⎩⎪⎪⎪⎩⎪⎩同位角相等，两直线平行直线平行的判定内错角相等，两直线平行同旁内角相等，两直线平行两直线平行，同位角相等平行线直线平行的性质两直线平行，内错角相等平行线与相交线两直线平行，同旁内角互补作一条线段等于已知线段尺规作图作一个角等于已知角相交线：补角、余角、对顶角二、要点诠释1.两条直线的位置关系(1)在同一平面内,两条直线的位置关系只有两种:相交与平行。

(2)平行线:在同一平面内,不相交的两条直线交平行线。

2.几种特殊关系的角(1)余角与补角:①定义:如果两个角的与就是直角,称这两个角互为余角;如果两个角的与就是平角,称这两个角互为补角。

②性质:同角或等角的余角相等,同角或等角的补角相等。

(2)对顶角:①定义:两条直线相交所得有公共顶点、没有公共边的两个角②性质:对顶角相等。

(3)同位角、内错角、同旁内角两条直线分别与第三条直线相交,构成八个角。

①在两条直线同一侧并且在第三条直线的旁边的两个角叫同位角。

②在两条直线之间并且在第三条直线的两旁的两个角叫做内错角。

③在两条直线之间并且在第三条直线的同旁的两个角叫做同旁内角。

三、主要内容(1)平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角相等,两直线平行;平行于同一直线的两条直线平行;垂直于同一条直线的两直线平行。

(2)平行线的性质两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;经过直线外一点有且只有一条直线与已知直线平行。

第二章:二元一次方程组2、1二元一次方程含有两个未知数,且含有未知数的项的次数都就是一次的方程叫做二元一次方程。

使二元一次方程两边的值相等的一对未知数的值,叫做二元一次方程的一个解。

2、2二元一次方程组由两个二元一次方程组成,并且含有两个未知数的方程组,叫做二元一次方程组。

浙教版七年级下册数学各章知识点第一章：平行线与相交线一、知识结构⎧⎧⎧⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎪⎪⎨⎨⎨⎪⎪⎩⎪⎪⎪⎪⎧⎪⎪⎨⎪⎪⎩⎪⎪⎪⎩⎪⎩同位角相等，两直线平行直线平行的判定内错角相等，两直线平行同旁内角相等，两直线平行两直线平行，同位角相等平行线直线平行的性质两直线平行，内错角相等平行线与相交线两直线平行，同旁内角互补作一条线段等于已知线段尺规作图作一个角等于已知角相交线：补角、余角、对顶角二、要点诠释1.两条直线的位置关系（1）在同一平面内，两条直线的位置关系只有两种：相交与平行。

（2）平行线：在同一平面内，不相交的两条直线交平行线。

2.几种特殊关系的角（1）余角和补角：①定义：如果两个角的和是直角，称这两个角互为余角；如果两个角的和是平角，称这两个角互为补角。

②性质：同角或等角的余角相等，同角或等角的补角相等。

（2）对顶角：①定义：两条直线相交所得有公共顶点、没有公共边的两个角②性质：对顶角相等。

（3）同位角、内错角、同旁内角两条直线分别与第三条直线相交，构成八个角。

①在两条直线同一侧并且在第三条直线的旁边的两个角叫同位角。

②在两条直线之间并且在第三条直线的两旁的两个角叫做内错角。

③在两条直线之间并且在第三条直线的同旁的两个角叫做同旁内角。

三、主要内容（1）平行线的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角相等，两直线平行；平行于同一直线的两条直线平行；垂直于同一条直线的两直线平行。

（2）平行线的性质两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；经过直线外一点有且只有一条直线与已知直线平行。

第二章：二元一次方程组2.1二元一次方程含有两个未知数，且含有未知数的项的次数都是一次的方程叫做二元一次方程。

使二元一次方程两边的值相等的一对未知数的值，叫做二元一次方程的一个解。

2.2二元一次方程组由两个二元一次方程组成，并且含有两个未知数的方程组，叫做二元一次方程组。

新浙教版七年级下册数学各章知识点第一章：平行线与订交线一、知识构造同位角相等，两直线平行直线平行的判断内错角相等，两直线平行同旁内角相等，两直线平行两直线平行，同位角相等平行线与订交线平行线直线平行的性质两直线平行，内错角相等两直线平行，同旁内角互补尺规作图作一条线段等于已知线段作一个角等于已知角订交线：补角、余角、对顶角二、重点解说1. 两条直线的地点关系（1）在同一平面内，两条直线的地点关系只有两种：订交与平行。

（2）平行线：在同一平面内，不订交的两条直线交平行线。

2. 几种特别关系的角（1）余角和补角：①定义：假如两个角的和是直角，称这两个角互为余角；假如两个角的和是平角，称这两个角互为补角。

②性质：同角或等角的余角相等，同角或等角的补角相等。

（2）对顶角：①定义：两条直线订交所得有公共极点、没有公共边的两个角②性质：对顶角相等。

（3）同位角、内错角、同旁内角两条直线分别与第三条直线订交，构成八个角。

①在两条直线同一侧而且在第三条直线的旁边的两个角叫同位角。

②在两条直线之间而且在第三条直线的两旁的两个角叫做内错角。

③在两条直线之间而且在第三条直线的同旁的两个角叫做同旁内角。

三、主要内容（1）平行线的判断：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角相等，两直线平行；平行于同向来线的两条直线平行；垂直于同一条直线的两直线平行。

（2）平行线的性质两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；经过直线外一点有且只有一条直线与已知直线平行。

第二章：二元一次方程组2.1 二元一次方程含有两个未知数，且含有未知数的项的次数都是一次的方程叫做二元一次方程。

使二元一次方程两边的值相等的一对未知数的值，叫做二元一次方程的一个解。

2.2 二元一次方程组由两个二元一次方程构成，而且含有两个未知数的方程组，叫做二元一次方程组。

同时知足二元一次方程组中各个方程的解，叫做这个二元一次方程组的解。

浙教版初中数学七年级下册知识点（整理）及典型例题第一章三角形的初步认识1.1认识三角形①由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

“三角形”用符号“△”表示，顶点是ABC的三角形记做“△ABC”读作“三角形ABC”。

由两点之间线段最短，可以得到如下性质：三角形任何两边的和大于第三边。

②三角形三个内角的和等于180°。

由三角形一条边的延长线和另一条相邻的边组成的角，叫做该三角形的外角。

三角形的一个外角等于和它不相邻两个内角的和。

1.2三角形的平分线和中线在三角形中，一个内角的角平分线与它对边相交，这个角的顶点与交点之间的线段叫做三角形的三角形的平分线。

在三角形中，连结一个顶点与它对边中点的线段，叫做这个三角形的中线。

1.3三角形的高从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高。

锐角三角形的三条高在三角形的内部，垂足在相应顶点的对边上。

直角三角形的直角边上的高分别与另一条直角边重合，垂足都是直角的顶点。

而在钝角三角形中，夹钝角两边上的高都在三角形的外部，它们的垂足都在相应顶点的对边的延长线上。

1.4全等三角形能够重合的两个图形称为全等图形。

能够重合的两个三角形称为全等三角形。

两个全等三角形重合时，能互相重合的顶点叫做全等三角形的对应顶点，互相重合的边叫做全等三角形的对应边，互相重合的角叫做全等三角形的对应角。

“全等”可用符号“≌”来表示。

全等三角形的性质：全等三角形对应边相等，对应角相等。

1.5三角形全等的条件①三边对应相等的两个三角形全等（简写成“边边边”或“SSS”）。

当三角形三边长确定是，三角形的形状、大小完全被确定，这个性质叫做三角形的稳定性，这是三角形特有的性质。

②有一个角和夹这个角的两边对应相等的两个三角形全等（简写成“边角边”或“SAS ”）。

垂直于一条线段，并且平分这条线段的直线叫做这条线段的垂直平分线，简称中垂线。