2012-2013海淀区九年级期末考试分析

北京市海淀区2012届上学期初中九年级期末练习英语试卷 2012.1一、听对话，从下面各题所给的A、B、C三幅图片中选择与对话内容相符的图片。

每段对话读两遍。

（共4分，每小题1分）二、听对话或独白，根据对话或独白的内容，从下面各题所给的A、B、C三个选项中选择最佳选项。

每段对话或独白读两遍。

（共12分，每小题1分）请听一段对话，完成第5至第6小题。

5. How is Kate going to Qingdao?A. By plane.B. By car.C. By ship·6. What is she going to do there?A. She's going sightseeing.B. She's going to study in Qingdao.C. She's visiting her grandparents.请听一段对话，完成第7至第8小题。

7. What did the girl enjoy about last year's festival?A. Singing with other students.B. Playing in the school band.C. Listening to nice music.8. When does the festival start this year?A. October 17.B. October 7.C. October 6.请听一段对话，完成第9至第10小题。

9. Why is the man interested in this job?A. He likes public speaking.B. He likes working on weekends.C. He likes travelling and meeting people.10. How many foreign languages can the man speak?A. One.B. Two.C. Three.请听一段对话，完成第11至第13小题。

海淀区九年级第二学期期末练习数学试卷答案及评分参考2012. 6 说明: 与参考答案不同, 但解答正确相应给分.一、选择题（本题共32分，每小题4分）1. B2. C3. A4. C5. B6. D7. D8. C二、填空题（本题共16分，每小题4分）9. 10. 511. 12 12．8。

（每空各2分）三、解答题（本题共30分，每小题5分）13．解：= …………………………………………………4分= . …………………………………………………5分14．解：去分母，得．………………………………2分. ……………………………………………………3分整理，得．解得．………………………………………………………………4分经检验，是原方程的解．所以原方程的解是．……………………………………………………5分15．证明：∵AC //EG，∴．…………1分∵BC //EF，∴．∴．…………………………………………2分在△ABC和△GFE中，∴△ABC≌△GFE．…………………………………………………4分∴．…………………………………………………5分16. 解：原式= ……………………………………………2分= …………………………………………………3分= …………………………………………………4分由，得. ∴原式= . …………………………………………………5分17．解：（1）依题意设一次函数解读式为. …………………………………1分∵点A( )在一次函数图象上，∴. ∴k=1. ……………………………………………………2分∴一次函数的解读式为. …………………………………3分（2）的度数为15︒或105︒．（每解各1分）……………………5分18．解: ∵∠ADB=∠CBD =90︒，∴DE∥CB. ∵BE∥CD，∴四边形BEDC是平行四边形. ………1分∴BC=DE. 在Rt△ABD中，由勾股定理得. ………2分设，则．∴．在Rt△BDE中，由勾股定理得. ∴．……………………………………………………3分∴．∴．……………………………………………………4分∴………… 5分四、解答题（本题共20分，第19题、第20题各5分，第21题6分, 第22题4分）19．解：（1）甲图文社收费（元）与印制数（张）的函数关系式为. ……1分（2）设在甲、乙两家图文社各印制了张、张宣传单，依题意得………………………………………… 2分解得……………………………………………… 3分答：在甲、乙两家图文社各印制了800张、700张宣传单. ………………4分（3）乙. ……………………………………………………… 5分20.（1）证明：连结OC.∴∠DOC =2∠ A. …………1分∵∠ D = 90°，∴∠D+∠DOC =90°. ∴∠OCD=90°. ∵OC是⊙O的半径，∴直线CD是⊙O的切线. ………………………………………………2分（2）解: 过点O作OE⊥BC于E, 则∠OEC=90︒. ∵BC=4, ∴CE= BC=2. ∵BC//AO, ∴∠OCE=∠DOC. ∵∠COE+∠OCE=90︒, ∠D+∠DOC=90︒, ∴∠COE=∠ D. ……………………………………………………3分∵= , ∴. ∵∠OEC =90︒, CE=2, ∴. 在Rt △OEC中, 由勾股定理可得在Rt △ODC中, 由，得, ……………………4分由勾股定理可得∴…………………………………5分21．解：（1）. 所以李老师一共调查了20名学生. …………………1分（2）C类女生有 3 名，D类男生有 1 名；补充条形统计图略. 说明：其中每空1分，条形统计图1分. ……………………………………4分（3）解法一：由题意画树形图如下：………………………5分从树形图看出，所有可能出现的结果共有6种，且每种结果出现的可能性相等，所选两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P(所选两位同学恰好是一位男同学和一位女同学)= . ………………6分解法二：由题意列表如下：A类D类男女女男（男，男）（女，男）（女，男）女（男，女）（女，女）（女，女）………………………5分由上表得出，所有可能出现的结果共有6种，且每种结果出现的可能性相等，所选两位同学恰好是一位男同学和一位女同学的结果共有3种. 所以P(所选两位同学恰好是一位男同学和一位女同学)= . ………………6分22.解：（1）画图如下：(答案不唯一) …………………………………2分图 3 （2）图3中△FGH的面积为. …………………………………4分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23. 解：（1）∵抛物线与x轴交于A、B两点，∴由①得，由②得，∴m的取值范围是且．……………………………………………2分（2）∵点A、B是抛物线与x轴的交点，∴令，即．解得，．∵，∴∵点A在点B左侧，∴点A的坐标为，点B的坐标为. …………………………3分∴OA=1，OB= ．∵OA : OB=1 : 3，∴. ∴．∴抛物线的解读式为．………………………………………4分（3）∵点C是抛物线与y轴的交点，∴点C的坐标为. 依题意翻折后的图象如图所示．令，即．解得, ．∴新图象经过点 D . 当直线经过D点时，可得. 当直线经过C点时，可得．当直线与函数的图象仅有一个公共点P(x0, y0)时，得.整理得由，得．结合图象可知，符合题意的b的取值范围为或．……………7分说明：（2分），每边不等式正确各1分；（1分）24.解：（1）∵，∴抛物线的顶点B的坐标为. ……………………………1分（2）令，解得, . ∵抛物线与x轴负半轴交于点A，∴ A (m, 0), 且m<0. …………………………………………………2分过点D作DF⊥x轴于 F. 由D为BO中点，DF//BC, 可得CF=FO= ∴DF = 由抛物线的对称性得AC = OC. ∴AF : AO=3 : 4. ∵DF //EO, ∴△AFD∽△AOE.∴由 E (0, 2)， B ，得OE=2, DF= . ∴∴m = -6. ∴抛物线的解读式为. ………………………………………3分（3）依题意，得A（-6,0）、B (-3, 3)、C (-3, 0).可得直线OB的解读式为, 直线BC为. 作点C关于直线BO的对称点 C '(0，3)，连接AC '交BO 于M，则M即为所求. 由A（-6，0），C'(0, 3)，可得直线AC'的解读式为. 由解得∴点M的坐标为(-2, 2). ……………4分由点P在抛物线上，设P (t，). (ⅰ)当AM为所求平行四边形的一边时.ϕ如右图，过M作MG⊥x轴于G, 过P1作P1H⊥BC于H, 则xG= xM =-2, xH= xB =-3. 由四边形AM P1Q1为平行四边形，可证△AMG≌△P1Q1H . 可得P1H= AG=4. ∴t -(-3)=4. ∴t=1. ∴. ……………………5分κ如右图，同ϕ方法可得P2H=AG=4. ∴-3- t =4. ∴t=-7. ∴. ……………………6分(ⅱ)当AM为所求平行四边形的对角线时, 如右图，过M作MH⊥BC于H, 过P3作P3G⊥x轴于G, 则xH= xB =-3，xG= =t. 由四边形AP3MQ3为平行四边形，可证△A P3G≌△MQ3H . 可得AG= MH =1. ∴t -(-6)=1. ∴t=-5. ∴. ……………………………………………………7分综上，点P的坐标为、、.25. 解：（1）BN与NE的位置关系是BN⊥NE；= . 证明：如图，过点E作EG⊥AF于G, 则∠EGN=90°．∵矩形ABCD中, AB=BC，∴矩形ABCD为正方形. ∴AB =AD =CD, ∠A=∠ADC =∠DCB =90°．∴EG//CD, ∠EGN =∠A, ∠CDF =90°．………………………………1分∵E为CF的中点，EG//CD, ∴GF=DG = ∴∵N为MD(AD)的中点，∴AN=ND= ∴GE=AN, NG=ND+DG=ND+AN=AD=AB. ……………………………2分∴△NGE≌△BAN．∴∠1=∠ 2. ∵∠2+∠3=90°，∴∠1+∠3=90°．∴∠BNE =90°. ∴BN⊥NE．……………………………………………………………3分∵∠CDF =90°, CD=DF, 可得∠ F =∠FCD =45°，. 于是……………………………………4分（2）在（1）中得到的两个结论均成立. 证明：如图，延长BN交CD的延长线于点G，连结BE、GE，过E作EH⊥CE，交CD于点H．∵四边形ABCD是矩形，∴AB∥CG．∴∠MBN=∠DGN，∠BMN=∠GDN. ∵N为MD的中点，∴MN=DN．∴△BMN≌△GDN．∴MB=DG，BN=GN. ∵BN=NE，∴BN=NE=GN. ∴∠BEG=90°．……………………………………………5分∵EH⊥CE，∴∠CEH =90°．∴∠BEG=∠CEH．∴∠BEC=∠GEH．由（1）得∠DCF =45°．∴∠CHE=∠HCE =45°．∴EC=EH, ∠EHG =135°．∵∠ECB =∠DCB +∠HCE =135°，∴∠ECB =∠EHG．∴△ECB≌△EHG．∴EB=EG，CB=HG．∵BN=NG，∴BN⊥NE. ……………………………………………6分∵BM =DG= HG-HD= BC-HD =CD-HD =CH= CE，∴= . ……………………………………………7分（3）BN⊥NE；不一定等于. ………………………………………………8分11 / 11。

海淀区2012-2013学年第一学期期末考试九年级语文试卷一、选择。

下面各题均有四个选项，其中只有一个符合题意，选出答案后在答题纸上用铅笔把对应题目的选项字母涂黑涂满。

（共12分。

每小题2分）1.下列词语中加点字的读音完全正确的一项是A.镂．空（lîu）模．样（mï）炫．耀（xuàn）相辅．相成（pǔ）B.霎．时（chà）恣．意（zì）瞥．见（piě）锐不可当．（dāng）C.殉．职（xùn）虔．诚（qián）执拗．（niù）贻．笑大方（yí）D.自诩．（xǔ）殷．红（yīn）隐瞒．（mán）妄自菲．薄（fēi）2.对下列各组词语中两个加点字的解说都正确的一项是A.悠．扬——悠．闲解说：两个“悠”字意思相同，都是“闲适”的意思。

B.照．管——照．例解说：两个“照”字意思不同，“照管”的“照”是“照料”的意思；“照例”的“照”是“按照”的意思。

C.诗情画意．——言简意．赅解说：两个“意”的意思相同，都是“意境”的意思。

D.闲情逸致．——专心致．志解说：两个“致”字意思不同，“闲情逸致”的“致”是“情趣”的意思；“专心致志”的“致”是“达到”的意思。

3.下列句子中加点成语或俗语使用有误的一项是A.此幅《墨梅图》在构图上与现藏于台北故宫博物院的《南枝春早图》有异曲同工．．．．之妙，都讲究主宾相宜，虚实相生。

B.《海洋生物插图集》记录了这位科学家对海洋研究的重大发现，并以照片的形式生动地展现了鲜为人知．．．．的海底世界。

C.在年级篮球联赛开局的关键时刻，队员们只要谨记“行百里者半九十．．．．．．．”的古训，戒骄戒躁，团结协作，就能取得胜利。

D.俗话说，“曲不离口．．．．”，学习写作也是如此，只有勤于动笔，反复训练，我．．．．，拳不离手们的写作能力才能提高。

4.下列作家作品表述有误的一项是A.《战国策》着重记录了战国时期一些谋臣策士的言论和谋略，由西汉刘向编订，《邹忌讽齐王纳谏》是其中的名篇。

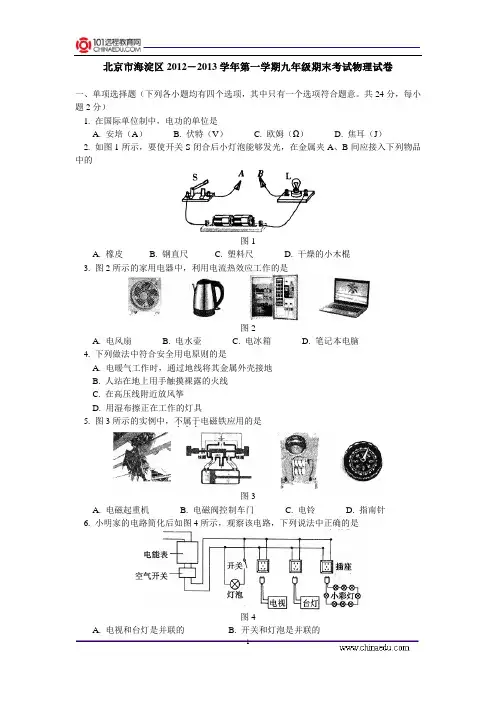
北京市海淀区2012－2013学年第一学期九年级期末考试物理试卷一、单项选择题（下列各小题均有四个选项，其中只有一个选项符合题意。

共24分，每小题2分）1. 在国际单位制中，电功的单位是A. 安培（A）B. 伏特（V）C. 欧姆（Ω）D. 焦耳（J）2. 如图1所示，要使开关S闭合后小灯泡能够发光，在金属夹A、B间应接入下列物品中的图1A. 橡皮B. 钢直尺C. 塑料尺D. 干燥的小木棍3. 图2所示的家用电器中，利用电流热效应工作的是图2A. 电风扇B. 电水壶C. 电冰箱D. 笔记本电脑4. 下列做法中符合安全用电原则的是A. 电暖气工作时，通过地线将其金属外壳接地B. 人站在地上用手触摸裸露的火线C. 在高压线附近放风筝D. 用湿布擦正在工作的灯具5. 图3所示的实例中，不属于．．．电磁铁应用的是图3A. 电磁起重机B. 电磁阀控制车门C. 电铃D. 指南针6. 小明家的电路简化后如图4所示，观察该电路，下列说法中正确的是图4A. 电视和台灯是并联的B. 开关和灯泡是并联的C. 各个小彩灯之间是并联的D. 不插用电器时，插座处火线和零线是连通的7. 分析图5所示的用电器铭牌，各用电器在正常工作时，相同时间内消耗电能最多的是保温式自动电饭锅型号：CFXB40－90 2B额定容量：4L 额定功率：700W额定电压：220V～额定频率：50HzA. 电饭锅煮饭型号：42E60HR彩色液晶电视机电源：220V～50Hz/60Hz功率：135WB. 液晶电视机播放电视贮水式电热水器额定电压220～型号RCD－JTM060－Ⅱ容积60L 额定频率50Hz额定最高温度75℃额定功率2000W防水等级（防溅型）额定内压0.75MPaC. 电热水器烧水家用电冰箱有效容积：254L 制冰量：1.5kg/24h额定电压：220V～除霜输入功率：160W额定频率：50Hz 灯的额定输入功率：15W额定电流：0.86A 耗电量：0.8kWh/24hD. 电冰箱保持箱内低温图58. 下列说法中正确的是A. 电流做功的过程就是电能转化为内能的过程B. 电功率是表示电流做功快慢的物理量C. 用电器的电功率越大，做功就越多D. 用电器的额定功率越大，消耗的电能就越多9. 图6所示电路中，电源两端电压保持不变，开关S闭合后与闭合前相比较，下列说法中正确的是图6A. 电压表的示数变大B. 电流表的示数不变C. 电路中的总电阻变小D. 电路消耗的总功率变小10. 图7所示电路中，电源两端电压保持不变。

数学试卷答案及评分参考 2012.01说明: 与参考答案不同, 但解答正确相应给分.一、选择题（本题共32分，每小题4分）1. B2.D3.A4.B5. B6. C7.D8. C二、填空题（本题共16分，每小题4分）9. x =0或x =4 10. 15 11. 1 12. π(2分); 32π12n(2分)三、解答题（本题共29分,第13题～第15题各5分,第16题4分,第17题、第18题各5分）13．解法一： a =1, b =-8, c =1, …………………………1分24600b ac ∆=-=>. …………………………2分 86022b x a -±∆±==. …………………………3分 ∴ 154,15421-=+=x x . …………………………5分 解法二：281x x -=-.2816116x x -+=-+. …………………………1分 2(4)15x -=. …………………………2分 415x -=±. …………………………3分 ∴154,15421-=+=x x . …………………………5分14．证明: 在△AED 和△ACB 中，∵ ∠A =∠A , ∠AED =∠C , ……………………………2分 ∴ △AED ∽△ACB. ……………………………3分∴ .ABAD AC AE = ……………………………4分 ∴ .645=AE ∴ .310=AE ……………………………5分 15．（1）① (-2 ,0), (1, 0)；② 8; ③增大 (每空1分) ……………………………3分（2）依题意设抛物线解析式为 y =a (x +2) (x -1).由点 (0, -4)在函数图象上，得-4=a (0+2) (0-1). (4)分解得 a =2.∴ y =2 (x +2) (x -1). …………………………………………………5分即所求抛物线解析式为y =2x 2+2x -4.16．（1）正确画图（1分）标出字母（1分） ……………………………………2分（2）正确画图（1分），结论（1分） ………………………………………………4分17．解：由题意得{220,[2(2)]4(2)(1)0.k k k k -≠∆=---+≥ …………………1分 由①得 2k ≠. ………………………………………………………2分由②得 2k ≤. ………………………………………………………4分∴2k <.∵k 为正整数， ∴1k =. ……………………………………………………5分18．解法一：由题意画树形图如下：…………………3分① ②第二次摸球第一次摸球312321233211从树形图看出，所有可能出现的结果共有9个，这些结果出现的可能性相等，标号之和等于4的结果共有3种. ………………………………………………………4分所以P (标号之和等于4)=3193=. ………………………………………………………5分 解法二：……………………………………3分由上表得出，所有可能出现的结果共有9个，这些结果出现的可能性相等，标号之和等于4的结果共有3种. ………………………………………………………4分所以P (标号之和等于4)=3193=. ………………………………………………………5分 四、解答题（本题共21分, 第19题、第20题各5分, 第21题6分，第22题5分）19．（1）(20)(280)(20)y w x x x =-=-+- ……………………………………2分221201600x x =-+-.（2）22(30)200y x =--+.∵2040x ≤≤, a =-2<0,∴当30x =时，200y =最大值. ……………………………………4分答：当销售单价定为每双30元时，每天的利润最大，最大利润为200元. ………5分20．（1）∵二次函数y ＝m x 2+(3-m )x -3 (m >0)的图象与x 轴交于点 (x 1, 0)和(x 2, 0), ∴ 令0y =，即 m x 2+(3-m )x -3=0．………………………………………………1分 (m x +3)( x -1)=0.∵m >0，∴0m >.解得 1x =或3x m=-． …………………………………………………………2分 ∵ x 1 <x 2，103<<-m,∴21x =. ……………………………………………………………3分 （2）由（1）13x m =-，得13x m =-. 由13x m=-是方程mx 2+(3-m )x -3=0的根， 得m x 12+(3-m )x 1=3. ∴mx 12 +m x 12 +(3-m ) x 1+ 6m x 1+9 =m x 12 +(3-m ) x 1+(m x 1+3)2=3. ………5分21．解：（1）证明：∵CE AB ⊥, ∴ 90CEB ∠= . ∵ CD 平分ECB ∠, BC =BD , ∴ 12∠=∠, 2D ∠=∠. ∴ 1D ∠=∠. …………………………1分标号标号 标号 之和 1 2 3 1 2 3 4 2 3 4 5 3 4 5 6 21E F O B C A∴ CE ∥BD .∴ 90DBA CEB ∠=∠= .∵ AB 是⊙O 的直径,∴ BD 是⊙O 的切线. ………………………………………………………2分（2）连接AC ，∵ AB 是⊙O 直径，∴ 90ACB ∠= .∵CE AB ⊥,可得 2CE AE EB =⋅.∴ .162==AECE EB ………………………………………………………3分 在Rt △CEB 中，∠CEB =90︒, 由勾股定理得 2220.BC CE EB =+= ……………4分 ∴ 20BD BC ==.∵ 1D ∠=∠, ∠EFC =∠BFD ,∴ △EFC ∽△BFD. ………………………………………………………5分∴ BFEF BD EC =. ∴101620BF BF-=. ∴ BF =10. ………………………………………………………………………6分 22．（1）画图: 图略(1分); 填空： a (1分) …………………………………2分（2）a 85 (1分), a n n 1212++ （2分） ……………………………………………5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．（1）∵A (a , -3)在4a y x+=的图象上, ∴43a a +=-. 解得1a =-. ……………………………………1分 ∴反比例函数的解析式为3y x=. ……………………………………2分 （2）过A 作AC ⊥y 轴于C .∵ A (-1, -3),∴ AC =1，OC =3.∵ ∠ABO =135︒， ∴ ∠ABC =45︒. 可得 BC =AC =1. ∴ OB =2. ∴ B (0, -2). …………………3分由抛物线2y ax bx c =++与y 轴交于B ，得c = -2. ∵ a = -1, ∴22y x bx =-+-. ∵ 抛物线过A (-1，-3), ∴ 123b ---=-.∴ b =0.∴ 二次函数的解析式为22y x =--. (4)C BA 234-2-3-4-4-3-243211-1-1y x O分（3）将22y x =--的图象沿x 轴翻折，得到二次函数解析式为22y x =+. ……………5分设将22y x =+的图象向右平移后的二次函数解析式为2()2y x m =-+ (m >0).∵ 点P （x 0, 6）在函数3y x=上， ∴036.x = ∴012x =. ∴2()2y x m =-+的图象过点1(,6)2P . ∴62)21(2=+-m . 可得1253,22m m ==-（不合题意，舍去）. ∴ 平移后的二次函数解析式为25()22y x =-+. …………………………6分∵ a =1>0,∴ 当2521≤≤x 时，62≤≤y ; 当325≤<x 时，492≤<y . ∴ 当132x ≤≤时，26y ≤≤. ……………………………………7分 ∴ 平移后的二次函数y 的取值范围为 26y ≤≤.24. （1）CD =AF +BE . …………………1分（2）解：（1）中的结论仍然成立. 证明：延长EA 到G ，使得AG =BE ，连结DG .∵ 四边形ABCD 是平行四边形, ∴ AB =CD , AB ∥CD ，AD =BC . ∵ AE ⊥BC 于点E ,∴ ∠AEB =∠AEC =90︒.∴∠AEB =∠DAG =90︒. ∴ ∠DAG =90︒.∵ AE =AD , ∴ △ABE ≌△DAG . …………………………………………………………………3分 ∴∠1=∠2, DG =AB .∴∠GFD =90︒-∠3.∵ DF 平分∠ADC ,∴∠3=∠4.∴∠GDF =∠2+∠3=∠1+∠4=180︒-∠FAD -∠3=90︒-∠3.∴∠GDF =∠GFD . ………………………………………………………………4分 ∴ DG =GF .∴ CD =GF =AF +AG = AF + BE .即 CD = AF +BE . ………………………………………………………………5分（3）a CD AF BE b =+或bCD aAF bBE =+或b b CD AF BE a a=+. …………………7分 25. 解：（1）∵ 抛物线过原点和A (23,0-)，4321GD A F CE B O x y -1-111234-2-3-4-4-3-2432A B C∴ 抛物线对称轴为3-=x .∴ B (3,3-). 设抛物线的解析式为2+33y a x =+（）.∵ 抛物线经过(0, 0),∴ 0=3a +3.∴ a =-1. ∴3)3(2++-=x y ……………………………………………1分 =.322x x --∵ C 为AB 的中点, A (23,0-)、B (3,3-)，可得 C (333,22-) . 可得直线OC 的解析式为x y 33-=. ……………………………………………2分 （2）连结OB . 依题意点E 为抛物线x x y 322--=与直线x y 33-=的交点（点E 与点O 不重合）.由23323,y x y x x ⎧=-⎪⎨⎪=--⎩， 解得 53,35,3x y ⎧=-⎪⎪⎨⎪=⎪⎩或0,0.x y =⎧⎨=⎩（不合题意，舍）. ∴ E （535,33-） …………………………3分 过E 作EF ⊥y 轴于F , 可得OF =53， ∵ OE =DE ，EF ⊥y 轴， ∴ OF=DF .∴ DO =2OF =103. ∴ D (0, 10)3. ………………………………………………………………………4分∴ BD =2210233733-+-=（）（）. ……………………………………………5分 （3）E 点的坐标为(333,22-)或(31,22-). ……………………………………………8分 说明：此问少一种结果扣1分.F C D E B A y x O。

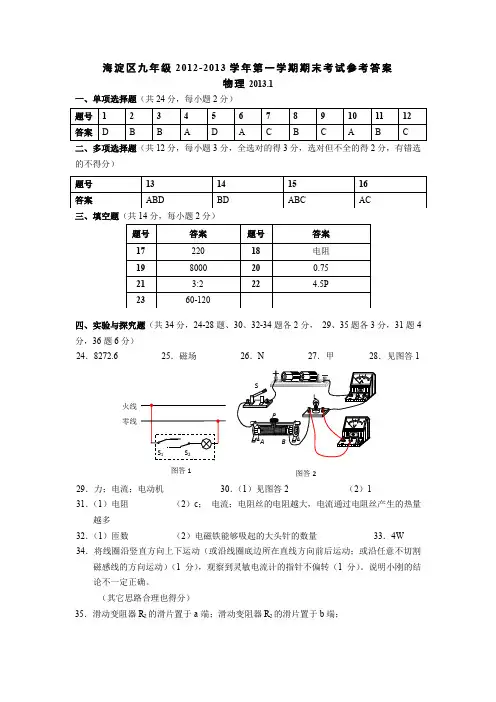
2012-2013 学年北京市海淀区九年级（上）期末数学试卷一、选择题（本题共32 分，每小题4 分）下面各题均有四个选项，其中只有一个是符合题意的．1．（4 分）若代数式有意义，则x 的取值范围是（）A． B．x≥ C．x≤ D．x≠﹣2．（4分）将抛物线y＝x2 平移得到抛物线y＝x2+5，正确的叙述是（）A．向上平移5 个单位B．向左平移5 个单位C．向下平移5 个单位D．向右平移5 个单位3．（4 分）如图，AC 与BD 相交于点E，AD∥BC．若AE：EC＝1：2，则S△AED：S△CEB 为（）A．1： B．1：2 C．1：3 D．1：44．（4分）下列一元二次方程中有两个相等的实数根的是（）A．x2+2x﹣4＝0 B．x2﹣2x﹣6＝0 C．x2﹣4x+4＝0 D．x2+3x+5＝0 5．（4分）如图，⊙O 是△ABC 的外接圆，∠OCB＝40°，则∠A 的度数等于（）A．60°B．50°C．40°D．30°6．（4 分）如图，平面直角坐标系中的二次函数图象所对应的函数解析式可能为（）A． B．C． D．7．（4 分）已知a＜0，那么|﹣2a|可化简为（）A．﹣a B．a C．﹣3a D．3a8．（4分）如图，以G（0，1）为圆心，半径为2 的圆与x 轴交于A、B 两点，与y 轴交于C、D 两点，点E 为⊙G 上一动点，CF⊥AE 于F．当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长为（）A． B． C． D．二、填空题（本题共16 分，每小题4 分）9．（4 分）计算＝．10．（4 分）若二次函数y＝2x2﹣3 的图象上有两个点A（1，m）、B（2，n），则m n（填“＜”或“＝”或“＞”）．11．（4 分）如图，将半径为2cm 的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB 的长为cm．12．（4 分）小聪用描点法画出了函数的图象F，如图所示．结合旋转的知识，他尝试着将图象F 绕原点逆时针旋转90°得到图象F1，再将图象F1 绕原点逆时针旋转90 °得到图象F2，如此继续下去，得到图象F n．在尝试的过程中，他发现点P（﹣4，﹣2）在图象上（写出一个正确的即可）；若点P（a，b）在图象F127 上，则a＝（用含b 的代数式表示）．三、解答题（本题共30 分，每小题5 分）13．（5 分）计算：．14．（5 分）解方程：x2+2x﹣8＝0．15．（5 分）已知a+b＝3，求代数式a2﹣b2+2a+8b+5 的值．16．（5 分）如图，正方形网格中，△ABC 的顶点及点O 在格点上．（1）画出与△ABC 关于点O 对称的△A1B1C1；（2）画出一个以点O 为位似中心的△A2B2C2，使得△A2B2C2 与△A1B1C1 的相似比为2．17．（5 分）如图，在△ABC 与△ADE 中，∠C＝∠E，∠1＝∠2，AC＝AD＝2AB＝6，求AE 的长．18．（5 分）如图，二次函数y＝﹣x2+2x+3 的图象与x 轴交于A、B 两点，与y 轴交于点C，顶点为D，求△BCD 的面积．四、解答题（本题共20 分，每小题5 分）19．（5 分）已知关于x 的方程．（1）如果此方程有两个不相等的实数根，求m 的取值范围；（2）在（1）中，若m 为符合条件的最大整数，求此时方程的根．20．（5 分）已知：二次函数y＝ax2+bx+c（a≠0）中的x 和y 满足下表：x…0 1 2 3 4 5 …y… 3 0 ﹣1 0 m8 …（1）可求得m 的值为；（2）求出这个二次函数的解析式；（3）当0＜x＜3 时，则y 的取值范围为．21．（5 分）图中是抛物线形拱桥，当水面宽为4 米时，拱顶距离水面2 米；当水面高度下降1 米时，水面宽度为多少米？22．（5 分）如图，AB 为⊙O 的直径，BC 切⊙O 于点B，AC 交⊙O 于点D，E 为BC 中点．（1）求证：DE 为⊙O 的切线；（2）延长ED 交BA 的延长线于F，若DF＝4，AF＝2，求BC 的长．五、解答题（本题共22 分，第23 题7 分，第24 题8 分，第25 题7 分）23．（7 分）小明利用等距平行线解决了二等分线段的问题．作法：（1）在e 上任取一点C，以点C 为圆心，AB 长为半径画弧交c 于点D，交d 于点E；（2）以点A 为圆心，CE 长为半径画弧交AB 于点M；∴点M 为线段AB 的二等分点．解决下列问题：（尺规作图，保留作图痕迹）（1）仿照小明的作法，在图2 中作出线段AB 的三等分点；（2）点P 是∠AOB 内部一点，过点P 作PM⊥OA 于M，PN⊥OB 于N，请找出一个满足下列条件的点P．（可以利用图1 中的等距平行线）①在图3 中作出点P，使得PM＝PN；②在图4 中作出点P，使得PM＝2PN．24．（8 分）抛物线y＝mx2+（m﹣3）x﹣3（m＞0）与x 轴交于A、B 两点，且点A 在点B 的左侧，与y 轴交于点C，OB＝OC．（1）求这条抛物线的解析式；（2）若点P（x1，b）与点Q（x2，b）在（1）中的抛物线上，且x1＜x2，PQ＝n．①求的值；②将抛物线在PQ 下方的部分沿PQ 翻折，抛物线的其它部分保持不变，得到一个新图象．当这个新图象与x 轴恰好只有两个公共点时，b 的取值范围是．25．（7 分）如图1，两个等腰直角三角板ABC 和DEF 有一条边在同一条直线l 上，DE＝2，AB＝1．将直线EB 绕点E 逆时针旋转45°，交直线AD 于点M．将图1 中的三角板ABC 沿直线l 向右平移，设C、E 两点间的距离为k．解答问题：（1）①当点C 与点F 重合时，如图2 所示，可得的值为；②在平移过程中，的值为（用含k 的代数式表示）；（2）将图2 中的三角板ABC 绕点C 逆时针旋转，原题中的其他条件保持不变．当点A 落在线段DF 上时，如图3 所示，请补全图形，计算的值；（3）将图1 中的三角板ABC 绕点C 逆时针旋转α度，0＜α≤90，原题中的其他条件保持不变．计算的值（用含k 的代数式表示）．2012-2013 学年北京市海淀区九年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共32 分，每小题4 分）下面各题均有四个选项，其中只有一个是符合题意的．1．（4 分）若代数式有意义，则x 的取值范围是（）A． B．x≥ C．x≤ D．x≠﹣【分析】根据二次根式的性质，被开方数大于等于0，就可以求解．【解答】解：根据题意得：2x﹣1≥0，解得：x≥．故选：B．【点评】本题考查的知识点为：二次根式的被开方数是非负数．2．（4 分）将抛物线y＝x2 平移得到抛物线y＝x2+5，正确的叙述是（）A．向上平移5 个单位B．向左平移5 个单位C．向下平移5 个单位D．向右平移5 个单位【分析】找到两个抛物线的顶点，根据抛物线的顶点即可判断是如何平移得到．【解答】解：原抛物线的顶点为（0，0），新抛物线的顶点为（0，5），∴是抛物线y＝x2 向上平移5 个单位得到，故选：A．【点评】上下平移抛物线时，顶点的横坐标不变，而纵坐标发生了改变，向上平移时，纵坐标增加，向下平移时纵坐标减小．3．（4 分）如图，AC 与BD 相交于点E，AD∥BC．若AE：EC＝1：2，则S△AED：S△CEB 为（）A．1： B．1：2 C．1：3 D．1：4【分析】由AD∥BC 可证明△ADE∽CBE，再由相似三角形的性质就可以得出结论【解答】解：∵AD∥BC．∴△ADE∽CBE，∴S△AED：S△CEB＝AE2：EC2，∵AE：EC＝1：2，∴S△AED：S△CEB＝1：4，故选：D．【点评】本题考查了相似三角形的判定及相似三角形的面积之比等于相似比的平方运用．解答本题求出两三角形相似是关健．4．（4 分）下列一元二次方程中有两个相等的实数根的是（）A．x2+2x﹣4＝0 B．x2﹣2x﹣6＝0 C．x2﹣4x+4＝0 D．x2+3x+5＝0 【分析】判断上述方程的根的情况，只要看根的判别式△＝b2﹣4ac 的值的符号就可以了．有两个相等实数根的一元二次方程就是判别式的值是0 的一元二次方程．【解答】解：因为方程x2﹣4x+4＝0 中，a＝1，b＝﹣4，c＝4，所以△＝b2﹣4ac＝0，所以方程有两个相等的实数根，故选：C．【点评】本题考查了一元二次方程根的判别式的应用．总结一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△＝0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．5．（4 分）如图，⊙O 是△ABC 的外接圆，∠OCB＝40°，则∠A 的度数等于（）A．60°B．50°C．40°D．30°【分析】在等腰三角形OCB 中，求得两个底角∠OBC、∠0CB 的度数，然后根据三角形的内角和求得∠COB＝100°；最后由圆周角定理求得∠A 的度数并作出选择．【解答】解：在△OCB 中，OB＝OC（⊙O 的半径），∴∠OBC＝∠0CB（等边对等角）；∵∠OCB＝40°，∠C0B＝180°﹣∠OBC﹣∠0CB，∴∠COB＝100°；又∵∠A＝∠C0B（同弧所对的圆周角是所对的圆心角的一半），∴∠A＝50°，故选：B．【点评】本题考查了圆周角定理：同弧所对的圆周角是所对的圆心角的一半．解题时，借用了等腰三角形的两个底角相等和三角形的内角和定理．6．（4 分）如图，平面直角坐标系中的二次函数图象所对应的函数解析式可能为（）A． B．C． D．【分析】根据二次函数图象得出顶点位置，进而根据各选项排除即可．【解答】解：根据二次函数顶点坐标位于第三象限，只有选项D 的顶点符合要求，故选：D．【点评】此题主要考查了二次函数图象，根据图象得出顶点位置是解题关键．7．（4 分）已知a＜0，那么|﹣2a|可化简为（）A．﹣a B．a C．﹣3a D．3a【分析】已知a＜0，利用二次根式的性质化简．【解答】解：∵a＜0∴＝﹣a∴|﹣2a|＝|﹣3a|＝﹣3a．故选：C．【点评】本题考查了根据二次根式的意义化简．二次根式规律总结：当a≥0 时，＝a，当a≤0 时，＝﹣a．8．（4分）如图，以G（0，1）为圆心，半径为2 的圆与x 轴交于A、B 两点，与y 轴交于C、D 两点，点E 为⊙G 上一动点，CF⊥AE 于F．当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长为（）A． B． C． D．【分析】连接AC，AG，由OG 垂直于AB，利用垂径定理得到O 为AB 的中点，由G 的坐标确定出OG 的长，在直角三角形AOG 中，由AG 与OG 的长，利用勾股定理求出AO 的长，进而确定出AB 的长，由CG+GO 求出OC 的长，在直角三角形AOC 中，利用勾股定理求出AC 的长，由CF 垂直于AE，得到三角形ACF 始终为直角三角形，点F 的运动轨迹为以AC 为直径的半径，如图中红线所示，当E 位于点B 时，CO⊥AE，此时F 与O 重合；当E 位于D 时，CA⊥AE，此时F 与A 重合，可得出当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长，在直角三角形ACO 中，利用锐角三角函数定义求出∠ACO 的度数，进而确定出所对圆心角的度数，再由AC 的长求出半径，利用弧长公式即可求出的长．【解答】解：连接AC，AG，∵GO⊥AB，∴O 为AB 的中点，即AO＝BO＝AB，∵G（0，1），即OG＝1，∴在Rt△AOG 中，根据勾股定理得：AO＝＝，∴AB＝2AO＝2 ，又CO＝CG+GO＝2+1＝3，∴在Rt△AOC 中，根据勾股定理得：AC＝＝2 ，∵CF⊥AE，∴△ACF 始终是直角三角形，点F 的运动轨迹为以AC 为直径的半圆，当E 位于点B 时，CO⊥AE，此时F 与O 重合；当E 位于D 时，CA⊥AE，此时F 与A 重合，∴当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长，在Rt△ACO 中，tan∠ACO＝＝，∴∠ACO＝30°，∴度数为60°，∵直径AC＝2，∴的长为＝π，则当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长π．故选：B．【点评】此题属于圆综合题，涉及的知识有：坐标与图形性质，勾股定理，锐角三角函数定义，弧长公式，以及圆周角定理，其中根据题意得到点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长是解本题的关键．二、填空题（本题共16 分，每小题4 分）9．（4 分）计算＝﹣3 ．【分析】先进行二次根式的乘法运算，然后化简即可．【解答】解：原式＝﹣＝﹣3．故答案为：﹣3 ．【点评】本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，再进行二次根式的乘除运算，然后合并同类二次根式．10．（4 分）若二次函数y＝2x2﹣3 的图象上有两个点A（1，m）、B（2，n），则m＜n （填“＜”或“＝”或“＞”）．【分析】根据二次函数图象的增减性即可解答．【解答】解：y＝2x2﹣3 的对称轴为x＝0，开口方向向上，顶点为（0，﹣3）．对于开口向上的函数，x 距离对称轴越近，y 值越小，1 比2 距离近，所以m＜n．【点评】本题主要考查二次函数的性质．对于开口向上的函数，x 距离对称轴越近，y 值越小．11．（4 分）如图，将半径为2cm 的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB 的长为 2 cm．【分析】通过作辅助线，过点O 作OD⊥AB 交AB 于点D，根据折叠的性质可知OA＝2OD，根据勾股定理可将AD 的长求出，通过垂径定理可求出AB 的长．【解答】解：过点O 作OD⊥AB 交AB 于点D，连接OA，∵OA＝2OD＝2cm，∴AD＝＝＝cm，∵OD⊥AB，∴AB＝2AD＝cm．故答案为：2．【点评】本题综合考查垂径定理和勾股定理的运用．12．（4 分）小聪用描点法画出了函数的图象F，如图所示．结合旋转的知识，他尝试着将图象F 绕原点逆时针旋转90°得到图象F1，再将图象F1 绕原点逆时针旋转90 °得到图象F2，如此继续下去，得到图象F n．在尝试的过程中，他发现点P（﹣4，﹣2）在图象 F2 上（写出一个正确的即可）；若点P（a，b）在图象F127 上，则a＝（用含b 的代数式表示）．【分析】根据题意知，F1 的图象位于第二象限，F2 的图象位于第三象限，F3 的图象位于第四象限…据此确定F n 图象位于的象限．【解答】解：根据旋转的规律知：F1 的解析是：y＝x2，其图象位于第二象限，F2 的解析是：y＝﹣，其图象位于第三象限，F3 的解析是：y＝﹣x2，其图象位于第四象限，F4 的解析是：y＝，其图象位于第一象限，…则127÷4＝31…3，即F127 的图象位于第4 象限．该图象的函数解析式是y＝﹣．∵P（﹣4，﹣2）位于第三象限，∴点P 所在的图象是F2．∵点P（a，b）在图象F127 上，则b＝﹣a2，∴a＝．故答案是：．【点评】本题考查了坐标与图形变化．根据图象的旋转，找出解析式的规律是解题的关键．三、解答题（本题共30 分，每小题5 分）13．（5 分）计算：．【分析】分别进行二次根式的化简、绝对值、负整数指数幂及零指数幂的运算，然后合并即可．【解答】解：原式＝﹣1+9﹣1﹣2＝7﹣．【点评】本题考查了实数的运算，涉及了二次根式的化简，零指数幂，负整数指数幂及绝对值，熟练掌握各部分的运算法则是关键．14．（5 分）解方程：x2+2x﹣8＝0．【分析】分解因式后得到（x+4）（x﹣2）＝0，推出方程x+4＝0，x﹣2＝0，求出方程的解即可．【解答】解：x2+2x﹣8＝0，分解因式得：（x+4）（x﹣2）＝0，∴x+4＝0，x﹣2＝0，解方程得：x1＝﹣4，x2＝2，∴方程的解是x1＝﹣4，x2＝2．【点评】本题主要考查对解一元一次方程，等式的性质，解一元二次方程等知识点的理解和掌握，能把一元二次方程转化成一元一次方程是解此题的关键．15．（5 分）已知a+b＝3，求代数式a2﹣b2+2a+8b+5 的值．【分析】所求式子前两项利用平方差公式分解因式，将a+b 的值代入计算，去括号合并后再将a+b 的值代入计算，即可求出值．【解答】解：∵a+b＝3，∴a2﹣b2+2a+8b+5＝（a+b）（a﹣b）+2a+8b+5＝3（a﹣b）+2a+8b+5＝5（a+b）+5＝15+5＝20．【点评】此题考查了因式分解的应用，对所求式子进行适当的变形是解本题的关键．16．（5 分）如图，正方形网格中，△ABC 的顶点及点O 在格点上．（1）画出与△ABC 关于点O 对称的△A1B1C1；（2）画出一个以点O 为位似中心的△A2B2C2，使得△A2B2C2 与△A1B1C1 的相似比为2．【分析】（1）根据对称中心平分对应点连线可找到各点的对应点，然后顺次连接即可；（2）根据△A2B2C2 与△A1B1C1 相似比是2，得出对应点坐标即可得出答案．【解答】解：（1）如图所示△A1B1C1 为所求；（2）如图所示△A2B2C2 为所求．【点评】本题考查了作简单平面图形的中心对称图形以及作为似图形，解答本题的关键是根据中心对称的性质和位似图形性质找到各点的对应点，然后顺次连接．17．（5 分）如图，在△ABC 与△ADE 中，∠C＝∠E，∠1＝∠2，AC＝AD＝2AB＝6，求AE 的长．【分析】由已知条件和相似三角形的判定方法证明△ABC∽ADE，利用相似三角形的性质：对应边的比值相等即可求出AE 的长．【解答】解：∵∠1＝∠2，∴∠CAB＝∠EAD，∵∠C＝∠E，∴△ABC∽△ADE，∴，∵AC＝AD＝2AB＝6，∴，∴AE＝12．【点评】本题考查了相似三角形的判定和性质，是中考中常见的题型．18．（5 分）如图，二次函数y＝﹣x2+2x+3 的图象与x 轴交于A、B 两点，与y 轴交于点C，顶点为D，求△BCD 的面积．【分析】延长DC 交x 轴于E，利用S△BCD＝S△BED﹣S△BCE 计算即可．【解答】解：依题意，可得y＝﹣x2+2x+3＝﹣（x﹣1）2+4．∴顶点D（1，4）．令y＝0，可得x＝3 或x＝﹣1．∴令x＝0，可得y＝3．∴C（0，3）．∴OC＝3，∴直线DC 的解析式为y＝x+3．设直线DE 交x 轴于E．∴BE＝6．∴S△BCD＝S△BED﹣S△BCE＝3．∴△BCD 的面积为3．【点评】熟练掌握二次函数图象与x 轴，y 轴交点的意义，二次函数顶点坐标与解析式之间的关系，二次函数对称轴的性质和特点，注意二次函数与一次函数以及三角形之间＝．，x 2＝．可能出现的出题点．四、解答题（本题共 20 分，每小题 5 分） 19．（5 分）已知关于 x 的方程．（1）如果此方程有两个不相等的实数根，求 m 的取值范围； （2）在（1）中，若 m 为符合条件的最大整数，求此时方程的根．【分析】（1）先根据方程有两个不相等的实数根可知△＞0，由△＞0 可得到关于 m 的 不等式，求出 m 的取值范围即可；（2）由（1）中 m 的取值范围得出符合条件的 m 的最大整数值，代入原方程，利用求 根公式即可求出 x 的值．【解答】解：（1）∵该方程有两个不相等的实数根， ∴△＝32﹣4×1×＝9﹣3m ＞0． 解得 m ＜3． ∴m 的取值范围是 m ＜3； （2）∵m ＜3，∴符合条件的最大整数是 m ＝2． 此时方程为 x 2+3x +＝0，解得 x ＝＝ ． ∴方程的根为 x 1＝，x 2故答案为：m ＜3，x 1＝【点评】本题考查的是一元二次方程 ax 2+bx +c ＝0（a ≠0）的根与△的关系及求根公 式，是一个综合性的题目，难度适中．20．（5 分）已知：二次函数 y ＝ax 2+bx +c （a ≠0）中的 x 和 y 满足下表：x … 0 1 2 3 4 5 … y…3﹣1m8…（1）可求得 m 的值为 3 ；（2）求出这个二次函数的解析式；（3）当 0＜x ＜3 时，则 y 的取值范围为 ﹣1≤y ＜3 ．【分析】（1）（2）把表中的三个点（0，3），（1，0），（2，﹣1）代入函数的解析式，得到关于a，b，c 的方程组，即可求得解析式，把x＝4 代入即可求得m 的值；（3）根据函数的图象开口方向，增减性即可确定．【解答】解：（1）（2）根据题意得：，解得：，则函数的解析式是：y＝x2﹣4x+3，当x＝4 时，m＝16﹣16+3＝3；（3）函数的顶点坐标是：（2，﹣1），当0＜x＜3 时，则y 的取值范围为：﹣1≤y＜3．故答案是：3；﹣1≤y＜3．【点评】本题考查了待定系数法求函数的解析式以及二次函数的性质，理解函数的增减性是关键．21．（5 分）图中是抛物线形拱桥，当水面宽为4 米时，拱顶距离水面2 米；当水面高度下降1 米时，水面宽度为多少米？【分析】根据已知得出直角坐标系，进而求出二次函数解析式，再根据通过把y＝﹣1 代入抛物线解析式得出水面宽度，即可得出答案．【解答】解：建立平面直角坐标系如图：则抛物线顶点C 坐标为（0，2），设抛物线解析式y＝ax2+2，将A 点坐标（﹣2，0）代入，可得：0＝4a+2，解得：a＝﹣0.5，故抛物线解析式为y＝﹣0.5x2+2，当水面下降1 米，通过抛物线在图上的观察可转化为：当y＝﹣1 时，对应的抛物线上两点之间的距离，也就是直线y＝﹣1 与抛物线相交的两点之间的距离，将y＝﹣1 代入抛物线解析式得出：﹣1＝﹣0.5x2+2，解得：x＝±，所以水面宽度为2米，【点评】此题主要考查了二次函数的应用，根据已知建立坐标系从而得出二次函数解析式是解决问题的关键，难度一般．22．（5 分）如图，AB 为⊙O 的直径，BC 切⊙O 于点B，AC 交⊙O 于点D，E 为BC 中点．（1）求证：DE 为⊙O 的切线；（2）延长ED 交BA 的延长线于F，若DF＝4，AF＝2，求BC 的长．【分析】（1）连接OD 和DB，根据直角三角形斜边上中线性质得出DE＝BE，推出∠2 ＝∠4，根据等腰三角形性质得出∠1＝∠3，根据∠3+∠4＝∠1+∠2＝∠ABC＝90°，根据切线的判定推出即可；（2）在Rt△FDO 中，根据勾股定理求出半径，证△FDO∽△FBE，得出比例式求出BE，即可求出BC．【解答】解（1）如图，连接DB，OD，∵OD＝OB∴∠1＝∠3．∵AB 是⊙O 的直径，∴∠ADB＝90°＝∠CDB，∵E 为BC 中点，∴DE＝BE，∴∠2＝∠4．∵BC 切⊙O 于点B，∴∠ABC＝90°＝∠3+∠4，∴∠1+∠2＝90°，∴OD⊥DE，∵OD 为⊙O 半径，∴DE 为⊙O 的切线；（2）∵OD⊥DE，∴∠FDO＝90°，设OA＝OD＝r．∵OF2＝FD2+OD2，DF＝4，AF＝2，∴（r+2）2＝42+r2，解得r＝3，∴OA＝OD＝3，FB＝8，∵∠F＝∠F，∠FDO＝∠FBE＝90°，∴△FDO∽△FBE，∴，∴BE＝6，∵E 为BC 中点，∴BC＝2BE＝12．【点评】本题考查了相似三角形的性质和判定，直角三角形斜边上中线性质，勾股定理，切线的判定，等腰三角形的性质等知识点的综合运用．五、解答题（本题共22 分，第23 题7 分，第24 题8 分，第25 题7 分）23．（7 分）小明利用等距平行线解决了二等分线段的问题．作法：（1）在e 上任取一点C，以点C 为圆心，AB 长为半径画弧交c 于点D，交d 于点E；（2）以点A 为圆心，CE 长为半径画弧交AB 于点M；∴点M 为线段AB 的二等分点．解决下列问题：（尺规作图，保留作图痕迹）（1）仿照小明的作法，在图2 中作出线段AB 的三等分点；（2）点P 是∠AOB 内部一点，过点P 作PM⊥OA 于M，PN⊥OB 于N，请找出一个满足下列条件的点P．（可以利用图1 中的等距平行线）①在图3 中作出点P，使得PM＝PN；②在图4 中作出点P，使得PM＝2PN．【分析】（1）作法：①在e 上任取一点C，以点C 为圆心，AB 长为半径画弧交b 于点D，交d 于点E，交c 于点F；②以点A 为圆心，CE 长为半径画弧交AB 于点P1，再以点B 为圆心，CE 长为半径画弧交AB 于点P2；则点P1、P2 为线段AB 的三等分点；（2）①以O 为圆心，任意长为半径画弧，交OA 于G，交OB 于H；在d 上任取一点C，以点C 为圆心，GH 长为半径画弧交b 于点D，交c 于点E；以点G 为圆心，CE 长为半径画弧交GH 于点P；则P 点为所求；②以O 为圆心，任意长为半径画弧，交OA 于G，交OB 于H；在d 上任取一点C，以点C 为圆心，GH 长为半径画弧交a 于点D，交c 于点E，交b 于点F；②以点G 为圆心，CF 长为半径画弧交GH 于点P；则则P 点为所求．【解答】解：（1）如下图所示，点P1、P2 为线段AB 的三等分点；（2）①如下图所示，点P 即为所求；②如下图所示，点P 即为所求．【点评】本题考查了作图﹣应用与设计作图，学生的阅读理解能力及知识的迁移能力，理解等距平行线的含义及平行线分线段成比例定理是解题的关键．24．（8 分）抛物线y＝mx2+（m﹣3）x﹣3（m＞0）与x 轴交于A、B 两点，且点A 在点B 的左侧，与y 轴交于点C，OB＝OC．（1）求这条抛物线的解析式；（2）若点P（x1，b）与点Q（x2，b）在（1）中的抛物线上，且x1＜x2，PQ＝n．①求的值；②将抛物线在PQ 下方的部分沿PQ 翻折，抛物线的其它部分保持不变，得到一个新图象．当这个新图象与x 轴恰好只有两个公共点时，b 的取值范围是﹣4＜b＜﹣2 或b＝0 ．【分析】（1）先确定点C 的坐标，根据OB＝OC，A 在点B 的左侧，可得出点B 的坐标，将点B 坐标代入可得出抛物线解析式；也可采取解法二；（2）①由抛物线y＝x2﹣2x﹣3 可知对称轴为x＝1，因为点P 与点Q 纵坐标相等，可得出两点关于抛物线对称轴对称，从而可得出x1，x2 的表达式，变形后代入即可得出答案．②画出图形，结合图形可直接得出b 的范围．【解答】解：（1）解法一：∵抛物线y＝mx2+（m﹣3）x﹣3（m＞0）与y 轴交于点C，∴C（0，﹣3），∵抛物线与x 轴交于A、B 两点，OB＝OC，∴B（3，0）或B（﹣3，0），∵点A 在点B 的左侧，m＞0，∴抛物线经过点B（3，0），∴0＝9m+3（m﹣3）﹣3，∴m＝1，∴抛物线的解析式为y＝x2﹣2x﹣3．解法二：令y＝0，∴mx2+（m﹣3）x﹣3＝0．∴（x+1）（mx﹣3）＝0．∴x＝﹣1，x＝，∵m＞0，点A 在点B 的左侧，∴A（﹣1，0），B（），令x＝0，可得y＝﹣3，∴C（0，﹣3），∴OC＝3，∵OB＝OC，∴，∴m＝1，∴y＝x2﹣2x﹣3．（2）①由抛物线y＝x2﹣2x﹣3 可知对称轴为x＝1，∵点P（x1，b）与点Q（x2，b）在这条抛物线上，且x1＜x2，PQ＝n，∴x1＝1﹣，x2＝1+，∴2x1＝2﹣n，2x2＝2+n，∴原式＝（2﹣n）2﹣（2+n）n+6n+3＝7．②结合图形可得当这个新图象与x 轴恰好只有两个公共点时，b 的取值范围是：﹣4＜b＜﹣2 或b＝0．【点评】本题考查了二次函数的综合应用，涉及了待定系数法求函数解析式、代数式求值及根与系数的关系，综合考察的知识点较多，解答本题要求同学们熟练掌握各个知识点，并将所学知识融会贯通．25．（7 分）如图1，两个等腰直角三角板ABC 和DEF 有一条边在同一条直线l 上，DE＝2，AB＝1．将直线EB 绕点E 逆时针旋转45°，交直线AD 于点M．将图1 中的三角板ABC 沿直线l 向右平移，设C、E 两点间的距离为k．解答问题：（1）①当点C 与点F 重合时，如图2 所示，可得的值为 1 ；②在平移过程中，的值为（用含k 的代数式表示）；（2）将图2 中的三角板ABC 绕点C 逆时针旋转，原题中的其他条件保持不变．当点A落在线段DF 上时，如图3 所示，请补全图形，计算的值；（3）将图1 中的三角板ABC 绕点C 逆时针旋转α度，0＜α≤90，原题中的其他条件保持不变．计算的值（用含k 的代数式表示）．【分析】（1）①根据题意可得EM 垂直平分DF，直线AF∥EM，从而转化为，继而得出结论；②仿照①的思路进行求解即可；（2）先补全图形，连接AE，分别求出AM 及DM 的值，然后可确定比值．（3）先画出图形，然后证明△ABG≌△CBE，继而推出AG∥DE，△AGM∽△DEM，利用相似三角形的性质即可得出答案．【解答】解：（1）①如图，∵∠MEB＝45°，∠AFB＝45°，∴EM 垂直且平分DF，AF∥EM，∴＝＝1；②如图由①可得＝＝＝＝；（2）连接AE，∵△ABC，△DEF 均为等腰直角三角形，DE＝2，AB＝1，∴EF＝2，BC＝1，∠DEF＝90°，∠4＝∠5＝45°∴DF＝2 ，AC＝，∠EFB＝90°，∴DF＝2AC，AD＝，∴点A 为CD 的中点，∴EA⊥DF，EA 平分∠DEF，∴∠MAE＝90°，∠AEF＝45°，AE＝，∵∠BEM＝45°，∴∠1+∠2＝∠3+∠2＝45°，∴∠1＝∠3，∴△AEM∽△FEB，∴，∴AM＝，∴DM＝AD﹣AM＝，∴．（3）过B 作BE 的垂线交直线EM 于点G，连接AG、BG，，∴∠EBG＝90°，∵∠BEM＝45°，∴∠EGB＝∠BEM＝45°，∴BE＝BG，∵△ABC 为等腰直角三角形，∴BA＝BC，∠ABC＝90°，∴∠1＝∠2，∴△ABG≌△CBE，∴AG＝EC＝k，∠3＝∠4，∵∠3+∠6＝∠5+∠4＝45°，∴∠6＝∠5，∴AG∥DE，∴△AGM∽△DEM，∴．【点评】本题考查了相似形综合题，涉及了相似三角形的判定与性质、平行线的性质、旋转的性质及等腰直角三角形的性质，考察的知识点比较多，难度较大，解答本题之前一定要将图形画出来，这样可以使我们的思考方向更准确一些，另外要求我们熟练掌握各个基础知识点的内容．。

2012-2013海淀区九年级第一学期期末练习数学试卷答案及评分参考一、选择题（本题共32分，每小题4分） 题 号 1 2 3 4 5 6 7 8 答 案 B A D A B DC B二、填空题（本题共16分，每小题4分） 题 号 9 101112答 案332- > 232F （答案不唯一）、b - 三、解答题（本题共30分，每小题5分） 13. 计算：20112()(3)83π--+---.解：原式=219122-+-- …………………………………………4分=72-. …………………………………………5分14. 解方程：2280x x +-= .解法一：(4)(2)0x x +-=. …………………………………………3分40x +=或20x -=.∴ 124,2x x =-=. …………………………………………5分解法二： 1,2,8a b c ===-, …………………………………1分2241(8)360∆=-⨯⨯-=>. ……………………………………2分∴ 23621x -±=⨯. …………………………………………3分∴ 124,2x x =-=. …………………………………………5分15．解法一：∵3a b +=，∴ 22285a b a b -+++=()()285a b a b a b +-+++ ………………………2分 =3()285a b a b -+++ ………………………3分 =5()5a b ++ ………………………4分 =535⨯+=20. ………………………5分 解法二：∵3a b +=，∴3b a =-. .…………………………1分原式= 22(3)28(3)5a a a a --++-+.…………………………2分=22(96)22485a a a a a --+++-+ .…………………………3分 =582426922+-++-+-a a a a a .…………………………4分=20. ………………………5分16.例如：∴△111A B C 、△222A B C 为所求.(注：第（1）问2分；第（2）问3分，画出一个正确的即可.) 17. 解：∵12∠=∠，∴C A B E A D ∠=∠. ………………………1分∵C E ∠=∠，∴△C A B ∽△EAD . ………………………3分 ∴A BA CA D A E=. ………………………4分∵AC AD =2AB ==6，∴=3A B . ∴36=6A E.∴12A E =. ………………………5分18. 解法一：依题意，可得223y x x =-++=214x --+（）. ∴顶点(1,4)D . ……………1分令0y =，可得3x =或1x =-.∴A (1,0)-、B (3,0). ……………2分令0x =，可得3y =.∴(0,3)C . ……………3分∴直线C D 的解析式为3y x =+. 设直线C D 交x 轴于E . ∴(3,0)E -.∴6B E =. …….………….…………4分 ∴3BC D BED BC E S S S =-= .∴△BCD 的面积为3. …….………….…………5分解法二：同解法一，可得A (1,0)-、B (3,0)、(0,3)C 、(1,4)D . ……………3分∴直线B C 的解析式为3y x =-+. 过点D 作D E ∥B C 交x 轴于E ,连接C E . ∴设过D 、E 两点的直线的解析式为y x b =-+.∵(1,4)D ，∴直线D E 的解析式为5y x =-+. ∴(5,0)E .∴2B E =. ….…………4分 ∵D E ∥B C ， ∴132B C D B C E S S B E O C ==⨯⨯= .∴△BCD 的面积为3. . .………….………………5分 四、解答题（本题共20分，每小题5分） 19．解：（1）∵关于x 的方程04332=++m x x有两个不相等的实数根，∴∆930m =->. …………………………1分∴3m <. .…………………………2分 （2）∵m 为符合条件的最大整数， ∴2m =. .…………………………3分 ∴23302x x ++=.2223333()()222x x ++=-+.233()24x +=.2331-=x ，2332--=x .∴方程的根为2331-=x ，2332--=x . .…………………………5分20．解：(1)m 的值为3； .…………………………1分 (2) ∵二次函数的图象经过点（1，0），（3，0），∴设二次函数的解析式为(1)(3)y a x x =--. .…………………………2分 ∵图象经过点(0,3)，∴1a =. .…………………………3分∴这个二次函数的解析式为243y x x =-+. .…………………………4分 (3) 当03x <<时，则y 的取值范围为 1-≤3<y . .…………………5分 21. 解：如图所示，建立平面直角坐标系.设二次函数的解析式为2y ax =(0)a ≠. .…………………1分 ∵图象经过点(2,2)-， .…………………2分∴24a -=，12a =-.∴212y x =-. .…………………3分当3y =-时，6x =±. .…………………4分答：当水面高度下降1米时，水面宽度为26米. .…………………5分 22．（1）如图，连接,OD BD . ………………1分∵在⊙O 中，O D O B =，∴∠1=∠2.∵A B 是⊙O 的直径， ∴90AD B C D B ∠=∠=︒. ∵E 为BC 中点， ∴12E D B C E B ==.∴∠3=∠4.∵BC 切⊙O 于点B ，∴90E B A∠=︒.∴132490∠+∠=∠+∠=︒,即90O D E∠=︒.∴O D⊥D E.∵点D在⊙O上，∴D E是⊙O的切线. ……………2分（2）∵O D⊥D E，∴90F D O∠=︒.设O A O D r==.∵222OF FD OD=+, DF=4，AF=2，∴222(2)4r r+=+.解得3r=. ……………………………………3分∴3,8OA OD FB===.∵,90F F FDO FBE∠=∠∠=∠=︒,∴△F D O∽△FBE. ……………………………………4分∴F D O DF B B E=.∴ 6.B E=∵E为BC中点，∴212.B C B E==……………………………………5分五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）23. 解：（1）……………………2分（注：直接等分不给分，在等距平行线上有正确痕迹的给分,作出一个给1分.）(2)①②……………………4分……………………7分24．解：（1）解法一：∵抛物线2(3)3(0)y m x m x m =+-->与y 轴交于点C ，∴(0,3)C -. ……………………1分 ∵抛物线与x 轴交于A 、B 两点，OB=OC ， ∴B (3,0)或B (-3,0).∵点A 在点B 的左侧，0m >，∴抛物线经过点B (3,0). ……………………2分 ∴093(3)3m m =+--. ∴1m =.∴抛物线的解析式为322--=x x y . ……………………3分 解法二：令0y =, ∴2(3)3=0m x m x +--. ∴(1)(3)0x mx +-=. ∴31,=x x m=-.0m > ，点A 在点B 的左侧，∴3(1,0),(,0)A B m-. ……………………1分令0x =，可得3y =-. ∴(0,3)C -.∴3O C =. ……………………2分 O B O C = , ∴33m =.∴1m =.∴322--=x x y . ……………………3分（2）①由抛物线322--=x x y 可知对称轴为1x =. ……………4分∵点P 1(,)x b 与点Q 2(,)x b 在这条抛物线上，且12x x <，PQ n =， ∴121,122n n x x =-=+. ……………………5分∴1222,22x n x n =-=+.∴原式=736)2()2(2=+++--n n n n . ……………………6分②42b -<<-或0b =. ……………………8分 （注：答对一部分给1分.） 25．解：（1）①1；……………………1分②2k ；……………………2分（2）解：连接AE .∵ABC DEF ∆∆，均为等腰直角三角形，2,1DE AB ==，∴2,1,90,4545.EF BC DEF ==∠=︒∠=∠=︒ ∴22,2,90.D F AC EFB ==∠=︒ ∴2, 2.D F AC AD ==∴点A 为C D 的中点. ……………………3分 ∴,.EA DF EA DEF ⊥∠平分 ∴90,45MAE AEF ∠=︒∠=︒, 2.AE =∵45,BEM ∠=︒ ∴1+2=3+2=45∠∠∠∠︒. ∴1= 3.∠∠∴A E M ∆∽F E B ∆. ∴.A M A E B FE F= ……………………4分∴22A M =.∴22222D M AD AM =-=-=.∴1A M D M=. ……………………5分（3） 过B 作B E 的垂线交直线EM 于点G ，连接A G 、B G . ∴90E B G ∠=︒. ∵45B E M ∠=︒，∴45EG B BEM ∠=∠=︒. ∴B E B G =.∵△A B C 为等腰直角三角形， ∴90.BA BC ABC =∠=︒， ∴12∠=∠.∴△ABG ≌△C B E . ……………………6分 ∴34AG EC k ==∠=∠，.∵3+65+4=45∠∠=∠∠︒， ∴65∠=∠. ∴A G ∥D E .∴△A G M ∽△D EM . ∴.2A M A G k D MD E== ……………………7分(注：本卷中许多问题解法不唯一,请老师根据评分标准酌情给分.)。

海淀区九年级第一学期期末测评数 学 试 卷（分数：120分 时间：120分钟） 2013.1班级 姓名 学号 成绩 一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1.若代数式21x -有意义，则x 的取值范围是 A ．12x ≠B ．x ≥12C ．x ≤12D ．x ≠-122.将抛物线2y x =平移得到抛物线25y x =+，下列叙述正确的是 A .向上平移5个单位 B .向下平移5个单位C .向左平移5个单位D .向右平移5个单位3.如图，A C 与BD 相交于点E ，A D ∥BC .若:1:2AE EC =，则:AED C EB S S ∆∆为 A.2:1 B. 1:2 C.3:1 D. 1:44.下列一元二次方程中，有两个相等的实数根的是 A ．2210x x -+=B ． 2240x x +-=C ．2250x x --=D ．2240x x ++=5.如图，⊙O 是△ABC 的外接圆，∠A =40°，则∠OCB 等于 A ．60°B ．50°C ．40°D ．30°6.如图，平面直角坐标系中的二次函数图象所对应的函数解析式可能为 A ．212y x =-B ．21(1)2y x =-+C ．1)1(212---=x y D ． 21(1)12y x =-+-7．已知0a <，那么22a a -可化简为A . a -B . aC . 3a -D . 3a 8. 如图，以(0,1)G 为圆心，半径为2的圆与x 轴交于A 、B 两点,与y 轴交于C 、D 两点,点E 为⊙G 上一动点，C F AE ⊥于F .当点E 从点B 出发顺时针运动到点D 时，点F 所经过的路径长为 A ．32π B ．33π C ．34π D ．36π二、填空题（本题共16分，每小题4分） 9．计算3(16)-= ．10. 若二次函数223y x =-的图象上有两个点(3,)A m -、(2,)B n ，则m n （填“<”或“=”或“>”）. 11.如图，将半径为2cm 的圆形纸片折叠后，圆弧恰好经过圆心O ，则折痕AB 的长为 _________cm . 12.小聪用描点法画出了函数y x =的图象F ，如图所示.结合旋转的知识，他尝试着将图象F 绕原点逆时针旋转90︒得到图象1F ，再将图象1F 绕原点逆时针旋转90︒得到图象2F ，如此继续下去，得到图象n F .在尝试的过程中，他发现点P (4,2)--在图象 上（写出一个正确的即可）；若点P （a ，b ）在图象127F 上，则a = (用含b 的代数式表示) . 三、解答题（本题共30分，每小题5分） 13. 计算：20112()(3)83π--+---.(0,1)I14. 解方程：2280x x +-= .15．已知3a b +=，求代数式22285a b a b -+++的值.16.如图，正方形网格中，△ABC 的顶点及点O 在格点上． (1)画出与△ABC 关于点O 对称的△111A B C ；(2)画出一个以点O 为位似中心的△222A B C ，使得△222A B C 与△111A B C 的相似比为2.17．如图，在△ABC 与△A D E 中，C E ∠=∠，12∠=∠,AC AD =2AB ==6,求AE 的长．18.如图,二次函数223y x x =-++的图象与x 轴交于A 、B 两点，与y 轴交于点C ，顶点为D , 求△BCD的面积.四、解答题（本题共20分，每小题5分） 19．已知关于x 的方程04332=++m x x 有两个不相等的实数根.（1）求m 的取值范围；（2）若m 为符合条件的最大整数，求此时方程的根.20. 已知：二次函数2y ax bx c =++(0)a ≠中的x 和y 满足下表：x… 0 1 23 4 5 … y…31-m8…(1) 可求得m 的值为 ； (2) 求出这个二次函数的解析式；(3) 当03x <<时，则y 的取值范围为 .21．图中是抛物线形拱桥，当水面宽为4米时，拱顶距离水面2米；当水面高度下降1米时，水面宽度为多少米？22.如图，AB 为⊙O 的直径，BC 切⊙O 于点B ，AC 交⊙O 于点D ，E 为BC 中点. 求证：（1）DE 为⊙O 的切线；（2）延长ED 交BA 的延长线于F ，若DF =4，AF =2，求BC 的长.五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）23. 小明利用等距平行线解决了二等分线段的问题.作法：（1）在e上任取一点C，以点C为圆心，AB长为半径画弧交c于点D，交d于点E；（2）以点A为圆心，CE长为半径画弧交AB于点M；∴点M为线段AB的二等分点.图1解决下列问题：（尺规作图，保留作图痕迹）（1）仿照小明的作法，在图2中作出线段AB的三等分点；图2（2）点P是∠AOB内部一点，过点P作PM⊥OA于M，PN⊥OB于N，请找出一个满足下列条件的点P. （可以利用图1中的等距平行线）①在图3中作出点P，使得P M P N=.=；②在图4中作出点P，使得2P M P N图3 图424．抛物线2(3)3(0)y m x m x m =+-->与x 轴交于A 、B 两点，且点A 在点B 的左侧，与y 轴交于点C ，OB=OC ． （1）求这条抛物线的解析式；（2）若点P 1(,)x b 与点Q 2(,)x b 在（1）中的抛物线上，且12x x <，PQ=n . ①求2124263x x n n -++的值；② 将抛物线在PQ 下方的部分沿PQ 翻折，抛物线的其它部分保持不变，得到一个新图象.当这个新图象与x 轴恰好只有两个公共点时，b 的取值范围是 .25．如图1，两个等腰直角三角板ABC 和DEF 有一条边在同一条直线l 上，2D E =，1A B =．将直线E B 绕点E 逆时针旋转45︒，交直线A D 于点M ．将图1中的三角板ABC 沿直线l 向右平移，设C 、E 两点间的距离为k ．图1 图2 图3解答问题：（1）①当点C 与点F 重合时，如图2所示，可得A M D M的值为 ；②在平移过程中，A M D M的值为 （用含k 的代数式表示）；（2）将图2中的三角板A B C 绕点C 逆时针旋转，原题中的其他条件保持不变.当点A 落在线段D F 上时，如图3所示，请补全图形，计算A M D M的值；（3）将图1中的三角板ABC 绕点C 逆时针旋转α度，0α<≤90，原题中的其他条件保持不变.计算A M D M的值（用含k 的代数式表示）．海淀区九年级第一学期期末练习数学试卷答案及评分参考一、选择题（本题共32分，每小题4分） 题 号 1 2 3 4 5 6 7 8 答 案 B A D A B DC B二、填空题（本题共16分，每小题4分） 题 号 9 101112答 案332- > 232F （答案不唯一）、b - 三、解答题（本题共30分，每小题5分） 13. 计算：20112()(3)83π--+---.解：原式=219122-+-- …………………………………………4分=72-. …………………………………………5分14. 解方程：2280x x +-= .解法一：(4)(2)0x x +-=. …………………………………………3分40x +=或20x -=.∴ 124,2x x =-=. …………………………………………5分解法二： 1,2,8a b c ===-, …………………………………1分2241(8)360∆=-⨯⨯-=>. ……………………………………2分∴ 23621x -±=⨯. …………………………………………3分∴ 124,2x x =-=. …………………………………………5分15．解法一：∵3a b +=，∴ 22285a b a b -+++=()()285a b a b a b +-+++ ………………………2分 =3()285a b a b -+++ ………………………3分 =5()5a b ++ ………………………4分 =535⨯+=20. ………………………5分 解法二：∵3a b +=，∴3b a =-. .…………………………1分原式= 22(3)28(3)5a a a a --++-+.…………………………2分=22(96)22485a a a a a --+++-+ .…………………………3分 =582426922+-++-+-a a a a a .…………………………4分=20. ………………………5分16.例如：∴△111A B C 、△222A B C 为所求.(注：第（1）问2分；第（2）问3分，画出一个正确的即可.) 17. 解：∵12∠=∠，∴C A B E A D ∠=∠. ………………………1分∵C E ∠=∠，∴△C A B ∽△EAD . ………………………3分 ∴A BA CA D A E=. ………………………4分∵AC AD =2AB ==6，∴=3A B . ∴36=6A E.∴12A E =. ………………………5分18. 解法一：依题意，可得223y x x =-++=214x --+（）. ∴顶点(1,4)D . ……………1分令0y =，可得3x =或1x =-.∴A (1,0)-、B (3,0). ……………2分令0x =，可得3y =.∴(0,3)C . ……………3分∴直线C D 的解析式为3y x =+. 设直线C D 交x 轴于E . ∴(3,0)E -.∴6B E =. …….………….…………4分 ∴3BC D BED BC E S S S =-= .∴△BCD 的面积为3. …….………….…………5分解法二：同解法一，可得A (1,0)-、B (3,0)、(0,3)C 、(1,4)D . ……………3分∴直线B C 的解析式为3y x =-+. 过点D 作D E ∥B C 交x 轴于E ,连接C E . ∴设过D 、E 两点的直线的解析式为y x b =-+.∵(1,4)D ，∴直线D E 的解析式为5y x =-+. ∴(5,0)E .∴2B E =. ….…………4分 ∵D E ∥B C ， ∴132B C D B C E S S B E O C ==⨯⨯= .∴△BCD 的面积为3. . .………….………………5分 四、解答题（本题共20分，每小题5分） 19．解：（1）∵关于x 的方程04332=++m x x有两个不相等的实数根，∴∆930m =->. …………………………1分∴3m <. .…………………………2分 （2）∵m 为符合条件的最大整数， ∴2m =. .…………………………3分 ∴23302x x ++=.2223333()()222x x ++=-+.233()24x +=.2331-=x ，2332--=x .∴方程的根为2331-=x ，2332--=x . .…………………………5分20．解：(1)m 的值为3； .…………………………1分 (2) ∵二次函数的图象经过点（1，0），（3，0），∴设二次函数的解析式为(1)(3)y a x x =--. .…………………………2分 ∵图象经过点(0,3)，∴1a =. .…………………………3分∴这个二次函数的解析式为243y x x =-+. .…………………………4分 (3) 当03x <<时，则y 的取值范围为 1-≤3<y . .…………………5分 21. 解：如图所示，建立平面直角坐标系.设二次函数的解析式为2y ax =(0)a ≠. .…………………1分 ∵图象经过点(2,2)-， .…………………2分∴24a -=，12a =-.∴212y x =-. .…………………3分当3y =-时，6x =±. .…………………4分答：当水面高度下降1米时，水面宽度为26米. .…………………5分 22．（1）如图，连接,OD BD . ………………1分∵在⊙O 中，O D O B =，∴∠1=∠2.∵A B 是⊙O 的直径， ∴90AD B C D B ∠=∠=︒. ∵E 为BC 中点， ∴12E D B C E B ==.∴∠3=∠4.∵BC 切⊙O 于点B ，∴90E B A ∠=︒.∴132490∠+∠=∠+∠=︒,即90O D E ∠=︒.∴O D ⊥D E .∵点D 在⊙O 上，∴D E 是⊙O 的切线. ……………2分（2）∵O D ⊥D E ，∴90F D O ∠=︒.设O A O D r ==.∵222OF FD OD =+, DF =4，AF =2，∴222(2)4r r +=+.解得3r =. ………3分∴3,8OA OD FB ===.∵,90F F FDO FBE ∠=∠∠=∠=︒,∴△F D O ∽△FBE . ……………4分∴F D ODF B B E =.∴ 6.B E =∵E 为BC 中点，∴212.B C B E ==……………………………………5分五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）23. 解：（1）……………………2分（注：直接等分不给分，在等距平行线上有正确痕迹的给分,作出一个给1分.）(2)① ②……………………4分 ……………………7分24．解：（1）解法一：∵抛物线2(3)3(0)y m x m x m =+-->与y 轴交于点C ，∴(0,3)C -. ……………………1分∵抛物线与x 轴交于A 、B 两点，OB=OC ，∴B (3,0)或B (-3,0).∵点A 在点B 的左侧，0m >，∴抛物线经过点B (3,0). ……………………2分∴093(3)3m m =+--.∴1m =.∴抛物线的解析式为322--=x x y . ……………………3分 解法二：令0y =,∴2(3)3=0m x m x +--.∴(1)(3)0x mx +-=. ∴31,=x x m =-. 0m > ，点A 在点B 的左侧， ∴3(1,0),(,0)A B m-. ……………………1分 令0x =，可得3y =-.∴(0,3)C -. ∴3O C =. ……………………2分 O B O C = ,∴33m =.∴1m =.∴322--=x x y . ……………………3分（2）①由抛物线322--=x x y 可知对称轴为1x =. ……………4分 ∵点P 1(,)x b 与点Q 2(,)x b 在这条抛物线上，且12x x <，PQ n =， ∴121,122n n x x =-=+. ……………………5分 ∴1222,22x n x n =-=+.∴原式=736)2()2(2=+++--n n n n . ……6分②42b -<<-或0b =. ……………………8分（注：答对一部分给1分.）25．解：（1）①1；……………………1分 ②2k；……………………2分（2）解：连接AE .∵ABC DEF ∆∆，均为等腰直角三角形，2,1DE AB ==，∴2,1,90,4545.EF BC DEF ==∠=︒∠=∠=︒∴22,2,90.D F AC EFB ==∠=︒∴2, 2.D F AC AD == ∴点A 为C D 的中点. ……………………3分∴,.EA DF EA DEF ⊥∠平分∴90,45MAE AEF ∠=︒∠=︒, 2.AE =∵45,BEM ∠=︒∴1+2=3+2=45∠∠∠∠︒.∴1= 3.∠∠ ∴A E M ∆∽F E B ∆. ∴.A M A E B F E F = ……………………4分 ∴22A M =.∴22222D M AD AM =-=-=. ∴1A M D M =. ……………………5分（3） 过B 作B E 的垂线交直线EM 于点G ，连接A G 、B G . ∴90E B G ∠=︒.∵45B E M ∠=︒，∴45EG B BEM ∠=∠=︒.∴B E B G =.∵△A B C 为等腰直角三角形，∴90.BA BC ABC =∠=︒，∴12∠=∠.∴△ABG ≌△C B E . ……………………6分∴34AG EC k ==∠=∠，.∵3+65+4=45∠∠=∠∠︒，∴65∠=∠.∴A G ∥D E .∴△A G M ∽△D EM . ∴.2A M A G k D M D E == ……………………7分(注：本卷中许多问题解法不唯一,请老师根据评分标准酌情给分.)。

2012-2013海淀区初三期末试卷分析——语文一、期末考试意义这次期末考试是初三学生进入初三以来第一次非常重要的大考，其考试成绩和排名对初三下学期的中考语文复习冲刺具有十分重要的指导意义，而且对学生接下来的学习状态和信心有直接影响。

这次考试出题角度和命题趋势，也和中考紧密相连，这种关联度应引起学生的重视。

期末考试意义之大不言而喻，同时也应看到不少学校存在押分现象，如首师附、中关村中学、交大附、理工附等。

如有同学很期待知道自己的语文实际水平，可携带试卷到观止堂找老师解答。

二、试卷难度整体来说属于中上难度。

●选择题：难度适中，需要较好的基础知识积累。

第5、6题难度稍大，做对需极为细心。

●填空题：基础题，在张兴东老师的《考点破解》可见原题。

●综合性学习：难度较小，第11题需分析逻辑关系。

●文言文阅读：难度小，《考点破解》和《文言文练死你系列》均有原题。

●现代文阅读：记叙文：难度较大。

概括题难度不大，含义作用题和人物形象分析难度较大，因情节曲折对主题理解有障碍，“伏笔”作用是新题型。

据笔者研究发现，自2006起，北京的模拟题和中考题从未出现超过“承、铺、照、点、引”这五类范围的题目。

说明文：难度较小，需概括到位。

议论文：题型不常见，难度小●作文：难度较高。

题目本身很难转化为写作素材。

但分析题目“有疑惑，问题解决了”即遇到疑惑，有所感悟后疑惑解决了或疑惑解决后得到某种感悟、启示，所以成长类、亲情类有感悟的素材都能用了。

但我们也发现，从2012中考“少年风采”到2012年期中考试“_____正当时”再到“解惑”，似乎成长类的题目一直在延续，同时也要多练习亲情类文章。

三、各知识板块及诊断说明阅读和作文为拉分题，基础和文言文大部分为课内知识，送分题。

四、试卷判断整体判断：基础不牢：基本功不扎实，学习习惯不好，懒写懒记，眼高手低习惯不好：订正马虎、卷面不清、没有用不同色笔区分、试卷乱涂乱画、集错本阅读不好：审题不清，答题套路不规范，漏答要点作文不好：主题、语言、结构三大块，（1）构思：故事没有新意，只是一个人云亦云的故事；没有扣题、没有感悟（2）语言：语言干涩，不生动不形象，没有文采。

11．海淀区九年级第一学期期末测评数 学 试 卷 2012.1一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1．下列说法正确的是 ( )A. 掷两枚硬币，一枚正面朝上，一枚反面超上是不可能事件 B ．随意地翻到一本书的某页，这页的页码为奇数是随机事件 C ．经过某市一装有交通信号灯的路口，遇到红灯是必然事件 D ．某一抽奖活动中奖的概率为1001,买100张奖券一定会中奖 2．下列图形中，既是轴对称图形，又是中心对称图形的是 ( )A B C3. 将抛物线y =x 2平移得到抛物线y =x 2+3,则下列平移过程正确的是 ( ) A. 向上平移3个单位 B. 向下平移3个单位 C. 向左平移3个单位 D. 向右平移3个单位4.下列一元二次方程中，有两个相等的实数根的是 ( )A ．x 2+1=0B ．9x 2-6x +1=0C ．x 2-x +2=0D ．x 2-2x -3=05. 已知圆锥的底面半径为2cm ，母线长为5cm ，则此圆锥的侧面积为 ( ) A. 5πcm 2 B. 10πcm 2 C. 14πcm 2 D. 20πcm 26. 如图，为了测量某棵树的高度，小明用长为2m 的竹竿作 测量工具，移动竹竿，使竹竿顶端、树的顶端的影子恰好落在地面的同一点．此时竹竿与这一点相距6m,与树相距 15m ，则树的高度为 ( )A. 4mB. 5mC. 7mD. 9m7. 已知二次函数y ＝ax 2＋bx ＋c 的图象如右图所示，则下列 结论中正确的是 ( )A ．a >0B ．c ＜0C ．042<-ac bD ．a ＋b ＋c >011xOy 15m 6m 2m8.已知O为圆锥顶点, OA、OB为圆锥的母线, C为OB中点, 一只小蚂蚁从点C开始沿圆锥侧面爬行到点A, 另一只小蚂蚁绕着圆锥侧面爬行到点B，它们所爬行的最短路线的痕迹如右图所示. 若沿OA剪开, 则得到的圆锥侧面展开图为( )A B C D二、填空题（本题共16分，每小题4分）9. 方程042=-xx的解是.10.如图, △ABD与△AEC都是等边三角形, 若∠ADC = 15︒,则∠ABE= ︒ .11. 若432zyx==（x, y, z均不为0），则zzyx-+2的值为 .12．用两个全等的含30︒角的直角三角形制作如图1所示的两种卡片, 两种卡片中扇形的半径均为1, 且扇形所在圆的圆心分别为长直角边的中点和30︒角的顶点, 按先A后B的顺序交替摆放A、B两种卡片得到图2所示的图案. 若摆放这个图案共用两种卡片8张，则这个图案中阴影部分的面积之和为; 若摆放这个图案共用两种卡片(2n+1)张( n为正整数), 则这个图案中阴影部分的面积之和为. (结果保留π )……A种B种图1 图2，三、解答题（本题共29分, 第13题～第15题各5分, 第16题4分, 第17题、第18题各5分）13．解方程：x2-8x +1=0.解:14．如图，在△ABC中，D、E分别是AC、AB边上的点，∠AED=∠C，AB=6，AD=4，AC=5, 求AE的长．解:ACBDEADB CEOB(A)COABC OAB(A)COAB(A)COAB(A)CC(A)BAOBA15. 抛物线y =ax 2+bx +c 上部分点的横坐标x ，纵坐标y 的对应值如下表：（1）根据上表填空：① 抛物线与x 轴的交点坐标是 和 ；② 抛物线经过点 (-3, )；③ 在对称轴右侧，y 随x 增大而 ； （2）试确定抛物线y =ax 2+bx +c 的解析式.解: （1）① 抛物线与x 轴的交点坐标是 和 ；② 抛物线经过点 (-3, )；③ 在对称轴右侧，y 随x 增大而 .（2）16. 如图, 在正方形网格中，△ABC 的顶点和O 点都在格点上． （1）在图1中画出与△ABC 关于点O 对称的△A ′B ′C ′；（2）在图2中以点O 为位似中心，将△ABC 放大为原来的2倍(只需画出一种即可). 解:图1 图2结论: 为所求.17．已知关于x 的方程(k -2)x 2＋2(k -2)x ＋k ＋1=0有两个实数根，求正整数k 的值． 解:18．在一个口袋中有3个完全相同的小球,把它们分别标号为1, 2, 3, 随机地摸出一个 小球记下标号后放回, 再随机地摸出一个小球记下标号, 求两次摸出小球的标号 之和等于4的概率． 解:四、解答题（本题共21分，第19题、第20题各5分, 第21题6分, 第22题5分） 19．某商店销售一种进价为20元/双的手套，经调查发现，该种手套每天的销售量w (双) 与销售单价x (元)满足280w x =-+(20≤x ≤40),设销售这种手套每天的利润为y （元）. （1）求y 与x 之间的函数关系式；（2）当销售单价定为多少元时, 每天的利润最大？最大利润是多少？ 解:20．已知二次函数y 2+(3x -3 (m >0)的图象与x 轴交于点 (x 1, 0)和(x 2, 0), 且x 1<x 2.（1）求x 2的值;（2）求代数式96)3(112121++-++x m x m x m x m 的值.21. 如图，AB 是⊙O 的直径， 点C 在⊙O 上，CE ⊥ AB 于E , CD 平分∠ECB , 交过 点B 的射线于D , 交AB 于F , 且BC=BD . （1）求证：BD 是⊙O 的切线； （2）若AE =9, CE =12, 求BF 的长.解:22. 已知△ABC 的面积为a ，O 、D 分别是边AC 、BC 的中点.（1）画图：在图1中将点D 绕点O 旋转180︒得到点E , 连接AE 、CE . 填空：四边形ADCE 的面积为 ；（2）在（1）的条件下，若F 1是AB 的中点，F 2是AF 1的中点, F 3是AF 2的中点,…,F n 是AF n -1的中点 (n 为大于1的整数), 则△F 2CE 的面积为 ; △F n CE 的面积为 .解: （1）画图:图1填空：四边形ADCE 的面积为 .（2）△F 2CE 的面积为 ; △F n CE 的面积为 .备用图五、解答题（本题共22分，第23题7分, 第24题7分，第25题8分）23. 已知二次函数y =ax 2+bx +c 的图象与反比例函数xa y 4+=的图象交于点A (a , -3)，与 y 轴交于点B .（1）试确定反比例函数的解析式;（2）若∠ABO =135︒, 试确定二次函数的解析式;（3）在（2）的条件下,将二次函数y =ax 2 + bx + c 的图象先沿x 轴翻折, 再向右平移到与反比例函数xa y 4+=的图象交于点P (x 0, 6) . 当x 0 ≤x ≤3时, 求平移后的二 次函数y 的取值范围.解:24. 已知在□ABCD 中，AE ⊥BC 于E ，DF 平分∠ADC 交线段AE 于F .（1）如图1，若AE =AD ，∠ADC =60︒, 请直接写出线段CD 与AF +BE 之间所满足的等量关系;（2）如图2, 若AE =AD ，你在（1）中得到的结论是否仍然成立, 若成立,对你的结论 加以证明, 若不成立, 请说明理由；（3）如图3, 若AE : AD =a : b ，试探究线段CD 、AF 、BE 之间所满足的等量关系， 请直接写出你的结论.解: （1）线段CD 与AF +BE 之间所满足的等量关系为:.（2） 图1图2（3）线段CD 、AF 、BE 之间所满足的等量关系为:.图3DA FC EB A B EC DFB EC DA F25.如图, 已知抛物线经过坐标原点O及)0,32(A，其顶点为B(m,3),C是AB中点，点E是直线OC上的一个动点(点E与点O不重合)，点D在y轴上, 且EO=ED .（1）求此抛物线及直线OC的解析式；（2）当点E运动到抛物线上时, 求BD的长；（3）连接AD, 当点E运动到何处时，△AED的面积为433，请直接写出此时E点的坐标.解:11．海淀区九年级第一学期期末练习数学试卷答案及评分参考 2012.01说明: 与参考答案不同, 但解答正确相应给分. 一、选择题（本题共32分，每小题4分）1. B2.D3.A4.B5. B6. C7.D8. C 二、填空题（本题共16分，每小题4分）9. x =0或x =4 10. 15 11. 1 12. π(2分);32π12n + (2分) 三、解答题（本题共29分,第13题～第15题各5分,第16题4分,第17题、第18题各5分） 13．解法一： a =1, b =-8, c =1, …………………………1分24600b ac ∆=-=>. …………………………2分x ==…………………………3分 ∴ 154,15421-=+=x x . …………………………5分 解法二：281x x -=-.2816116x x -+=-+. …………………………1分2(4)15x -=. …………………………2分4x -= …………………………3分∴154,15421-=+=x x . …………………………5分 14．证明: 在△AED 和△ACB 中，∵ ∠A =∠A , ∠AED =∠C , ……………………………2分 ∴ △AED ∽△ACB. ……………………………3分 ∴ .ABADAC AE = ……………………………4分 ∴.645=AE ∴ .310=AE ……………………………5分 15．（1）① (-2 ,0), (1, 0)；② 8; ③增大 (每空1分) ……………………………3分 （2）依题意设抛物线解析式为 y =a (x +2) (x -1).由点 (0, -4)在函数图象上，得-4=a (0+2) (0-1). ……………………………………4分 解得 a =2.∴ y =2 (x +2) (x -1). …………………………………………………5分 即所求抛物线解析式为y =2x 2+2x -4. 16．（1）正确画图（1分）标出字母（1分） ……………………………………2分 （2）正确画图（1分），结论（1分） ………………………………………………4分 17．解：由题意得{220,[2(2)]4(2)(1)0.k k k k -≠∆=---+≥ …………………1分 ① ②由①得 2k ≠. ………………………………………………………2分 由②得 2k ≤. ………………………………………………………4分 ∴2k <. ∵k 为正整数，∴1k =. ……………………………………………………5分 18．解法一：由题意画树形图如下：…………………3分从树形图看出，所有可能出现的结果共有9个，这些结果出现的可能性相等，标号之和等于4的结果共有3种. ………………………………………………………4分所以P (标号之和等于4)=3193=. ………………………………………………………5分解法二：……………………………………3分由上表得出，所有可能出现的结果共有9个，这些结果出现的可能性相等，标号之和等于4的结果共有3种. ………………………………………………………4分所以P (标号之和等于4)=3193=. ………………………………………………………5分四、解答题（本题共21分, 第19题、第20题各5分, 第21题6分，第22题5分） 19．（1）(20)(280)(20)y w x x x =-=-+- ……………………………………2分221201600x x =-+-.（2）22(30)200y x =--+. ∵2040x ≤≤, a =-2<0,∴当30x =时，200y =最大值. ……………………………………4分 答：当销售单价定为每双30元时，每天的利润最大，最大利润为200元. ………5分 20．（1）∵二次函数y 2+(3x -3 (m >0)的图象与x 轴交于点 (x 1, 0)和(x 2, 0), ∴ 令0y =，即2+(3x -3=0．………………………………………………1分+3)( x -1)=0. ∵m >0， 0.第二次摸球第一次摸球312321233211解得 1x =或x = …………………………………………………………2分 ∵ x 1 <x 2，103<<-m, ∴21x =. ……………………………………………………………3分（2）由（1）1x =，得3x -.由1x =是方程mx 2+(3x -3=0的根，12+(3x 1=3. ∴mx 1212 +(3x 1112 +(3x 11+3)2=3. ………5分 21．解：（1）证明：∵CE AB ⊥,∴ 90CEB ∠=o.∵ CD 平分ECB ∠, BC =BD , ∴ 12∠=∠, 2D ∠=∠.∴ 1D ∠=∠. …………………………1分 ∴ CE ∥BD .∴ 90DBA CEB ∠=∠=o .∵ AB 是⊙O 的直径,∴ BD 是⊙O 的切线. ………………………………………………………2分 （2）连接AC ，∵ AB 是⊙O 直径，∴ 90ACB ∠=o . ∵CE AB ⊥, 可得 2CE AE EB =⋅.∴ .162==AECE EB ………………………………………………………3分在Rt △CEB 中，∠CEB =90︒, 由勾股定理得20.BC == ……………4分 ∴ 20BD BC ==.∵ 1D ∠=∠, ∠EFC =∠BFD ,∴ △EFC ∽△BFD. ………………………………………………………5分 ∴ BFEFBD EC =. ∴121620BFBF-=. ∴ BF =10. ………………………………………………………………………6分 22．（1）画图: 图略(1分); 填空： a (1分) …………………………………2分（2）a 85(1分), a n n 1212++ （2分） ……………………………………………5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分）23．（1）∵A (a , -3)在4a y x+=的图象上,∴43a a +=-. 解得1a =-. ……………………………………1分 ∴反比例函数的解析式为3y x=. ……………………………………2分 （2）过A 作AC ⊥y 轴于C .∵ A (-1, -3),∴ AC =1，OC =3. ∵ ∠ABO =135︒， ∴ ∠ABC =45︒. 可得 BC =AC =1. ∴ OB =2.∴ B (0, -2). …………………3分由抛物线2y ax bx c =++与y 轴交于B ，得c = -∵ a = -1, ∴22y x bx =-+-. ∵ 抛物线过A (-1，-3), ∴ 123b ---=-. ∴ b =0.∴ 二次函数的解析式为22y x =--. ……………………………………4分 （3）将22y x =--的图象沿x 轴翻折，得到二次函数解析式为22y x =+. ……………5分设将22y x =+的图象向右平移后的二次函数解析式为2()2y x m =-+ (m >0). ∵ 点P （x 0, 6）在函数3y x=上， ∴036.x =∴012x =. ∴2()2y x m =-+的图象过点1(,6)2P .∴62)21(2=+-m .可得1253,22m m ==-（不合题意，舍去）. ∴ 平移后的二次函数解析式为25()22y x =-+. …………………………6分∵ a =1>0, ∴ 当2521≤≤x 时，62≤≤y ; 当325≤<x 时，492≤<y .∴ 当132x ≤≤时，26y ≤≤. ……………………………………7分 ∴ 平移后的二次函数y 的取值范围为 26y ≤≤.24. （1）CD =AF +BE . …………………1分 （2）解：（1）中的结论仍然成立. 证明：延长EA 到G ，使得AG =BE ，连结DG .∵ 四边形ABCD 是平行四边形, ∴ AB =CD , AB ∥CD ，AD =BC . ∵ AE ⊥BC 于点E , ∴ ∠AEB =∠AEC =90︒.∴∠AEB =∠DAG =90︒. ∴ ∠DAG =90︒. ∵ AE =AD ,∴ △ABE ≌△DAG . …………………………………………………………………3分 ∴∠1=∠2, DG =AB . ∴∠GFD =90︒-∠3. ∵ DF 平分∠ADC , ∴∠3=∠4.∴∠GDF =∠2+∠3=∠1+∠4=180︒-∠FAD -∠3=90︒-∠3.∴∠GDF =∠GFD . ………………………………………………………………4分 ∴ DG =GF .∴ CD =GF =AF +AG = AF + BE .即 CD = AF +BE . ………………………………………………………………5分 （3）a CD AF BE b =+或bCD aAF bBE =+或b bCD AF BE a a=+. …………………7分 25. 解：（1）∵ 抛物线过原点和A(0-)，∴ 抛物线对称轴为3-=x . ∴ B(3).设抛物线的解析式为23y ax =+（. ∵ 抛物线经过(0, 0),∴ 0=3a +3. ∴ a =-1.∴3)3(2++-=x y ……………………………………………1分 =.322x x --∵ C 为AB 的中点, A(0-)、B(3)，4321G D A FC EB可得 C(32) . 可得直线OC 的解析式为x y 33-=. ……………………………………………2分 （2）连结OB . 依题意点E 为抛物线x x y 322--=与直线x y 33-=的交点（点E 与点O 不重合）.由2,y y x ⎧=⎪⎨⎪=--⎩， 解得5,3x y ⎧=⎪⎪⎨⎪=⎪⎩或0,0.x y =⎧⎨=⎩（不合题意，舍）.∴ E（53） …………………………3分 过E 作EF ⊥y 轴于F , 可得OF =53，∵ OE =DE ，EF ⊥y 轴， ∴ OF=DF .∴ DO =2OF =103. ∴ D (0,10)3.∴ BD （3）E 点的坐标为(32)或12-). 说明：此问少一种结果扣1分.。