excel排幻方20140626
- 格式:xls
- 大小:16.87 MB
- 文档页数:14

幻方常规解法汇总没法,组合数学还考幻方构造。
这东西不看解法真不会写,虽然没见有啥用,但还是记录下,免得日后再找。
按目前填写幻方的方法,是把幻方分成了三类,即奇数阶幻方、双偶阶幻方、单偶阶幻方。
下面按这三类幻方,列出最常用解法(考试用,不求强大,只求有效!)。
奇数阶幻方(罗伯法)奇数阶幻方最经典的填法是罗伯法。
填写的方法是:把1(或最小的数)放在第一行正中;按以下规律排列剩下的(n×n-1)个数:1、每一个数放在前一个数的右上一格;2、如果这个数所要放的格已经超出了顶行那么就把它放在底行,仍然要放在右一列;3、如果这个数所要放的格已经超出了最右列那么就把它放在最左列,仍然要放在上一行;4、如果这个数所要放的格已经超出了顶行且超出了最右列,那么就把它放在前一个数的下一行同一列的格内;5、如果这个数所要放的格已经有数填入,那么就把它放在前一个数的下一行同一列的格内。
例,用该填法获得的5阶幻方:双偶数阶幻方(对称交换法)所谓双偶阶幻方就是当n可以被4整除时的偶阶幻方,即4K阶幻方。
在说解法之前我们先说明一个“互补数”定义:就是在n 阶幻方中,如果两个数的和等于幻方中最大的数与 1 的和(即n×n+1),我们称它们为一对互补数。
如在三阶幻方中,每一对和为10 的数,是一对互补数;在四阶幻方中,每一对和为17 的数,是一对互补数。
双偶数阶幻方的对称交换解法:先看看4阶幻方的填法:将数字从左到右、从上到下按顺序填写:内外四个角对角上互补的数相易,(方阵分为两个正方形,外大内小,然后把大正方形的四个对角上的数字对换,小正方形四个对角上的数字对换)即(16,11)(7,10)互换即可。
对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4×4把它划分成k×k个方阵。
因为n是4的倍数,一定能用4×4的小方阵分割。
然后把每个小方阵的对角线,象制作4阶幻方的方法一样,对角线上的数字换成互补的数字,就构成幻方。

Excel2020 中进行排列的操作方法
翻开要排列的 excel 文档,在菜单栏找到数据,点开。
先选定要排列的列,点列的上部就全选了,还要注意后边留下一空列。
点击排列,调出排列窗口,我是依据分开符来排列,我用的分开符就是空格。
勾选其余,在其余后边输入一个空格。
这个空格是前方列中姓名与证件号的分开符。
下方还有数据预览,能够看到有一条线分开了。
点下一步,而后点达成。
就行了。
假如后边不空出一列,就会被排列后的数据覆盖,自然会有提示的。
自然我也能够用固定宽度来排列。
在需要的地方点一下就能够了。

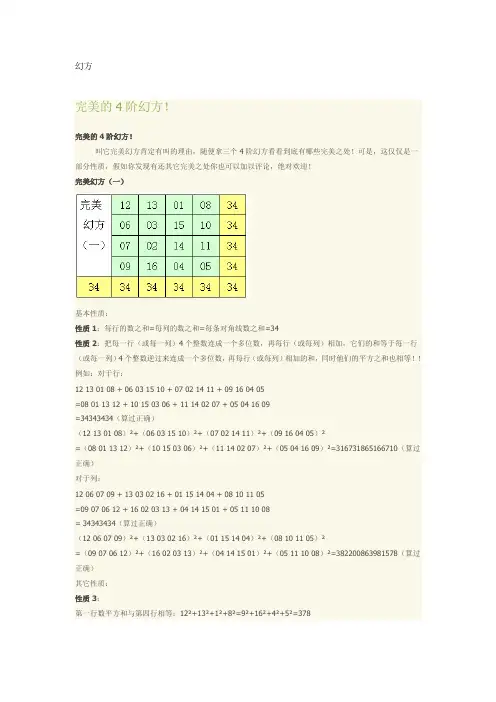
幻方完美的4阶幻方!完美的4阶幻方!叫它完美幻方肯定有叫的理由,随便拿三个4阶幻方看看到底有哪些完美之处!可是,这仅仅是一部分性质,假如你发现有还其它完美之处你也可以加以评论,绝对欢迎!完美幻方(一)基本性质:性质1:每行的数之和=每列的数之和=每条对角线数之和=34性质2:把每一行(或每一列)4个整数连成一个多位数,再每行(或每列)相加,它们的和等于每一行(或每一列)4个整数逆过来连成一个多位数,再每行(或每列)相加的和,同时他们的平方之和也相等!!例如:对于行:12 13 01 08 + 06 03 15 10 + 07 02 14 11 + 09 16 04 05=08 01 13 12 + 10 15 03 06 + 11 14 02 07 + 05 04 16 09=34343434(算过正确)(12 13 01 08)²+(06 03 15 10)²+(07 02 14 11)²+(09 16 04 05)²=(08 01 13 12)²+(10 15 03 06)²+(11 14 02 07)²+(05 04 16 09)²=316731865166710(算过正确)对于列:12 06 07 09 + 13 03 02 16 + 01 15 14 04 + 08 10 11 05=09 07 06 12 + 16 02 03 13 + 04 14 15 01 + 05 11 10 08= 34343434(算过正确)(12 06 07 09)²+(13 03 02 16)²+(01 15 14 04)²+(08 10 11 05)²=(09 07 06 12)²+(16 02 03 13)²+(04 14 15 01)²+(05 11 10 08)²=382200863981578(算过正确)其它性质:性质3:第一行数平方和与第四行相等:12²+13²+1²+8²=9²+16²+4²+5²=378第二行数平方和与第三行相等:6²+3²+15²+10²=7²+2²+14²+11²=370两条对角线的数平方和相等:12²+3²+14²+5²=8²+15²+2²+9²=374推广,一二行的数平方和、三四行的数平方和与两对角线的数平方和相等:12²+13²+1²+8²+6²+3²+15²+10²=9²+16²+4²+5²+7²+2²+14²+11²=12²+3²+14²+5²+8²+15²+2²+9²=748性质4:对称小“田”和及平方相等、中“田”对称四角和及平方相等。

六阶幻方解法 Revised by Hanlin on 10 January 2021
一、奇阶幻方:罗伯法(适合编制所有的奇阶幻方)一居上行正中央,依次斜填切莫忘,上出格时往下填,右出格时左边放,排重便在下格填,角上出格一个样。
例:用
?偶阶幻方分两类:双偶数阶幻方和单偶数阶幻方
双偶数:四阶幻方,八阶幻方,……4K阶幻方,
?可用<对称交换法>,方法很简单:
1)把自然数依次排成方阵
2)把幻方划成4×4的小区,每个小区划对角线
3)把这些对角线所划到的数,保持不动
4)把没划到的数,按幻方的中心,以中心对称的方式,进行对调。
单偶数:六阶幻方,十阶幻方,……4K+2阶幻方
?方法是很繁的,有一种称<同心方阵法>:
1)把幻方分成两个区:一是边框一圈;二是里面一个双偶数方阵,
2)把(3+8K)到(16K2+8K+2)按双偶数幻方方法填入双偶数方阵
?3)把余下的数,在边上试填,调整到符合为止。
?例题:用自然数1-36完成六阶幻方。
首先因为4×1+2,k=1,把11~26填入中间4×4方格中,
然后将1-10,27-36这20个自然数成对填入余下空中。
“九子斜排,上下对易,左右相更,四维挺出”。

幻方做题技巧幻方啊,就像一个神秘的数字魔法阵。
咱要解开它的奥秘,可得有点小窍门。
先说说三阶幻方吧。
这就好比是幻方里的小老弟,简单又有趣。
你得知道幻和这个概念,啥是幻和呢?就像是这个幻方里的一个小目标。
对于三阶幻方来说,它的幻和特别好算,你把这九个数里最大的数加上最小的数,然后乘以个1.5就成了。
比如说1到9这九个数,最大的是9,最小的是1,那幻和就是(9 + 1)×1.5 = 15。
知道了幻和,就像手里有了一把小钥匙。
咱再看这九个数怎么往幻方里填。
中间数那可是个关键的主儿,就像一个小班长,在三阶幻方里,这中间数就得填5。
为啥呢?因为它在这堆数里位置特殊呗。
你把5填在中间,就像在这个魔法阵的中心定了个桩。
然后呢,你就可以试着把和为10的数对往幻方里填,像1和9,2和8,3和7,4和6,就像给小朋友找小伙伴,一对一对的。
不过这填的时候也得有点小技巧,不能瞎填。
你可以先在角上找个位置给1,为啥是角上呢?角上的数啊,它要跟更多的数相加凑幻和呢。
你把1填在角上,那跟1凑幻和15的数就有9和5了,这样就比较容易确定其他数的位置。
再讲讲五阶幻方。
这五阶幻方可比三阶的复杂点了,就像从小学的数学题跳到了初中的难度。
这时候幻和的计算也有点不一样了。
你得把这25个数里最小的数加上最大的数,然后乘以个2.5。
这时候填数也有个小办法。
你可以先把1填在最上面一行中间的位置,就像在舞台的正中央先放了个小演员。
然后呢,你就按照斜着往上走的规则填数。
要是走到幻方的外面了,你就像这个数字坐了时光机一样,从幻方的对面钻出来接着填。
要是斜着走的位置已经被占了,那这个数字就乖乖地填在这个被占数字的下面,就像排排坐吃果果一样。
还有一种幻方是偶数阶幻方。
偶数阶幻方就像两个好朋友手拉手。
比如说四阶幻方,你可以把这个幻方分成四个小方阵。
先把1到16这16个数按顺序填进去,然后呢,你就像个调皮的小精灵,把对角线上的数进行交换。
把左上角小方阵和右下角小方阵里的对角线的数交换,右上角小方阵和左下角小方阵里的对角线的数也交换。

幻方1.概念简析:幻方:是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的3×3的数阵称作三阶幻方,4×4的数阵称作四阶幻方,5×5的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样.2.构造幻方常用的方法:(1)适用于所有奇数阶幻方的填法—罗伯法.口诀是:一居上行正中央,后数依次右上连.上出框时往下填,右出框时往左填.排重便在下格填,右上排重一个样.(2)仅适用于三阶幻方—九宫格口诀.口诀是:九宫者,二四为肩,六八为足,左七右三,戴九履一,五居中央。
(3)适用于所有偶数阶幻方的填法—对称交换的方法1.将数依次填入方格中,对角线满足要求。
2.调整行,对角线数不动,对称行的其它数对调;调整列,对角线数不动,对称列的其它数对调。
3.三阶幻方的性质:1.幻和相等,幻和等于9个数的和除以3.2.中间数必位于幻方中心,中间数等于幻和除以3.3.黄金三角: 黄金三角顶点的数为两腰之和除以2.视频描述把0、2、4、6、8、10、12、14、16这9个数填在下面图中的方格内,使每行、每列和每条对角线上的三个数的和都相等。
1.1.请用11、13、15、17、19、21、23、25、27编制一个三阶幻方。
注:此题答案默认为0,正确答案见解析!2.2.把7—15这九个数构成一个三阶幻方。
注:此题答案默认为0,正确答案见解析!3.3.请用1、4、7、10、13、16、19、22、25编制一个三阶幻方。
注:此题答案默认为0,正确答案见解析!视频描述将下面左边方格中的9个数填入右边方格中,使每一行、每一列、每条对角线中的三个数相加的和都相等。
1.1.将图中的数重新排列,使横行、竖行、对角线上的三个数的和都相等。
注:此题答案默认为0,正确答案见解析!2.2.把3、4、5、8、9、10、13、14、15编成一个三阶幻方,并求出幻和是多少?3.3.将图中的数重新排列,使横行、竖行、对角线上的三个数的和都相等。


如何利用Excel进行数据的时间序列分析数据分析在当今社会中扮演着至关重要的角色,其中时间序列分析是一种常用的数据分析方法。
Excel作为一款功能强大且广泛使用的电子表格软件,具备处理和分析时间序列数据的能力。
本文将介绍如何利用Excel进行数据的时间序列分析,以帮助读者更好地应用Excel进行数据分析。
一、时间序列分析简介时间序列分析是指对一系列按时间顺序排列的数据进行统计方法的分析。
时间序列分析的目的是通过对历史数据的分析,揭示数据内在的规律性和趋势,从而预测未来的发展趋势。
时间序列分析的应用广泛,包括经济预测、市场调研、环境监测等领域。
二、Excel中的时间序列分析工具Excel提供了多种功能和工具,可以帮助我们进行时间序列分析。
下面我们将介绍其中一些常用的工具。
1. 数据准备在进行时间序列分析之前,首先需要准备好要分析的数据。
在Excel中,我们可以将时间序列数据按照日期顺序排列在一个列中,并在旁边的列中记录相应的数值。
确保数据的连续性和准确性是进行时间序列分析的基础。
2. 移动平均图移动平均图是一种常见的时间序列分析方法,用于显示数据的趋势变化。
在Excel中,我们可以使用“数据分析工具包”中的“移动平均”功能绘制移动平均图。
将要分析的数据选中,点击菜单栏的“数据”选项,选择“数据分析”,在弹出的对话框中选择“移动平均”,填写相应参数后,Excel会自动绘制移动平均图。
3. 分解趋势分解趋势是指将时间序列数据分解为趋势、季节性和残差三个部分,以便更好地理解数据的规律性。
在Excel中,我们可以使用“数据分析工具包”中的“指数平滑法”进行趋势分析。
选择要分析的数据,点击菜单栏的“数据”选项,选择“数据分析”,在弹出的对话框中选择“指数平滑法”,填写相应参数后,Excel会自动生成趋势分析结果。
4. 预测模型预测模型是根据历史数据的规律性,对未来的趋势进行预测和估计。
在Excel中,我们可以使用“数据分析工具包”中的“趋势拟合”功能进行预测模型的分析。

双偶幻方和excel所谓幻方,也叫纵横图,就是在n×n的方阵中,放入从某个自然数开始的n平方个自然数;在一定的布局下,其各行、各列和两条对角线上的数字之和正好都相等,这个和数就叫“幻和”。
幻方分为奇幻方(2K+1,K为非零自然数)和偶幻方,偶幻方又分为单偶幻方(4K+2,K为非零自然数)和双偶幻方(4K,K为非零自然数)。
由于幻方具有奇特性质,几千年来吸引着许多数学家和数学爱好者的兴趣,填幻方也是广大中小学生非常喜欢的一项数学游戏活动,但是由于幻方计算量大,制作繁琐,一定程度上制约给广大数学爱好者对幻方的探索。
Excel是微软公司出品的Office系列办公软件中的一个组件,是一个电子表格软件,可以用来制作电子表格、完成许多复杂的数据运算,进行数据的分析和预测并且具有强大的制作图表的功能。
excel的应用给广大中小学数学爱好者探索幻方奥秘带来了极大的方便,为进一步探索幻方提供了保障。
让我一起随着excel遨游、探索神奇的幻方世界,启迪思想、开阔视野,锻炼思维能力。
双偶幻方双偶幻方:n=4K,K为非零自然数,这样的方阵叫做双偶幻方。
双偶幻方有很多种填法,对称交换法是其中的一种填法:一个重要的概念互补:如果两个数字的和,等于幻方中最大数与最小数的和,称为互补。
当K=1时,n=4,就叫做4阶幻方,当K=2时,n=8,就叫做8阶幻方,当K=3时,n=12,就叫做12阶幻方……对于n=4k阶幻方,我们先把数字按顺序填写。
写好后,按4×4把它划分成k×k个方阵。
因为n是4的倍数,一定能用4×4的小方阵分割。
然后把每个小方阵的对角线上单元格内的数字,用幻方中最大数与最小数的和减这个单元格里的数,换成互补的数字,就构成幻方。
第一课时4阶幻方4阶幻方在excel中快速的填法把1至16这16个连续自然数分别填入excel中4乘4的方格中,使得第行每列每条对角线的和都相等。
●写数:将数字从左到右、从上到下按顺序填写,操作过程如下图。

Excel60甲子排列组合算法一、引言在Excel中,我们经常需要进行排列和组合的计算,特别是在处理数据分析和统计的过程中。
而对于我国传统的六十甲子,也是一种十分有趣的排列组合。
接下来,我们将探讨Excel中如何使用排列组合算法来实现六十甲子的计算,并将其应用于实际的数据处理中。
二、六十甲子简介六十甲子是我国古代用于纪年的一种方法,它是通过干支纪年的方式来表示年份。
干支纪年是由“天干”和“地支”两个周期性纪年方法相合并而来的纪年法。
天干包括甲、乙、丙、丁、戊、己、庚、辛、壬、癸,地支包括子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥。
将天干和地支相合并得到六十个甲子,在我国传统文化中具有重要的纪年意义。
三、Excel中的排列组合算法在Excel中,可以使用排列组合算法来计算六十甲子的排列组合。
在实际操作中,可以通过以下步骤来实现:1. 使用Excel的数据填充功能,输入天干和地支的数据。
2. 利用Excel的排列组合函数,计算出所有可能的排列组合。
3. 使用筛选和排序功能,将计算结果进行整理和展示。
四、排列组合算法的应用在数据分析和统计的过程中,我们可以利用排列组合算法来进行各种计算,比如在确定某一年份的干支纪年之后,可以通过排列组合算法来计算出该年份对应的六十甲子。
在文化研究和历史考证方面,排列组合算法也可以被广泛应用,比如在研究古代历法和纪年法时,可以利用排列组合算法来进行相关计算和推论。
五、个人观点和理解对于六十甲子的排列组合算法,我个人认为它不仅具有很高的纪年价值,而且也是我国传统文化中的一种独特而有趣的计算方法。
在今天的信息时代,我们可以借助现代化的工具和技术,比如Excel,来更加便捷地进行六十甲子的计算和应用。
这也充分展现了传统文化与现代科技的结合和发展。
六、总结与展望通过本文的探讨,我们了解了在Excel中利用排列组合算法来计算六十甲子的方法和应用。
通过实际操作,我们可以更深入地理解和应用六十甲子,并发现其中的更多魅力和价值。
一、奇阶幻方:罗伯法(适合编制所有的奇阶幻方)
一居上行正中央,依次斜填切莫忘,
上出格时往下填,右出格时左边放,
排重便在下格填,角上出格一个样。
例:用1-25组成五阶幻方。
二、偶阶幻方:
偶阶幻方分两类:双偶数阶幻方和单偶数阶幻方
双偶数:四阶幻方,八阶幻方,……4K阶幻方,
可用<对称交换法>,方法很简单:
1) 把自然数依次排成方阵
2) 把幻方划成4×4的小区,每个小区划对角线
3) 把这些对角线所划到的数,保持不动
4) 把没划到的数,按幻方的中心,以中心对称的方式,进行对
调。
单偶数:六阶幻方,十阶幻方,……4K+2阶幻方
方法是很繁的,有一种称<同心方阵法>:
1) 把幻方分成两个区:一是边框一圈;二是里面一个双偶数方阵,
2) 把(3+8K)到(16K2+8K+2)按双偶数幻方方法填入双偶数方阵
3) 把余下的数,在边上试填,调整到符合为止。
例题:用自然数1-36完成六阶幻方。
首先因为4×1+2,k=1,把11~26填入中间4×4方格中,
然后将1-10,27-36这20个自然数成对填入余下空中。
“九子斜排,上下对易,左右相更,四维挺出”。
幻方解题公式幻方是一种数学谜题,由数字排列在一个正方形内以形成一个阶数相同的网格而形成。
每行、每列和对角线的数字之和相等。
在这篇文章中,我们将介绍一些幻方解题的公式,让您更好地理解和解决这个谜题。
1. 幻方基本公式在一个n阶幻方中,每个数字的位置可以表示为 (i,j)。
其中i 和j是数字的行和列。
幻方基本公式是S=n(n+1)/2。
这个公式是幻方中每行、每列和每个对角线数字之和的值。
例如,一个3阶幻方中的S值是15。
2. 幻方奇数阶公式在奇数阶的幻方中,我们可以使用以下公式来找出每个数字的位置。
如果我们要找出数字x的位置,那么行和列可以表示为:行 = (n+1)/2 + p列 = (n+1)/2 - q其中p和q是数字在幻方中的偏移量,可以使用以下公式计算: p = (x-1) mod nq = (x-1) div n例如,在一个5阶幻方中,数字17的位置可以计算为:行 = (5+1)/2 + (17-1) mod 5 = 3 + 1 = 4列 = (5+1)/2 - (17-1) div 5 = 3 - 3 = 0因此,数字17在第4行第1列。
3. 幻方偶数阶公式在偶数阶的幻方中,我们需要使用不同的公式来找出每个数字的位置。
我们可以将幻方分成四个相等的部分,并使用以下公式来计算每个数字的位置:如果数字x位于左上或右下的网格中:行 = (n/2) - p列 = (n/2) - q如果数字位于右上或左下的网格中:行 = (n/2) + p列 = (n/2) - q其中p和q的计算方法与奇数阶幻方相同。
例如,在一个4阶幻方中,数字14位于左下角的网格中。
因此,我们可以计算其位置为:行 = (4/2) + (14-1) div 4 = 2 + 3 = 5列 = (4/2) - (14-1) mod 4 = 2 - 1 = 1因此,数字14在第5行第1列。
以上是一些幻方解题的基本公式,希望能对您的幻方解题有所帮助。
excel如何做排列组合?[五篇]第一篇:excel如何做排列组合?怎样做排列组合?比如现在有一个长度是9 位的字符串(ABCDEFGHI),想列出全部的只取其中7个字符的组合值:CDEFGHIADEFGHIABEFGHIABCFGHIABCDGHI……共36个。
用函数或VBA均可。
多谢用公式的解:=REPLACE(REPLACE($M$1,MIN(IF(ROW()第二篇:排列组合排列组合方法一:相邻元素捆绑法:所谓“捆绑法”就是在解决对于某几个元素要求相邻问题时,可整体考虑将相邻元素视为一个“大”元素例:6名同学排成一排,其中甲,乙两人必须在一起的不同徘法共有(C)A.720种 B.360种 C.240种 D.120种因甲,乙两人排在一起,故甲乙两人捆在一起视作一人,与其余四个全排列A5种排法,但甲乙两人之间有A2种52排法,由分布计数原理可知:共有A5•A2=240种不同排法,故选C 方法二:相离问题插空法:不相邻问题是指要求某些元素不能相邻,由其他元素将它隔开,此类问题可以先将其他元素排好,再将所指定的不相邻的元素插入到它们的空隙及两端位置,故称“插空法”例:要排一张有6个歌唱节目和4个舞蹈节目的演出节目单,任何两个舞蹈节目不得相邻,问有多少种不同的排法?先将6个歌唱节目排好,其不同的排法A6种,这6个歌唱节目的空隙及两端共7个位置中再排4个舞蹈节目有A746种排法,由分步计数原理可知,任何两个舞蹈节目不得相邻的排法为A7.•A6方法三:定序问题缩倍法:在排列问题中限制某几个元素必须保持一定顺序成为定序问题,这类问题用缩小倍数的方法求解比较方便。
例:信号兵吧红旗与白旗从上到下挂在旗杆上表示信号,现有3面红旗,2面白旗,把这5面旗都挂上去,可表示不同信号的种数是_________(10种)5解法一:5面旗全排列有A5种挂法,由于3面红旗与2面白旗分别全排列只能做一次挂法,故共有不同的信号5A5总数是3=10种2A3•A22解法二:定序问题属组合。
幻方罗伯法证明方法幻方,这玩意儿可神奇啦!就像一个神秘的魔法盒子,里面藏着无尽的奇妙。
而罗伯法呢,就是打开这个魔法盒子的一把钥匙。
咱先来说说幻方是啥。
简单来讲,就是把一些数字巧妙地排列在一个方阵里,让每行、每列和对角线上的数字之和都相等。
这就好比是一场数字的大派对,每个数字都要找到自己最合适的位置,才能让整个派对热闹而和谐。
那罗伯法是怎么做到让这些数字乖乖听话,排列出完美幻方的呢?这可就得好好研究研究啦。
你看啊,罗伯法就像是一个聪明的指挥家,它指挥着数字们依次就座。
先从第一行中间那个位置开始,这就是整个幻方的起点。
然后呢,数字们就一个一个地按照一定的规则排下去。
比如说,下一个数字要放在右上方,如果右上方已经有数字了,那就放到下方。
这就好像是数字们在玩跳房子游戏,一格一格地跳着,找到自己的落脚点。
这听起来是不是很简单?但这里面可藏着大学问呢!就好像解一道超级复杂的谜题,每一步都要小心翼翼,不能出错。
想象一下,这些数字就像是一群调皮的小孩子,要让他们乖乖听话,按照罗伯法的规则来排列,可不是一件容易的事啊。
但一旦排列成功,哇,那感觉就像是创造了一个小小的奇迹。
咱们来具体分析分析罗伯法的神奇之处。
它为什么能这么准确地让数字们排列成幻方呢?这背后其实有着深刻的数学原理。
就好像是一条隐藏在数字世界里的秘密通道,只有通过罗伯法,我们才能找到它。
比如说,通过罗伯法排列出来的幻方,它的对称性是非常美妙的。
每一行、每列和对角线都像是一面镜子,反射出同样的和谐与完美。
这难道不是数学的魅力所在吗?而且啊,罗伯法可不是随便想出来的,那是经过无数数学家们的努力和探索才发现的。
他们就像是一群勇敢的探险家,在数字的海洋里寻找着宝藏,而罗伯法就是他们找到的最珍贵的宝藏之一。
你说,这多有意思啊!一个小小的罗伯法,却能让我们看到数学的博大精深。
它就像是一把钥匙,打开了幻方这个神秘世界的大门,让我们可以尽情地探索其中的奥秘。
总之,幻方罗伯法证明方法真的是太神奇啦!它让我们感受到了数学的无穷魅力,也让我们对这个世界有了更深的理解。
填幻方(奇数阶)关于幻方的起源,中国有“河图”和“洛书”之说。
相传在远古时期,伏羲氏取得天下,把国家治理得井井有条,感动了上天,于是黄河中跃出一匹龙马,背上驮着一张图,作为礼物献给他,这就是“河图”,也是最早的幻方。
伏羲氏凭借着“河图”而演绎出了八卦,后来大禹治洪水时,洛水中浮出一只大乌龟,它的背上有图有字,人们称之为“洛书”。
“洛书”所画的图中共有黑、白圆圈45个。
把这些连在一起的小圆和数目表示出来,得到九个数,这九个数就可以组成一个纵横图,如果用数字翻译出来,就是三阶幻方。
幻方是指横行、竖列、对角线上数的和都相等的数的方阵,具有这一性质的3×3的数阵称作三阶幻方,4×4的数阵称作四阶幻方,5×5的称作五阶幻方…如图为三阶幻方。
求幻和:幻和是指每行、每列及两条对角线上几个自然数的和,这个和是相等的,因此求幻和的方法是:n个数之和÷幻方的阶 = 幻和求中心数:(即上图中的5),可以根据求出的幻和来计算,我们可以得到求这个中心数的方法是:幻和÷ n =中心数幻方的填写一、口诀法:九宫之义,法以灵龟,二四为肩,六八为足,左七右三,戴九履一,五居中央。
二、九子斜排法:宋朝数学家杨辉在《续古摘奇算法》中,总结“洛书”幻方的编排方法时说:三阶幻方的编排方法是“九子斜排,上下对易,左右相更,四维挺出”。
这就是九子斜排法。
同样的方法也适用于奇数阶幻方(五阶、七阶……)三、罗伯法法国人罗伯总结出了构造奇数阶,连续自然数幻方的简单易行的方法“罗伯法”。
(适用于奇数阶幻方,适合于连续自然数或者等差数列的奇数阶幻方)口诀:1居首行正中央,依次右上切莫忘,上出框时往下放,右出框时往左放,重复便往自下放,右上出框一个样。
口诀解读:1居首行正中央——将填入的数列中最小的数填在首行中间的格子中。
依次右上切莫忘——向右上角斜行,依次填入数字。
上出框时往下放——如果右上方向出了上边界,就以出框后的虚拟方格位置为基准,将数字竖直降落至底行对应的格子中。
幻方专题王红1104班1130140223一、幻方一般地说,在n×n的方格里,既不重复也不遗漏地填上n²个连续的自然数,每个数占一格,并使每行、每列及两条对角线上n个自然数的和都相等,这样排成的数表称为n阶幻方。
这个相等的和叫幻和。
1.奇数阶幻方奇数阶幻方的方法可以简单概括为方阵斜线对换法:(1)三阶幻方(九宫幻方):具体可以概括为以下几步:第一步:将1——9九个整数如图1那样排列成方阵;第二步:如图2,画斜线;第三部:如图3,将图2中得到的正方形外四角的数字1、3、7、9,分别向斜线对面数三格,把数字填入空格内,即1和9交换,3和7交换入幻方格内。
便得到了图4的三阶幻方(九宫幻方),横排、数列,对角线上每三个数字的和都为15。
(2)五阶幻方:五阶幻方具体可以概括为以下几步:第一步:将1——25这二十五个整数如图5排列成方阵;第二步:如图6,画斜线;第三部:如图7,将图2中得到的正方形外四角的数字(1、2、6),(4、5、10);(16、21、22),和(20、24、25)分别向斜线对面数五格,把数字填入空格内,即1 和25交换,2和20交换,6 和24交换,5和21交换,4和16交换,10和22交换填入幻方格内便得到了图8的五阶幻方,横排、数列,对角线上每三个数字的和都为65。
2.偶数阶幻方偶数阶幻方的方法可以简单概括为方阵对角线数字互换和对面数字互换的方法:比如四阶幻方四阶幻方比较简单,只需要交换对角线上的数字就能使横排、竖列、对角线上的和分别都等于34。
具体步骤为:第一步:将1——16十六个整数如图9排列成方阵;第二步:如图10那样画出对角线和方框;第三步:如图10—图11,将方阵中对角线上的数字1和16,4和13,6和12,以及7和10对换,便得到了图12的四阶幻方,而六阶幻方就要复杂得多了,不仅仅需要交换对角线上的数字,还需要横排对面交换,竖列对面交换。
3.反幻方将1~9九个自然数,填在3×3正方形表格内,使其中每一横行、每一竖列及任一条对角线上的三数之和都不等,并且相邻的两个数在图中位置也相邻。