当前位置：文档之家 › 电容元件与电感元件

电容元件与电感元件

  • 格式：ppt
  • 大小：737.00 KB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

电容元件与电感元件

电容元件与电感元件

二、 电容元件
任何两个彼此靠近而且又相互绝缘的 导体都可以构成电容器 ，这两个导体叫做 电容器的极板 ，它们之间的绝缘物质叫做
介质。
1.线性电容元件的图形符号
2.线性电容元件中电荷量q与其两端 的电压u关系
4. 电容元件的电压电流关系（关联参考方向）
1）任何时刻 ，线性电容元件的电流与该时刻电压变 化率成正比。 2）只有当极板上的电荷量发生变化时 ，极板间的电 压才发生变化 ， 电容电路中才出现电流。 3）当电压不随时间变化时 ，则电流为零 ，这时电容 元件相当于开路 ，故电容元件有隔直流，通交流的 作用。
3 、 电感的单位
在SI（国际单位制） 中 ， 电感的单 位为亨[利]。
符号：H mH uH
换算关系： 1 mH=10-3H
1 uH=10-6H
4、 电感元件的电压电流关系
楞次定律： 变化的磁通与感应电动 势（或感应电流） 在方向上的关系： 在电磁感应过程中 ，感应电流所产生 的磁通 ，总是力图阻止原磁通的变化。
电工电子技术
一 、电感元件
1 、 电感线圈： 用导线绕制的空心线圈或具有铁芯
的线圈在工程中称为电感线圈或电感。
线圈的磁通和磁链
图形符号：
2 、 自感磁链 与元件的电流i关系 （关联参考方向）
L称电感元件的自感系数源自注意：电感元件的电感为常量 ，而不随通过它 的电流的改变而改变 ，则称为线性电感元件。
谢谢！！！
通常设定感应电动势与磁通的参考 方向符合右手螺旋关系。
根据电磁感应定律有：
若电感上的电流的参考方向与磁链满足
右手螺旋定则 ，则
，代入上
式得
1） .任何时刻 ， 线性电感元件上的电压与 其 电流的变化率成正比。

《电容元件和电感元 》课件

《电容元件和电感元 》课件

PART 03
电容元件和电感元件的特 性比较
REPORTING
静态特性比较
总结词
在静态条件下，电容元件和电感元件的特性存在显著差异。
详细描述
电容元件在静态时表现为隔直流通交流的特性，其两端电压 与电流相位差为90度；而电感元件在静态时表现为通直阻交 流的特性，其两端电压与电流相位差为0度。
动态特性比较
机械应力
电感元件应能承受一定的 机械应力，如振动和冲击 。
THANKS
感谢观看
REPORTING
选频。
扼流：在高频电路中，电 感可以抑制高频信号的突
变。
旁路：在高频信号下，电 容可以作为旁路，使信号
顺利通过。
电感元件
滤波：对于高频信号，电 感可以滤除特定频率的信
号。
PART 05
电容元件和电感元件的选 用原则
REPORTING
根据电路需求选择合适的元件
滤波电路
耦合电路
选择低损耗、高绝缘电阻的电容或电 感元件。
电容
电容元件的电学量，表示电容器 容纳电荷的本领，与电容器极板 的面积、距离和介质有关。
电容元件的种类
01
02

固定电容
电容量固定的电容器，常 见有瓷介电容、薄膜电容 等。
可变电容
电容量可调的电容器，常 见有空气电容、可变电容 器等。
电解电容
有极性的电容器，正极和 负极材料不同，常见有铝 电解电容、钽电解电容等 。
总结词
在动态条件下，电容元件和电感元件的特性也表现出不同的特点。
详细描述
电容元件在动态时表现为充电和放电的过程，其阻抗随频率的升高而减小；而电 感元件在动态时表现为电流的磁效应，其阻抗随频率的升高而增大。

电容元件及电感元件

电容元件及电感元件
位的正弦量，它们之间关系如下:
图3-4-1
3.4.1 电阻元件
其电压与电流的波形图如图3-4-2所示
图3-4-2
3.4.1 电阻元件
那么，电压与电流的相量关系为： 电压电流的相量模型及相量图如图3-4-3所示
相量模型
图3-4-3
相量图
3.4.1 电阻元件
2、功率 1）瞬间功率
在关联参考方向下电阻元件吸收的瞬时功率p=ui，为了
电容的单位为法拉，简称法，符号为F。常用单位有：微法(μ
F)，皮法(pF)。
3.3.1 电容元件
3、库伏特性 C不随u和q改变称为线性电容，上式表示的电容元件电荷量
与电压之间的约束关系，称为线性电容的库伏特性，它是过坐标原 点的一条直线。如图3-3-3所示。
图3-3-3
3.3.1 电容元件
4、电容元件的伏安特性 图3-3-4给出了电容元件的电压电流参考方向，
L表示。 电感的单位为亨(利)，符号为H，常用的单位有毫亨(mH)、微
亨(μH)。 电感元件的电感为一常数，磁链Ψ总是与产生它的电流i成线性
关系，即
3.3.2 电感元件
3、韦安特性 上式所表示的电感元件磁链与产生它的电流之间的约束关系称为
线性电感的韦安特性,是过坐标原点的一条直线。如图3-3-9所示。
3.4.3 电容元件
2）平均功率
电容元件在一个周期内的平均功率为零（正、负波形相抵 消）。表明电容元件不消耗能量，只是在电源和元件间进行能量 的转换，同时说明电容元件确实为储能元件。
3.4.3 电容元件
3）无功功率（Q） 无功功率是用来描述储能元件与电源交换能量的规模。
单位是乏（var)
介质可以是绝缘纸、真空、 玻璃、陶瓷、云母、聚苯乙烯等 绝缘材料。

第五章 电容元件与电感元件.

第五章 电容元件与电感元件.

1 2
Li2

1 ψ2 2L
结论
(1) 元件方程是同一类型；
(2) 若把 u-i，q- ，C-L互换,可由电容元件
的方程得到电感元件的方程；
(3) C 和 L称为对偶元件, 、q等称为对偶
元素。
电容器和电感器的模型
电容器模型（按照近似程度分） 0 级模型：不考虑损耗和产生的磁场。 I 级模型：考虑损耗不考虑产生的磁场。 II级模型：考虑损耗和产生的磁场。
i
i dq
dt
+
+ dq =Cduc
uc
C
–
–
i C duc dt
uc(
t
)
1 C
t

i

t
dt


uc
(
t
0
)
1 C
t
t 0
i

t
dt

例 5-1 5-2
2. 线性电容的充、放电过程
u,i i u
o
ωt
i ii i
+ u
+u
u
u
- -++
(1) u>0，du/dt>0，则i>0，q , 正向充电(电流流向正极板)；

1 2
Li 2 (t 2)
1 2
Li 2 (t1)
wL( t2 ) wL( t1 )
wL ( t 2 ) wL ( t1 )元件充电，吸收能量
wL ( t 2 ) wL ( t1 )元件放电，释放能量
五、电感电流不能跃变（连续性）
电感 L 储存的磁场能量
wL

电工学 电容,电感元件

电工学 电容,电感元件

4 2
iS/A
2
W / J
4 6 （b）
8
t/s
由题意知L=2H,故电感上的储能为:
16
t0 0 2 4t 0 t 2 1 2 2 w(t ) li 4t 64t 256 2 2t 8 9 9 9 0 t 8
2
4
6
8
（
e ）
例4-4 图所示电路,t<0时开关K闭合，电路已达到稳态。 t=0时刻，打开开关K, 球初始值il(0+), Uc(0+), i(0+), ic(0+), UL(0+)的值。
㈣电容的单位
在国际单位制中，电容C的单位为法拉 （F），但因法拉这个单位太大，所以 通常采用微法（μF）或皮法（pF）作 为电容的单位，其换算关系为
1F 10 F，
6
1F 10 pF
6
㈤电容的伏安关系 设电容上流过电流与其两端电压为关联参 考方向，如图所示，则根据电流的定义有
dq(t ) i(t ) dt
所以
1 1 uc (1) uc (0) ic (t )dt C 0
1 1 V 0 5tdt 1.25 2 0
10 0 -10
iC/A
t/s
1
2
3
4
5
（b）
1 4 uc (4) uc (0) ic (t )dt C 0
1 2 1 4 5tdt (10)dt 2 0 2 0
u(t ) u(t )
(4-4)
等式两边分别为电容电压在t时刻左右极限值.上 式说明在 t 和 t 时刻电压值是相等的。在动态 电路分析中常用这一结论，并称之为“换路理 论”。

电容元件与电感元件

电容元件与电感元件

第六章 电容元件与电感元件电路在任一时刻t 的相应与激励的全部过去历史有关，因此动态电路是有记忆的。

由于动态元件的V AR 是对时间变量t 的微分或积分关系，所以动态电路需要用微分方程或积分方程来描述。

动态元件：电容元件、电感元件动态电路：至少包含一个动态元件的电路。

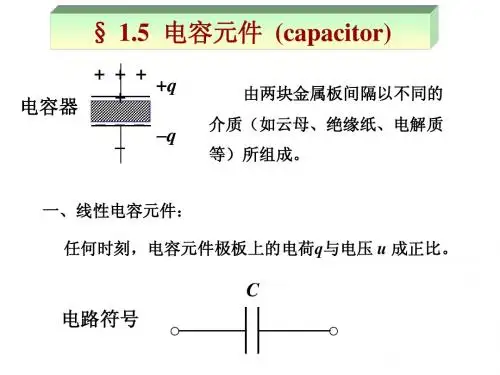
6-1 电容元件1、定义：一个二端元件，如果在任一时刻t ，它所存储的电荷和它的端电压 之间的关系可以用平面上的一条曲线来确定，则该二端元件称为电容元件。

线性时不变电容：平面上通过原点的一条直线，且不随时间变化。

电容元件的符号及线性电容的u-q 曲线对于线性电容有6-2 电容的伏安关系（V AR 关系）若采用关联方向,V AR 关系为讨论： 1、任何时刻i 与 成正比，即与电容电压的变化率成正比。

2、若电容电压为直流电压，则 ＝0，i =0。

所以电容具有隔直作用。

3、在某一时刻t 时，电容电压的数值并不取决于该时刻的电流值，而是取决于从－∞到t 所有时刻的电流值，也就是说与电流全部过去历史有关。

)()(t Cu t qdt du dt du为电容电压的初始值，它反映了电容初始时刻的储能状况。

电容是一个记忆电流的记忆元件。

4、由于实际电路中，电流i 为有限值，即 为有限值，所以u 必为连续函数，电压值在某一时刻不能跃变，即6-3 电容电压的连续性质和记忆性质1、电容电压的连续性质： 若电容电流i(t)在闭区间〔ta 、tb 〕内为有界的，则电容电压uc(t)在开区间（ta 、tb ）内为连续的。

特别是，对任何时间t ，且ta ＜t ＜tb ，2、电容电压的记忆性质：电容是一种记忆元件。

通常只知道在某一时刻t0后作用于电容的电流情况，而对在此之前电容电流的情况并不了解。

在求解具体电路时，给出或求解初始电压是必不可少的。

例：p15页，当u 为9.9V 时，作用过的脉冲数目是多少？解：电容电压为对节点a 由KCL 得：)(0t u )0()0(+-=u u )()(+-=t u t u CC ⎰=tt id C t u 199.01)(ξ0)(,311==t u s t 且设其中μ5099.0su i +=5001.0su i =即su i 2=即u 由0线性增长至0.099V 。

电感元件、电容元件

电感元件、电容元件

-的值及 t =2π/300 时的电流。
解： 电压 u的最大值为60V，所以
+ i
uC
-
i
+ uL e –
三、电感元件储存的能量
电感 L 在任一瞬间吸收的功率：（关联参考方向） P>0 吸收能量
电感 L 在 dt 时间内吸收的能量： P<0 释放能量
电感 L 从 0 到 t 时间内吸收的能量：设i ( 0 ) = 0
即
例1.2 电感电流 i =100e-0.02t mA, L =0.5H , 求其电压 表达式、t =0 时的电感电压和 t =0 时的磁场能量。
三、 电容元件储存的能量
电容 C在任一瞬间吸收的功率：（关联参考方向） P>0 吸收能量 P<0 释放能量
电容 C在 dt 时间内吸收的能量：
电容 C从 0 到 t 时间内吸收的能量： 设u(0) =0
即
例1.3 电容元件及其参考方向如图所示，已知u=
-60sin100t V，电容储存能量最大值为18J，求电容C
[ 名称]： 空心线圈 特性：体积小高频特性好滤波效果好 用途：BB机、电话机、手提电脑等超薄型电器
1.6.1 电感元件
一、线性电感（L为常数） i
N— 匝数
Ψ— 磁链
电感
Φ — 磁通
+
u
–
韦伯（Wb）
亨利（H）
（安）A
N
i
+
u
L
–
二、电感元件的电压电流关系
u、i 、e（电动势）的参考方向为关联参考方向
解： u、i 参考方向一致时
i
+
u
L
–

电容与电感-PPT课件

电容与电感-PPT课件
电容元件的VCR方程 （元件约束方程） 可见线性电容的端口电流并不取决于当前时刻电 压，而与端口电压的时间变化率成正比，所以电 容是一种动态元件。
已知电流 i，求电荷 q ，反映电荷量的积储过程
q ( t) i( )d

t
物理意义：t 时刻电容上的电荷量是此刻以前由电流 充电（或放电）而积累起来的。所以某一瞬刻的电荷 量不能由该瞬间时刻的电流值来确定，而须考虑此刻 以前的全部电流的“历史”，所以电容也属于记忆元 件。对于线性电容有
并联电容的总电荷等于各电容的电荷之和，即
q q q q ( C CC ) u C u 1 2 N 1 2 N e q
q q q q ( C CC ) u C u 1 2 N 1 2 N e q
所以并联等效电容等于各电容之和，等效电路如 图 所示
12 u 32 V 24V u 32 V u 8 V 1 2 1 ( 12 4 )
所以两个电容储存的电场能量分别为：
1 2 w 1 4 4 J ; 1 Cu 1 1 2
1 2 w2 C2u2 8J 2
例5.2、设 0.2F 电容流过的电流波形如图 (a)所示，已知 u(0)=30V 。试计算电容电压的变化规律并画出波形。
同时电容的输入功率与能量变化关系为:
p d we d t
电容储能随时间 的增加率
反之截止到 t 瞬间，从外部输入电容的能量为 ：
t
t d u 1 2 u ( t ) w ( t ) p ( ) d ( C u ) d C u d u C u 5 . 9 ) e u ( ) ( d 2 t
i + u

05电容和电感元件

05电容和电感元件

或
t u(t ) = 1 ∫− ∞ idξ C
du i=C dt
q =Cu
q(t ) = q(t0 ) + ∫ idξ
t t
0
1 t idξ + 1 t idξ = ∫− ∞ C C ∫t 1 t idξ = u(t0 ) + ∫t C
0 0
0
若 t0=0
1 t u( t ) = u( 0) + ∫0 idξ C
L
u
对于线性电感,有： ψ =Li 对于线性电感 有
ψ L= i
def
ψ =NΦ 为电感线圈的磁链
N为电感线圈的匝数。 为电感线圈的匝数。
ψ 单位：Wb （韦伯） 单位： 韦伯）
L 称为自感系数或电感，L是一个正实常数。 称为自感系数或电感， 是一个正实常数 是一个正实常数。
的单位： 亨 电感 L 的单位：H(亨) (Henry，亨利 ，亨利)
u( 2) = 0 V
1 t t ≥ 2 S u( t ) = u( 2) + ∫2 0dξ = 0 2
i/ A
2
1 2
0
−2
t/S
uC / V
1 1
0
2
t/S
思考： 思考：
(1) 一般来说，电容、电感的电压波形与电流波形是不相同 一般来说，电容、 的，为什么？ 为什么？ (2)如果一个电感线圈两端电压为零，它所储存的磁场能量 如果一个电感线圈两端电压为零， 如果一个电感线圈两端电压为零 也为零，对吗？为什么？ 也为零，对吗？为什么？ (3) 电路元件的电压与电流都是有一定的关系的，因此， 电路元件的电压与电流都是有一定的关系的，因此， 某时刻电容储能与该时刻的电压有关， 某时刻电容储能与该时刻的电压有关，也可以说与该时 刻的电流有关，对不对？ 刻的电流有关，对不对？

电容元件和电感元件

电容元件和电感元件

例2-1 C =4F，其上电压如图(b)，试求
iC(t), pC(t)和 wC(t),并画出u波S 形。
+
+ iC
1
uS uC C
-
-
12
-1
34 t
(b) 解：
pC 4
12 -4
34
t
iC 4
12
-4
34 t
wC 2
0 1234 t
uS 1
12
-1
34 t
(b)
iC 4
12
-4
34 t
pC 4
1. 电容是动态元件 电容的电流与其电压对时间的变化率 成正比。假如电容的电压保持不变， 则电容的电流为零。电容元件相当于 开路(i=0)。
2. 电容是惯性元件 当i 有限时，电压变化率 必然有 限；电压只能连续变化而不能跳变。
3. 电容是记忆元件
电容电压u有“记忆”电流全部历史
的作用。取决于电流
u
线性时不变电容的特性
线性电容——特性曲线是通过坐标原点 一条直线，否则为非线性电容。时不 变——特性曲线不随时间变化，否则为 时变电容元件。
线性非时变电容元件的数学表达式：
Cq u
系数 C 为为只与元件本身有关的常 量，为直线的斜率，称为电容，表征 积聚电荷的能力。
单位是法[拉],用F表示。
电容元件的电压电流关系
定义：如果一个二端元件在任一时刻，
其磁链与电流之间的关系由
平
面上一条曲线所确定，则称此二端 元件
为电感元件。
符号和特性曲线：
斜率为L
i(t) L (t)
+ u (t) -
iБайду номын сангаас

电容和电感的关系

电容和电感的关系

电容和电感的关系电容和电感是电路中常见的两种元件，它们在电路中起着不同的作用。

电容是一种能够存储电荷的元件，而电感则是一种能够存储磁场能量的元件。

虽然它们的作用不同，但是在电路中它们之间存在着密切的关系。

一、电容和电感的基本概念电容是指两个导体之间的电荷储存能力，通常用法拉（F）作为单位。

电容器是一种能够存储电荷的元件，它由两个导体板和介质组成。

当电容器两端加上电压时，电荷会在两个导体板之间积累，形成电场。

电容器的电容量与介质的介电常数、导体板的面积和板间距离有关。

电感是指导体中存储磁场能量的能力，通常用亨利（H）作为单位。

电感器是一种能够存储磁场能量的元件，它由导体线圈和铁芯组成。

当电流通过导体线圈时，会在铁芯中产生磁场，导体线圈中存储的能量与电流的大小和铁芯的磁导率有关。

二、电容和电感的作用电容和电感在电路中起着不同的作用。

电容器可以用来存储电荷，当电容器两端加上电压时，电荷会在两个导体板之间积累，形成电场。

电容器可以用来滤波、稳压、调节电压等。

电感器则可以用来存储磁场能量，当电流通过导体线圈时，会在铁芯中产生磁场，导体线圈中存储的能量可以用来产生电磁感应、滤波、稳压等。

三、电容和电感之间存在着密切的关系，它们可以相互转换。

当电容器两端加上电压时，电荷会在两个导体板之间积累，形成电场。

当电容器两端的电压发生变化时，电容器中的电荷也会发生变化，从而产生电流。

这个过程中，电容器的电流与电容器两端的电压成正比，电容器的比例系数就是电容量。

而当电流通过导体线圈时，会在铁芯中产生磁场，导体线圈中存储的能量可以用来产生电磁感应、滤波、稳压等。

这个过程中，电感器的电压与电流成正比，电感器的比例系数就是电感。

在电路中，电容和电感可以组成谐振电路。

谐振电路是一种能够产生共振的电路，它可以用来产生稳定的振荡信号。

当电容和电感的数值满足一定的条件时，谐振电路就会产生共振，产生稳定的振荡信号。

综上所述，电容和电感在电路中起着不同的作用，但是它们之间存在着密切的关系。

电容元件和电感元件

电容元件和电感元件

+
t u(ξ )dξ
t0
∫ ∫ i(t) = 1 L
t u(ξ )dξ
−∞
=
i(t0 )
+
1 L
t u(ξ )dξ
t0
(5.19) (5.20)
此两式表明，电感中某一瞬间的磁链和电流决定于此瞬间以前 的全过程的电压，因此电感也属于记忆元件。
线性电感吸收的功率为
p = ui = iL di = d ( 1 Li 2 ) = dwm
∫ u = u(3s) + 1 t i(ξ )dξ
C 3s
i
∫ = 105V + 1 t (−2)Adξ = 135V − 10t
0.2F 3s
5A
iC +u−
并且 u(7s) = 65V
(3) t ≥ 7s ：此时 i = 0 ，电容电压
保持不变， u(t) = u(7s) = 65V
0
t
3s
7s
在下图中，可明显地判断自感磁链和互感磁链的相对方向。 但当将实际线圈抽象成电路模型时，就靠电流进、出同名端来 判断互感磁链的+（或 -）。
12 ＋ i1
u1 ψ 11
从全过程来看，电容本身既不提供任何能量，也不消耗能量， 所以电容是无源元件。
综上所述，电容是一种动态、记忆、储能、无源元件。
例题 5.1 图示RC串联电路，设uC(0)=0，i ( t )=I e-t /RC。求在 0<t<∞时间内电阻消耗的电能和电容存储的电能，并比较二者大
小。
i
[解] 电阻消耗的电能为
e
d
)
相交链的磁通(flux)Φ （两者的方向遵循右手螺旋法则），与线

电容元件与电感元件

电容元件与电感元件

第二篇 动态电路的时域分析第五章 电容元件与电感元件● 电容元件 ● 电容的VCR● 电容电压的连续性质与记忆性质 ● 电容的储能 ● 电感元件 ● 电感的VCR● *电容与电感的对偶性 状态变量学 习 目 标本章重点：理解动态元件L 、C 的特性，并能熟练应用于电路分析。

一．动态原件包括电容元件和电感元件。

电压电流关系都涉及对电流、电压的微分或积分。

电路模型中出现动态元件的原因：1）有意接入电容器或电感器，实现某种功能；2）信号变化很快时，实际器件已不能再用电阻模型表示。

二．电阻电路与动态电路1.电阻电路是无记忆性（memoryless ）即时的（instantaneous)；2.动态电路（至少含有一个动态元件的电路 ）在任一时刻的响应与激励的全部过去历史有关。

注:电阻电路和动态电路均服从基尔霍夫定律。

动态电路分析与电阻电路分析的比较电阻电路动态电路组成 独立源,受控源,电阻 电感,电容 (独立源,受控源,电阻)特性 耗能 贮能(电能,磁能) ——贮能状态 电路方程 代数方程微分、积分（一阶、 二阶）VCRi R u =⎰∞-==tc cd i c u dt du ci ) (1 ττ§5.1 电 容 元 件一、电容元件的基本概念电容器是一种能储存电荷的器件电容元件是电容器的理想化模型是一个理想的二端元件。

图形符号如右所示：u q C =电容的SI 单位为法［拉］, 符号为F;1 F=1 C ／V常采用微法（μF ）皮法（pF ）作为其单位。

F pF F F 126101101--==μ§5.2 电 容 的VCR一、电容元件的VCR ——电压表示电流1.当电容上电压与电荷为关联参考方向时，电荷q 与u 关系为：q(t)=Cu(t) C 是电容的电容量，亦即特性曲线的斜率。

2.当u 、i 为关联方向时,据电流强度定义有：dt du C dt dCu dt dq t i ===)(非关联时:表明：在某一时刻电容的电流取决于该时刻电容电压的变化率。

电容元件与电感元件

电容元件与电感元件

§ 5－2
电感元件
电感的记忆性质：电感电流对电压有记忆作用 ； 电感电流的连续性：若电感电压有界，则电感电流 不跃变：
il (0 ) il (o )
或
il (t0 ) il (t0 )
三、电感元件的贮能 在t1-- t2时间内，电感贮存的能量为： 1 2 1 2 W（ Lil (t 2 ) Lil (t1 ) WL (t 2 ) WL (t1 ) L t1 , t 2 ) 2 2 1 2 电感在任一时间t时的贮能为： WL (t ) Lil (t ) 2
电流只与电压的变化率有关，当电压为直流时， 电流为0。电容有隔直流的作用。
§5－1 电容元件
1 t （2）、uc (t ) uc ( t 0 ) ic (t )d (t ) , C t0 1 t0 其中， uc (t0 )＝ ic (t ) d (t ) C －
uc(t0) （一般取 t0 ＝0） 称为电容电压的初始值， 体现了t0时 刻以前电流对电压的贡献。
0
§ 5－2
四、实际电感器
电感元件
R

实际电容器比较容易做的理想，即损耗可以近似 认为零。而实际电感器很难做的理想，损耗大，一般 不可忽略不计。
§5－1 电容元件
三、电容元件的储能 在t1--t2时间段内，电容贮存的能量为：
1 1 2 2 W（ t , t ) Cu ( t ) Cu C 1 2 c 2 c (t1 ) WC (t 2 ) WC (t1 ) 2 2 1 电容在任一时间t时的贮能为: WC (t ) Cu c 2 (t ) 0 2 结论：电容在某段时间内的贮能只与该段时间起点 的贮能和终点的贮能有关，与这段时间中其它时刻的 能量无关。

电路分析第五章 电容元件与电感元件

电路分析第五章 电容元件与电感元件

u=L di dt
WL
=
1 2
Li
2
5.7、电容与电感的对偶性
电感和电容的串并联
电感的串联
n
Leq
Lk
k 1
电感的并联
1
n1
Leq
k 1 Lk
电容的串联 电容的并联
1 n 1
Ceq
k 1 Ck
n
Ceq
Ck
k 1
习题课
5-12
习题1 已知u(0)=4V，则该电容t≥0时的VCR为
C a
2Ω电阻的功率：P2 2V2 /2Ω 2W
习题3 答案（续1）
5-18
解
电感储存能量：WL
1 2
Li2
1 2H2A2
2
4J
电容储存能量：WC
1 Cu 2 2
1 1F4V2
2
8J
电路总共储存能量为4J+8J=12J。该项能量 是电源接入时，由电源提供的。在电源持续作用 下，这能量始终储存在电路内，其值不变，故PL 和PC均为零。
功率平衡。
消耗功率 6W+2W+4W=12W
习题课
5-20
习题4 已知uc(t)=2cos(2t)V、C=1F、R=1Ω， 受控源电压u(t)=2ic(t)，求uR(t)、is(t)。
R
iS
+ ic + uR- +
u-c C
2ic
-
答案
P1 2A2 1 4W P2 2V 2 /2 2W
习题4 答案
2dt 0.25V
4 1
例题 (续)
（4） t ≥ 0时的等效电路
u1(t)+-

电容元件和电感元件

电容元件和电感元件

电容元件和电感元件电容元件电感元件公式q(t)=cu c(t)伏安关系式功率p=u c(t)i c(t)p=u L(t)i L(t)贮能W(t)=cu c2(t)/2W(t)=Li L2(t)/2电容电压不能跃变电感电流不能跃变共同点：都是记忆元件，惯性元件。

零输入响应当外加激励为零,仅有动态元件初始储能所产生的电流和电压,称为动态电路的零输入响应.RC电路的零输入响应右图(a) 所示的电路中，在t<0时开关在位置1，电容被电流源充电，电路已处于稳态，电容电压u C(0-)=R0I S，t=0时，开关扳向位置2，这样在t≥0时，电容将对R放电，电路如图 (b)所示，电路中形成电流i。

故 t>0后，电路中无电源作用，电路的响应均是由电容的初始储能而产生，故属于零输入响应。

换路后由图（b）可知，根据KVL有-u R+u c=0,而u R=i R,代入上式可得上式是一阶常系数齐次微分方程，其通解形式为u c=Ae pt（t≥0）式中A为待定的积分常数，可由初始条件确定。

p为１式对应的特征方程的根。

将２式代入１式可得特征方程为RC+1=0p从而解出特征根为则通解将初始条件u c(0+)=R0I S代入,求出积分常数A为(t≥0)令τ=RC，它是具有时间的量纲，即故称τ为时间常数, 这样两式可分别写为(t≥0)(t≥0)由于为负，故u c和i均按指数规律衰减，它们的最大值分别为初始值u c(0+)=R0I S 及当t→∞时，u c和i 衰减到零。

画出u c及i的波形如图所示。

RL电路的零输入响应一阶RL电路如图(a)所示，t=0-时开关S闭合，电路已达稳态，电感L相当于短路，流过L的电流为I0。

即i L(0-)=I0，故电感储存了磁能。

在t=0时开关S打开，所以在t≥0时，电感L储存的磁能将通过电阻R 放电，在电路中产生电流和电压，如图(b)所示。

由于t>0后，放电回路中的电流及电压均是由电感L的初始储能产生的，所以为零输入响应。

电容器与电感器基本特性

电容器与电感器基本特性

电容器与电感器基本特性电容器和电感器是电路中常见的两种元件，它们具有不同的基本特性和应用场景。

本文将介绍电容器与电感器的基本特性，包括其定义、符号表示、物理特性和主要应用等方面。

一、电容器的基本特性电容器是一种能够储存电荷的被动元件，其主要特性是具有电容。

电容的定义为电荷量与电压之比，用C表示，单位是法拉（F）。

电容器通常由两个电极和介电层构成，电荷通过导电材料在两个电极之间储存，并且通过介电层的阻挡，阻止电荷直接在两个电极之间流动。

电容器的电容量与电极面积、电极间距和介电系数相关。

1. 电容器的符号表示电容器的电路符号常用两条平行线表示两个电极，中间夹有一个垂直于平行线的直线表示介电层，如图1所示。

2. 电容器的物理特性电容器的物理特性主要包括电容量、极性和频率响应。

（1）电容量：电容量表示单位电压下所储存的电荷量，单位是法拉。

电容量越大，电容器储存的电荷量越多。

（2）极性：大部分电容器为无极性元件，即两个电极没有正负之分。

然而有一些电容器，如电解电容器，具有极性，需要按照正负电极进行接线。

（3）频率响应：电容器的电容量会随着交流信号的频率而变化，呈现频率响应特性。

在高频信号下，电容器的电容量会变小，而在低频信号下则会变大。

3. 电容器的主要应用电容器的主要应用包括能量储存、信号耦合和滤波等方面。

（1）能量储存：电容器能够储存电能，在一些电路中用来提供瞬态能量。

（2）信号耦合：电容器可以用于实现信号的耦合和隔离，将一个信号传递到其他电路中。

（3）滤波：电容器可以通过对特定频率的信号进行滤波，去除噪音和杂散信号。

二、电感器的基本特性电感器是一种能够储存磁能的被动元件，其主要特性是具有电感。

电感的定义为电流变化速率与电压之比，用L表示，单位是亨利（H）。

电感器通常由线圈构成，线圈上的电流在通过时会产生磁场，进而储存磁能。

电感器的电感与线圈的匝数、线圈的形状和材料等参数有关。

1. 电感器的符号表示电感器的电路符号常用两个相互垂直的平行线表示线圈，如图2所示。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 2 t Cu wC t 2 上式表明，电容储能与该时刻电压的平方成正比，为非负值，说明 电容是一种储能元件，电容的储能是电容电压具有记忆的本质。

5.2
电容元件的性质
0
0
t = u (t0 ) + 1 i( ) d C t
0
t ≥ t0
在某一时刻t电容电压的数值取决于从 到t所有时刻的电流值， 也就是说，电容电压与电流的“全部过去历史”有关。 电容电压具有记忆电流的作用 如果知道了由初始时刻t0开始作用的电流 i (t )以及电容的初始电 压 u (t0 ) ，就能唯一地确定 t ≥ t0 时的电容电压 u (t )
电容的储能 wc (t )为
0 2 1 2 t wc (t ) Cuc (t ) 2 2 ( t 2) 0 ( t 0) (0 t 1s) (1s t 2s) (2s t )
) 例 如图 (a) 所示，电流 i (t波形如图 (b) 所示，试求电容
1 i( ) d 0 C
0.25 103 s ≤ t ≤ 0.75 103 s 0.75 103 s ≤ t ≤ 1.25 103 s
当 0 ≤ t ≤ 0.25 103 s 时
u t = u t0 +
1 i( ) d 0 C
= 106 4000 d 2 109 t 2V
1 1
则在t1～t2期间，电容C吸收的能量为
t2 t2
t2
Cu ( )
1
du d d
=C

u ( t2 )
u ( t1 )
1 2 udu= Cu 2
u ( t2 ) = u ( t1 )
1 C [u 2 (t2 ) u 2 (t1 )] 2
电容C在某一时刻t的储能只与该时刻t的电压有关，即
电压。设 u(0) =0。
解
已知电容电流求电容电压时，可用 u t = u t0 +
1 0.25 103 t 4000t i (t ) 4000(t 0.5 103 ) 4000t 2 4000(t 103 ) 4000t 4 0 ≤ t ≤ 0.25 103 s
0
t
电压随时间按抛物线规律上升，当t＝0.25ms时，电压为 125 V。
当
1 t u (t ) = u(0.25 10 )+ i( ) d 0.25 10 t C 6 (4000 2) d = 125+ 10
3
3
0.25 103 s ≤ t ≤ 0.75 103时 s
0.25103
=(-250+2×106t-2×109t2)V
此为一开口向下的抛物线方程，其顶点在t＝0.5ms、u＝250V处。 当 t＝0.75ms时，电压下降到125V。
当 0.75 103 s ≤ t ≤1.25 103 s 时
3
3
t 1 t 6 u(t ) u(0.75 10 ) i( ) d 125 10 (4000 4)d 0.75 10 0.75 10 C (2000 4 106 t 2 109 t 2 )V
5.1
电容元件
5.1.1 电容元件的定义
一个二端元件，如果在任一时刻 t,它的电荷q(t)同 它的端电压u(t)之间的关系可以用u-q平面上的一条 曲线来确定，则此二端元件称为电容元件。
i q u
+
5.1.2 电容元件的伏安关系
i q u
对线性电容，得
qt Cut
dq t it dt
3
此为一开口向上的抛物线方程，其顶点在t＝1ms，u＝0处。
5.1.3
电容元件的储能

若电容电压、电流为关联参考方向，则任一瞬间电容吸 收的瞬时功率为
pt ut it 来自电容功率的特点：电容有时吸收功率， 有时却又放出功率。
由于
dw p dt
wC (t ) p( )d u ( )i( )d = t t t
uc (0) 0
解
根据 it
dq t ，得电流 dt
( t 0) (0 t 1s ) (1s t 2s ) (2 s t )
0 dus (t ) 2 i (t ) 2 d(t ) 2 0
) 瞬时功率 p (t为
0 2t p (t ) 2(t 2) 0 ( t 0) (0 ≤ t ≤ 1s ) (1s ≤ t ≤ 2 s ) (2 s t )
例
c 2F 如图(a)所示电路，其中
0 t u ( t ) s ，电源电压为 (t 2) 0
( t 0) (0 ≤ t ≤ 1s ) (1s ≤ t ≤ 2s) (2s t )
试求电容上电流 i (t ) 、瞬时功率 p (t )以及在t时刻的储能 wc (t。已知 )
dCu t du t i t C dt dt du i t C 若u和i的参考方向不一致，则
dt
电容有隔断直流的作用
+
1 t u(t ) i( )d C
1 t t 1 u(t ) i( ) d + i( ) d C C t
第5章 电容元件与电感元件
5.1 5.2 5.3 5.4 5.5

电容元件 电容元件的性质 电感元件 电感元件的性质 应用—混合电池(超级电容器件)
返回
上一节
下一节
上一页
下一页
教学提示
电容元件和电感元件的电压、电流关系都 涉及对电压、电流的微分或积分，这种元 件统称为动态元件。 至少包含一个动态元件的电路称为动态电 路。 动态电路在任一时刻的响应与激励的全部 过去历史有关，可见动态电路是有记忆的。 本章将讨论电容元件和电感元件的定义、 VCR、性质及储能情况，为动态电路的分析 奠定基础。