上海初三物理一模压强计算汇编备课讲稿

知识要点初三物理压强计算知识点1 基本计算公式密度公式： ρ =V，密度、质量、体积知道任意两个量，求第三个量。

压强定义公式：P = F，分析压力的施力物体和受力物体，明确受力面积。

S液体内部压强的大小：p = ρgh，注意：当柱体放在水平面上，对水平面的压力的大小等于物体重力时，可以用这一公式。

知识点2 基本方法与技巧（1）牢记两个压强公式，理解式中各个物理量的意义，注意统一用国际单位；（2）要能正确地确定压力、确定受力面积、确定深度；（3）相关的物理量（如重力、质量、密度等）及计算也要搞清楚；（4）液体对容器底部的压力并不一定等于液体的重力；（5）计算有关固体、液体的压力和压强问题时，先求压力还是压强的次序一般不同。

例题精讲正确理解物体间的压力【例题1】有一重50N，边长为20㎝的正方体木块，放在水平地面上。

若用10N的力竖直向上拉木块，但没有拉起来，求此时木块对地面的压强。

【分析】压强的计算，需要确定压力、面积。

要注意面积的计算与单位，其中压力的确定是难点。

如果认为压力F=G=50N，那就要犯错误了。

本题中压力虽然是由于物体受到重力产生的，但用10N的力竖直向上拉木块，虽然没有拉起来（那样对地面的压力就为零了），却减轻了木块对地面的压力。

要问减轻了多少压力？向上用多少力，压力就减少多少。

即此时木块对地面的压力为F=50N–10N=40N。

当然，还可以对木块进行受力分析：木块共受三个力：重力G=50N，方向竖直向下；施加的力F1=10N，方向竖直向上；地面对木块向上的力F2，方向竖直向上．由于木块静止，所有向上的力等于向下的力。

即F2=G-F1=50N-10N=40N。

根据物体间力的作用是相互的，木块对地面的压力大小就等于F2。

木块对水平地面的压强P = F2 =S40 N0.2m ⨯ 0.2m= 1000Pa【答案】1000Pa正确理解受力面积【例题2】正方体铝块的质量为 2.7kg，分别放在以下的水平桌面中央，那么受力面积各是多少？产生的压强各是多大?（ρ铝=2.7×103㎏/m3，取g=10N/㎏）⑴每边长1m的正方形水平面。

沪教版九年级物理第六章压力压强复习教案复习目标：1.理解压力。

知道压力和重力的区别，学会压力的计算，知道影响压力作用效果的因素。

2.掌握压强。

根据压强公式进行相关的计算，知道增大和减小压强的方法。

3.理解液体内部压强的规律，会根据公式p=pgh进行简单计算。

知道连通器在生产和生活中的应用。

4.知道大气压强的存在，解释一些与大气压有关的简单现象。

知道托里拆利实验的方法和原理。

5.理解阿基米德原理。

知道浮力概念，知道浮力产生的原因，学会用弹簧测力计测浮力。

理解阿基米德原理，根据阿基米德原理完成简单的讨论和计算。

6.学会探究液体内部压强与哪些因素有关。

7.学会验证阿基米德原理。

能通过实验找出浮力大小与物体排开液体所受重力之间的关系。

一、复习重点：1.压强的综合应用。

2.液体内部压强的分布规律。

3.理解阿基米德原理。

二、知识梳理（一）压强1.压力：垂直作用在物体表面并指向物体表面的力。

F 单位：牛。

2.压力的作用效果：使物体发生形变。

压力的作用效果的影响因素：压力的大小和受力面积的大小。

结论：当压力相同时，受力面积越小，压力的作用效果越明显。

当受力面积相同时，压力越大，压力的作用效果越明显。

当压力和受力面积都不同时，比较：单位面积上受到的压力，越大，压力的作用效果越明显。

4.压强（1）引入目的：反映了压力的形变效果；（2）定义：单位面积上受到的压力；（3）公式p=F/s（4）单位：牛/米2=1帕，表示的物理意义：每平方米上受到的压力为1牛。

5.压强的改变：增大压强的方法：增大压力或减小受力面积；减小压强的方法：减小压力或增大受力面积。

（二）液体内部压强1.液体内部产生压强的原因：液体受重力且具有流动性。

2.液体内部压强的测量工具：U形管压强计，从两液面的高度差反映压强的大小。

3.液体内部压强的分布规律：液体内部存在压强；同一液体，同一深度，各个方向的压强相等；同一液体，深度越深，压强越大；同一深度，液体的密度越大，压强也大。

2019 年上海中考物理一模试题分类汇编——压强计算固体压强1．（ 19 宝山区一模）以下列图，质量为240 千克，边长分别为0.3 米、 0.4 米和 1 米的实心长方体直立在水平川面上。

（ 1）求该长方体的密度ρ。

（2）若沿竖直（或水平）方向将长方体一分为二，再将它们重新放置在水平川面上，使得地面碰到的压力大小不变、地面碰到的压强均匀且比切割前的压强要小些。

（a）请你说明一种满足上述要求的切割部位和放置方式。

（ b）求出它对水平川面的最小压强P 最小。

2．（ 19 长宁区一模）如图，实心均匀正方体甲、乙放置在水平川面上，它们的重力G 均为 90 牛，甲的边长 a 为 0.3 米，乙的边长 b 为 0.2 米。

求：① 正方体甲对地面的压强p 甲；② 若沿水平方向将甲、乙截去相同的厚度△h 后，它们节余部分对地面的压强p 甲′和 p 乙′相等，请计算截去的厚度△ h。

液体压强3．（ 19 闵行区一模）如图，质量为0.2 千克的薄壁圆柱形容器置于水平川面上，容器内装有 4.8 千克的浓盐水。

容器足够高、底面积为0.02 米2，浓盐水密度为1200 千克 /米3。

（1）求浓盐水的体积。

（2）求容器对桌面的压强。

（3）现有质量为m的冰块，将其放入盐水中静止后，冰块飘扬在液面上。

待冰块完好消融，溶液再次均匀牢固后，盐水密度变为 1100 千克 /米3。

① 请比较冰块消融前后液体对容器底部压强的大小关系，并说明原由；②液体中有一点 A ，它到容器底的距离 d 为0.05 米，请计算冰块消融前后 A 点处液体压强的变化量△p A。

14．（ 19 松江区一模）以下列图，质量为0.2 千克、底面积为1× 10﹣2米2的圆柱形容器，内盛 2 千克的水后置于水平川面上，现将一质量为 2.6 千克、密度为× 103千克 /米3的物块，完好吞没在容器的水中后，测得容器底部碰到水的压强为 2450帕。

专题03 压强计算—在柱体或液体中加物体一、常见题目类型1. 将物体甲全部或切去一部分体积浸没在容器乙的液体中（见图1）。

2. 将乙容器放在甲的上方（见图1）。

3. 将另一物体A 分别放在柱体甲表面的上方或浸没在容器乙的液体中（见图2）。

4. 将一实心物体A 分别浸没于甲、乙液体中（见图3）。

二、常用到的基础知识与分析方法1. 压强： p =ρgh ， p ＝F/S2. 变化（增大或减小）的压强： △p ＝△F / S △p =ρg △h3. 把物体放入柱形液体中浸没时，液体对容器底部产生的压力：F=pS =ρghS+ρg △h S =G 液+ G 排（F 浮）即等于原来液体的重力与物体受到的浮力之和。

增大的压力△F =G 排=F 浮=ρ液gV 排 就是物体排开的液体所受到的重力（即浮力）。

4. 区别液体的压强与固体的压强（容器对地面的压强） 在液体不溢出时，则液体对容器底部的压强p 液=ρ液gh 液=F 液/S 容器 容器对地面的压强p 地=F 地/S 容器=G 物体+G 容器/S 容器5. 区别液体的压强与固体的压强（容器对地面的压强） 在液体不溢出时，则液体对容器底部压强的增加量Δp 液=ρ液g Δh 液=ρ液gV 物体/S 容器容器对地面压强的增加量Δp 地=ΔF 地/S 甲==G 物体/S 甲=ρ物体gV 物体/S 容器 6. 理解“轻质薄壁”容器甲乙图3即容器的重力为0，内部液体的受力面积与水平面的受力面积相等。

三、例题分析【例题1】（2023闵行二模）将足够高的薄壁柱形容器甲、乙放置在水平地面上，如图9所示，甲、乙两容器中分别盛有深度为米的酒精和质量为1千克的水。

已知容器乙的底面积为1×102 米2，酒精的密度为0.8×103千克/米3。

①求水的体积V 水。

②现将密度为2×103千克/米3的小球放入某个容器内，小球浸没于液体中，此时两液体对容器底部的压强恰好相等，求该容器对地面压强的增加量Δp 地。

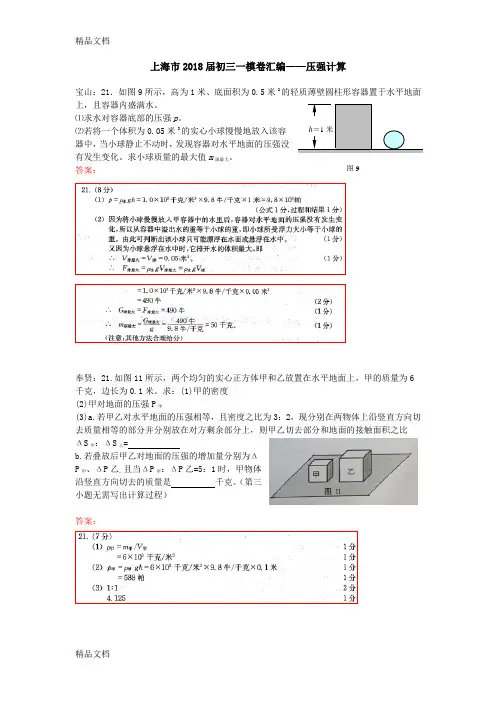
上海市2018届初三一模卷汇编——压强计算宝山：21．如图9所示，高为1米、底面积为0.5米2的轻质薄壁圆柱形容器置于水平地面上，且容器内盛满水。

⑴求水对容器底部的压强p。

⑵若将一个体积为0.05米3的实心小球慢慢地放入该容器中，当小球静止不动时，发现容器对水平地面的压强没有发生变化。

求小球质量的最大值m球最大。

答案：奉贤：21.如图11所示，两个均匀的实心正方体甲和乙放置在水平地面上，甲的质量为6千克，边长为0.1米。

求：(1)甲的密度(2)甲对地面的压强P甲(3)a.若甲乙对水平地面的压强相等，且密度之比为3：2，现分别在两物体上沿竖直方向切去质量相等的部分并分别放在对方剩余部分上，则甲乙切去部分和地面的接触面积之比ΔS甲：ΔS乙=b.若叠放后甲乙对地面的压强的增加量分别为ΔP甲、ΔP乙，且当ΔP甲：ΔP乙=5：1时，甲物体沿竖直方向切去的质量是千克。

（第三小题无需写出计算过程）答案：图9h＝1米甲乙图14虹口：22. 如图10所示，轻质薄壁圆柱形容器置于水平地面，容器盛有质量为4千克的水.①求水的体积V水；②求0.1米深处水的压强P水；③现有质量为4千克的物体，其底面积是容器的一半。

若通过两种方法增大地面受到的压强，并测出压强的变化量，如下表所示.根据表中的信息，通过计算判断将物体放入容器时是否有水溢出，若有水溢出请求出溢出水的重力G溢水，若无水溢出请说明理由.答案：金山：23．如图14所示，底面积为102米2、高为0.4米长方体甲（ρ甲＝2×103千克/米3）和底面积为2102米2的薄壁柱形容器乙放在水平地面上。

乙容器足够高，内盛有0.1米深的水。

（1）求甲的质量m甲。

（2）求水对乙容器底部的压强p水。

（3）现沿水平方向将长方体甲截取一定的厚度，并将截取部分竖直放入乙容器中，使得水对容器底部的压强最大，且长方体甲对地面的压强减少量最小，请求出甲对地面的压强减少量。

答案：静安：22．盛有水的薄壁圆柱形容器置于水平地面，其底面积为2×10-2米2，甲和乙是由同种金属制成、体积不同的圆柱体。

专题02 压强计算——液体的抽取与加入一、常见题目类型在柱形容器中抽取（或加入）液体：某一深度（体积或质量）（图1）。

甲图1 乙二、常用到的基础知识1. 液体的压强：p=ρgh，p＝F/S2. 密度：ρ=m/V3. 柱形容器中，液体对容器底部压力的大小等于液体的重力大小：F =G液体=m液体g4. 柱形液体的体积：V= sh三、常用的分析方法1. 液体对容器底部压强的变化量计算：Δp=ρ液体gΔh液体；Δp=ΔF/S=ΔG液体/S；数学方法：ΔP=P1-P2。

2. 压力的变化量计算：ΔF=Δmg、ΔF=ΔpS或ΔF=F1-F2等分析计算。

四、例题分析【例题1】（2022嘉定一模）如图所示，底面积不同足够高的圆柱形容器甲、乙（S甲>S乙）置于水平地面上。

（1）若容器甲重为10牛，底面积为1×10-2米2，内部盛有深度为0.4米的水。

求：（a）水对容器甲底部的压强p水；（b）容器甲对水平地面的压强p地；（2）若容器甲、乙中的液体A、B对容器底部的压强相等。

为使A液体对容器甲底部的压强大于B液体对容器乙底部的压强，有如下方案：（a）在容器甲、乙中同时抽取相同质量的液体；（b）在容器甲、乙中同时加入相同高度的原有液体；请分析每种方案的可行性。

【答案】（1）3920Pa；4900Pa；（2）a可行，b不可行【详解】（1）（a）水对容器甲底部的压强为p水=ρ水gh水=1.0×103千克/米3×9.8牛/千克×0.4米=3920帕（b）容器甲内水的体积为V=Sh=1.0×10-2m2×0.4m=4×10-3m3水的质量为m水=ρ水V水=1.0×103kg/m3×4×10-3m3=4kg容器甲对对水平地面的压力为F 地=G水+G甲容=m水g+G甲容=4kg×10N/kg+10N=50N容器甲对地面的压强为p 地=F地S甲=50N1×10-2m2=5000Pa（2）已知液体对容器底部的压强为p甲=p乙两个容器是圆柱形的，液体对容器底的压力等于液体的重力，F甲=G甲，F乙=G乙，所以液体对容器底的压强为p 甲=G甲S甲p乙=G乙S乙（a）在容器甲、乙中同时抽取相同质量的液体，设抽取液体的质量为m，则剩余液体对容器底的压强为p甲剩=G甲-mgS甲=G甲S甲-mgS甲=p甲-mgS甲p乙剩=G乙-mgS乙=G乙S乙-mgS乙=p乙-mgS乙因为S甲>S乙，所以p甲剩>p乙剩此方案可行；（b）已知液体对容器底部的压强为p甲=p B，即ρ甲gh甲=ρ乙gh乙因为h甲>h乙，所以液体的密度关系为ρ甲<ρ乙在容器甲、乙中同时加入相同高度的原有液体，由压强的计算公式可知，增大的压强为Δp=ρgΔh，所以Δp甲<Δp乙后来液体对容器底的压强为p 甲1=p 甲+Δp 甲 p 乙1=p 乙+Δp 乙 所以p 甲1<p 乙1 此方案不可行。

2022年中考一模汇编-压强计算一、综合题 1．（2022·上海金山·一模）如图（a ）所示，在水平桌面上放有一个底面为0.2米×0.2米正方形的柱形容器甲，内盛有深度为h 的水，容器足够高，密度为3510⨯千克/米3的实心长方体乙竖放在桌面上，其边长如图（b ）所示，求：（1）当0.2h =米时，水对容器甲底部的压强p 水= ______； （2）长方体乙的质量m 乙= ______；（3）若将长方体乙以不同方式放入甲容器中：①当0.04h =米时，采用______方式可以使水对容器底部的压强增加量较大（选填“平放”、“竖放”或“平放或竖放相同”），求出该增加量Δp 水= ______；②通过计算说明，h 至少为______米时，采用平放或竖放都能使水对容器底部的压强增加量相同。

【答案】1960Pa 10kg 平放 392Pa 0.15 【详解】（1）[1]当0.2h =米时，水对容器甲底部的压强331.010kg /m 9.8N/kg 0.2m 1960Pa p gh ρ==⨯⨯⨯=水水（2）[2]长方体乙的体积为V 乙=0.2m×0.1m×0.1m=2×10-3m 3长方体乙的质量3333510kg /m 210m 10kg m V ρ-==⨯⨯⨯=乙乙乙（3）①[3]当0.04h =米时，容器内水的体积为V 水=0.2m×0.2m×0.04m=1.6×10-3m 3当将实心长方体平放在底面为0.2米×0.2米正方形的柱形容器甲中，假设此时实心长方体的高度足够高，则此时容器内的水的高度为33121.610m 0.08m 0.50.50.04m V h S -⨯===⨯水容器小于平放实心长方体的高度0.1米，即当将实心长方体平放在底面为0.2米×0.2米正方形的柱形容器甲中，实心长方体也不能浸没在水中；可知当将实心长方体竖放在底面为0.2米试卷第2页，共21页×0.2米正方形的柱形容器甲中时，此时容器中水的深度小于0.08米，根据液体压强公式p gh ρ=有ΔΔp g h ρ= ①可知当容器内水增加的深度较大时，水对容器底部的压强增加量较大，即当0.04h =米时，采用平放方式可以使水对容器底部的压强增加量较大。