第章时间序列预测习题答案

第10章时间序列预测教材习题答案下表是1981年一1999年国家财政用于农业的支出额数据（1）绘制时间序列图描述其形态。

（2）计算年平均增长率。

（3）根据年平均增长率预测2000年的支出额。

详细答案：（1）时间序列图如下：从时间序列图可以看出，国家财政用于农业的支出额大体上呈指数上升趋势（2）年平均增长率为：G = - 1 = 035 76 -1 = 113.55% -1 = 13.55%Y 打y110.21。

（3）。

下表是1981年一2000年我国油彩油菜籽单位面积产量数据（单位：kg / hm2 ）19901260 2000 1519(1)绘制时间序列图描述其形态。

(2)用5期移动平均法预测2001年的单位面积产量。

(3)采用指数平滑法，分别用平滑系数a二和a=预测2001年的单位面积产量说明用哪一个平滑系数预测更合适？详细答案：(1)时间序列图如下:（2）2001年的预测值为：冲1367 + 1479 + 1272 + 1469+W1? 7106 一小①^ooi = -------------- 7 -------------- 二 F 二14笨2- 」I (3)由Excel输出的指数平滑预测值如下表:年份单位面积产量指数平滑预测a= 误差平方指数平滑预测a=误差平方11981 14511982 1372，分析预测误差，年谕2001年a=时的预测值为：耳观=购 + (1-⑵耳=0.3x1519 + (1-03)x1380 2 = 1^21 8 =时的预测值为:耳DM=叱+ &讯=0.5x1519 + (1-0.5)x14074 = 1463 1比较误差平方可知，a二更合适月份营业额（万元）月份营业额（万元）1 295 10 4732 283 11 4703 322 12 4814 355 13 4495 286 14 5446 379 15 6017 1381 16 5878 431 17 6449 424 18 660（1）用3期移动平均法预测第19个月的营业额（2）采用指数平滑法，分别用平滑系数a二、a=和a二预测各月的营业额，分析预测误差，用哪一个平说明滑系数预测更合适？（3）建立一个趋势方程预测各月的营业额，计算出估计标准误差详细答案：(1)第19个月的3期移动平均预测值为:587 + 644 + 6601891630.33(2)F19= 0 3x660+(1 -0.3)x567.9 = 595.5 误差均方=。

第五章时间序列练习题1、时间序列中，数值大小与时间长短没有关系的是（C）。

A.平均数时间序列B.时期序列C.时点序列D.相对数时间序列2、采用几何平均法计算平均发展速度的依据是（ A ）。

A.各年环比发展速度之积等于总速度B.各年环比发展速度之和等于总速度C.各年环比增长速度之积等于总速度D.各年环比增长速度这和等于总速度3、下列数列中哪一个属于动态数列（D）。

A.学生按学习成绩分组形成的数列B.职工按工资水平分组形成的数列C. 企业按产量多少形成的分组数列D. 企业生产成本按时间顺序形成的数列4．由两个等时期数列相应项对比所形成的相对数动态数列算序时平均数的基本公式是（D）。

A.n aa∑=B.ncc∑=C.∑--++++++=ffaafaafaaannn11232121222D.∑∑=bac5．间隔不等的间断时点数列的序时平均数的计算公式是（ C ）。

A.n aa∑=B.12121121-++++=-naaaaannC.∑--++++++=ffaafaafaaannn11232121222D.∑∑=fafa6．累计增长量与逐期增长量的关系是（ A ）A.逐期增长量之和等于累计增长量B.逐期增长量之积等于累计增长量C.累计增加量之和等于逐期增长量D.两者没有直接关系7．环比发展速度与定基发展速度之间的关系是（ C ）。

A.定基发展速度等于环比发展速度之和B.环比发展速度等于定基发展速度的平方根C.环比发展速度的连乘积等于定基发展速度D.环比发展速度等于定基发展速度减18．某现象前期水平为1500万吨，本期水平为2100万吨，则增长1%的绝对值为( C )。

A.1500万吨B.600万吨C.15万吨D.2100万吨9．已知各期的环比增长速度为9%、8%、10%，则定基增长速度为( C )。

A.9%×8%×10% B.9%×8%×10%-100%C.109%×108%×110%-100%D.109%×108%×110%10．某车间6月、7月、8月、9月末职工人数分别为250人、265人、280人和290人，该公司三季度月职工平均人数为( D )。

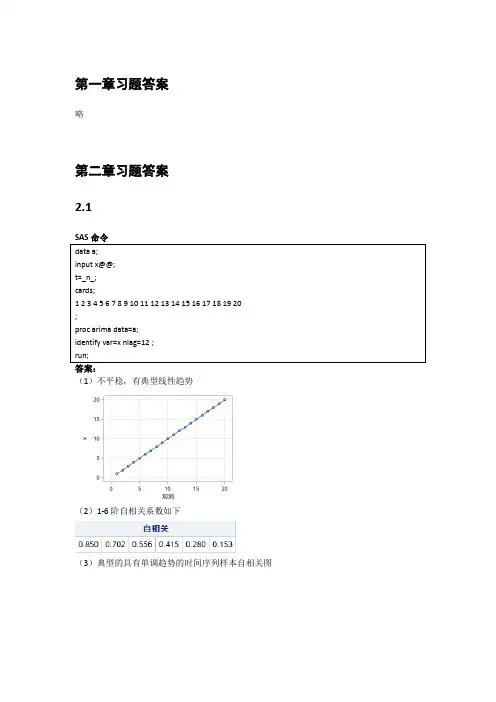
第一章习题答案略第二章习题答案2.1答案：（1）不平稳，有典型线性趋势（2）1-6阶自相关系数如下（3）典型的具有单调趋势的时间序列样本自相关图2.2答案：（1）不平稳（2）延迟1-24阶自相关系数（3）自相关图呈现典型的长期趋势与周期并存的特征2.3答案：（1）1-24阶自相关系数（2）平稳序列（3）非白噪声序列2.4计算该序列各阶延迟的Q统计量及相应P值。

由于延迟1-12阶Q统计量的P值均显著大于0.05，所以该序列为纯随机序列。

2.5答案（1）绘制时序图与自相关图（2）序列时序图显示出典型的周期特征，该序列非平稳（3）该序列为非白噪声序列2.6答案（1）如果是进行平稳性图识别，该序列自相关图呈现一定的趋势序列特征，可以视为非平稳非白噪声序列。

如果通过adf检验进行序列平稳性识别，该序列带漂移项的0阶滞后P值小于0.05，可以视为平稳非白噪声序列（2）差分后序列为平稳非白噪声序列2.7答案（1）时序图和自相关图显示该序列有趋势特征，所以图识别为非平稳序列。

（2）单位根检验显示带漂移项0阶延迟的P值小于0.05，所以基于adf检验可以认为该序列平稳（3）如果使用adf检验结果，认为该序列平稳，则白噪声检验显示该序列为非白噪声序列如果使用图识别认为该序列非平稳，那么一阶差分后序列为平稳非白噪声序列2.8答案（1）时序图和自相关图都显示典型的趋势序列特征（2）单位根检验显示该序列可以认为是平稳序列（带漂移项一阶滞后P值小于0.05）（3）一阶差分后序列平稳第三章习题答案 3.10101()0110.7t E x φφ===--（） 221112() 1.96110.7t Var x φ===--（） 22213=0.70.49ρφ==（）12122221110.490.7=0110.71ρρρφρρ-==-（4） 3.21111222211212(2)7=0.515111=0.30.515AR φφφρφφφρφρφφφ⎧⎧⎧=⎪=⎪⎪⎪--⇒⇒⎨⎨⎨⎪⎪⎪=+=+⎩⎩⎪⎩模型有：,2115φ=3.312012(1)(10.5)(10.3)0.80.15()01t t t t t tt B B x x x x E x εεφφφ----=⇔=-+==--,22121212()(1)(1)(1)10.15=(10.15)(10.80.15)(10.80.15)1.98t Var x φφφφφφ-=+--+-+--+++=（）1122112312210.83=0.70110.150.80.70.150.410.80.410.150.70.22φρφρφρφρφρφρ==-+=+=⨯-==+=⨯-⨯=（） 1112223340.70.15=0φρφφφ====-（）3.41211110011AR c c c c c ⎧<-<<⎧⎪⇒⇒-<<⎨⎨<±<⎪⎩⎩（） （）模型的平稳条件是 1121,21,2k k k c c k ρρρρ--⎧=⎪-⎨⎪=+≥⎩（） 3.5证明:该序列的特征方程为：320c c λλλ--+=，解该特征方程得三个特征根：11λ=，2λ=3λ=无论c 取什么值，该方程都有一个特征根在单位圆上，所以该序列一定是非平稳序列。

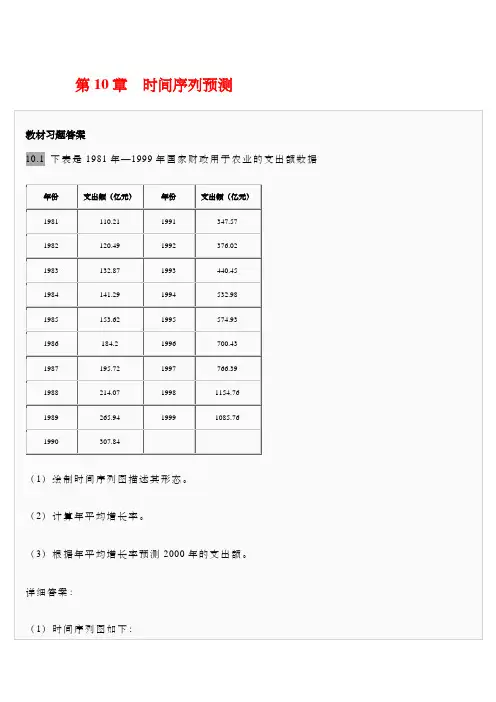
第10章时间序列预测从时间序列图可以看出，国家财政用于农业的支出额大体上呈指数上升趋势。

（2）年平均增长率为：。

（3）。

10.2 下表是1981年—2000年我国油彩油菜籽单位面积产量数据（单位：kg / hm2）年份单位面积产量年份单位面积产量1981 1451 1991 12151982 1372 1992 12811983 1168 1993 13091984 1232 1994 12961985 1245 1995 14161986 1200 1996 13671987 1260 1997 14791988 1020 1998 12721989 1095 1999 14691990 1260 2000 1519（1）绘制时间序列图描述其形态。

（2）用5期移动平均法预测2001年的单位面积产量。

（3）采用指数平滑法，分别用平滑系数a=0.3和a=0.5预测2001年的单位面积产量，分析预测误差，说明用哪一个平滑系数预测更合适？详细答案：（1）时间序列图如下：（2）2001年的预测值为：|（3）由Excel输出的指数平滑预测值如下表：2001年a=0.3时的预测值为：a=0.5时的预测值为：比较误差平方可知，a=0.5更合适。

10.3 下面是一家旅馆过去18个月的营业额数据月份营业额（万元）月份营业额（万元）1 295 10 4732 283 11 4703 322 12 4814 355 13 4495 286 14 5446 379 15 6017 381 16 5878 431 17 6449 424 18 660（1）用3期移动平均法预测第19个月的营业额。

（2）采用指数平滑法，分别用平滑系数a=0.3、a=0.4和a=0.5预测各月的营业额，分析预测误差，说明用哪一个平滑系数预测更合适？（3）建立一个趋势方程预测各月的营业额，计算出估计标准误差。

详细答案：（1）第19个月的3期移动平均预测值为：（2）月份营业额预测a=0.3误差平方预测a=0.4误差平方预测a=0.5误差平方1 2952 283 295.0 144.0 295.0 144.0 295.0 144.03 322 291.4 936.4 290.2 1011.2 289.0 1089.04 355 300.6 2961.5 302.9 2712.3 305.5 2450.35 286 316.9 955.2 323.8 1425.2 330.3 1958.16 379 307.6 5093.1 308.7 4949.0 308.1 5023.37 381 329.0 2699.4 336.8 1954.5 343.6 1401.68 431 344.6 7459.6 354.5 5856.2 362.3 4722.39 424 370.5 2857.8 385.1 1514.4 396.6 748.510 473 386.6 7468.6 400.7 5234.4 410.3 3928.711 470 412.5 3305.6 429.6 1632.9 441.7 803.112 481 429.8 2626.2 445.8 1242.3 455.8 633.513 449 445.1 15.0 459.9 117.8 468.4 376.914 544 446.3 9547.4 455.5 7830.2 458.7 7274.815 601 475.6 15724.5 490.9 12120.5 501.4 9929.416 587 513.2 5443.2 534.9 2709.8 551.2 1283.317 644 535.4 11803.7 555.8 7785.2 569.1 5611.718 660 567.9 8473.4 591.1 4752.7 606.5 2857.5合计——87514.7—62992.5—50236由Excel输出的指数平滑预测值如下表：a=0.3时的预测值：，误差均方＝87514.7。

第九章 时间数列分析与预测一、填空题9.1.1 时间数列一般由两个基本要素构成：一是现象所属的 时间 ，二是反映客观现象的 观察值 。

9.1.2 时间数列按其观察值具体表现形式不同可分为三种：绝对数时间数列、 相对数时间数列和 平均数时间 数列。

9.1.3 同一时间数列中，各期环比发展速度的连乘积等于相应的 定基发展速度 。

9.1.4 绝对数时间数列中， 时期 数列中，各期的指标值直接相加有意义。

9.1.5 某公司2007年的利额比2003年增长25%，2006年比2003年增长20%，则2007年比2006年增长 4.17% ，2004年至2007年平均每年增长 5.74% 。

9.1.6 某地2006年1季度的GDP 为100亿元，2006年3季度的GDP 为115亿元，则其年度化增长率为 32.25% 。

9.1.7 计算平均发展速度有两种方法，即 几何平均法 和 高次方程法 ，它们的数理依据、侧重点、计算方法和应用场合都不相同。

9.1.8 影响时间序列的因素主要有四种，它们是 长期趋势 、 季节变动 、 循环变动 和 不规则变动 。

9.1.9 时间数列变动的趋势有直线趋势和曲线趋势。

在建立模型之前，先要确定现象变动的形态。

判定趋势变动形态的方法常用的有两种，即 画散点图的方法 和 指标判别法 。

9.1.10 若时间数列的 逐期增减量 大致相等，则该现象的发展趋势近似于一条直线，可拟合一条直线趋势方程。

9.1.11 如果时间数列中各期二次逐期增减量大致相等，则应拟合 二次曲线 方程；如果各期环比发展速度大致相等，则应拟合 指数曲线 方程。

9.1.12 某些社会经济现象，随着季节的更换或社会因素的影响而引起的在年度内比较有规律性的变动称 季节变动 ，测定它的变动常用且最简便的方法是 同期平均法 。

9.1.13 客观社会经济现象在一个相当长的时间内，受某些基本因素的影响所呈现的一种基本发展趋势称 长期趋势 。

第一章数据的采集课后习题答案一、判断题1. (×)2. (×)3. (×)4. (√)5. (×)6.（×）7.（√） 8.（√） 9.（×）二、单选题1.(B)2.(C)3.(A)4.(D)5.(C)6.(D）7.(B）8.(A）9.（B） 10.（C）11.（C）三、多选题1.(ABCDE)2.(ABCD)3.(CE)4.(CDE)5.(ABCD)第二章数据的整理与展示课后习题答案一、判断题1. (√)2. (√)3. (√)4. (×)5. (×)二、单项选择题1.(C)2.(D)3.(A)4.(A)5.(D)三、多项选择题1.(A)(D)2.(C)(D)3.(B)(C)(E)4.(A)(B)(C)(D)(E)5.(A)(B) (C)(D)第三章数据分布的测度课后习题答案一、判断题1-5 ×√××× 6-8 ×√×二、单项选择题1. C2.B3.B4. A5. C三、多项选择题1.AB2.DE3.CE五、计算题1、75%3400085%7000095%3600085.14%140000x⨯+⨯+⨯==该产品的平均合格率为85.14%。

2、11920085.14%25500595003420075%85%95%x==++该产品的平均合格率为85.14%。

3、105700+120900+1371100==123.042700317900==117.74126009600095900105120137x x ⨯⨯⨯++甲乙元（）件元（）件 商品在甲市场上的平均价格为123.04 元件，在乙市场上的平均价格为117.74元件。

4、332200==123.04735001080001507001051201371051200+120800+137700==117.742700x x ++⨯⨯⨯甲乙元（）件元（）件 商品在甲市场上的平均价格为123.04 元件，在乙市场上的平均价格为117.74元件。

第十章时间数列分析和预测一、填空题1.同一现象在不同时间的相继____________排列而成的序列称为_______________。

2.时间序列在__________重复出现的____________称为季节波动。

3.时间序列在___________呈现出来的某种持续_______________称长期趋势。

4.增长率是时间序列中_________观察值与基期观察值______减1 后的结果。

5.由于比较的基期不同，增长率可分为_____________和______________。

6.复合型序列是指含有___________季节性和___________的序列。

7.某企业2005年的利润额比2000年增长45%，2004年2000年增长30%，则2005年比2004年增长_______；2004年至2000年平均增长率__________。

8.指数平滑法是对过去的观察值__________进行预测的一种方法。

9.如果时间序列中各期的逐期增减量大致相等,则趋势近似于_____________；各期环比值大体相等，则趋势近似于___________。

10.测定季节波动的方法主要有____________和_____________。

二、单项选择题1.用图形描述时间序列，其时间一般绘制在（）A. 纵轴上B. 横轴上C. 左端D. 右端2.求解（）趋势参数方法是先做对数变换，将其化为直线模型，然后用最小二乘法求出模型参数A. 三次曲线B. 指数曲线C. 一次直线D. 二次曲线3.对运用几个模型分别对时间序列进行拟合后，（）最小的模型即位最好的拟合曲线模型A. 判定系数B. 相关系数C. 标准误差D.D—W值4.当数据的随机波动较大时，选用的移动间隔长度K应该（）A. 较大B. 较小C. 随机D. 等于n5.在进行预测时，最新观察值包含更多信息，可考虑权重应（）A. 更大B. 更小C. 无所谓D. 任意6. 按季度资料计算的季节指数S的取值范围是（）A. 0≤ S ≤4B. 0 ≤S≤ 1C. 1 ≤S ≤4D. 1≤ S≤ 2三、多项选择题1. 时间序列可以分解为下列因素的影响 ( )A. 长期趋势B. 季节变动C. 周期波动D. 不规则变动E. 随机误差因素2. 某地区国民收入2000年为140亿元，2005年比2000年增长45%，则（）A. 国民收入2005年比2000年增加了63亿元B. 2000年每增长1%的绝对值为1.4亿元C. 五年间平均增长率是9%D. 国民收入2005年达到210亿元E. 国民收入2005年达到203亿元3．测定季节变动A. 可以依据年度资料B. 可以依据月度资料C. 可以依据季度资料D. 需要三年以上资料E. 可以依据任何资料4. 时间序列分解较常用的模型有（）A. 加法模型B. 乘法模型C. 直线模型D. 指数模型E. 多项式模型5．一次指数平滑法的初值的确定可以（）A. 取第一期的实际值B. 取最初三期的加权平均值C. 取最初几期的平均值D. 取初值=1E. 取任意值四、简答题1. 简述时间序列的构成要素2. 利用增长率分析时间序列时应注意哪些问题3. 简述用平均趋势剔除法求季节指数的步骤4. 简述用剩余法求循环波动的基本步骤5. 试比较移动平均法与一次指数平滑法五、计算题1．某企业利润额资料如下：要求：(1) 求出直线趋势方程（2）预测2006年的利润额2．已知某煤矿（1）求五期移动平均；（2）取α= 0.9，求一次指数平滑3．某地财政收入资料如下试用指数曲线拟合变动趋势4．某商场销售资料如下：（单位：百万元）试就其进行季节变动分析5．某企业职工人数逐年增加,有1992—2004年的资料,求得∑t = 0，∑ty=9100，∑y = 15600；试求出直线趋势方程,并估计2006年职工人数。

一、单项选择题1．时间数列与变量数列( )A都是根据时间顺序排列的 B都是根据变量值大小排列的 C前者是根据时间顺序排列的，后者是根据变量值大小排列的D前者是根据变量值大小排列的，后者是根据时间顺序排列的2．时间数列中，数值大小与时间长短有直接关系的是( )A平均数时间数列 B时期数列 C时点数列 D相对数时间数列 3．发展速度属于( )A比例相对数 B比较相对数 C动态相对数 D强度相对数4．计算发展速度的分母是( )A报告期水平 B基期水平 C实际水平 D计划水平5．某车间月初工人人数资料如下：则该车间上半年的平均人数约为( )A 296人B 292人C 295 人D 300人6．某地区某年9月末的人口数为150万人，10月末的人口数为150．2万人，该地区10月的人口平均数为( )A150万人 B150．2万人 C150．1万人 D无法确定7．由一个9项的时间数列可以计算的环比发展速度( )A有8个 B有9个 C有10个 D有7个8．采用几何平均法计算平均发展速度的依据是( )A 各年环比发展速度之积等于总速度B 各年环比发展速度之和等于总速度C 各年环比增长速度之积等于总速度D 各年环比增长速度之和等于总速度9．某企业的产值2005年比2000年增长了58．6％，则该企业2001—2005年间产值的平均发展速度为( )A 5%6.58B 5%6.158C 6%6.58D 6%6.15810．根据牧区每个月初的牲畜存栏数计算全牧区半年的牲畜平均存栏数，采用的公式是( )A 简单平均法B 几何平均法C 加权序时平均法D 首末折半法 11、时间序列在一年内重复出现的周期性波动称为（ ）A 、长期趋势B 、季节变动C 、循环变动D 、随机变动1．C 2．B 3．C 4．B 5．C 6．C 7．A 8．A 9．B 10．D 11、B二、多项选择题1．对于时间数列，下列说法正确的有( )A 数列是按数值大小顺序排列的B 数列是按时间顺序排列的C 数列中的数值都有可加性D 数列是进行动态分析的基础E 编制时应注意数值间的可比性 2．时点数列的特点有( )A 数值大小与间隔长短有关B 数值大小与间隔长短无关C 数值相加有实际意义D 数值相加没有实际意义E 数值是连续登记得到的3．下列说法正确的有( )A 平均增长速度大于平均发展速度B 平均增长速度小于平均发展速度C 平均增长速度=平均发展速度-1D 平均发展速度=平均增长速度-1E 平均发展速度×平均增长速度=14．下列计算增长速度的公式正确的有( )A%100⨯=基期水平增长量增长速度 B %100⨯=报告期水平增长量增长速度C 增长速度= 发展速度—100％D%100⨯-=基期水平基期水平报告期水平增长速度E%100⨯=基期水平报告期水平增长速度5．采用几何平均法计算平均发展速度的公式有( )A1231201-⨯⨯⨯⨯=n n a a a a a a a a n x K Ba a nx n =C1a a n x n = D nR x = En xx ∑=6．某公司连续五年的销售额资料如下：根据上述资料计算的下列数据正确的有( )A第二年的环比增长速度=定基增长速度=10％B第三年的累计增长量=逐期增长量=200万元C第四年的定基发展速度为135％D第五年增长1％绝对值为14万元E第五年增长1％绝对值为13．5万元7．下列关系正确的有( )A环比发展速度的连乘积等于相应的定基发展速度B定基发展速度的连乘积等于相应的环比发展速度C环比增长速度的连乘积等于相应的定基增长速度D环比发展速度的连乘积等于相应的定基增长速度E平均增长速度=平均发展速度-18．测定长期趋势的方法主要有( )A时距扩大法 B方程法 C最小平方法 D移动平均法 E几何平均法9．关于季节变动的测定，下列说法正确的是( )A目的在于掌握事物变动的季节周期性B常用的方法是按月(季)平均法C需要计算季节比率D按月计算的季节比率之和应等于400％E季节比率越大，说明事物的变动越处于淡季10．时间数列的可比性原则主要指( )A时间长度要一致 B经济内容要一致 C计算方法要一致 D总体范围要一致E计算价格和单位要一致答案1．BDE 2．BD 3．BC 4．ACD 5．ABD 6．ACE 7．AE8．ACD 9．ABC 10．ABCDE三、判断题1．时间数列中的发展水平都是统计绝对数。